Similar presentations:
Исследование устойчивости методом Ляпунова
1. Исследование устойчивости методом Ляпунова
2.
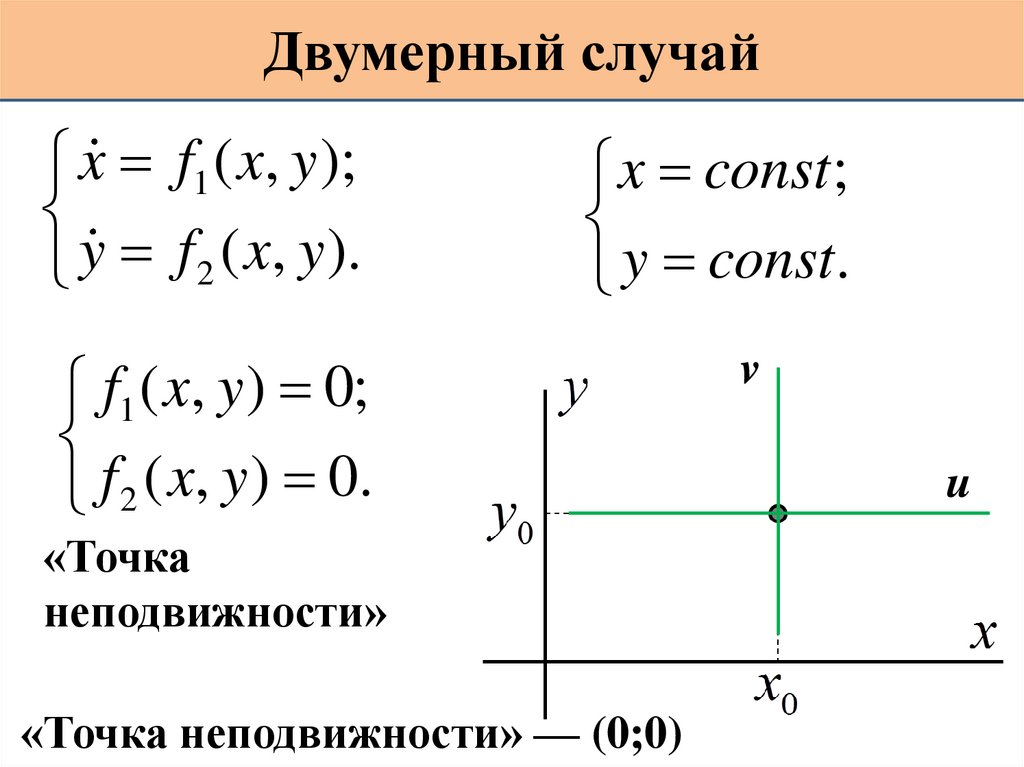
Двумерный случайx f1 ( x, y );
y f 2 ( x, y ).
x const ;
y const.
f1 ( x, y ) 0;
f 2 ( x, y ) 0.
«Точка
неподвижности»
«Точка неподвижности» — (0;0)
v
u
3.
Теорема Ляпунова об устойчивостиНулевое решение (0;0) асимптотически
устойчиво
4.
Вычисление полной производнойdL L
L
x
y
dt x
y
x f1 ( x, y );
y f 2 ( x, y ).
L
L
f1 ( x, y )
f 2 ( x, y )
x
y
5.
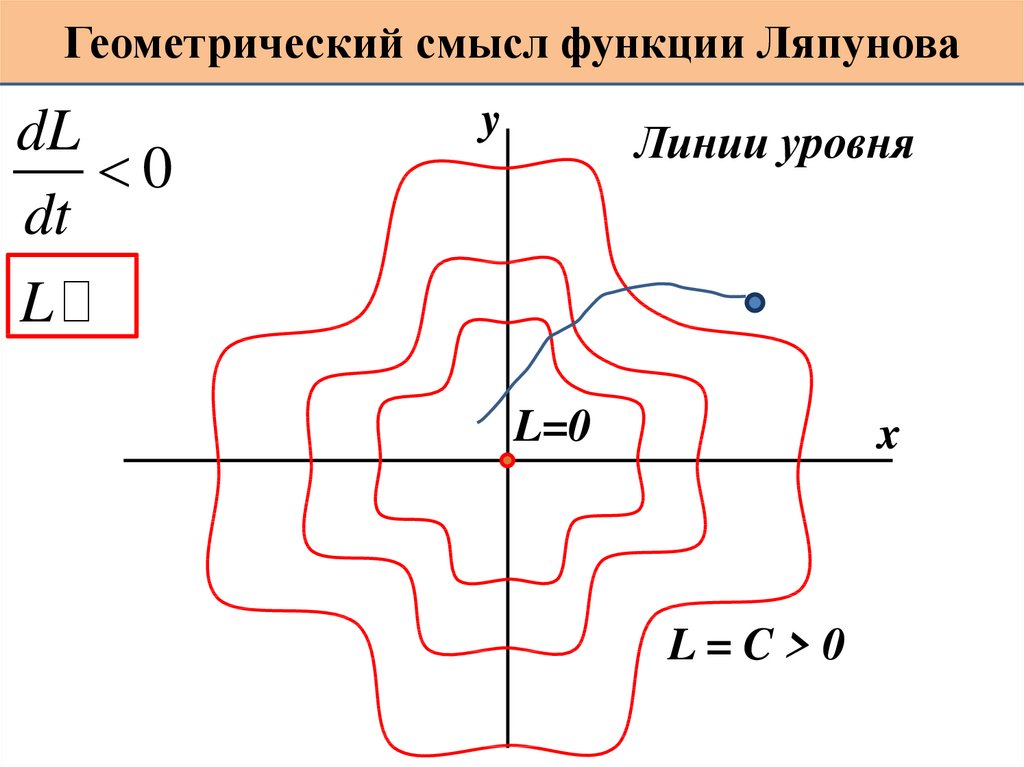
Геометрический смысл функции ЛяпуноваdL
0
dt
L
y
Линии уровня
L=0
x
L=C>0
6.
Пример применения теоремы Ляпуноваx x y;
3
y x y .
3
x y
L ( x, y )
0
2
L
L
y
x
y
x
2
2
dL
x x y y
dt
3
3
x x y y x y
x y 0
4
4
7.
Теорема Ляпунова о неустойчивостиНулевое решение (0;0) неустойчиво
8.
Пример применения теоремы Ляпуноваx x y;
3
y x y .
3
x y
V ( x, y )
0
2
V
V
y
x
y
x
2
2
dV
x x y y
dt
3
3
4
4
x x y y x y x y 0
9.
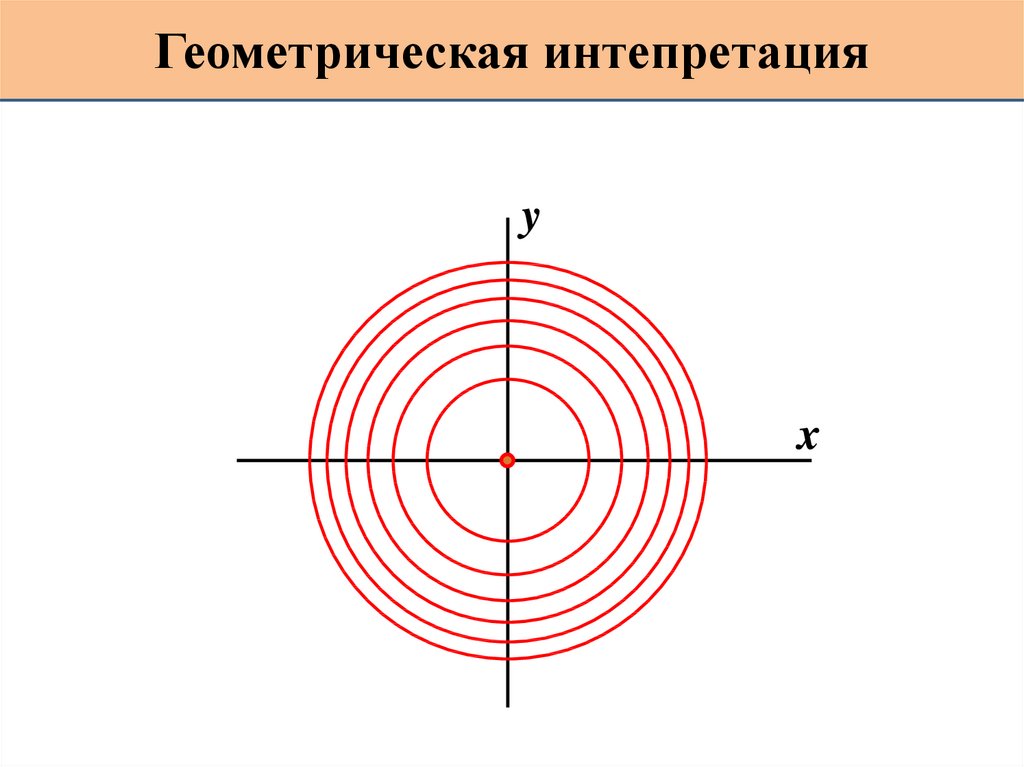
Геометрическая интерпретация10.
Недостаточность линейного приближенияx x y;
3
y x y .
3
3 x
1
стационарная
точка (0;0)
У
Н
1
2
3 y
Матрица
Якоби
Матрица
линеаризованной
системы:
0 1
1 0
2
x x y;
3
y x y .
3
3x
1
2
1
2
3y
1,2 i
«Центр»
11.
Теорема Четаеваy
V>0
D
V=0
O — предельная точка D
x
dV
0
dt
( x, y ) D
Нулевое
решение
неустойчиво
12.
Применение теоремы Четаеваx x xy ;
3
2
y x y y .
3
2
x y
V ( x, y )
2
2
| x | | y |
2
V
x
x
V
y
y
13.
Применение теоремы ЧетаеваV
x x xy ; V
y
x
3
2
x
y
.
y
y
x
y
dV
3
2
2
3
x x xy y x y y
dt
3
2
x x y x y y x y 0
при | x | | y |
4
2
2
2
2
4
4
Нулевое решение неустойчиво
4
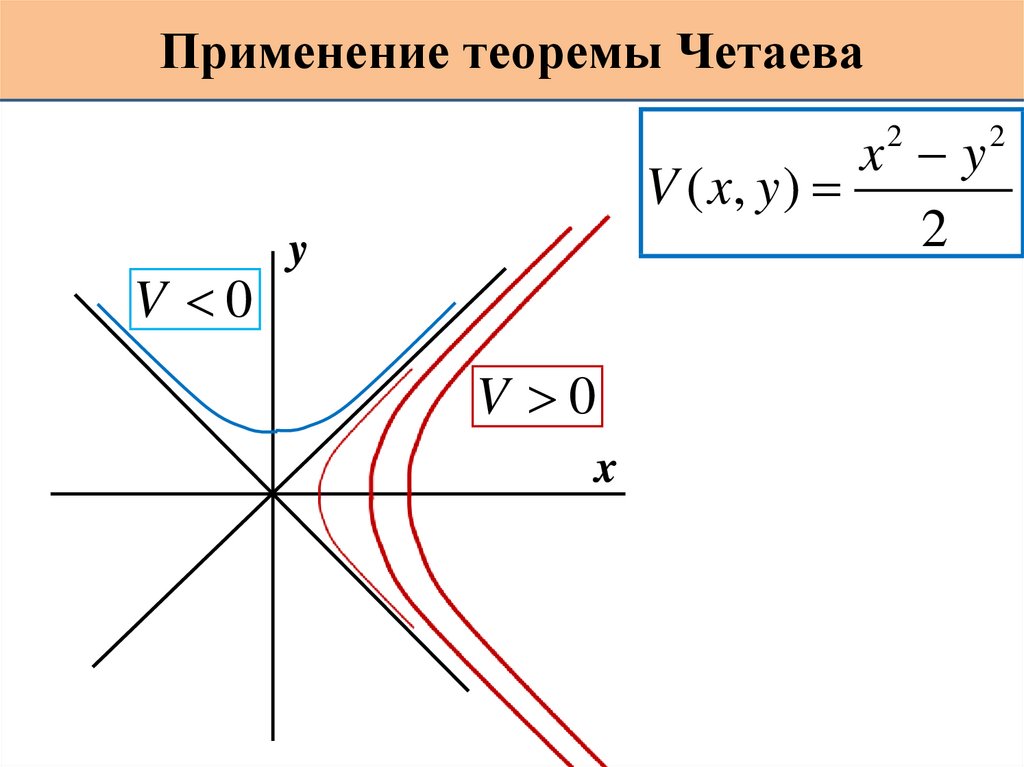
14.
Применение теоремы Четаеваx y
V ( x, y )
2
2
V 0
y
V 0
x
2
15.
Построение функции Ляпуноваu Ax Bxy Cy
2
x
x
2
u y A B C
y
y
2
Условие сохранения знака: D B 4 AC 0
2
2
16.
Построение функции Ляпунова17.
Построение функции ЛяпуноваdL
(2 x By ) x 4 y
dt
( Bx 2Cy ) x 2 y
2 x 8 xy Bxy 4 By
2
2
Bx 2 Bxy 2Cxy 4Cy
2
2
(2 B) x (8 B 2C ) xy (4 B 4C ) y
2
B 2
B C
2
18.
Построение функции ЛяпуноваB 4C (8 B 2C ) 4(2 B)(4 B 4C )
2 B C
C B
B 2
2
2
C
2
B
C
4
B
2
B 3
Подбор:
C 4
19.
Построение функции ЛяпуноваB 4C 2 B C
2
(8 B 2C ) 4(2 B)(4 B 4C )
Подбор:
B 3
C 4
2
(8 3 8) 4(2 3)(12 16)? 9 16
2
L( x, y ) x 3 xy 4 y 0
2
2
dL
2
2
(2 B) x (8 B 2C ) xy (4 B 4C ) y
dt
dL
2
2
x 3 xy 4 y 0
dt
20.
Геометрическая интепретацияy
x
















 mathematics
mathematics








