Similar presentations:
Методы исследования потоков и аппаратов
1. Методы исследования потоков и аппаратов
ДисциплинаМоделирование химическо-технологических
процессов
Тема №4
Методы исследования
потоков и аппаратов
Воробьев Евгений Сергеевич
2. Основные цели исследования
Начиная любое исследование объекта необходимо выяснить тумодель потока, которая в нем существует или хотя бы оценить
наличие в объекте различных зон (РИВ, РИС) и самое главное
наличие застойных зон, которые просто исключают часть объема
аппарата из работы.
Пользуясь этими приемами можно исследовать не только поток,
но и другие характеристики объекта, например, теплофизику,
массопередачу и т.п. Надо только правильно подобрать
исследуемый сигнал, который посылается в объект и модель,
которая должна описать полученный после прохождения объекта
сигнал.
3. Исследование потоков
Основной задачей при проектировании технологическихпроцессов и аппаратов является исследование потоков и выбор
оптимального аппарата для решаемой задачи.
При исследовании потоков используются следующие сигналы:
Ступенчатый (F(t))
Импульсный (C(t))
Синусоидальный
Эти импульсы в виде трассеров запускаются в поток и потом
регистрируется отклик на них.
На основании полученных кривых строится модель потока и
делается заключение о исследуемом аппарате. Чаще всего
используется статистический подход в решении данной задачи, в
предположении, что все объекты описываются нормальным
законом распределении.
4. Модели потоков
Существует достаточно много вариантов описания потоков ваппаратах. Их можно разделить на несколько групп:
Идеальные модели;
Приближенные к реальным модели;
Комбинированные модели.
Модели в каждой из групп имеют право на использование в
определенных условиях и на определенных этапах исследования.
Первые модели позволяют строить идеальные аппараты для
предварительного анализа эффективности выбранной схемы
процесса. Вторые приближают модель к реальным условиям
функционирования аппарата и позволяют найти возможные
проблемы в его работе. Третьи дают достаточно хороший анализ
работы реального аппарата для его модернизации.
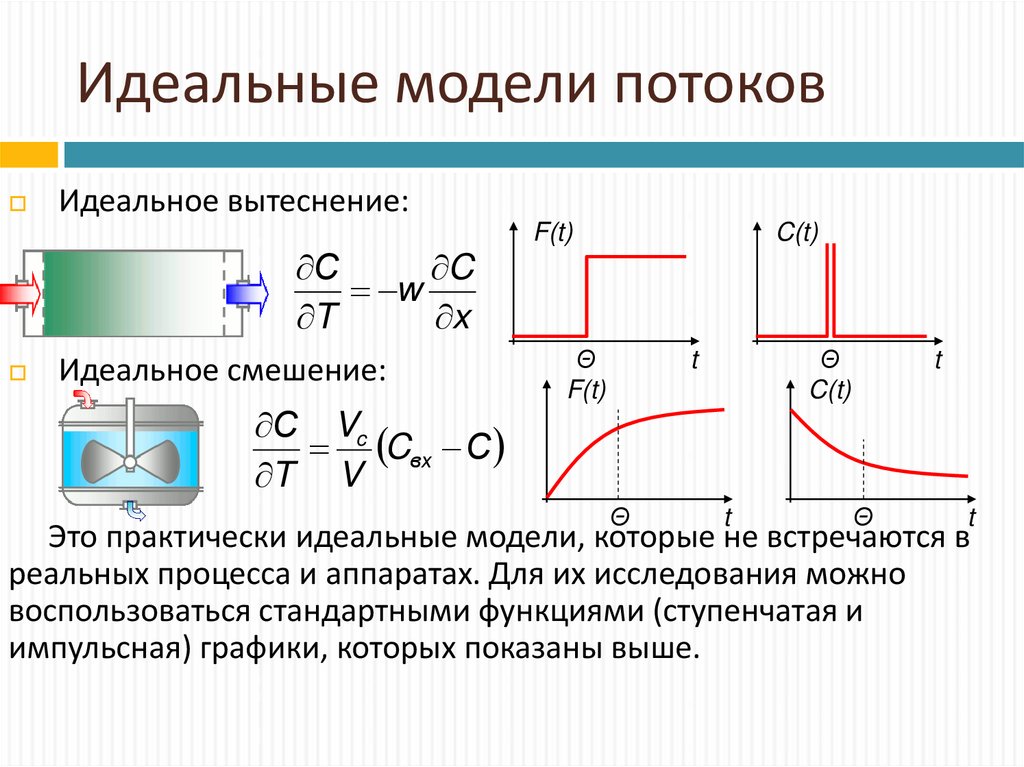
5. Идеальные модели потоков
Идеальное вытеснение:С
C
w
T
x
Идеальное смешение:
С Vc
Cвх С
T V
F(t)
C(t)
Θ
F(t)
Θ
C(t)
t
Θ
t
t
Θ
t
Это практически идеальные модели, которые не встречаются в
реальных процесса и аппаратах. Для их исследования можно
воспользоваться стандартными функциями (ступенчатая и
импульсная) графики, которых показаны выше.
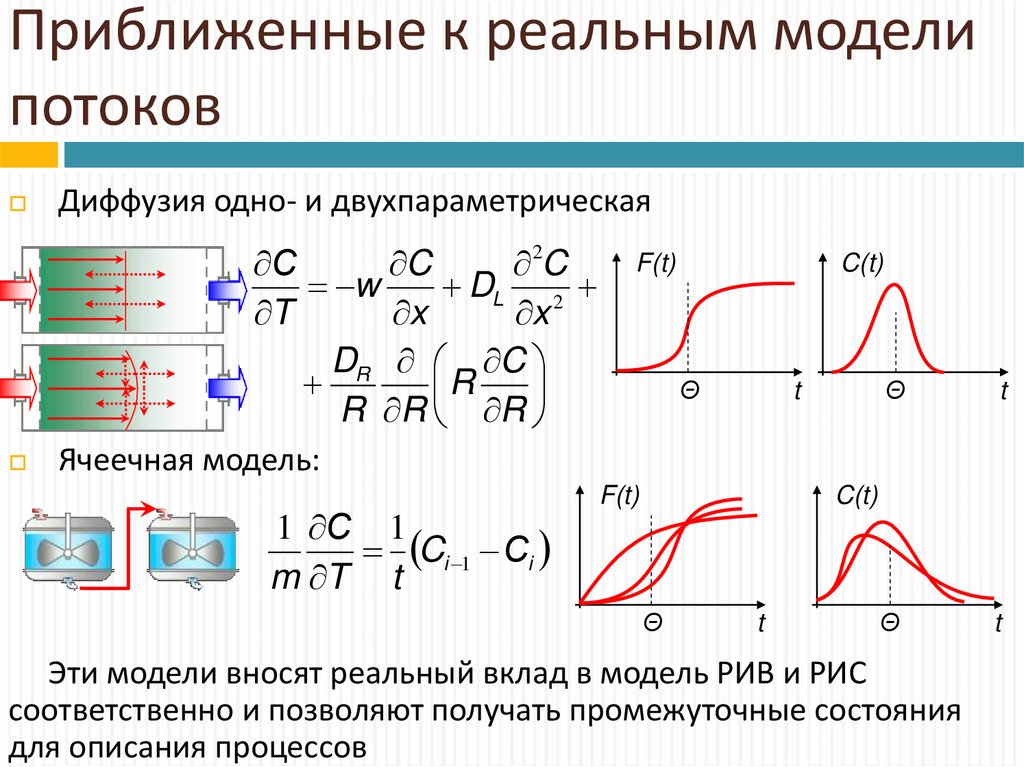
6. Приближенные к реальным модели потоков
Диффузия одно- и двухпараметрическаяС
C
2C
w
DL 2
T
x
x
DR C
R
R R R
Ячеечная модель:
1 С 1
Ci 1 Сi
m T t
F(t)
C(t)
Θ
t
F(t)
Θ
t
Θ
t
C(t)
Θ
t
Эти модели вносят реальный вклад в модель РИВ и РИС
соответственно и позволяют получать промежуточные состояния
для описания процессов
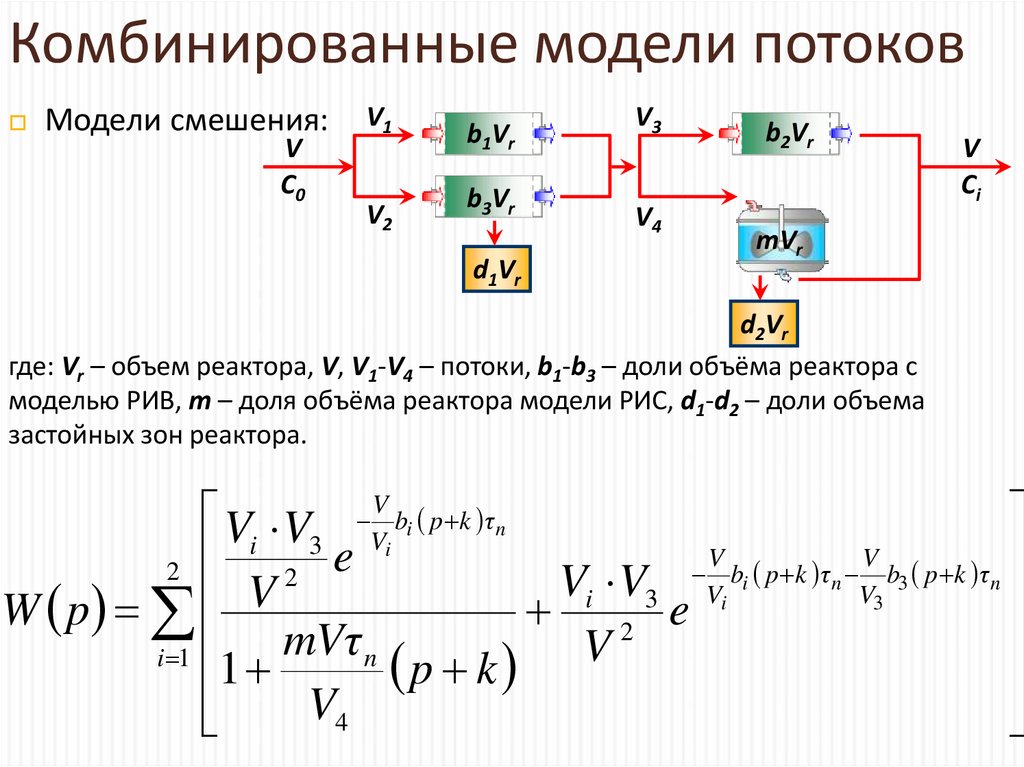
7. Комбинированные модели потоков
Модели смешения:V
C0
V1
V2
b1Vr
b3Vr
d1Vr
V3
V4
b2Vr
V
Ci
mVr
d2Vr
где: Vr – объем реактора, V, V1-V4 – потоки, b1-b3 – доли объёма реактора с
моделью РИВ, m – доля объёма реактора модели РИС, d1-d2 – доли объема
застойных зон реактора.
Vi V3 VVi bi p k τn
V
V
e
2
b
p
k
τ
b3 p k τ n
2
i
n
V
V
Vi
V3
V
i
3
W p
2 e
mVτ n
i 1
p k V
1
V4
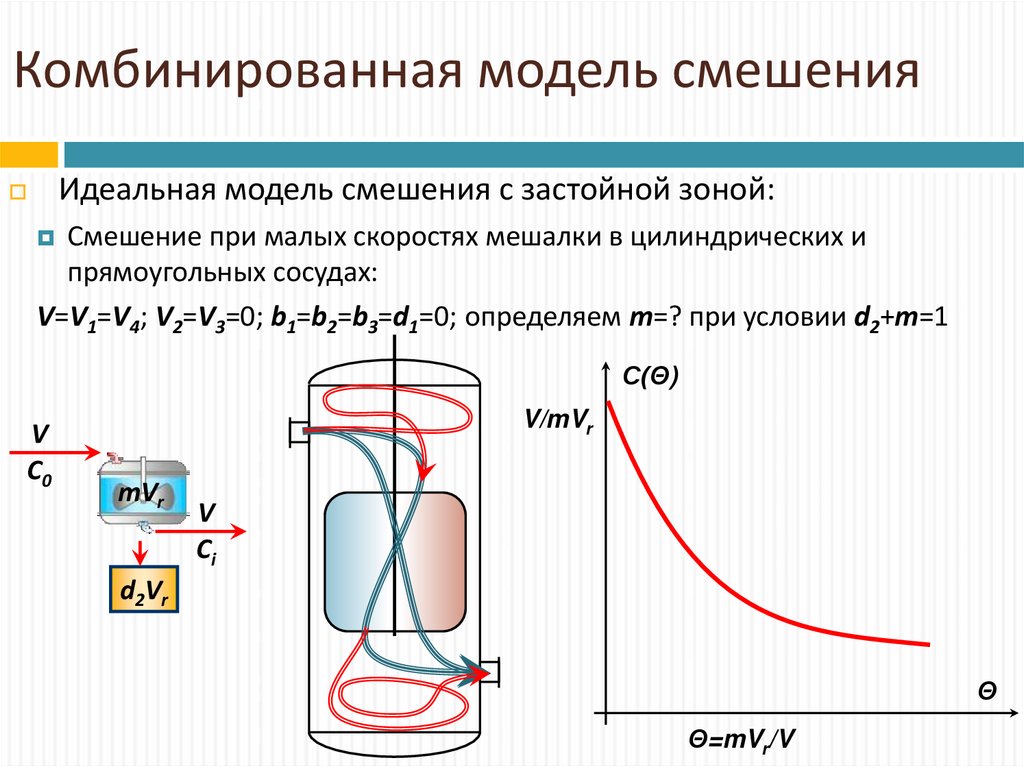
8. Комбинированная модель смешения
Идеальная модель смешения с застойной зоной:Смешение при малых скоростях мешалки в цилиндрических и
прямоугольных сосудах:
V=V1=V4; V2=V3=0; b1=b2=b3=d1=0; определяем m=? при условии d2+m=1
С(Θ)
V
C0
V/mVr
mVr
V
Ci
d2Vr
Θ
Θ=mVr/V
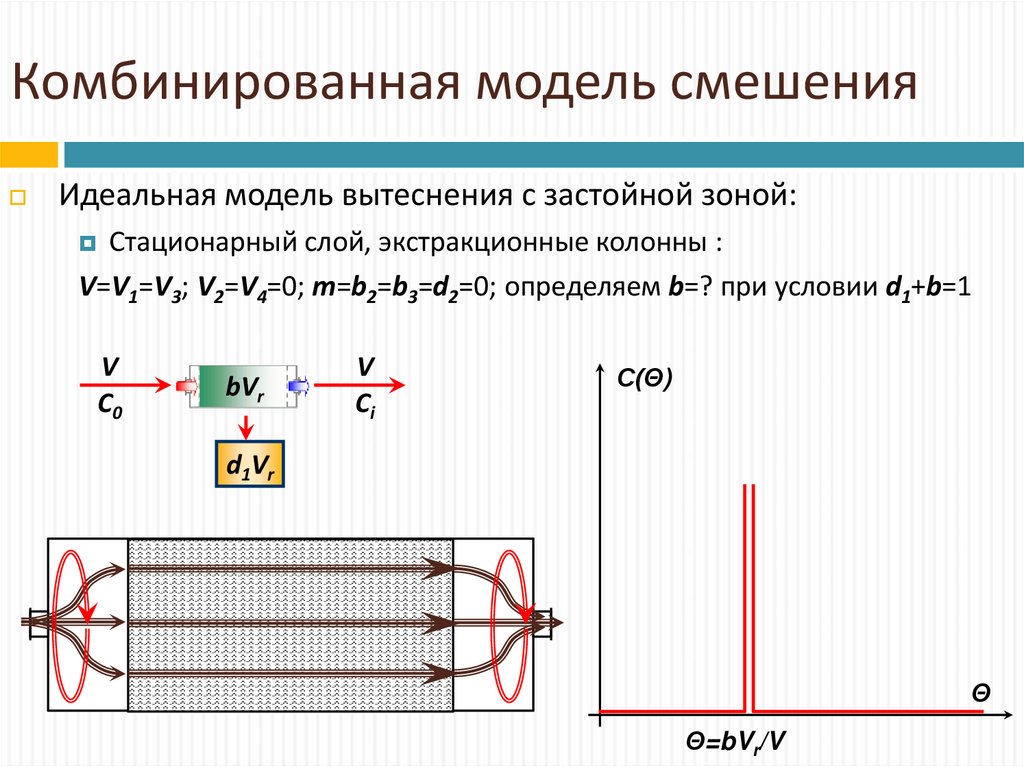
9. Комбинированная модель смешения
Идеальная модель вытеснения с застойной зоной:Стационарный слой, экстракционные колонны :
V=V1=V3; V2=V4=0; m=b2=b3=d2=0; определяем b=? при условии d1+b=1
V
C0
bVr
V
Ci
С(Θ)
d1Vr
Θ
Θ=bVr/V
10. Комбинированная модель смешения
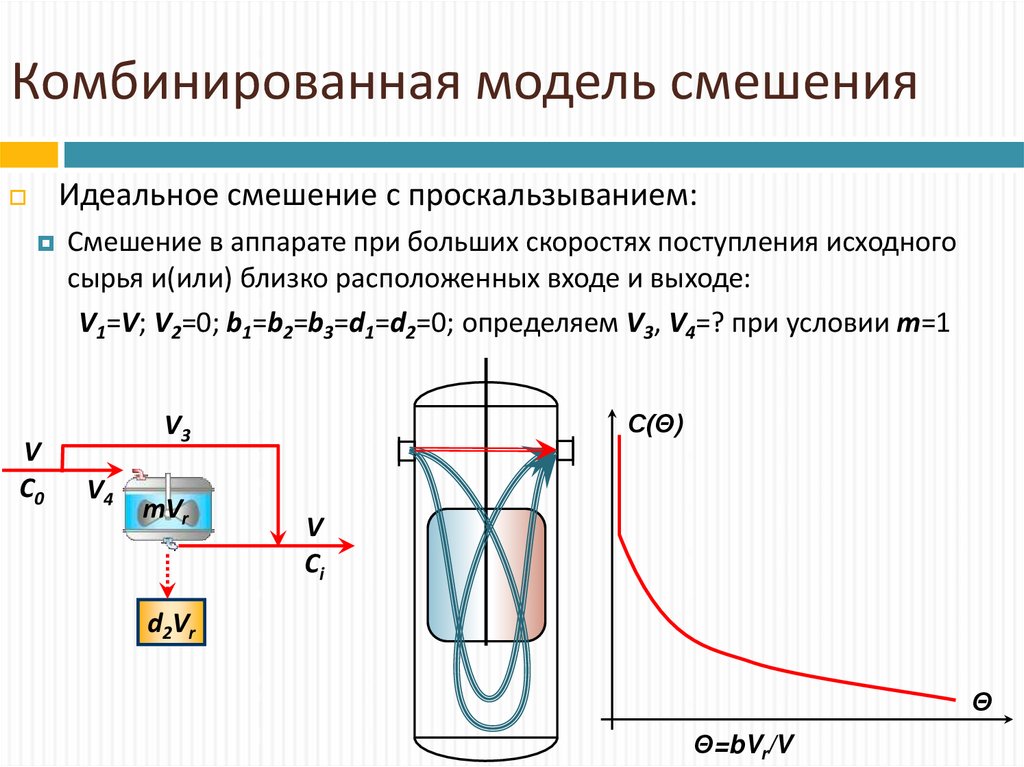
Идеальное смешение с проскальзыванием:V
C0
Смешение в аппарате при больших скоростях поступления исходного
сырья и(или) близко расположенных входе и выходе:
V1=V; V2=0; b1=b2=b3=d1=d2=0; определяем V3, V4=? при условии m=1
С(Θ)
V3
V4
mVr
V
Ci
d2Vr
Θ
Θ=bVr/V
11. Комбинированная модель смешения
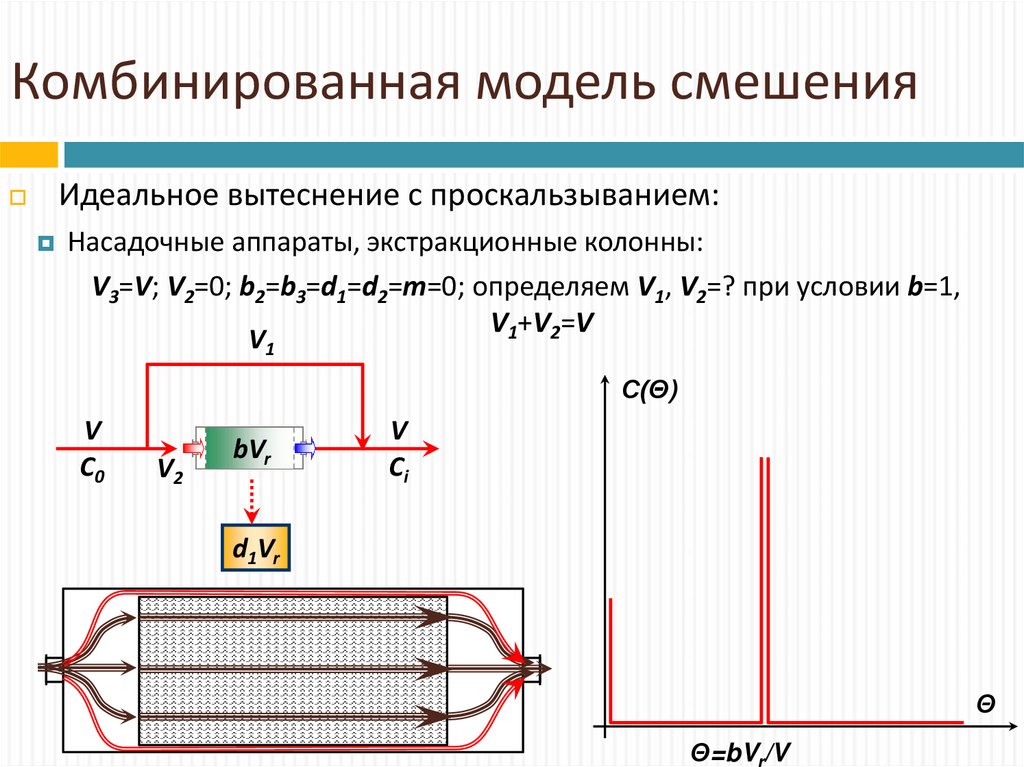
Идеальное вытеснение с проскальзыванием:Насадочные аппараты, экстракционные колонны:
V3=V; V2=0; b2=b3=d1=d2=m=0; определяем V1, V2=? при условии b=1,
V1+V2=V
V1
С(Θ)
V
C0
V2
bVr
V
Ci
d1Vr
Θ
Θ=bVr/V
12. Комбинированная модель смешения
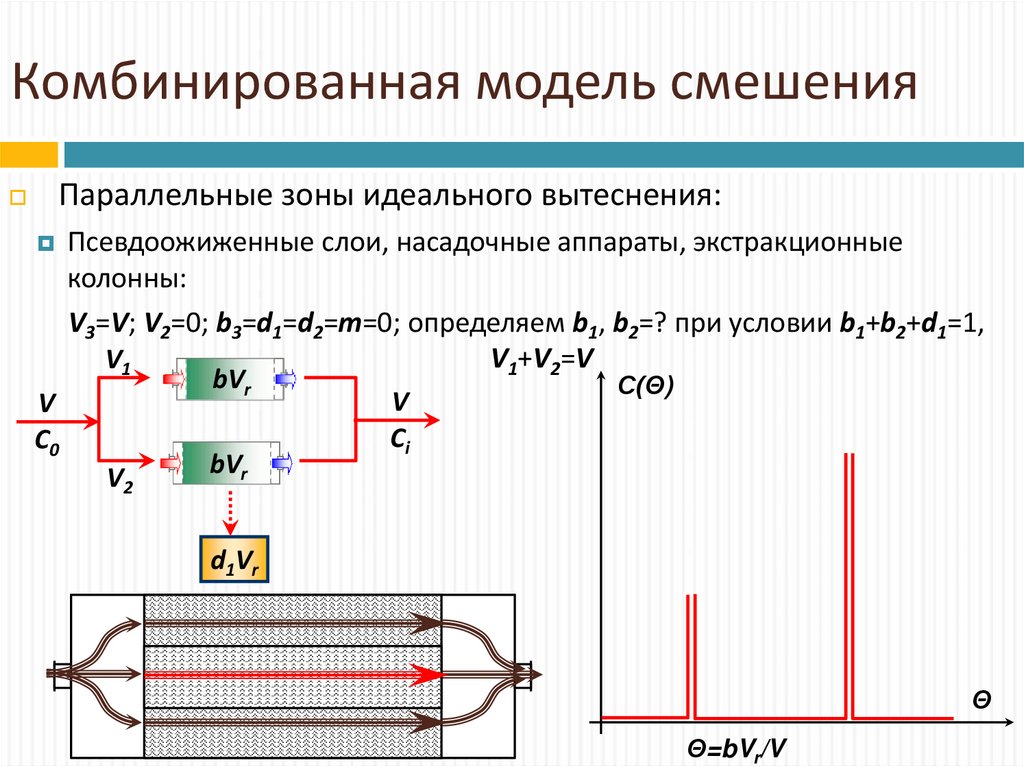
Параллельные зоны идеального вытеснения:Псевдоожиженные слои, насадочные аппараты, экстракционные
колонны:
V3=V; V2=0; b3=d1=d2=m=0; определяем b1, b2=? при условии b1+b2+d1=1,
V1+V2=V
V1
bVr
С(Θ)
V
V
Ci
C0
bVr
V2
d1Vr
Θ
Θ=bVr/V
13. Комбинированная модель смешения
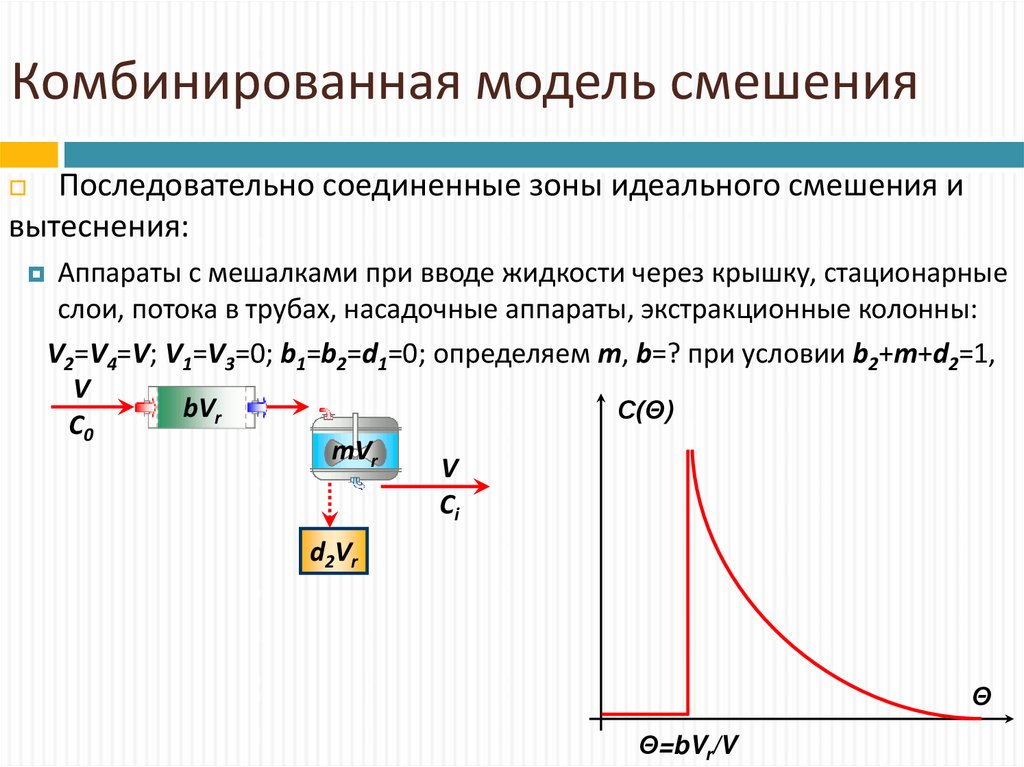
Последовательно соединенные зоны идеального смешения ивытеснения:
Аппараты с мешалками при вводе жидкости через крышку, стационарные
слои, потока в трубах, насадочные аппараты, экстракционные колонны:
V2=V4=V; V1=V3=0; b1=b2=d1=0; определяем m, b=? при условии b2+m+d2=1,
V
bVr
С(Θ)
C0
mVr
V
Ci
d2Vr
Θ
Θ=bVr/V
14. Комбинированная модель смешения
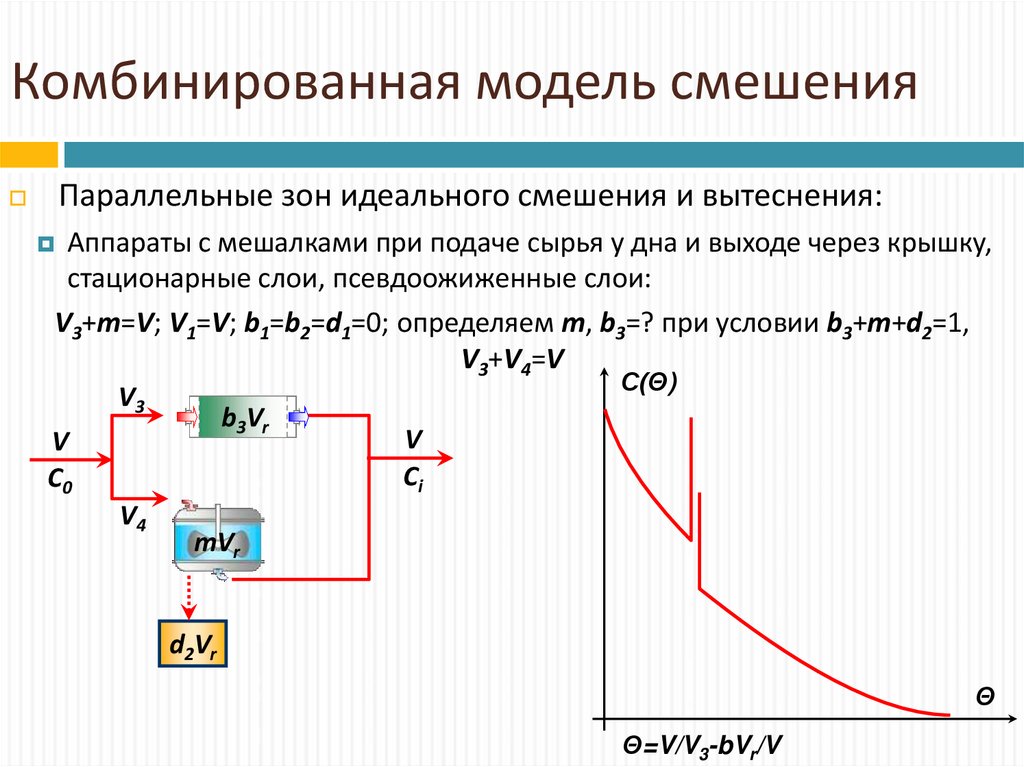
Параллельные зон идеального смешения и вытеснения:Аппараты с мешалками при подаче сырья у дна и выходе через крышку,
стационарные слои, псевдоожиженные слои:
V3+m=V; V1=V; b1=b2=d1=0; определяем m, b3=? при условии b3+m+d2=1,
V3+V4=V
С(Θ)
V3
b3Vr
V
V
Ci
C0
V4
mVr
d2Vr
Θ
Θ=V/V3-bVr/V
15. Комбинированная модель смешения
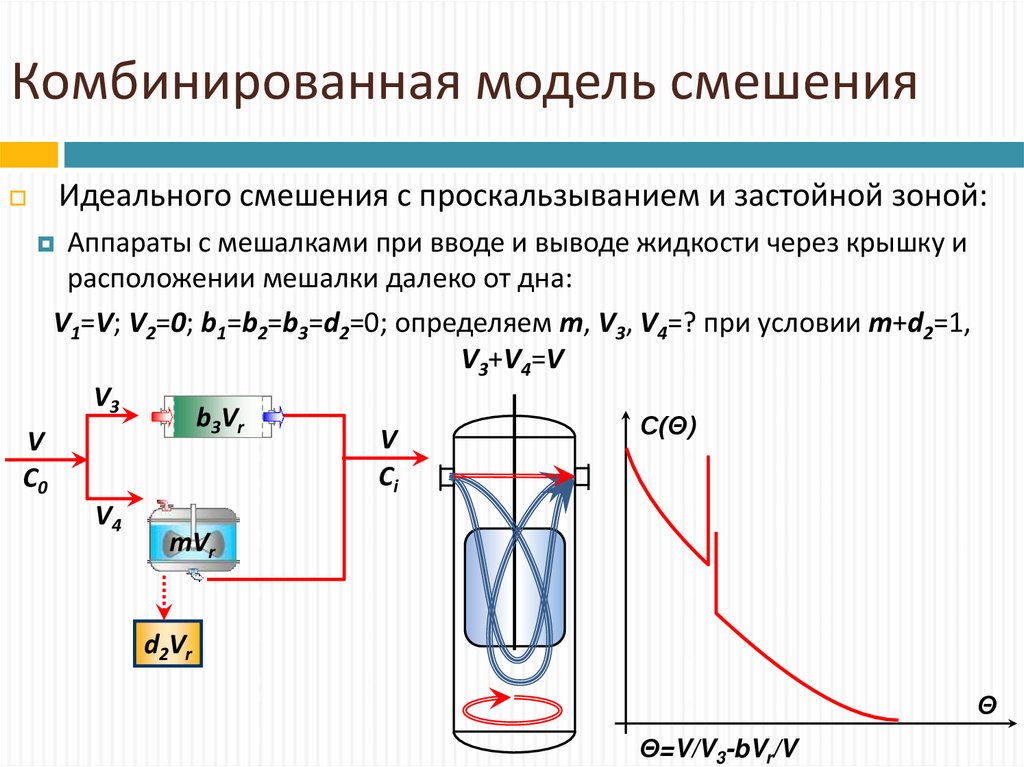
Идеального смешения с проскальзыванием и застойной зоной:Аппараты с мешалками при вводе и выводе жидкости через крышку и
расположении мешалки далеко от дна:
V1=V; V2=0; b1=b2=b3=d2=0; определяем m, V3, V4=? при условии m+d2=1,
V3+V4=V
V3
b3Vr
С(Θ)
V
V
Ci
C0
V4
mVr
d2Vr
Θ
Θ=V/V3-bVr/V
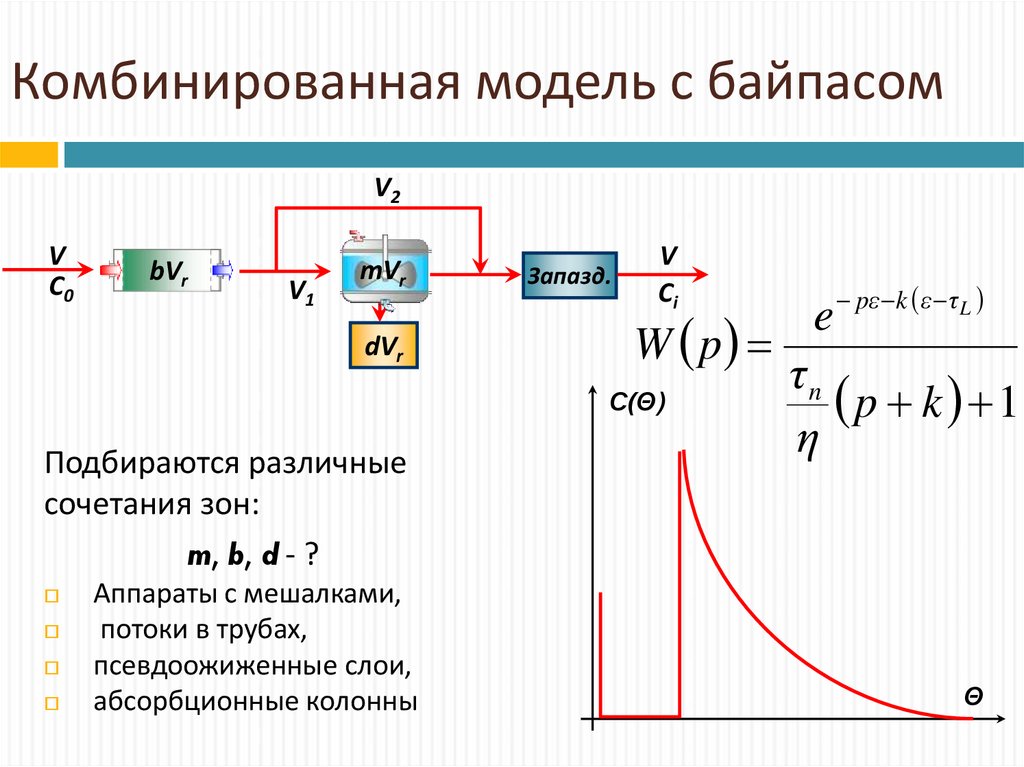
16. Комбинированная модель с байпасом
V2V
C0
bVr
V1
mVr
dVr
Запазд.
V
Ci
W p
С(Θ)
Подбираются различные
сочетания зон:
m, b, d - ?
Аппараты с мешалками,
потоки в трубах,
псевдоожиженные слои,
абсорбционные колонны
e
pε k ε τ L
τn
p k 1
η
Θ
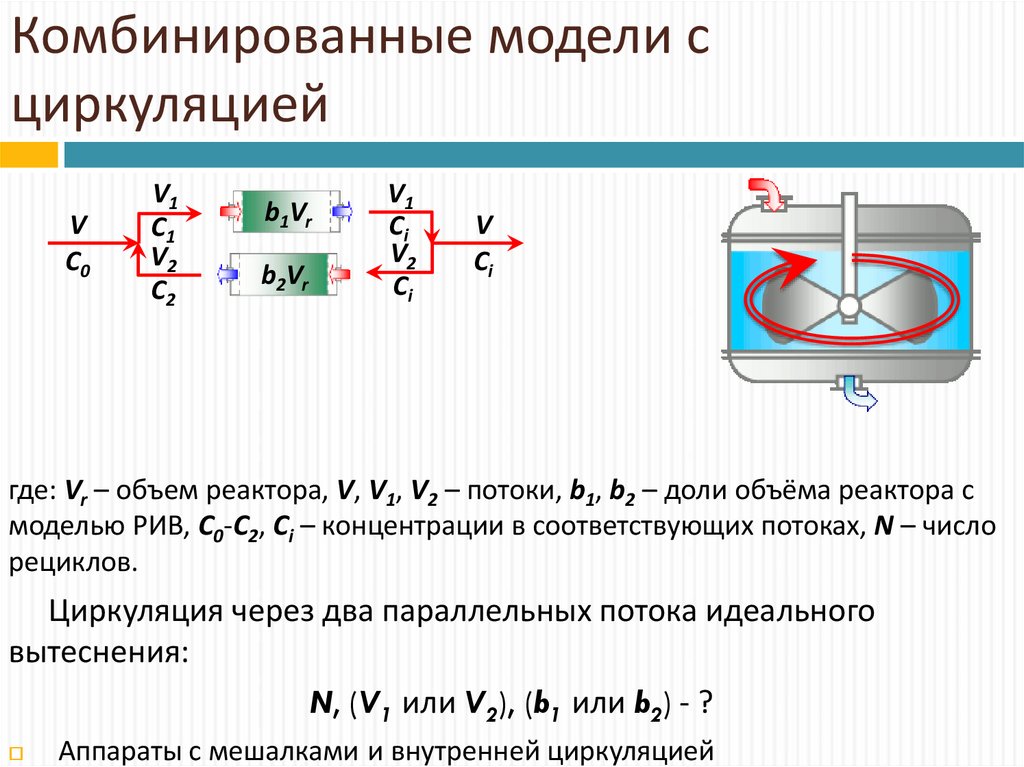
17. Комбинированные модели с циркуляцией
VC0
V1
C1
V2
C2
b1Vr
b2Vr
V1
Ci
V2
Ci
V
Ci
где: Vr – объем реактора, V, V1, V2 – потоки, b1, b2 – доли объёма реактора с
моделью РИВ, С0-С2, Сi – концентрации в соответствующих потоках, N – число
рециклов.
Циркуляция через два параллельных потока идеального
вытеснения:
N, (V1 или V2), (b1 или b2) - ?
Аппараты с мешалками и внутренней циркуляцией
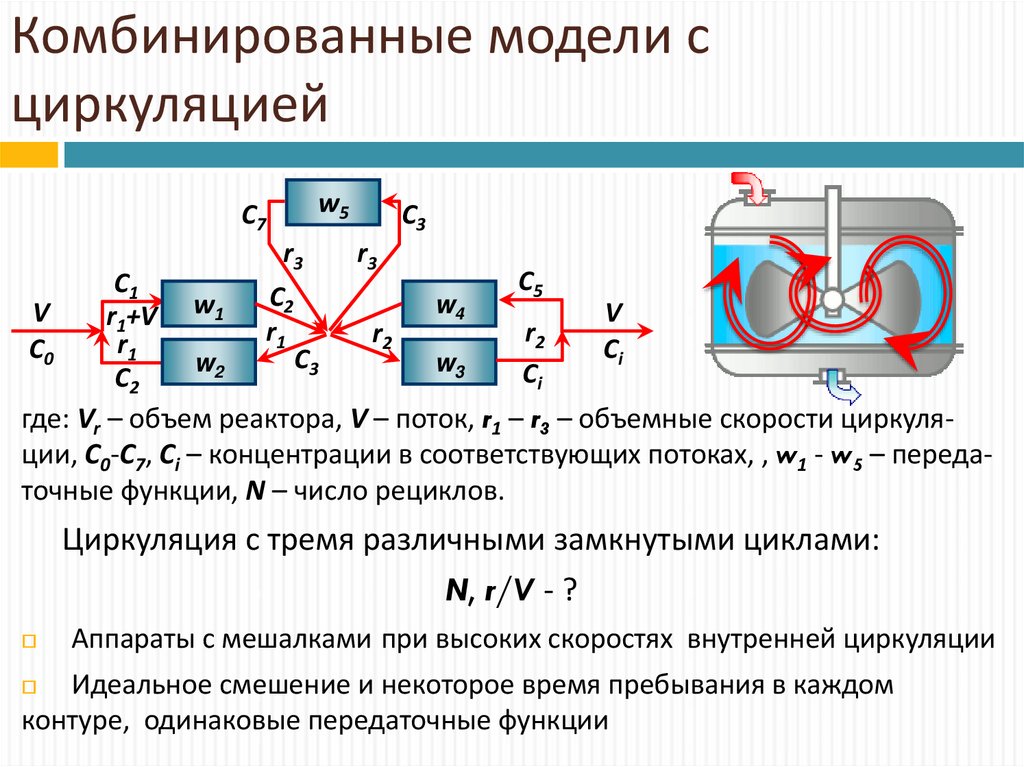
18. Комбинированные модели с циркуляцией
w5C7
r3
C3
r3
C5
C1
C
2
w4
V
V
r1+V w1
r1
r2
r2
r1
C0
Ci
C3
w2
w3
Ci
C2
где: Vr – объем реактора, V – поток, r1 – r3 – объемные скорости циркуляции, С0-С7, Сi – концентрации в соответствующих потоках, , w1 - w5 – передаточные функции, N – число рециклов.
Циркуляция с тремя различными замкнутыми циклами:
N, r/V - ?
Аппараты с мешалками при высоких скоростях внутренней циркуляции
Идеальное смешение и некоторое время пребывания в каждом
контуре, одинаковые передаточные функции
19. Пример решения данной задачи
Запускаем в исследуемый поток маркер:Для импульсного воздействия вводим
единовременно заданный объем индикатора;
Для ступенчатого потока переключаем поток с
одного веществе на другое;
Синусоидальные сигналы обычно используются
в исследовании электрических, магнитных и
тепловых параметров системы.
Рассмотрим расчет для импульсного сигнала
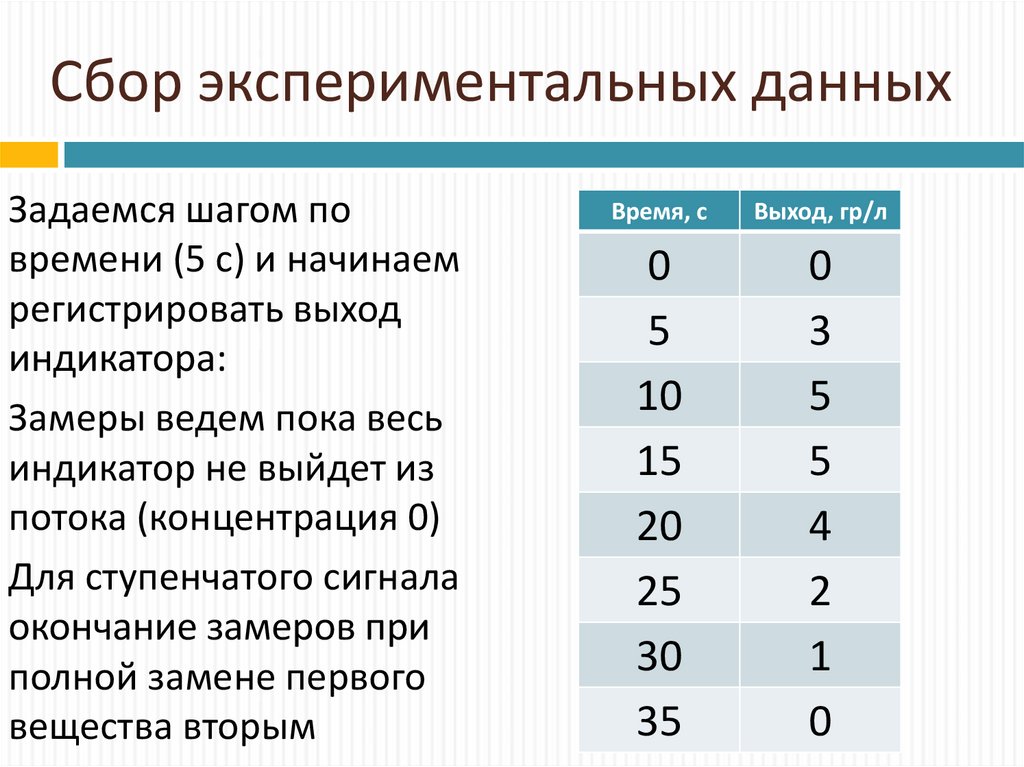
20. Сбор экспериментальных данных
Задаемся шагом повремени (5 с) и начинаем
регистрировать выход
индикатора:
Замеры ведем пока весь
индикатор не выйдет из
потока (концентрация 0)
Для ступенчатого сигнала
окончание замеров при
полной замене первого
вещества вторым
Время, с
Выход, гр/л
0
5
10
15
20
25
30
35
0
3
5
5
4
2
1
0
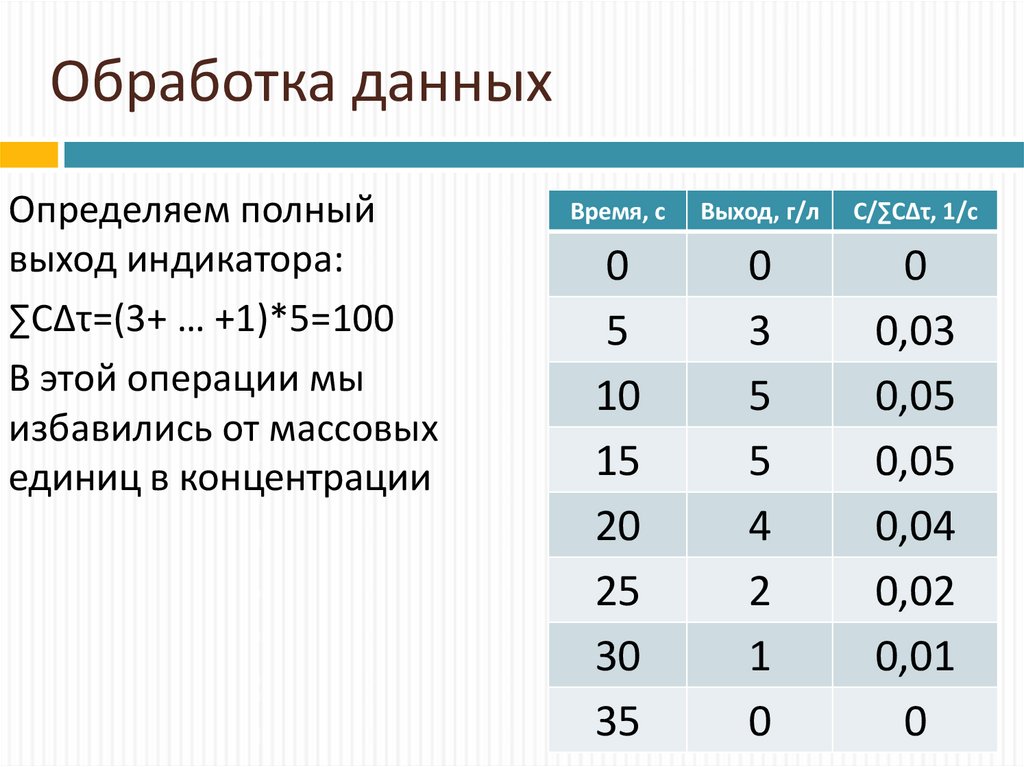
21. Обработка данных
Определяем полныйвыход индикатора:
∑С∆τ=(3+ … +1)*5=100
В этой операции мы
избавились от массовых
единиц в концентрации
Время, с
Выход, г/л
С/∑С∆τ, 1/с
0
5
10
15
20
25
30
35
0
3
5
5
4
2
1
0
0
0,03
0,05
0,05
0,04
0,02
0,01
0
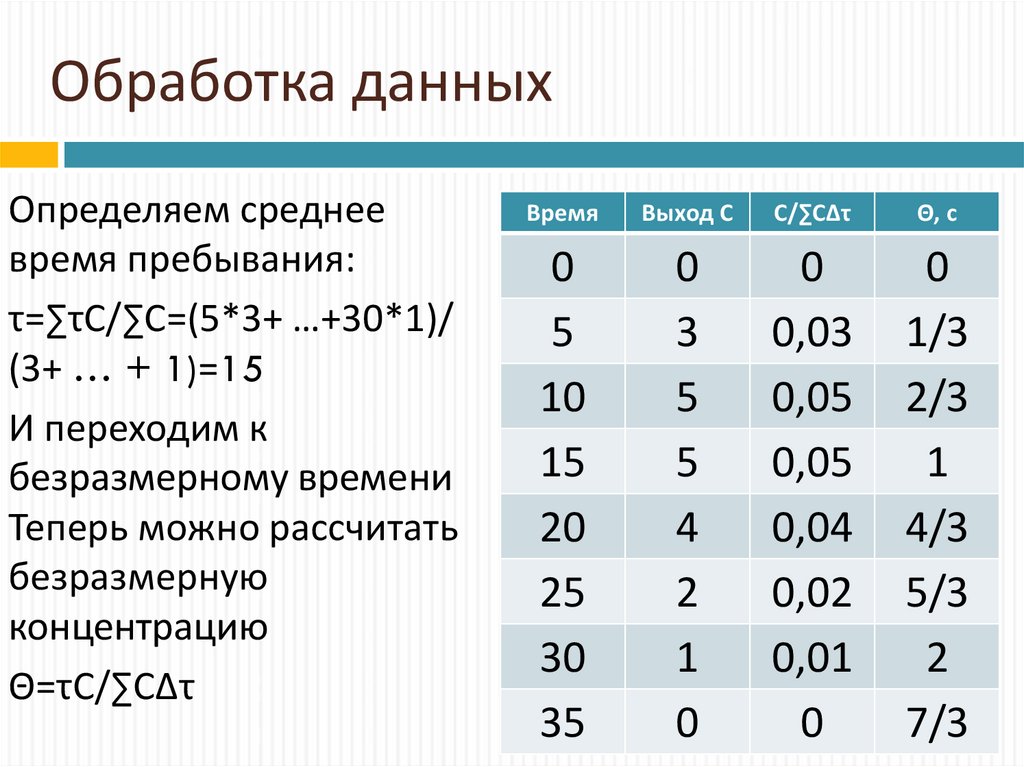
22. Обработка данных
Определяем среднеевремя пребывания:
τ=∑τС/∑С=(5*3+ …+30*1)/
(3+ … + 1)=15
И переходим к
безразмерному времени
Теперь можно рассчитать
безразмерную
концентрацию
Θ=τС/∑С∆τ
Время
Выход С
С/∑С∆τ
Θ, с
0
5
10
15
20
25
30
35
0
3
5
5
4
2
1
0
0
0,03
0,05
0,05
0,04
0,02
0,01
0
0
1/3
2/3
1
4/3
5/3
2
7/3
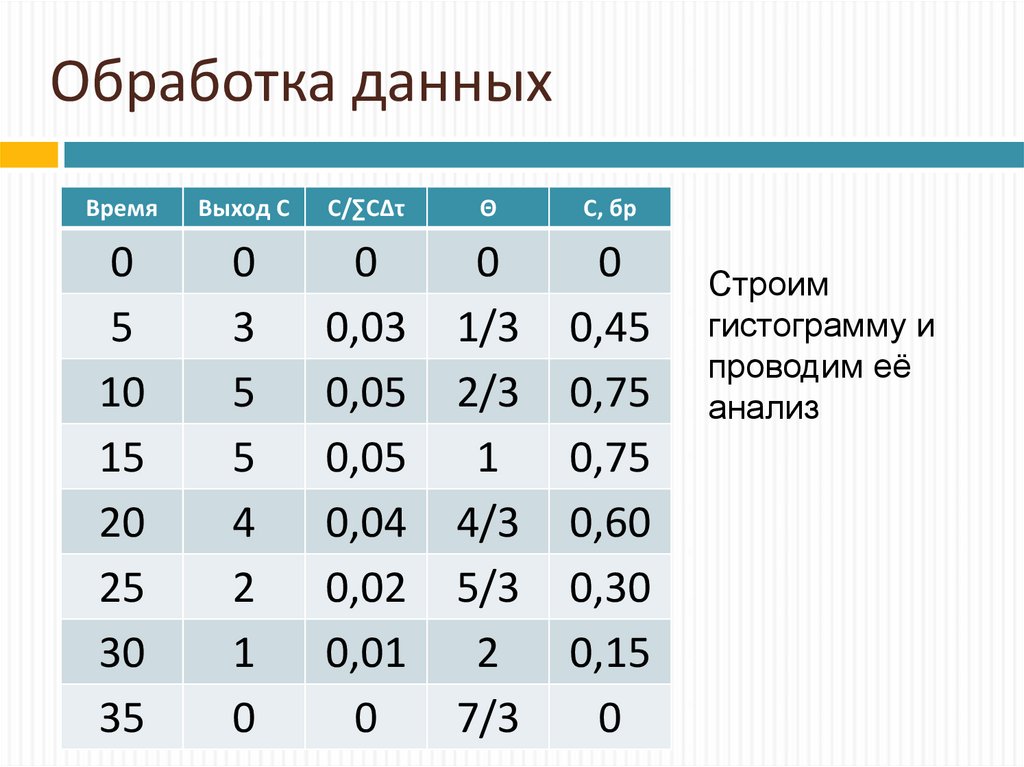
23. Обработка данных
ВремяВыход С
С/∑С∆τ
Θ
С, бр
0
5
10
15
20
25
30
35
0
3
5
5
4
2
1
0
0
0,03
0,05
0,05
0,04
0,02
0,01
0
0
1/3
2/3
1
4/3
5/3
2
7/3
0
0,45
0,75
0,75
0,60
0,30
0,15
0
Строим
гистограмму и
проводим её
анализ
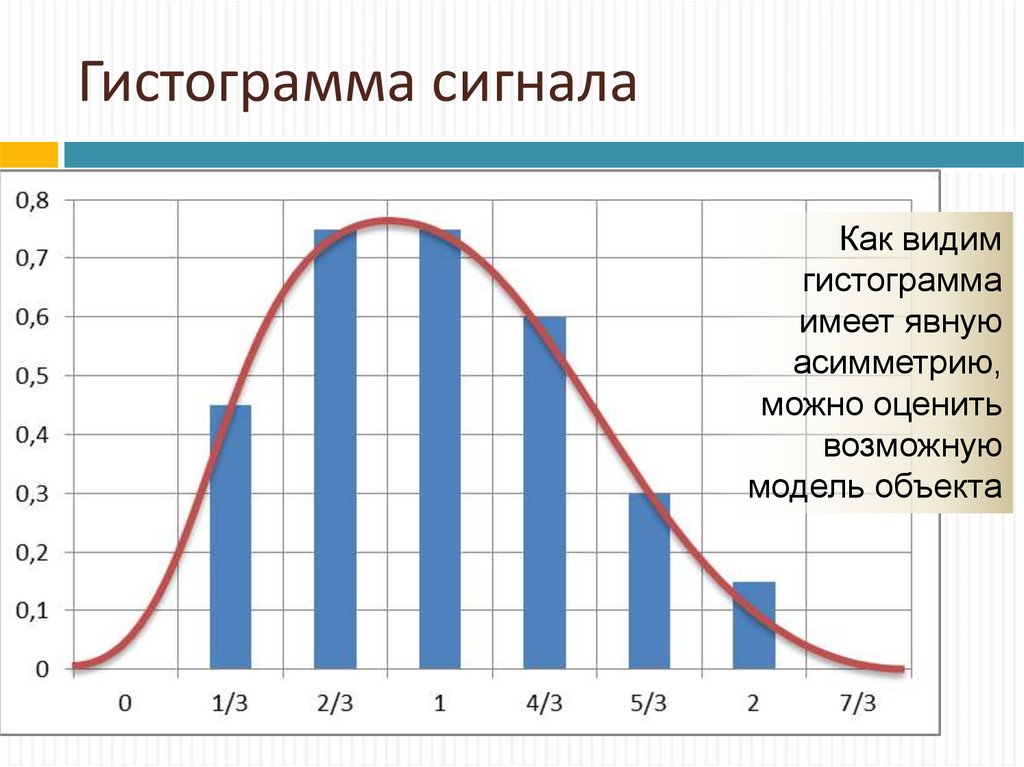
24. Гистограмма сигнала
Как видимгистограмма
имеет явную
асимметрию,
можно оценить
возможную
модель объекта
25. Расчет критерия Пекле для диффузионной модели
Коэффициент продольного перемешивания DL,характеризующим диффузионную модель, представляется в
виде безразмерного диффузионного критерия Пекле:
С-кривая описывается с помощью вероятностных
характеристик:
αk – начальные моменты k-го порядка (k=1,2,3,4);
σ2
– дисперсия;
αk
σ 2 α2 α12
A – показатель асимметрии;
Э – эксцесса;
n
Э
C
α3 3α1α2 2α13
α
2 α
α4 4α1α3 6α2 α12 3α14
2
i 1
n
i 1
A
α
k
C
θ
2 2
1
α
2
1
3
2
ωL
Pe
DL
k 1,4
26.
Последние две характеристики (m и Сm) находятся непосредственно из кривойраспределения, где Сm – максимальное значение по ординате на гистограмме,
m – значение для Сm по оси абсцисс
Теперь вычисляются все варианты Ре по следующим формулам:
1
α1 1
Pe
4
4
9
30
30
α2 1
2 α3 1
2 3
Pe Pe
Pe Pe
Pe
16 108 336 336
α4 1
2 3 4
Pe Pe
Pe
Pe
A
12 Pe 20
3 2 Pe 2
1
2
3
σ
2
Pe Pe
210 120 Pe
Э
2
3 2 Pe
2
Pe
m
2 Pe
2 Pe
1 Pe
1 Pe
Cm
exp
erfc
π
2 Pe 2
2 Pe
Из 9 найденных значений отбрасываются сильно
отличающиеся и из остальных находя среднее значение и
вычисляем коэффициент диффузии
ωL
DL
Pe
27. Расчет числа ячеек для ячеечной модели
Пользуясь результатами исследования потока находим связи междустатистическими характеристиками и числом ячеек в модели по следующим
формулам:
n 1
n 1 n 2
n 1 n 2 n 3
α1n 1; α2 n
; α3n
; α4 n
2
n
n
n3
1
σ
n
2
6
Э
n
2
A
n
n 1
m
n
Окончательное значение n определяется как среднее арифметическое:
k
n
ni
i 1
k
где: k – число вероятностных характеристик, имеющие близкие значения n.
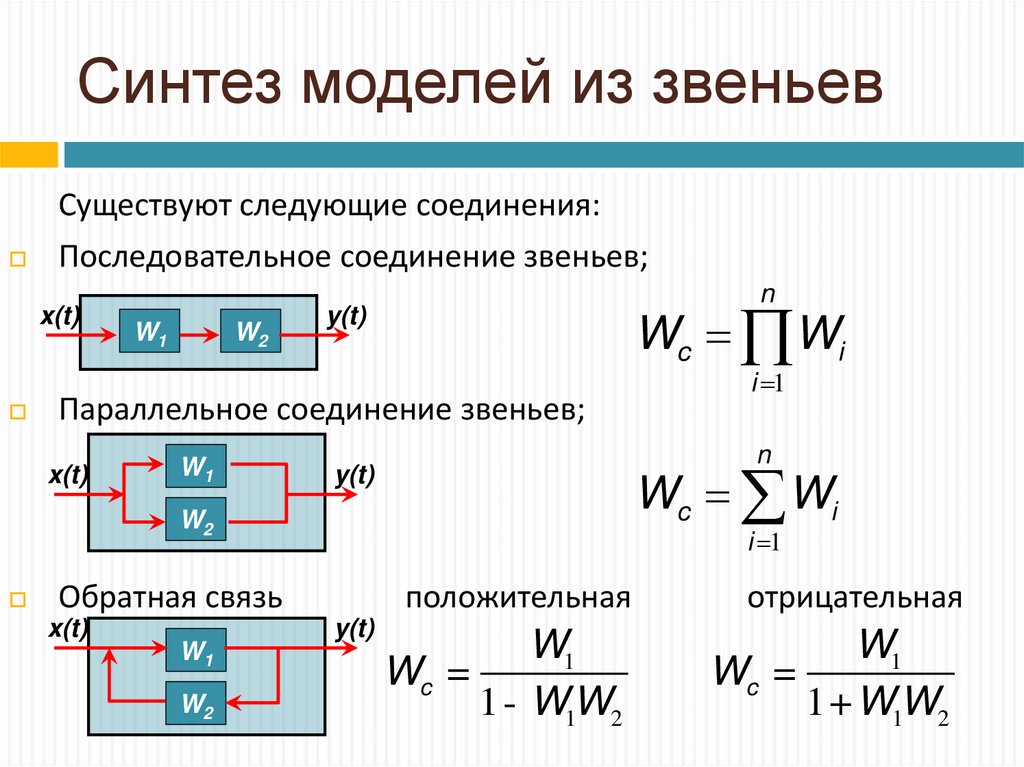
28. Синтез моделей из звеньев
Существуют следующие соединения:Последовательное соединение звеньев;
x(t)
W1
W2
n
Wc Wi
y(t)
Параллельное соединение звеньев;
x(t)
W1
n
Wc Wi
y(t)
W2
i 1
Обратная связь
x(t)
W1
W2
i 1
положительная
y(t)
W1
Wc =
1 - W1W2
отрицательная
W1
Wc =
1 + W1W2








 mathematics
mathematics physics
physics








