Similar presentations:
Методы оптимальных решений в линейном программировании
1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
2. ОБЩАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Общая задача математического программирования:найти экстремум целевой функции F(X) =f (х1, х2, ...,
хп) → max (min)
(1.1)
при системе ограничений
i x1 , x2 ,..., xn 0, i 1,2,...,l ,
(1.2)
i x1 , x2 ,..., xn 0 , i l 1,l 2,...,m.
3.
Если целевая функция (1.1) и системаограничений
(1.2)
линейны,
то
задача
математического программирования называется
задачей линейного программирования.
Математическая модель задачи на нахождения
максимального значения целевой функции
записывается в виде:
4.
F(X) = с1 х1 + с2 х2 + ... + сп хп→max,а11 х1 а12 х2 ... а1n xn b1 ,
а х а х ... а x b ,
21 1
22 2
2n n
2
..........
..........
..........
..........
.
аm1 х1 аm 2 х2 ... аmn xn bm ,
x j 0 , j 1,2 ,...,n.
5.
В задаче на нахождение минимального значенияцелевой функции математическая модель её
запишется в виде F(X) = с1 х1 + с2 х2 + ...
+ сп хп→min,
а11 х1 а12 х2 ... а1n xn b1 ,
а х а х ... а x b ,
21 1
22 2
2n n
2
.........................................
а m1 х1 аm 2 х2 ... а mn xn bm ,
x j 0,
j 1,2 ,...,n.
6. Рассмотрим варианты составления математической модели для следующих задач
РАССМОТРИМ ВАРИАНТЫ СОСТАВЛЕНИЯМАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ
СЛЕДУЮЩИХ ЗАДАЧ
Задача 1. (Планирование производства.)
Некоторое предприятие выпускает три типа
продукции П1,П2,П3 двумя
технологическими способами S1 и S2.
Количество продукции j-гo вида (j = 1,2,3),
произведенного i -м способом (i = 1,2) за
единицу времени задано таблицей
7.
ПродукцииП1
П2
П3
Лимит
времени
S1
20
25
30
10
S2
30
20
15
8
Стоимость 1 ед.
продукции
5
3
6
Т.способ
8.
Необходимо так организовывать производство,чтобы получить наибольшую прибыль при
реализации продукции по указанной стоимости.
9. Математическая модель задачи
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЗАДАЧИОбозначим через хi j — время, затраченное на
изготовление продукции Пj (j = 1,2,3) i -м способом. Тогда
план производства будет иметь вид:
S1
х11
х12
х13
S2
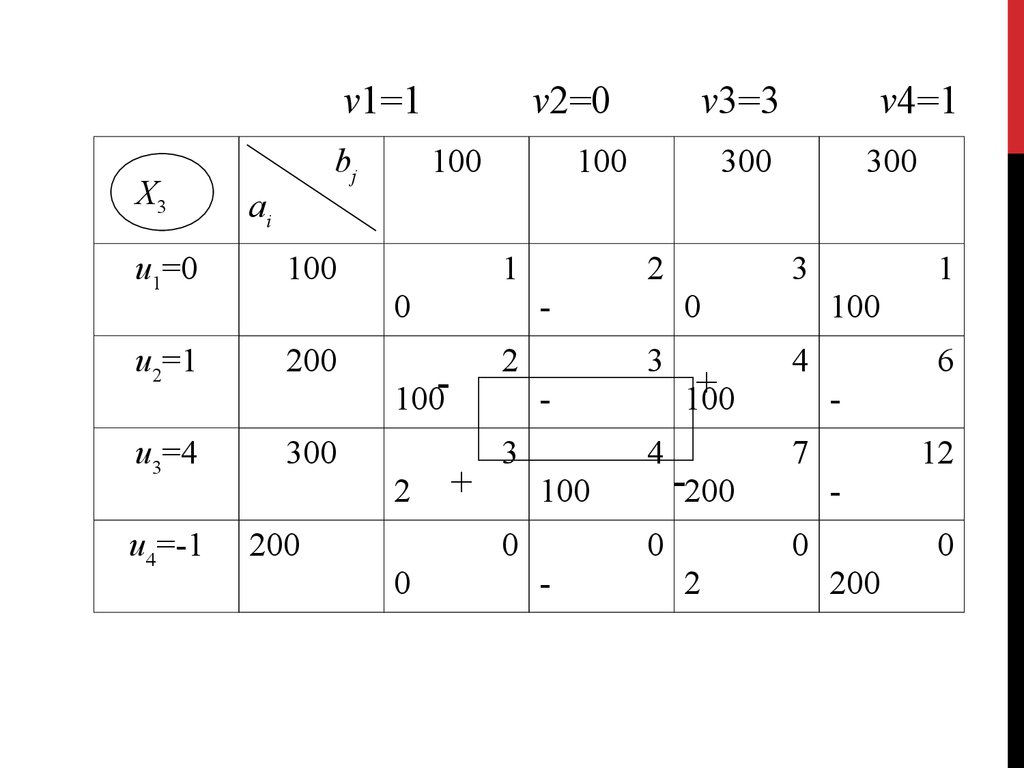
х21
х22
х23
10.
При этом продукции 1-го вида будет выпущено 20х11+ 30х21 , 2-го вида25х12+20х22 , 3-го вида 30х13+ 15х23.
Стоимость всей продукции (обозначим ее за F) равна 5(20х11+
30х21)+3(25х12+20х22)+6(30х13+
15х23)
и
она
должна
быть
максимальной. Но при этом есть ограничения по времени: х11+ х12 + х13
≤10, х21+ х22 + х23 ≤8 и очевидно, все хi j ≥ 0.
11. Окончательно получаем математическую модель задачи
ОКОНЧАТЕЛЬНОПОЛУЧАЕМ
МАТЕМАТИЧЕСКУЮ
МОДЕЛЬ
ЗАДАЧИ
F=5(20х11+ 30х21)+3(25х12+20х22)+6(30х13+ 15х23)
→ max,
х11 х12 х13 10 ,
х
х
х
8
,
все
х
0
.
21
22
23
i
j
12. Задача 2. (Задача о смеси.)
ЗАДАЧА 2. (ЗАДАЧА О СМЕСИ.)Известно, что при правильном питании
человек должен получать в день не менее 20
единиц витамина А, не менее 15 единиц
витамина В. Содержание этих витаминов в
одной единице каждого из продуктов П1, П2,
П3 задано таблице. Составить наиболее
дешевый рацион питания.
Все данные занесены в таблицу.
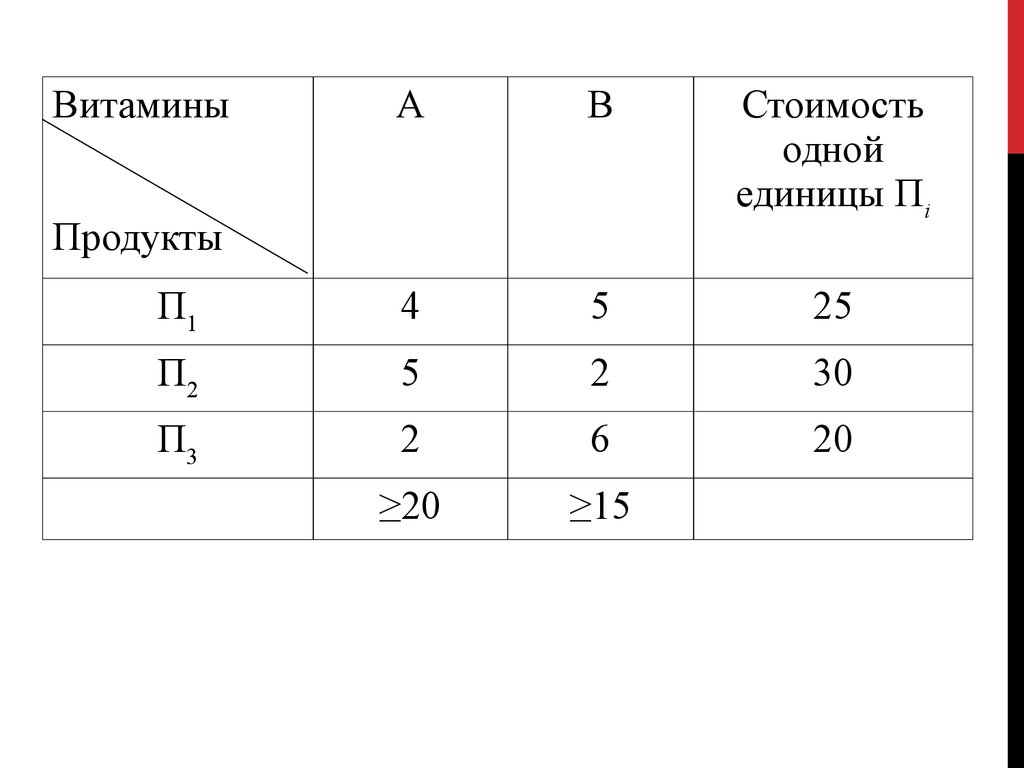
13.
ВитаминыА
В
Стоимость
одной
единицы Пi
П1
4
5
25
П2
5
2
30
П3
2
6
20
≥20
≥15
Продукты
14.
Математическая модель задачиПусть хi — количество продукта Пi, потребляемого
в день (i=1,2,3), тогда стоимость всех продуктов
(обозначим F) будет равна F=25х1 +30x2 + +20х3.
При этом количество витамина А равно 4x1 + 5х2 +
2х3 , витамина В — 5x1 + 2х2 + 6х3, получаем
математическую модель:
15.
F=25х1 +30x2 +20х3 → min,4 х1 5 х2 2 х3 20,
5 х1 2 х2 6 х3 15, х1 , х2 , х3 0.
16. Задача 3. (О раскрое материала.)
ЗАДАЧА 3. (О РАСКРОЕ МАТЕРИАЛА.)Для изготовления некоторого изделия требуется 2
планки по 2 м, 3 — по 2,5 м и одна трехметровая.
Для этого используют 100 досок по 7 м длиной.
Как распилить доски, чтобы получить возможно
большее число комплектов?
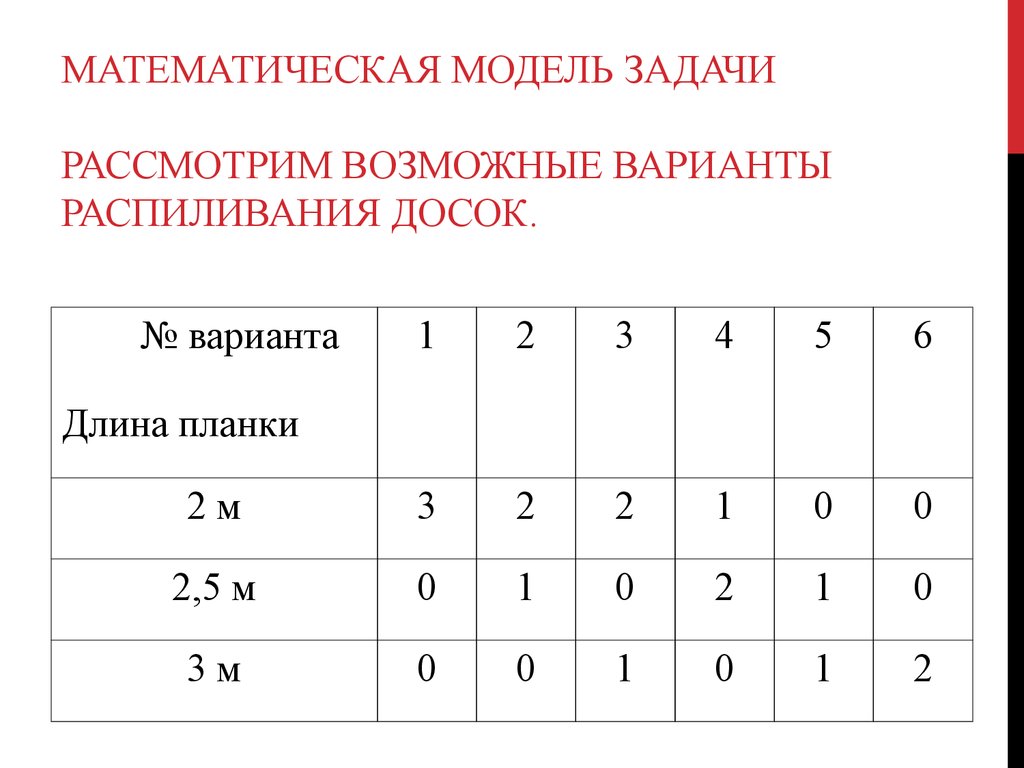
17. Математическая модель задачи Рассмотрим возможные варианты распиливания досок.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЗАДАЧИРАССМОТРИМ ВОЗМОЖНЫЕ ВАРИАНТЫ
РАСПИЛИВАНИЯ ДОСОК.
№ варианта
1
2
3
4
5
6
2м
3
2
2
1
0
0
2,5 м
0
1
0
2
1
0
3м
0
0
1
0
1
2
Длина планки
18.
Обозначим через хi— количество досок,распиленных i-м способом, тогда заготовок по 2 м
получится 3x1+ 2х2 + 2х3 + х4, по 2,5 м — x2 + 2x4
+ х5; по 3 м — х 3 + x5 + 2x6. Обозначим через к
— число полученных изделий, тогда
к
3x1+ 2х2 + 2х3 + х4 =
2
или
x2 + 2x4 + х5 =
к
3
2(3x1+ 2х2 + 2х3 + х4 )=к,
или
3(x2 + 2x4 + х5 )=к,
19.
х 3 + x5 + 2x6=к. Исключим к.2(3x1+ 2х2 + 2х3 + х4 )= 3(x2 + 2x4 + х5 )
или 6x1+ х2 + 4х3 -4х4 -3х5 =0,
2(3x1+ 2х2 + 2х3 + х4 )= х 3 + x5 + 2x6
или 6x1+ 4х2 + 3х3 +2х4 -х5-2х6=0.
20.
Окончательно получим математическую модельк=х 3 + x5 + 2x6→ max,
6 х1 х2 4 х3 4 х4 3 х5 0 ,
6 х1 4 х2 3 х3 2 х4 х5 2 х6 0 ,
х х х х х х 100 ,
2
3
4
5
6
1
все хi ≥0.
21. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача с двумя переменнымиПусть требуется найти максимальное значение
функции F(X) = с1 х1 + с2 х2
при ограничениях
а11 х1 а12 х 2 b1 ,
а х а х b ,
21 1
22 2
2
........................
а m1 х1 а m 2 х 2 bm ,
x1 0 , х 2 0.
22.
Алгоритм решения ЗЛП с двумя переменными графическимметодом:
1. Строится область допустимых решений.
2. Строится вектор = (с1, с2) с точкой приложения в начале
координат.
3. Перпендикулярно вектору проводится одна из линий
уровня, например линия уровня, соответствующая
уравнению с1х1 + с2х2 = 0.
4. Линия уровня перемещается до положения опорной
прямой. На этой прямой и будет находиться максимум или
минимум функции.
23.
Пример1.
Решить
задачу
программирования
графическим
F(X)=2x1+4x2→ max,
2 х1 3 х2 12 ,
х1 х2 9 ,
3 х 2 х 12 ,
2
1
х1 0 , х 2 0.
линейного
методом:
24.
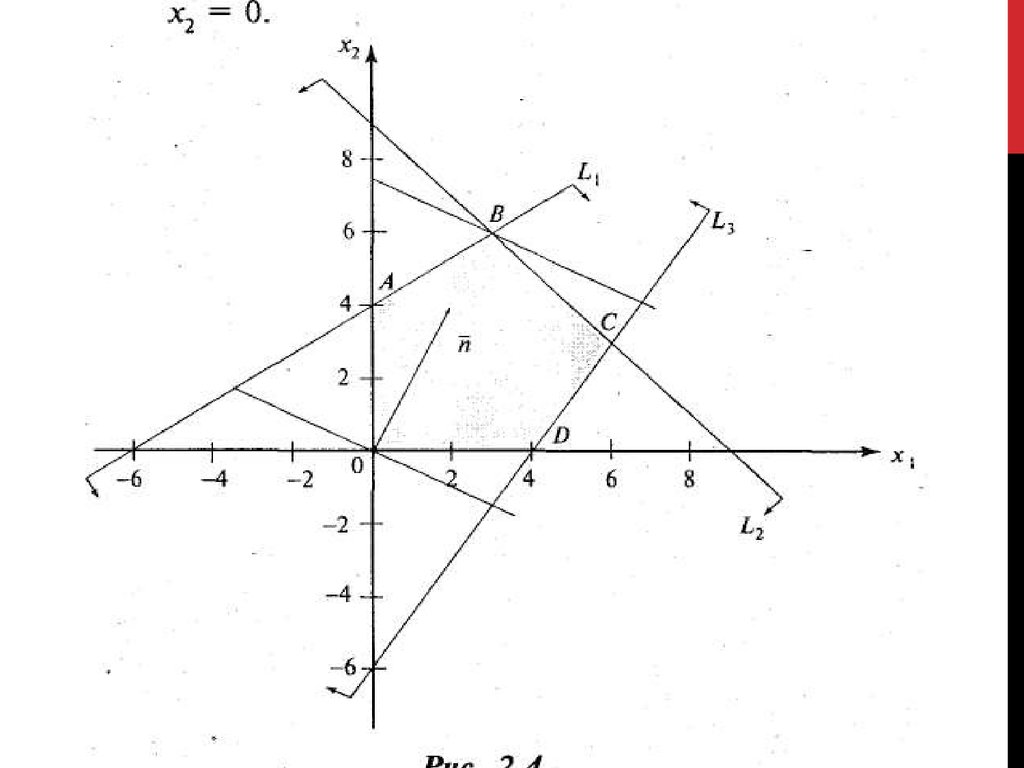
Решение. Изобразим на плоскости системукоординат Ох1х2 и построим граничные прямые
области допустимых решений (номера прямых
соответствуют их порядковому номеру в системе).
Область допустимых решений определяется
многоугольником OABCD (рис.).
Для линий уровня 2х1 + 4х2 = с (с = const) строим
нормальный вектор
n
= (2, 4).
25.
Перпендикулярно вектору nпостроим одну из линий
уровня (на рис. она проходит через начало координат).
Так как задача на максимум, то перемещаем линию
уровня в направлении вектора
прямой.
n
до опорной
26.
27.
В данном случае опорной прямой являетсяпрямая, проходящая через точку пересечения
граничных прямых L1 и L2, т.е. через точку В =
L1∩L2. Для определения координат точки В
решаем систему уравнений
2 х1 3 х2 12 ,
х1 х2 9.
Получаем х1 = 3, х2 = 6. Это и будет оптимальное
решение данной задачи, которому соответствует
максимальное значение целевой функции
max F(X) = 2 · 3 + 4 · 6 = 30.
28.
Пример2.
Найти
минимум
F(X)=2x1+x2→ min при ограничениях
2 х1 3 х2 12 ,
х1 2 х2 8,
х х 8,
2
1
х1 0 , х2 0.
функции
29.
А (6/7; 25/7) и Fmin = 37/7.30. ДВОЙСТВЕННАЯ ЗАДАЧА
В теории двойственности используютсячетыре пары двойственных задач (приведем
их в матричной форме записи):
31.
Исходная задачаДвойственная
задача
Симметричные пары
1. F(X)=CX→max,
Z(Y)=YA0→min
AX≤ A0 ,
YA≥ C,
X≥θ;
Y≥θ.
2. F(X)=CX→min,
Z(Y)=YA0→ max,
AX≥ A0 ,
YA≤ C,
X≥θ;
Y≥θ.
32.
Несимметричные пары1. F(X)=CX→max,
Z(Y)=YA0→min
AX= A0 ,
YA≥ C.
X≥θ;
2. F(X)=CX→min,
Z(Y)=YA0→
max,
AX=A0 ,
YA≤ C.
X≥θ;
33.
Здесь С=(с1, с2,…, сn), Y= (у1, у2,… …,ут),а11 а12 ... а1n
b1
x1
а21 а22 ... а2 n
b2
x2
А
,
A
,
X
.
0
...................
b
x
а а ... а
m
m
m1 m 2
mn
34.
Пример 1. Составить задачу, двойственную кданной
F(X) = х1 + 4х2 +3 х3→min,
х1 х2 x3 10 ,
2 х1 х2 6 ,
х 2 х 3x 12 ,
2
3
1
x j 0,
j 1,2 ,3.
35.
Решение.Умножим
первое
ограничениенеравенство на -1. Задача примет вид исходной
задачи симметричной пары двойственных задач:
F(X) = х1 + 4х2 +3 х3→min,
х1 х2 x3 10 , у1
у2
2 х1 х2 6,
х 2 х 3 x 12 , у
2
3
3
1
x j 0,
j 1,2 ,3.
36.
Окончательно двойственная задача имеетвид
Z(Y) = -10у1 + 6у2 + 12у3→ max,
у1 2 у 2 у3 1,
у1 у 2 2 у3 4 ,
у 3 у 3,
3
1
уi 0 ,
i 1,2 ,3.
37.
Первая теорема двойственностиТеорема. Если одна из пары двойственных задач
имеет оптимальное решение, то и двойственная к
ней имеет оптимальное решение; причем
значения целевых функций задач на своих
оптимальных решениях совпадают. Если же одна
из пары двойственных задач не имеет решения
ввиду неограниченности целевой функции, то
другая не имеет решения ввиду несовместности
системы ограничений.
38.
Вторая теорема двойственностиПусть имеется симметричная пара
двойственных задач
n
F ( X ) c j x j max,
j 1
n
ai j x j bi ,
i 1,2 ,...m ,
j 1
x j 0, j 1,2 ,...n;
m
Z ( Y ) bi yi min,
i 1
m
ai j y i c j ,
j 1,2 ,...n ,
i 1
yi 0 ,
i 1,2 ,...,m.
39.
Теорема. Для того чтобы допустимые решенияХ= (х1, х2, ..., хп), Y=(y1, y2, ..., yт) являлись
оптимальными решениями пары двойственных
задач, необходимо и достаточно, чтобы выполнялись
следующие равенства:
m
х j aij yi c j 0 , j 1,2 ,...,n;
i 1
n
yi aij x j bi 0 ,i 1,2,...,m.
j 1
40.
Пример 1. Для данной задачи составитьдвойственную, решить ее графическим методом и,
используя вторую теорему двойственности, найти
решение исходной задачи:
F(X) = -2x1 + 2х2 + 10х3 + 4х4 + 2х5→ min,
х1 х2 2 х3 2 х5 2 ,
х1 х2 х3 х4 х5 3,
х j 0 j .
y1
y2
41.
Решение. Составим двойственную задачу: Z(Y) = 2у1+ 3у2→ max,
у1 у 2 2 ,
у у 2,
1
2
2 у1 у 2 10 ,
у 4,
2
2 у1 у 2 2.
42.
Решим эту задачу графическим методом. На рис.изображены область допустимых решений задачи,
нормаль п = (2, 3) линий уровня, линии уровня 2у1
+ 3у2 = с и оптимальное решение задачи Y* = (3, 4).
43.
44.
Y * L3 L4 ,2 y1 y 2 10
y2 4
2у1=6
(1 )
( 1 )
у1*=3, у2*=4.
Y *=(3,4).
Z(Y *)=2·3+3·4=18.
45.
Подставим оптимальное решение Y *= (3, 4) всистему ограничений. Получим, что первое, второе и
пятое ограничения выполняются как строгие
неравенства:
3 4 2 ,
0,
*
3 4 2 , х2 0
2 3 4 10 ,
4 4 ,
2 3 4 2 х5* 0.
*
х1
46.
По второй теореме двойственности следует, чтосоответствующие
координаты
оптимального
решения двойственной задачи, т.е. исходной
задачи, равны нулю: х1* = х2* = х5*=0. Учитывая
это, из системы ограничений исходной задачи
получим
2 х3 2 ,
х3 х4 3.
47.
Отсюда находим х3*= 1, х4* = 2. Окончательнозаписываем X*=(0,0,1,2,0).
Ответ: min F(X) = 18 при X* = (0, 0, 1, 2, 0).
48. ТРАНСПОРТНАЯ ЗАДАЧА
Формулировка транспортной задачиОднородный груз сосредоточен у т поставщиков в
объемах a1, a2,..., ат. Данный груз необходимо
доставить п потребителям в объемах b1, b2, ..., bn.
Известны сij, i= 1, 2, ..., m, j = 1, 2, ..., п — стоимости
перевозки единицы груза от каждого i-го поставщика
каждому j-му потребителю. Требуется составить такой
план перевозок, при котором запасы всех поставщиков
будут вывезены полностью, запросы всех потребителей
полностью удовлетворены и суммарные затраты на
перевозку всех грузов минимальны.
Исходные данные транспортной задачи обычно
записываются в таблице:
49.
bjb1
b2
…
bn
a1
с11
с12
…
с1n
a2
с21
с22
…
с2n
…
…
…
…
…
ат
ст1
ст2
…
стn
ai
50.
Исходные данные задачи могут быть представленытакже в виде вектора запасов поставщиков
А=(a1,a2,...,ат), вектора запросов потребителей
В=(b1,b2, ..., bn) и матрицы стоимостей
с11 с12 ... с1n
c
c
...
c
21
22
2n
С
.......................
cm1 cm 2 ... cmn
51.
52. Опорное решение транспортной задачи
ОПОРНОЕ РЕШЕНИЕТРАНСПОРТНОЙ ЗАДАЧИ
53.
Свойствосистемы
ограничений
транспортной задачи:
ранг системы векторов ― условий
транспортной задачи равен N=т + п — 1.
54.
Клетки таблицы транспортной задачи, вкоторых находятся отличные от нуля или
базисные нулевые перевозки, называются
занятыми, остальные — незанятыми или
свободными.
55.
56.
57. МЕТОДЫ ПОСТРОЕНИЯ НАЧАЛЬНОГО ОПОРНОГО РЕШЕНИЯ МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА
Существует ряд методов построения начального опорногорешения, наиболее простым из которых является метод
северо-западного угла. В данном методе запасы очередного
поставщика используются для обеспечения запросов
очередных потребителей до тех пор, пока не будут
исчерпаны полностью, после чего используются запасы
следующего по номеру поставщика.
Заполнение таблицы транспортной задачи начинается с
левого верхнего угла и состоит из ряда однотипных шагов.
На каждом шаге, исходя из запасов очередного поставщика и
запросов очередного потребителя, заполняется только одна
клетка и соответственно исключается из рассмотрения один
поставщик или потребитель.
58.
Во избежание ошибок после построенияначального опорного решения необходимо проверить,
что число занятых клеток равно т + п — 1 и векторыусловия, соответствующие этим клеткам, линейно
независимы.
Теорема.
Решение
транспортной
задачи,
построенное методом северо-западного угла, является
опорным.
59.
60.
61. Переход от одного опорного решения к другому
ПЕРЕХОД ОТ ОДНОГО ОПОРНОГОРЕШЕНИЯ К ДРУГОМУ
В транспортной задаче переход от одного опорного
решения к другому осуществляется с помощью
цикла. Для некоторой свободной клетки таблицы
строится цикл, содержащий часть клеток, занятых
опорным
решением.
По
этому
циклу
перераспределяются объемы перевозок. Перевозка
загружается в выбранную свободную клетку, и
освобождается одна из занятых клеток, получается
новое опорное решение.
62.
Теорема(о
существовании
и
единственности цикла).
Если
таблица
транспортной
задачи
содержит опорное решение, то для любой
свободной клетки таблицы существует
единственный цикл, содержащий эту клетку и
часть клеток, занятых опорным решением.
63.
64.
Сдвигом по циклу на величину θ называетсяувеличение объемов перевозок во всех нечетных
клетках цикла, отмеченных знаком «+», на θ и
уменьшение объемов перевозок во всех четных
клетках, отмеченных знаком «—», на θ.
Теорема.
Если таблица транспортной задачи содержит
опорное решение, то при сдвиге по любому циклу,
содержащему одну свободную клетку, на величину
θ = получится опорное решение.
65. МЕТОД ПОТЕНЦИАЛОВ
66.
67.
Числа Δij называются оценками свободных клеток таблицыили векторов ― условий транспортной задачи,
68.
69. ОСОБЕННОСТИ РЕШЕНИЯ ТРАНСПОРТНЫХ ЗАДАЧ С НЕПРАВИЛЬНЫМ БАЛАНСОМ
70.
Следовательно, чтобы задача в рассматриваемом случаеимела решение, необходимо ввести фиктивного
потребителя с запросами bn+1, равными разности
суммарных запасов поставщиков и запросов
потребителей, и нулевыми стоимостями перевозок
единиц груза
71.
72.
Следовательно, чтобы в этом случае задачаимела
решение,
необходимо
ввести
фиктивного поставщика с запасами ат+1,
равными
разно
суммарным
запросам
потребителей и запасам поставщиков, и
нулевыми стоимостями перевозок единиц
груза
73.
Алгоритм решения транспортной задачи методомпотенциалов
1. Проверяют
выполнение
необходимого
и
достаточного условия разрешимости задачи.
Если задача имеет неправильный баланс, то
вводят
фиктивного
поставщика
или
потребителя с недостающими запасами или
запросами и нулевыми стоимостями перевозок.
2. Строят начальное опорное решение и проверяют
правильность его построения, для чего
подсчитывают количество занятых клеток (их
должно быть т+п—1) и убеждаются в линейной
независимости векторов-условий.
74.
3.Строят систему потенциалов, соответствующихопорному решению. Для этого решают систему
уравнений u v c при х 0.
i
j
ij
ij
Для того чтобы найти частное решение системы,
одному из потенциалов задают произвольно некоторое
значение (чаще нуль). Остальные потенциалы
однозначно определяются по формулам:
ui cij v j
при
если известен потенциал
vj
хij 0 ,
75.
v j cij uiпри
хij 0 ,
ui
если известен
потенциал
.
76.
4. Проверяют, выполняется ли условиеоптимальности для свободных клеток таблицы.
Для этого вычисляют оценки для всех свободных
клеток по формулам. ij ui v j cij
ij
Если для всех свободных клеток
< 0, то
вычисляют значение целевой функции, и
решение задачи заканчивается, так как
полученное решение является оптимальным.
Если же имеется хотя бы одна клетка с
положительной оценкой, то опорное решение не
является оптимальным.
77.
Переходят к новому опорному решению, накотором значение целевой функции будет
меньше. Для этого находят клетку таблицы
задачи, которой соответствует наибольшая
положительная оценка
max
5.
ij
0
ij
lk
78.
Строят цикл, включающий в свой состав даннуюклетку и часть клеток, занятых опорным решением.
В клетках цикла расставляют поочередно знаки «+»
и «-», начиная с «+» в клетке с наибольшей
положительной оценкой. Осуществляют сдвиг
(перераспределение груза) по циклу на величину
θ=
min xij
"-"
Клетка со знаком «-», в которой достигается
min xij
"-"
79.
Если минимум достигается в несколькихклетках, то одна из них остается пустой, а в
остальных проставляют базисные нули,
чтобы число занятых клеток оставалось
равным т+п—1. Возвращаются к пункту 3.
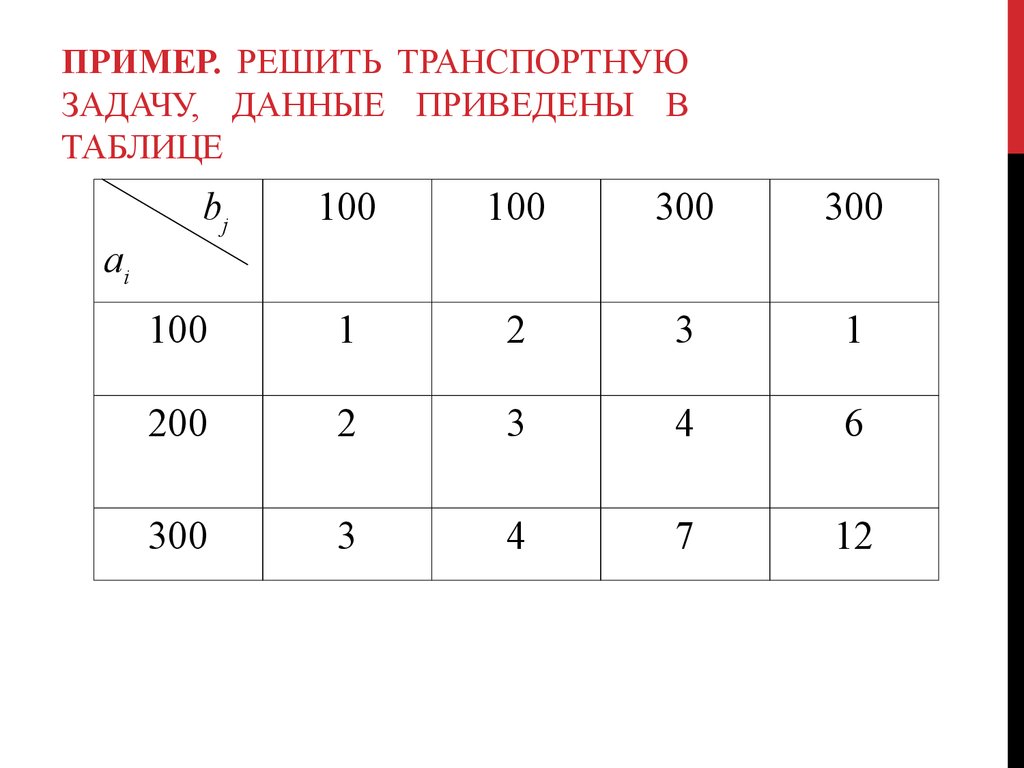
80. Пример. Решить транспортную задачу, данные приведены в таблице
ПРИМЕР. РЕШИТЬ ТРАНСПОРТНУЮЗАДАЧУ, ДАННЫЕ ПРИВЕДЕНЫ В
ТАБЛИЦЕ
bj
100
100
300
300
100
1
2
3
1
200
2
3
4
6
300
3
4
7
12
ai
81.
Решение. 1. Проверяем выполнение необходимогои достаточного условия разрешимости задачи.
Находим суммарные запасы поставщиков и запросы
потребителей:
3
аi
i 1
= 100 + 200 + 300 = 600,
4
100 + 100 + 300 + 300 = 800.
bj =
Задача с неправильным балансом.
j 1
Вводим
четвертого,
фиктивного
поставщика с запасами а4 = 800 — 600
= 200 и нулевыми стоимостями
перевозки единиц груза
82.
2. Составляем начальное опорное решениеметодом минимальной стоимости. Записываем
матрицу стоимостей С:
bj
100
100
300
300
ai
100
1
2
3
1
2
3
4
6
7
12
100
200
0
100
300
3
100
4
200
200
0
0
100
0
0
200
83.
Полученное решение Х1 имеет т + п — 1=4 + 4 — 1= 7 базисных переменных. Опорное решение
является вырожденным, так как одна из его
координат равна нулю. Вычислим значение целевой
функции
на
этом
опорном
решении
F(X1)=100·1+0·2+100·3+100·4+200·7+100·12+200·0
=3400.
84.
3. Для проверки оптимальности опорного решениянеобходимо найти потенциалы. По признаку
оптимальности в каждой занятой опорным
решением клетке таблицы транспортной задачи
сумма потенциалов равна стоимости
(
ui v j cij при хij 0
).
Записываем систему уравнений для нахождения
потенциалов:
85.
u1 v1 1,u v 2 ,
2 1
u 2 v2 3,
u 2 v3 4,
u v 7 ,
3
3
u3 v4 12 ,
u 4 v4 0.
86.
Система состоит из семи уравнений и имеетвосемь
переменных.
Система
неопределенная. Одному из потенциалов
задаем значение произвольно: пусть и2 = 0.
Остальные
потенциалы
находятся
однозначно:
87.
u 2 0 ,v 2 u 2 0 2 ,
2
1
v2 3 u 2 3 0 3,
v3 4 u 2 4 0 4 ,
u
1
v
1
2
1
,
1
1
u3 7 v3 7 4 3,
v4 12 u3 12 3 9 ,
u 0 v 0 9 9.
4
4
88.
4. Проверяем опорное решение Х1 на оптимальность.С этой целью вычисляем оценки
ij
для всех незаполненных клеток таблицы
12 u1 v2 c12 1 3 2 0;
14 u1 v4 c14 1 9 1 7;
13 u1 v3 c13 1 4 3 0;
24 u 2 v4 c24 0 9 6 3;
89.
31 u3 v1 c31 3 2 3 2;41 u 4 v1 c41 9 2 0 7;
43 u 4 v3 c43 9 4 0 5.
32 u3 v2 c32 3 3 4 2;
42 u 4 v2 c42 9 3 0 6;
90.
5. Переходим к новому опорному решению.Находим клетку таблицы, которой соответствует
наибольшая положительная оценка:
max ij max{7,3,2,2}=7
ij
для клетки (1,4). Для этой клетки строим цикл. Ставим
в нее знак «+»
Цикл изображен в таблице.
91.
v1=2ai
Х
1
u1=-1
bj
100
u2=0
200
u3=3
300
u4=-9
200
v2=3
100
100
1
100
0
2
0+
2
3
-100
2
200
+
6
100 -
0
-
1
3
7
0
-
7
+
4
4
0
300
0
100
2
v4=9
300
3
3
-
v3=4
12
0
200
92.
Положительные оценки записываем в левыенижние углы соответствующих клеток
таблицы, вместо отрицательных ставим знак
«—». Начальное опорное решение не
является оптимальным, так как имеются
положительные оценки.
93.
В данном случае минимум перевозок в клетках,отмеченных знаком «-», достигался сразу в трех
клетках, поэтому для того, чтобы число занятых
клеток опорного решения было по-прежнему
равно т + п — 1 = 7, в клетки с номерами (1, 1) и
(2, 3) поставлены нулевые базисные перевозки.
Следует освобождать клетку с большей
стоимостью перевозки, т.е. клетку (3, 4).
Вычисляем значение целевой функции на втором
опорном решении:
F(X) = 0·1 + 100·1 + 100·2 + 100·3 + 0·4 + 300·7 +
200·0 = 2700.
94.
6. Проверяем второе опорное решение Х2 наоптимальность. Находим, потенциалы и оценки.
Решение не является оптимальным, так как
имеются положительные оценки Δ31=2, Δ32=2,
Δ42=1 и Δ43=2. Наибольшая из них равна 2
одновременно для трех клеток (3, 1), (3, 2) и (4, 3).
В одну из них, пусть в клетку (3, 2), ставим знак
«+». Для этой клетки строим цикл и находим
величину груза по циклу: θ=min{100,300}=100.
Осуществляем сдвиг по циклу на величину
θ=100. Получаем третье опорное решение Х3.
95.
v1=1Х3
bj
100
v3=3
100
v4=1
300
300
ai
u1=0
100
u2=1
200
u3=4
300
u4=-1
v2=0
1
0
2
1002
200
2
-
+
4
100
0
0
0
3
3
3
+
100
-200
0
-
1
100
4
6
-
7
12
-
0
2
0
200
96.
Вычисляем значение целевой функции натретьем опорном решении:
F(X3)= 0·1 + 100·1 + 100·2 + 100·4 + 100·4 + 200·7 +
200·0 =2500.
7. Решение не является оптимальным, так как
имеются положительные оценки Δ31=2 и Δ43=2.
Ставим знак «+» пусть в клетку (3, 1), Для этой
клетки строим цикл и находим величину груза
для
перераспределения
по
циклу:
θ=min{100,200}=100. Осуществляем сдвиг по
циклу на величину θ=100. Получаем четвертое
опорное решение Х4:
97.
v1=1Х4
bj
100
v3=3
100
300
v4=1
300
ai
u1=-2
100
u2=-3
200
u3=0
300
u4=-3
v2=0
1
0 -
2
0
2
3
2
3
1
100
+
4
6
7
12
0
0
200
3
100
+
200
0
4
100
0
1
100
0
4 +
200
98.
Вычисляем значение целевой функции начетвертом опорном решении: F(Х4) = 0·l + 100·1
+200·4+ 100·3 + 100·4+ 100·7 + 200·0 =2300.
8. Проверяем решение Х4 на оптимальность.
Находим потенциалы и оценки. Они приведены в
таблице. Положительными являются оценки Δ13=2,
Δ42=1 и Δ43=4. Для клетки (4, 3), которой
соответствует наибольшая оценка, строим цикл и
находим величину груза для перераспределения по
циклу: θ=min{200,0,100}=0. Осуществляем сдвиг по
циклу на величину θ=0. Получаем пятое опорное
решение Х5:
99.
Х5bj
v2=4
100
v3=7
300
v4=3
300
ai
u1=-6
100
u2=-3
200
u3=0
300
u4=-7
v1=3
100
1
-
2
-
2
-
3
3
200
6
-
7
100
0
-
100
200
100
1
4
4
0
-
-
-
100
3
12
-
0
-
0
200
100.
Решение Х5 является оптимальным, так как всеоценки отрицательные. Значение целевой
функции F(X5) = F(X4) = 2300.
Ответ: min F(Х)=2300 при
0 0 0 100
0 200 0
Х *= 0
100 100 100 0
.



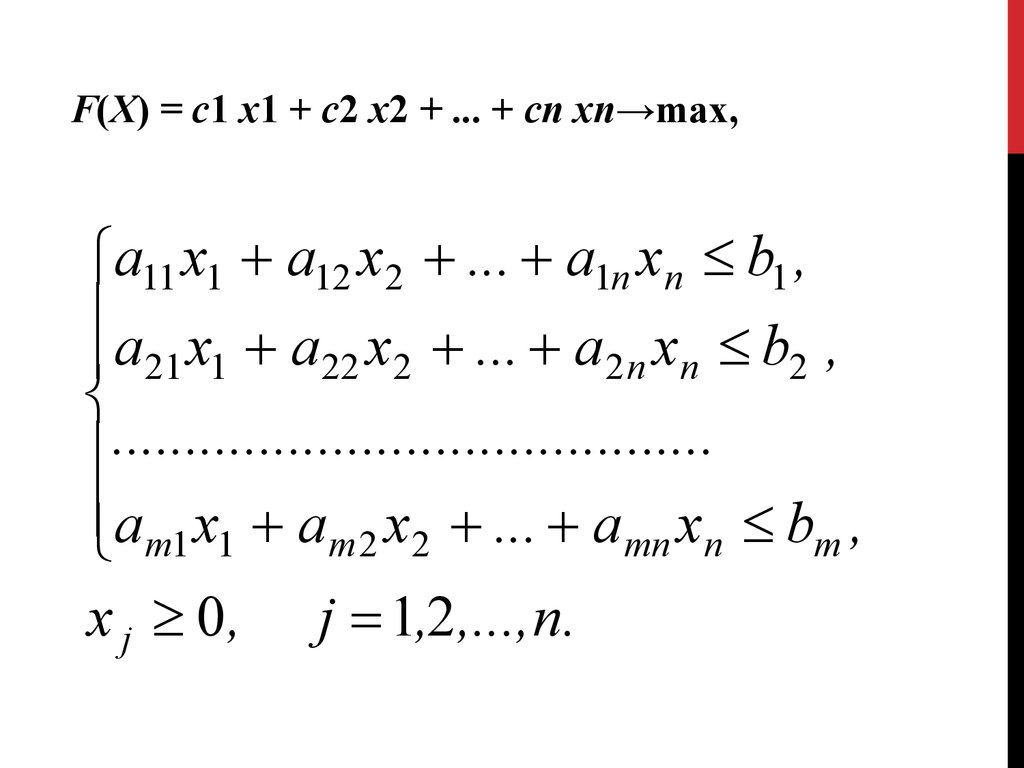









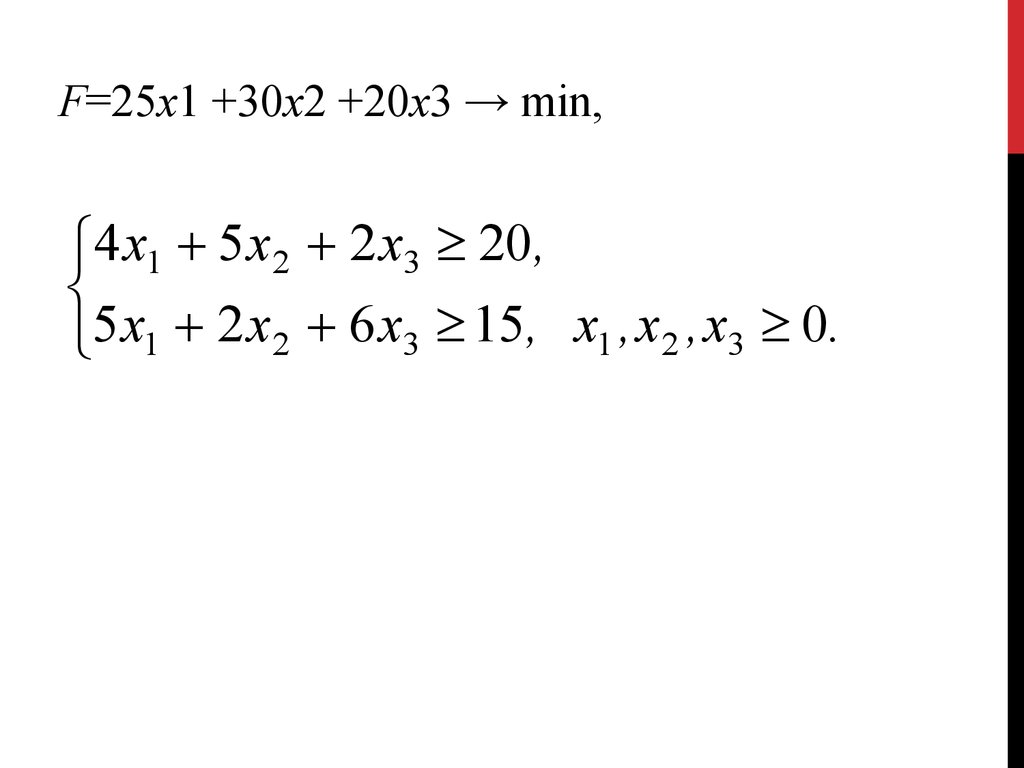


























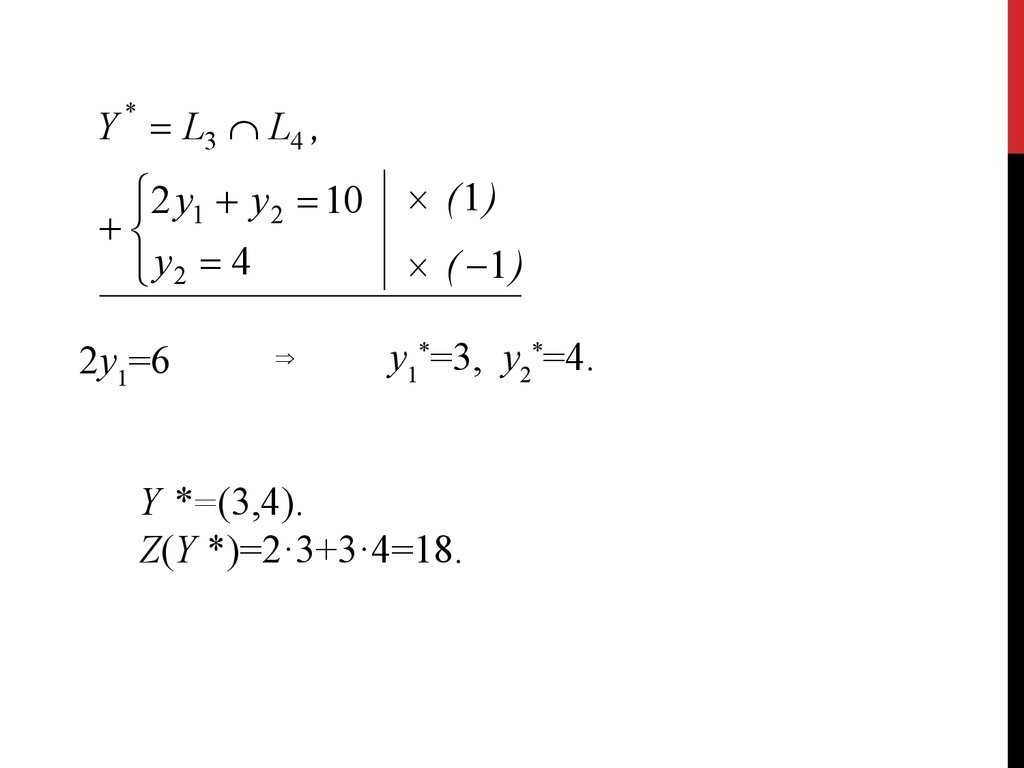







































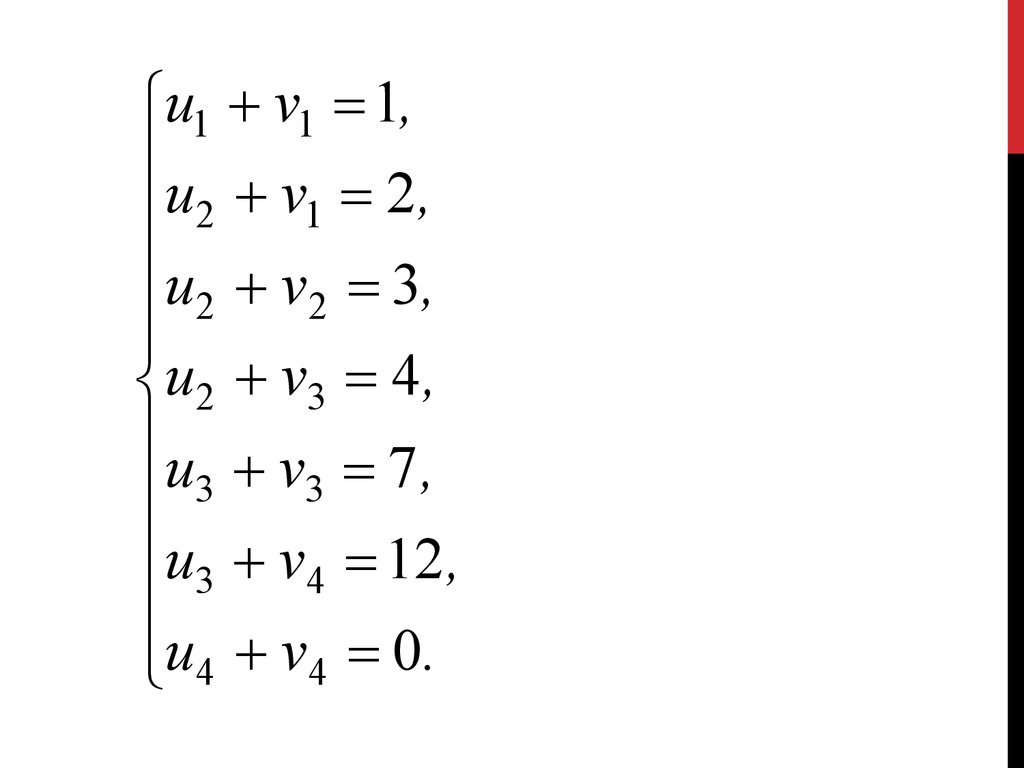

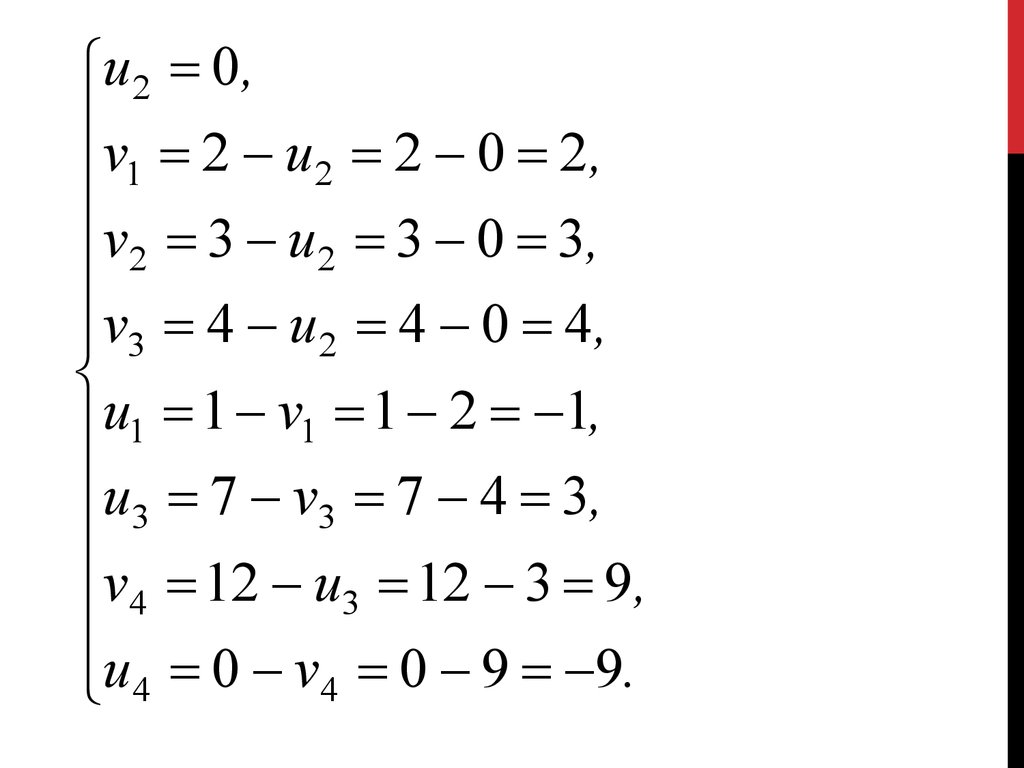

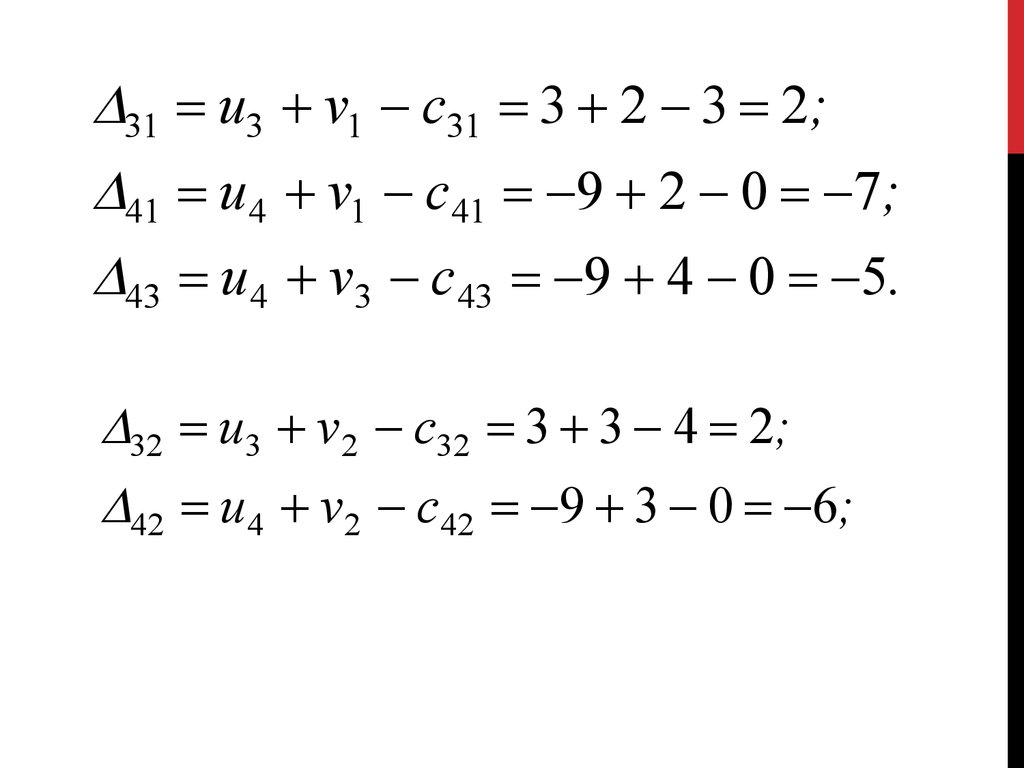










 mathematics
mathematics








