Similar presentations:
Математические методы принятия оптимальных решений
1. Математические методы принятия оптимальных решений
Элементы математическогопрограммирования
2. 1. Примеры задач математического программирования
1.1. Максимизация полезности набора п благ,приобретаемых по ценам p1 , p 2 ,..., p n при
ограниченном бюджете М:
U ( x ) U ( x1 ; x2 ;...; xn ) max
p1 x1 p2 x2 ... pn xn M
xi mi минимальный объем i - го блага (1 i n),
U ( x ) – полезность набора x ( x1 ; x2 ;...; xn ) .
3.
1.2. Минимизация издержек производства приобеспечении валового объема продукцииY0 :
w1 x1 w2 x2 ... wn xn min ,
A x1 1 x 2 2 ... x n n Y0
xi 0 (1 i n),
1 2
F ( x) A x1 x2 ... x n n – производственная функция,
wi – цена единицы i-го ресурса, используемого в
производстве, xi – его количество.
4.
1.3. Размещение ресурсов с наибольшей прибылью.Заемные средства банка и депозиты: 200 млн. €.
По уставу банка:
в кредитах размещается не менее 80 млн. €,
ликвидные активы (ценные бумаги: акции, векселя,…) –
не менее 40% размещенных средств (кредитов и ликвидов).
Средняя доходность операций с ценными бумагами – 15%,
прибыль от кредитов – 20% от вкладываемых средств.
Как разместить средства с наибольшей прибылью?
5.
1.5. Транспортная задача с минимизацией стоимости.Требуется перебросить 10 и 6 соединений к двум ТВД
с
трех
баз.
Для
переброски
одного
соединения
на первый театр требуется соответственно а, b, с часов,
а на второй театр – u, v, w часов;
транспортные расходы оцениваются в s тыс.$ в час.
Как найти наиболее экономичный план переброски
войск, если на базах мобилизовано соответственно
4, 5 и 7 соединений?
6.
s (ax1 bx 2 cx3 uy1 vy2 wy3 ) minx1 x2 x3 10,
y1 y2 y3 6,
x y 4,
1
1
x y 5,
2
2
x3 y3 7,
xi , y j 0.
1.6. Транспортная задача с минимизацией времени.
z max( a x1 , b x2 , c x3 , u y1 , v y2 , w y3 )
z min
при тех же ограничениях.
( x sgn x – знак числа x).
7. 2. Теоретические сведения
2.1. Существованиенаибольшего или
наименьшего значения
непрерывной функции
на множестве ,
x ( x1; x2 ;...; xn ) R n ,
: i ( x ) 0 (1 i k ),
( x ) 0 (1 j l ).
j
Теорема Вейерштрасса: Если функция f непрерывна на
ограниченном замкнутом множестве , то
x m , x M :
x f ( x m ) f ( x ) f ( x M ) , т.е. xm , x M –
точки нестрогого глобального минимума и максимума
функции f на множестве .
8.
называется ограниченным подмножествомR , еслиn
C : x x C , где x x12 x22 ... xn2 .
замкнуто, если содержит все точки своей границы;
n
x
R
точка
лежит на границе множества
( x ) , если в любой ее окрестности есть как точки
множества , так и точки, ему не принадлежащие.
Если функции i , j непрерывны (1 i k , 1 j l ) ,
то замкнуто.
9.
2.2. Необходимое условие экстремума гладкой функции.Пусть x * – внутренняя точка множества
( x* , x* ) .
Если
grad f ( x*) , x * – точка максимума или
минимума, то
grad f ( x*) 0 .
f
f f
grad f
;
; ... ;
xn
x1 x2
2.3.Условный экстремум (ограничения в виде равенств):
n
x R i ( x ) 0 (1 i k ) .
10.
k 1 : Если поверхность (x) 0 обладает вискомой точке
x * касательной плоскостью П, то
grad f ( x*) – иначе в П нашлось бы направление
f ( x*)
(grad f ( x*), e) 0 .
е, в котором f растет:
e
grad x L( x*, ) 0 , где L f – функция
Лагранжа.
11. 3. Три картинки
f ( x1, x2 ) c1x1 c2 x2 max .x1 x2 0,
x1 0.
12.
3.1.f ( x1, x2 ) x1 x2
3.2.
f ( x1, x2 ) x1 x2
3.3.
f ( x1, x2 ) x1 x2
Решений нет.
Бесконечно много
решений.
Единственное решение.
13. 4. Задачи линейного программирования (ЗЛП)
4.1. Определения.f ( x ) max (min)
Ω – множество
допустимых
планов (МДП).
x ( x1; x2 ;...; xn ),
n
(
x
)
0
(
1
i
k
),
x
R
i
( x ) 0 (1 j l ).
j
– Задача линейного программирования, если f , i , j
линейны:
f ( x ) c0 c1 x1 c2 x2 ... cn xn c0 (c , x ) c0 c x T
14.
x1c x T (c1; c2 ;...; cn ) x2
xn
4.2. Если f 0 , то grad f ( x ) (c1 ; c2 ;...; cn ) 0
постоянный вектор.
4.3.
i ( x) 0
пространстве R
n
задает
гиперплоскость i
, разбивающую его на две части:
в
i ( x ) 0
i ( x) 0
(
x
)
0
задает
полупространство
P
i
i ;
задает полупространство Pi ,
15.
i Pi Pi ;i , Pi , Pi – выпуклые множества.
Всякий
отрезок
полупространствах
с
Pi
концами
имеет
в
общую
разных
точку
гиперплоскостью i .
4.4. МДП Ω – пересечение 2l+k полупространств
–выпуклое многогранное множество (ВММ).
с
16.
Определения и комментарии.Множество
называется
выпуклым, если
u,v
1 u v .
0, 0
-- вместе с парой точек, принадлежащих множеству ,
ему принадлежит и всякая точка отрезка с концами в
этих точках.
Выпуклым многогранным множеством называется
пересечение семейства полупространств.
Обозначение:
x ( x1; x2 ;...; xn ) 0 x j 0 (1 i n)
17.
4.5. Основные формы ЗЛП:c1x1 c2 x2 ... cn xn max
a11x1 a12 x2 ... a1n xn b1
– симметрическая
...
...
...
(стандартная);
a x a x ... a x b
mn n
m
m1 1 m 2 2
x1, x2 , ... xn 0
то же в матричной записи:
c x max
Ax T b ,
x 0
T
а также:
c x min
Ax T b
x 0
T
18.
c x T max/ minAx T b
– каноническая.
x 0
a11 a12
b1
b
a21 a22
b 2 b , A
... ...
b
m
a
m1 am2
... a1n
... a2n
... ...
... amn
19.
4.6. ai j x j bi ai j x j xn i bij 1
j 1
xn i 0 –
n
n
ai j x j bi ai j x j xn i bi балансовая
переменная.
j 1
j 1
4.7. x j R (без ограничения x j 0 )
x j x j x j , x j , x j 0 .
n
n
4.8. min f ( x ) c0 min (c x ) c0 max (( c ) x )
T
x
x
T
x
max f ( x ) c0 min (( c ) x T ) .
x
x
20.
4.9. Пример. 3 x1 x2x2 5 x3 3
4 x1 2 x2 7
x 6
2
x1 , x2 0
8 x3 min
x3 x3 x3 : x3 , x3 0;
4x – балансовые
x переменные;
5
3 x1 x2 8 x3 8 x3 max
x2 5 x3 5 x3 3
4 x1 2 x2 x4 7
x2 x5 6
x1 , x2 , x3 , x3 , x4 , x5 0
21. 5. Свойства множества допустимых планов ЗЛП
5.1. Пусть ВММ Ω задается системой m линейныхнеравенств
Ax b
T
Ax T b
x
x
– все неравенства строгие
(х – внутренняя точка);
– хотя бы одно неравенство
превратилось в равенство
(х – граничная точка).
22.
5.2. Определение. Точка x называется вершинойВММ Ω (угловой точкой), если она не является
внутренней точкой никакого отрезка с концами в Ω:
x u v ,
1; 0, 0; u v (u,v ) .
5.3.Замечание. Вершины ВММ R , задаваемого
системой неравенств, получаются так:
(i) выбирают п неравенств системы, заменяют на =;
(ii) решают эту систему п уравнений с п неизвестными;
(iii) если ее решение х единственно и x ,
то х – вершина Ω.
n
23.
5.4. Утверждение. Пусть v1 , v 2 ,...v p – все вершиныограниченной ВММ Ω, тогда
1v1 2 v 2 ... p v p 1 2 ... p 1, i 0
– выпуклая линейная оболочка множества своих вершин;
такая ВММ называется выпуклым многогранником.
5.5. Теорема. Если и f ограничена на Ω, то
(i) существует хотя бы одно решение ЗЛП
f ( x ) max(min)
x
;
24.
(ii) если при этом Ω имеет хотя бы одну вершину,то некоторое решение ЗЛП является вершиной.
называемой оптимальной;
(iii) так будет, если Ω ограничено, и тогда множество
всех решений ЗЛП является выпуклой линейной
оболочкой семейства всех оптимальных вершин.
– Среди всех вершин v1 , v 2 ,...v p надо найти те, на
которых f принимает оптимальное значение
max/ min f (v1 ), f (v 2 ),... f (v p ) .
x
25. 6. Двойственность в линейном программировании.
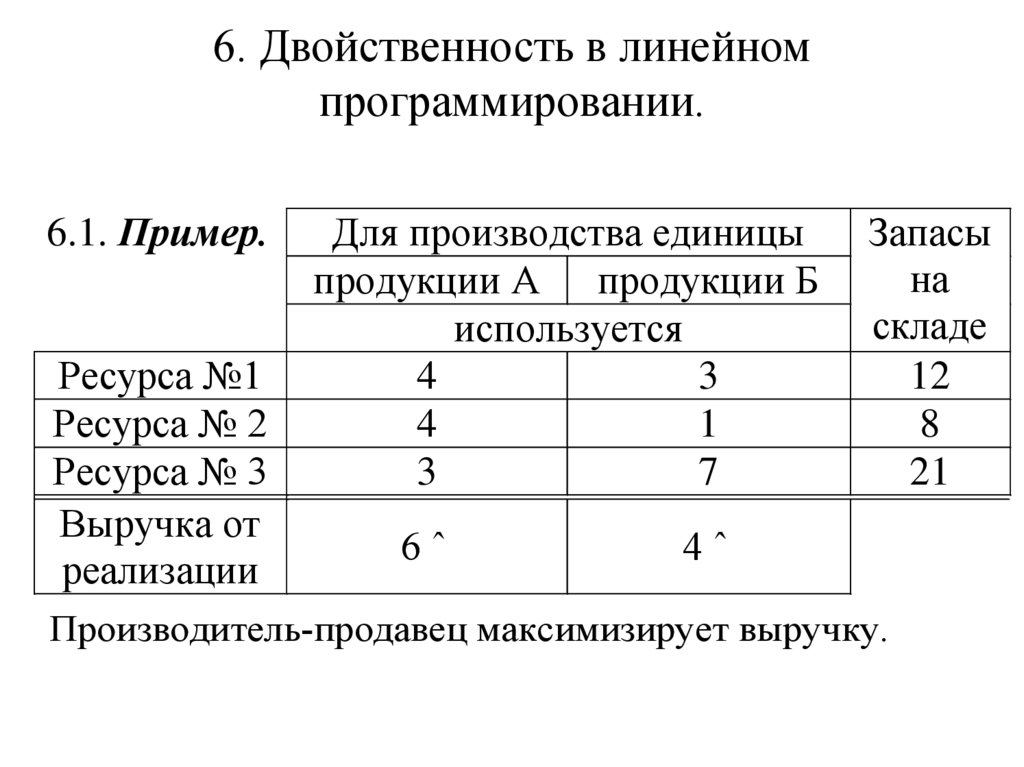
6.1. Пример.Ресурса №1
Ресурса № 2
Ресурса № 3
Выручка от
реализации
Для производства единицы
продукции А продукции Б
используется
4
3
4
1
3
7
6ˆ
Запасы
на
складе
12
8
21
4ˆ
Производитель-продавец максимизирует выручку.
26.
f x1; x2 6 x1 4 x2 max :4 x1 3 x2 12;
4 x1 x2 8;
3 x 7 x 21;
2
1
x1 , x2 0.
( x1; x2 ) – план
производства.
Производитель выступает как продавец ресурсов –
готов продать их целиком лишь когда выручит за них
не менее, чем за произведенную из них продукцию.
27.
12 y1 8 y2 21y3 min4 y1 4 y2 3 y3 6
3 y1 y2 7 y3 4
y1 , y2 , y3 0
y1 , y2 , y3 –цены в €
за единицу ресурса.
Пара двойственных задач:
c x max
A x b
:
x 0
y b min bT y min
y A c AT y c
:
y 0 y 0
28.
4A 4
3
c (6 ,
3
12
1 , b 8
7
21
4)
4
4
3
T 6
A
,c
3 1 7
4
T
b (12, 8, 21)
T
29.
Теоремы двойственности6.2. Для любых допустимых планов x, y c x y b
(вся выручка не превосходит суммарной оценки ресурсов).
4 y1 4 y2 3 y3 6... x1
3 y1 y2 7 y3 4... x2
y1 ( 4 x1 3 x2 ) y 2 ( 4 x1 x2 ) y3 (3 x1 7 x2 )
6 x1 4 x2 ,
т.е. y A x c x ;
аналогично A x b y A x y b
c x y A x y b .
30.
cx
y
b
x
,
y
6.3. Если
(
),
то x, y – оптимальные планы.
6.4. Если в одной задаче ЦФ неограничена,
то МДП двойственной задачи пусто.
6.5. Основная теорема. Если имеет решение одна
задача, то разрешима и другая и
max (c x ) min ( y b ) .
x
y
6.3 – необходимое и достаточное условие
оптимальности допустимых планов.
31.
6.6. Теорема равновесия.x , y – оптимальны
( y a j c j ) x j 0 (1 j n)
yi (bi ai x ) 0 (1 i m)
yb c x 0
Условия
дополняющей
нежесткости.
(yb y Ax ) (y Ax c x ) 0
y (b A x ) ( y A c ) x 0
все cлагаемые
неотрицате льны
каждое слагаемое = 0.
32.
y ajxj
cj
0 y
xj
aj
0 (j-е изделие убыточно),
c j ; yi
0 bi ai x ;
ai x bi yi 0 (оценка избыточного ресурса =0).
6.7. Дополнительное увеличение на ε дефицитного
y
ресурса № i увеличит выручку на i :
f ( x*)
yi .
bi
Принудительный выпуск δ единиц убыточной продукции
№ j уменьшит оптимальную выручку на ( y * a j
c j ).
33.
6.8. Пример.Решили задачу графически:
f ( x1; x2 ) 6 x1 4 x2 ; f max f (1.5; 2) 17 .
x3 12 4 x1 3x2 ; -- ввели балансовые переменные
x4 8 4 x1 x2 ;
x 21 3x 7 x x* (1.5; 2; 0; 0; 2.5)
1
2
5
x1 ,..., x5 0
g ( y1; y2 ; y3 ) 12 y1 8 y2 21 y3
y4 4 y1 4 y2 3 y3 6;
y5 3 y1 y2 7 y3 4 ;
y1 ,..., y5 0.
34.
основныебалансовые
x1 0 x2 0 x3 x4 x5 0
y5 y1 y2 y3
y4
балансовые
x1 0 6.6.
x2 0
x5 0
– всюду *.
основные
y4 0
y5 0 ;
y3 0 -- третий ресурс недефицитен.
35.
0 4 y1 4 y2 3 0 6;0 3y y 7 0 4 y 4 3y
2
1
1
2
4 y1 4(4 3 y1 ) 6 0 y1 1.25 ; y2 0.25 .
y* (1.25; 0.25; 0; 0; 0)
g min y *b 12 1.25 8 0.25 17 .
36.
6.9. Другие формы двойственности.c x max
y b min
A x b
x 0
y A c
n
y R
c x min
y b max
A x b
x 0
y A c
n
y R
37.
Замечания о предмете.Математическое программирование – научная дисциплина,
изучающая теорию и методы решения экстремальных задач
– часть науки об исследовании операций, т.е. о построении,
разработке и приложениях математических моделей
принятия оптимальных решений.
Средством достижения цели часто служит оптимизация
количественных показателей (целевых) этой деятельности –
достижение масимальных или минимальных
(экстремальных) значений этих показателей.
38.
Стадии (этапы) работы над проблемой:1. Формулировка задачи.
2. Разработка математической модели изучаемой
системы.
3. Отыскание решения задачи в рамках выбранной
модели.
4. Проверка выбранной модели и решения.
5. Уточнение модели и решения.
6. Практические применения.


















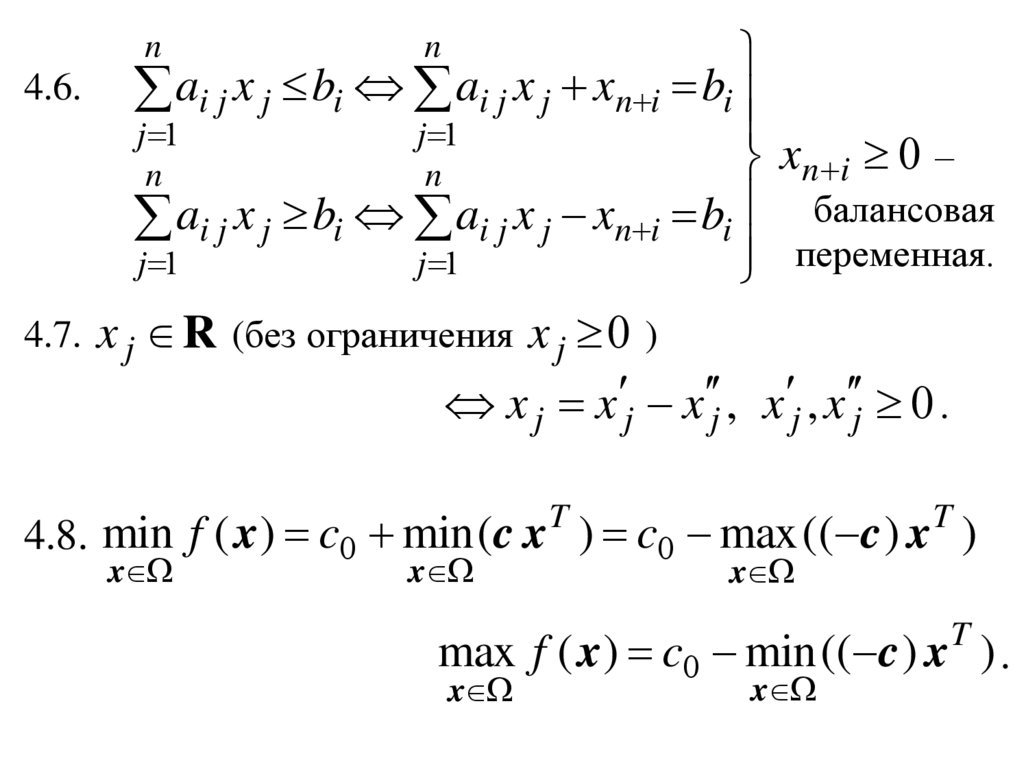







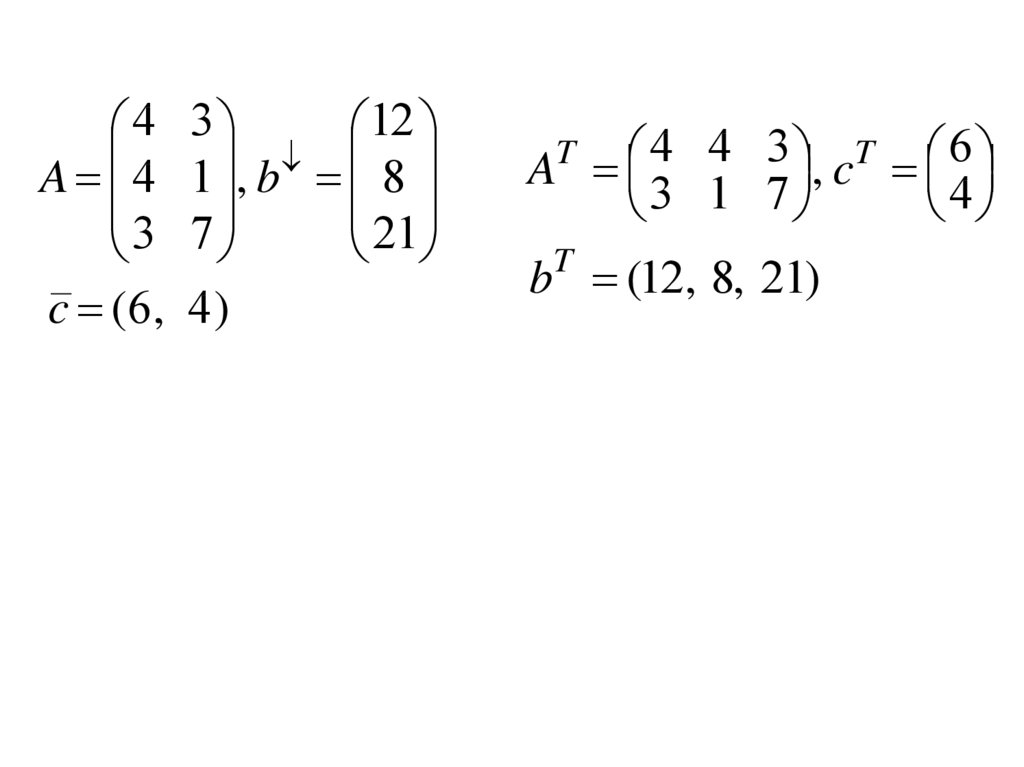






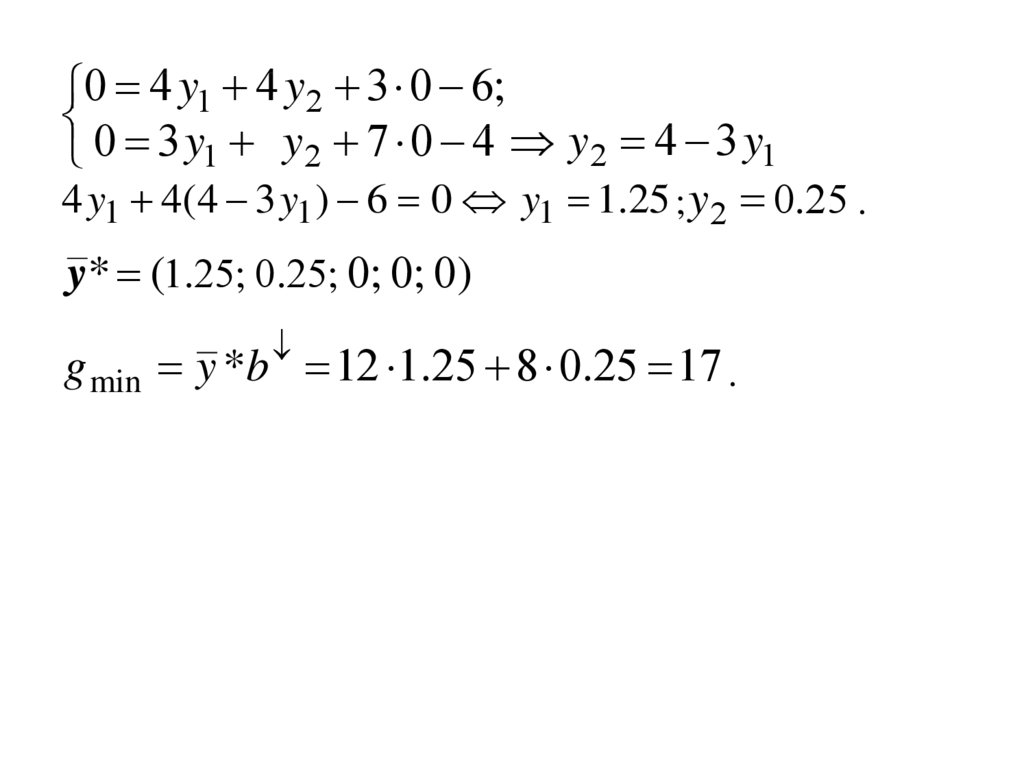



 mathematics
mathematics








