Математические методы исследования экономики (математическая экономика)

1. Математические методы исследования экономики (математическая экономика)

2006-07 учеб. год, семестр II, зачет
Преп. Мунипов Рафаил
1

2. Литература

• Аллен Р. Математическая экономика.
• Альсевич В.В. Введение в математическую экономику.
Конструктивная теория.
• Ашманов С.А. Введение в математическую экономику.
• Интрилигатор М. Математические методы оптимизации и
экономическая теория.
• Канторович Л.В. Горстко А.Б. Оптимальные решения в экономике.
• Кевеш П. Теория индексов и практика экономического анализа.
• Клейнер Г.Б. Методы анализа производственной функции.
• Колемаев В.А. Математическая экономика.
• Ланкастер К. Математическая экономика.
• Никайдо Х. Выпуклые структуры и математическая экономика.
• Петров А.А., Поспелов И.Г., Шананин А.А. Опыт математического
моделирования экономики.
2

3.

Производственная функция
Функциональная зависимость F определяющая взаимосвязь
между производимой продукцией X и факторами
X1, X 2 ,
, Xn
ее обеспечивающими называется производственной функцией.
X F ( X1, X 2 ,
, Xn)
Отсутствие любого фактора производства с необходимость
обуславливает невозможность выпуска продукции
i : F
X i 0
0
3

4.

Неограниченность любого фактора производства с обуславливает
неограниченность выпуска продукции
i : lim F
X i
Рост любого фактора производства с необходимостью влечет
увеличение выпуска продукции
F
i :
0
X i
4

5.

С ростом любого фактора производства его значимость для
увеличения выпуска продукции убывает (закон Госсена
убывающей эффективности)
F
1 F 2 F
2 F
2 F
i : 2 0
Xi
1 F
X i
X i
Xi
5

6.

1. i : F
X i 0
0
2. i : lim F
X i
F
3. i :
0
X i
2 F
4. i : 2 0
Xi
Производственная функция удовлетворяющая условиям 1-4
называется неоклассической
K основные фонды
L труд (трудозатраты)
F ( K , L) AK 1 L 2
Мультипликативная
производственная функция
6

7.

F ( K , L) AK 1 L 2
F ( K , L) K 0 AK 1 L 2
F ( K , L) L 0 AK 1 L 2
K 0
L 0
0
0
F
F ( K , L)
K
K
F
F ( K , L)
L
L
1 2
2
1
F ( K , L)
AK
L
AL
K
K
K
K
1 2
AK
L
F
1 1 2
AK L
0
K
K
1 0
1 2
1
2
F ( K , L)
AK
L
AK
L
L
L
L
2 0
1 2
AK L
F
1 2 1
AK L
0
7
L
L

8.

1 2
2
lim F lim AK L AL lim K
K
K
K
1
1 0
lim F lim AK 1 L 2 AK 1 lim L 2 2 0
L
L
L
2
2
1 2
1 2
F ( K , L)
AK L
AK L
2
2
K
K
K K
1 1 2
2
1 1
AK
L
AL
K
K
K
1
K 2
2
1 2
AL 1 1 K
1 1 A 2 L
K
F
1 1 2 0
K
1 1 0
1 1
8

9.

2
2
1 2
1 2
F ( K , L) 2 AK L
AK L
2
L
L
L L
1 2 1
1
2 1
AK L AK
L
L
L
AK 1 2 1 L 2 2 2 1 AK 1
L 2
2
L
F
2 1 2 0
L
2 1 0
2 1
9

10.

0 1 1
F
F ( K , L)
K
0 2 1 K
F L const
K
F
K
F L const
F
F
F
K
K
K
K
F F
L const
K K
Параметр 1 характеризует отношение относительного прироста
производственной функции F (или выпуска продукции) к
относительному приросту основных фондов K при условии
постоянства трудозатрат L .
Параметр 1 называют коэффициентом эластичности по
фондам, который определяет на сколько процентов изменится
выпуск продукции X при увеличении основных фондов K
на один процент
10

11.

0 1 1
F
F ( K , L)
L
0 2 1 L
F K const
L
F
L
F K const
F
F
F
L
L
L
L
F F
K const
L L
Параметр 2 характеризует отношение относительного прироста
производственной функции F (или выпуска продукции) к
относительному приросту трудозатрат L при условии
постоянства основных фондов K .
Параметр 2 называют коэффициентом эластичности по
труду, который определяет на сколько процентов изменится
выпуск продукции X при увеличении трудозатрат L на один
процент
11

12.

0 1 1
Типы экономик
0 2 1
Эластичности по факторам производства
1 2
Экономика называется
трудосберегающей, когда
эластичность по фондам больше
эластичности по труду. Суть такой
экономики в том, что наибольшую
значимость для прироста выпуска
продукции имеют фонды
2 1
Экономика называется
фондосберегающей, когда
эластичность по труду больше
эластичности по фондам. Суть такой
экономики в том, что наибольшую
значимость для прироста выпуска
12
продукции имеет труд

13.

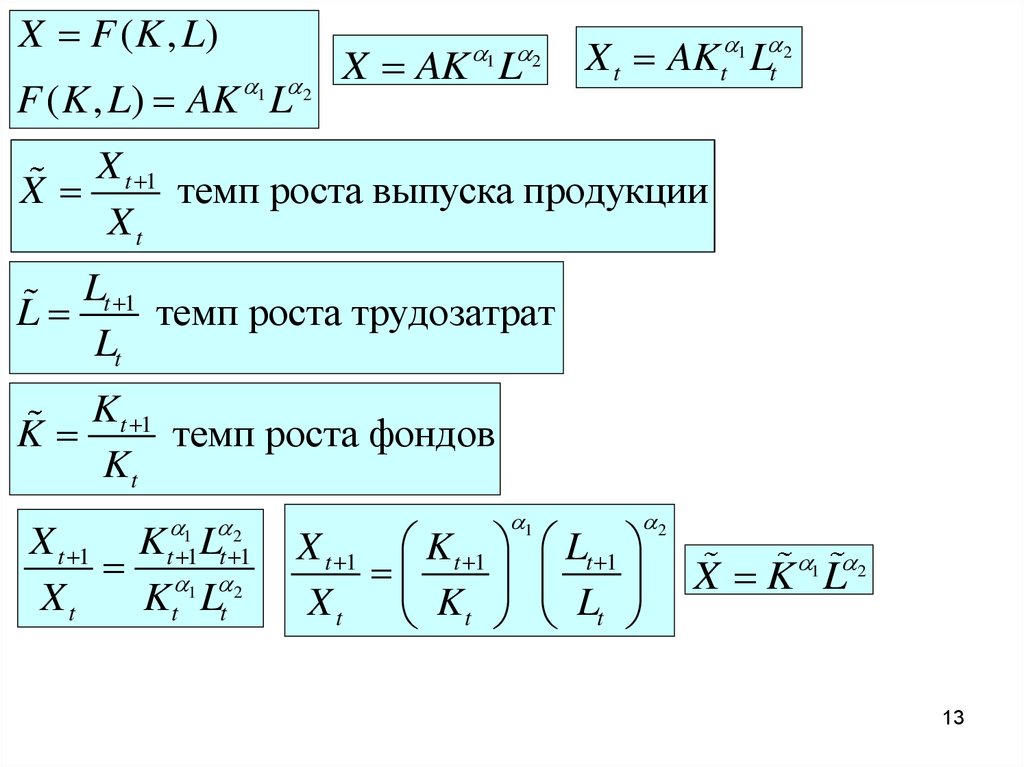
X F ( K , L)
1 2
F ( K , L) AK L
1 2
X AK L
X t AKt 1 L t 2
X t 1
X
темп роста выпуска продукции
Xt
Lt 1
L
темп роста трудозатрат
Lt
Kt 1
K
темп роста фондов
Kt
1
2
X t 1 Kt 1Lt 1
1 2
Xt
Kt Lt
1
2
X t 1 K t 1 Lt 1
X t K t Lt
X K 1 L 2
13

14.

1
1 2
X t AK t Lt
2
X t 1 Kt 1 Lt 1
1 2
Xt
Kt Lt
X t 1 AKt 11 L t 21
1
2
X t 1 K t 1 Lt 1
X t K t Lt
1 2
X t 1
X
K
L
X
темп роста выпуска продукции
Xt
K t 1
K
темп роста основных фондов
Kt
Lt 1
L
темпы роста трудозатрат
Lt
X
1
1 2
1 2
K
1
1 2
X K
2
1 2
L
1
1 2
2
1 2
L
1
1 2
2
1
1 2
Выражение
для темпов
роста выпуска
продукции
через темпы
роста
факторов
производства
14

15.

X K 1 L 2
X
1
1 2
K
1
1 2
2
1 2
L
Темп роста выпуска продукции
определяется темпами роста
факторов производства
1
1 2
Относительный (приведенный) коэффициент
эластичности по фондам
2
1 2
Относительный (приведенный) коэффициент
эластичности по труду
1
2
1
1 2 1 2
X
1
1 2
K L1
1
15

16.

X
1
1 2
K
1
1 2
2
1 2
L
1
1 2
2
1
1 2
1 2
X K L1
Приведенный коэффициент
эластичности по фондам
Приведенный коэффициент
эластичности по труду
Корень степени суммы эластичностей
по факторам производства из темпов
роста выпуска продукции равен
произведению темпов роста факторов
производства со степенями равные
приведенным коэффициентам
эластичности соответствующего
фактора
16

17.

1 2
X K L1
1 2 1
1 2
X X
1
1 2
X K 1 L 2
1 2 1
1 2
X X
1
1 2
X K 1 L 2
Сумма эластичностей по
факторам производства
больше единицы, тогда
увеличение факторов
производства на один процент
влечет увеличение выпуска
продукции более чем на один
процент
Сумма эластичностей по
факторам производства
меньше единицы, тогда
увеличение факторов
производства на один процент
влечет увеличение выпуска
продукции менее чем на один
процент
17

18.

Виды экономик
Эластичности по фактора производства
1 2
Экономика называется прогрессивной:
увеличение факторов производства на
1 один процент влечет увеличение выпуска
продукции более чем на один процент
1 2
Экономика называется регрессивной:
1 увеличение факторов производства на
один процент влечет увеличение выпуска
продукции менее чем на один процент
1 2
Экономика называется экономикой
Дугласа-Коба: увеличение факторов
1 производства на один процент влечет
увеличение выпуска продукции на один
процент
18

19.

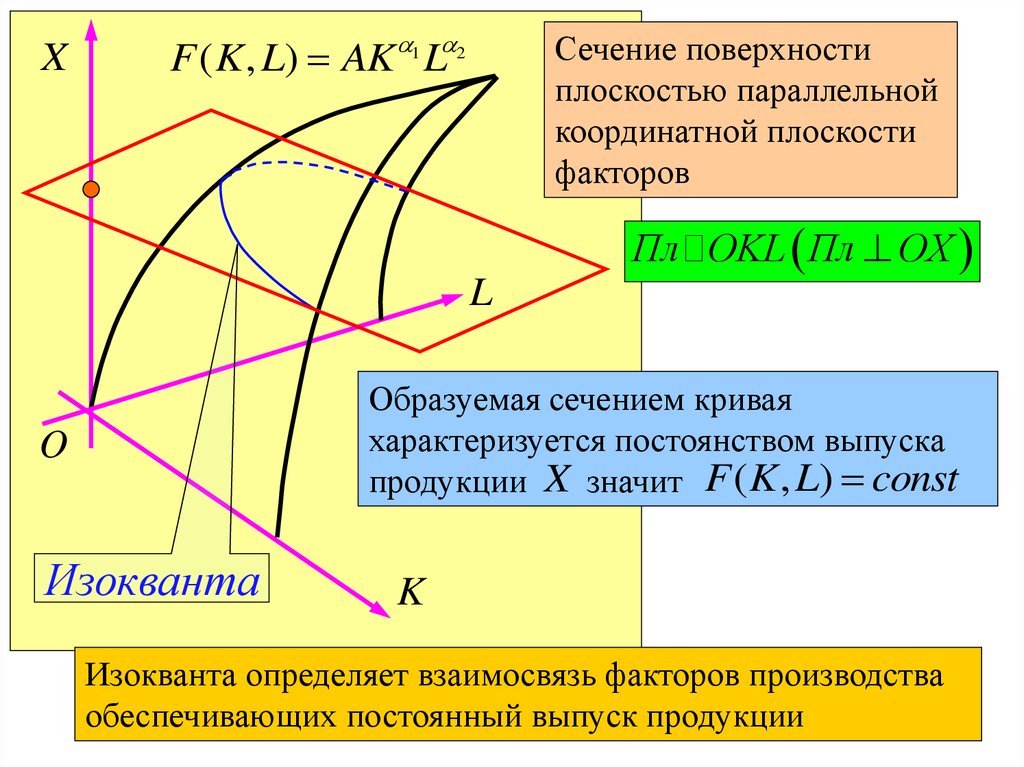
X
F ( K , L) AK 1 L 2
Сечение поверхности
плоскостью параллельной
координатной плоскости
факторов
Пл OKL Пл OX
L
Образуемая сечением кривая
характеризуется постоянством выпуска
продукции X значит F ( K , L) const
O
Изокванта
K
Изокванта определяет взаимосвязь факторов производства
19
обеспечивающих постоянный выпуск продукции

20.

F ( K , L) AK 1 L 2
1 2
AK
L
F ( K , L) ( const )
1 2
K L
L
K 1 L 2
2
K 1 L 2
Характер изоквантных кривых
мультипликативной
производственной функции
соответствует гиперболической
зависимости
K 1 L 2
3
K 1 L 2
O
A
1
K
20

21.

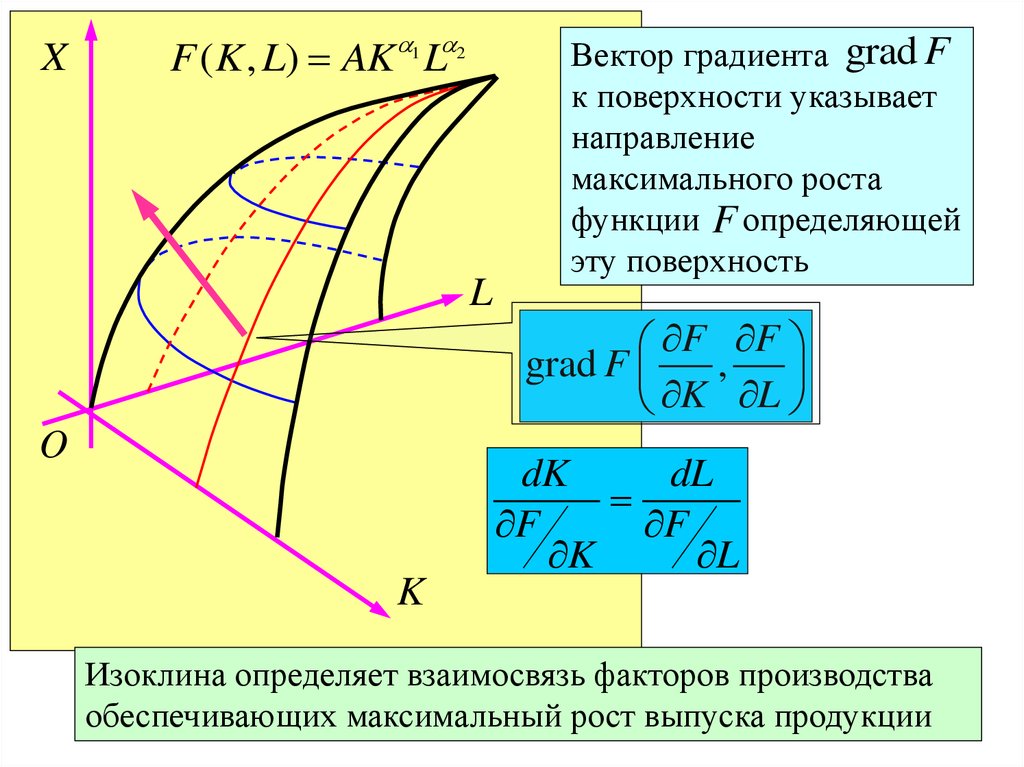
X
F ( K , L) AK 1 L 2
L
O
Вектор градиента grad F
к поверхности указывает
направление
максимального роста
функции F определяющей
эту поверхность
F F
grad F
,
K
L
dK
dL
F
F
K
L
K
Изоклина определяет взаимосвязь факторов производства
обеспечивающих максимальный рост выпуска продукции 21

22.

dK
dL
F
F
K
L
1
1
dK
dL
F
F
1
2
K
L
1
LdL
2
1
2
KdK
LdL
KdK
LdL
K
1
2
1
2
2 1
2 2
L
K
1
1
KdK
1
1L2 2 K 2
L
L2
2
K2
1
1 2
L
2 2
1
1
L K
2
K
Главная изоклиналь
22

23.

X
1
1 2
K L1
X EM
Интенсивное увеличение
выпуска продукции есть
повышение эффективности
использования ресурсов,
факторов производства, что
можно назвать
эффективностью
производства или
эффективностью.
M M K, L
1
M K L
Экстенсивное увеличение
выпуска продукции есть
увеличение затрат
ресурсов, факторов
производства, что можно
назвать увеличением
масштаба производства
или масштабностью.
X EK L1
23

24.

X
E 1
K L
1
X EK L
1
X X
E 1
K L
X X 1
E 1
K L
1
X X
E
K L
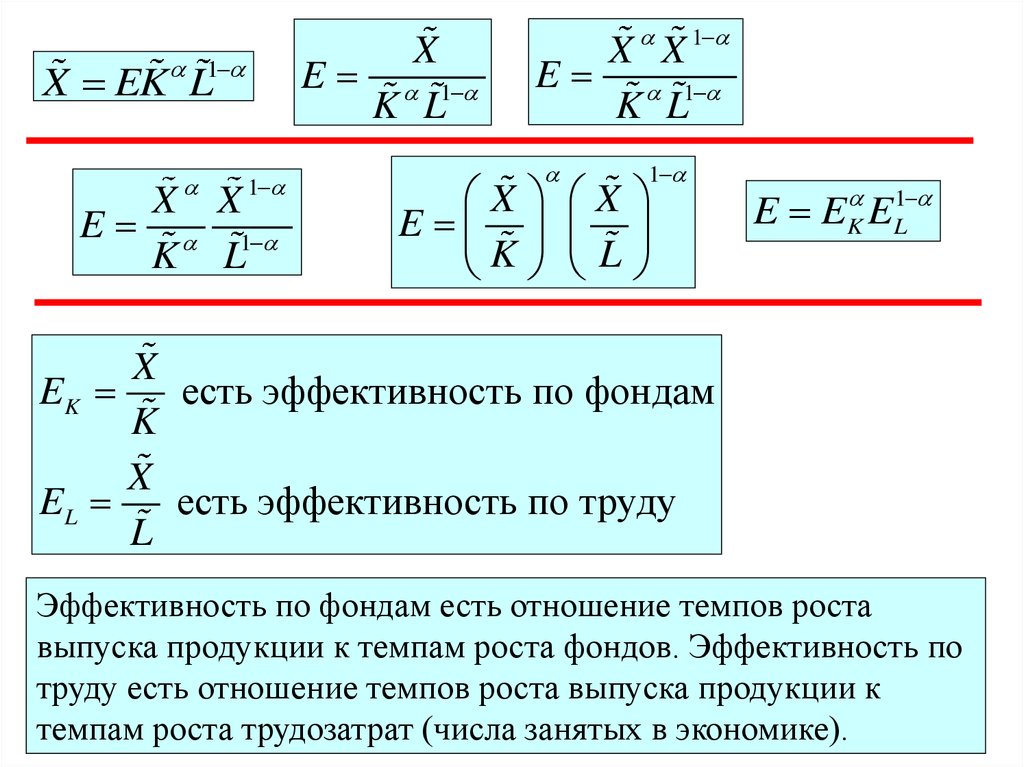
E EK EL1
X
EK
есть эффективность по фондам
K
X
EL
есть эффективность по труду
L
Эффективность по фондам есть отношение темпов роста
выпуска продукции к темпам роста фондов. Эффективность по
труду есть отношение темпов роста выпуска продукции к
24
темпам роста трудозатрат (числа занятых в экономике).

25.

За рассматриваемый период времени для экономики с
X 2,655,
производственной функцией
F ( K , L) 2,38K 0,567 L0,683
K 1,94
выпуск продукции увеличился в 2,655 раз, при этом
L 2, 41
основные фонды увеличились в 1,94 раза, соответственно
трудозатраты в 2,41 раза.
X 2,655
эффективность фондов: EK
1,369
K
1,94
X 2,655
эффективность трудозатрат: EL
1,102
L
2,41
1
0,567
0, 4536
1 2 0,567 0,683
1 0,5464
Приведенные
эластичности по
фондам и труду 25

26.

E EK EL1
E 1,3690,45361,1020,5464 1,216 X 2,655,
K 1,94
0,4536
0,5464
M
1,94
2,41
2,184 L 2, 41
M K L
EM 1,126 2,184 2,655
1
E
1,126
E
0,352 (35,2%)
E M 1,126 2,184
M
2,184
M
0,642 (64,2%)
E M 1,126 2,184
Доля
эффективности
факторов
производства в
увеличении
выпуска
продукции
Доля
масштабности
производства в
увеличении
выпуска
продукции
26

27.

t
время
x x (t )
переменная величина (экономический показатель)
зависящая от времени t
x
изменение (прирост) за время t
x
x
относительный прирост (темп) равный (const )
x
t
x
x
x
t
x
lim
x
t 0 t
xt x x x
При постоянных темпах скорость изменения величины
пропорциональна самой величине с коэффициентом
пропорциональности равный постоянному темпу
27

28.

x
x x Координатная плоскость, ось
ординат которой есть скорость
изменения переменной по времени
от переменной на оси абсцисс
называется фазовой плоскостью
0
x
0
Для величины с постоянным
темпом фазовая кривая есть
прямая проходящая через
начало координат
dx
x dt ln x t ln
Линия на фазовой плоскости
определяющая взаимосвязь
скорости изменения величины от
самой этой величины называется
фазовой кривой
dx
x
x x
dt
ln x ln
t
dx
dt
x
ln
x
t
28

29.

ln
x
x
t
t 0 : x t 0 x0
e t
x e t
x0 x t 0 e
0
x
x x0e t
x0
x x
0
x
0
x
0
0
t
При постоянном темпе показатель
по времени изменяется
29
экспоненциально

30.

t
время
x x (t )
переменная величина (экономический показатель)
зависящая от времени t
x
изменение (прирост) за время t
x
x
относительный прирост (темп) линейно убывает
относительно переменной x ( , const )
x
x t
x
x
x
x x lim
x x
t 0 t
t
xt x x
x x x
30

31.

x x x
При линейно убывающих темпах скорость
изменения величины определяется
параболической кривой
x
4
2
0
xmax
2
x
2
при x
4
x x x x
2
x
2
2
=
2 2 4
Фазовая кривая для величины с
линейно убывающим темпом
есть параболическая кривая,
ветви которой направлены вниз
и пересекают ось абсцисс в
точках 0 и .
31

32.

dx
x x x
x x
dt
dx
1 kx x
dt
dx
1
dt
dx
1 kx x
dt
dx
dx
1 kx x dt t 1 kx x
x x
k
dx
dt
1 kx x
1
1
k
1 kx x x 1 kx
dx
kdx
k
1
t
dx t x 1 kx
x 1 kx
t ln x ln 1 kx ln
t ln
x
1 kx
x
e t
1 kx 32

33.

x0
x
t
e t 0:
e0
1 kx
1 kx0
x0
1 kx0
выпуск продукции в начальный
t 0 : x x0
момент времени
x
1 kx e
t
e t
x
1 ke t
xпр lim x lim
t
t
t
x e kxe
x(t )
e t
e
t
k
1
k k
t
x 1 ke t e t
Предельное значение
величины с линейно
убывающими темпами
есть величина
постоянная не
зависящая от времени
33

34.

x(t )
e
t
k
x0
1 kx0
Определим условия
монотонности, когда величина
возрастает и убывает
x x x
x 0
x (t ) возростает x 0 :
x 0
1
x xпр
k
x 0
x (t ) убывает x 0 :
x 0
1
x xпр
k
34

35.

x(t )
e
t
k
x0
1 kx0
Определим условия
выпуклости вогнутости кривой
графика функции.
x x x
d
x x x x 2 xx 2 x x
dt
x 2 x x x
x 0 x(t ) выпукла вниз
x 0 x(t ) выпукла вверх
35

36.

x 2 x x x
x 0
a) x
x
2
x 0
a ) x 0
2 x 0
x (t ) выпукла вниз x 0 :
x 0
b) x 0
2 x 0
x 0
1 xпр
a) x
b) x
2
2
2
k
1
x
b) x xпр
2
k
36

37.

x 2 x x x
x 0
x 0
a ) x 0 a ) x
2 x 0
x (t ) выпукла вверх x 0 :
x
0
x
2
b) x 0
x
0
2 x 0
b) x xпр
xпр
a)
x xпр
2
2
xпр Невозможно
x
2
2 одновременное
xпр
a)
x xпр
исполнение этих
37
2
двух неравенств

38.

x(t )
e t k
x0
1 kx0
xпр
xкр
2
2
xпр
x
x0
Кривая насыщения
xпр
x0
xкр
Точка перегиба,
изменения направления
графика функции
x0
t
tкр
38

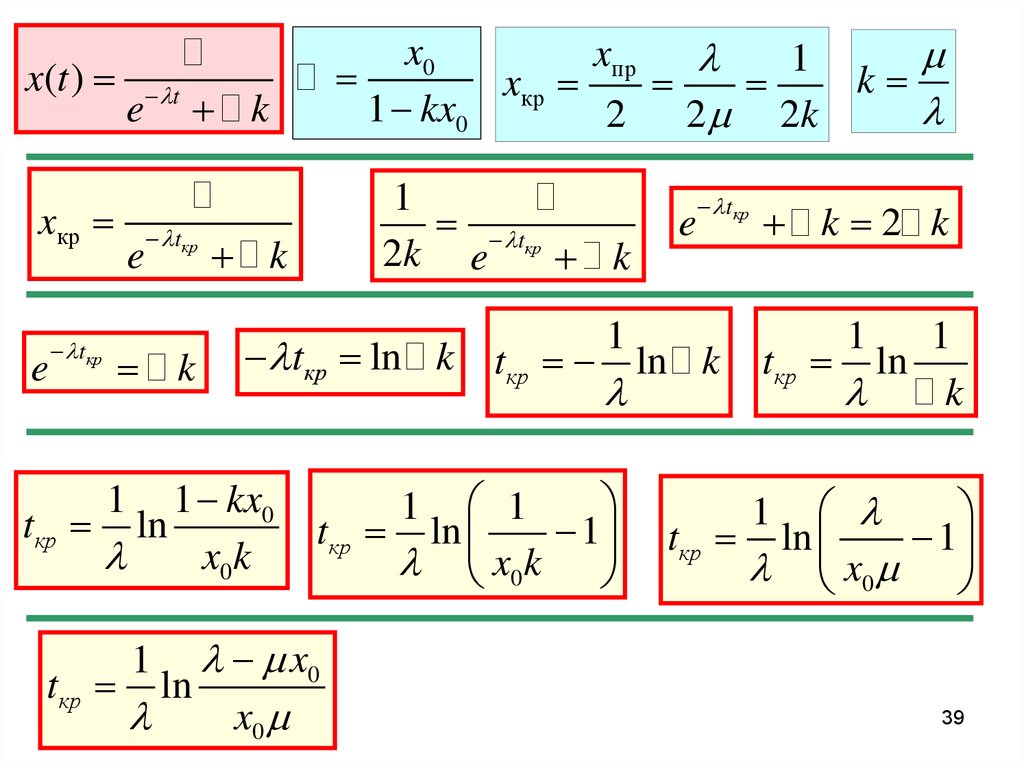
39.

x(t )
e t k
xкр
e
tкр
x0
xпр
1
k
xкр
1 kx0
2
2 2k
e
tкр
k
k
tкр ln k tкр
1 kx0
tкр ln
x0 k
1
1
tкр
2k e
k
1
1
tкр ln
1
x0 k
x0
tкр ln
x0
1
e
tкр
ln k
k 2 k
1
1
tкр ln
k
tкр ln
1
x0
1
1
39

40.

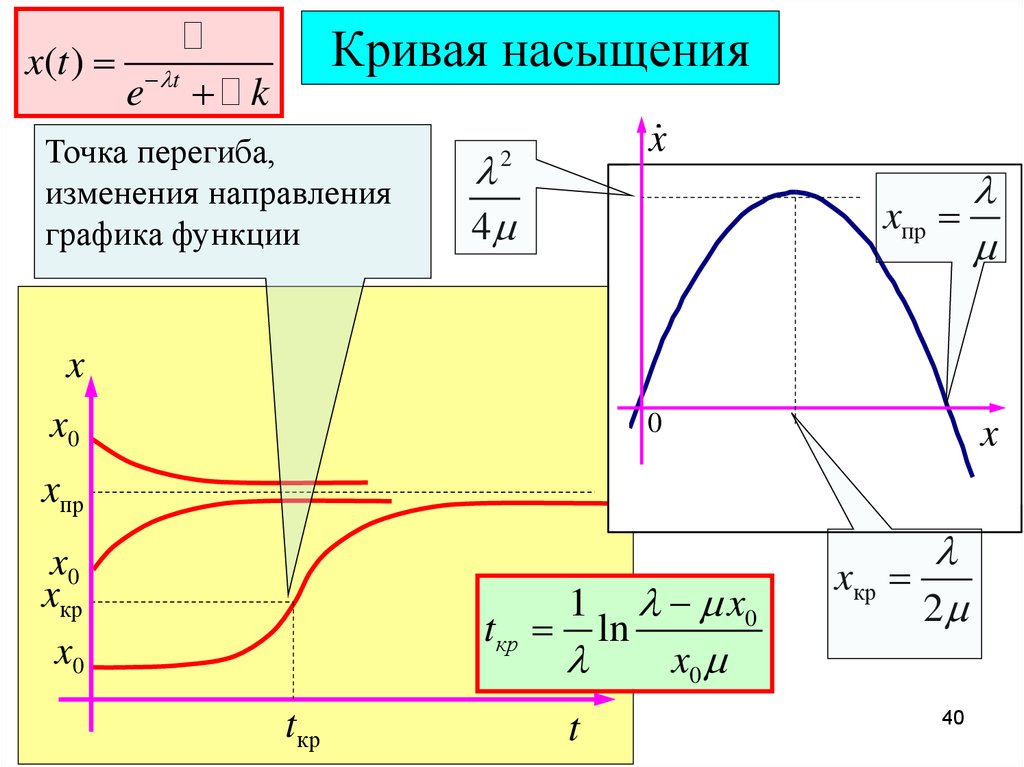
x(t )
Кривая насыщения
e t k
Точка перегиба,
изменения направления
графика функции
x
4
2
xпр
x
x0
0
x
xпр
x0
xкр
x0
x0
tкр ln
x0
1
tкр
t
xкр
2
40

41.

Продукт производимый
экономикой: X AK 1 L 2
а) автономное потребление
обеспечивающее
жизнеспособность экономики
б) инвестиции в экономику для
восстановления основных фондов,
которые убывают в результата
производственной деятельности
в) общественное
потребление,
обеспечивающее
трудоспособность
экономики
41

42.

a доля автономного потребления
aX есть продукт идущий на автономное потребление
1 a X
есть продукт оставшийся после
распределения его части на автономное потребление
есть доля продукта идущая на инвестиции
1 a X есть продукт идущий на инвестиции
1 1 a X есть продукт оставшийся после
распределения его на автономное потребление и
инвестиции, или общественное потребление
Автономное потребление
Aˆ aX
Инвестиции
I 1 a X
Общественное потребление
C 1 1 a X
42

43.

Логико-структурная схема экономики Солоу
Темпы роста труда
I 1 a X
L L0e t
X AK 1 L 2
C 1 1 a X
Aˆ aX
Труд (трудозатраты) в
начальный момент времени
43

44.

X AK 1 L 2
L L0e t
I 1 a X
C 1 1 a X
X AK 1 L 2
t
L
L
e
0
K K I
I 1 a X
C 1 1 a X
есть постоянные темпы выбытия
основных фондов K
K ( ) K
K
( )
I
Определяет выбытие
основных фондов в
результате
производственной
деятельности
Определяет
восстановление
основных фондов через
инвестиции
Система уравнений модели
Солоу для экономики в
абсолютных показателях
44

45.

X AK 1 L 2
t
L
L
e
0
K K I
I 1 a X
C 1 1 a X
Система уравнений
модели Солоу для
экономики ДугласаКоба в абсолютных
показателях
X
x
L
1
X AK L
K
k
t
L
L L0e
K K 1 a X i I
L
I 1 a X
C
c
C 1 1 a X
L
X xL
K kL
I iL
C cL
Производительность труда
Фондовооруженность
Удельные инвестиции,
инвестиции приходящиеся
на одного занятого в
экономике
Удельное общественное
потребление, т.е потребление
приходящиеся на одного
занятого в экономике
45

46.

X xL d
d
dk
dL
d
K
L k
K kL
K kL dt
dt
dt
dt
dt
I iL
t
d
K
kL
k
L
e
t
0
K
kL
k
L
e
0
C cL
dt
K
K
xL
A
L
k
L
L
t
L
L
e
0
kL kL kL 1 a xL
iL 1 a xL
cL 1 1 a xL
K kL k L
x Ak
t
L
L
e
0
k k k 1 a x
i 1 a x
c 1 1 a x
46

47.

Система уравнений модели
x Ak
Солоу для экономики
k k 1 a x
Дугласа-Коба в
относительных показателях
i
1
a
x
c 1 1 a x
k
k
A
1
a
k
k uv
k uv uv
uv uv uv A 1 a uv
uv u v v A 1 a uv
uv A 1 a uv
dv
v
v v 0 v v
dt
dv
dv
t
dt
dt
ln
v
t
v
e
v
v
47

48.

ue t A 1 a u e t
u A 1 a u e
1 t
du
1 t
A 1 a u e u du A 1 a e 1 t dt
dt
u
1
u
du A 1 a e
1 t
1 a 1 t
A
e
k uv
dt
1 a 1 t
u
A
e
1
1
1
1 a 1 t
u A
e
1 a 1 t
k A
e
1
1
1
1
e t
48

49.

k k A 1 a k
1 a 1 t
k A
e
Величина называется
стационарной если она
не зависит от времени
Для стационарной
величины производная
по времени равна нулю
dkst
kst
0 kst 0
dt
0 kst A 1 a k st
стационарная
фондовооруженность
k k
1 1 t
st
e
e t
k
1
1
1
1
1
st
e
A
1 a
1 a
kst A
1
1
t
49

50.

k k
1 1 t
st
e
1
1
e t
k0 kst1
t 0 : k k0
k
1
0
k
1
st
k k
1 1 t
st
e
k kst1 k01 kst1 e
1
0
1
st
1 t
1 k k
k kst
e
1
1
k
1
0
k
1
1 1
st
e
t
1
1 t 1
1
1
выражение для
фондовооруженности в
модели Солоу экономики
Дугласа-Коба
50

51.

1 k01 kst1
x A kst
1 t
e
1
1 k01 kst1
i A (1 a) kst
1 t
e
1 k01 kst1
k kst
1 t
e
1
1 k01 kst1
c A(1 )(1 a) kst
1 t
e
1
1
x Ak
k k 1 a x
i 1 a x
c 1 1 a x
1
Динамика производительности труда, удельных инвестиций и удельного
51
общественного потребления определяется динамикой фондовооруженности

52.

1 k01 kst1
k kst
1 t
e
kпр lim k lim k
t
t
1 a
kst A
1
1
1
1 1
st
1 k01 kst1
lim k lim kst
1 t
t
t
e
kst
xпр Akst
iпр A (1 a)kst
cпр A(1 )(1 a)kst
xпр lim x
0
1
1
1 a
xпр A A
1
1
t
1
1 a
iпр A (1 a) A
iпр lim i
t
cпр lim c
t
1
1 a
cпр A(1 )(1 a ) A
1
52

53.

1
0
1
st
1 t
1
1
d
d k
1 k k
k 0
0
k
0
k kst
2
dt
dt
e
k
1
k k A 1 a k
k A 1 a kкр
k 0
k0
2
kst
k
k0
kкр
k0
tкр
Точка
перегиба,
изменения
направления
графика
функции
1
кр
A
1 a
1 a
kкр A
1
1
t
53

54.

1
0
1
st
1 t
1 k k
k kst
e
1 a
kst A
kкр kst
k
1 k01 kst1
kкр kst 1 tкр
e
1
1
1 a
kкр A
1
1
1
1
1
st
kst
1
1
1
1
1 k01 kst1
kst 1 tкр
e
kst1 kst1
k01 kst1
1
e
1 k0 kst
1 tкр ln
1
1
1
1
1 tкр
e
1
1
k01 kst1
e
1 tкр
1 tкр
kst1 k01
1
kst 1
1 k0 kst
1
tкр
ln
1
1 54
1

55.

1 a
cst A(1 )(1 a) A
1
Логико-структурная схема
экономики Солоу
I 1 a X
L L0e t
X AK 1 L 2
C 1 1 a X
Aˆ aX
Определим долю инвестирования в основные фонды
55
обеспечивающее максимальное среднедушевое потребление

56.

1 a
cst A(1 )(1 a) A
1 a
cst A(1 a) A
1
1
(1 )
B обозначим
1
cst 0
B(1 ) 1 0
1
1
B (1 )
1 0
1
B
1
(1 )
1 0
1
cst B(1 )
B
1
1
0
1
B
1
2 1
1
0
56

57.

B
1
2 1
1
1 a
x A A
*
st
1 a
k A
*
st
0
*
1
1
1
ist* 1 A (1 a )
1
1 a
c A(1 )(1 a ) A
*
st
Золотое правило накопления:
среднедушевое потребление на
стационарной траектории
достигает максимального
значения когда доля
инвестирования в основные
фонды совпадает с
эластичностью по основным
фондам:
1
Выражения для
относительных показателей
обеспечивающих
максимальное
среднедушевое потребление
на стационарной траектории
57

58.

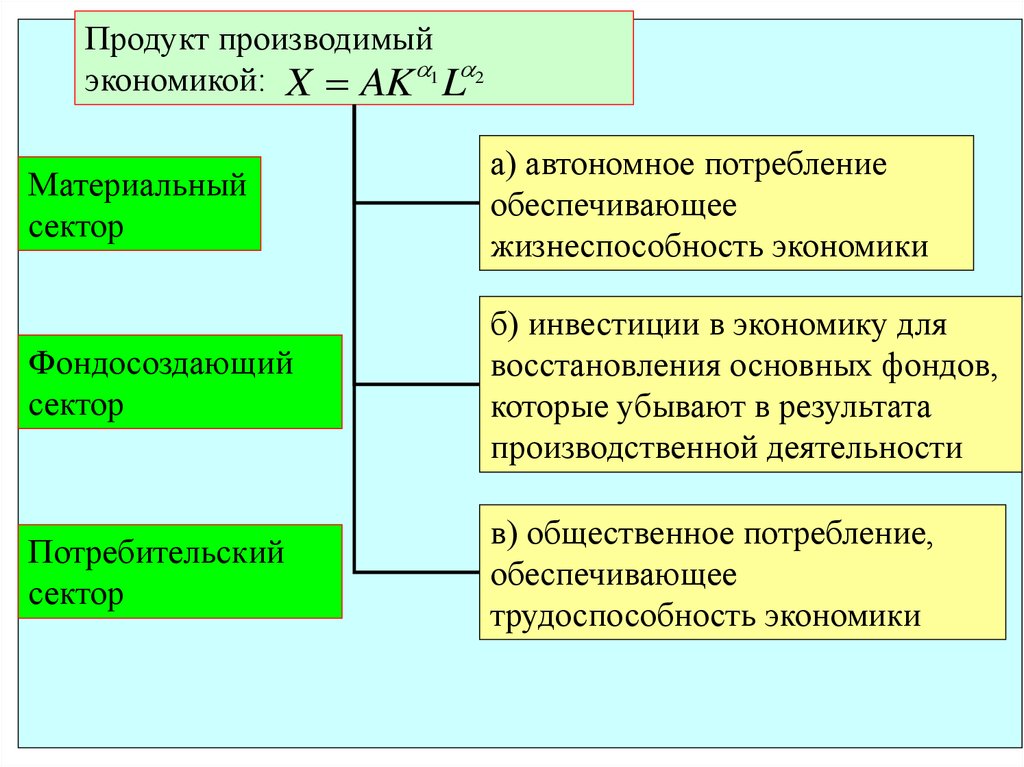
Продукт производимый
экономикой: X AK 1 L 2
Материальный
сектор
а) автономное потребление
обеспечивающее
жизнеспособность экономики
Фондосоздающий
сектор
б) инвестиции в экономику для
восстановления основных фондов,
которые убывают в результата
производственной деятельности
Потребительский
сектор
в) общественное потребление,
обеспечивающее
трудоспособность экономики
58

59.

Материальный сектор экономики производит предметы труда,
обеспечивая ими другие сектора, а также и предприятия своего
сектора
Фондосоздающий сектор экономики производит средства
труда, обеспечивая ими другие сектора, а также и предприятия
своего сектора
Потребительский сектор экономики производит лишь
предметы во благо общества
59

60.

Трехсекторная экономика
L L0e t
L1
L2
L3
I1
a1 X 1
1 2
X 1 A1K1 L1
I2
1 2
a2 X 1 X 2 AK2 L2
I3
X 3 AK3 1 L 32
C
a3 X 1
Материальный
сектор
Фондосоздающий
сектор
Потребительский
сектор
60

61.

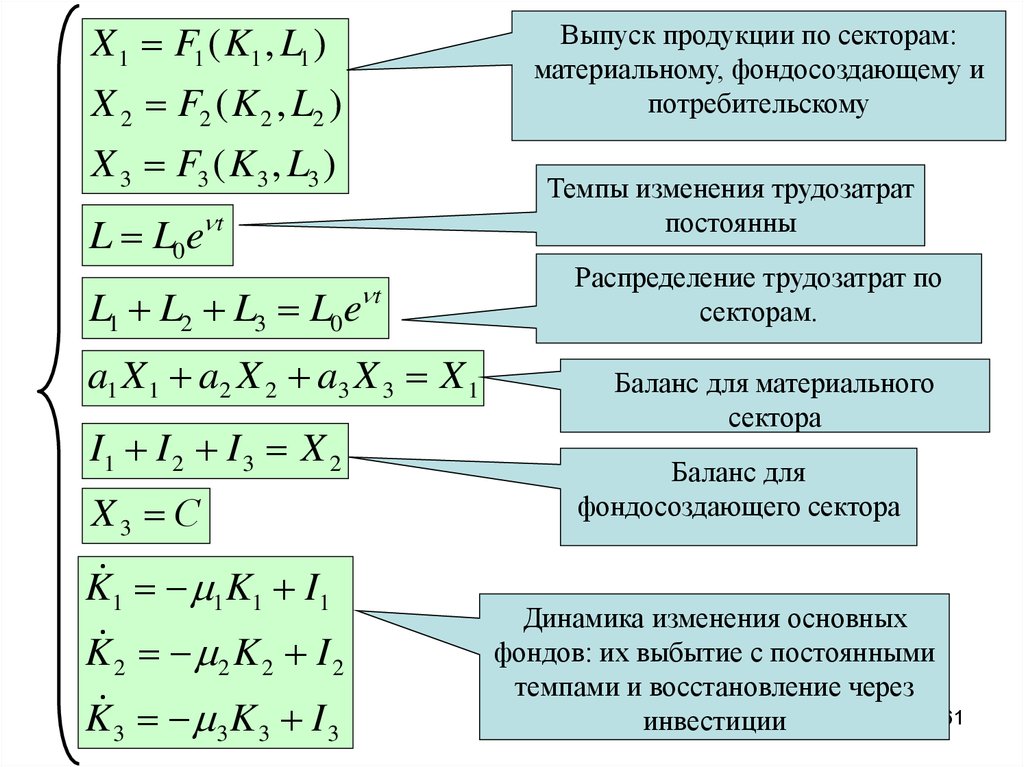
X 1 F1 ( K1 , L1 )
Выпуск продукции по секторам:
материальному, фондосоздающему и
потребительскому
X 2 F2 ( K 2 , L2 )
X 3 F3 ( K 3 , L3 )
Темпы изменения трудозатрат
постоянны
L L0e t
t
L1 L2 L3 L0e
a1 X 1 a2 X 2 a3 X 3 X 1
I1 I 2 I 3 X 2
X3 С
K1 1 K1 I1
K 2 2 K 2 I 2
K 3 3 K 3 I 3
Распределение трудозатрат по
секторам.
Баланс для материального
сектора
Баланс для
фондосоздающего сектора
Динамика изменения основных
фондов: их выбытие с постоянными
темпами и восстановление через
61
инвестиции

62.

X 1 F1 ( K1 , L1 )
X 1 A1 K1 1 L11 1
X 2 F2 ( K 2 , L2 )
X 2 A2 K 2 2 L21 2
X 3 F3 ( K 3 , L3 )
X 3 A3 K 3 3 L31 3
L L0e t
L L0e t
L1 L2 L3 L0e t
L1 L2 L3 L0e t
a1 X 1 a2 X 2 a3 X 3 X 1
a1 X 1 a2 X 2 a3 X 3 X 1
I1 I 2 I 3 X 2
I1 I 2 I 3 X 2
X3 С
X3 С
K1 1 K1 I1
K1 1 K1 I1
K 2 2 K 2 I 2
K 2 2 K 2 I 2
K 3 3 K 3 I 3
K 3 3 K 3 I 3
62

63.

X 1 A1 K1 1 L11 1
X 2 A2 K 2 2 L21 2
X 3 A3 K 3 3 L31 3
L L0e t
L1 L2 L3 L0e t
a1 X 1 a2 X 2 a3 X 3 X 1
a2 X 2 a3 X 3 1 a1 X 1
I1 I 2 I 3 X 2
X3 С
K1 1 K1 I1
K 2 2 K 2 I 2
K 3 3 K 3 I 3
63

64.

F ( K , L) AK 1 L 2
X F ( X1, X 2 ,
, Xn)
X 1 A1 K1 1 L11 1
X 2 A2 K 2 2 L21 2
X 3 A3 K 3 3 L31 3
1. i : F
X i 0
0
2. i : lim F
X i
K
F
3. i :
0
X i
F
4. i : 2 0
Xi
2
64