Исследование нелинейных явлений методами детерминированной динамики. Лекция 5

1. Лекция 5 Исследование нелинейных явлений методами детерминированной динамики

2. 1. Неустойчивость

Неустойчивость – это
состояние, чувствительное
к малым возмущениям,
флуктуациям, которые,
разрастаясь, вызывают
разрушение структуры
системы.

3.

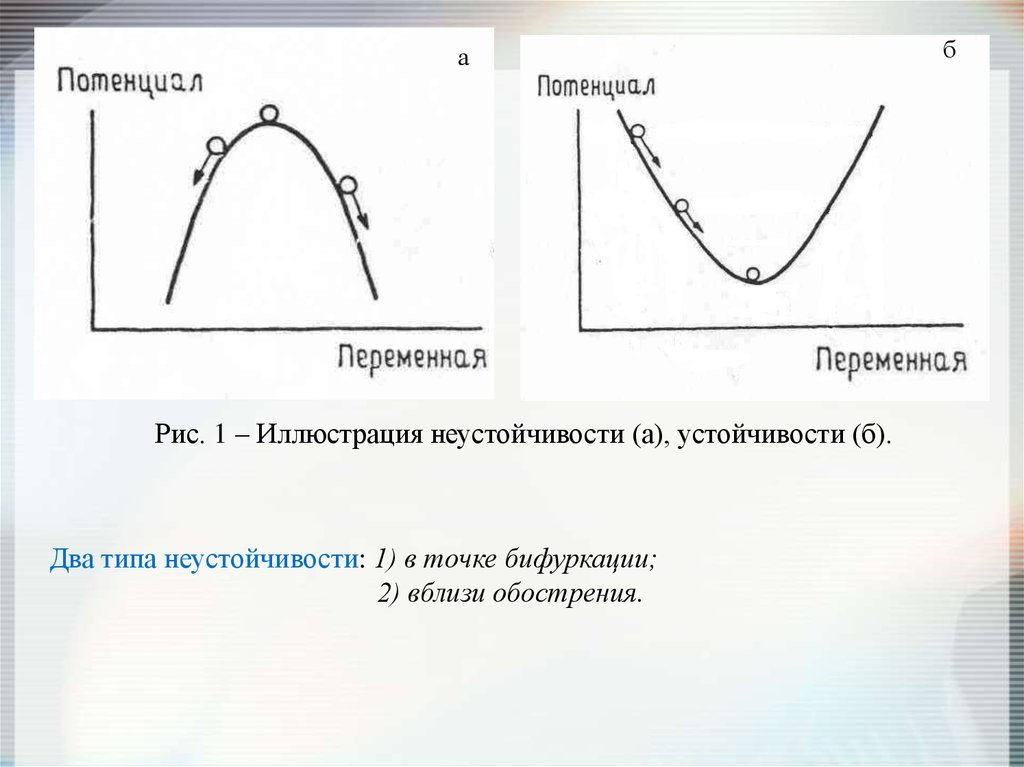
а
Рис. 1 – Иллюстрация неустойчивости (а), устойчивости (б).
Два типа неустойчивости: 1) в точке бифуркации;
2) вблизи обострения.
б

4.

1. Неустойчивость в точке бифуркации:

5.

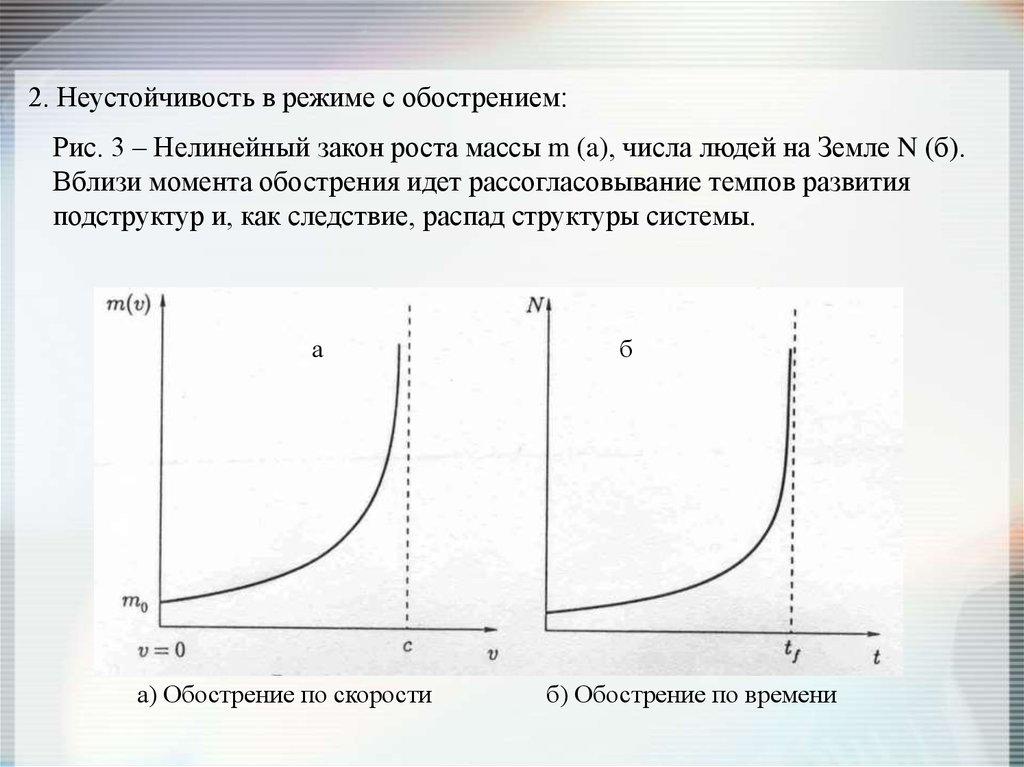
2. Неустойчивость в режиме с обострением:
Рис. 3 – Нелинейный закон роста массы m (a), числа людей на Земле N (б).
Вблизи момента обострения идет рассогласовывание темпов развития
подструктур и, как следствие, распад структуры системы.
а
а) Обострение по скорости
б
б) Обострение по времени

6.

• Вблизи критических точек (бифуркации, обострения) система:
не способна подавлять возмущения, флуктуации и теряет устойчивость;
меняет структуру и закон развития (испытывает переход к новому
экономическому укладу и др., например, демографический переход (б)).
• Неустойчивость приводит к появлению двух сценариев (С. П. Курдюмов)
развития системы:
1.структурному кризису, в процессе которого система выходит на новый
аттрактор, на новый режим функционирования;
2.системному кризису, в результате которого происходит распад сложной
структуры, гибель системы.

7.

• В системном анализе часто называют три сценария (П.М. Хомяков)
изменения экономической системы через неустойчивость:
1. кризис. Адаптация системы к новым условиям и сохранение её элементов;
2. катастрофа. Сохранение целостности системы. Отмирание некоторых и
появление новых элементов;
3. катаклизм. Гибель системы.
• В экономике обнаружены и исследуются неустойчивости в процессах типа
автокаталитических.

8. 2. Автокаталитические процессы

В химической реакции, протекающей при наличии катализатора:
k
X Y
Z
(1)
• катализатор может ускорять (активатор) или замедлять (ингибитор)
протекание химической реакции, то есть влиять на величину постоянной
реакции k.
• X, Y, Z – концентрации веществ.
Кинетическое уравнение реакции:
dZ
kXY
dt
(2)

9.

k
В реакции автокатализа: A 2 X
3 X
(3)
Для синтеза вещества Х из реагента А необходимо в качестве катализатора
само синтезируемое вещество Х.
А
3Х
Х
Нелин. полож. обратн связь
Рис. 4 – Синтезируемое
вещество Х в качестве и
катализатора, и положительной
обратной связи.
Х
Кинетика автокаталитического процесса описывается нелинейным
дифференциальным уравнением:
dX
kAX 2
dt
(4)
В каждом фрагменте системы производство вещества (товара,
капитала) пропорционально квадрату количества вещества (товара,
капитала) в этом фрагменте.

10.

Озоновая дыра, наблюдаемая из космоса (а), с поверхности Земли (б).
а)
б)
О О2 М О3 М

11.

Особенности уравнения (4):
• квадратичная нелинейность Х2, ускоряющая развитие
процесса;
• производимое вещество служит нелинейной положительной
обратной связью;
• автокаталитические процессы – нелинейные. Они широко
встречаются и изучаются в экономике;
• автокаталитические нелинейные процессы развиваются в так
называемом «режиме с обострением».

12. 3. Элементы теории режимов с обострением

Режимом с обострением называют процесс сверхбыстрого
неограниченного возрастания величины (вещества, товара,
капитала) за ограниченное время.
Математическая модель (теория)
«режима с обострением»
разработана в ИПМ РАН им. М.В.
Келдыша под руководством
академика С.П. Курдюмова.

13.

Можно представить, что в ходе экономического процесса скорость изменения
изучаемой величины Х пропорциональна не самой Х, а ее степени:
dX
Xn
dt
(5)
где Х(0) = Х0,
= Const.
n > 1,
При = 1 решение уравнения (5) имеет вид:
1 n
X
1 n
Xt
t Const
X0
(6)
Xt A t f t
A n 1
1
n 1
(7)
1
n 1
t f X 0 n 1
(8)
1
n 1
n 1
(9 )

14.

где:
Х0, Xt – значения изучаемой величины на начало процесса t = 0 и в момент
времени t соответственно;
tf – время обострения, параметр процесса «режим с обострением».
Рис. 5 – Характерный вид решения уравнения (5); при t tf , Xt .

15.

Из анализа уравнений следует:
• решение уравнения (5) существует только до момента tf;
• за ограниченное время t неограниченно растет Х термин «режим
с обострением»;
• причина сверхбыстрого роста величины Х – сильная нелинейная
положительная обратная связь Xn;
• в течение длительного времени в системе как будто бы «ничего не
происходит». однако затем, вблизи
взрывной рост решения.
tf
происходит сверхбыстрый,

16.

В экономике и экологии обнаружены нелинейные процессы, уравнения
которых содержат показатель n = 2, тогда уравнение (5) при = 1
приобретает вид:
dX
X2
(10)
dt
Решение:
1 n
X
1 n
Xt
t Const
X0
1
Xt
tf t
A 1,
(12) (11)
tf
X0
Xt
t
1
tf
1
t
t f 1
tf
1
X0
(11)
(12)
(13)

17.

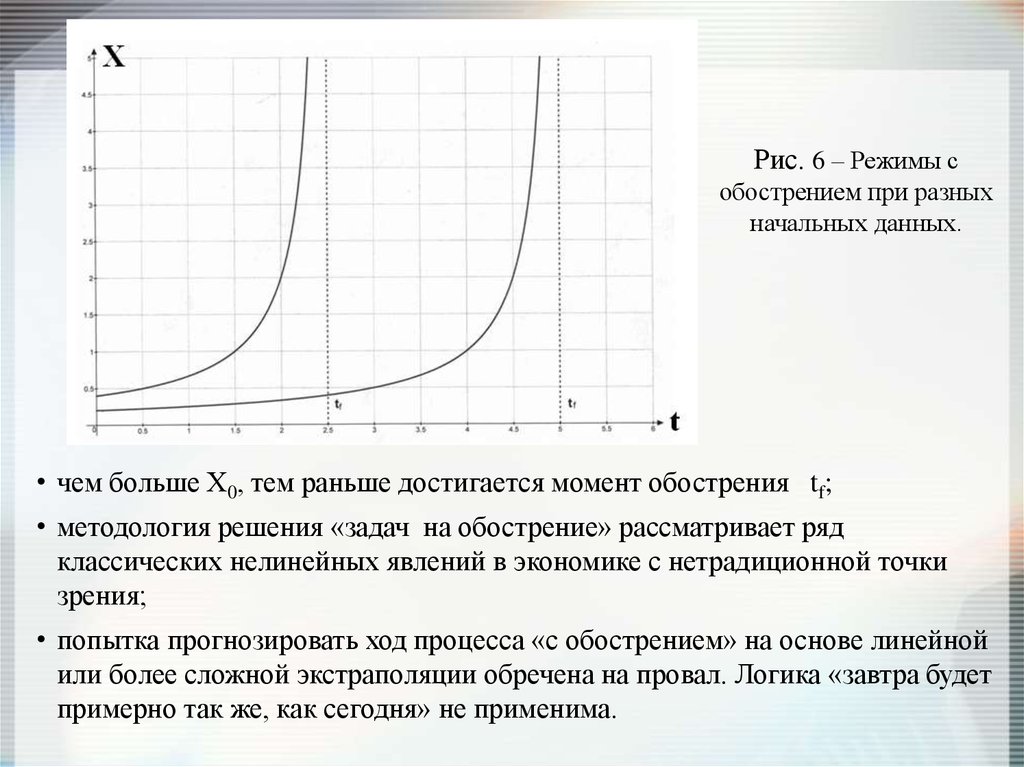
Рис. 6 – Режимы с
обострением при разных
начальных данных.
• чем больше Х0, тем раньше достигается момент обострения tf;
• методология решения «задач на обострение» рассматривает ряд
классических нелинейных явлений в экономике с нетрадиционной точки
зрения;
• попытка прогнозировать ход процесса «с обострением» на основе линейной
или более сложной экстраполяции обречена на провал. Логика «завтра будет
примерно так же, как сегодня» не применима.

18. 4. Нелинейная динамика капитала

Классический пример режима с обострением из экономики – быстрый рост
денежного капитала («капитал на капитал», «деньги к деньгам»).
Если свободные деньги С0 пускаются в оборот, вкладываются в какое-либо
дело (в производство, новые технологии и т.п.), то автокаталитический
процесс роста капитала можно представить упрощенной моделью:
С0
k
С 0 2С 3С
3С
(14)
С
dС
kС 0С 2
dt
Нелин. полож. обратн связь
(15)
С
Рис. 7 – Источник развития процесса – С2.

19.

k – постоянная, характеризующая эффективность влияния нелинейной
положительной обратной связи С2 на рост капитала.
Приняв условно kС0 = 1 и применяя теорию режимов с обострением, можно
считать, что рост капитала C (t) идет по закону:
C0
Сt
t
1
tf
(16)

20.

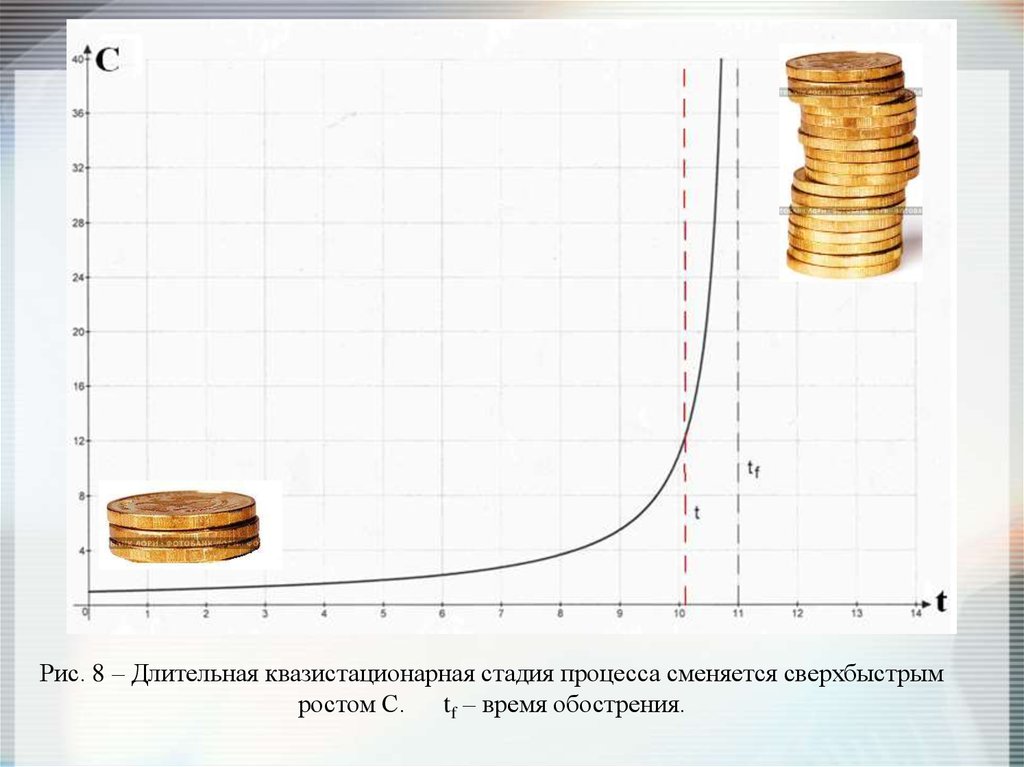
Рис. 8 – Длительная квазистационарная стадия процесса сменяется сверхбыстрым
ростом С.
tf – время обострения.

21.

• в задаче: k = Const, С0 = Const («жесткая модель»);
• теоретически при t tf , С ;
• в реальных условиях при t 0,9 tf , когда Сt 10 С0, система становится
неустойчивой;
• на квазистационарной стадии роста С различие в количестве денег в
соседних фрагментах системы не влияет на характер процесса;
• при t 0,9 tf рассогласованность моментов обострения, вызванная разным
количеством денег в различных фрагментах, приводит к разрушению
структуры системы (структурному кризису капитала – старая технология
отмирает, требуется переход на новую технологию).

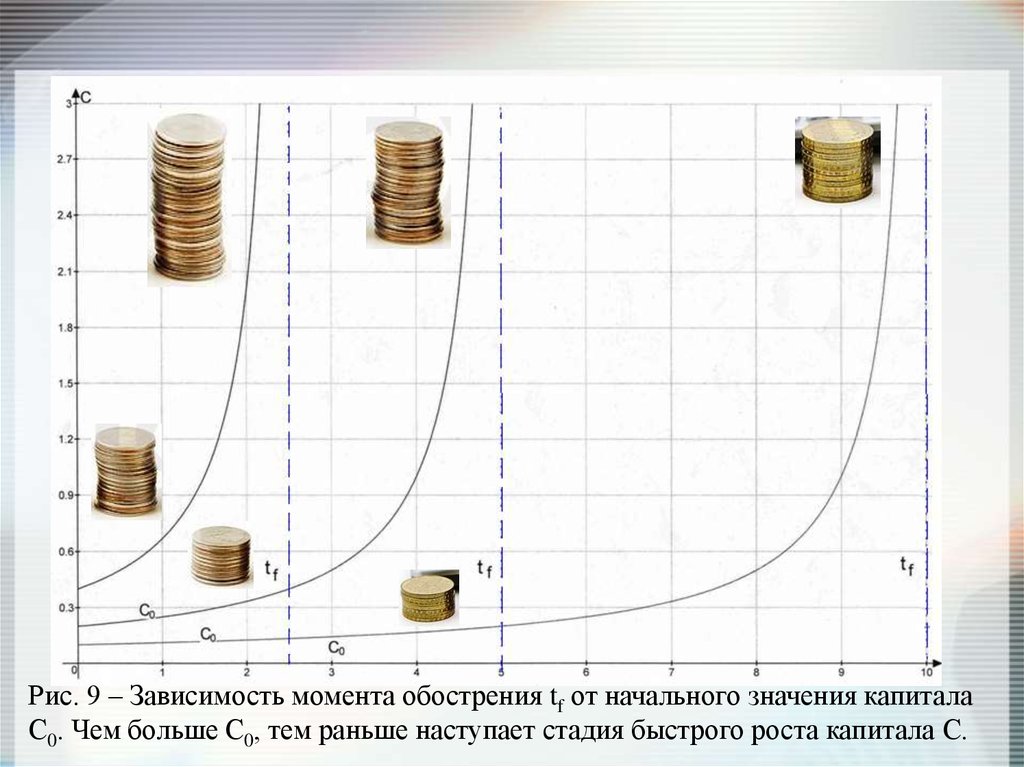
22.

Рис. 9 – Зависимость момента обострения tf от начального значения капитала
С0. Чем больше С0, тем раньше наступает стадия быстрого роста капитала С.

23. 5. Нелинейные процессы в выпуске и реализации продукции

Предприятие выпускает продукцию A по технологии А.
IА – выпуск продукции,
ПА – прибыль,
НАА – норма прибыли.
П А Н АА I А
(17)
dC
– скорость роста прибыли:
dt
dC
П АI А
(18)
dt
dC
2
Н АА I А
(17) (18)
(19)
dt
В «жесткой» модели при НАА = Const уравнение (19) – нелинейное.
В «мягкой» модели НАА Const , например, с насыщением рынка товаром А
норма прибыли будет уменьшаться:
0
1 I А ,
Н АА Н АА
(20)
где – коэффициент падения нормы прибыли.

24.

Затраты производителя должны компенсировать снижение НАА:
0
2
Н АА Н АА
1 I А f I A
(21)
где f – эффективность затрат.
Рис. 10 – Нелинейное уменьшение нормы прибыли;
характеризует насыщение рынка,
f – эффективность затрат.

25.

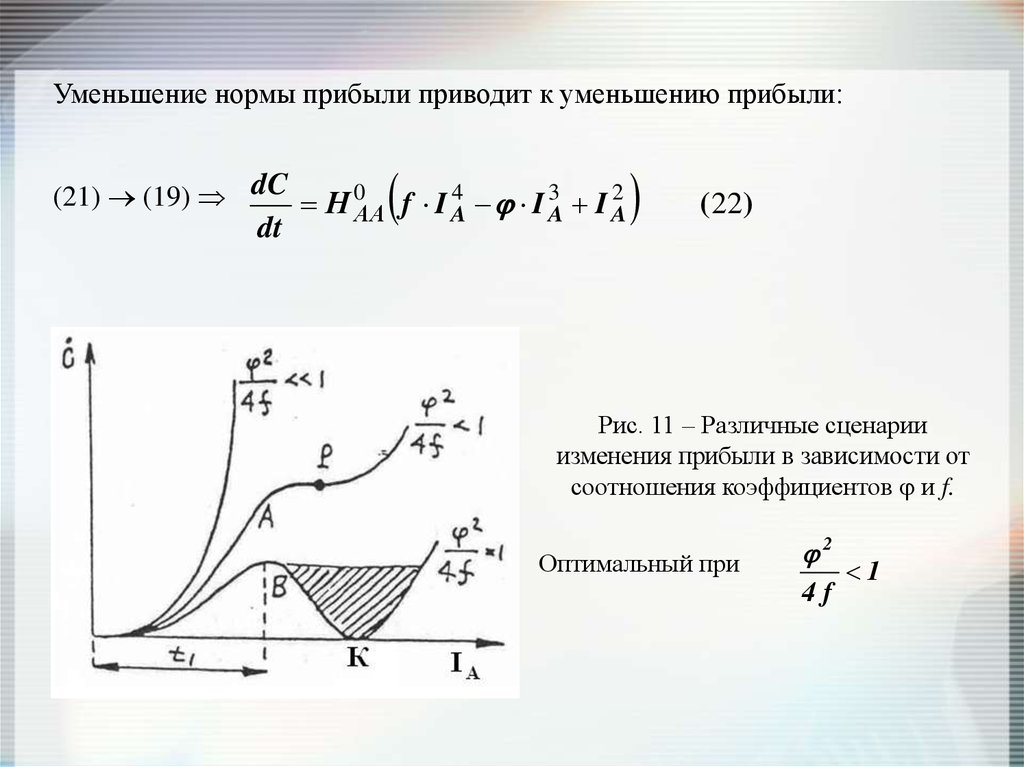
Уменьшение нормы прибыли приводит к уменьшению прибыли:
(21) (19) dC Н 0 f I 4 I 3 I 2
АА
A
A
A
dt
(22)
Рис. 11 – Различные сценарии
изменения прибыли в зависимости от
соотношения коэффициентов и f.
Оптимальный при
2
4f
1

26.

• в «мягкой» модели НAA = НАА (IА); две нелинейности (19) и (21);
• со временем (правее В) предприятие начинает терпеть убытки, прибыль
падает;
• чтобы ликвидировать угрозу, необходимо соблюдать условие
подбором численных значений коэффициентов и f ;
• на уровне К следует прекратить выпуск товара А.
2
4f
1

27. 6. Модель нелинейных явлений: жизненный цикл технологий

Задача:
Математически описать жизненный цикл технологии А, по которой
осуществляется производство товара группы А, как функцию технического
строения капитала КА на уровне предприятия (фирмы).

28.

VА – основной капитал предприятия, который участвует в производстве
товаров по технологии А;
С – цена капитала. Это функция, которая характеризует производственную
деятельность фирмы, С = С(VА).
КА
V А
, где К – техническое строение капитала
А
tж
(капиталовооруженность) фирмы, измеряется отношением накопленного
капитала VА к числу оплаченных часов (живого труда) tж ;
ПА
С
LА
,
где ПА– прибыль на единицу затрат живого труда, измеряемая
отношением фиксированной прибыли С к затратам живого труда LА.
LА = tж , где – средняя часовая ставка.

29.

В линейном приближении техническое строение капитала
(капиталовооруженность) КА определяет прибыль ПА :
П А Н АА К А
(23)
где НАА – норма прибыли:
Н АА
П А 1 С
К А V А
(24)
Норма прибыли равна приращению цены капитала, приходящегося на
единицу приращения основного капитала фирмы с точностью до
интегративного множителя.
Скорость изменения цены основного капитала (комплексная характеристика
производственной деятельности ) F фирмы:
F
dC
П А К А Н АА К А2
dt
Уравнение (25) есть нелинейное уравнение.
(25)

30.

Если оставаться в рамках старой технологии производства, то со временем
отдача от производства падает, и нелинейно падает норма прибыли:
0
2
Н АА Н АА
1 k К А К А
(26)
Рис.12 – Уменьшение нормы
прибыли фирмы по мере роста
капиталовооруженности КА.
Параметры k и определяют
степень нашего незнания о
причинах понижения нормы
прибыли.

31.

Нелинейное поведение нормы прибыли приводит S-образному виду кривой
скорости изменения цены основного капитала:
dC
0
F К А , k , Н АА
К А4 k К 3А К А2
dt
( 27)
Рис.13 – Зависимость
комплексной характеристики
производственной
деятельности фирмы F от КА
для различных соотношений,
понижающих k и повышающих
факторов: S-образная кривая
характеризует жизненный цикл
технологии А.

32.

• Время жизни технологии ограничено нелинейными явлениями производства.
• Жизненный цикл технологии А (S-образная кривая) включает стадии:
зарождение технологии, ускоренного роста, замедления роста и зрелости,
угасания, отмирания (0). Все стадии связаны с характеристиками капитала.
• Потенциал фирмы
2
если k 1.
4
F
dC
dt
может изменить знак (прибыль на убытки),

33.

• Нелинейная динамика технологии :
с одной стороны порождает желание фирмы окупить огромные
капиталовложения в действующую технологию, на что требуется
время.
с другой стороны, высокая прибыль в начале подъема дает возможность
финансировать НИОКР, в ходе которых открываются новые технологии.
• Неумение руководства фирмы вовремя осознать необходимость смены
технологии и может привести к крупным потерям на рынке. Новейшая
технология позволяет сохранить превосходство в конкурентной борьбе.

34.

35.

Таким образом, методы детерминированной динамики могут
успешно применяться для исследования нелинейных явлений в
экономике.