Исследование нелинейных процессов на рынке ВРП аналитическими методами. Лекция 7

1. Лекция 7 Исследование нелинейных процессов на рынке ВРП аналитическими методами

2. 1. Модель взаимовлияния спроса и предложения для слабонеравновесного рынка

Цель: найти математические уравнения кривых спроса и предложения.
• В слабонеравновесных процессах все коэффициенты эластичности не
меняются: Lii = Const, Lee = Const, Lei = Lie = Const, т.е. система линейная;
• Ii(t), Ie(t), Xi(t), Xe(t) – потоки и цены изменяются во времени.
В условиях сокращения выпуска продукции изменение предложения, спроса и
цен можно представить уравнениями:
dI i
Ii i
Lii X i Lie X e
dt
dI e
Ie e
Lee X e Lei X i
dt
dX i
X i I i Lii X i Lie X e
dt
dX e
X e I e Lee X e Lei X i
dt
(1)
(2)
(3)
(4)

3.

где
dI i – скорость и время сокращения выпуска продукции
, i
dt
соответственно;
dI e
, e – скорость и время повышения спроса на продукцию
dt
соответственно.
Из совместного решения (1) и (3), а также (2) и (4) следует:
dX i
dI
X i i i
dt
dt
dX e
dI
X e e e
dt
dt
После преобразования:
dX i
i dI i
Xi
dX e
e dI e
Xe
dt
Xi
dt
Xe

4.

Интегрирование дает уравнения:
ln X i i I i ln Const
ln X e e I e ln Const
После потенцирования имеем:
X i Const e i I i
X e Const e e Ie
где основание натурального логарифма е 2,7.
Из начальных условий можно найти значения Const:
если i = 0, Const = Xi = Xi ,
если e = 0, Const = Xe = Xe ,

5.

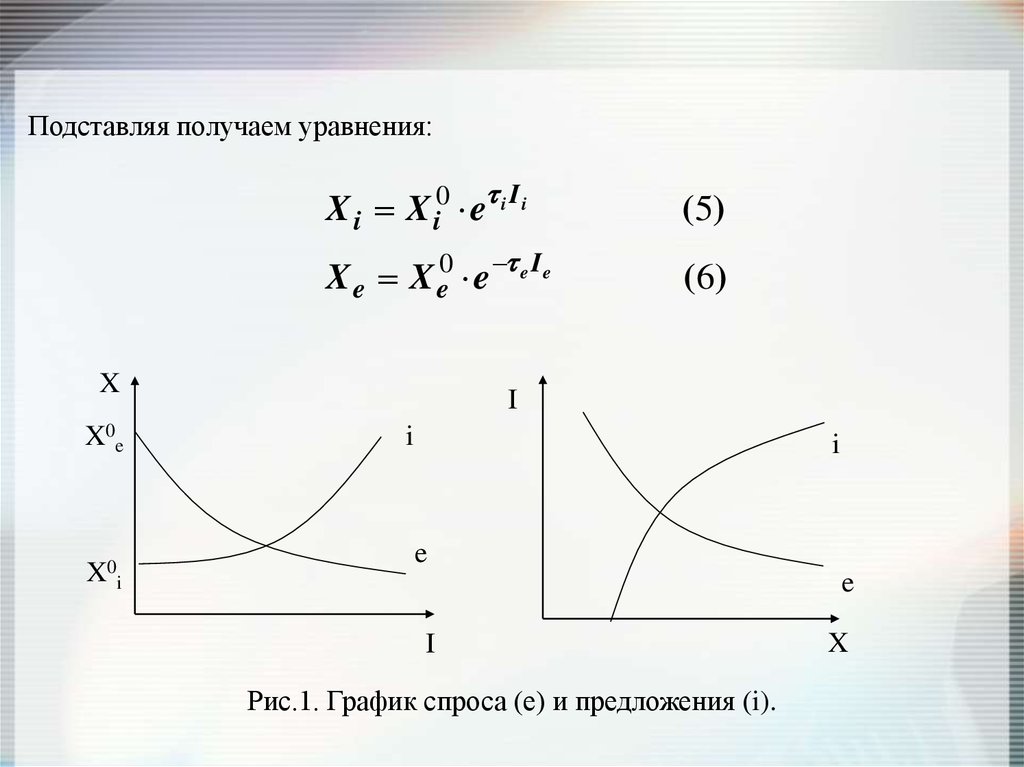
Подставляя получаем уравнения:
X i X i0 e i I i
(5)
X e X e0 e e Ie
( 6)
X
X0e
X0
I
i
i
e
e
i
I
Рис.1. График спроса (е) и предложения (i).
X

6.

• Кривая спроса: нисходящая экспонента устанавливает для
рынка ВРП количество продукции, покупаемой в течение e
(дня, месяца, года) по различным ценам;
• Кривая предложения: восходящая экспонента показывает цену,
ниже которой производитель продукции не может продавать
товар;
• Модель отражает реальные взаимовлияния спроса и
предложения вблизи стационарного состояния (линейные
процессы).

7.

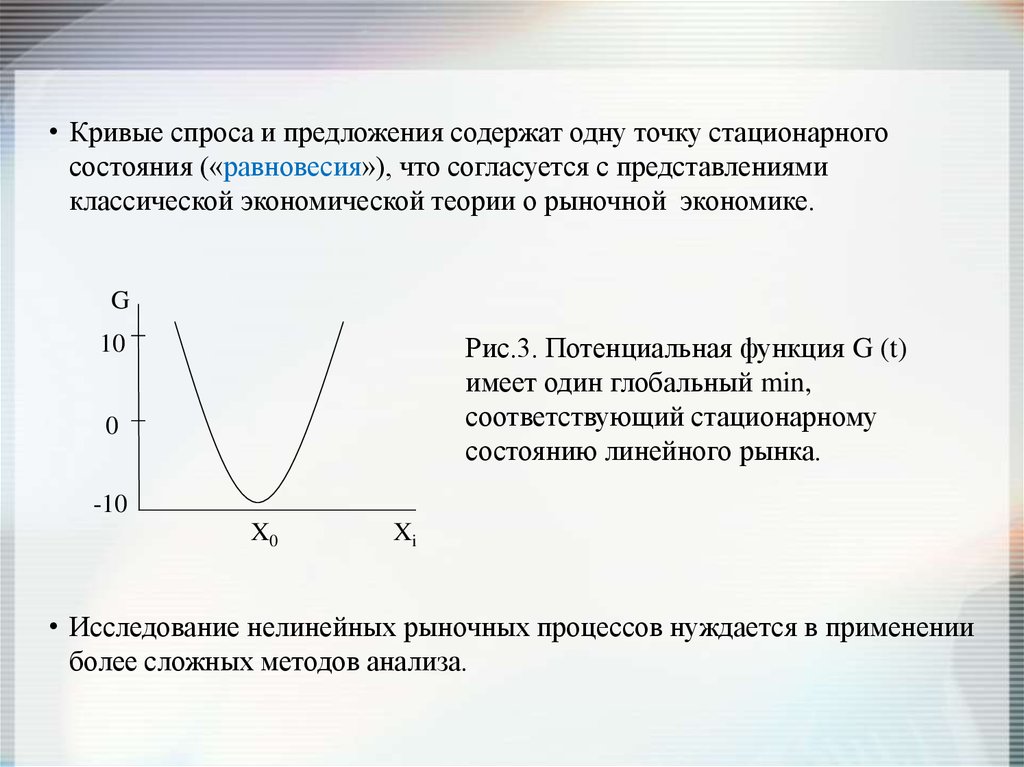
• Кривые спроса и предложения содержат одну точку стационарного
состояния («равновесия»), что согласуется с представлениями
классической экономической теории о рыночной экономике.
G
Рис.3. Потенциальная функция G (t)
имеет один глобальный min,
соответствующий стационарному
состоянию линейного рынка.
10
0
-10
X0
Xi
• Исследование нелинейных рыночных процессов нуждается в применении
более сложных методов анализа.

8. 2. Элементы теории катастроф

Катастрофами называются внезапные изменения в системах – резкие
переходы в новые состояния, происходящие при плавном изменении
управляющих параметров.
Теория катастроф позволяет исследовать нелинейную динамику систем в
зависимости от числа управляющих параметров.
Процессы, связанные с катастрофой, описываются уравнением:
dx
F x , a , b, c ...
dt
x
где х – переменная, параметр порядка;
а, b, с,… – управляющие параметры;
F – потенциальная функция.
(7)

9.

В зависимости от величины показателя степени переменной и числа
управляющих параметров можно назвать ряд катастроф:
1. Складка
1 3
F x ax
3
2. Сборка
F
3. Ласточкин хвост
1 5 1 3 1 2
F x ax bx cx
5
3
2
1
1
1
1
F x 6 ax 4 bx 3 cx 2 dx
6
4
3
2
4. Бабочка
5. Вигвам
F
1 4 1 2
x ax bx
4
2
1 7 1 5 1 4 1 3 1 2
x ax bx cx dx ex
7
5
4
3
2
• Все перечисленные и другие катастрофы используются при анализе
экономических процессов.
• В ряде случаев модели теории катастроф способны обнаружить новые
эффекты в нелинейных экономических системах.

10.

Сальвадор Дали
Катастрофа «Ласточкин хвост»

11.

А.А. Андронов
Рене Том
В.И. Арнольд
Ж.А. Пуанкаре
Л.С. Понтрягин

12. 3. Катастрофа сборки

В уравнении катастрофы сборки есть два управляющих параметра a и b.
dx
F x , a , b
(8)
dt
x
F x, a, b
где
1 4 1 2
x ax bx
4
2
(9)
(10)
dx
x 3 ax b
dt
тогда
х
1
К
2
а
b
К
B
L
Рис.3. Катастрофа сборки.
1 – лист состояний х; каждая точка
соответствует стационарным
решениям.
2 – лист управляющих параметров;
каждая точка соответствует
заданным значениям a и b.

13.

Особые точки:
1.
dF
0,
dx
2.
d 2F
0,
2
dx
3.
d 3F
0,
3
dx
3
4.
x 3 ax b 0 - вырожденные точки, соответствуют листу
состояний 1, т.е.ext F.
3 x 2 a 0 - дважды вырожденные точки, линии ВК, LK.
6 x 0 - трижды вырожденная точка К (х = 0, а = 0, b = 0)
2
a b
0
3 2
- уравнение сепаратрисы {LK, BK}. Сепаратриса
является предельной для метастабильных
состояний.

14.

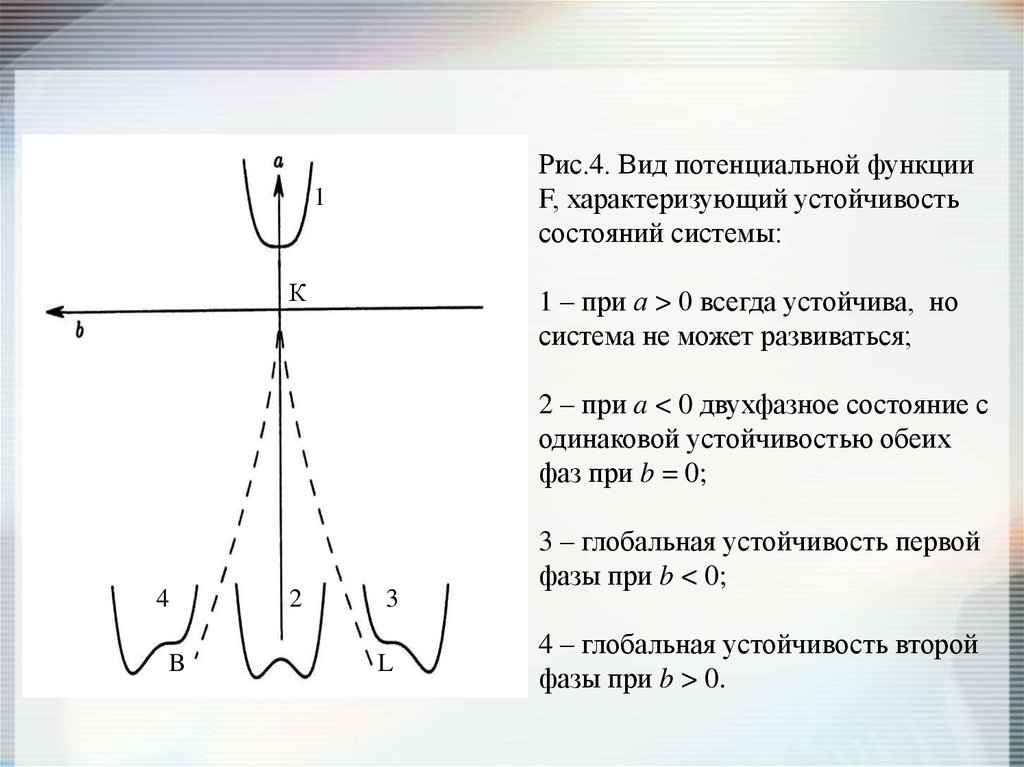
Рис.4. Вид потенциальной функции
F, характеризующий устойчивость
состояний системы:
1
К
1 – при а > 0 всегда устойчива, но
система не может развиваться;
2 – при a < 0 двухфазное состояние с
одинаковой устойчивостью обеих
фаз при b = 0;
4
B
2
3
L
3 – глобальная устойчивость первой
фазы при b < 0;
4 – глобальная устойчивость второй
фазы при b > 0.

15.

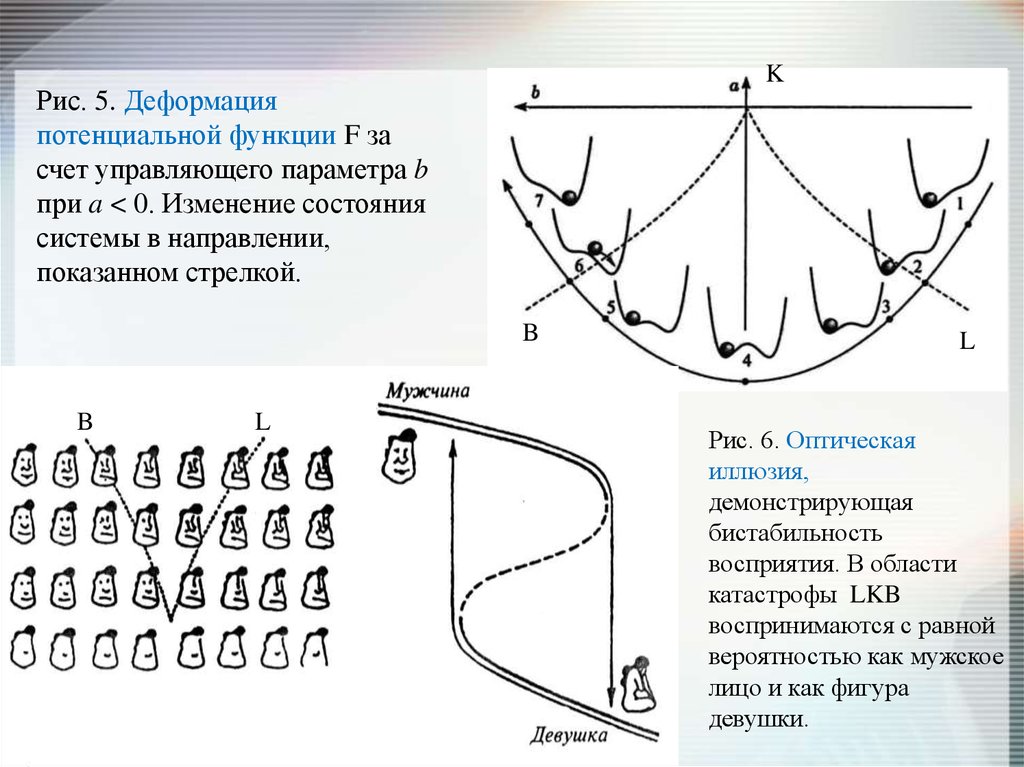
K
Рис. 5. Деформация
потенциальной функции F за
счет управляющего параметра b
при a < 0. Изменение состояния
системы в направлении,
показанном стрелкой.
B
B
L
L
Рис. 6. Оптическая
иллюзия,
демонстрирующая
бистабильность
восприятия. В области
катастрофы LKB
воспринимаются с равной
вероятностью как мужское
лицо и как фигура
девушки.

16.

• Система, динамика которой моделируется катастрофой сборки,
способна к развитию. Она является самоорганизующейся.
• Модель катастрофы сборки:
объясняет переход рынка ВРП из одного стационарного состояния в
другое через экономический кризис;
выясняет различные механизмы развития нелинейных экономических
систем;
решает ряд задач прогноза экономических кризисов.

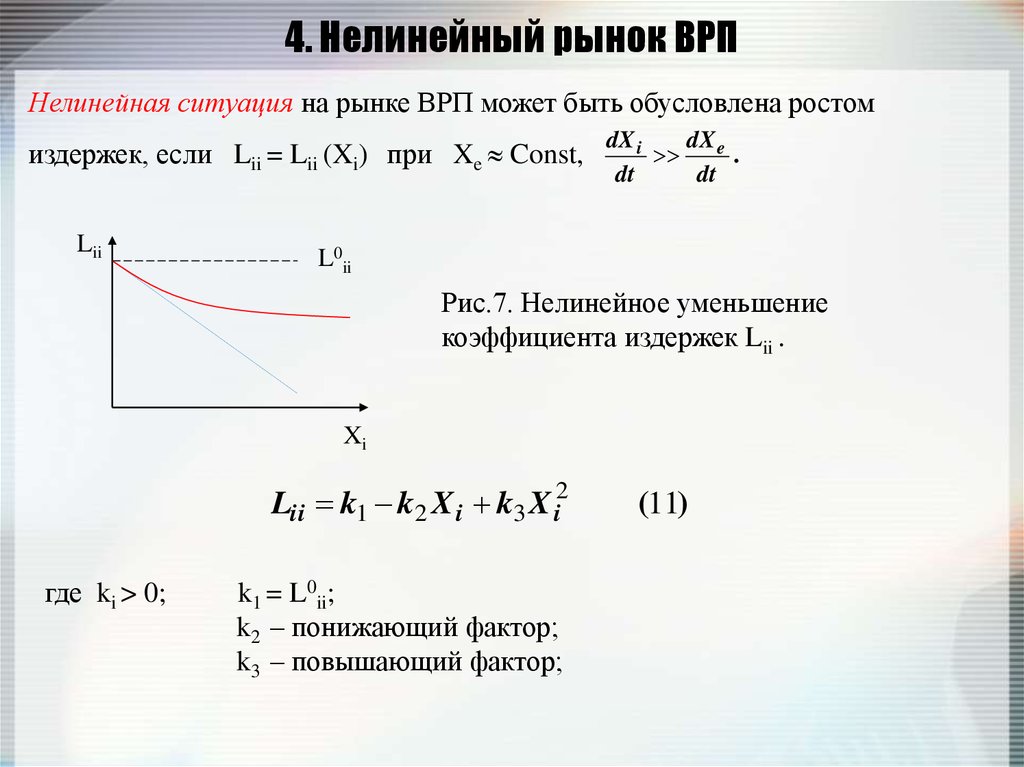
17. 4. Нелинейный рынок ВРП

Нелинейная ситуация на рынке ВРП может быть обусловлена ростом
издержек, если Lii = Lii (Xi) при Xe Const,
Lii
dX i
dX e
.
dt
dt
L0ii
Рис.7. Нелинейное уменьшение
коэффициента издержек Lii .
Xi
Lii k1 k2 X i k3 X i2
где ki > 0;
k1 = L0ii;
k2 – понижающий фактор;
k3 – повышающий фактор;
(11)

18.

В потенциальной функции G(t)
G
dS
Ie X e Ii X i
dt
учтем величину потерь регионального уровня введением показателя потерь :
1 I i X i
где 1
Тогда
где
(12)
при = 1, = 0.
G Ie X e Ii X i
(13)
I e Lee X e Lei X i ,
I i Lii X i Lie X e
После преобразования функция издержек выглядит так:

19.

G Lii X i2 Lie Lei X i X e Lee X e2
(14)
Производная функции издержек:
G
2 Lii X i Lie Lei X e
X i
(15)
Она связана со скоростью изменения цены Xi уравнением катастрофы:
dX i G
dt
X i
(16)
Подставив (11) (15) (16), получаем:
dX i
2 k3 X i3 k 2 X i2 k1 X i Lie Lei X e
dt
Если (11) (14), то функция издержек
G = G (X4i )
(17)
(18)
G 2 k3 X i4 k2 X i3 k1 X i2 Lie Lei X i X e Lee X e2
(18)

20.

• Кривые Xi и Xe имеют три точки пересечения;
• потенциальная функция G (X4i ) имеет два минимума;
• цена предложения Xi – внутренняя быстрая переменная, а цена спроса Xe
– внешняя медленная переменная;
• цена Xe – управляющий параметр, он определяет рыночную ситуацию.

21.

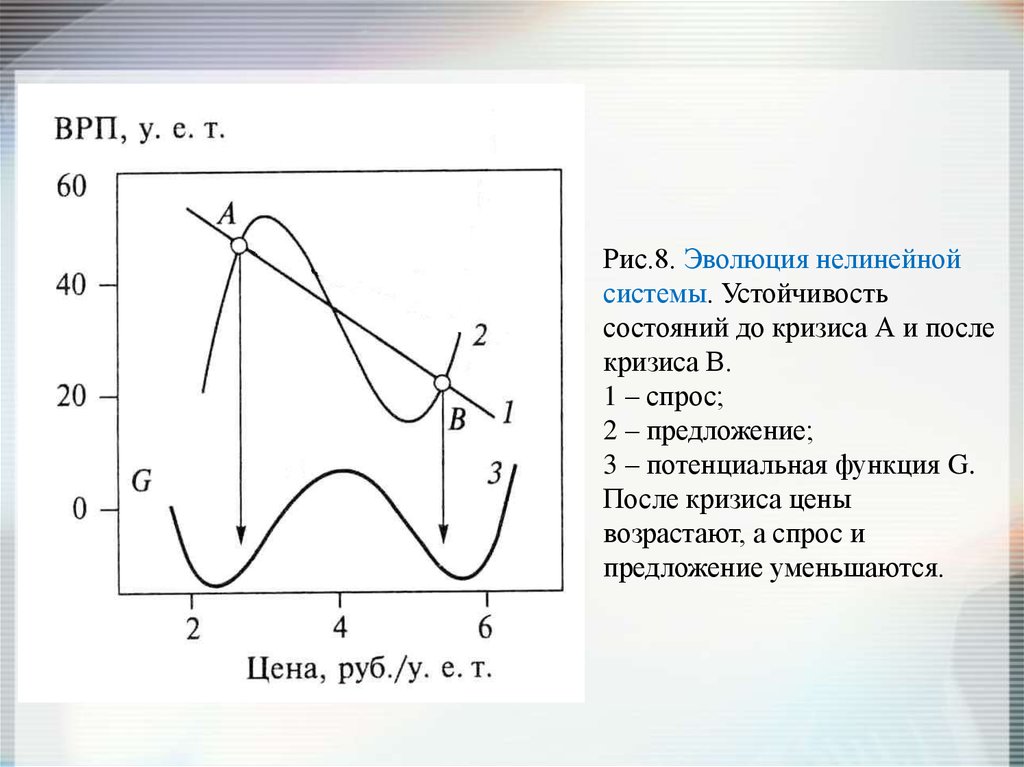
Рис.8. Эволюция нелинейной
системы. Устойчивость
состояний до кризиса А и после
кризиса В.
1 – спрос;
2 – предложение;
3 – потенциальная функция G.
После кризиса цены
возрастают, а спрос и
предложение уменьшаются.

22.

Переход к новой переменной х и управляющим параметрам (a, b) дает более
простые уравнения:
dx
x 3 ax b
dt
dx G
dt x
(19)
(20)
1 4 1 2
G ( x , a , b ) x ax bx
4
2
где G (x, a, b) <> 0.
( 21)

23.

x
Xi
X
0
XК XК
(22)
где x – определена по отклонению Xi от среднего значения X 0
XК – цена в точке К.
X
a 3 0
X К
b
2
1
X
Xe
X
3 0 2 0
XК
XК
XК
X A XB
;
2
(23)
3
(24)
Уравнения (19 - 21) соответствуют катастрофе сборки, здесь x – параметр
порядка, а, b – управляющие параметры и уравнение (17) переходит в
уравнение (19).

24.

х
В
К
А
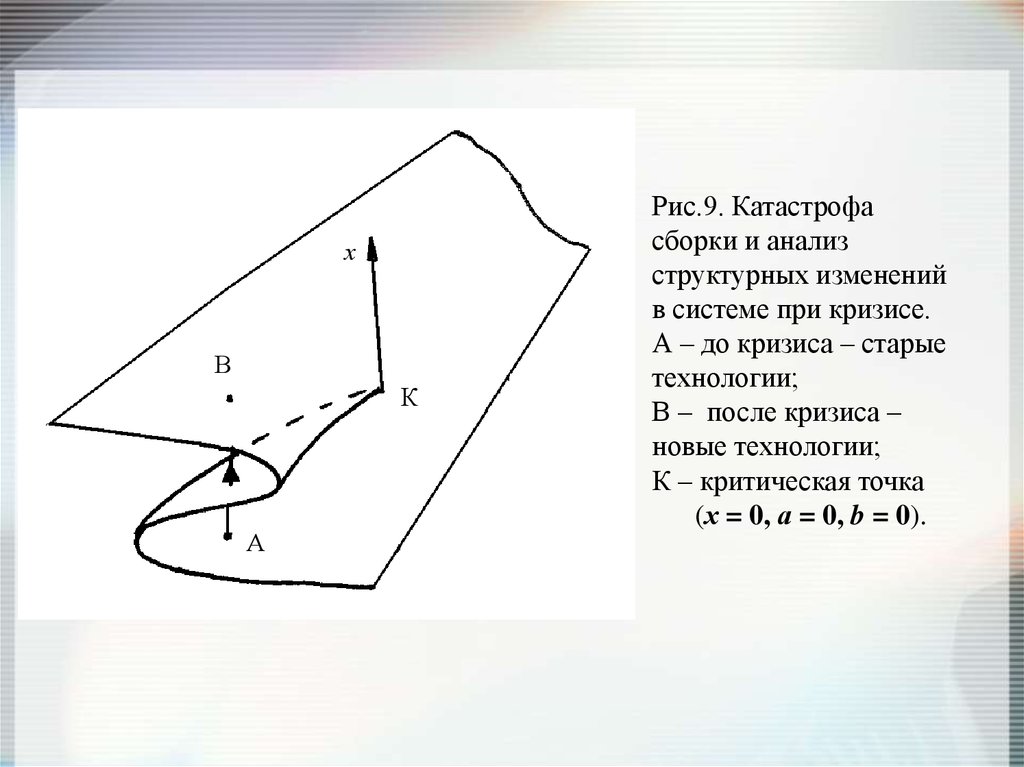
Рис.9. Катастрофа
сборки и анализ
структурных изменений
в системе при кризисе.
А – до кризиса – старые
технологии;
В – после кризиса –
новые технологии;
К – критическая точка
(х = 0, а = 0, b = 0).

25.

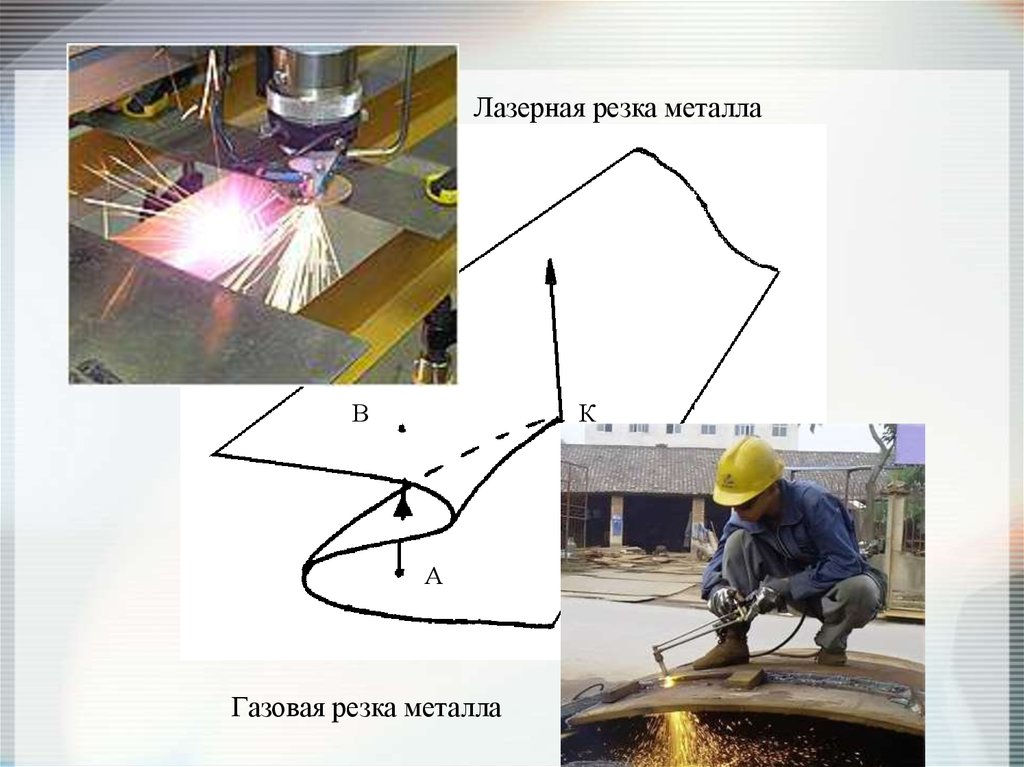
Лазерная резка металла
В
К
А
Газовая резка металла

26.

• Управляющий параметр b характеризует влияние цены спроса Xe (внешнее
рыночное поле) на развитие рыночной ситуации.
Величина в рамке
X0
Xe
X0
b
3
2
XК
XК
XК
3
(24)
составляет внутреннее самосогласованное рыночное поле.
• G < 0 – условие процессов самоорганизации, имеет место прибыль:
доходы > расходов;
• G > 0 – условие деградации, здесь убытки: издержки > доходов.
• Таким образом, нелинейные процессы на рынкеа ВРП, вызванные
нелинейным ростом издержек, описывается моделью (законом) –
катастрофа сборки.

27. 5. Устойчивость нелинейных экономических систем

Теорема. При постоянных граничных условиях (постоянном спросе
σe = Const) издержки в нелинейных системах стремятся убывать и достигают
минимального (положительного) значения в ближайшем стационарном
состоянии, локальная или глобальная устойчивость которого определяется
теоремой Тома теории катастроф.
Доказательство. Уравнения катастрофы сборки:
dx
x 3 ax b
dt
dx
dG
dt
dx
1 4 1 2
G ( x , a , b) x ax bx
4
2
(19)
( 20)
( 21)
где G >< 0 – функция издержек, равная относительной скорости изменения
убытков системы;
х – характеризует отклонение цены от среднего уровня цен;
b – параметр, связанный с ценой спроса Xe.

28.

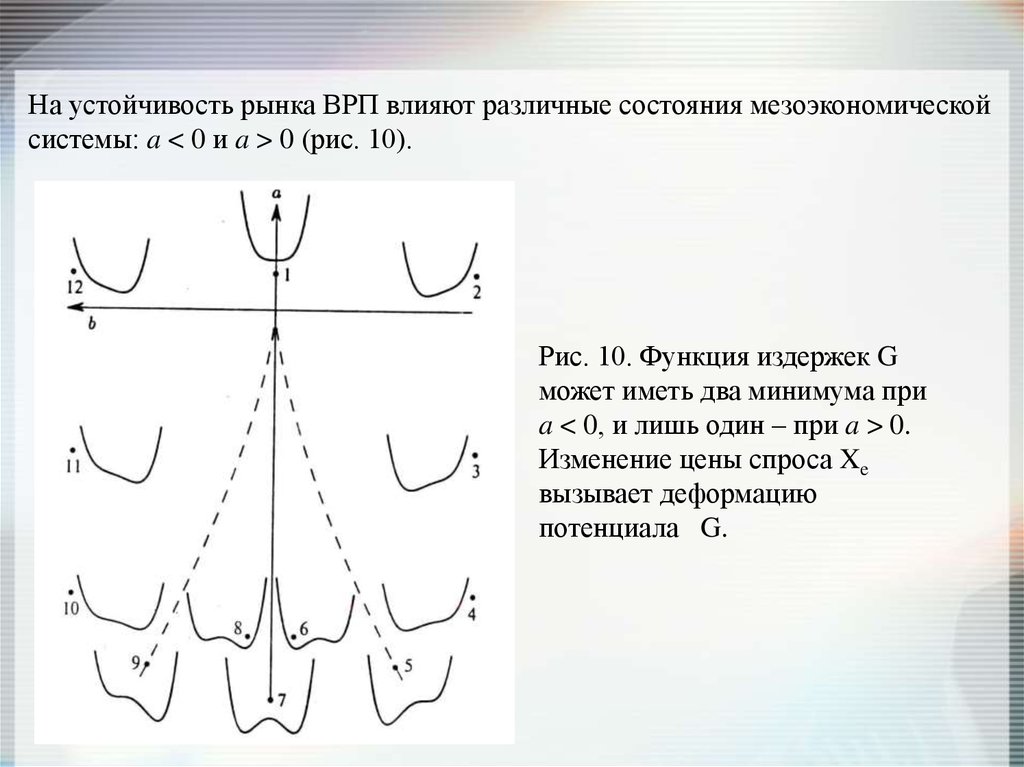
На устойчивость рынка ВРП влияют различные состояния мезоэкономической
системы: a < 0 и a > 0 (рис. 10).
Рис. 10. Функция издержек G
может иметь два минимума при
a < 0, и лишь один – при a > 0.
Изменение цены спроса Xe
вызывает деформацию
потенциала G.

29.

1. Устойчивость при a < 0.
G < 0 – условие самоорганизации. Система может иметь два
стационарных состояния (глобальный и локальный min при b 0),
определяемых по значениям параметров уравнения (19).
Относительно заданных параметров х и b (рис. 11):
• динамика системы нелинейна;
• медленным изменением приведенной цены спроса систему можно
перевести из одного стационарного в другое стационарное
состояние.

30.

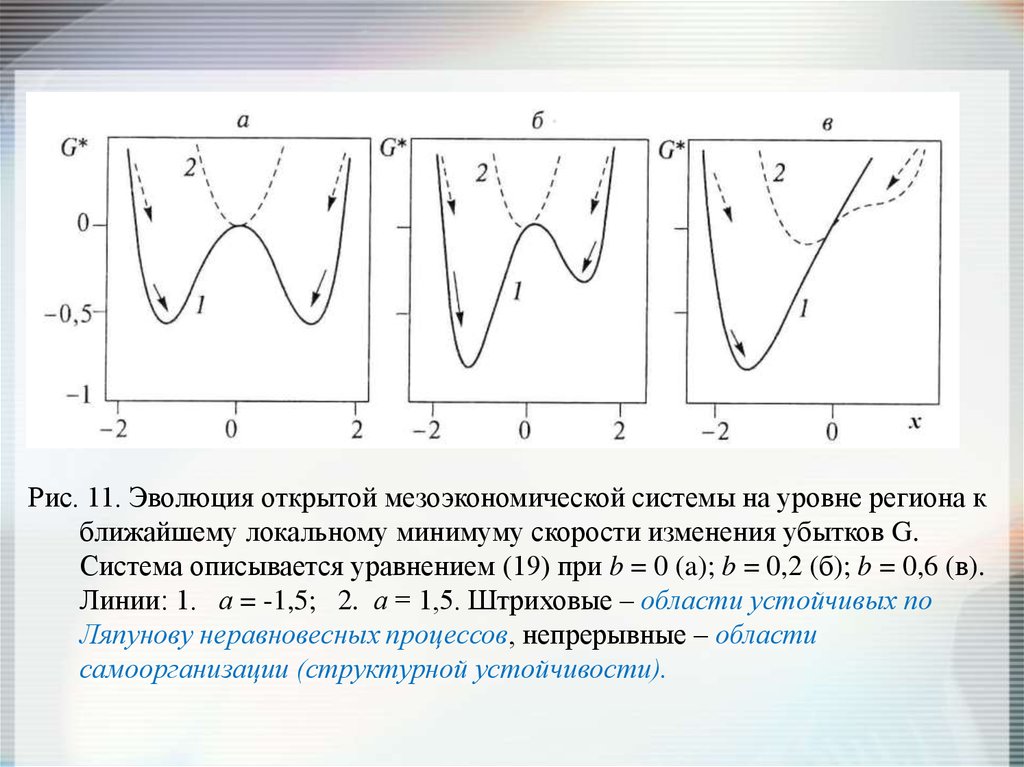
Рис. 11. Эволюция открытой мезоэкономической системы на уровне региона к
ближайшему локальному минимуму скорости изменения убытков G.
Система описывается уравнением (19) при b = 0 (a); b = 0,2 (б); b = 0,6 (в).
Линии: 1. а = -1,5; 2. а = 1,5. Штриховые – области устойчивых по
Ляпунову неравновесных процессов, непрерывные – области
самоорганизации (структурной устойчивости).

31.

2. Устойчивость при a > 0.
G > 0 – является функцией Ляпунова при b = 0).
1 4 1 2
x ax 0
4
2
dG dG dx
dt
dx dt
G
( 25)
dG
x 3 ax
dt
2
0
( 26)
G имеет min при х = 0 (кривая 2 рис. 11 (а)).
На рынке ВРП (a > 0, b = 0) нелинейные процессы устойчивы по
Ляпунову.

32.

3. Модель однопродуктового рынка описывает:
наличие двух стационарных состояний;
возможность перехода из одного стационарного состояния в другое;
изменение спроса, предложения и цен (экономический кризис).

33.

Итак, аналитические методы теории катастроф позволяют:
• исследовать временную деформацию потенциальных функций,
а значит, и формализовать на мезоуровне задачи устойчивого
развития объектов и управления ими;
• после обработки финансовых отчетов предприятий,
статистических данных по отраслям, по ВРП в целом дать
оценку состояния экономического объекта с точки зрения
устойчивости.

34. 6. О реальной выполнимости принципа минимальности издержек

Рассмотренные аналитические методы дополняет экономический принцип
minimax – минимизации издержек и максимизации прибыли.
Пример 1. Результаты исследования легкой промышленности Свердловской
области.
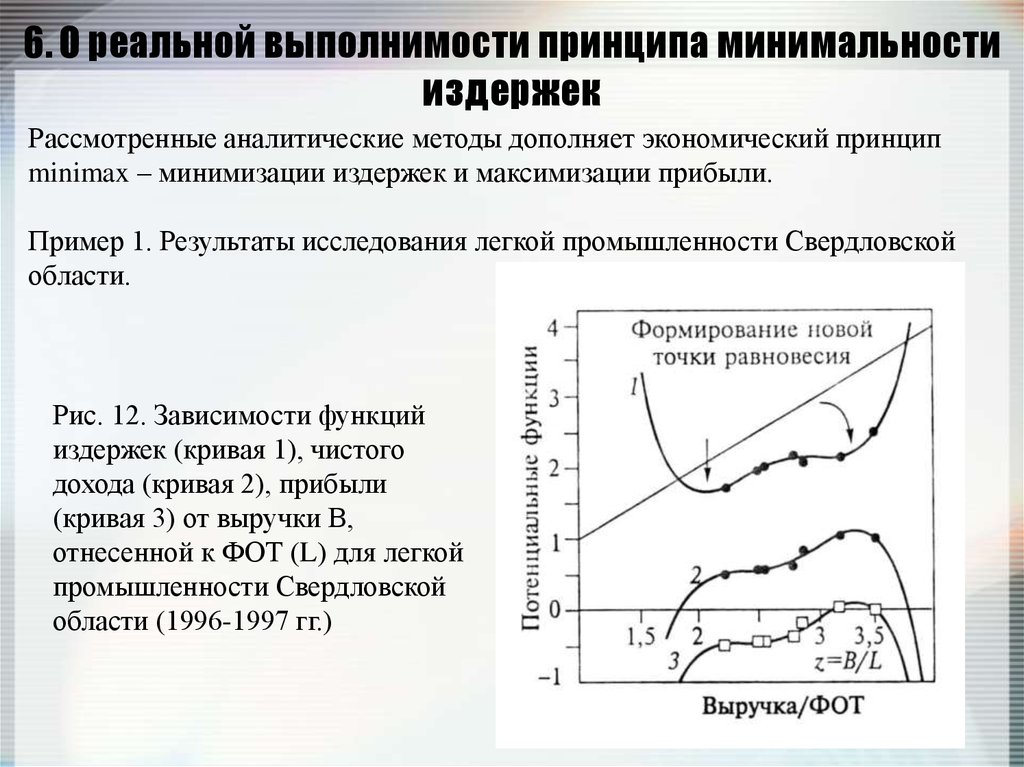
Рис. 12. Зависимости функций
издержек (кривая 1), чистого
дохода (кривая 2), прибыли
(кривая 3) от выручки В,
отнесенной к ФОТ (L) для легкой
промышленности Свердловской
области (1996-1997 гг.)

35.

• В издержках есть глобальный (z = 2,2) и локальный (z = 3,3)
минимумы;
• состояние при z = 3,3 неустойчиво;
• сдвиг стационарной точки за 1,5 года от z = 3,3 к z = 2,2
вызван завышенным размером ФОТ по сравнению с другими
отраслями;
• область прибыли неустойчива по Ляпунову (кривая 3).

36.

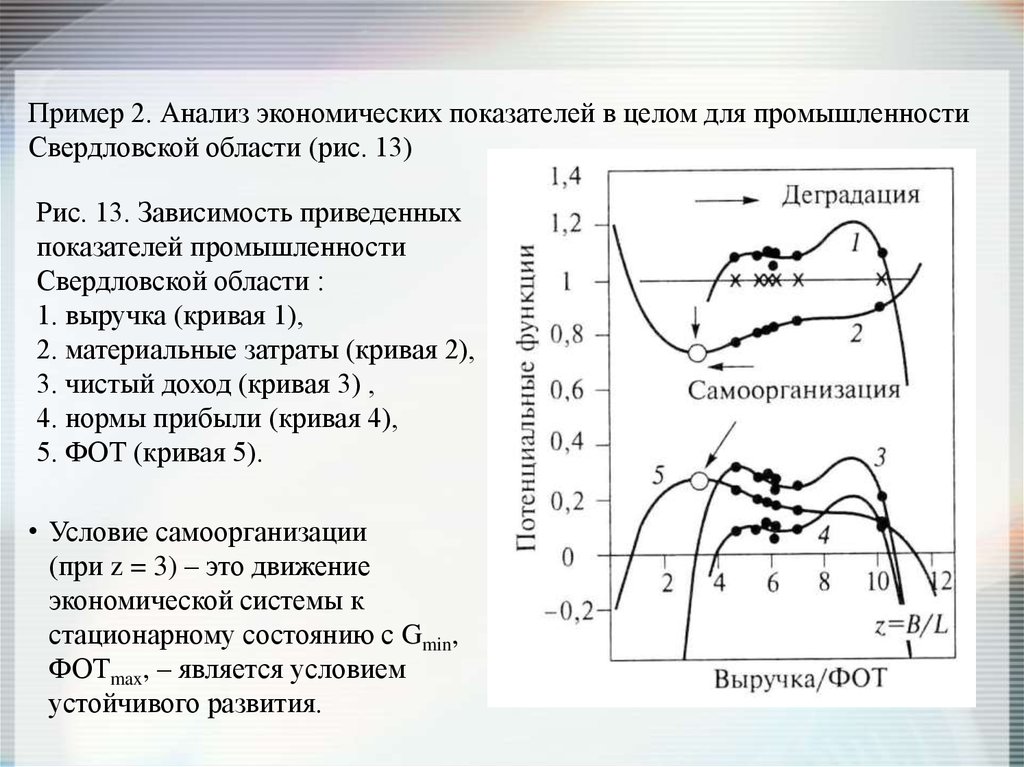
Пример 2. Анализ экономических показателей в целом для промышленности
Свердловской области (рис. 13)
Рис. 13. Зависимость приведенных
показателей промышленности
Свердловской области :
1. выручка (кривая 1),
2. материальные затраты (кривая 2),
3. чистый доход (кривая 3) ,
4. нормы прибыли (кривая 4),
5. ФОТ (кривая 5).
• Условие самоорганизации
(при z = 3) – это движение
экономической системы к
стационарному состоянию с Gmin,
ФОТmax, – является условием
устойчивого развития.

37.

Итак, результаты подтверждают возможность оценки
устойчивости при нелинейном развитии экономики региона.
Благодарю за внимание!