Нелинейные модели регрессии. (Лекция 7)

1.

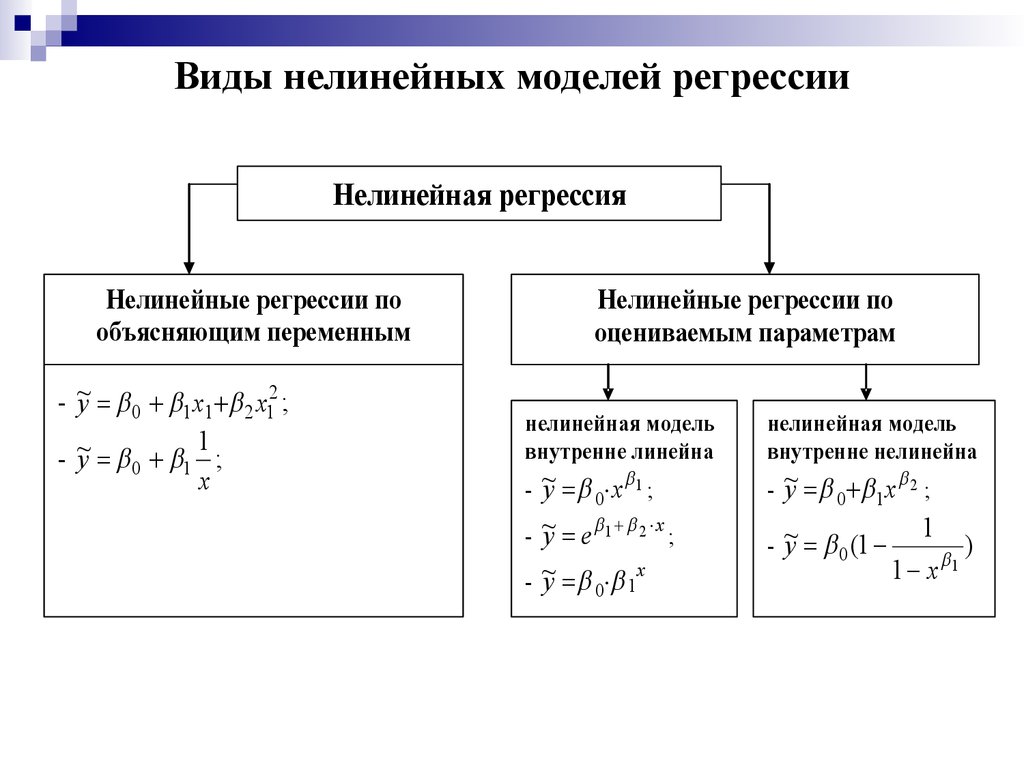
Нелинейные модели регрессии

2. Виды нелинейных моделей регрессии

Нелинейная регрессия
Нелинейные регрессии по
объясняющим переменным
- ~y 0 1 x1 2 x12 ;
1
- ~y 0 1 ;
x
Нелинейные регрессии по
оцениваемым параметрам
нелинейная модель
внутренне линейна
нелинейная модель
внутренне нелинейна
- ~
y e 1 2 x ;
- ~
y 0 (1
- ~
y 0 x 1 ;
- ~
y 0 1 x
- ~
y 0 1 x 2 ;
1
1 x
1
)

3. Подходы к оцениванию параметров нелинейных моделей регрессии

1. Линеаризация
- подбор преобразований к
анализируемым переменным y, x1 , x2 ,..., xk , которые позволили бы
представить искомую зависимость в виде линейного соотношения
между преобразованными переменными; другими словами.
Если 0 , 1 ,... p - искомые функции, которые определяют
переход
к
преобразованным
переменным,
т.е.
y* 0 ( y ), x1* 1 ( x1 ), ... x*p p ( x p ) ,
то связь между
y
и X ( x1 , x2 ,..., xk )
может быть представлена в виде линейной функции регрессии
X * , а именно:
yi* 0 1 xi* ... p x*p i ,
i 1, 2,..., n
y*
от

4. Подходы к оцениванию параметров нелинейных моделей регрессии

2.
В
случае
невозможности
линеаризации
модели
исследуется искомая регрессионная зависимость в терминах
исходных переменных:
yi f X i , i .
Если спецификация регрессионных остатков
i
соответствует
условиям классической модели, то для вычисления МНК-оценок
решается оптимизационная задача вида:
n
bМНК arg min ( yi f ( X i , )) 2
b
i 1

5. Некоторые виды нелинейных зависимостей, поддающиеся линеаризации

Зависимость гиперболического типа
1
ó
i ( 0 xi )
0
1
1. i
xi
f ( x, )
1 0
0
1 0
x
0
Рис.1
1
1
Преобразования объясняющей переменной x* , X * 1
x
x
1
ói 0 1 xi* i .
1
1
x2
...
....
1
1
xn
Т

6.

2. y i
1
, ( 0 x )
0 1 xi i
1
f ( x, )
f ( x, )
0
1
x
0
0
0
1
Рис. 2 а) 0 0, 1 0
x
Рис. 2 б ) 0 0, 1 0
1
1
Преобразования результативного признака y* , Y *
y
y1
ó*i 0 1 xi i
1
y2
...
1
yn
Т

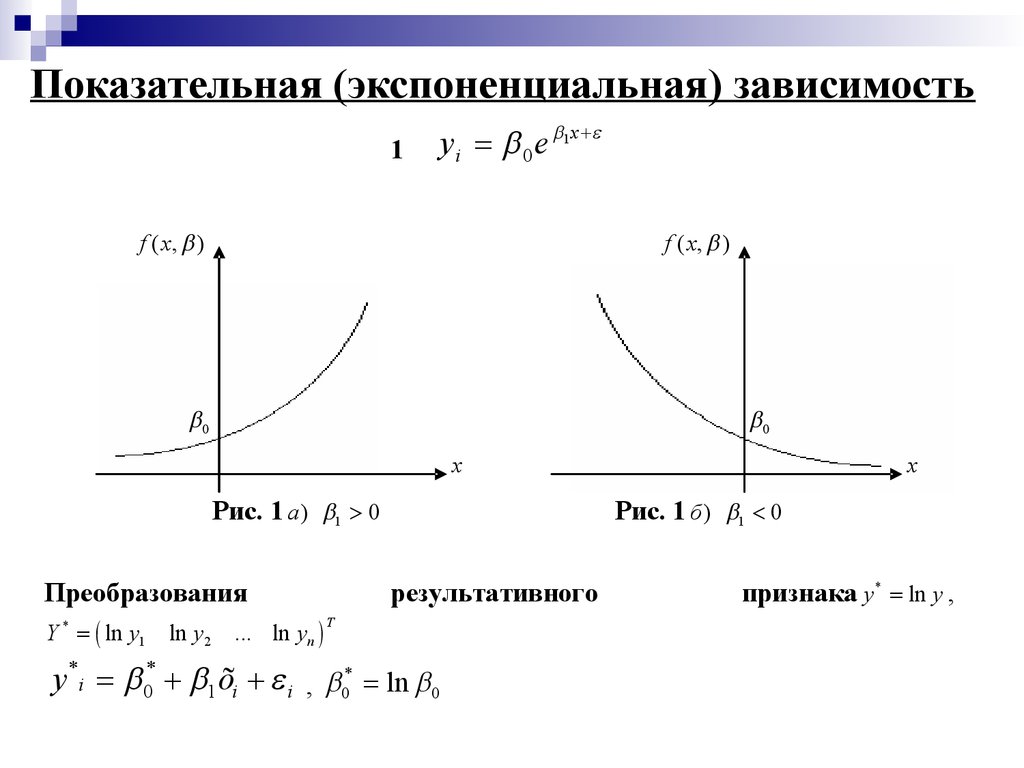
7. Показательная (экспоненциальная) зависимость

1
y i 0 e 1 x
f ( x, )
f ( x, )
0
0
x
Рис. 1 а ) 1 0
Преобразования
Y * ln y1
ln y2
... ln yn
x
Рис. 1 б ) 1 0
результативного
Т
y *i 0* 1 õi i , 0* ln 0
признака y* ln y ,

8.

2
f ( x, )
y i 0e
1
i
xi
f ( x, )
0
0
Рис. 2 а ) 1 0
Рис. 2 б ) 1 0
1
x
Преобразования переменных y * ln y , x* . Где 0* ln 0
Y * ln y1
ln y2
... ln yn
Т
1
*
и матрица X 1
x
1
1
1
x2
...
....
1
1
xn
Т

9.

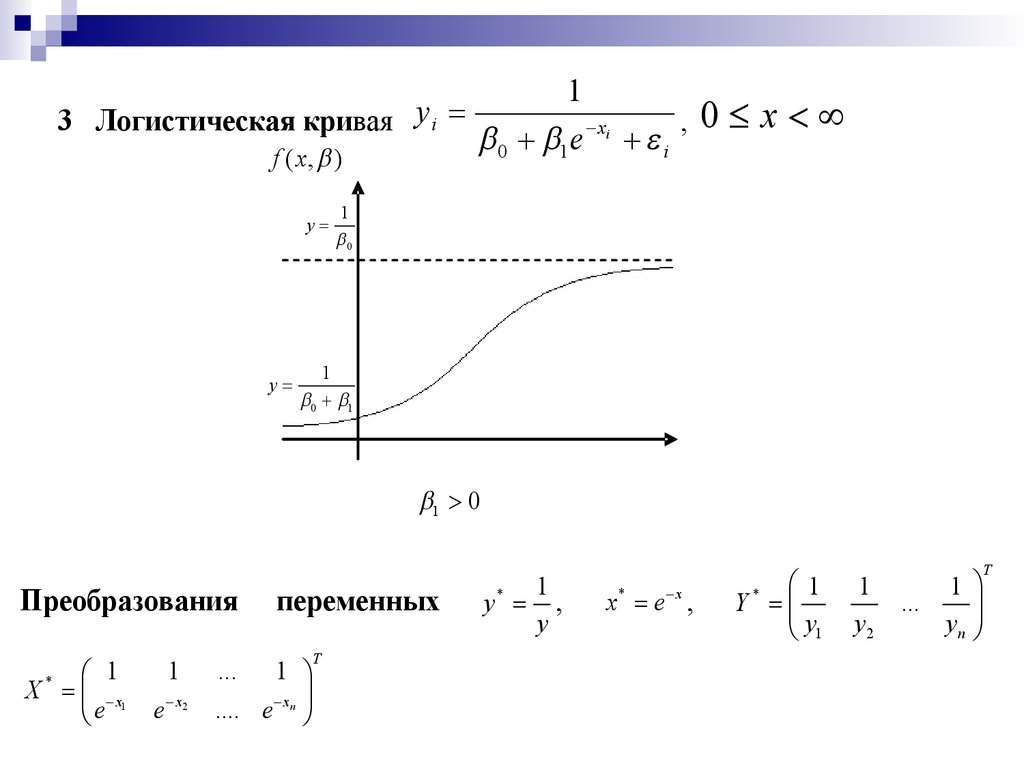
1
3 Логистическая кривая y i
, 0 x
xi
0 1e i
f ( x, )
y
y
1
0
1
0 1
1 0
Преобразования
1
X * x1
e
1
e x2
переменных
... 1
.... e xn
Т
1
y* ,
y
x* e x ,
1
Y*
y1
1
y2
...
1
yn
Т

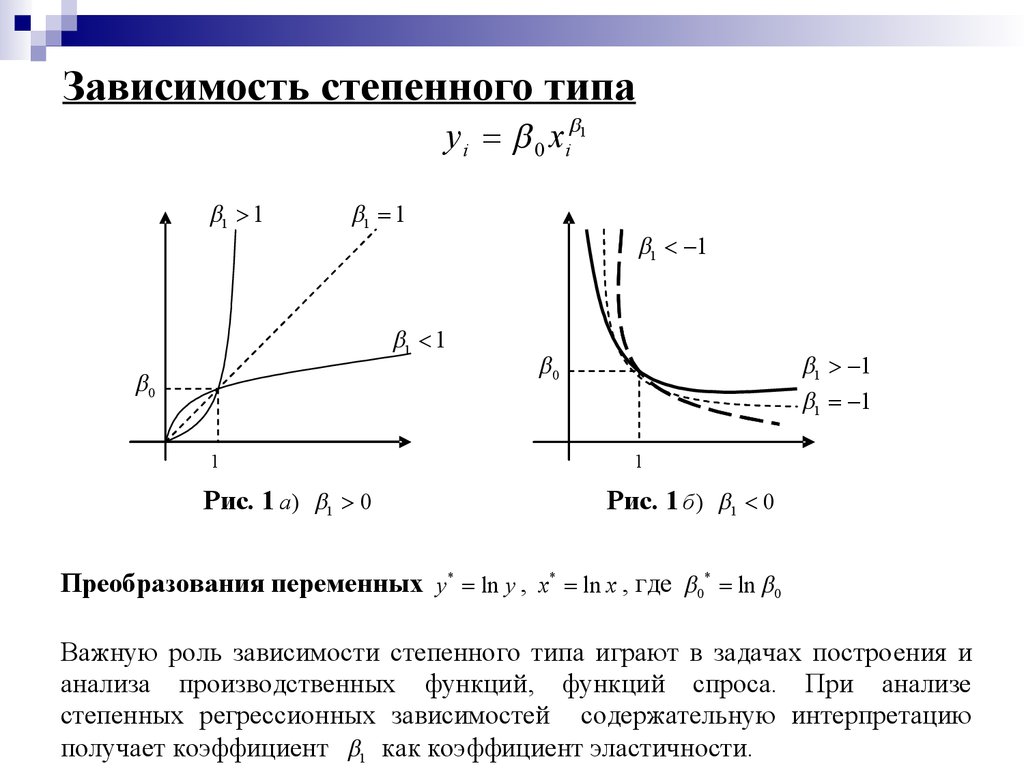
10. Зависимость степенного типа

y i 0 x i 1
1 1
1 1
1 1
0
1
Рис. 1 а) 1 0
1 1
0
1 1
1 1
1
Рис. 1 б ) 1 0
Преобразования переменных y* ln y , x* ln x , где 0* ln 0
Важную роль зависимости степенного типа играют в задачах построения и
анализа производственных функций, функций спроса. При анализе
степенных регрессионных зависимостей содержательную интерпретацию
получает коэффициент 1 как коэффициент эластичности.

11.

Метод Бокса-Кокса
Метод основан на степенном преобразовании переменных:
Y 1
X 1
Y ( )
, X ( )
, 0.
Линейная регрессия с учетом степенной трансформации переменных
примет вид:
Y ( ) 0 1 X 1 ( ) 2 X 2 ( ) ... k X k ( ) .
Задача состоит в определении оптимального . Наилучшим считается
то значение , при котором достигается максимум логарифма функции
правдоподобия:
n
n
2
ln L( ) ln ( ) ( 1) ln yi ,
2
i 1
где 2 ( ) – это оценка наибольшего правдоподобия для 2 при
данном .
Значение подбирают из диапазона от -2 до +2.