Similar presentations:
Экономическая и статистическая интерпретация линейной модели парной регрессии. Нелинейная регрессия. (Тема 2)
1. Тема 2. Экономическая и статистическая интерпретация линейной модели парной регрессии. Нелинейная регрессия.
1. Экономическая интерпретация параметров модели.Коэффициенты корреляции и детерминации в линейной
модели парной регрессии.
2. Оценка значимости уравнения регрессии в целом.
Оценка значимости отдельных параметров регрессии.
3. Расчет доверительных интервалов для параметров
регрессии. Интервалы прогноза по линейному уравнению
регрессии.
4. Нелинейная регрессия. Индекс корреляции.
5. Линеаризация нелинейных регрессий.
2.
1.Экономическая интерпретация параметров модели. Коэффициентыкорреляции и детерминации в линейной модели парной регрессии.
Коэффициент
регрессии b
Свободный
коэффициент a
• показывает среднее
изменение результата с
изменением фактора на
одну единицу
• b>0- связь прямая
• b<0- связь обратная
• Показывает значение Y при
х=0
• Если a>0, то Vx>Vy
• Если признак-фактор х не
имеет и не может иметь
нулевого значения, то
трактовка свободного
коэффициента а не имеет
смысла
3.
Задача: начальник отдела маркетинга кинотеатра«Отражение» поручил своим сотрудникам провести
исследование, в результате которого необходимо:
1) выявить фактор, в наибольшей степени влияющий на
среднее число зрителей за первые три дня проката
фильма;
2) построить прогнозную модель в виде линейной функции;
3) с помощью построенной модели получить прогнозные
оценки среднего числа зрителей на первые три дня проката
следующего фильма, при расходах на рекламу в 5000 руб.
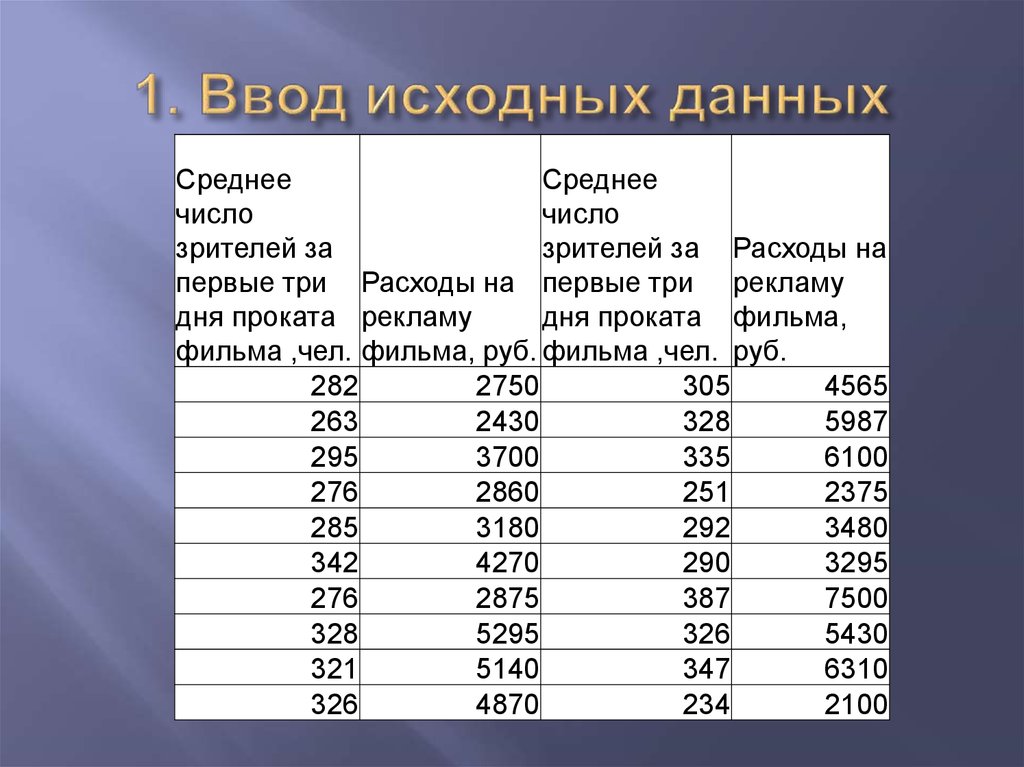
4. 1. Ввод исходных данных
СреднееСреднее
число
число
зрителей за
зрителей за Расходы на
первые три Расходы на первые три рекламу
дня проката рекламу
дня проката фильма,
фильма ,чел. фильма, руб. фильма ,чел. руб.
282
2750
305
4565
263
2430
328
5987
295
3700
335
6100
276
2860
251
2375
285
3180
292
3480
342
4270
290
3295
276
2875
387
7500
328
5295
326
5430
321
5140
347
6310
326
4870
234
2100
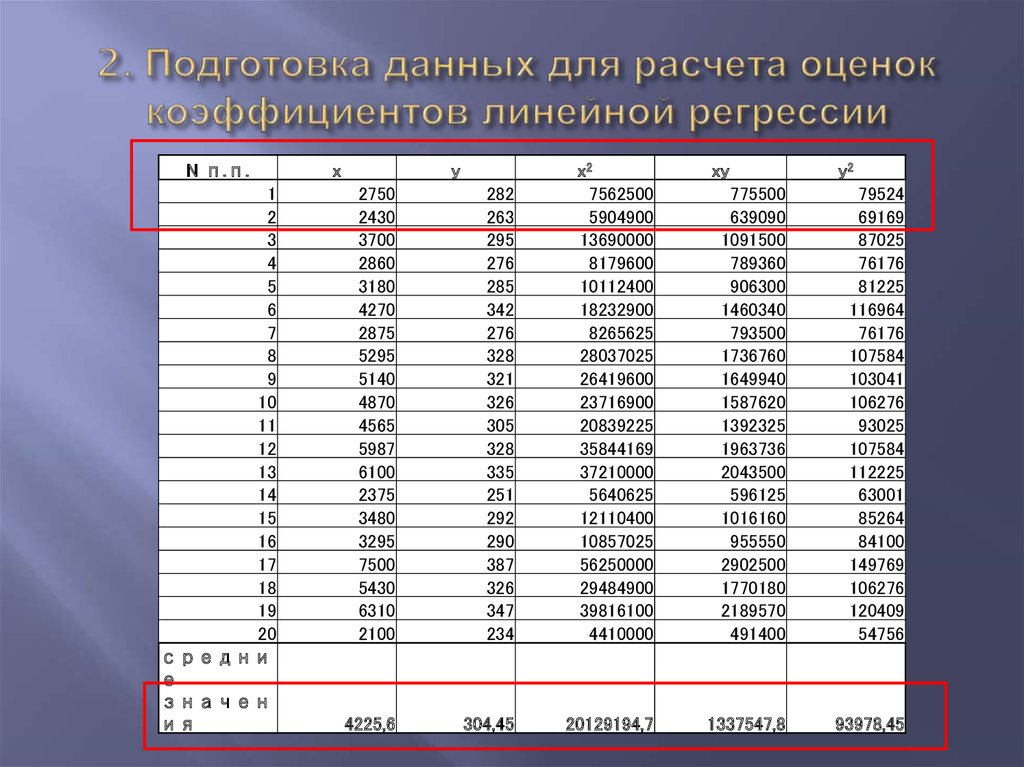
5. 2. Подготовка данных для расчета оценок коэффициентов линейной регрессии
N п.п.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
средни
е
значен
ия
2750
2430
3700
2860
3180
4270
2875
5295
5140
4870
4565
5987
6100
2375
3480
3295
7500
5430
6310
2100
282
263
295
276
285
342
276
328
321
326
305
328
335
251
292
290
387
326
347
234
x2
7562500
5904900
13690000
8179600
10112400
18232900
8265625
28037025
26419600
23716900
20839225
35844169
37210000
5640625
12110400
10857025
56250000
29484900
39816100
4410000
4225,6
304,45
20129194,7
x
y
xy
y2
775500
639090
1091500
789360
906300
1460340
793500
1736760
1649940
1587620
1392325
1963736
2043500
596125
1016160
955550
2902500
1770180
2189570
491400
79524
69169
87025
76176
81225
116964
76176
107584
103041
106276
93025
107584
112225
63001
85264
84100
149769
106276
120409
54756
1337547,8
93978,45
6. 3. Расчет оценок коэффициентов регрессии
a y b x,b
y x y x
x2 ( x )2
1337547,8 4225,6 304,5
b
0,022
2
20129194,7 4225,6
a 304,5 0,022 4225,6 209,541
y 209,541 0,022 x e
7.
Коэффициент b этой модели показывает, чтов среднем увеличение расходов на рекламу на
1000 рублей приводит к увеличению числа
зрителей за первые три дня проката фильма
на 22 человека.
8. Диаграмма Венна
2 вопросЕсли все точки лежат на построенной прямой, то регрессия Y на Х
«идеально» объясняет поведение зависимой переменной. Обычно
поведение Y лишь частично объясняется влиянием переменной Х.
X
Y
Y
X
Y
Y
X
Y=X
X
9. Линейный коэффициент парной корреляции
x cov( x, y ) yx y xryx b
y
x y
x y
1 ryx 1
Если b>0, то ryx>0; если b<0, то ryx<0
10.
По абсолютной величине чем ближе значение rxy к единице, темтеснее связь, чем ближе значение rxy к нулю, тем слабее связь
ryx 0,3 слабая
0,3 ryx 0,7 средняя
ryx 0,7 сильная , тесная
11.
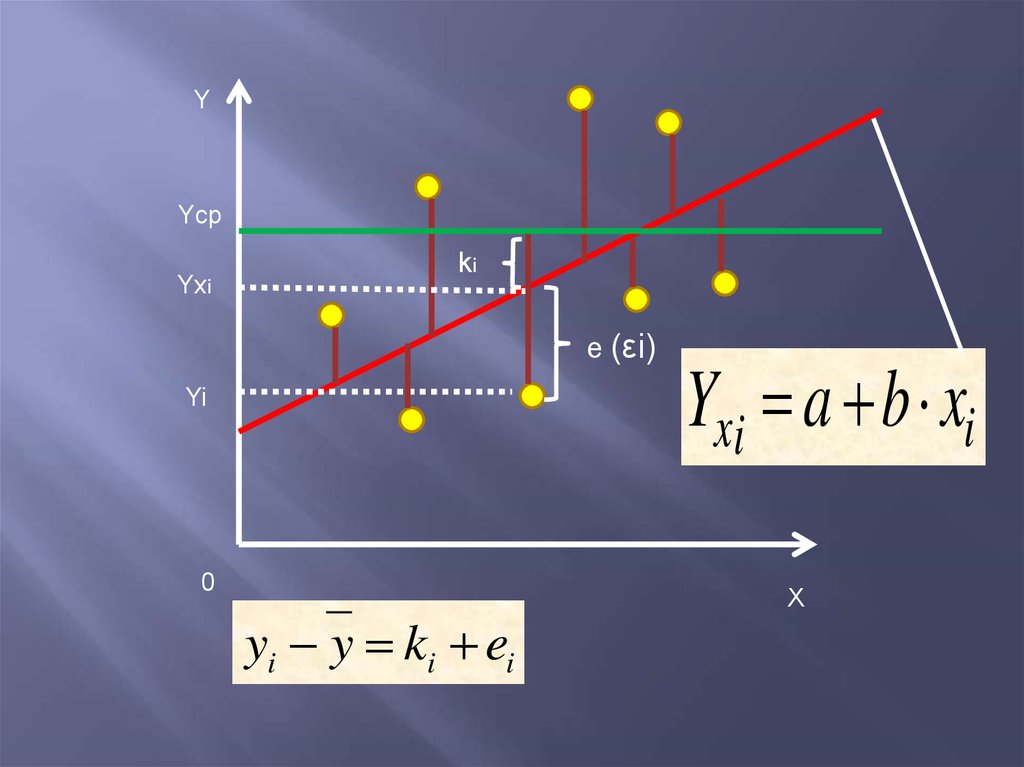
YYср
Yxi
ki
e (εi)
Yi
0
yi y ki ei
Yxi a b xi
X
12. Суммы квадратов отклонений
( yi y )2
( yx y)
2
( yi y x )
2
- Общая с. к.о. (TSS)
- Регрессионная с. к. о. (ESS)
- Остаточная с.к.о. (RSS)
2
2
2
(
y
y
)
(
y
y
)
(
y
y
)
i
x
i x
13. Выборочные оценки дисперсий
2S TSS
S
S
2
( yi y )
2
- Общая дисперсия
n 1
( yi y x )
RSS
2
n m 1
2
( yx y)
ESS
m
2
- Остаточная дисперсия
- Регрессионная дисперсия
14. Коэффициент детерминации
R2
( yx y)
2
( yi y)
R r
2
2
2
yx ;0
( yi y x )
1
2
( yi y)
2
R 1
2
Коэффициент детерминации определяет долю разброса
зависимой переменной Y, объяснимую регрессией Y на X.
15. 4. Расчет сумм квадратов отклонений
YN п.п.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
282
263
295
276
285
342
276
328
321
326
305
328
335
251
292
290
387
326
347
234
Yx
271,3073
264,12
292,6448
273,778
280,9653
305,4472
274,1149
328,4692
324,9879
318,9235
312,0731
344,0119
346,5499
262,8846
287,7035
283,5483
377,9946
331,5014
351,2666
256,708
(Yx-yср)2
1098,437
1626,512
139,3634
940,7733
551,53
0,994498
920,2195
576,9236
421,8037
209,4831
58,11144
1565,143
1772,403
1727,679
280,4463
436,8819
5408,806
731,7782
2191,796
2279,298
(y-Yx)2
114,3334
1,254327
5,547093
4,937407
16,2786
1336,104
3,553679
0,220181
15,90303
50,07641
50,02854
256,3804
133,4006
141,2447
18,46019
41,62469
81,09747
30,26539
18,20403
515,6537
(y-yср)2
504,0025
1718,103
89,3025
809,4025
378,3025
1410,003
809,4025
554,6025
273,9025
464,4025
0,3025
554,6025
933,3025
2856,903
155,0025
208,8025
6814,503
464,4025
1810,503
4963,203
22938,38
2834,568
25772,95
y 209,541 0,022 x e
Сумма
16. 5. Расчет коэффициентов корреляции и детерминации
x x 2 ( x )2 20129194 ,7 4225,62 1507 ,81y y 2 ( y )2 93978 ,45 304,452 35,90
x
1507 ,81
ryx b
0,022
0,94
y
35,90
22938 ,38
2834,57
R 0,94
1
0,89
25772 ,95
25772 ,95
2
2
17.
Коэффициент корреляции достаточновысокий (0,94), что свидетельствует о
существенной зависимости числа зрителей
за первые три дня проката фильма от
расходов на рекламу.
Коэффициент детерминации также
достаточно высокий, он показывает, что
89% разброса числа зрителей за первые
три дня проката фильма объясняется
зависимостью с расходами на рекламу.
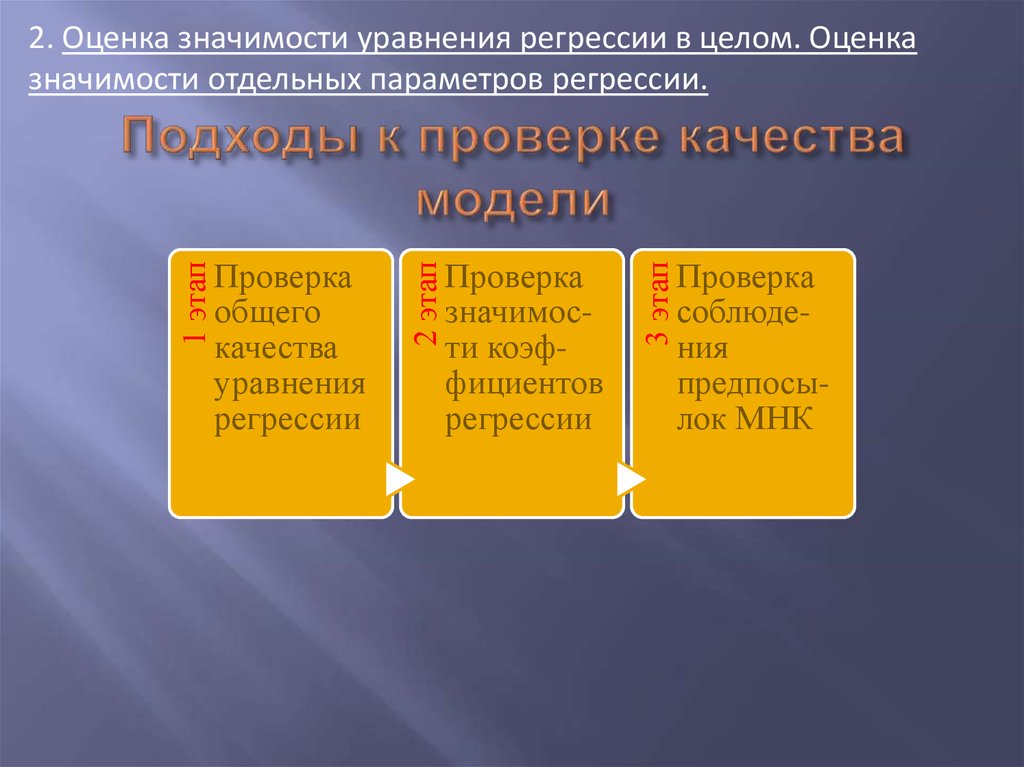
18. Подходы к проверке качества модели
Проверказначимости коэффициентов
регрессии
3 этап
Проверка
общего
качества
уравнения
регрессии
2 этап
1 этап
2. Оценка значимости уравнения регрессии в целом. Оценка
значимости отдельных параметров регрессии.
Проверка
соблюдения
предпосылок МНК
19. Оценка значимости уравнения регрессии в целом
F-тест (тест Фишера) состоит в проверке гипотезы H0 о статистическойнезначимости уравнения регрессии и показателя тесноты связи
H 0 : D 2 ESS D 2 RSS ( модельнезн ачима )
H1 : D 2 ESS D 2 RSS ( модельзнач има )
2
(
y
y
)
/m
x
r 2 xy
F
(n 2)
2
2
( yi y x ) /( n m 1) 1 r xy
F F ,v1 m ,v2 n m 1 H1
F F ,v1 m ,v2 n m 1 H 0
20. 1. Расчет выборочных оценок дисперсий
22938 ,38S ESS
22938 ,38
1
2834 ,57
2
S RSS
157 ,48
20 1 1
25772 ,95
2
S TSS
1356 ,47
20 1
2
21. 2. Расчет наблюдаемого значения Фишера и его сравнение с табличным
22938 ,38F
145,66
157 ,48
F0,05;1;18 4,41
145,66 4,41
Для нахождения табличного значения используем
функцию Excel FРАСПОБР (вероятность;
число степеней свободы «Регрессия»; число степеней
свободы «Остаток»)
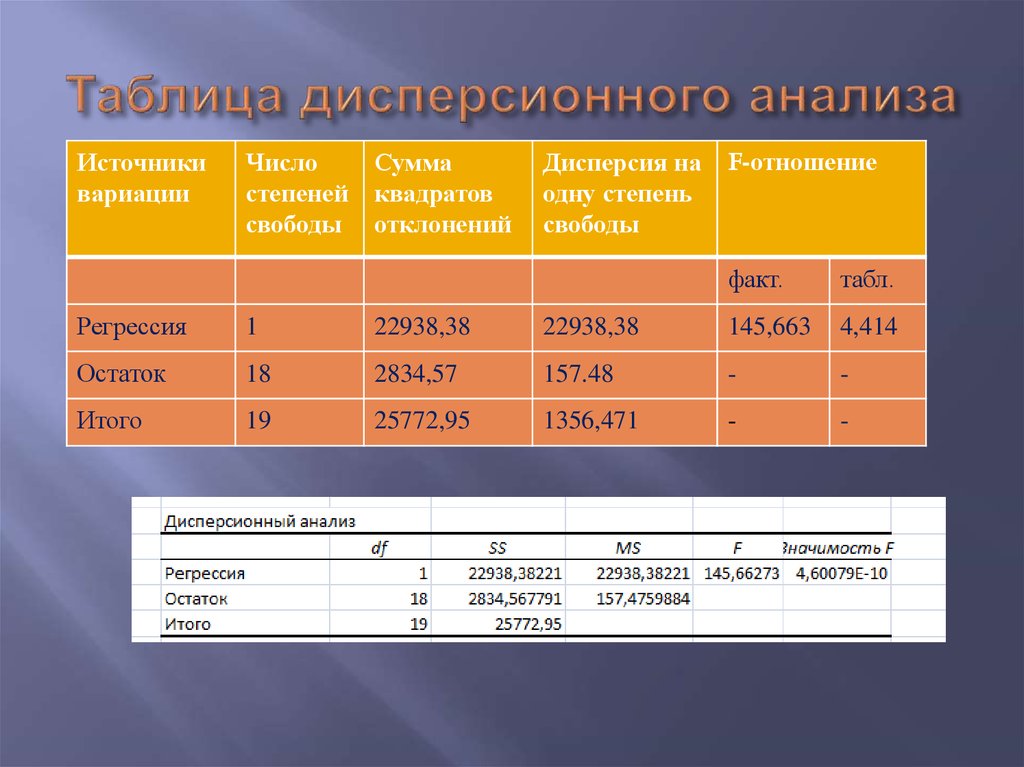
22. Таблица дисперсионного анализа
Источникивариации
Число
степеней
свободы
Сумма
квадратов
отклонений
Дисперсия на
одну степень
свободы
F-отношение
факт.
табл.
Регрессия
1
22938,38
22938,38
145,663
4,414
Остаток
18
2834,57
157.48
-
-
Итого
19
25772,95
1356,471
-
-
23. Оценка значимости отдельных параметров уравнения регрессии
T-тест (тест Стьюдента) состоит в проверке гипотезы Н0 о статистическойнезначимости коэффициентов регрессии и корреляции
b
t
mb
b
tb
mb
H0 : 0
H1 : 0
tb t / 2,n 2 H1
tb t / 2,n 2 H 0
24.
Стандартные ошибки параметроврегрессии
b
a
r
r
tb
; ta
; tr
n 2
2
mb
ma
mr
1 r
mb
2
(
y
y
)
x /( n 2)
( x x)
2
S 2 RSS
S RSS
2
( x x) x n
2
2
2
2
x
(
y
y
)
x
x
2
x
ma
S RSS 2 2 S RSS
2
(n 2)
n x
n x
n ( x x)
1 r2 2
mr
; t r t 2b F
n 2
25. 2. Расчет стандартных ошибок параметров регрессии
2S RSS
157 ,48
mb
0,002
2
45469986 ,8
(x x)
ma S RSS
x
n x
2
157 ,48
20129194 ,70 20
8,35
20 1 1
20 1507 ,81
26. 2. Расчет наблюдаемого значения Стьюдента и его сравнение с табличным
0,022209,54
tb
12,07; ta
25,10
0,002
8,35
t0,05;18 2,1009
12,07 2,10;
25,10 2,10.
Для нахождения табличного значения используем
функцию Excel СТЬЮДРАСПОБР (вероятность;
число степеней свободы «Остаток»)
27. Доверительные интервалы коэффициентов теоретического уравнения регрессии
3. Расчет доверительных интервалов для параметроврегрессии. Интервалы прогноза по линейному уравнению
регрессии.
b t / 2, n 2 mb ;
b b b b
a t / 2, n 2 ma ;
a a a a
28. 3. Расчет доверительных границ для параметров регрессии
b t / 2, n 2 mb 2,1009 0,002 0,0040,022 0,004 0,018
0,022 0,004 0,026
0,018 0,026
a t / 2, n 2 ma 2,1009 8,350 17,542
209,541 17,542 191,999
209,541 17,542 227 ,083
191,999 227 ,083
29. Предсказание среднего значения зависимой переменной
По уравнению регрессии определяется прогнозное значение зависимойпеременной Yx путем подстановки в уравнение прогнозного значения Xp.
Точечный прогноз дополняется интервальной оценкой прогноза Yx.
Yxp mYxp Y * Yxp mYxp ;
1 (x xp )
a b x p t / 2,n 2 S
2
n ( xi x)
2
30. Предсказание индивидуальных значений зависимой переменной
1 (x xp )a b x p t / 2,n 2 S 1
2
n ( xi x)
2
myxp – стандартная ошибка точечного прогноза
S2 – остаточная дисперсия на одну степень свободы
t – СВ, имеющая распределение Стьюдента с заданной вероятностью.
31. 6. Получение прогнозной оценки числа зрителей и расчет доверительных границ
Y * 209,541 0,022 5000 321,843 321S
2834 ,57
12,549 .
20 1 1
( x p x )2
1
a b x p t / 2, n 2 S 1
n ( xi x) 2
1 (5000 4225,6) 2
321 2,1009 12,549 1
294,658 295
20
45469986 ,8
1 (5000 4225,6) 2
321 2,1009 12,549 1
349,028 349 .
20
45469986 ,8
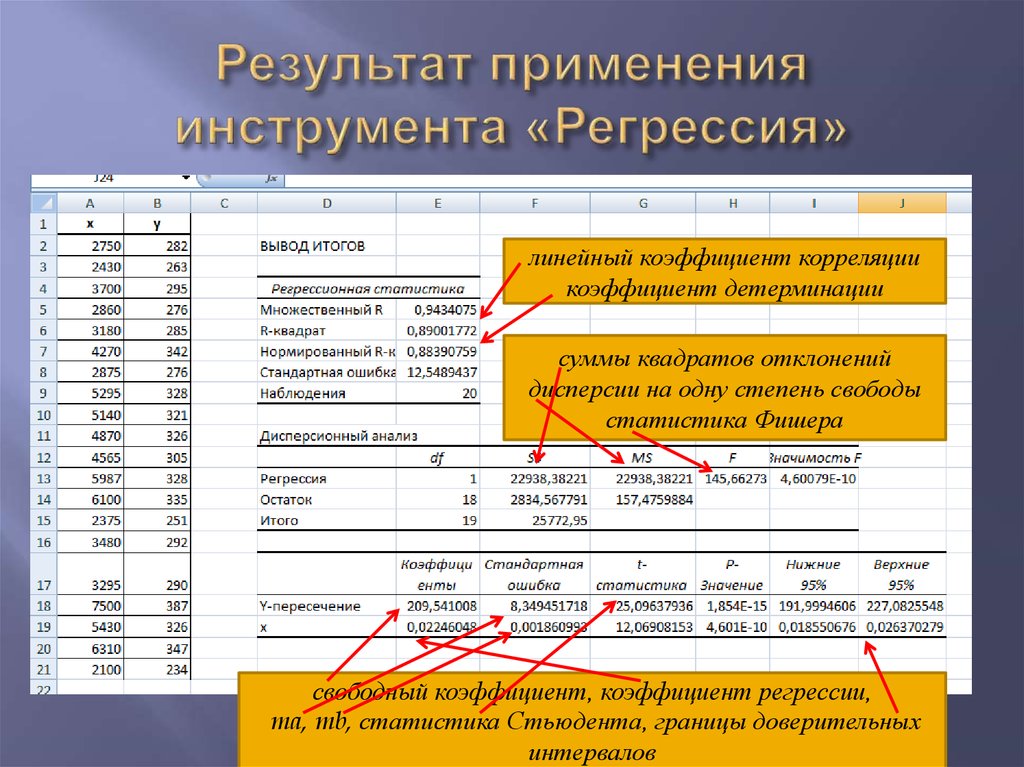
32. Результат применения инструмента «Регрессия»
линейный коэффициент корреляциикоэффициент детерминации
суммы квадратов отклонений
дисперсии на одну степень свободы
статистика Фишера
свободный коэффициент, коэффициент регрессии,
ma, mb, статистика Стьюдента, границы доверительных
интервалов
33.
4. Нелинейная регрессия. Индекс корреляции.Классы нелинейных регрессий
Регрессии, нелинейные
относительно
переменных
• линейные по
параметрам
Регрессии, нелинейные
по оцениваемым
параметрам
• линейные по
переменным
34.
Регрессии, нелинейныеотносительно переменных
y x a bx сx парабола
2
b
y x a гипербола
x
2
3
y x a bx сx dx полином
35.
Регрессии, нелинейные пооцениваемым параметрам
y x a x степенная
b
y x a b показательная
x
yx e
a bx
экспоненци альная
36.
Индекс корреляцииДля измерения тесноты связи между
переменными в нелинейных регрессиях
применяется индекс корреляции
R
(y y )
1
( y y)
2
x
2
37.
5. Линеаризация нелинейных регрессий.Способы линеаризации
Замена
переменных
Логарифмиро
вание обеих Комбиниро
частей
ванный
уравнения
38.
Замена переменных заключается в замененелинейных объясняющих переменных новыми
линейными переменными и сведении
нелинейной регрессии к линейной
Полиномиальная модель
y 0 1 x 2 x ... k x
2
k
y 0 1 z1 2 z2 ... k zk
39.
Гиперболическая модельy 0
1
x
y 0 1 z
1
1
1
z1 ; z 2 ;... z n
x1
x2
xn
40.
Кривая Филлипса (равносторонняя гипербола)х- норма безработицы,
y – процент прироста заработной платы
0
x
,
y
0 1 x 1
z 0 1 x
1
1
1
1
z1 , z 2 ,...z3
yn
y2
y1
41.
Кривая Энгелях- доход потребителей,
y – спрос на определенный вид товаров или услуг
0
x
,
y
0 x 1 x 1
z 0 1 z
x
1
1
1
z1 , z 2 ,...z3
yn
y2
y1
1
1
1
z1 , z 2 ,...z3
xn
x2
x1
42.
Полулогарифмические моделиln y 0 1 x
Такие модели обычно используются в тех случаях, когда
необходимо исследовать зависимость темпа роста или
прироста экономических показателей:
прирост объема выпуска от процентного увеличения
затрат ресурсов;
прирост бюджетного дефицита от темпа роста ВНП;
темп роста инфляции от объема денежной массы.
z ln y; z 0 1 x
43.
y 0 1 ln xИспользуется обычно в тех случаях, когда необходимо
исследовать , как процентное изменение независимой
переменной влияет на абсолютное изменение зависимой
переменной:
влияние относительного (процентного) увеличения
денежной массы на абсолютное изменение ВНП
z ln x; y 0 1 z
44.
Логарифмирование обеих частей уравненияприменяется обычно, когда мультипликативную модель
необходимо привести к линейному виду.
Степенные модели
1
2
k
y 0 x1 x2 ... x p
y ln y; x j ln x j ; ln ( j 1,2,...k )
y 0 1 x1 ... k xk , где 0 ln 0
45.
К классу степенных функций относятся:кривые спроса и предложения,
производственная функция Кобба-Дугласа,
кривые освоения для характеристики связи между
трудоемкостью продукции и масштабами производства в
период освоения и выпуска нового вида изделий,
зависимость валового национального дохода от уровня
занятости.
46.
Показательные (экспоненциальные) моделиШирокий класс экономических показателей характеризуется
приблизительно постоянным темпом относительного
прироста во времени. Этому соответствует следующая
форма зависимости показателя Y от времени X:
1 x
0
y e
y ln y
, (e 2,7182818).
y 0 1 x , 0 ln 0
b0 e
0
47.
Показательные (экспоненциальные) моделиy 0e
1
x
1
, (e 2,7182818).
1
y ln y, x
x
y 0 1 x , 0 ln 0
b0 e
0
48.
Логистическая криваяПрименяется для описания поведения показателей,
имеющих определенные «уровни насыщения»:
зависимость спроса на товар Y от дохода X,
развитие производства новых товаров,
рост численности населения (впервые применил
А. Кетле (1796-1874))
1
y
, ( x ).
x
0 1e
1
x
y ,x e
y
y 0 1 x
49.
Логлинейная модельИспользуется в банковском и финансовом анализе.
Y0 – начальная величина переменной Y (первоначальная
сумма вклада), r – сложный темп прироста величины Y
(процентная ставка); Yt – значение величины Y в момент
времени t (вклад в банке в момент времени t).
ln yt ln y0 t ln( 1 r ) ln
ln y0 0 , ln( 1 r ) 1 , ln t t
ln yt 0 1t t
50.
Коэффициент эластичностиВеличина коэффициента эластичности показывает, на
сколько процентов изменится результативный признак
Y, если факторный признак изменится на 1 %.
x
Ý f ( x)
y
Средний показатель эластичности:
x
Ý b
y
51.
Расчет коэффициента эластичностиФункция
y a bx
y a bx cx 2
y a
b
x
y ab x
Коэффициент эластичности
bx
a bx
(b 2cx) x
a bx cx 2
b
ax b
x ln b
52.
Расчет коэффициента эластичностиФункция
y ax b
y a b ln x
Коэффициент эластичности
b
b
a b ln x
c x
a
y
1 b e cx
1 cx
e 1
b
1
a bx
b x
a b x
y














































 mathematics
mathematics economics
economics








