Линейная парная регрессия

1. ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ

Лекция №2

2. ПОСТАНОВКА ЗАДАЧИ

Пусть объясняющая переменная X и объясняемая переменная Y
связаны соотношением:
Y=mX+b+ ,
Эта модель является регрессионной,
если MxY=mx+b, т. е. если М =0
где m и b - детерминированные величины, - случайное
возмущение.
Получены наблюдения: (x1,y1), (x2,y2), …, (xn,yn).
Требуется по наблюдениям
найти в некотором смысле
mˆ , bˆ
наилучшие оценки
значений m и b. Тогда оценивание Y по
известному x можно производить
(*)формуле:
yˆ mˆ x bˆ по
Далее дается два подхода к определению таких оценок и формулируются условия,
при которых эти подходы дают одинаковый результат.

3.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
(МНК)
Обозначим:
yˆi mˆ xi bˆ, ei yi yˆi ,
n
n
n
Qe ei ( yi yˆi ) ( yi mˆ xi bˆ) 2
2
i 1
i 1
2
i 1
y
yi
Qe- остаточная сумма
ei
поле корреляции
yˆ i
xi
x

4.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Параметры регрессии определяются из условия минимума
остаточной суммы:
n
2
ˆ
Qe ( yi mˆ xi b ) min
i 1
mˆ ,bˆ

5.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Необходимое условие экстремума:
n
Qe
ˆ mˆ xi ) 0
2
(
y
b
i
bˆ
i 1
n
Q
e
2 ( yi bˆ mˆ xi ) xi 0
mˆ
i 1
Откуда получаем нормальную систему уравнений:
n
n
ˆ
xi yi
bn mˆ i
1
i 1
(1)
n
n 2
n
bˆ x mˆ x x y
i
i i
i 1 i
i 1
i 1

6.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Тогда из (1) получим:
Обозначим:
n
xi
x i 1 среднее _ значение _ х,
n
n
yi
y i 1 среднее _ значение _ y,
n
n
__
xi yi
xy i 1
n
__
n
xi
, x 2 i 1
n
2
bˆ mˆ x y
__
__ ( 2)
bˆx mˆ x 2 xy
Решая систему (2), найдем:
__
ˆ
m
xy x y
__
2
x x
ˆ x.
bˆ y m
2
,
(3)
mˆ - выборочный коэффициент
регрессии

7.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
sx-выборочное среднее
квадратичное отклонение x
n
1
s x 2 x 2 x 2 ( xi x ) 2 - выборочная дисперсия Х
Заметим, что
__
n i 1
__
1 n
- выборочная
Coˆv( X , Y ) xy x y ( xi x )( yi y )
ковариация ХиY
n i 1
С учетом этих обозначений получим:
mˆ
Coˆv( X , Y )
sx
2
(4)

8.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Из (3): прямая y bˆ mˆ x проходит через точку ( x , y )
y
(xi,yi)
y bˆ mˆ x
y
x
x

9.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
При М i=0, i=1,…,n, (отсутствии систематических ошибок)
уравнение y b mx является уравнением регрессии, т. е.
M x y b mx.
Внимание! При получении МНК-оценок параметров b и m
не использовалось никаких предположений о распределении X и Y.

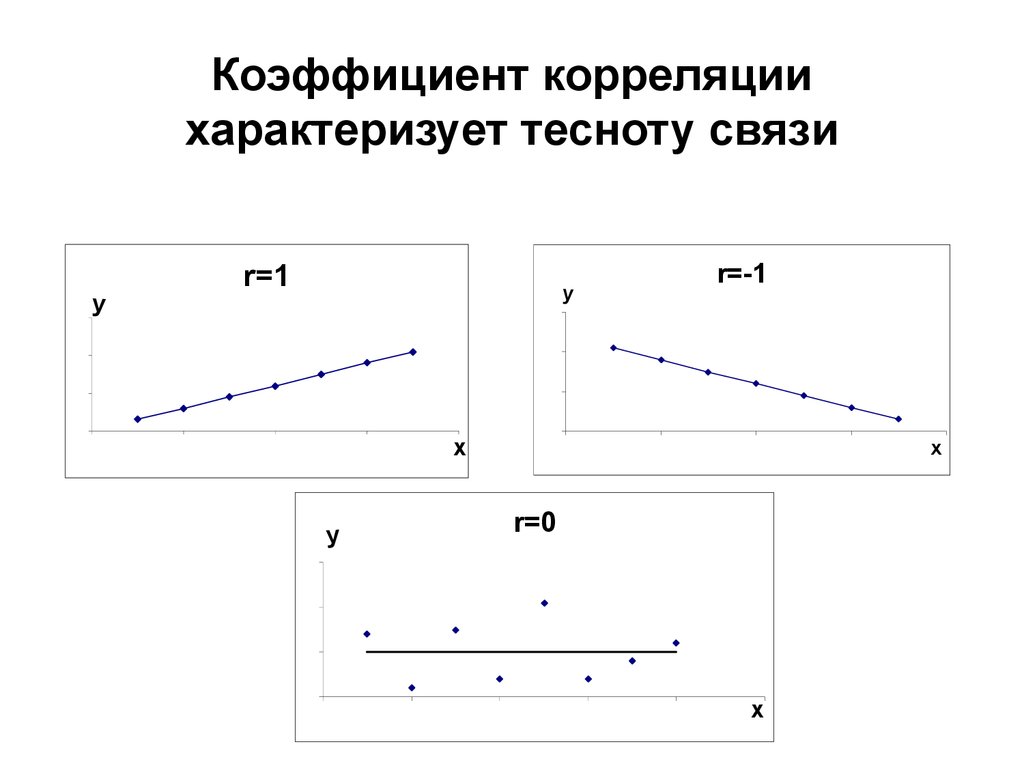
10. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Подставим (3) в yˆ bˆ mˆ x (*)
yˆ y mˆ x mˆ x
yˆ y mˆ ( x x )
Представим последнее соотношение в эквивалентном виде:
sx x x
yˆ y
mˆ
,
sy
s y sx
где sx, sy - выборочные средние квадратичные отклонения x и y.
Здесь используются нормированные и центрированные значения x, y.
Нормирование позволяет избежать зависимости от их единиц измерения.
Центрирование позволяет работать с приращениями.

11.

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Обозначив
получим
sx
r mˆ ,
sy
r - выборочный
коэффициент корреляции
yˆ y
x x
r
(**)
sy
sx
Коэффициент корреляции показывает, насколько величин sy
в среднем изменится y, если x изменится на sx.
Коэффициент корреляции характеризует тесноту связи X и Y.

12.

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
С учетом (4) получаем:
Coˆv( X , Y )
r
sx s y
Эта формула обычно используется как
определение выборочного коэффициента
корреляции
Для расчетов по таблице наблюдений применяется формула:
r
n
n
n
i 1
i 1
i 1
n xi yi ( xi )( yi )
n
2
n
n xi ( xi )
i 1
i 1
2
n
2
n
n yi ( yi ) 2
i 1
i 1

13. Свойства коэффициента корреляции

• 1. -1 r 1. Чем ближе r к 1, тем теснее связь.
• 2. При r= 1 корреляционная связь - линейная
(наблюдения располагаются на прямой)
• 3.
При r=0 связь отсутствует, линия регрессии
параллельна оси ОХ.

14. Коэффициент корреляции характеризует тесноту связи

y
r=1
y
r=-1
x
y
x
r=0
x

15.

Коэффициент корреляции
характеризует тесноту связи
слабая связь, r близок к 0
тесная связь, r близок к 1
x
x

16.

Классическая нормальная
линейная регрессионная
модель
Предположим, что:
X - детерминированная величина;
1, …, n- независимые нормальные одинаково распределенные
случайные величины: i~N(0, 2).
В этих предположениях соотношение
Y=mX+b+
называется классической нормальной линейной регрессионной
моделью
(Classical Normal Linear Regression model).

17.

МЕТОД МАКСИМАЛЬНОГО
ПРАВДОПОДОБИЯ
Для упрощения выкладок можно вместо функции (5) максимизировать ее
логарифм (т. к. логарифм - монотонная функция):
n
ln P ln( 2 ) ( yi b mx i ) 2 ln( 2 ) Qe (6)
i 1
Из (6) следует, что при известной дисперсии 2 для нахождения
оценок МП достаточно минимизировать Qe , и, следовательно,
МП-оценка совпадает с НК-оценкой.

18. Свойства оценок: несмещенность

~
Оценка n является несмещенной оценкой параметра , если:
~
M n
Математическое ожидание оценки равно оцениваемому параметру.
МП-оценки могут иметь смещение!

19. Свойства оценок: состоятельность

Обозначим
~
по n наблюдениям.
n-оценка параметра , полученная
~
~
nназывается состоятельной оценкой, если n сходится по
вероятности к
:
для состоятельной
несмещенной
оценки выполняется
закон больших чисел
~
n
P
n
или
0
lim
n
~
P n 1

20.

Свойства оценок:
состоятельность
Другая формулировка закона больших чисел -
неравенство Чебышева:
0
D~
~
~
n
P n M n 2
Может использоваться для определения необходимого числа
наблюдений, если задано допустимое отклонение оценки от
оцениваемого параметра и допустимая вероятность отклонения.

21. Свойства оценок: эффективность

Эффективной называется оценка, обладающая минимальной
дисперсией:
~
*
D n D n
*
n -любая другая оценка.
Для несмещенных оценок:
~
M ( n ) 2 M ( *n ) 2

22.

Несмещенность оценок
параметров регрессии
__
ˆ
m
xy x y
__
2
x x2
ˆ x.
bˆ y m
,
формула (3)
Доказательство несмещенности параметра m:
__
xy x y
ˆ
Mm M __
2 x2
x

23.

Несмещенность оценок
параметров регрессии
В силу детерминированности
X, свойств математического ожидания
__
и определения x , y , xy
1 n 1 n
1 n
1 n
M xi yi x yi
xi My i x My i
n i 1
n i 1 n i 1
n i 1
Mmˆ
__
__
2 x2
2 x2
x
x
Так как Myi=mxi+b, то, после приведения подобных членов,
получаем
Mmˆ m,
что и требовалось доказать

24.

Несмещенность оценок
параметров регрессии
Доказательство несмещенности параметра b:
Mbˆ M y mˆ x
В силу свойств математического ожидания и детерминированности X,
получаем: Mbˆ My x Mm
ˆ.
Так как Mmˆ m
и по определению y имеем:
n
1
Mbˆ M yi x m
n i 1

25.

Несмещенность оценок
параметров регрессии
Так как Myi=mxi+b, и в силу свойств математического ожидания
получаем:
n
n
1
1
Mbˆ (mxi b) mx m x i b mx mx mx b b,
n i 1
n i 1
что и требовалось доказать

26. Теорема Гаусса-Маркова

В условиях классической нормальной регрессионной
модели оценки (3) имеют наименьшую дисперсию в
классе всех линейных несмещенных оценок.
(3) - самые эффективные оценки Best Linear Unbiased Estimates (BLUE)

27. ОЦЕНИВАНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙ

n
1
2
2 Qe
ˆ ei
n i 1
n
Оценка
максимального правдоподобия
n
Qe
1
2
2
s
ei
n 2 i 1
n 2
где
ei y i yˆ i y i bˆ mˆ xi
Оценки b, m, независимы
?для нормированных наблюдений
Несмещенная оценка
Число неизвестных
параметров (m, b)

28.

ОЦЕНКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ
Обозначим:
yˆ i mˆ xi bˆ, ei yi yˆ i ,
n
n
2
n
Qe ei ( yi yˆ i ) ( yi mˆ xi bˆ) 2
i 1
2
i 1
i 1
y
yi
y
Qe- остаточная сумма
yˆi y
ei
поле корреляции
yˆ i
xi
x

29. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ

30. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ

• Чем меньше остаточная сумма Qe, тем выше
качество модели.
• Чем больше регрессионная сумма QR, тем
выше качество модели.
• Чем больше отношение QR/Qe, тем выше
качество модели.
• Для перехода к стандартному распределению
следует рассматривать не суммы, а средние
квадраты.

31.

ОЦЕНКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ
Q Q Qe
2Можно2доказать, что
sR ~ ( p)
R
se2 ~ 2 (n p 1) ВМаркова
условиях теоремы ГауссаQR
sR2
QR (n p 1)
p
F
2
Qe
Qe p
se
n p 1
F статистика _ с _ степенями _ свободы
k1 p, k2 n p 1

32.

ОЦЕНКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ
F показывает, в какой мере регрессия лучше оценивает значение
зависимой переменной по сравнению с ее средним значением
При
(!)
F f ,k1,k 2
гипотеза (предположение) о незначимости
регрессии отклоняется
с уровнем значимости .
Неравенство (!) - правило (критерий) проверки гипотезы
о незначимости линейной регрессии,
f ,k1,k2 – квантиль распределения Фишера, критическое (пороговое) значение F,
- вероятность отклонения гипотезы при условии, что она верна вероятность ошибки первого рода.

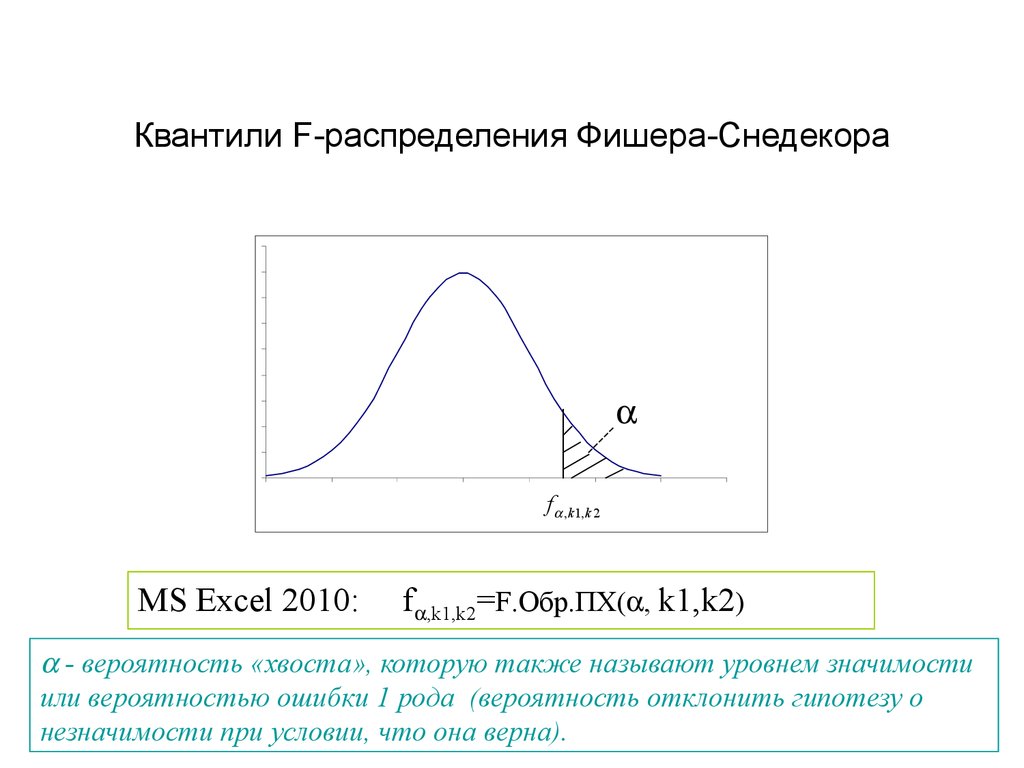
33. Квантили F-распределения Фишера-Снедекора

f ,k1,k 2
MS Excel 2010:
f ,k1,k2=F.Обр.ПХ( , k1,k2)
- вероятность «хвоста», которую также называют уровнем значимости
или вероятностью ошибки 1 рода (вероятность отклонить гипотезу о
незначимости при условии, что она верна).

34.

ОЦЕНКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ
Коэффициент детерминации: R 2 QR 1 Qe
Q
Q
Коэффициент детерминации показывает, какая часть изменения
зависимой переменной объясняется изменением объясняющей
переменной.
2
0 R 1
1. Чем ближе R2 к единице, тем лучше регрессия аппроксимирует
наблюдения.
2. Если R2=1, то наблюдения лежат на линии регрессии.
3. Если R2=0, то изменение зависимой переменной полностью
обусловлено неучтенными в модели факторами, и линия
регрессии параллельна оси ОХ.

35. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ

Можно доказать, что в случае парной регрессии:
R2=r2

36. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ

• QR>Qe – регрессионная модель
значима;
• QR<Qe – регрессионная модель
незначима;
• QR=Qe – граничный случай; R2=0.5;
• R2 0.5 (r 0.7) – регрессионная
модель значима.

37.

ОЦЕНКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ
Критерий (!) проверки гипотезы о незначимости регрессии
может использовать значение R2 :
QR (n p 1) QR (n p 1)
F
Qe p
(Q QR ) p
R 2 (n ( p 1))
f , p ,n ( p 1)
2
(1 R ) p
Статистика F Фишера (Фишера-Снедекора) и коэффициент
детерминации R2 связаны друг с другом

38.

ОЦЕНКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ
Другой способ оценки значимости уравнения ПАРНОЙ регрессии -
проверка гипотезы m=0
если m=0, то y не зависит от x.
Можно ли по значению оценки m судить о справедливости этой гипотезы?
2
mˆ ~ N (m, m
ˆ)
Если гипотеза верна, то m
ˆ ~ N (0, 2ˆ )
mˆ
P
x
mˆ
m
большие значения оценки
маловероятны
х - квантиль стандартного нормального
распределения, - суммарная вероятность
двух «хвостов» (в эконометрике =0.05)
СКО оценки m не знаем, используем выборочное СКО:

39. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ

СКО оценки m не знаем, используем выборочное СКО:
mˆ
P
t ;n 2
smˆ
mˆ
Tn 2
smˆ
-статистика Стьюдента с числом степеней
свободы n-2, t ;n-2 – ее квантиль уровня
(суммарная вероятность двух «хвостов»)
Правило проверки гипотезы о незначимости
уравнения регрессии: гипотеза отклоняется при
Tn-2 >t ,n-2,
(!!)

40. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ

Для парной регрессии правила(!) и (!!) эквиваленты и
F=T2,
2
f a;1;n 2 t
;n 2
Для парной регрессии значимость уравнения регрессии эквивалентна
значимости коэффициента регрессии

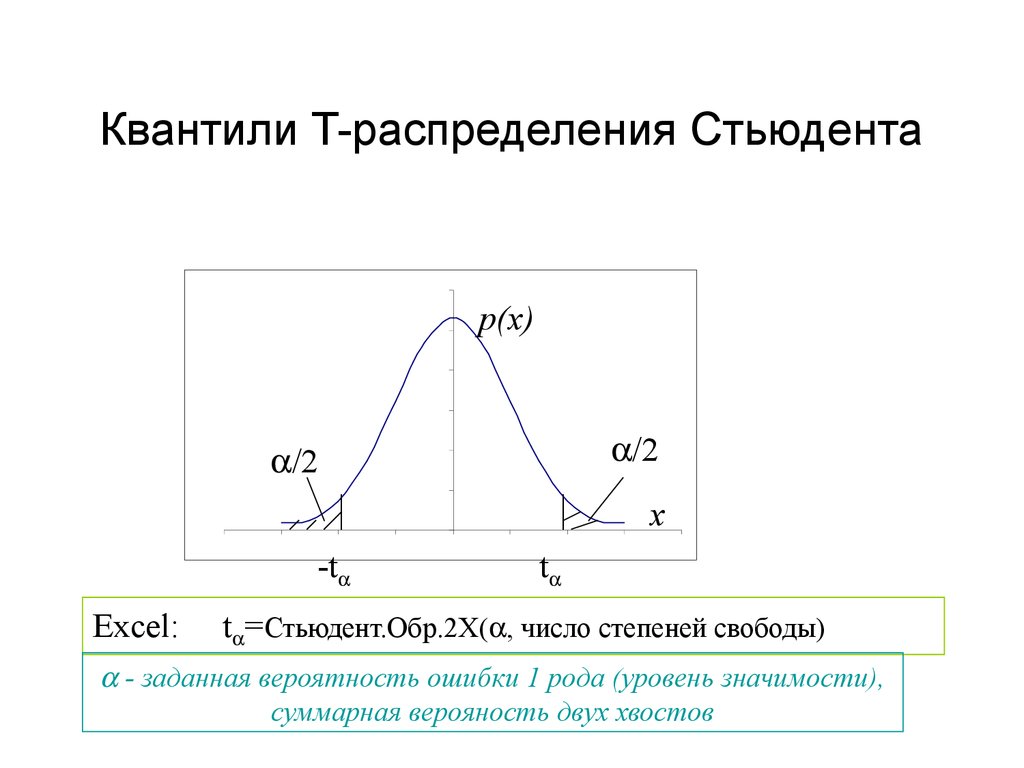
41. Квантили T-распределения Стьюдента

p(x)
/2
/2
x
-t
Excel:
t
t =Стьюдент.Обр.2Х( , число степеней свободы)
- заданная вероятность ошибки 1 рода (уровень значимости),
суммарная верояность двух хвостов