Similar presentations:
Парная регрессия и корреляция
1.
Тема 2. Парная регрессия икорреляция.
Вопросы
Статистическая
зависимость
(независимость)
случайных переменных. Ковариация.
Анализ линейной статистической связи экономических
данных,
корреляция;
вычисление
коэффициентов
корреляции.
Линейная модель парной регрессии.
Оценка параметров модели с помощью метода
наименьших квадратов (МНК).
Оценка существенности параметров линейной регрессии.
Интервалы прогноза по линейному уравнению регрессии.
Нелинейные модели и их линеаризация
2.
Категории зависимости:1) функциональные;
2) корреляционные.
Корреляционные связи:
1) между
изменением
факторного
и
результативного признака нет полного
соответствия,
2) воздействие
отдельных
факторов
проявляется лишь в среднем при массовом
наблюдении фактических данных.
3) Одновременное воздействие на изучаемый
признак большого количества самых
разнообразных факторов приводит к тому,
что одному и тому же значению признакафактора
соответствует
целое
распределение значений результативного
признака, поскольку в каждом конкретном
случае прочие факторные признаки могут
изменять силу и направленность своего
воздействия.
Функциональные связи
характеризуются:
1) полным соответствием между
изменением факторного признака
и изменением результативной
величины
2) каждому значению признакафактора соответствуют вполне
определенные
значения
результативного признака.
3) Функциональная
зависимость
может связывать результативный
признак с одним или несколькими
факторными признаками.
3.
Задачи корреляционного анализа:1) выявлении взаимосвязи между случайными переменными путем точечной и
интервальной оценки парных (частных) коэффициентов корреляции, вычисления и
проверки значимости множественных коэффициентов корреляции и детерминации.
2) отбор факторов, оказывающих наиболее существенное влияние на результативный
признак, на основании измерения степени связи между ними;
3) обнаружение ранее неизвестных причинных связей.
При проведении корреляционного анализа вся совокупность данных
рассматривается как множество переменных (факторов), каждая из которых содержит
n –наблюдений.
При изучении взаимосвязи между двумя факторами их, как правило, обозначают
X= ( x , x ,..., x ) и Y= ( y1 , y2 ,..., yn )
1
2
n
Ковариация - это статистическая мера
взаимодействия двух переменных.
4.
Ковариация между двумя переменными Х и У рассчитывается следующимобразом:
1 n
Cov( X , Y )
( xi x )( yi y )
n 1 i 1
где ( x1 , y1 ), ( x2 , y2 ),...,( xn , yn ) - фактические значения случайных переменных X и Y,
или
1 n
1 n
y
y
n
i 1
x
i
xi
n
i 1
Вычисление коэффициента парной корреляции.
Коэффициент парной корреляции
Для двух переменных Х и У коэффициент парной корреляции определяется
следующим образом:
n
n
rx, y
Где S 2 1
x
Cov( Х , Y )
Sx S y
(x
n 1
i
=
x )2
1
S y2
( yi y ) 2
и
n 1
- оценки дисперсий величин
1
( xi x )( yi y )
n 1 i 1
Sx S y
( x x )( y y )
i
i 1
i
n
(x x ) ( y y)
i 1
(1)
n
2
i
i 1
i
2
5.
Дисперсия (оценка дисперсии)n
1
2
S x2
(
x
x
)
i
n 1 i 1
характеризует степень разброса значений х1, х2, х3, …, хn (у1, у2, у3, …, уn )
вокруг своего среднего x ( y , соответственно) ), или вариабельность
(изменчивость) этих переменных на множестве наблюдений.
В общем случае для получения несмещенной оценки дисперсии
сумму квадратов следует делить на число степеней свободы оценки (n−p),
где n - объем выборки, p - число наложенных на выборку связей. В данном
случае p = 1, т.к. выборка уже использовалась один раз для определения
среднего X, поэтому число наложенных связей равно единице, а число
степеней свободы оценки (т.е. число независимых элементов выборки)
равно (n −1).
6.
Среднеквадратическое отклонение или стандартное отклонение, илистандартная ошибка переменной Х (переменной Y)
Sx S
2
x
Оценка значимости коэффициента корреляции при малых объемах
выборки выполняется с использованием t - критерия Стьюдента. При этом
фактическое (наблюдаемое) значение этого критерия определяется по
формуле:
tнабл
ry2, x
1 r
2
y,x
(n 2)
7. Парная линейная регрессия
Парная регрессия – это уравнение связи двух переменныхх и у
y f (x)
где
х - независимая, объясняющая переменная
(признак-фактор),
у
- зависимая переменная
(результативный признак).
Замечание. Число наблюдений должно в 7-8 раз превышать
число рассчитываемых параметров при переменной .
8.
Пусть имеется набор значений двух переменных: Y= (у1, у2, у3, …, уn)- объясняемая переменная и X= (х1, х2, х3, …, хn) - объясняющая переменная,
каждая из которых содержит n наблюдений, между которыми теоретически
существует некоторая линейная зависимость
Y f ( X ) f ( x1, x2 ,...xn ) x
Учитывая возможные отклонения, линейное уравнение связи двух
переменных (парную регрессию) представим в виде:
yi xi i
(2)
где - α постоянная величина (или свободный член уравнения),
- β коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны
данные наблюдений. Это показатель, характеризующий изменение переменной yi , при
изменении значения xi на единицу.
Если β > 0 - переменные xi и yi положительно коррелированные, если β 0 –
отрицательно коррелированны; εi - случайная переменная, или случайная
составляющая, или остаток, или возмущение. Она отражает тот факт, что изменение
yi будет неточно описываться изменением Х – присутствуют другие факторы,
неучтенные в данной модели.
9.
Таким образом, в уравнении (2) значение каждого наблюдения yi представленокак сумма двух частей — систематической xi и случайной εi
yˆi xi
таким образом
Y = Yˆ +
Предпосылки метода наименьших квадратов.
1) Математическое ожидание случайной составляющей
наблюдении должно быть равно нулю.
в
любом
M ( i ) = 0
2) Второе условие состоит в том, что в модели (2) возмущение εi (или
зависимая переменная уi) есть величина случайная, а объясняющая
переменная xi- величина неслучайная.
3) Третье условие предполагает отсутствие систематической связи между
значениями случайной составляющей в любых двух наблюдениях.
M ( i , j ) = 0 (i j )
4) Дисперсия случайной составляющей должна быть постоянна для всех
наблюдений.
5) Предположение о нормальности
10.
Свойства оценок МНК.1. Несмещенность оценки означает, что математическое ожидание
остатков равно нулю.
2. Оценки считаются эффективными, если они характеризуются
наименьшей дисперсией.
3. Состоятельность оценок характеризует увеличение их точности с
увеличением объема выборки
Оценка параметров регрессионного уравнения
МНК минимизирует сумму квадратов отклонения наблюдаемых значений
уi от модельных значений yi .
Согласно принципу метода наименьших квадратов, оценки и
находятся путем минимизации суммы квадратов:
Q( ,
n
yi yˆi
i 1
2
n
( yi xi ) 2
i 1
В результате применения МНК получаем формулы для вычисления
параметров модели парной регрессии.
n
ˆ
yi y xi x
i 1
n
xi x
i 1
2
,
y x
(3)
11.
Такое решение может существовать только при выполнении условияn
x
x 0 ,
2
что равносильно отличию от нуля
определителя системы нормальных уравнений. Действительно, этот определитель
равен
2
n
n
n
n 2
2
2
2
n xi xi n xi nx n xi x .
i 1
i 1
i 1
i 1
Последнее условие называется условием идентифицируемости модели наблюдений
i
i 1
yi xi i , i 1, , n
и означает, что не все значения x1 , , xn
совпадают между собой. При нарушении этого условия все точки xi , yi , i 1, , n
лежат на одной вертикальной прямой x x .
Оценки и называют оценками наименьших квадратов. Обратим
внимание на полученное выражение для параметра . В это выражение входят
суммы квадратов, участвовавшие ранее в определении выборочной дисперсии
n
S Var ( x) xi x
2
x
n
i 1
2
n 1
и выборочной ковариации
Cov( x, y ) xi x y i y n 1 , так что, в этих терминах параметр β можно
i 1
получить следующим образом:
12.
nˆ
=
Cov( X , Y )
Var ( x)
x x y y
n
=
xi x yi y n 1
=
i 1
S x2
i 1
i
n
xi x
i 1
n
=
rx , y
Sy
Sx
y x y x
x x
2
2
y x n y x
=
i
i 1
n
i
2
2
x
n
x
i
i 1
i
2
13.
Оценка качества уравнения регрессииПосле построения уравнения регрессии мы можем разбить значение Y, в каждом
наблюдении на две составляющих - yˆ i и ei .
yi yˆi ei
Остаток
представляет собой отклонение фактического значения зависимой
переменной от значения данной переменной, полученное расчетным путем:
( i 1: n ).
ei = yi yˆi
ei 0
14.
nn
( y y ) ( yˆ y )
2
.
i
i 1
n
2
i
i 1
yˆ
Где i - значения y, вычисленные по модели
yi yˆi ,
i 1
yˆi xi
n
2
(
y
y
)
i
Разделив правую и левую часть (4) на
i 1
n
n
(y
y)
(y
y )2
i 1
n
i 1
i
i
2
n
( yˆ
y)
(y
y )2
i 1
n
i 1
i
i
2
y
i 1
n
i
(y
i 1
i
yˆi
2
y )2
получим
n
1
2
ˆ
(
y
y
)
i
i 1
n
2
(
y
y
)
i
i 1
n
2
e
i
i 1
n
2
(
y
y
)
i
i 1
2
(4).
15.
Коэффициент детерминацииn
R2
объясняемая сумма квадратов
общая сумма квадратов
n
( yˆ y )
2
( yi y )
2
i 1
n
i 1
i
1
e
i 1
2
i
n
2
(
y
y
)
i
i 1
Коэффициент детерминации показывает долю вариации
результативного признака, находящегося под воздействием
изучаемых факторов, т. е. определяет, какая доля вариации
признака Y учтена в модели и обусловлена влиянием на него
факторов.
16.
для оценки качества регрессионных моделей целесообразноиспользовать среднюю ошибку аппроксимации:
1 n yi yˆi
1 n ei
E=
100% = 100%
n i 1 yi
n i 1 yi
17.
Для проверки значимости модели регрессии используется Fкритерий Фишера, вычисляемый как отношение дисперсииисходного ряда и несмещенной дисперсии остаточной компоненты.
Если расчетное значение с 1= k и 2 = (n - k - 1) степенями
свободы, где k – количество факторов, включенных в модель, больше
табличного при заданном уровне значимости, то модель считается
значимой.
Для модели парной регрессии:
2
2
y,x
r
R
F=
(
n
2)
=
(
n
2)
2
2
1 R
1 ry , x
18.
В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношениесуммы квадратов уровней остаточной компоненты к величине (n- k -1),
где k – количество факторов, включенных в модель. Квадратный корень
из этой величины ( S ) называется стандартной ошибкой
n
Se
i 1
ei2
n k 1
Для модели парной регрессии
n
Se
e
i 1
2
i
n 2
19.
Прогнозирование с применением уравнения регрессииПрогнозируемое значение переменной y получается при подстановке в
уравнение регрессии ожидаемой величины фактора x
yпрогн xпрогн
Доверительные интервалы, зависят от следующих параметров:
• стандартной ошибки,
• удаления xпрогн от своего среднего значения x
• количества наблюдений n
• и уровня значимости прогноза α.
В частности, для прогноза будущие значения yпрогн с вероятностью (1 α) попадут в интервал
yпрогн
yˆ прогн Se t
1 1
n
( xпрогн x ) 2
n
(x x )
i 1
i
2
; yˆ прогн Se t
( xпрогн x ) 2
1 1 n
n
( xi x ) 2
i 1
20.
Нелинейные модели и их линеаризацияЗадача построения нелинейной модели регрессии состоит в следующем:
Задана нелинейная спецификация модели
y = f(x,a,b,ε),
где
y - зависимая, объясняемая переменная;
x - независимая, объясняющая переменная;
a,b - параметры модели, для которых должны быть получены оценки;
ε - аддитивный или мультипликативный случайный фактор.
Требуется
1. Преобразовать исходные данные х → х*, у → у* так, чтобы
спецификация модифицированной регрессии была линейной:
y* = a* + b*x*
2. Методом наименьших квадратов получить оценки параметров a*, b*.
3. По оценкам a*, b* вычислить искомые оценки параметров a, b исходной
регрессии.
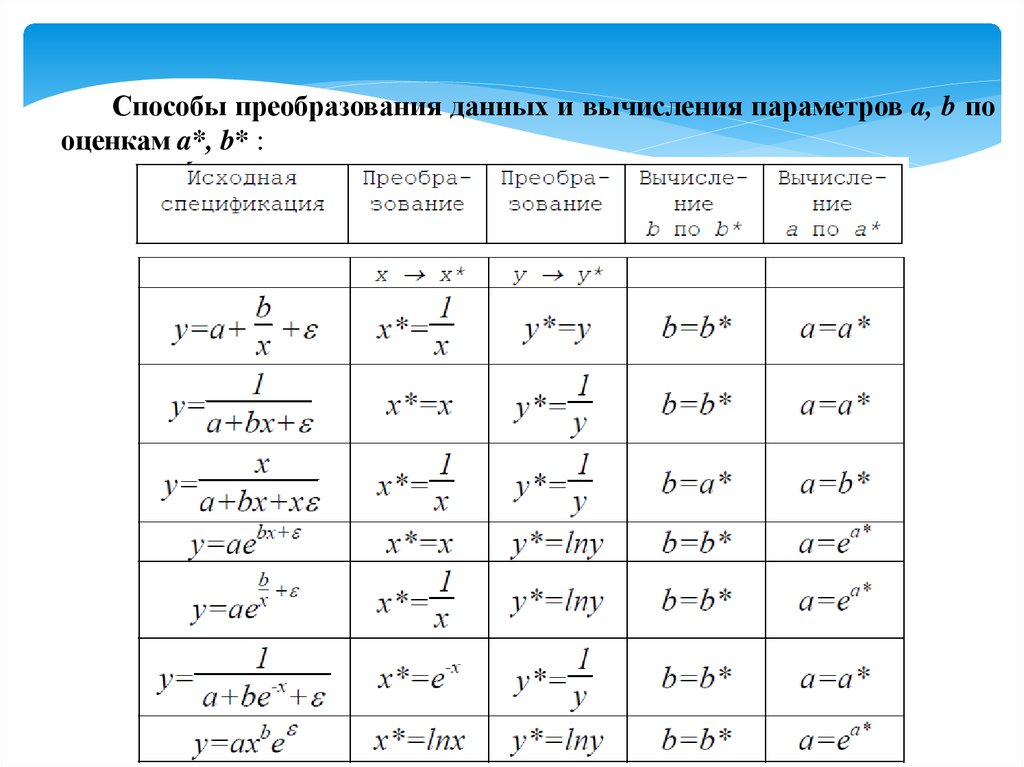
21.
Способы преобразования данных и вычисления параметров a, b пооценкам a*, b* :




















 mathematics
mathematics








