Эконометрика. Обратная и пропорциональная модель парной линейной регрессии. Фиктивная линейная зависимость

1. Эконометрика

Обратная и пропорциональная модель
парной линейной регрессии.
Фиктивная линейная зависимость.

2. «Обратная» модель парной линейной связи

Задача состоит в оценивании модели прямолинейной связи
между некоторыми переменными x и y на основе
наблюдений n пар xi , yi , i 1, , n, значений этих
переменных. Вопрос об оценивании параметров модели
наблюдений уже рассмотрен ранее. Встает вопрос о том,
что изменится, если исходить из «обратной» модели:
xi yi i , i 1, , n
Пусть xy , xy – оценки параметров и в модели
x
y
,
i
1
,
,
n
наблюдений i
, а yx , yx –
i
i
оценки параметров в модели наблюдений
yi xi i , i 1, , n . Тогда:
xy yx
2
Cov( x, y ) Cov( x, y )
Cov( x, y )
, т.е.
Var( y ) Var( x)
Var( y )
Var( x)
xy yx r ,
2
xy
или
xy yx R 2 .

3. Наилучшая прямая

По первой модели
наблюдений мы получаем наилучшую
прямую x xy xy y ,
xy
1
а по второй – прямую y yx yx x .
y x.
xy xy
Первую прямую мы можем записать в виде
Сравнивая коэффициенты при x в двух последних
уравнениях, находим, что эти коэффициенты равны в том
и только в том случае,
когда выполнено соотношение
1
yx ,
xy
2
1
,
R
1.
yx
xy
т. е.
или, с учетом предыдущего, когда
Что касается отрезков на осях, то они будут совпадать тогда и
только тогда, когда
xy
yx ,
xy
или yx xy xy .
Но yx y yx x , так что
yx xy ( y yx x ) xy = y xy - yx xy x .

4. Наилучшая прямая

При
R 1 получаем
2
yx xy y xy - x .
В то же время,
xy x xy y . При R 2 1 совпадают и отрезки на осях, т. е.
наилучшая прямая одна для обоих моделей, это прямая, на
которой расположены все наблюдаемые точки xi , yi , i 1, , n.
Наилучшие прямые, построенные по двум альтернативным
моделям, совпадают в том и только в том случае, когда все
точки , расположены на одной прямой (так что e1 , , en 0 );
при этом, R 2 1 . В противном случае R 2 1 , и
подобранные «наилучшие» прямые имеют разные угловые
коэффициенты.

5. Пропорциональная связь между переменными

Пусть получены наблюдения xi , yi , i 1, , n , такие, что
гипотетическая линейная связь между переменными и
имеет вид y x (пропорциональная связь между
переменными), и ей соответствует модель наблюдений:
yi xi i , i 1, , n.
Применение метода наименьших квадратов в этой ситуации
сводится к минимизации
суммы квадратов
n
Q( ) y i x i
2
i 1
по всем возможным значениям . Последняя сумма
квадратов является функцией единственной переменной
(при известных значениях xi , y i , i 1, , n ), и точка
минимума этой функции легко находится. Для этого мы
приравниваем нулю производную Q ( )по :
2 y i xi xi 0 ,
i 1
n
(нормальное уравнение)

6. Отсюда получаем,

n
y x
i 1
i
i
n
x
i 1
2
i
Оценка единственного параметра пропорциональной
модели будет:
n
y x
i 1
n
x
i 1
И, следовательно,
i
Cov( x, y )
,
Var ( x )
i
.
2
i
а точка ( x , y ) не лежит на
полученной прямой y x . Более того, в такой ситуации
n
y
i 1
y
2
i
2
2
n
y i y i y i y , где
i 1
i 1
n
y i xi ,

7. Коэффициент детерминации

выражение
2
yi y
R 2 i n1
2
yi y
n
не имеет смысла. И можно
i 1
воспользоваться формулой
R2 1
y
y
i i
y
yi
2
. Однако, такой
2
i
подход к определению коэффициента детерминации не
решает проблемы, поскольку, в принципе, при оценивании
модели без постоянной составляющей возможны ситуации,
2
при которых возникают отрицательные значения R .
Преодолеть возникающие затруднения можно, если
определить R 2 в модели наблюдений без постоянной
составляющей формулой:
yi yi
R2 1 n
yi2
i 1
2

8. Здесь используется

сумма квадратов, не центрированных значений переменной
y (отклонений значений переменной y от «нулевого
уровня»). При таком определении, неотрицательность
коэффициента гарантируется соотношением:
2
n
y yi y i y i ,
i 1
i 1
i 1
n
n
2
2
i
которое отражает геометрическую сущность метода
наименьших квадратов (аналог знаменитой теоремы
Пифагора для многомерного пространства) и выполняется
как для модели без постоянной составляющей, так и для
модели с наличием постоянной составляющей в правой
части модели наблюдений. Деля обе части последнего
равенства на
n
y
2
i
, приходим к соотношению:
i 1
2
n
2
y
y
y
i
i
i
i 1
i 1
1
n
,
n
yi2
yi2
n
i 1
i 1

9. Следовательно,

2
y
y
i
i
R 2 1 i 1 n
yi2
n
i 1
n
yi
2
i 1
n
y
i 1
0.
2
i
Доказать заявленное равенство не сложно. Действительно,
2
2
n
2
y i y i y i y i y i y i y i + 2 y i y i y i .
i 1
i 1
i 1
i 1
i 1
n
n
n
n
2
n
n
Но, y i y i y i = y i xi xi y i xi xi 0 ,
i 1
i 1
i 1
n
что и приводит к искомому результату.

10. Фиктивная линейная связь

На практике часто встречаются ситуации, при которых
существует заметный тренд (убывание или возрастание) в
динамике изменений различных показателей. Однако,
объективной связи между этими показателями не
существует. В этом случае принято говорить о фиктивной
(ложной, паразитной) линейной связи между показателями.
Для объяснения этого явления необходимо обратиться к уже
полученному ранее равенству R 2 ryx2 . Из него вытекает,
что близкие к единице значения коэффициента
детерминации соответствуют близким по абсолютной
величине к единице значениям коэффициента корреляции
между переменными x и y. Но коэффициент корреляции
Равен
ryx
Cov ( y , x )
Var ( y ) Var ( x )
,
где Cov ( y , x )
n
1
n 1
y
i 1
i
y xi x .

11. При фиксированных значениях

Var( x) и Var( y) , значение rxy
будет тем ближе к 1, чем
большим будет значение Cov( y, x) 0 . Последнее же
обеспечивается совпадением знаков разностей yi y и
x i x для максимально возможной доли наблюдений
переменных x и y, что как раз и имеет место, когда в
процессе наблюдения обе переменные возрастают или обе
переменные убывают по величине.
При этом превышение одной из переменных своего
среднего значения сопровождается, как правило, и
превышением второй переменной от своего среднего
значения. Если же одна из переменных принимает
значение, меньшее среднего значения этой переменной, то
и вторая переменная, как правило, принимает значение,
меньшее своего среднего.

12. Аналогичным образом,

rxy будет тем ближе к -1, чем меньшим будет
значение
значение Cov( y, x) 0 . Последнее же обеспечивается
несовпадением знаков разностей yi y и x i x
для максимально возможной доли наблюдений
переменных x и y, что имеет место, когда в процессе
наблюдения одна из переменных возрастает, а вторая
убывает. В этом случае, если одна из переменных
принимает значение, меньшее среднего значения этой
переменной, то вторая переменная, как правило,
принимает значение, большее своего среднего.
Из этого следует, что близость к единице наблюдаемого значения
коэффициента детерминации не обязательно означает наличие
причинной связи между двумя рассматриваемыми переменными,
а может являться лишь следствием тренда значений обеих
переменных.
Последнее обстоятельство часто наблюдается при анализе
различных экономических показателей, вычисленных без
поправки на инфляцию (недефлированные данные).

13. Эконометрика

Свойства МНК-оценок параметров
регрессии. Показатели качества регрессии

14. Свойства МНК-оценок параметров регрессии

Способ оценивания дает состоятельные оценки, если при
бесконечно большом объеме выборки значение
статистической оценки стремится к искомому значению
параметра (характеристики) генеральной совокупности.
Способ оценивания дает несмещенные оценки, если
математическое ожидание оценки при данном способе
оценивания тождественно искомому параметру
генеральной совокупности (при любом объеме выборки).
Оценка называется эффективной, если ее дисперсия
минимальна (при заданном объеме выборки n).
Оценки по методу наименьших квадратов являются
наилучшими, то есть несмещенными, состоятельными и
эффективными!!!

15. Докажем это:

Докажем, что является несмещенной оценкой . Если
выполнены предпосылки нормальной линейной модели
регрессии, то х – неслучайная величина, а x2 является
известной константой, а математическое ожидание
E(Cov(x, ))=0. Тогда
Cov( x, )
Cov( x, )
1
1
E ( ) E
E
E
(
Cov
(
x
,
))
0
2
2
2
2
x
x
x
x
Что и требовалось доказать. Аналогично доказывается
несмещенность .
Эффективность МНК–оценок параметров доказывается с
помощью теоремы Гаусса–Маркова, которая гласит, что
МНК дает оценки, имеющие наименьшую дисперсию в
классе всех линейных несмещенных оценок, если
выполняются предпосылки нормальной линейной модели.
Состоятельность МНК-оценок параметров является
следствием закона больших чисел теории вероятностей.

16. Оценка дисперсии случайной составляющей

Дисперсии МНК–оценок параметров регрессии будут
2
2
x
2
1 2 ,
n x
2
2 2
n x
2
2
где
– дисперсия случайной составляющей,
–
x
2
дисперсия фактора х. А так как
неизвестна, то
пользуются оценкой
S e2 .
Оценка дисперсии случайной составляющей применяется в
эконометрических задачах для анализа качества
полученной модели регрессии. В случае парной линейной
регрессии несмещенная оценка дисперсии случайной
составляющей будет:
1 n
1 n
2
2
S
(
y
y
)
(
e
)
i i n 2
i
n 2 i 1
i 1
где ei – остаток, равный разности между фактическим и
рассчитанным по уравнению регрессии значениям y.
2
e

17. Качество модели регрессии

связывают с адекватностью модели по наблюдаемым
(эмпирическим) данным. Проверка адекватности (или
соответствия) модели регрессии наблюдаемым данным
проводится на основе анализа остатков – ei.
Если значения остатков для всех наблюдений ei=0, то
фактическое значение значимой (результирующей)
переменной совпадает с расчетным: y i y i , но на практике
это, зачастую, не верно.
При анализе качества модели используется теорема о
разложении дисперсии, согласно которой общая
дисперсия результативного признака может быть
разложена на две составляющие – объясненную и
необъясненную уравнением регрессии.

18. Теорема о разложении общей дисперсии

n
где
2
( y y)
i 1
i
2 2 2
2
– объясненная уравнением регрессии
n
n
дисперсия результирующего признака, а 2
( y
i 1
i
yi )
n
n
2
e
– необъясненная уравнением регрессии дисперсия
результирующего признака. На основе этой теоремы
рассчитываются показатели качества модели регрессии.
n
Общая дисперсия при этом будет:
2
(y
i 1
i
y) 2
n
i 1
n
2
i

19. Показатели качества модели регрессии

1.
Теоретический коэффициент детерминации (индекс для
нелинейных форм связей)
2
2
. Этот коэффициент характеризует долю
R2
1
y ( x)
2
2
вариации (дисперсии) результирующего признака,
объясняемую регрессией y i
в общей дисперсии и,
2
соответственно, 1– R y ( x ) характеризует долю вариации
необъясненную уравнением регрессии, вызванную
влиянием прочих неучтенных в модели факторов. В
2
2
R
r
случае парной регрессии: y ( x )
yx . Коэффициент
детерминации изменяется на промежутке [0; 1], близость
его к 0 означает отсутствие линейной связи, а близость к
1 наличие тесной линейной зависимости.

20. Показатели качества модели регрессии

2.
Коэффициент (индекс) множественной корреляции
рассчитывается как корень квадратный из коэффициента
детерминации
3.
Ry ( x )
2
2
1 2 .
2
Он тоже изменяется на промежутке [0; 1]. Для случая
парной регрессии R y ( x ) r yx .
Средняя квадратическая ошибка уравнения регрессии
n
Se
( y
i 1
i
yi )2
n h
n 1 R y2( x ) y2
n h
,
где h – число параметров модели. Величину Se можно
сравнить с дисперсией
результирующего признака
n
( yi y ) 2
. Если Se< y , то
2
i 1
y
n
использование данной модели регрессии
является целесообразным.

21. Показатели качества модели регрессии

4.
Средняя ошибка аппроксимации
A
yi yi
1
100%.
n i 1 yi
n
Чем меньше рассеяние эмпирических точек вокруг
теоретической линии регрессии, тем меньше средняя
ошибка аппроксимации. Ошибка аппроксимации менее
7% свидетельствует о хорошем качестве модели.

22. Эконометрика

ПРОВЕРКА ГИПОТЕЗ О ЗНАЧИМОСТИ ПАРАМЕТРОВ
РЕГРЕССИИ, КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ И
УРАВНЕНИЯ РЕГРЕССИИ В ЦЕЛОМ

23. Проверка гипотез о значимости параметров регрессии

С помощью метода наименьших квадратов
можно получить лишь оценки параметров
модели, чтобы проверить, значимы ли они
(значимо ли отличаются от нуля) в «истинном»
уравнении (в генеральной совокупности), значим
ли коэффициент корреляции, требуется
обратиться к проверке гипотез.
В качестве основной гипотезы (Н0) выдвигают
гипотезу о незначительном отличии от нуля
«истинного» параметра или коэффициента
корреляции. Альтернативной гипотезой (Н1)
является обратная – о неравенстве нулю
«истинного» параметра или коэффициента.

24. Проверка гипотез о значимости параметров регрессии

Для проверки гипотез используют t–статистику
распределения Стьюдента, критическое значение которой
определяется по таблице (или с помощью функции
СТЬЮДРАСПОБР пакета Excel) в зависимости от уровня
значимости и числа степеней свободы равного (n–h), где
n – число наблюдений, а h – число параметров модели.
Если фактическое значение t–статистики (по модулю)
меньше критического, то нет оснований отвергать
основную гипотезу, то есть «истинный» параметр
регрессии (либо коэффициент корреляции) незначительно
отличается от нуля при заданном уровне значимости.

25. Проверка гипотез о значимости параметров регрессии

Для проверки гипотезы: =0 статистика критерия будет
t( 0 )
,
где – оценка параметра , полученная по наблюдаемым
данным, а – стандартная ошибка
оценки коэффициента регрессии .
Для линейной парной регрессии:
n
( y
i 1
i
yi )2
n
( n 2) ( x i x ) 2
i 1
2
Se
n x2

26. Проверка гипотез о значимости параметров регрессии

Для проверки гипотезы: =0 статистика критерия будет
t( 0)
.
В случае парной линейной регрессии:
n
(y
i 1
i
n
yi ) xi2
2
i 1
n
n (n 2) ( xi x) 2
i 1
.

27. Проверка гипотез о значимости коэффициента корреляции

Для проверки гипотез о незначительном отклонении от нуля
«истинного» коэффициента линейной парной корреляции
используют статистику
t( r 0 )
при этом:
r
ryx
r
(1 r yx2 )
( n 2)
,

28. В случае парной линейной регрессии

Существует взаимосвязь
t( 0 ) t( r 0) .
Рассмотренная формула статистики критерия проверки
гипотез применима, если:
1.
2.
Оценки делаются по большому числу наблюдений n.
Величина
не близка к единице.
r yx

29. В случае парной линейной регрессии

Если же величина выборочного коэффициента корреляции
близка к 1, то распределение его оценок отличается от
распределения Стьюдента. В данном случае используют
статистику Фишера. Вводится вспомогательная величина
1 ryx
,
z 0,5 ln
1 r
yx
при этом можно пользоваться готовыми таблицами
преобразований. Эта величина изменяется на промежутке
(– ; + ), что соответствует нормальному распределению.
Для проверки гипотезы о незначительном отклонении от
нуля «истинного» значения коэффициента парной
z
линейной корреляции используется статистика t z
,
1
. Критическое значение находят по таблице z
где z
n 3
стандартного нормального распределения с доверительной
вероятностью (1– ). Основную гипотезу отвергают, если
t z t кр.

30. Проверка гипотез о значимости уравнения регрессии в целом

Оценка значимости уравнения регрессии производится для
того, чтобы узнать, пригодно ли уравнение для
практического применения. Основная гипотеза утверждает,
что уравнение регрессии незначительно в целом, что
формально сводится к равенству нулю параметров модели
или коэффициента детерминации. Для ее проверки
используют F–статистику:
R2 n h
F
.
2
1 R h 1
Данная статистика имеет распределение Фишера–
Снедоккора, критическое значение которой можно найти в
таблицах этого распределения для =0,05 и двух степеней
свободы k1=h –1 и k1=n –h. В случае парной линейной
регрессии существует взаимосвязь :
t( 0 ) t( r 0 ) F .

31. Эконометрика

ПРОГНОЗ ОЖИДАЕМОГО ЗНАЧЕНИЯ
РЕЗУЛЬТИРУЮЩЕГО ПРИЗНАКА.

32. Прогноз ожидаемого значения результирующего признака

Предположим, необходимо определить для заданного
значения фактора xp с доверительной вероятностью (1– )
прогнозируемое значение результирующего признака.
Тогда, прогнозируемое значение результата должно
принадлежать интервалу (yp–t p; yp+t p), где yp – точечный
прогноз, t – коэффициент доверия (определяется по
таблицам распределения Стьюдента в зависимости от
уровня значимости и числа степеней свободы (n–2)), а p
– средняя ошибка прогноза.
Точечный прогноз рассчитывается по линейному уравнению
регрессии:
yp= + xp,
а средняя ошибка прогноза будет:
2
p
1
x x
p S e2 1 n
n
( xi x)2
i 1

33. Доверительный интервал

Вокруг линии регрессии образуется доверительный интервал
(«коридор», в который попадет прогнозируемое значение
результирующего признака):
y
y +t p
y –t p
x
Точечная и интегральная оценка прогноза
x

34. Эконометрика

НЕЛИНЕЙНАЯ
РЕГРЕССИЯ

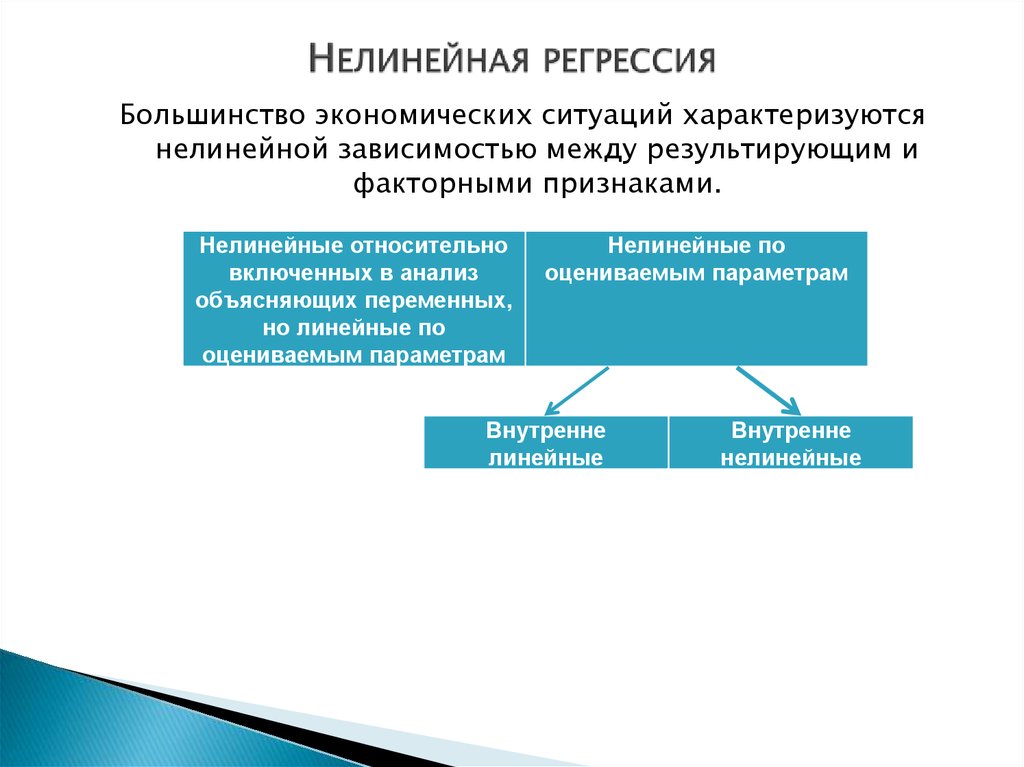
35. Нелинейная регрессия

Большинство экономических ситуаций характеризуются
нелинейной зависимостью между результирующим и
факторными признаками.
Нелинейные относительно
включенных в анализ
объясняющих переменных,
но линейные по
оцениваемым параметрам
Нелинейные по
оцениваемым параметрам
Внутренне
линейные
Внутренне
нелинейные

36. Примеры нелинейных регрессий относительно включенных в анализ объясняющих переменных, но линейных по оцениваемым параметрам

Полиномы различных степеней –
yi=a0+ a1 xi+…+ am xim+ i.
Равностороння гипербола –
yi a
b
i
xi

37. Примеры регрессий (внутренне линейных) нелинейных по оцениваемым параметрам

Степенная функция –
yi a xi i ;
b
Показательная функция –
y i a b xi i ;
Экспоненциальная функция –
yi e
a bxi
i
.

38. Рассмотрим степенную функцию

Модель описывается уравнением:
yi a xi i
b
y – спрашиваемое количество товара, x – цена, i– случайная
составляющая.
Преобразуем данную модель к линейному виду. Так как
данная модель нелинейна относительно оцениваемых
параметров, то необходимо произвести преобразование
переменных. Логарифмическое преобразование приведет
данное уравнение к линейному виду:
ln yi ln a b ln xi ln i
~
~
~
~
ln yi yi , ln a a, ln xi xi , ln i i
~
~
~
~
yi a b xi i
Введя новые переменные и введя новое обозначение для
параметра а и ошибки, получим линейную регрессию.