Эконометрика. Модель парной и множественной линейной регрессии

1. ЭКОНОМЕТРИКА

ЭКОНОМЕТРИ
КА

2. БРС эконометрика

• 1. Модель парной линейной регрессии 5
• 2. Модель множественной линейной 10
регрессии
3. Итоговый коллоквиум
4. Итоговая контрольная работа
1
5. Модель временного ряда
0
6. Презентация
1
0
10
5
2

3. ИТОГ

Эконометрика — это наука, в которой на
базе реальных статистических данных
• строятся,
• анализируются и
• совершенствуются
математические модели
реальных экономических явлений.
3

4. Эконометрическая модель – главный инструмент эконометрических исследований

• В эконометрике модель относится
классу математических моделей.
• Модели экономических объектов,
создаваемые именно в эконометрике,
являются дескриптивными
(описывающими реальность такой,
как она есть, в отличие от
оптимизационных моделей).
4

5. Этапы построения эконометрических моделей

постановка задачи; набора показателей, взаимосвязи между
которыми нас интересуют;
априорный, предмодельный анализ содержательной сущности
моделируемого явления;
информационно-статистический этап – получение данных,
анализ их качества;
этап спецификации модели;
этап параметризации модели – определяем вид
эконометрической модели, выражаем в математической
форме взаимосвязь между её переменными, формулируем
исходные предпосылки и ограничения модели.
этап идентификации модели – статистический анализ модели,
оценка качества её параметров по имеющимся статистическим
данным;
этап верификации модели, анализа её точности и адекватности;
интерпретация полученных результатов.
5

6. Три основных класса моделей

Регрессионные модели с одним
уравнением
Модели временных рядов
Системы одновременных
уравнений
6

7. Виды зависимости

• Функциональной называется взаимосвязь, при которой каждому
значению одного показателя соответствует строго определенное значение
другого.
Статистической (стохастической, вероятностной) называется
взаимосвязь, при которой одному значению первого показателя может
соответствовать несколько значений второго показателя.
Среди статистических зависимостей наибольший интерес представляют
корреляционные зависимости.
Корреляционная зависимость заключается в том, что средняя величина
одного показателя изменяется в зависимости от значения другого.
Корреляционной зависимостью между двумя переменными
величинами называется функциональная зависимость между значениями
одной из них и условным математическим ожиданием (средним
значением) другой.
7

8. Модель парной линейной регрессии

• 1. Постройте поле корреляции и сформулируйте гипотезу
о форме связи.
2. Рассчитайте параметры выборочного уравнения
линейной регрессии с помощью МНК.
3. Оцените тесноту связи с помощью показателей
корреляции (выборочный коэффициент корреляции) и
детерминации.
4. Используя критерий Стьюдента оцените
статистическую значимость коэффициентов регрессии и
корреляции.
5. Постройте интервальные оценки параметров регрессии.
Проверьте, согласуются ли полученные результаты с
выводами, полученными в предыдущем пункте.

9. Модель парной линейной регрессии

• 6. Постройте таблицу дисперсионного анализа для
оценки значимости уравнения в целом.
• 7. С помощью теста Гольдфельда – Квандта
исследуйте гетероскедастичность остатков.
Сделайте выводы.
• 8. В случае пригодности линейной модели
рассчитайте прогнозное значение результата, если
значение фактора увеличится на 5% от его среднего
уровня. Определите доверительный интервал
прогноза для уровня значимости =0,05.
• 9. Оцените полученные результаты,
проинтерпретируйте полученное уравнение
регрессии.

10.

Количес
тво
пропуск Результа
ов
ты теста
3
10
4
8
5
7
5
6
6
4
6
5
7
4
7
2
8
3
9
1
Оценка параметров
регрессии МНК
y i b0 b1 xi
b0 y b1 x
b1
cov( x, y ) x y y x
2
x
x2 x 2
 
+13,8

11.

результаты теста
12
10
f(x) = - 1.47x + 13.8
R² = 0.92
8
Axis Title
6
4
2
0
2
3
4
5
6
Axis Title
7
8
9
10

12. Оцените тесноту связи с помощью показателей корреляции (выборочный коэффициент корреляции) и детерминации

• Коэффициент корреляции
rxy b1
rxy
x cov( x, y ) x y y x
y
x y
x y
n
n
n
i 1
i 1
i 1
n y i xi y i x i
n
n
n
n
(n x ( xi ) ) (n y ( y i ) 2 )
i 1
2
i
i 1
2
i 1
2
i
i 1

13. Коэффициент детерминации R2

• Коэффициент детерминации характеризует
долю дисперсии результативного признака Y,
объясняемую регрессией, в общей дисперсии
результативного признака. Соответственно
величина 1- R2 характеризует долю дисперсии
Y, вызванную влиянием остальных, не
SS
SS R
учтенных в модели факторов.
R 2 1 ост
• Коэффициент детерминации
• R2 = rxy2
SS общ
SS общ

14. Используя критерий Стьюдента оцените статистическую значимость коэффициентов регрессии и корреляции

• Н 0 : b1 = 0
• Н 1 : b1 ≠ 0
t
S b1
S
2
b1
S b1
Статистика критерия при нулевой гипотезе имеет
распределение Стьюдента с (n-2) степенями свободы
S
(x
i
x)2
e
2
i
n 2
Стандартная ошибка коэффициента
регрессии
Несмещенная оценка дисперсии случайных
отклонений

15.

Если вычисленное значение t – статистики - |tфакт| при заданном
уровне значимости α больше критического (табличного) t табл , т.е.
|tфакт| > t табл = t(α ; n-2),
то гипотеза Н
0
: b1 = 0, отвергается в пользу альтернативной при
выбранном уровне значимости. Это подтверждает статистическую
значимость коэффициента регрессии b1.

16.

МНК
Стандартная
ошибка
коэффициента
b1
Коэффициент
детерминаци
и
 
+13,8
1,46667 13,8
0,15092 0,94251
3
4
0,92190
5
0,82664
94,4390
2
8
64,5333 5,46666
3
7
Уравнение
парной
линейной
регрессии
Стандартная
ошибка
коэффициента
b0
Стандартная
ошибка
регрессии

17.

Регрессионная
статистика
 
Множественный 0,9601
R
59
R-квадрат
0,9219
05
Нормированный 0,9121
R-квадрат
43
Стандартная
ошибка
0,8266
4
Наблюдения
10
ЗНАК!!
!
Коэффициент
корреляции
Коэффициент
детерминации

18.

Число Сумма
степен квадрато
ей
в
Дисперсион свобод отклонен
ный анализ
ы 
ий 
 
df
Регрессия
1
Остаток
Итого
8
9
 
 
 
Значимо
сть F
SS
MS
F
64,5333 64,5333 94,439
3
3
02
1,05E-05
5,46666 0,68333
7
3
 
 
70
 
 
 

19.

 
Стандарт
tPКоэффиц
ная
статист Значен Нижни Верхни
иенты
ошибка
ика
ие
е 95% е 95%
Yпересечен
0,94251 14,641 4,65E- 11,626 15,973
ие
13,8
4
69
07
56
44
Количеств
о
0,15092 9,7179 1,05E1,1186
пропусков -1,46667
3
7
05
1,8147
4

20.

ВЫВОД
ОСТАТКА
Количество пропусков
График остатков
Наблюде
ние
1
2
3
4
5
6
7
8
9
Предс
казан
2
ное
1
резуль
таты Остат Остатки 0
2
теста
ки
-1
9,4
0,6
-2
7,9333 0,0666
33
67
6,4666 0,5333
67
33
6,4666 0,4666
67
7
5
-1
5
0
3,5333 0,4666
33
67
3,5333 1,5333
33
3
2,0666 0,9333
67
33
3
4
5
6
7
Количество пропусков
8
9
10

21.

22.

потребительские расходы
1000
900
f(x) = 0.21x + 263.41
R² = 0.63
800
700
600
500
400
300
200
100
0
500
1000
1500
2000
2500
3000
3500

23.

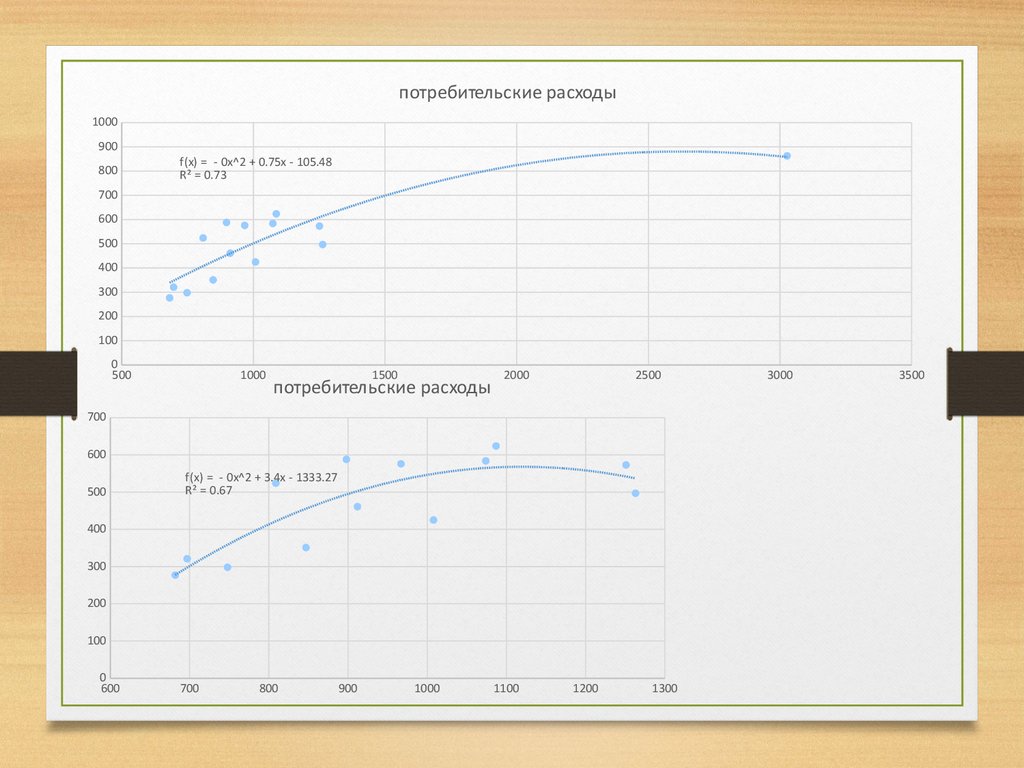
потребительские расходы
700
средняя
заработная
плата
потребитель
ские
расходы
912
461
809
524
748
298
847
351
1087
624
1074
584
1008
425
682
277
697
321
1251
573
967
576
898
588
1263
497
3027
863
600
f(x) = 0.45x + 44.8
R² = 0.49
500
400
300
200
100
0
600
700
800
900
1000
1100
1200
1300

24.

потребительские расходы
1000
900
800
f(x) = - 0x^2 + 0.75x - 105.48
R² = 0.73
700
600
500
400
300
200
100
0
500
1000
1500
потребительские расходы
2000
2500
700
600
500
f(x) = - 0x^2 + 3.4x - 1333.27
R² = 0.67
400
300
200
100
0
600
700
800
900
1000
1100
1200
1300
3000
3500

25.

потребительские расходы
1000
900
f(x) = 363.51 l n(x) - 2015.87
R² = 0.73
800
700
600
500
400
300
200
100
0
500
1000
1500
2000
2500
3000
потребительские расходы
700
600
500
f(x) = 447.53 l n(x) - 2586.99
R² = 0.54
400
300
200
100
0
600
700
800
900
1000
1100
1200
1300
3500

26. ПРИМЕР

X
Y

27.

x
y

28.

29.

y
1
2
3
4
5
6
7
8
9
10
11
12
∑
4
4
4
3
3
5
4
5
4
5
7
7
55
x
x
20
5
24
6
24
6
18
6
18
6
35
7
28
7
35
7
32
8
40
8
63
9
10 70
85 407
16
25
16
36
16
36
9
36
9
36
25
49
16
49
25
49
16
64
25
64
49
81
49
100
271
625
Остатки
6,8
0,2
3,76
0,24
5,28
-1,28
5,28
-0,28
3,76
0,24
4,52
0,48
3,76
-0,76
4,52
-0,52
6,04
0,96
3,76
-0,76
3
1
4,52
0,48
55
0

30.

31.

32.

33.

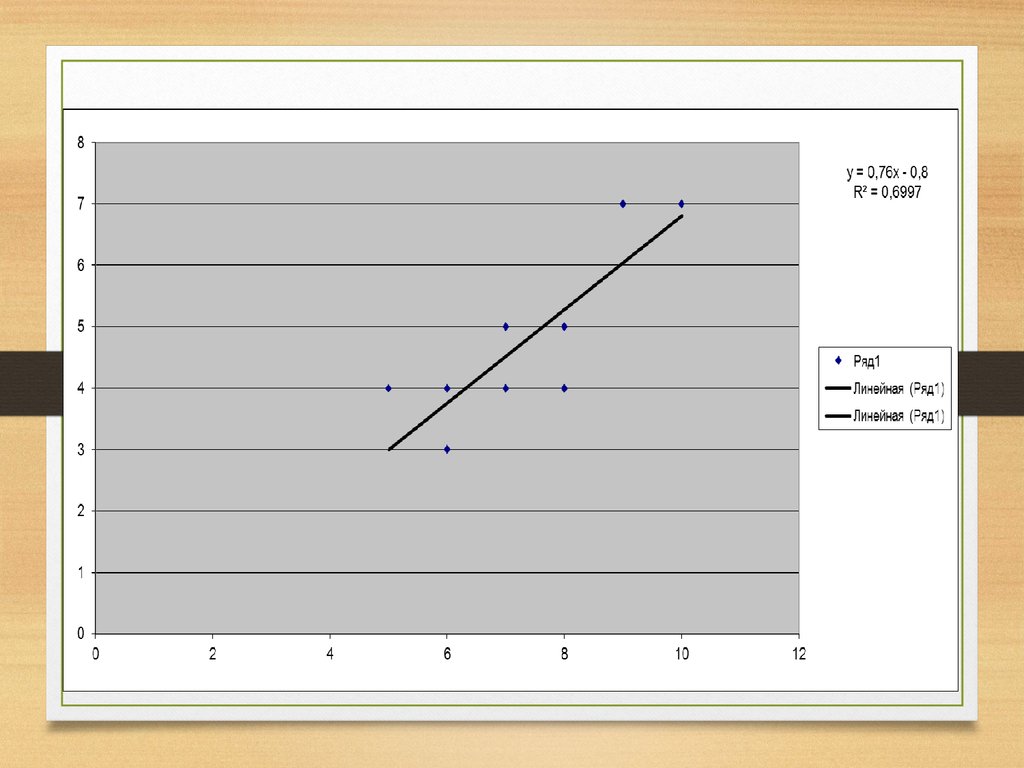
34. Постройте поле корреляции и сформулируйте гипотезу о форме связи

• Пусть имеется два ряда
эмпирических данных
• X (x1, x2, …, xn) и
• Y (y1, y2, …, yn),
соответствующие им точки с
координатами (xi, yi), где i=1,2,
…,n, отобразим на
координатной плоскости.
Такое изображение называется
полем корреляции.
Визуальный анализ корреляционного поля
позволяет сделать предположение о форме
взаимосвязи двух исследуемых показателей.
По форме взаимосвязи корреляционные
зависимости принято разделять на линейные и
нелинейные.

35. Парная корреляция

35