Similar presentations:
Эконометрика. Модель парной регрессии
1. ЭКОНОМЕТРИКА
Группа в VK Эконометрика ГМУ ВолГУ заочники2. ЭКОНОМЕТРИКА ЛИТЕРАТУРА К КУРСУ:
ОсновнаяК.Доугерти
«Введение в эконометрику» , М.: Инфра-М
(пер. под ред. Замкова)
(желательно последнее издание 2007г!!!)
3. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
B – потреблении мяса в США B в 1980 – 2007 годах (фунты на душунаселения)
YD – располагаемый доход (тысяч долларов в расчете на душу
населения)
Нас интересует влияет ли доход на потребление и если да, то насколько
сильно и какова форма зависимости.
4. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
B – потреблении мяса в США B в 1980 – 2007 годах (фунты на душунаселения)
YD – располагаемый доход (тысяч долларов в расчете на душу
населения)
5. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
B – потреблении мяса в США B в 1980 – 2007 годах (фунты на душунаселения)
YD – располагаемый доход (тысяч долларов в расчете на душу
населения)
Диаграмма рассеяния
140
120
B
100
80
60
40
20
0
0
2
4
6
YD
8
10
12
6. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
B – потреблении мяса в США B в 1980 – 2007 годах (фунты на душунаселения)
YD – располагаемый доход (тысяч долларов в расчете на душу
населения)
Степень зависимости измеряется коэффициентом корреляции.
7. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Свойства коэффициент корреляцииКоэффициент корреляции принимает значения от -1 до 1.
Значения близкие к 1 – есть тесная прямая связь между показателями
Значения близкие к -1 – есть тесная обратная связь между показателями
Значения близкие к 0 – связь между показателями отсутствует
8. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
B – потреблении мяса в США B в 1980 – 2007 годах (фунты на душунаселения)
YD – располагаемый доход (тысяч долларов в расчете на душу
населения)
Вычисляем корреляцию с помощью функции КОРРЕЛ
9. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
B – потреблении мяса в США B в 1980 – 2007 годах (фунты на душунаселения)
YD – располагаемый доход (тысяч долларов в расчете на душу
населения)
Вычисляем корреляцию с помощью функции КОРРЕЛ
Связь умеренная, прямая
(с ростом дохода YD потребление B растет)
10. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Зависимость есть. Строим модель парной линейной регрессииB a YD b
11. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
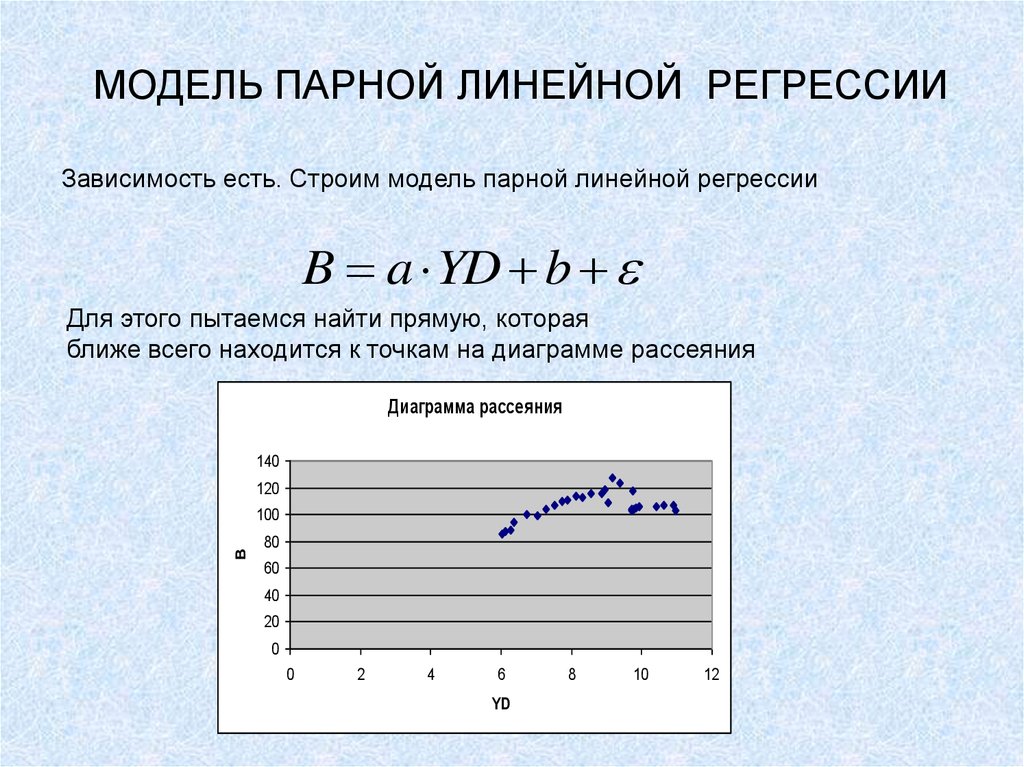
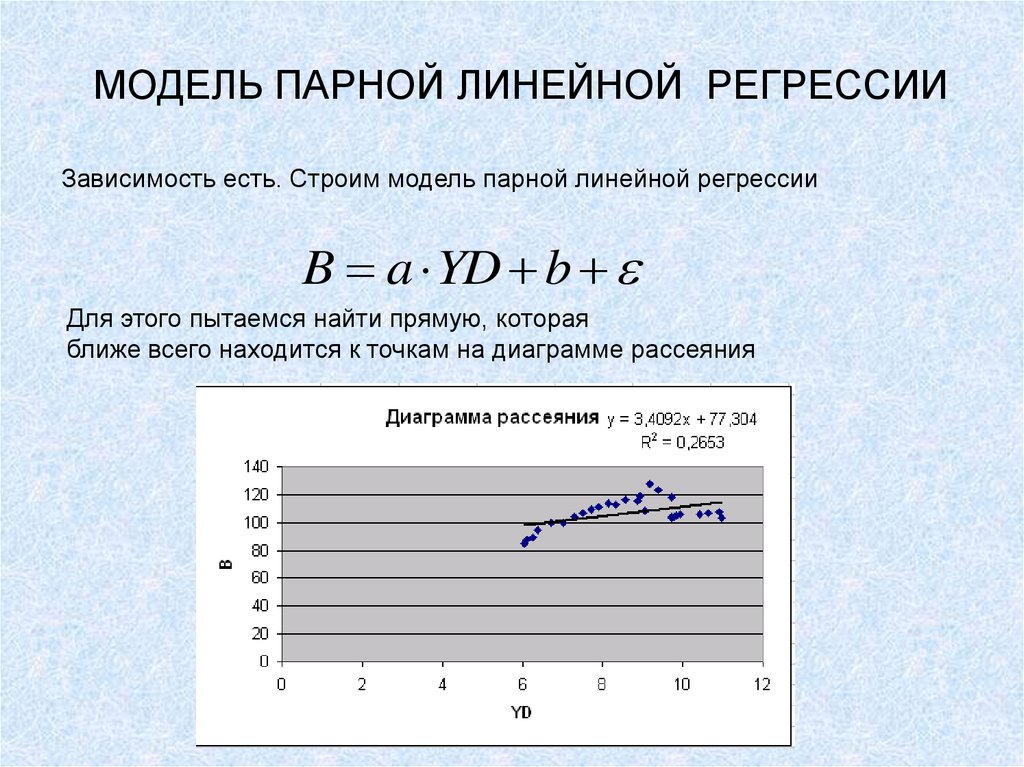
Зависимость есть. Строим модель парной линейной регрессииB a YD b
Для этого пытаемся найти прямую, которая
ближе всего находится к точкам на диаграмме рассеяния
Диаграмма рассеяния
140
120
B
100
80
60
40
20
0
0
2
4
6
YD
8
10
12
12. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Зависимость есть. Строим модель парной линейной регрессииB a YD b
Для этого пытаемся найти прямую, которая
ближе всего находится к точкам на диаграмме рассеяния
13. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
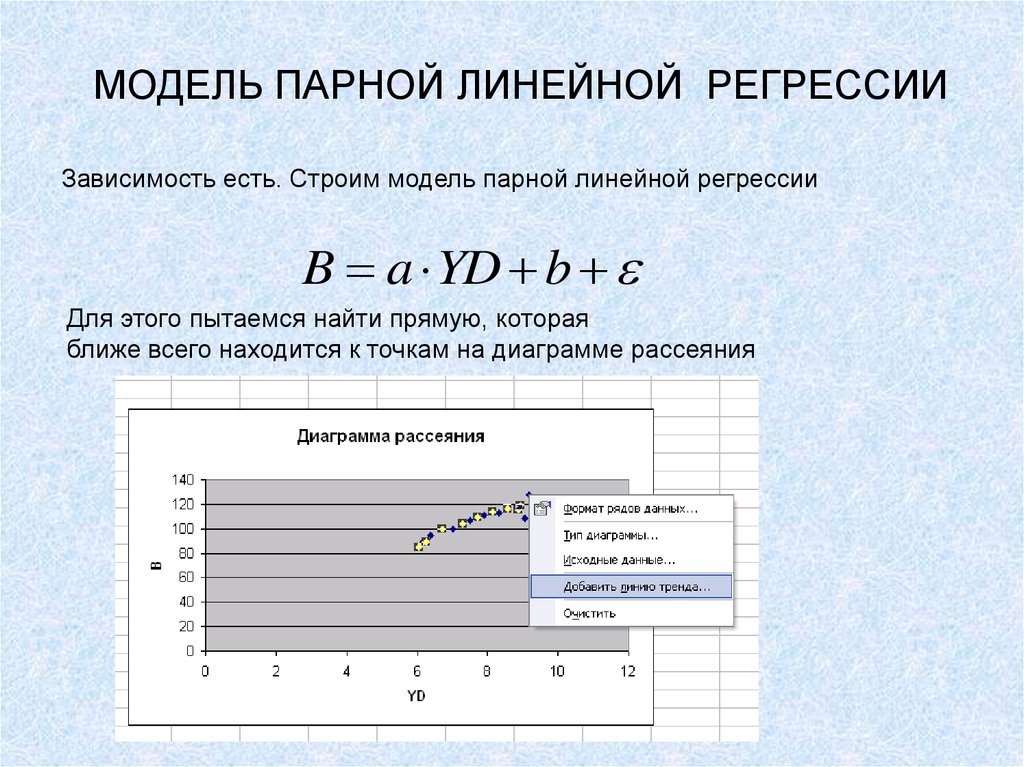
Зависимость есть. Строим модель парной линейной регрессииB a YD b
Для этого пытаемся найти прямую, которая
ближе всего находится к точкам на диаграмме рассеяния
14. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
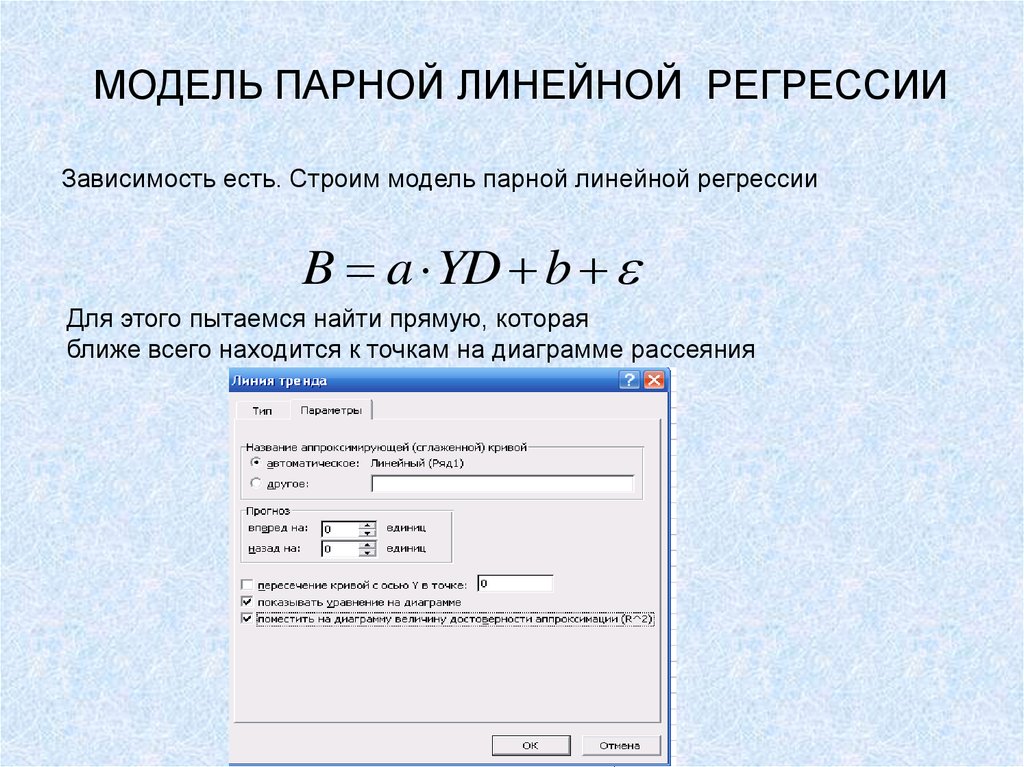
Зависимость есть. Строим модель парной линейной регрессииB a YD b
Для этого пытаемся найти прямую, которая
ближе всего находится к точкам на диаграмме рассеяния
15. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Зависимость есть. Строим модель парной линейной регрессииB a YD b
Для этого пытаемся найти прямую, которая
ближе всего находится к точкам на диаграмме рассеяния
16. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
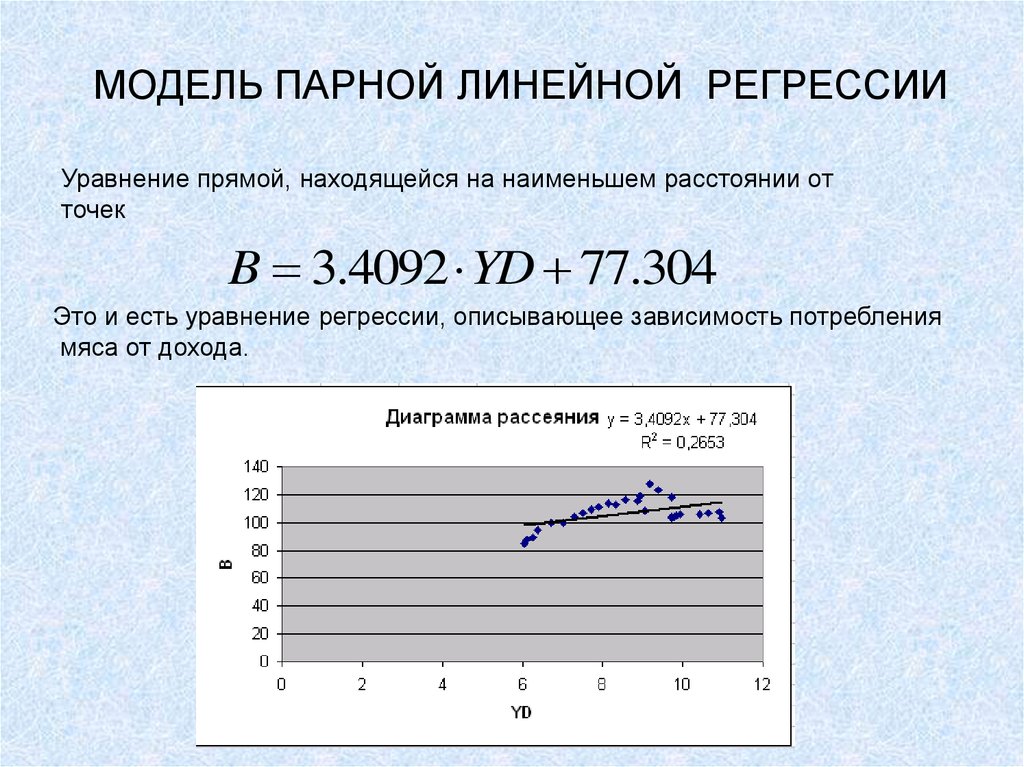
Уравнение прямой, находящейся на наименьшем расстоянии отточек
B 3.4092 YD 77.304
Это и есть уравнение регрессии, описывающее зависимость потребления
мяса от дохода.
17.
B 3.4092 YD 77.304Интерпретация: при увеличении располагаемого денежного дохода на 1 тысячу
долларов в расчете на душу населения потребление мяса увеличится на
3,41 фунта на душу населения.
18.
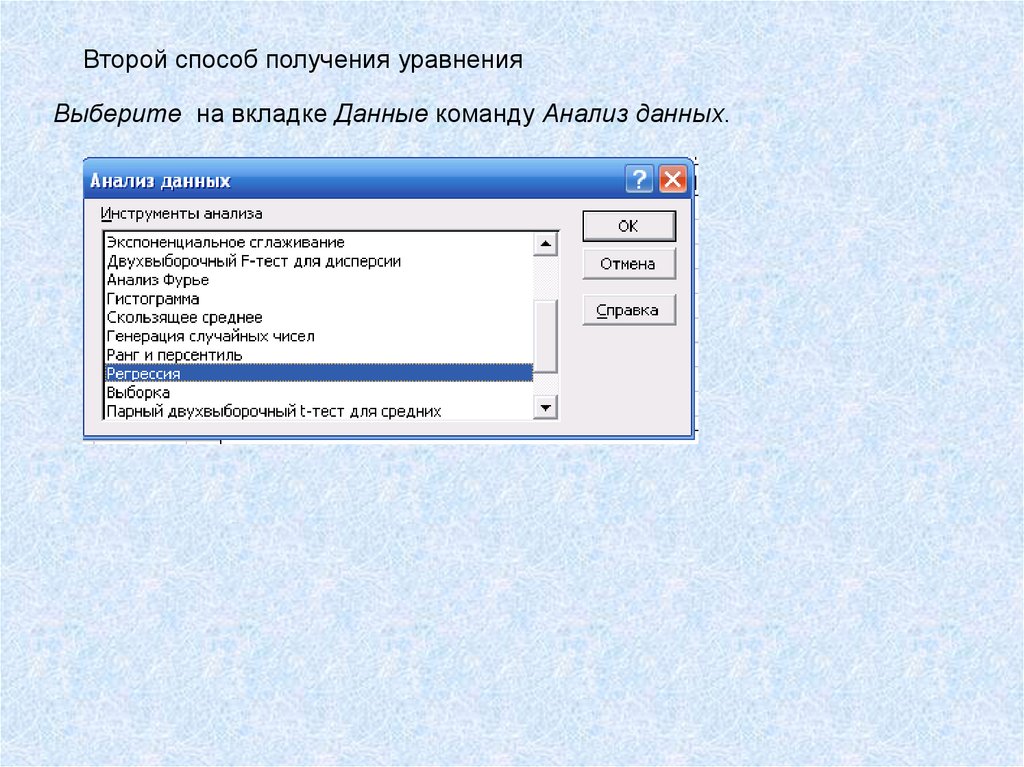
Второй способ получения уравненияВыберите на вкладке Данные команду Анализ данных.
19.
Второй способ получения уравненияВыберите на вкладке Данные команду Анализ данных.
столбец В вместе
с названием
столбец YD вместе
с названием
Куда выводить результат
20.
B 3.4092 YD 77.30421. Как оценить качество построенной модели?
Одной из характеристик качества является коэффициент детерминацииКоэффициент детерминации это доля вариации зависимой переменной,
объясненная уравнением.
Коэффициент детерминации принимает значения от 0 до 1.
Чем ближе к 1, тем выше качество модели.
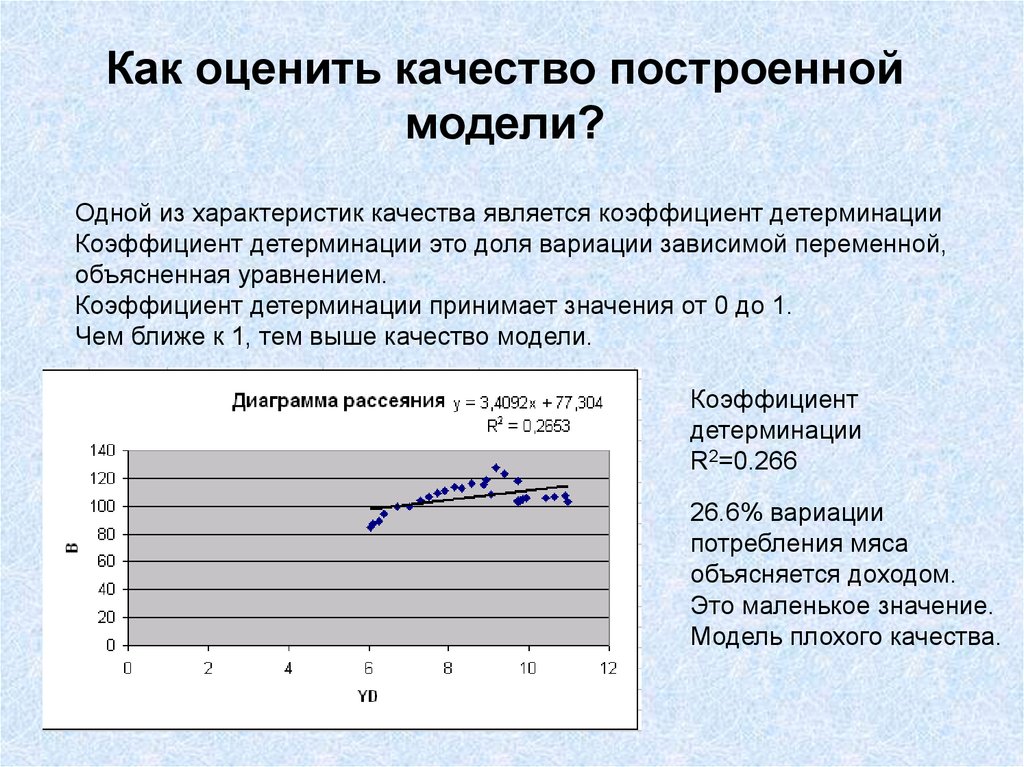
22. Как оценить качество построенной модели?
Одной из характеристик качества является коэффициент детерминацииКоэффициент детерминации это доля вариации зависимой переменной,
объясненная уравнением.
Коэффициент детерминации принимает значения от 0 до 1.
Чем ближе к 1, тем выше качество модели.
Коэффициент
детерминации
R2=0.266
26.6% вариации
потребления мяса
объясняется доходом.
Это маленькое значение.
Модель плохого качества.















 mathematics
mathematics economics
economics








