Similar presentations:
Эконометрика. Модель парной регрессии
1. Эконометрика
Модель парной регрессии2.
Простейшая регрессионная модель:y=α+βx+u
у - зависимая переменная, объясняемая,
регрессант
х – независимая переменная,
объясняющая, регрессор
α и β — параметры модели
U – случайная составляющая
3.
* Р4Q3
Р1
х
Q2
Y
*
Yˆ
* Р3
х
U1
х
Q1
*
х
Р2
(α+βx1)
Х1
Х2
Х3 Х4
Q4
4.
Величина у - зависимая переменная,состоит из двух частей:
1) Неслучайной составляющей – (α+βx),
2) Случайной составляющей - u.
5.
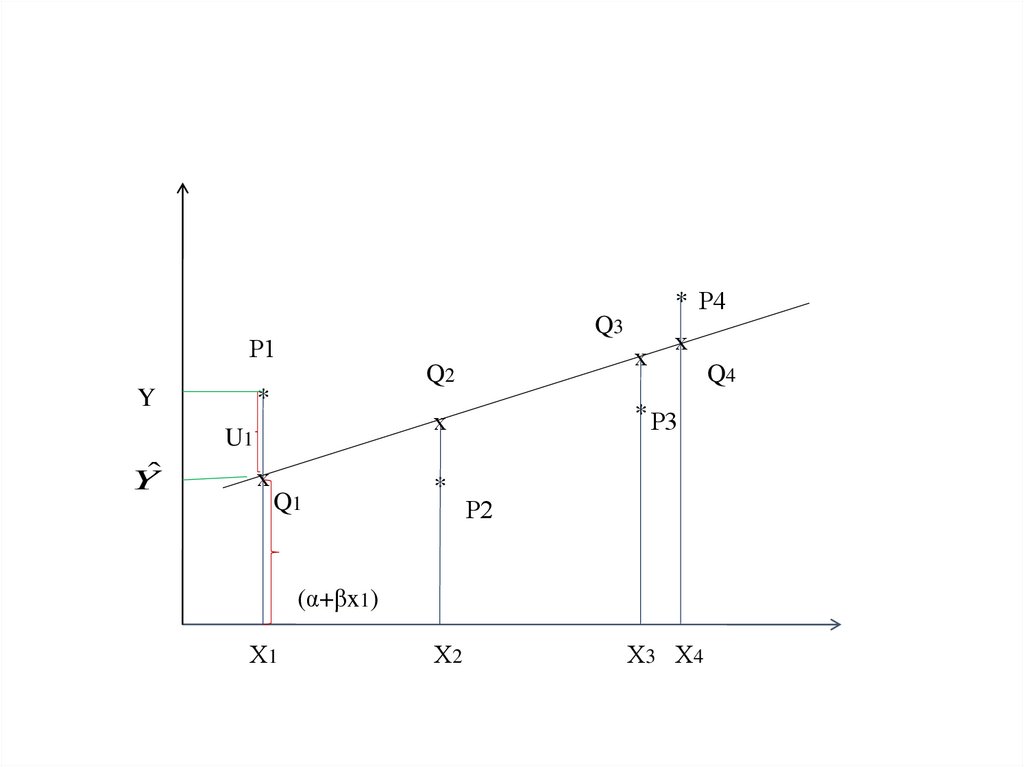
Точки Р1, Р2, Р3 и Р4 – это фактические илинаблюденные значения.
Точки Q1, Q2, Q3 и Q4 – это теоретические
значения, т.е. в отсутствии случайной
компоненты.
6.
Задача регрессионного анализасостоит в нахождении оценок α и β и
в определении положения
регрессионной прямой по известным
или наблюденным значениям X и Y
при неизвестных значениях U
7.
Метод наименьших квадратовМНК является наиболее популярным
методом нахождения оценок
неизвестных параметров. Критерий
выбора наилучших параметров:
минимизация суммы квадратов
остатков.
8.
Остаток или отклонение (е) –разница между наблюдаемым
значением переменной Y и ее
теоретическим значением
Yˆ
в каждом наблюдении, т.е. при
каждом значении X.
9.
(Y1 Yˆ1)2 e12x1
x2
2
2
ˆ
(Y2 Y2 ) e2
3) x3
2
2
ˆ
(Y3 Y3 ) e3
1)
2)
n)
xn
2
2
ˆ
(Yn Yn ) en
10.
Критерий оптимизации:n
n
2
ˆ
S e (Yi Yi )
i 1
2
i
i 1
Предположим, что между Y и X существует
прямая связь, т.е.
Yˆi a bxi
11.
Тогда можно записать:n
(Yi a bxi ) min
2
i 1
12. Функция принимает свое минимальное значение в точке, где все ее частные производные равны нулю
S0
a
S
0
b
13.
Данная система называетсясистемой нормальных уравненний,
решая эту систему относительно a и b,
мы получаем рабочие формулы
для нахождения оценок
неизвестных параметров α и β исходного
уравнения.
14.
Формулы для нахождения оценок a и b:a y b x
b
xy x y
x (x )
2
2
15.
Причины существованияслучайной компоненты
16.
1. Не включение объясняющих переменныхСоотношение между у и х - очень большое
упрощение. Существуют и другие факторы,
влияющие на у, которые не учтены в модели.
Влияние этих факторов приводит к тому, что
наблюдаемые точки лежат вне прямой.
17.
• Невозможность измерения.• Слабое влияние фактора.
• Отсутствия опыта или знаний.
18.
2. Агрегирование переменныхВо многих случаях зависимость — это попытка
объединить
вместе
микроэкономических
некоторое
соотношений.
число
Отдельные
соотношения имеют разные параметры, любая
попытка определить соотношение между ними
является лишь аппроксимацией.
19.
3. Неправильное описание структурымодели
Если зависимость относится к данным о
временном ряде, то значение Y может зависеть
не от фактического значения Х, а от значения,
которое ожидалось в предыдущем периоде.
20.
Еслиожидаемое
значения
тесно
и
фактическое
связаны,
то
будет
казаться, что между Y и X существует
зависимость,
но
аппроксимация.
это
будет
лишь
21.
4. Неправильная функциональнаяспецификация
Функциональное соотношение между Y и X
математически
может
быть
определено
неправильно. Истинная зависимость может не
являться линейной, а быть более сложной.
22.
5. Ошибки измеренияЕсли
в
измерении
взаимосвязанных
одной
переменных
или
более
имеются
ошибки, то наблюдаемые значения не будут
соответствовать точному соотношению.
23.
Случайная компонента является суммарнымпроявлением
всех
факторов.
Если
бы
случайной компоненты не существовало, то
мы бы знали, что любое изменение Y вызвано
только изменением X и смогли бы точно
вычислить β.
24.
Однако в действительности каждое изменениеY отчасти вызвано изменением U. Поэтому мы
не можем вычислить истинные значения
параметров (α и β), а можем определить лишь
их оценки, т.е. приближенные значения (a и b).
25. Свойства коэффициентов регрессии и условия нормальной линейной регрессии (Гаусса-Маркова)
26.
Фактическое значение Y состоит из двухэлементов: из неслучайной части и случайной
компоненты, поэтому вычисленные оценки а и b
также состоят из двух элементов. Неслучайной
частью для а является α, для b – β.
Следовательно,
свойства
коэффициентов
регрессии существенным образом зависят от свойств
случайной компоненты.
27.
Для того чтобы регрессионный анализ,основанный на обычном МНК, давал
наилучшие результаты, случайный член
должен удовлетворять четырем
условиям, известным как условия
Гаусса—Mapкова.
28.
1-е условие Гаусса—МарковаМатематическое ожидание случайной компоненты
в любом наблюдении должно быть равно нулю.
Иногда величина случайной компоненты будет
положительной, иногда отрицательной, но она не
должена иметь систематического смещения ни в
одном из двух возможных направлений.
29.
Фактически если уравнение регрессиивключает константу, то можно предположить,
что это условие выполняется автоматически,
так как роль константы состоит в определении
любой систематической тенденции в
поведении Y, которую не учитывают
объясняющие переменные, включенные в
уравнение регрессии.
30.
2-е условие Гаусса—МарковаДисперсия
2
u
случайной компоненты
должна быть постоянна для всех наблюдениях.
Иногда случайная компонента будет больше,
иногда меньше, однако не должно быть
априорной причины для того, чтобы она
порождала
большую
ошибку
наблюдениях, чем в других.
в
одних
31.
Если это условие выполняется, тоговорят, что дисперсия ошибки
гомоскедастична,
если нет, то - гетероскедастична.
32.
3-е условие Гаусса—МарковаДаное условие предполагает отсутствие систематической
связи между значениями случайной компоненты в любых
двух наблюдениях. Например, если случайная компонента
велика и положительна в одном наблюдении, это не должно
обусловливать систематическую тенденцию к тому, что она
будет большой и положительной в следующем наблюдении
33.
Или большой и отрицательной, илималой и положительной, или малой и
отрицательной.
Случайные
компоненты
должна
абсолютно независимы друг от друга.
быть
34.
Выполнение данного условия гарантируетотсутствие автокорреляции.
В противном случае, говорят, что
случайная компонета
автокоррелирована.
35. 4-е условие Гаусса—Маркова:
• Случайная компонента должна быть распределена независимо отобъясняющих переменных.
36.
Предположение о нормальности:Наряду с условиями Гаусса—Маркова обычно
также
предполагается
распределения
нормальность
случайного
члена.
Если
случайный член нормально распределен, то так
же
будут
регрессии.
распределены
Предположение
основывается
теореме:
на
и
коэффициенты
о
центральной
нормальности
предельной
37.
«Если случайная величина является общимрезультатом взаимодействия большого числа
других случайных величин, ни одна из которых не
является доминирующей, то она будет иметь
приблизительно нормальное распределение, даже
если отдельные составляющие не имеют
нормального распределения».
38.
Интерпретация линейного уравнениярегрессии
ŷ=а+bx
Оценки a и b имеют математическую и экономическую
интерпретацию.
Математическая:
Коэффициент а называется регрессионной постоянной
или const. Это значение
ŷ,
в том случае когда х=0.
Геометрически это точка с координатами: (0,а)
39.
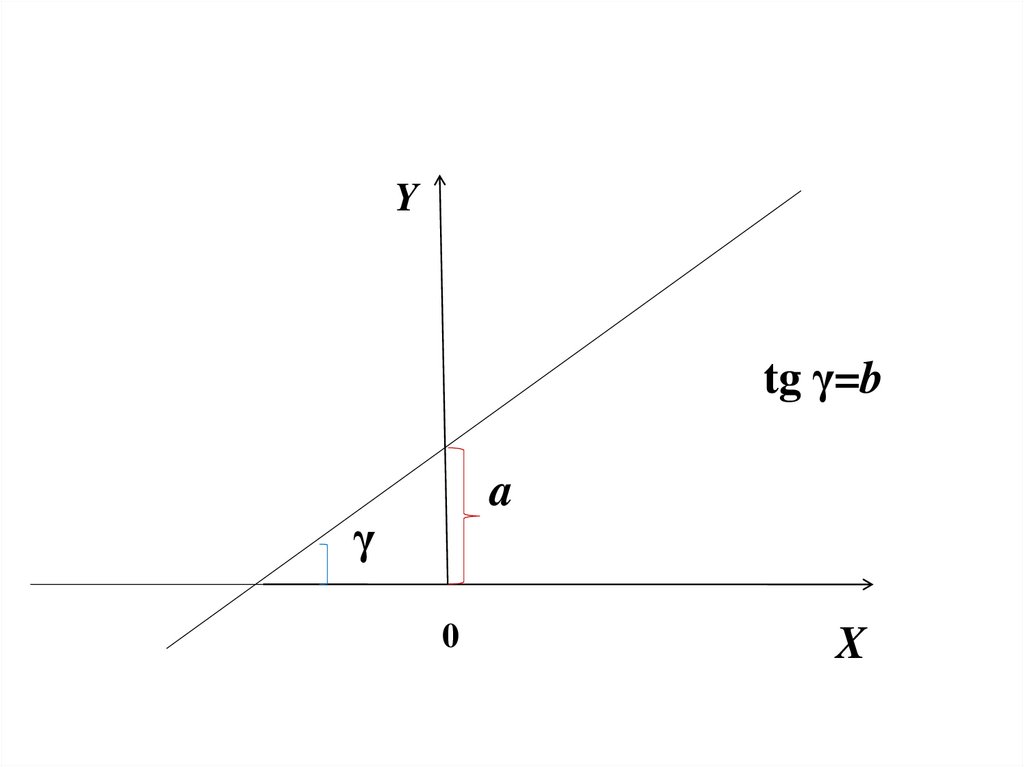
Коэффициентb
–
коэффициент
регрессии – это тангенс угла наклона к
оси OX.
40.
Ytg γ=b
a
γ
0
X
41.
Экономическая:а – регрессионная постоянная, const
Дает прогнозное значение
когда
факторный
у, в том случае,
признак
равен
нулю.
Экономически это может иметь или не иметь
ясного смысла.
42.
b – коэффициент регрессииПоказывает на сколько изменится
значение у (в единицах измерения у),
если х возрастет на одну единицу (в
единицах
измерения
среднего уровня.
x)
от
своего
43.
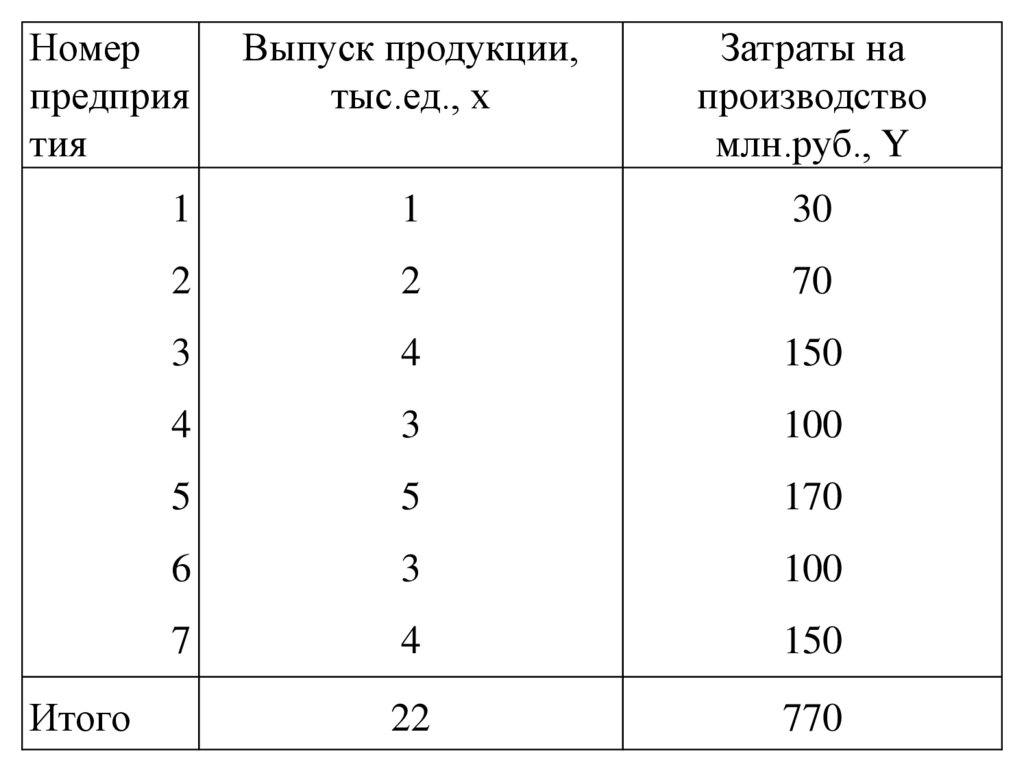
По группе предприятий, выпускающих одини тот же вид продукции, рассматривается функция
издержек
y=α+βx+u ,
где x – объем выпуска продукции (тыс.шт.),
Y – затраты на производство (млн.руб.)
44.
Номерпредприя
тия
Итого
Выпуск продукции,
тыс.ед., х
Затраты на
производство
млн.руб., Y
1
1
30
2
2
70
3
4
150
4
3
100
5
5
170
6
3
100
7
4
150
22
770
45.
Оценив параметры модели методом наименьшихквадратов, получим следующее уравнение:
ˆ
Y 5,79 36,84 x
46.
В данном случае величина параметра aне имеет экономического смысла.
Параметр b показывает, что если выпуск продукции
возрастет на одну тысячу штук (от своего среднего
уровня), то затраты на производство увеличатся на
36,84 млн.руб.
47.
Суточноепотребление
сливочного
масла
обследованных семьях связано с доходом потребителя
прямолинейной регрессией следующим образом:
ŷ=3,87+0,418*х
х – доход (руб.)
у – сливочное масло (г/сут.)
в
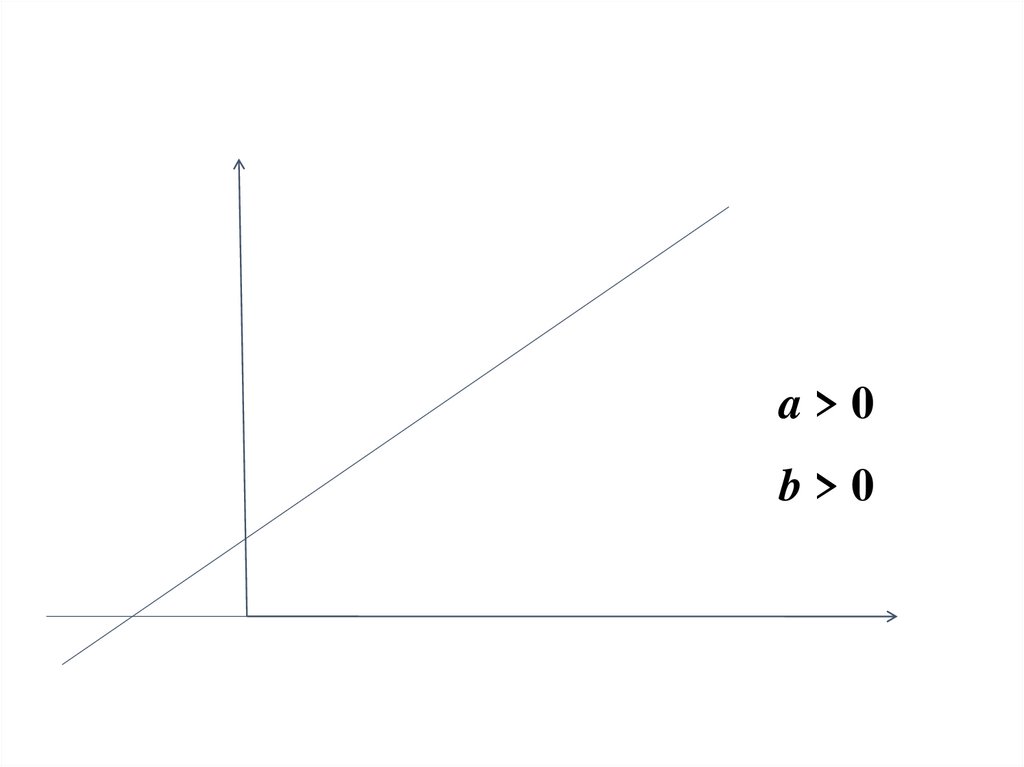
48.
a>0b>0
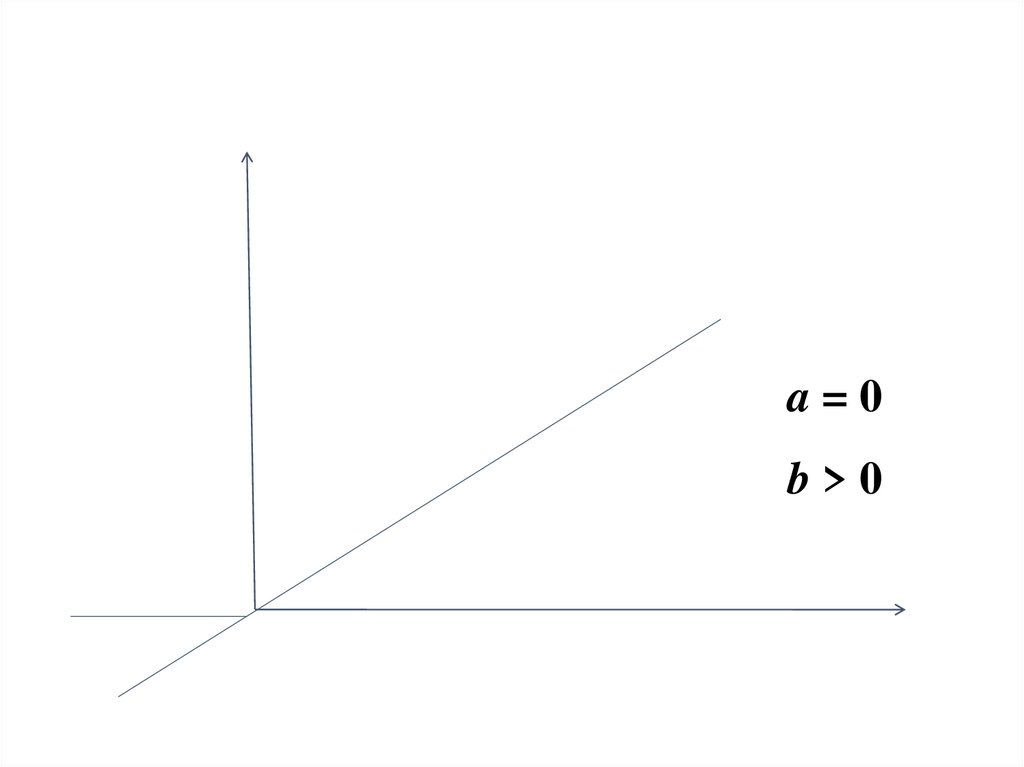
49.
a=0b>0
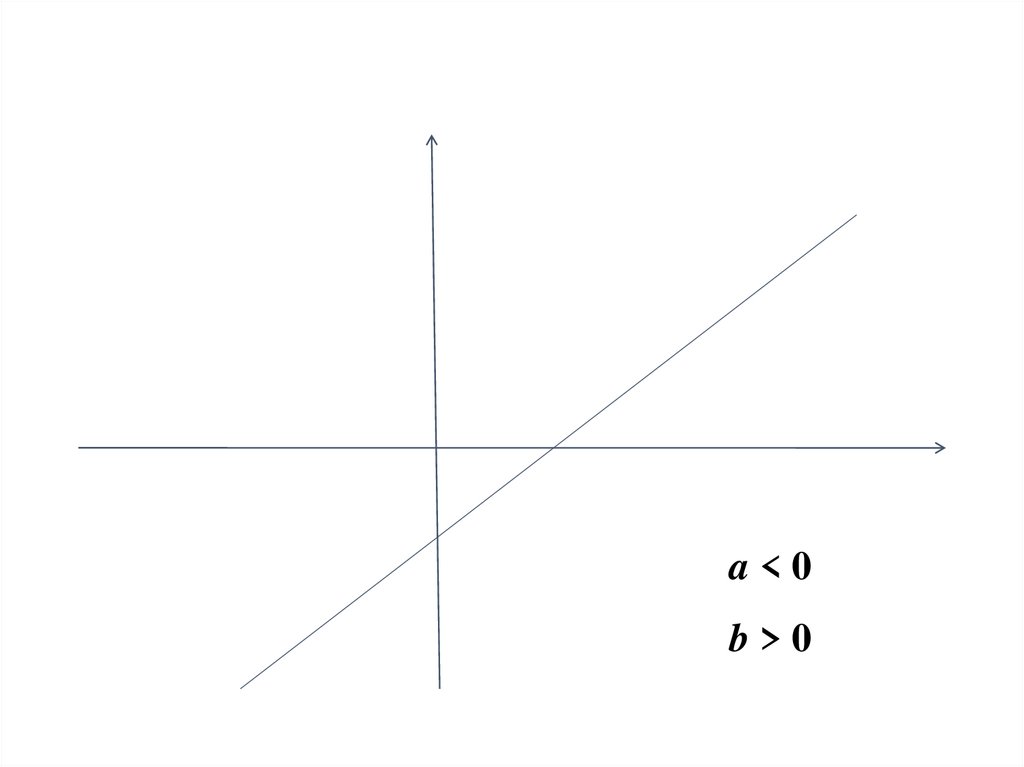
50.
a<0b>0
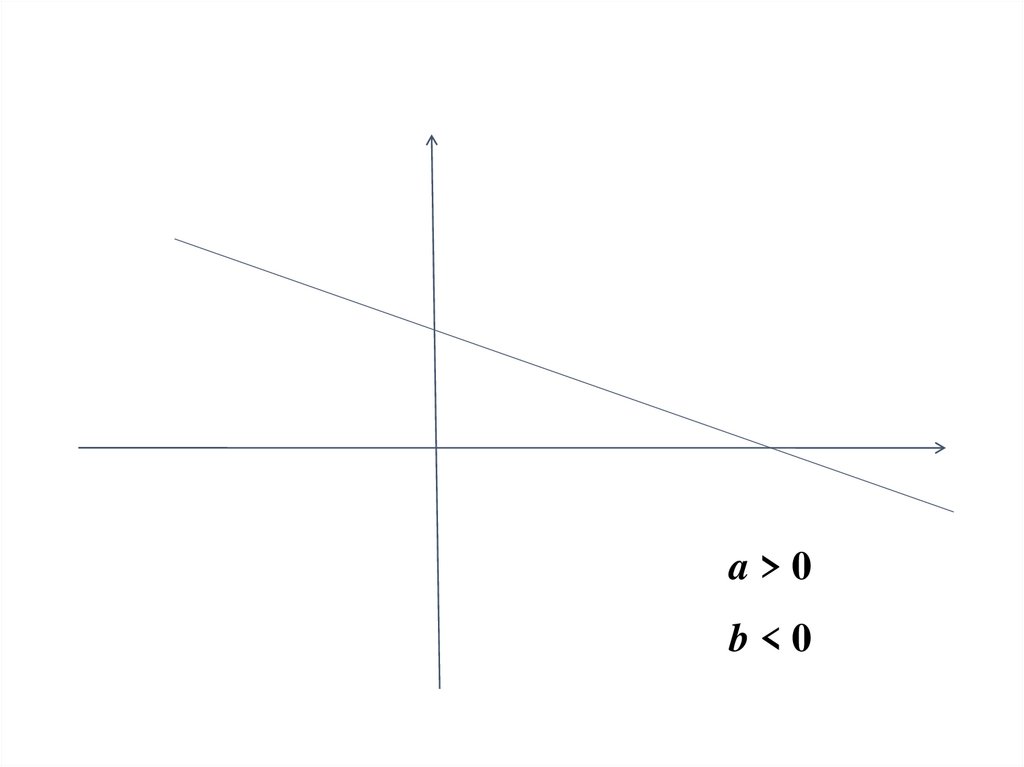
51.
a>0b<0
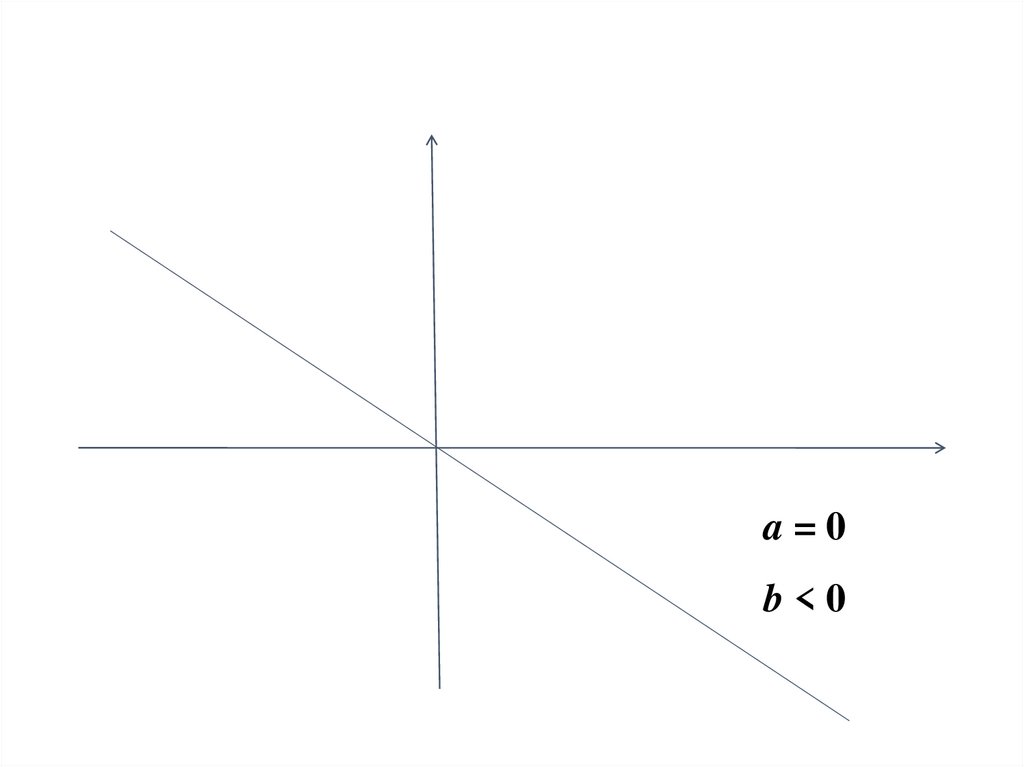
52.
a=0b<0
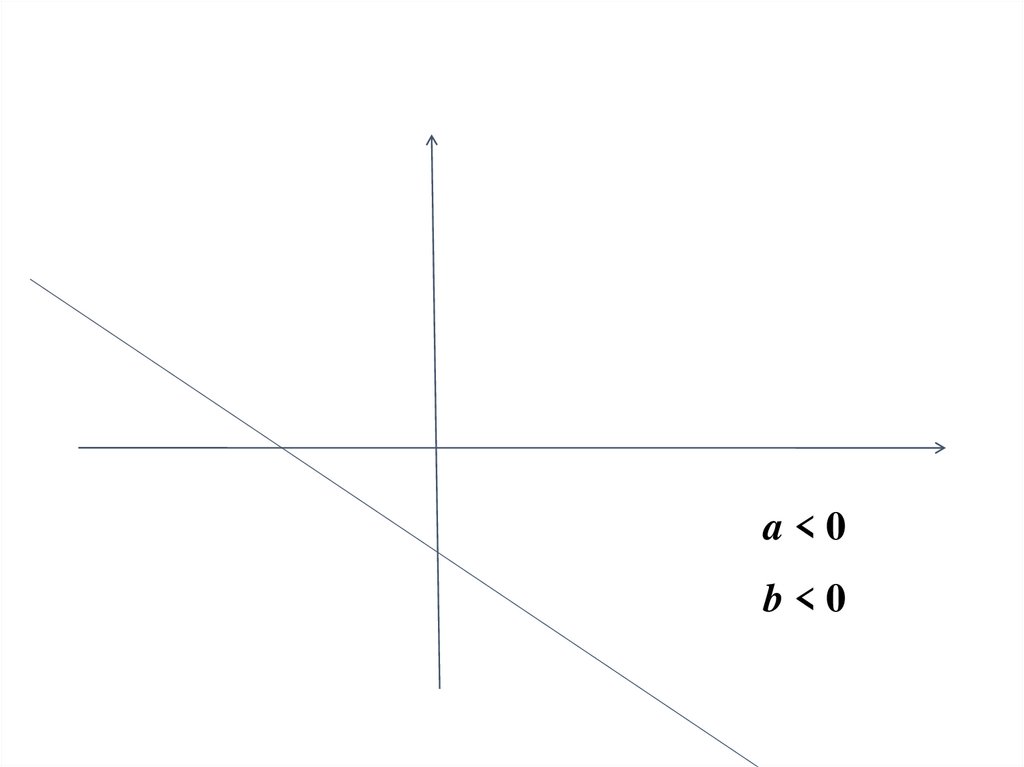
53.
a<0b<0
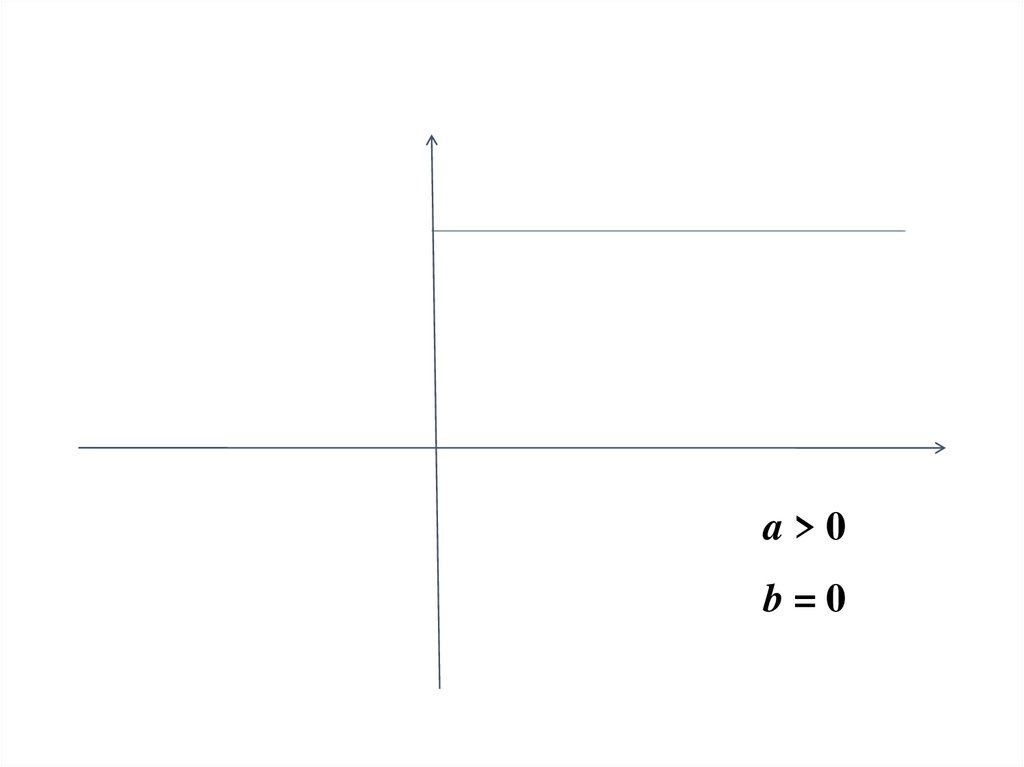
54.
a>0b=0
55.
Определение тесноты связи между факторамиВ
качестве
меры
тесноты
связи
используется
линейный коэффициент корреляции:
r
xy x y
x y
56.
гдеx x (x )
2
2
y y ( y)
2
2
57.
Линейныйкоэффициент
корреляции
может
принимать любые значения в пределах от минус 1 до
плюс 1. Чем ближе коэффициент корреляции по
абсолютной величине к 1, тем теснее связь между
признаками.
Знак при линейном коэффициенте корреляции
указывает на направление связи - прямой зависимости
соответствует знак плюс, а обратной зависимости знак минус.
58.
Еслисравнить
формулы
для
расчета
коэффициентов
регрессии и корреляции, то можно увидеть, что между этими
коэффициентами существует связь
b
r
xy x y
x (x )
2
2
xy x y
x y
59.
Можно выразить коэффициент корреляции черезкоэффициент регрессии:
x
r b
y
Если b < 0
Если b > 0
=> -1 ≤ r < 0
=> 0 < r ≤ 1
60.
r = 0 ==> связь между х и у отсутствует0 <│r│≤ 0,3 => связь практически
отсутствует
0,3 <│r│≤ 0,5 => слабая связь между х и у.
0,5 <│r│≤ 0,7 => средняя (умеренная
связь).
0,7 <│r│< 1 => сильная связь.
│r│ =1 => функциональная связь.
61.
d – коэффициент детерминации.Коэффициент детерминации показывает на
сколько процентов изменение у обусловлено
изменением х.
d r 100%
2
62.
Оставшаяся доля приходится на влияниепрочих факторов, не учтенных в модели.
(1 r ) *100
2
63.
Дляинтерпретации
полученных
результатов можно также использовать
коэффициент
эластичности,
который
показывает насколько процентов в среднем
изменится
признака,
значение
если
результативного
факторный
увеличится на один процент.
признак
64.
xЭ f ( x)
f ( x)
x
Э b
a b x
65.
В силу того, что коэффициент эластичностидля линейной функции не является величиной
постоянной, а зависит от соответствующего
значения x, то обычно рассчитывается средний
показатель эластичности по формуле:
66.
xЭ b
a b x
67.
Внашем
примере
коэффициент
эластичности равен 1,03 %.
Это означает, что с ростом выпуска
продукции на 1 % затраты на производство в
среднем увеличатся на 1,03 %.
68.
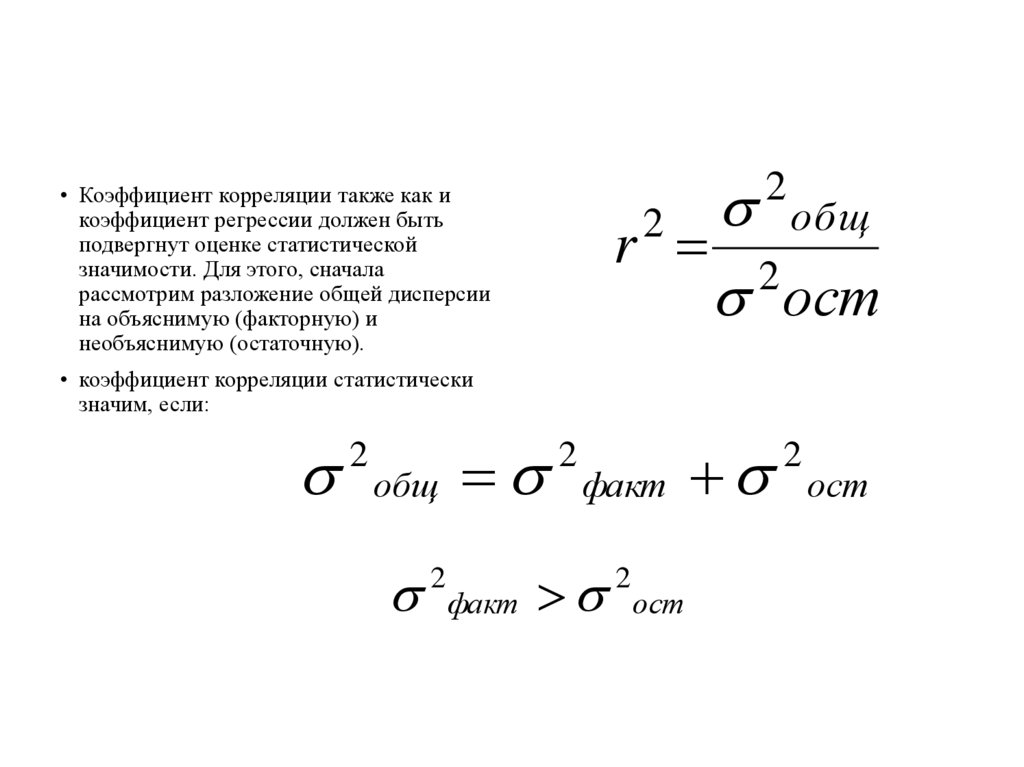
общr 2
ост
• Коэффициент корреляции также как и
коэффициент регрессии должен быть
подвергнут оценке статистической
значимости. Для этого, сначала
рассмотрим разложение общей дисперсии
на объяснимую (факторную) и
необъяснимую (остаточную).
2
2
• коэффициент корреляции статистически
значим, если:
2
общ
2
факт
2
факт
2
ост
2
ост
69. Любая сумма квадратов отклонений связана с числом степеней свободы df, то есть с числом свободы независимого варьирования
признака, который определяетсяразмером выборки и числом определяемых по ней констант.
2
2
2
ˆ
ˆ
(
y
y
)
(
y
y
)
(
y
y
)
x
x
• Степени свободы:
• Дисперсия на 1 степень
свободы:
(n 1) 1 (n 2)
Dобщ
2
(
y
y
)
Dфакт
Dост
n 1
2
ˆ
(
y
y
)
x
1
2
ˆ
(
y
y
)
x
n 2
70. F-статистика:
FF-статистика:
• Проверка:
2
• 1. H 0 : r
• 2.
0; H 1 : r 0
0,05
• 3. F-статистика
• 4.
Fкр ( n 2, )
2
r
• 5. F
* (n 2)
2
1 r
2
Dфакт
Dост
71.
• 1.• 2.
• 3.
• 4.
H 0 : Dфакт Dост ; H 1 : Dфакт Dост
1 r2
mr
n 2
r
tr
t
2
1 r
r
2
* n 2
F
– стандартная ошибка.
–(*)
72. Формула (*) рекомендуется при большом n и если r не стремится к 1 или к -1. Если же , то распределение его оценок отличается от
нормального распределенияили распределения Стьюдента.
Чтобы избежать этого затруднения Фишером было предложено ввести
вспомогательную величину Z:
1
1 r
Z * ln
2
1 r
Если
1 r , 1
, то
Тогда стандартная ошибка для Z:
Тогда:
H 0 : r 0; H1 : R 0
( ) Z ( )
mz
1
n 3
Z
tz
mz
Существуют таблицы для оценки значимости по этим формулам.







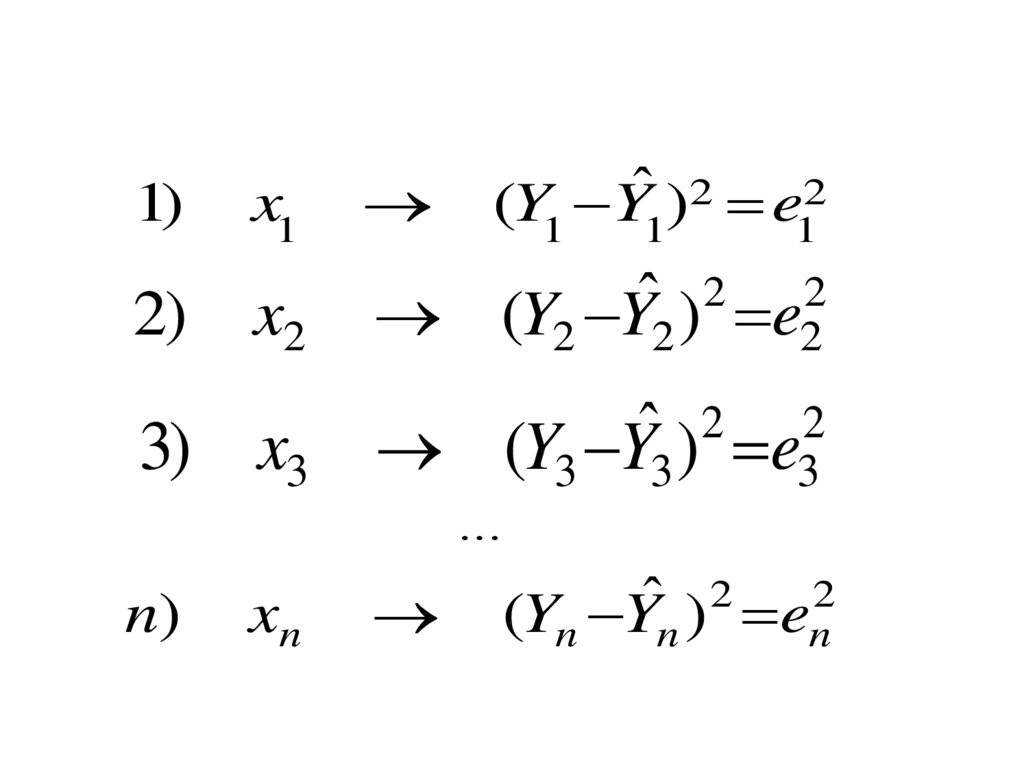

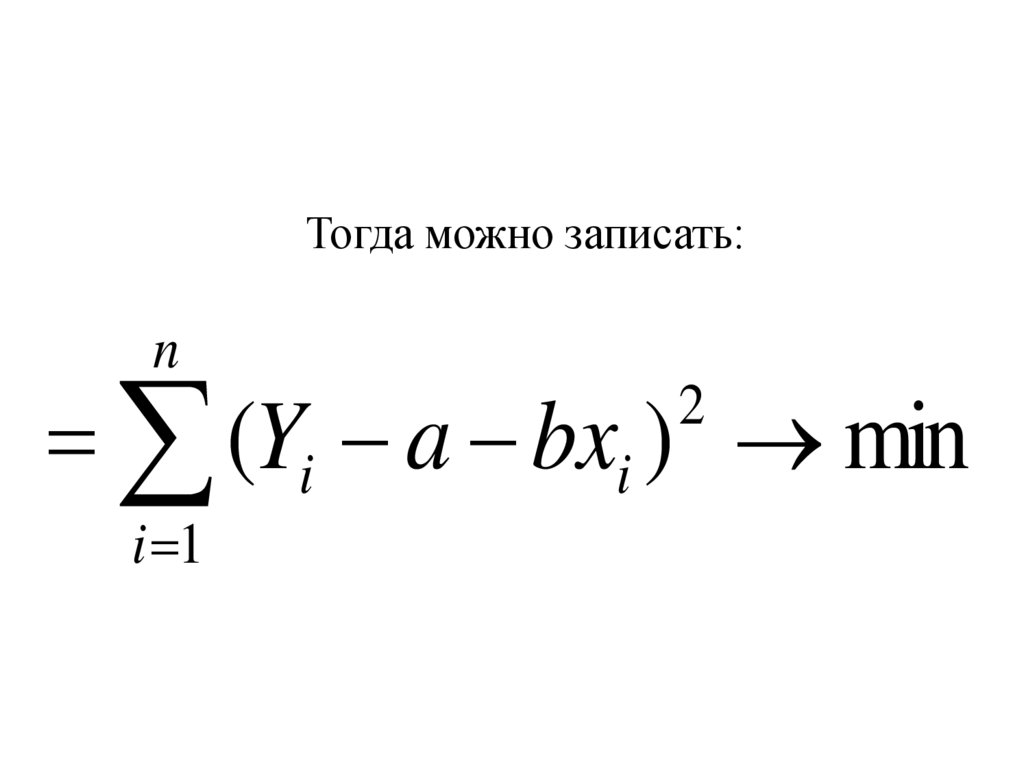











































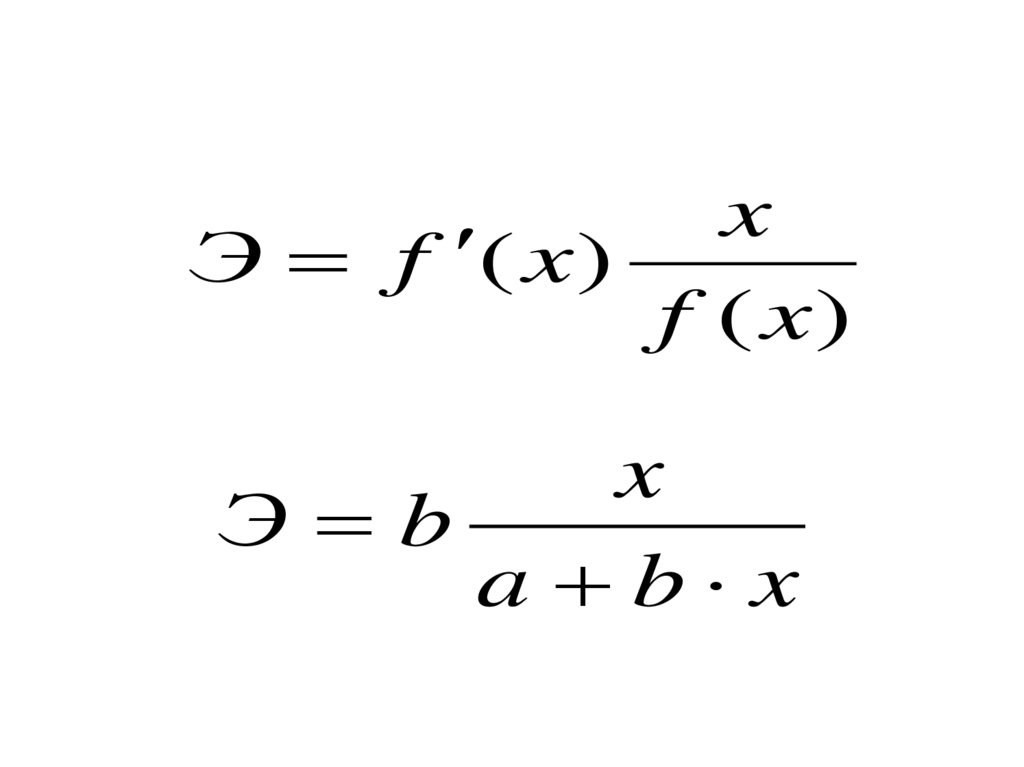

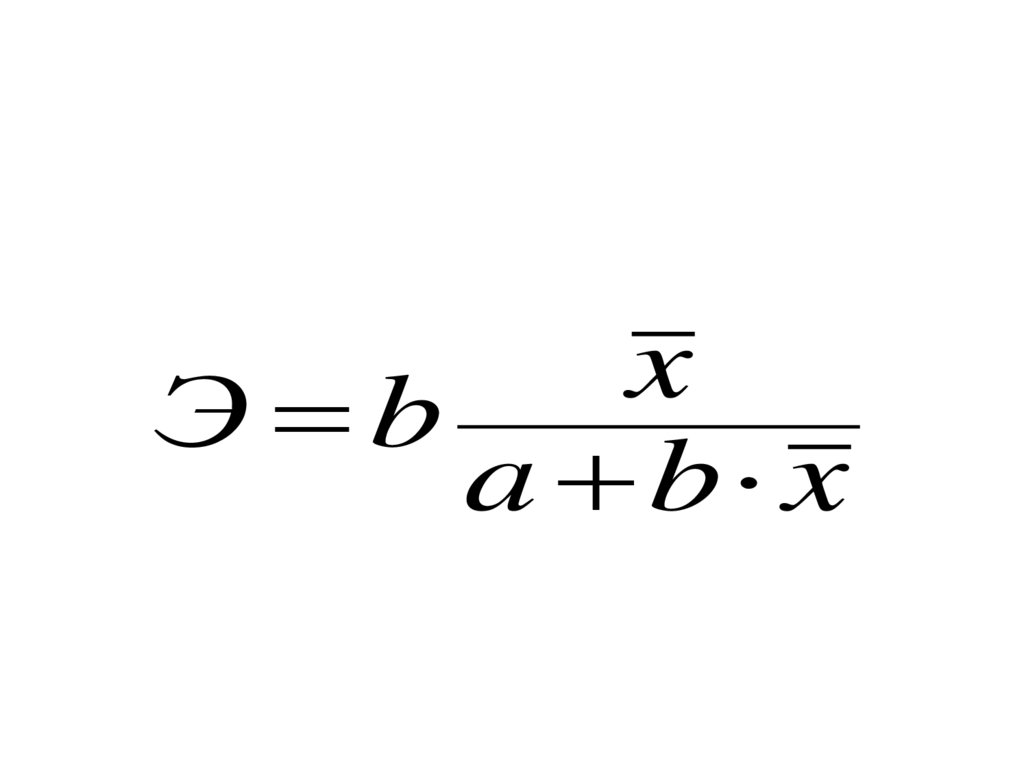



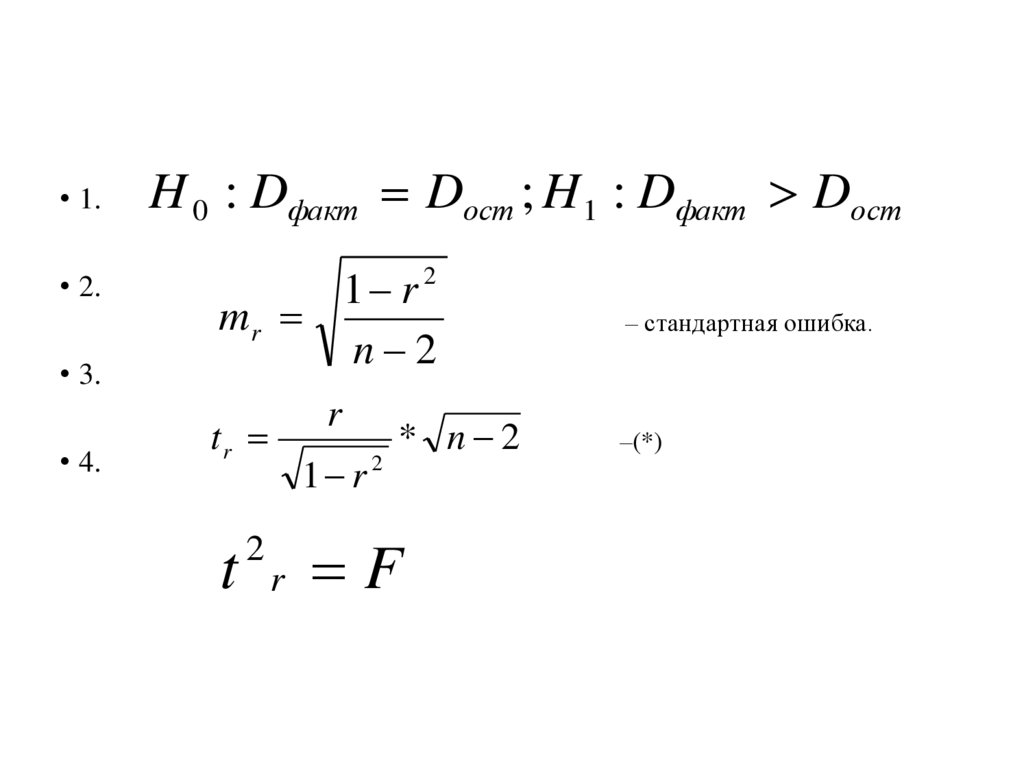

 mathematics
mathematics








