Similar presentations:
Линейная модель множественной регрессии, оценка ее параметров. (Тема 3)
1. Тема 3. Линейная модель множественной регрессии, оценка ее параметров
1. Общая модель множественной регрессии.Линейная модель множественной регрессии.
Эмпирическая форма записи.
2. Оценка параметров модели с помощью МНК.
3. Показатели качества множественной регрессии.
4. Мультиколлинеарность.
2. Спецификация модели множественной регрессии
1 вопросСпецификация модели
множественной регрессии
Множественная регрессия представляет собой модель,
где среднее значение зависимой переменной Y рассматривается как функция нескольких независимых переменных Xj.
Y f ( x1 , x2 , x3 ,...xm )
3.
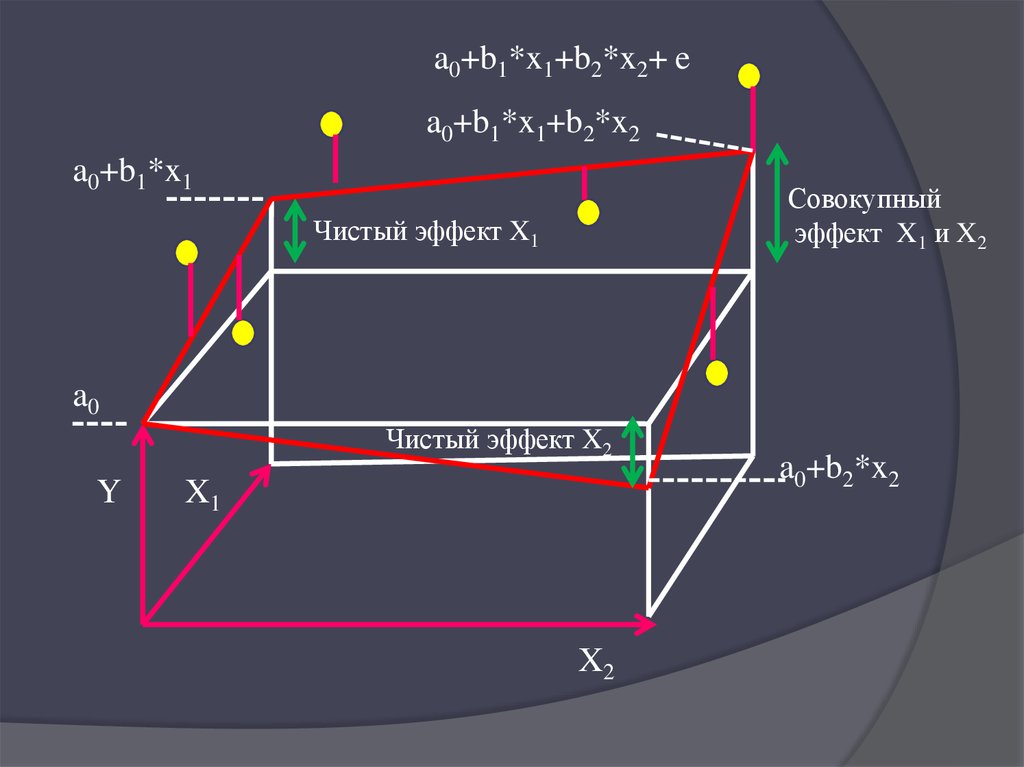
a0+b1*x1+b2*x2+ ea0+b1*x1+b2*x2
a0+b1*x1
Совокупный
эффект X1 и X2
Чистый эффект X1
a0
Чистый эффект X2
Y
X1
X2
a0+b2*x2
4.
Y= a0+b1*x1+b2*x2+ eY-общая величина расходов на питание
X1- располагаемый личный доход,
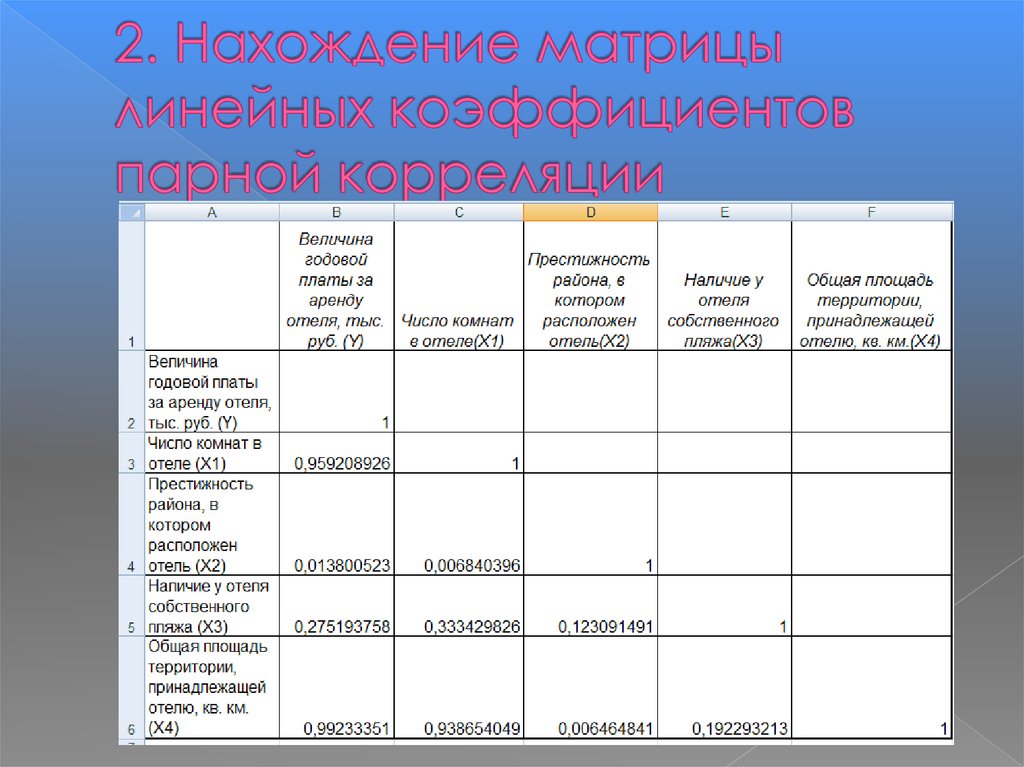
X2- цена продуктов питания
Экономическая интерпретация: При каждом увеличении
располагаемого личного доходаX1 на 1 единицу собственного
измерения, расходы на питание (Y) увеличиваются на b1
единиц измерения при сохранении постоянных цен.
На каждую единицу индекса цен X2 эти расходы уменьшаются
на b2 единиц измерения при сохранении постоянных доходов.
Если a0>0, то вариация расходов меньше вариации факторов;
если a0<0, то вариация расходов больше вариации факторов.
5.
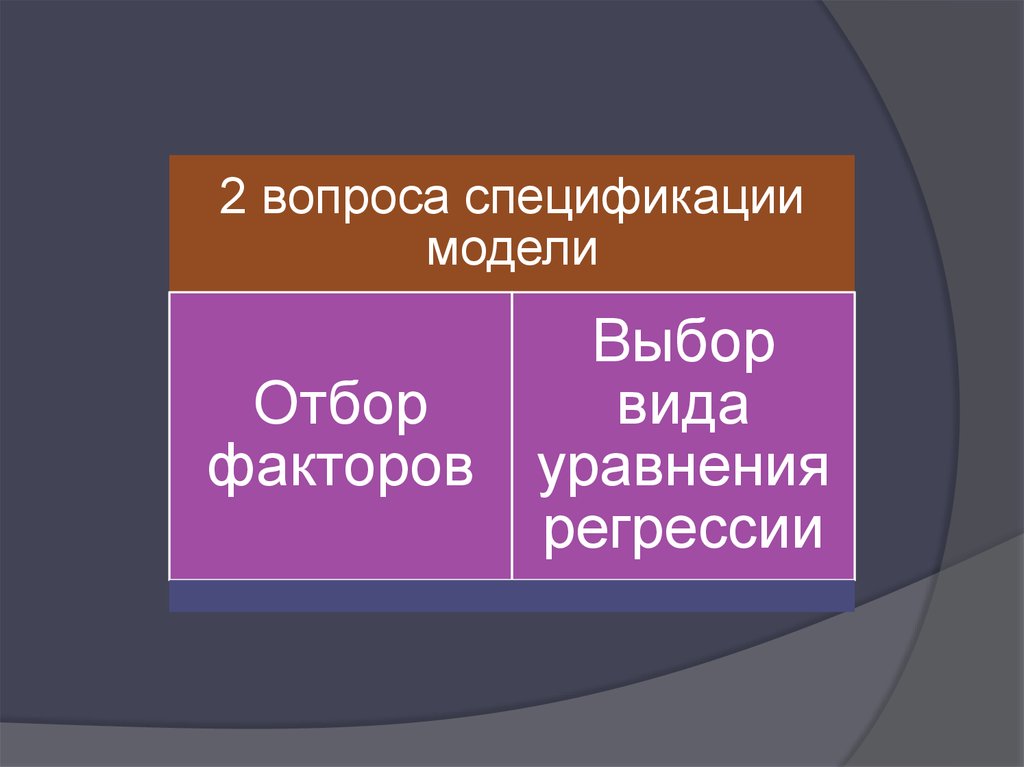
2 вопроса спецификациимодели
Отбор
факторов
Выбор
вида
уравнения
регрессии
6. Линейная модель множественной регрессии
Y a0 b1 x1 b2 x2 ... bm xmФакторы, включаемые во множественную регрессию:
- должны быть количественно измеримы;
- не должны быть коррелированы между собой и тем более
находиться в точной функциональной связи.
7.
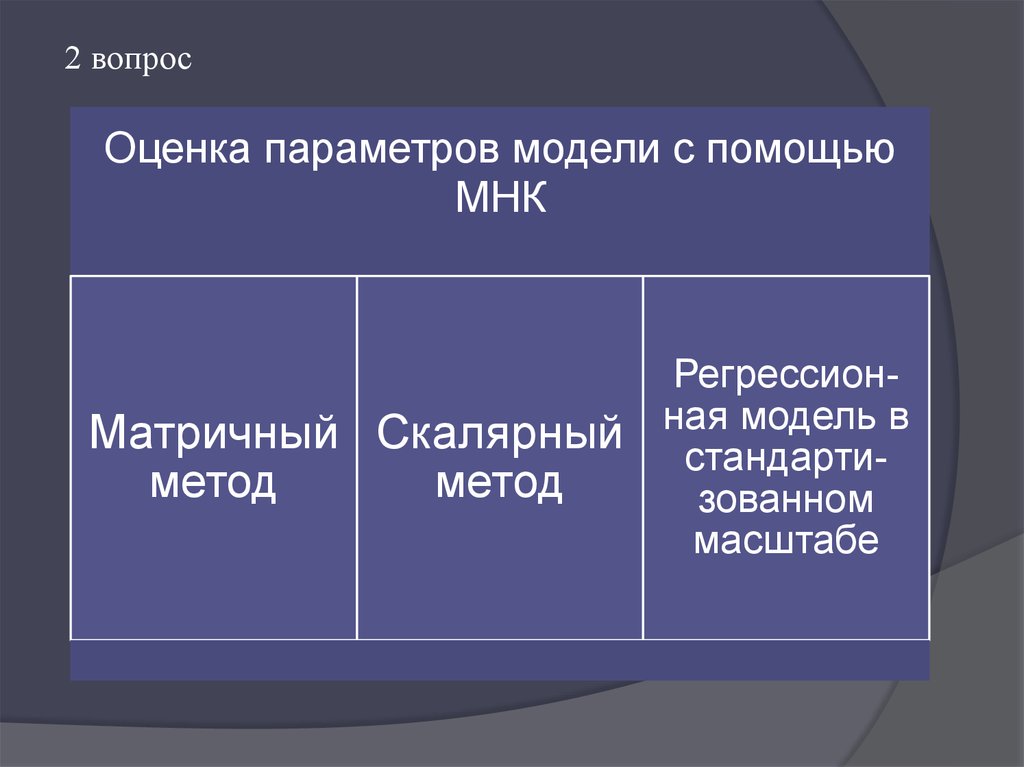
2 вопросОценка параметров модели с помощью
МНК
Регрессионмодель в
Матричный Скалярный ная
стандартиметод
метод
зованном
масштабе
8. Матричный метод
Y y1, y2 ,..., yn-вектор значений Y;
e e1, e2 ,...en
-вектор параметров
регрессии;
-вектор остатков
-регрессии .
B a, b1, b2 ,...bm
1 x11
1 x
21
X
... ...
1 xn1
... x1m
... x2 m
... ...
... xnm
- матрица значений X.
9. Матричный метод
Y B X ee Y B X
Q ei e e
2
Q
2 X Y 2( X X ) B
B
1
B ( X X ) X Y
10. Скалярный метод
ei yi a0 b1 x1 ... bm xmn
n
m
Q ei ( yi (a0 b j xij )) min
i 1
2
2
i 1
j 1
11. МНК-оценки множественной регрессии
nm
Q
a 2 ( yi ( a0 b j xij )),
i 1
j 1
0
n
m
Q
2 ( yi ( a0 b j xij )) xij
b j
i 1
j 1
m
n
( yi ( a0 b j xij )) 0,
j 1
i 1
n
m
( yi ( a0 b j xij )) xij 0
j 1
i 1
12. МНК-оценки множественной регрессии
y n a0 b1 x1 b2 x2 ... bm xm ,2
y x1 a0 x1 b1 x1 b2 x1 x2 ... bm xm x1 ,
......
2
y xm a0 xm b1 x1 xm b2 x2 xm ... bm xm
13. Регрессионная модель в стандартизованном масштабе
t y 1 t x 1 2 t x 2 ... m t xmty
y y
y
; t xj
xj xj
x
;
j
t y t x j 0; ty tx 1
14. Стандартизованные коэффициенты регрессии ()
Стандартизованныекоэффициенты регрессии ( )
Ryx1 1 2 Rx 2 x1 3 Rx 3 x1 ... m Rx m x1 ,
Ryx 2 1 x2 x1 2 3 Rx 3 x2 ... m Rx m x2 ,
......
Ryx x x Rx x Rx x ...
m
m 1
2
m 2
3
3 m
m
15.
Благодаря тому, что в стандартизованномуравнении все переменные заданы как
центрированные и нормированные,
β-коэффициенты сравнимы между собой.
Сравнивая друг с другом β-коэффициенты,
можно ранжировать факторы по силе их
влияния на зависимую переменную Y.
Коэффициенты «чистой» регрессии (bj)
несравнимы между собой.
16.
Стандартизованные коэффициентырегрессии показывают, на сколько
средних квадратических отклонений
(σy) изменится в среднем результат,
если соответствующий фактор xj
изменится на одну сигму (σxi) при
неизменном среднем уровне других
факторов
17.
В парной зависимости стандартизованныйкоэффициент регрессии есть линейный
коэффициент корреляции:
rxy
Во множественной регрессии зависимость
следующая:
y
bj j
x
j
18. Частный коэффициент эластичности
Эy x b jj
xj
y x j x1x2 ... x j 1x j 1 ... xm
показывает, на сколько % изменяется в среднем
результативный признак Y при изменении фактора Xj на
1% и при неизменных других факторах, включенных в модель
19. Индекс множественной корреляции
3 вопросИндекс множественной корреляции независимо от формы
связи оценивает тесноту совместного влияния факторов
на результативный признак Y:
Ryx1x2 ... xm
(y y
1
( y y)
x1 x2 ... xm
2
)
2
0 Ryx1x2 ... xm 1
При линейной регрессии:
Ryx1x2 ... xm
xj
ryx j
20.
Коэффициент детерминацииКоэффициент детерминации:
R
2
yx1 x2 ... xm
1
2
(
y
y
)
x1 x2 ... xm
( y y)
2
Скорректированный коэффициент детерминации:
R 2 yx1x2 ... xm 1
2
(
y
y
)
/( n m 1)
x1 x2 ... xm
( y y)
2
/( n 1)
21.
Когда m - число параметров при Xj –приближается к объему наблюдений (n), то
остаточная дисперсия будет близка к нулю и
R2 приблизится к 1 даже при слабой связи
факторов с результатом. Скорректированный
R2 содержит поправку на число степеней
свободы, что не допускает возможного
преувеличения тесноты связи.
22.
Частные коэффициентыкорреляции
характеризуют тесноту
представляют собой
связи между
отношение сокращения
результатом и
остаточной дисперсии
соответствующим
за счет включения
фактором при
нового фактора к
устранении влияния
остаточной дисперсии,
других факторов,
имевшей место до
включенных в уравнение
введения его в модель
регрессии
23. Частные коэффициенты корреляции
1 R yx1x2 ... x j ... xm1
2
1 R yx1x2 ... x j 1x j 1 ... xm
2
ryx j x1x2 ... x j 1x j 1 ... xm
R2yx1x2…xj…xm – множественный коэффициент детерминации
всего комплекса факторов с результатом;
R2yx1x2…xj-1xj+1…xm – тот же показатель детерминации, но без
введения в модель фактора xj
24.
Порядок частного коэффициента корреляции определяетсяколичеством факторов, влияние которых исключается.
Коэффициенты частной корреляции первого порядка:
1 r x x
1 r x x
x
;
r
yx
x
x
2
2
2
1 r yx
1 r yx
2
ryx x
1
2
1 2
2
1
1 2
2
1
2
ryx x
1
2
ryx ryx rx x
1
2
1 (rx x )
1 2
1 2
2
1
; ryx x
2
1
ryx ryx rx x
2
1
1 (rx x )
Коэффициенты парной корреляции называются
коэффициентами нулевого порядка
1 2
1 2
2
25. F-критерий Фишера
2 вопросЗначимость уравнения множественной регрессии в целом,
так же как и в парной регрессии, оценивается с помощью
F-критерия Фишера:
D ESS
R
n m 1
F 2
2
m
D RSS 1 R
2
2
26. t-статистика Стьюдента
- оценка значимости коэффициентов регрессииH 0 : i 0
H1 : i 0
bi
tb i
,
mb i
tb i t / 2,n m 1 H 1
27.
Задача: Предприниматель желает сдать в арендуна один год принадлежащий ему отель (80
комнат), расположенный в престижной
курортной зоне, обладающий собственным
пляжем, общая площадь территории отеля
составляет 3,42 кв. км. Для установления
величины арендной платы, предприниматель
решил изучить объявления владельцев подобных
отелей и смоделировать величину арендной
платы.
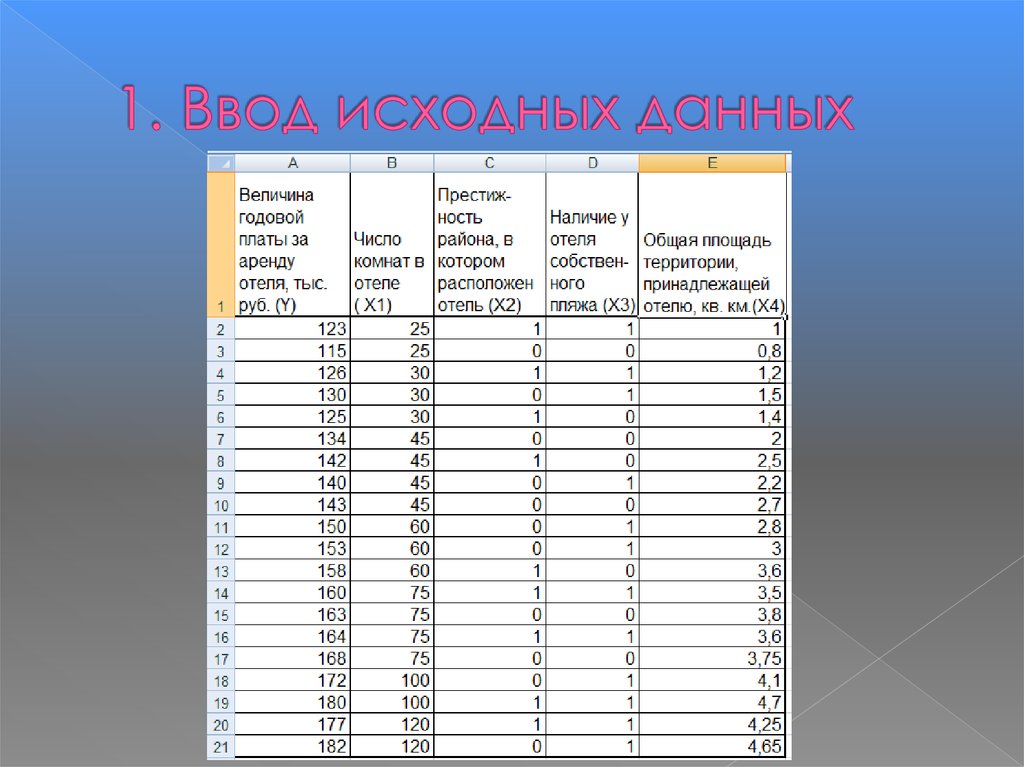
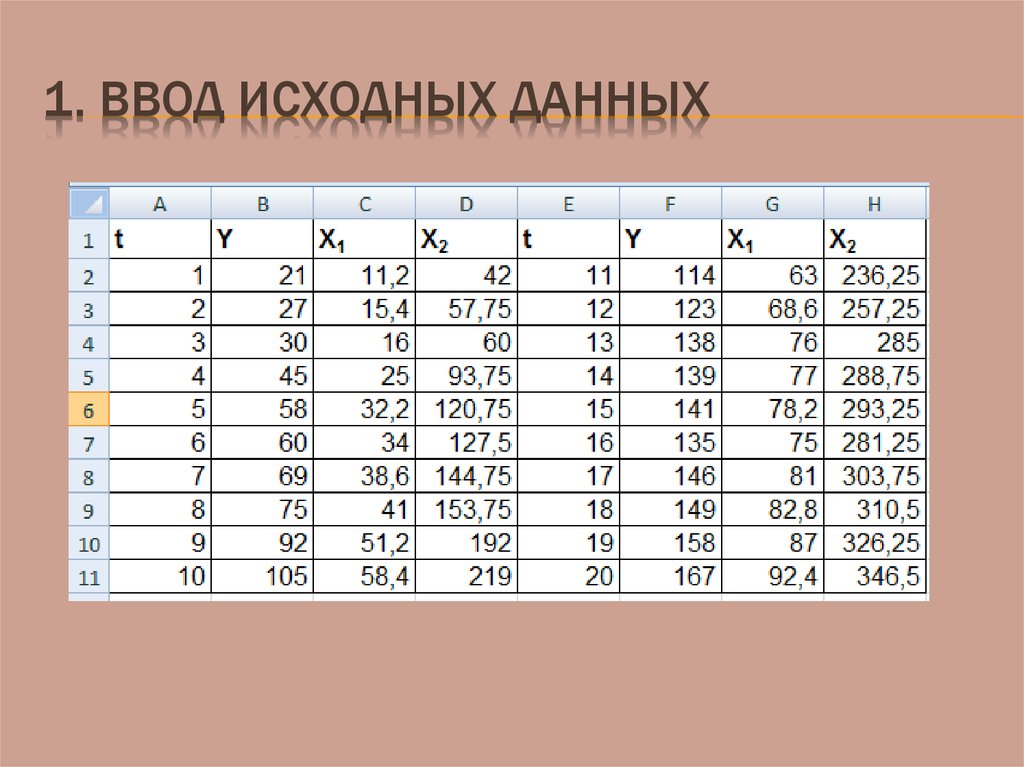
28. 1. Ввод исходных данных
29. 2. Нахождение матрицы линейных коэффициентов парной корреляции
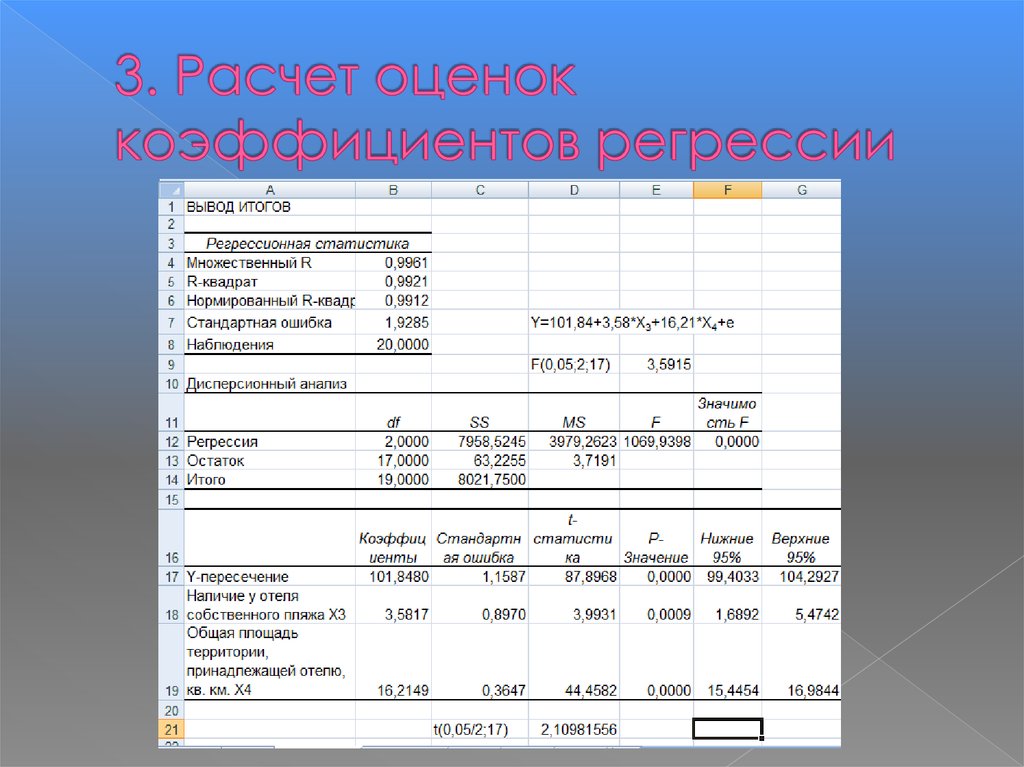
30. 3. Расчет оценок коэффициентов регрессии
31.
Таким образом, построенная модель может бытьзаписана в виде Y=101,84+3,58*X3+16,21*X4+e .
Коэффициент b3 этой модели показывает, что
наличие у отеля собственного пляжа приводит к
удорожанию арендной платы в среднем на 3,58
тыс. руб. при неизменной общей территории,
принадлежащей отелю.
Коэффициент b4 этой модели показывает, что
увеличение
общей территории на 1 кв.км приводит к
удорожанию
арендной платы на 16,21 тыс.руб.
32. 4.Множественный коэффициент корреляции
Множественный коэффициент корреляциидостаточно высокий, что свидетельствует о
существенной зависимости величины арендной
платы от включенных в модель факторов.
33. 5. Скорректированный коэффициент детерминации
Скорректированный коэффициент детерминациисвидетельствует, что 99,12% дисперсии арендной
платы
формируется под влиянием факторов, включенных
в модель.
34. 6. Расчет бетта-коэффициентов
0,2752 0,9923 0,19233
0,0876;
2
1 0,1923
0,9923 0,2752 0,1923
4
0,9755 .
2
1 0,1923
Полученные значения бетта-коэффициентов
позволяют проранжировать факторы по степени
их влияния на арендную плату следующим
образом:
1) общая площадь территории, принадлежащей
отелю;
2) наличие собственного пляжа.
35. 7. F-тест
Сравнение расчетного значения F-критерия стабличным
(1069,9398 > 3,5915) с вероятностью 95% позволяет
сделать
вывод об адекватности и статистической
значимости модели
в целом.
36. 8. t-тест
Сравнение модулей полученных t- статистикс табличным значением (2,1098)
подтверждает значимость коэффициентов
регрессии b0,b3,b4.
37. 9. Расчет средней прогнозируемой величины арендной платы
Y=101,84+3,58*X3+16,21*X4+e; X3=1; X4=3,42 кв.кмYx=101,84+3,58*1+16,21*3,42=160,8846≈161 тыс.руб.
38. Понятие мультиколлинеарности
4 вопросПОНЯТИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ
Мультиколлинеарность - это линейная
взаимосвязь нескольких объясняющих
переменных (х1, х2, … хm). Если
объясняющие переменные связаны строгой
функциональной зависимостью, то говорят о
совершенной мультиколлинеарности.
39. Диаграмма Венна
ДИАГРАММА ВЕННАМультиколлинерность не позволяет однозначно разделить
вклады объясняющих переменных x1,x2,…xm в их влияние
на зависимую переменную Y.
Y
Y X
X1
2
X1 X2
х1 и х2 не коллинеарны
х1 и х2 коллинеарны
Y
X1=X2
совершенная коллинеарность х1 и х2
40. Последствия мультиколлинеарности
ПОСЛЕДСТВИЯМУЛЬТИКОЛЛИНЕАРНОСТИ
Увеличиваются стандартные ошибки оценок
Уменьшаются t-статистики МНК-оценок регрессии
МНК-оценки чувствительны к изменениям данных
Возможность неверного знака МНК-оценок
Трудность в определении вклада независимых
переменных в дисперсию зависимой переменной
41. Признаки мультиколлинеарности
2 вопросПРИЗНАКИ МУЛЬТИКОЛЛИНЕАРНОСТИ
Высокий R2
Близкая к 1 парная корреляция между
малозначимыми независимыми переменными
Высокие частные коэффициенты корреляции
Сильная дополнительная регрессия между
независимыми переменными
42.
Задача: Руководство коммерческого банка ищет путиуменьшения расходов, связанных с основным видом
деятельности – размещением вкладов физических лиц. С
этой целью по данным за последние 20 кварталов было
решено проанализировать , в какой мере
среднеквартальное число клиентов (Y) определяется
величиной затрат на рекламу (X1) и суммой расходов на
связи с общественностью (X2).
43. 1. Ввод исходных данных
1. ВВОД ИСХОДНЫХ ДАННЫХ44. 2. Построение уравнения регрессии
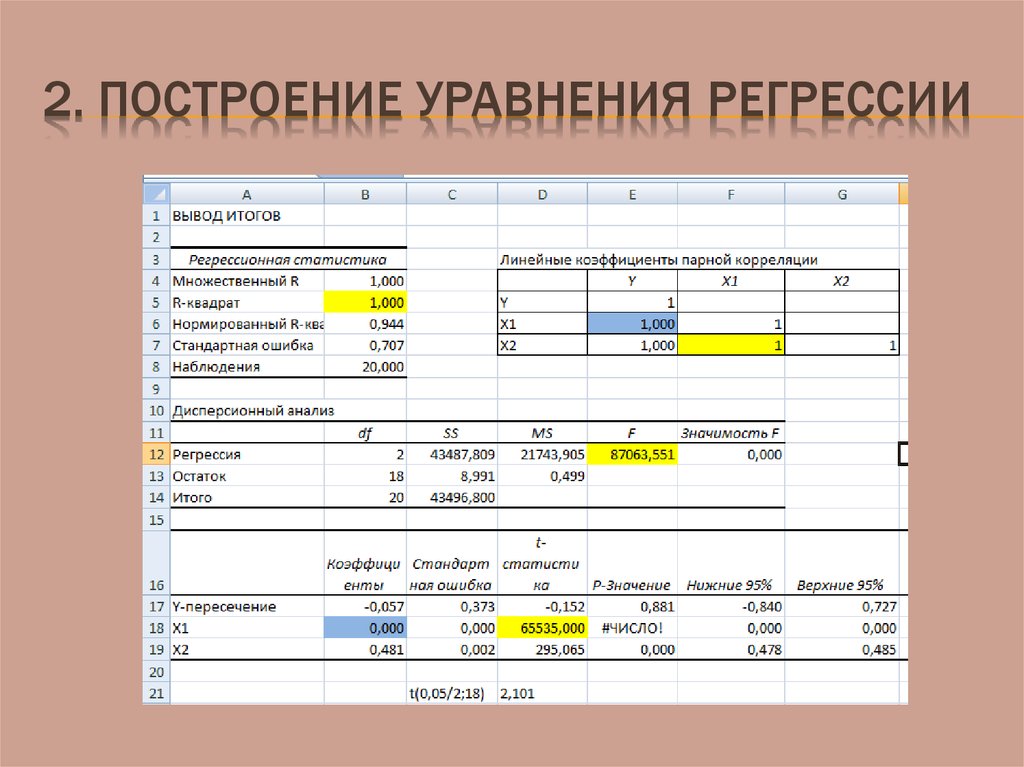
2. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ45.
Полученный результатпозволяет выдвинуть
гипотезу о наличии
коллинеарности факторов
X1, X2!
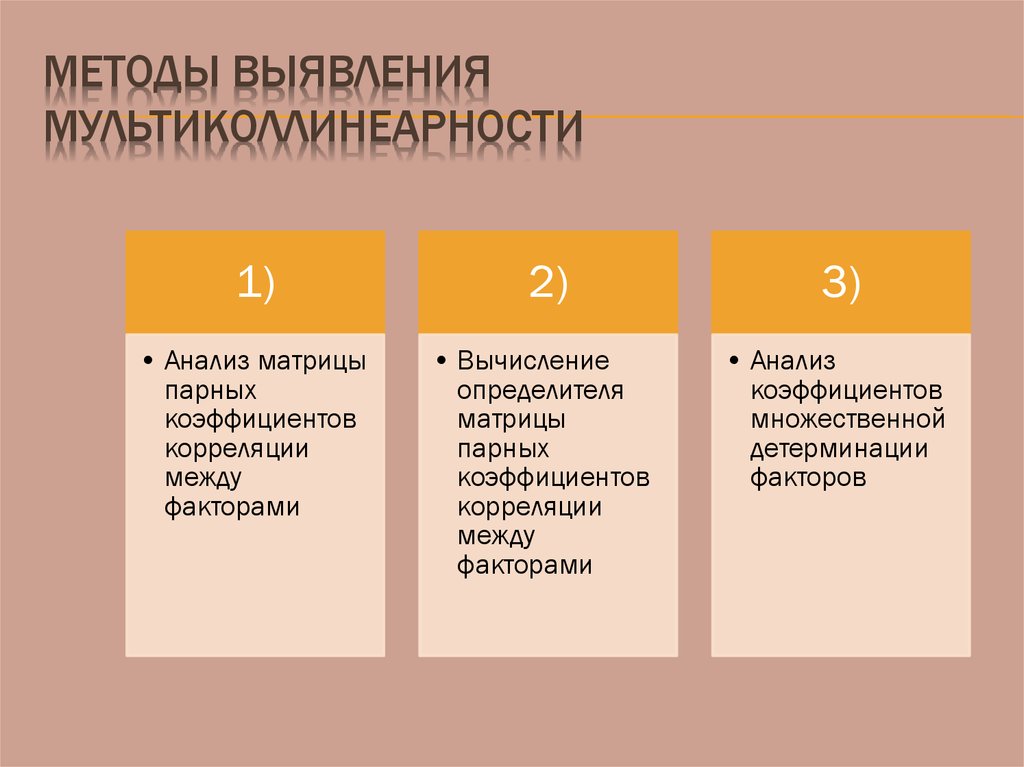
46. Методы выявления мультиколлинеарности
МЕТОДЫ ВЫЯВЛЕНИЯМУЛЬТИКОЛЛИНЕАРНОСТИ
1)
2)
3)
• Анализ матрицы
парных
коэффициентов
корреляции
между
факторами
• Вычисление
определителя
матрицы
парных
коэффициентов
корреляции
между
факторами
• Анализ
коэффициентов
множественной
детерминации
факторов
47.
Первый метод: Две переменные коллинеарны, т. е.находятся между собой в линейной зависимости,
если rxixj ≥ 0,7. По величине парных коэффициентов
корреляции обнаруживается явная коллинеарность
двух факторов.
Y
X1
X2
Y
1
X1
0,8
1
X2
0,7
0,8
1
X3
0,6
0,5
0,2
X3
1
rx1x2= 0,8 - x1 и x2 коллинеарны.
ryx1>ryx2, при этом rx1x3>rx2x3, поэтому исключается x1.
48.
Предпочтение при этомотдается тому фактору,
который при достаточно
тесной связи с результатом
имеет наименьшую тесноту
связи с другими факторами!
49.
Второй метод: Если между факторами существует полнаялинейная зависимость, и все коэффициенты межфакторной
корреляции равны единице, то определитель такой матрицы
равен нулю. Следовательно, чем ближе к нулю определитель,
тем сильнее мультиколлинеарность факторов.
Линейные коэффициенты парной корреляции
Y
X1
X2
Y
1
X1
1,000
1
1
X2
1,000
1
1
Δ=1*1-1*1=0. Равенство определителя нулю говорит о наличии
мультиколлинеарности в строгом смысле. Следовательно, необходимо
исключить один из факторов и перестроить модель заново.
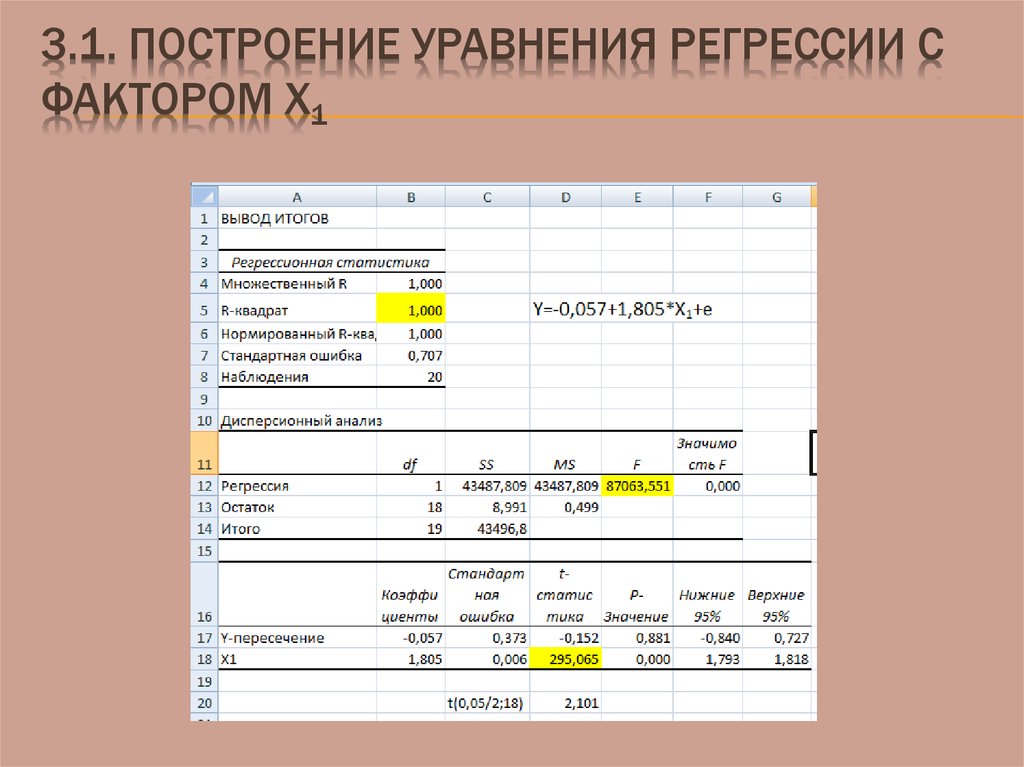
50. 3.1. Построение уравнения регрессии с фактором X1
3.1. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ СФАКТОРОМ X1
51. 3. Построение уравнения регрессии с фактором X2.
3. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ СФАКТОРОМ X2.
52.
Третий метод: Для расчета коэффициентов множественнойдетерминации факторов в качестве зависимой переменной
рассматривается каждый из факторов. Например,
xˆ1 c d 2 x2 d3 x3 ... d p x p .
Чем ближе такой коэффициент множественной детерминации
к единице, тем сильнее проявляется мультиколлинеарность
факторов. В уравнении регрессии оставляют факторы с
минимальным коэффициентом множественной детерминации.
Если коэффициент детерминации статистически значим, то в
этом случае xj является линейной комбинацией других
факторов, и его можно исключить из регрессии.
R2 j n p
Fj
2
1 R j p 1
F j F ( ; p 1; n p ).
53. Методы устранения мультиколлинеарности
МЕТОДЫ УСТРАНЕНИЯМУЛЬТИКОЛЛИНЕАРНОСТИ
Исключение из модели коррелированных
переменных ( при отборе факторов)
Сбор дополнительных данных или новая выборка
Изменение спецификации модели
Использование предварительной информации о
параметрах
Преобразование переменных
54. Методы отбора факторов
МЕТОДЫ ОТБОРА ФАКТОРОВМетод
включения
Метод
исключения
Пошаговая
регрессия
•Последовательное введение в
модель факторов, дающих
увеличение скорректированного R2
•Включаются все факторы, а затем
исключаются незначимые по критерию tстатистики
•Последовательное увеличение
факторов в модели с учетом
результатов предыдущего шага
55. Исключение k объясняющих переменных
ИСКЛЮЧЕНИЕ K ОБЪЯСНЯЮЩИХПЕРЕМЕННЫХ
2
2
H 0 : R1 R2
2
2
H1 : R1 R2
2
2
R1 R2
F
2
1 R1
0
n p 1
k
F F ( ; k ; n p 1) H1(исключение некорректно)
56. Включение k объясняющих переменных
ВКЛЮЧЕНИЕ K ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ2
H 0 : R2 R1
2
2
H1 : R2 R1
2
2
R2 R1
F
2
1 R2
2
0
n p 1
k
F F ( ; k ; n p 1) H1 (включение оправдано)














































 mathematics
mathematics economics
economics








