Модели нелинейной регрессии

1.

Модели нелинейной регрессии
№
домохозяйства
Среднедушевой
доход
Объем спроса, кг в
домохозяйства, месяц
тыс. д.е.
1
1
1,71
2
2
6,88
3
3
8,25
4
4
9,52
5
5
9,81
6
6
11,43
7
7
11,09
8
8
10,87
9
9
12,15
10
10
10,94

2.

14
x
Спрос (y), кг
12
y
10
1
1,71
8
2
6,88
3
8,25
2
4
9,52
0
5
9,81
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
6
4
0
Доход (x),тыс. д.е.
Зависимость нелинейная!

3.

14
y = 0,8448x + 4,6187
Спрос (y), кг
12
x
y
10
1
1,71
8
2
6,88
3
8,25
2
4
9,52
0
5
9,81
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
6
4
0
Доход (x),тыс. д.е.
Попытка провести прямую

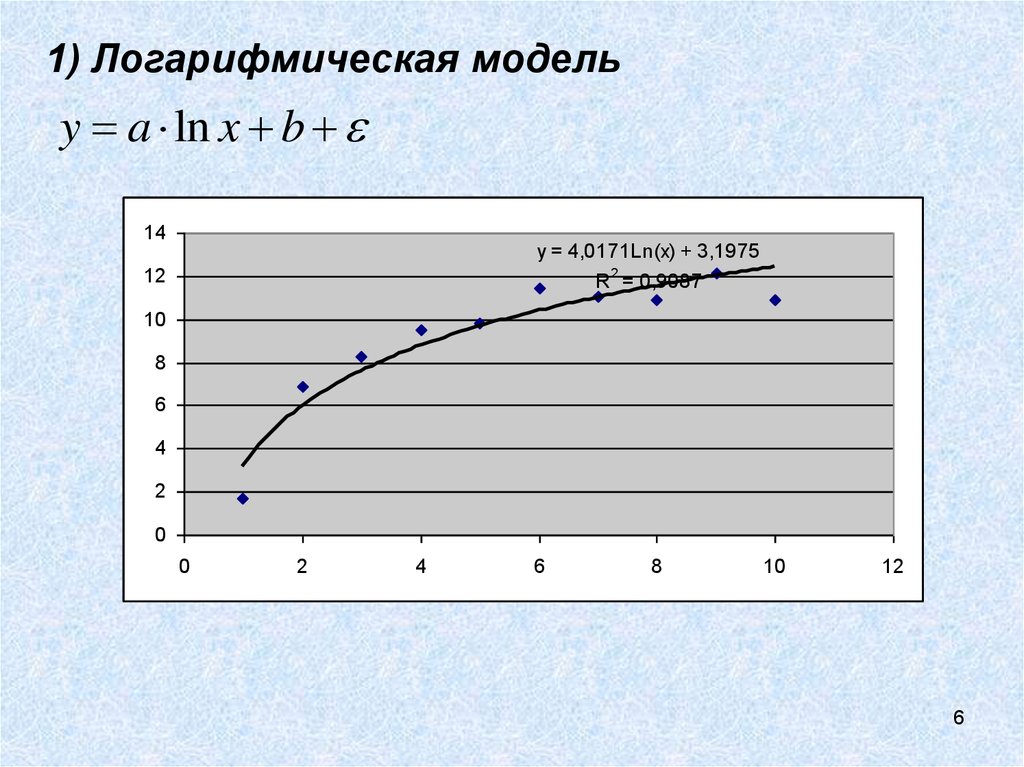
4. 1) Логарифмическая модель

y a ln x b
Для оценки такой зависимости создаем столбец с ln(x)
4

5. 1) Логарифмическая модель

y a ln x b
Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной y, а в качестве независимой ln(x).
Y=4.017ln(x)+3.197
5

6. 1) Логарифмическая модель

y a ln x b
14
y = 4,0171Ln(x) + 3,1975
12
2
R = 0,9087
10
8
6
4
2
0
0
2
4
6
8
10
12
6

7. 1) Логарифмическая модель

y a ln x b
Интерпретация коэффициента а: при увеличении х на 1% y увеличится на
а/100 единиц.
Y=4.017ln(x)+3.197
При увеличении дохода на 1% спрос на товар увеличится на
0,0417 единиц.
7

8. 1) Логарифмическая модель

Также как в линейной модели рассчитывается средняя относительная ошибка
аппроксимации
Y=4.017ln(x)+3.197
8

9.

14
x
Спрос (y), кг
12
y
1
1,71
2
6,88
3
8,25
4
9,52
2
5
9,81
0
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
10
8
6
4
0
Доход (x),тыс. д.е.
2) Попробуем провести гиперболу
наилучшим образом.
1
y a b
x

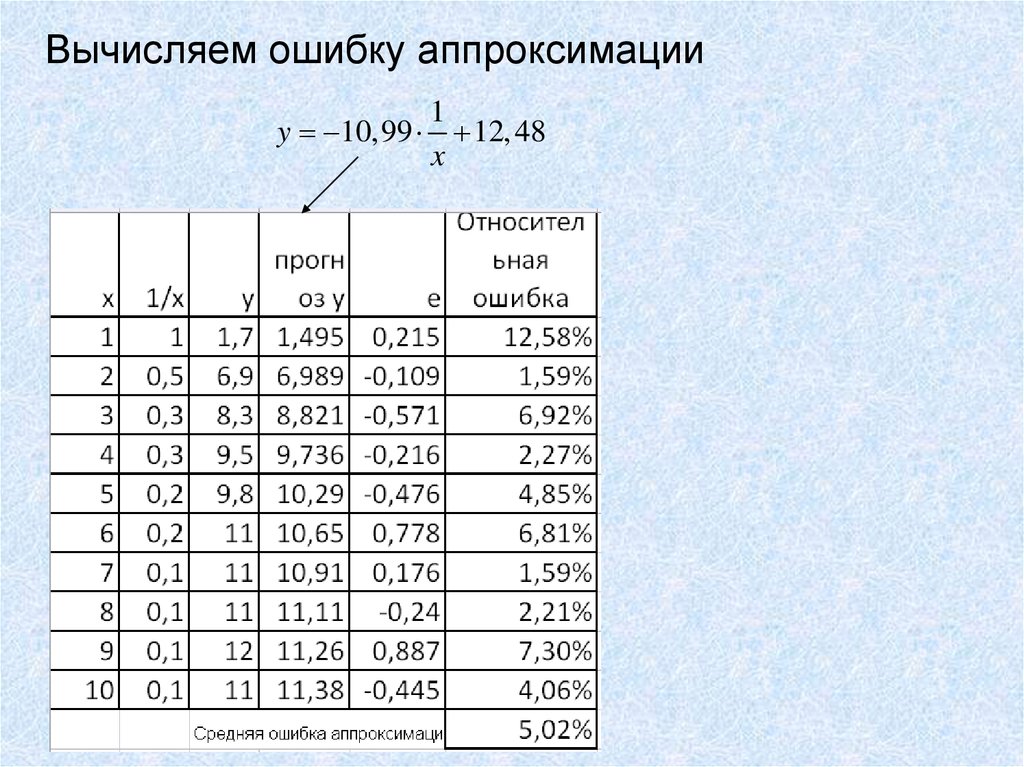
10.

Сначала рассчитаем столбик 1/x

11.

1
y 10,99 12, 48
x

12.

14
12
10
8
1
y 10,99 12, 48
x
6
4
2
0
0
1
2
3
4
5
6
7
8
9
10
11
С ростом дохода объем потребления товара стремится к 12.48 ед.
12

13.

Вычисляем ошибку аппроксимации
1
y 10,99 12, 48
x

14. 3) Степенная модель

y bx
a
Интерпретация коэффициента a – эластичность
зависимой переменной по объясняющей переменной
a показывает, на сколько процентов возрастает y при
возрастании x на 1%.
14

15. Степенная модель

y bx
a
Сводится к линейной модели логарифмированием
ln y ln b a ln x
15

16. Степенная модель

Создаем столбцы с логарифмами
16

17.

Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
17

18.

Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
ln y a ln x ln b
ln b 1.063 b exp(1.063) 2.9
18

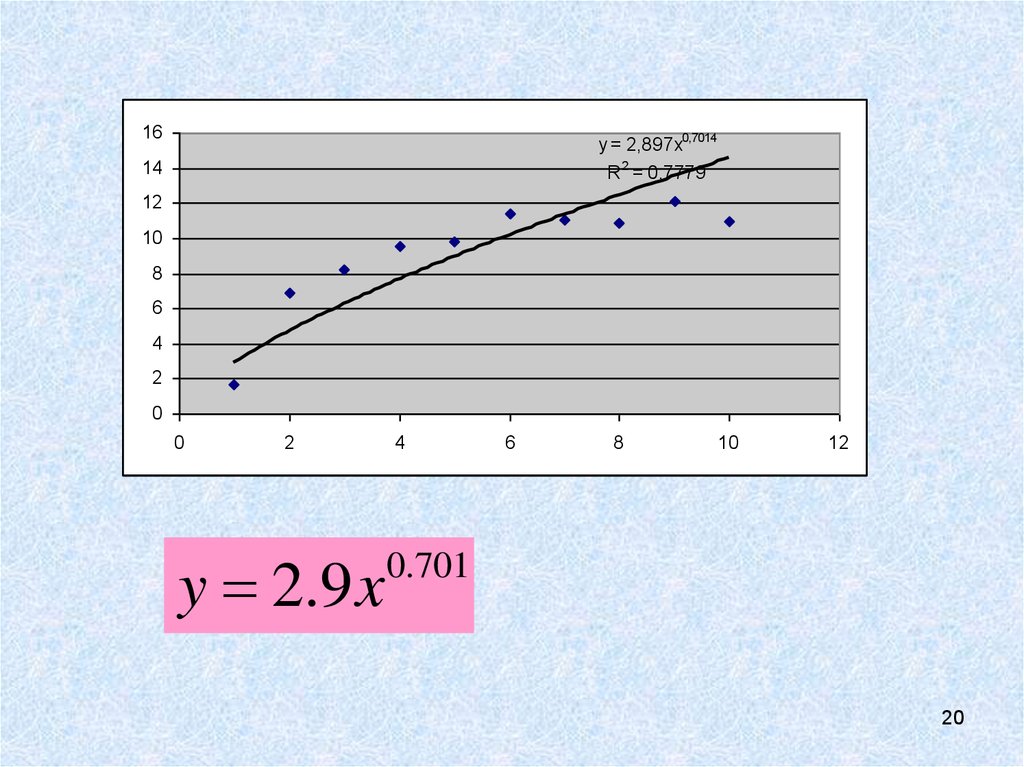
19.

Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
y bx
a
b exp(1.063) 2.9
y 2.9 x
0.701
19

20.

16
y = 2,897x0,7014
14
R = 0,7779
2
12
10
8
6
4
2
0
0
2
y 2.9 x
4
6
8
10
12
0.701
20

21.

Также как в линейной модели рассчитывается средняя относительная ошибка
аппроксимации
y 2.9 x
0.701
21

22.

1
y 10,99 12, 48 - наилучшая функция спроса
x
в зависимости от дохода.
1)Выполнить прогноз потребления продукта
домохозяйством с доходом 4 тыс.д.е.
2) Имеется ли уровень насыщения для данного
продукта? Если да, найти его.
2)Найти предельную склонность к потреблению
продукта.
3) Найти эластичность спроса по доходу при
доходе 1000 д.е. и 10000 д.е.

23. Модели парной нелинейной регрессии

Существует 2 типа нелинейных моделей:
1. модели, сводящиеся к линейным;
2. модели, не сводящиеся к линейным.

24. 1 тип моделей 1) Гиперболическая модель

1
y a b
x

25. 1 тип моделей 3) Экспоненциальная модель

y b eax
25

26.

Пример применения экспоненциальной модели для моделирования
оплаты труда
140
120
zpl
100
80
60
40
20
0
0
5
10
15
20
25
n
Данные 2002 г. о часовой заработной плате ($ США) и уровне образования (лет) по 540
респондентам из национального опроса в США.
12 лет – средняя школа
13-16 лет – колледж (бакалавриат)
17-18 лет – университет ( магистратура)
19-20 лет - PhD

27.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Zpl=-12,617+2,3651N
140
y = 2,3651x - 12,617
R2 = 0,1714
120
zpl
100
80
60
40
20
0
0
5
15
10
20
25
n
Увеличении уровня образования на один год приведет в среднем к увеличению
почасовой заработной платы на $2.37

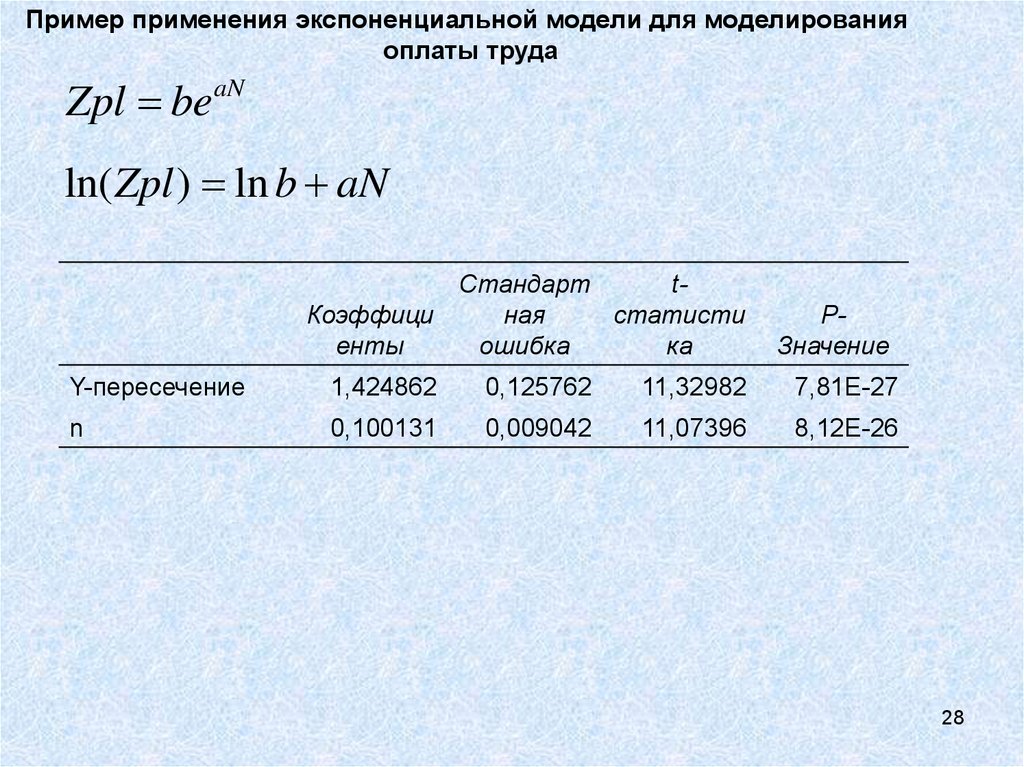
28.

Пример применения экспоненциальной модели для моделирования
оплаты труда
aN
Zpl be
ln( Zpl ) ln b aN
Стандарт
tКоэффици
ная
статисти
енты
ошибка
ка
PЗначение
Y-пересечение
1,424862
0,125762
11,32982
7,81E-27
n
0,100131
0,009042
11,07396
8,12E-26
28

29.

Пример применения экспоненциальной модели для моделирования
оплаты труда
aN
Zpl be
ln( Zpl ) ln b aN
Стандарт
tКоэффици
ная
статисти
енты
ошибка
ка
PЗначение
Y-пересечение
1,424862
0,125762
11,32982
7,81E-27
n
0,100131
0,009042
11,07396
8,12E-26
ln( Zpl ) 1, 42 0,1N
1,42 0,1N
Zpl e
Zpl 4,14e
0,1N
29

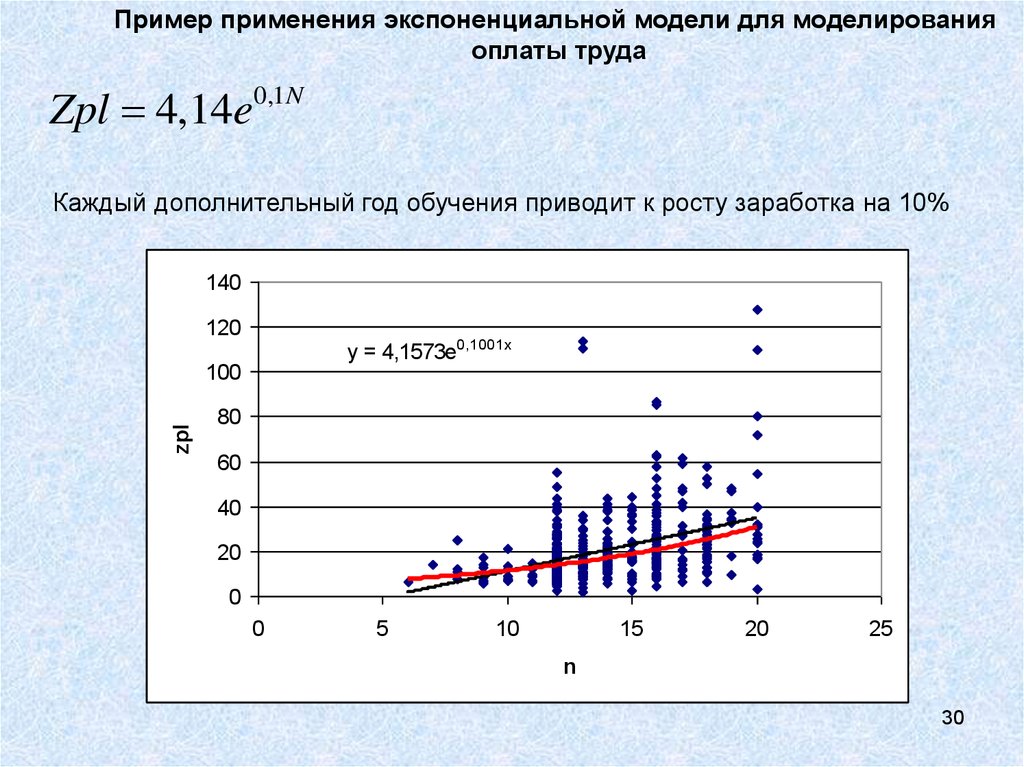
30.

Пример применения экспоненциальной модели для моделирования
оплаты труда
Zpl 4,14e0,1N
Каждый дополнительный год обучения приводит к росту заработка на 10%
140
120
y = 4,1573e0,1001x
zpl
100
80
60
40
20
0
0
5
10
15
20
25
n
30

31.

Пример применения экспоненциальной модели для моделирования
оплаты труда
Преимущества экспоненциальной модели:
1) Она не предсказывает отрицательного заработка индивидам с низким
образовательным уровнем
2) Она показывает возрастание прироста заработков в расчете на 1
дополнительный год обучения при повышении образовательного уровня.
140
120
y = 4,1573e0,1001x
zpl
100
80
60
40
20
0
0
5
10
15
20
25
n
31

32. 4) Степенная модель

y bx
a
32

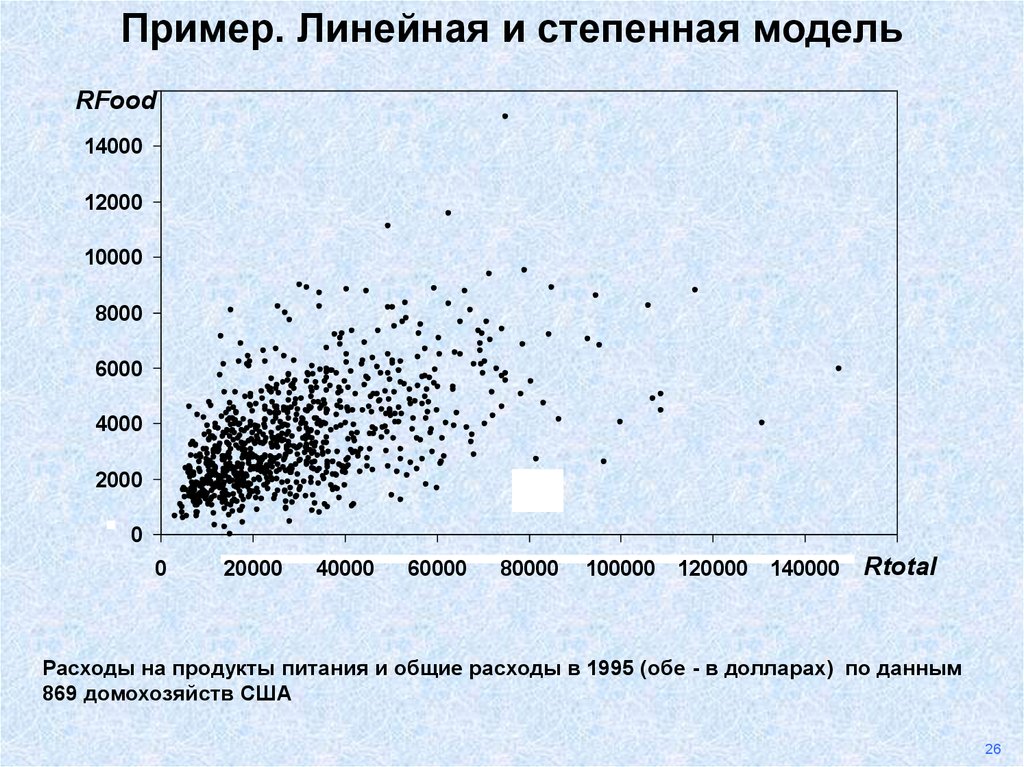
33.

Пример. Линейная и степенная модель
16000
RFood
14000
12000
10000
8000
6000
4000
2000
0
0
20000
40000
60000
80000
Rtotal
100000 120000 140000 160000
Расходы на продукты питания и общие расходы в 1995 (обе - в долларах) по данным
869 домохозяйств США
26

34.

Линейная модель
Number of obs
F( 1,
867)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
869
381.47
0.0000
0.3055
0.3047
1549.5
-----------------------------------------------------------------------------Rtotal|
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
---------+-------------------------------------------------------------------RFood|
.0528427
.0027055
19.531
0.000
.0475325
.0581529
_cons |
1916.143
96.54591
19.847
0.000
1726.652
2105.634
------------------------------------------------------------------------------
Коэффициенты представляются разумными, хотя
предельный эффект несколько занижен, а константазавышена.
27

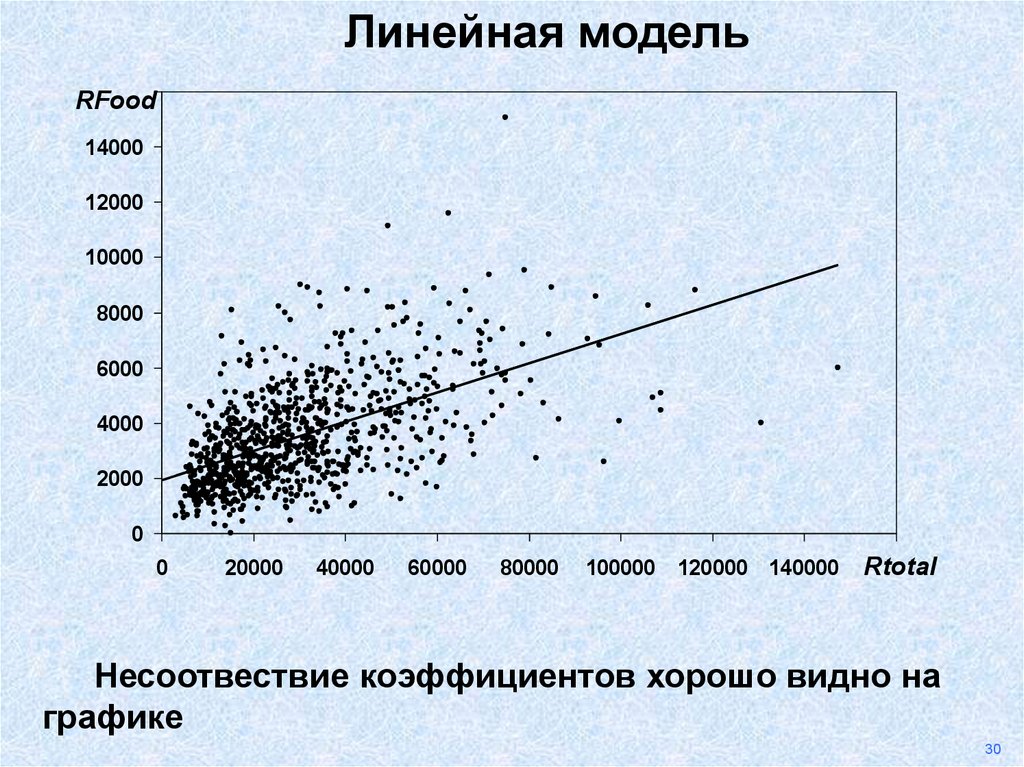
35.

Линейная модель
16000
RFood
14000
12000
10000
8000
6000
4000
2000
0
0
20000
40000
60000
80000
100000 120000 140000 160000
Rtotal
Несоотвествие коэффициентов хорошо видно на
графике
30

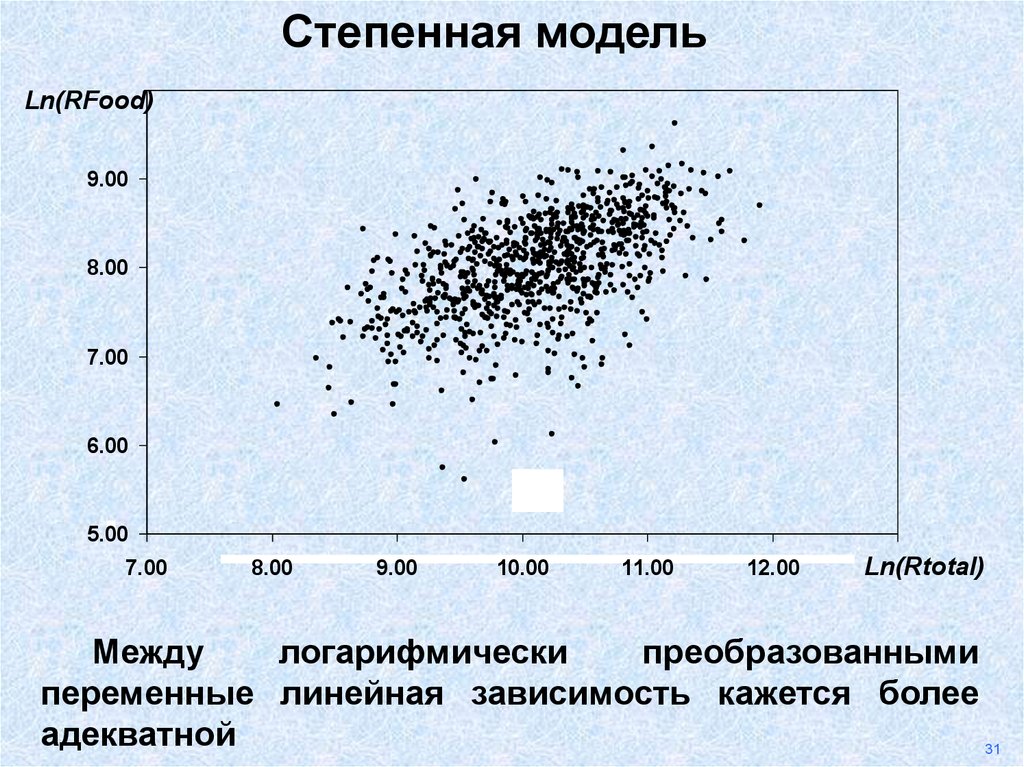
36.

Степенная модель
10.00
Ln(RFood)
9.00
8.00
7.00
6.00
5.00
7.00
8.00
9.00
10.00
11.00
12.00
Ln(Rtotal)
13.00
Между
логарифмически
преобразованными
переменные линейная зависимость кажется более
адекватной
31

37.

Степенная модель
Number of obs
F( 1,
866)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
868
396.06
0.0000
0.3138
0.3130
.46167
-----------------------------------------------------------------------------LnRtotal |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
---------+-------------------------------------------------------------------LnRFood |
.4800417
.0241212
19.901
0.000
.4326988
.5273846
_cons |
3.166271
.244297
12.961
0.000
2.686787
3.645754
------------------------------------------------------------------------------
Модель высокозначима. Коэффициент эластичности расходов на товары питания по
совокупным расходам положителен и меньше единицы, как и полагается для
нормального товара первой необходимости
LnRFood 3.17 0.48LnRtotal RFood 23.8EXP0.48 Rtotal
Константа не имеет хорошей интерпретации. e3.16 =23.8, то есть просто некий
масштабный множитель
32

38.

Степенная модель
16000
RFood
14000
12000
10000
8000
6000
4000
2000
0
0
20000
40000
60000
80000
100000 120000 140000 160000
RTotal
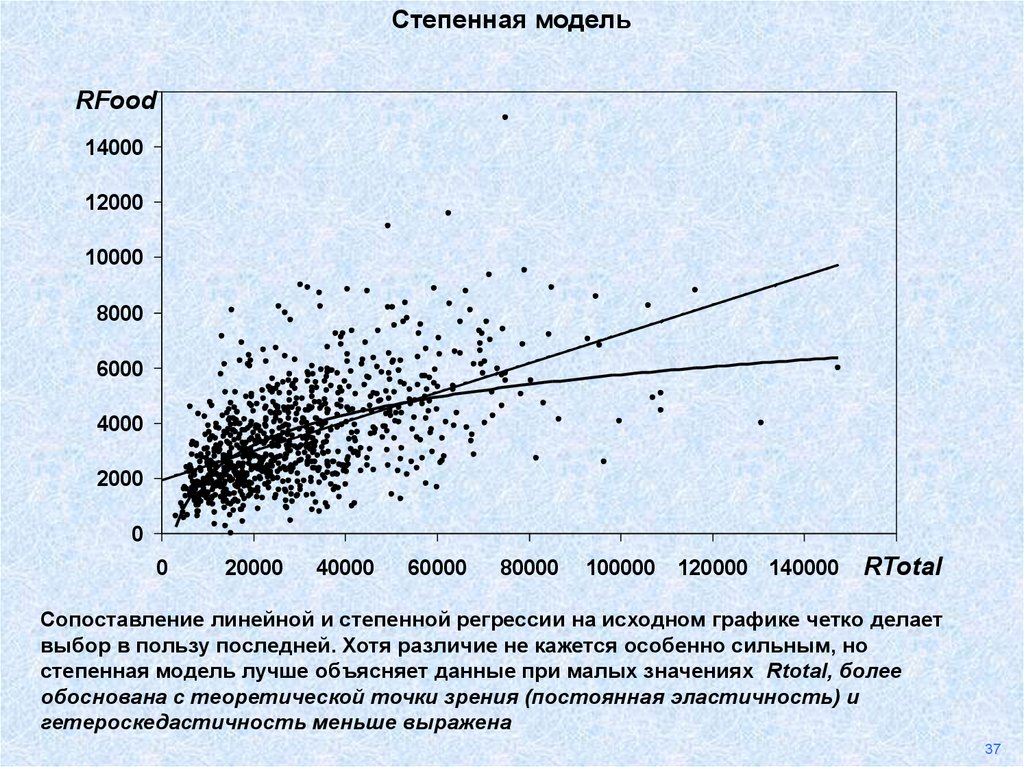
Сопоставление линейной и степенной регрессии на исходном графике четко делает
выбор в пользу последней. Хотя различие не кажется особенно сильным, но
степенная модель лучше объясняет данные при малых значениях Rtotal, более
обоснована с теоретической точки зрения (постоянная эластичность) и
гетероскедастичность меньше выражена
37

39.

Полиномиальная модель
y a0 a1 x a2 x 2
ak x k
Появляются возможность исследования
зависимостей, для которых существенно
наличие максимумов и минимумов
y a0 a1 x a2 x
2
квадратичная модель
37

40.

Полиномиальная модель
y a0 a1 x a2 x 2
x1 x
x2 x
2
y a0 a1 x1 a2 x2
- модель множественной регрессии.
37

41.

Полиномиальная модель
Примеры
1) Пусть Q – объем выпуска продукции, MC – предельные издержки производства.
MC aQ2 bQ c
a>0, b<0
MC
Q
b
2a
37

42.

Полиномиальная модель
Примеры
2) x – возраст работника физического труда, y – заработная плата
y ax2 bx c
a<0, b<0
MC
b
2a
Q
37

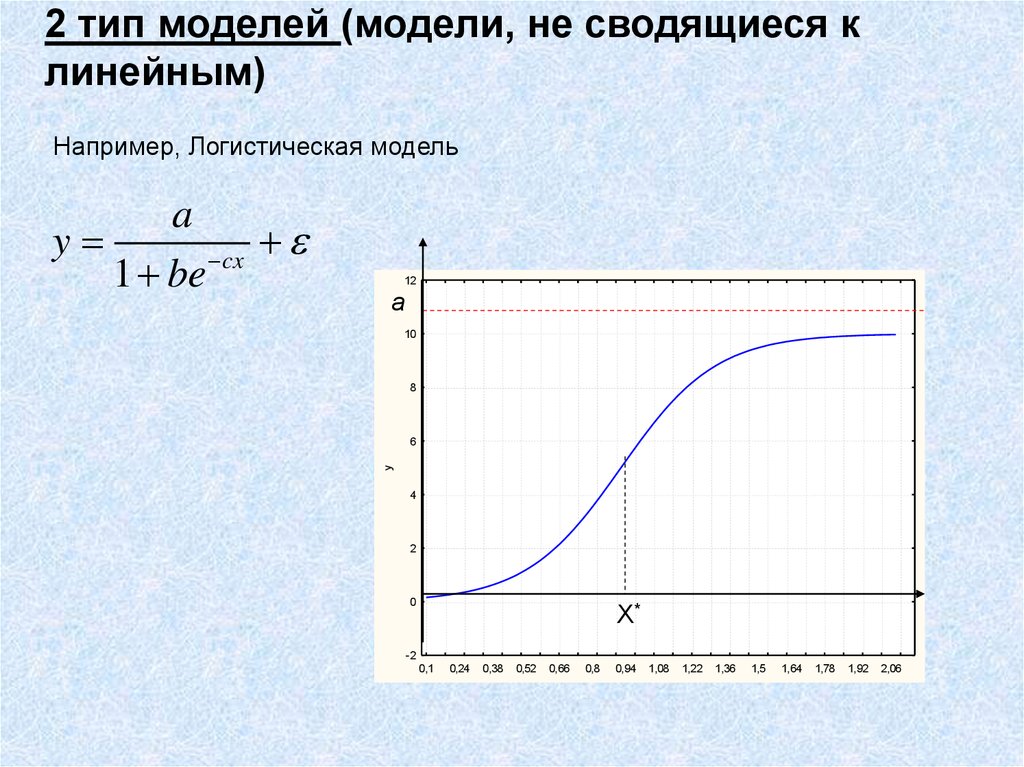
43. 2 тип моделей (модели, не сводящиеся к линейным)

Например, Логистическая модель
12
a
10
8
6
y
a
y
cx
1 be
4
2
0
X*
-2
0,1
0,24
0,38
0,52
0,66
0,8
0,94
1,08
1,22
1,36
1,5
1,64
1,78
1,92
2,06

44. 2 тип моделей (модели, не сводящиеся к линейным)

Для оценки коэффициентов таких моделей используется МНК:
a
y
cx
1 be
a
S (a, b, c) yi
cxi
1
be
i 1
n
2
minS (a, b, c)
a ,b ,c
S a 0
Sb 0
S 0
c
Задача решается численными методами.
В Excel через поиск решения