Similar presentations:
Нелинейные регрессионные модели. Тема 5
1. Тема 5. Нелинейные регрессионные модели
2.
5.1. Общие сведения5.2. Регрессионные модели,
нелинейные по переменным
5.3. Регрессионные модели,
нелинейные по параметрам
5.4. Нелинеаризуемые
регрессионные модели
3. Полиномиальная зависимость
Y 0 1 X 2 X2
... m X
m
4. кубическая функция
Y 0 1 X 2 X2
3 X
3
5. Квадратичная функция
Y 0 1 X 2 X2
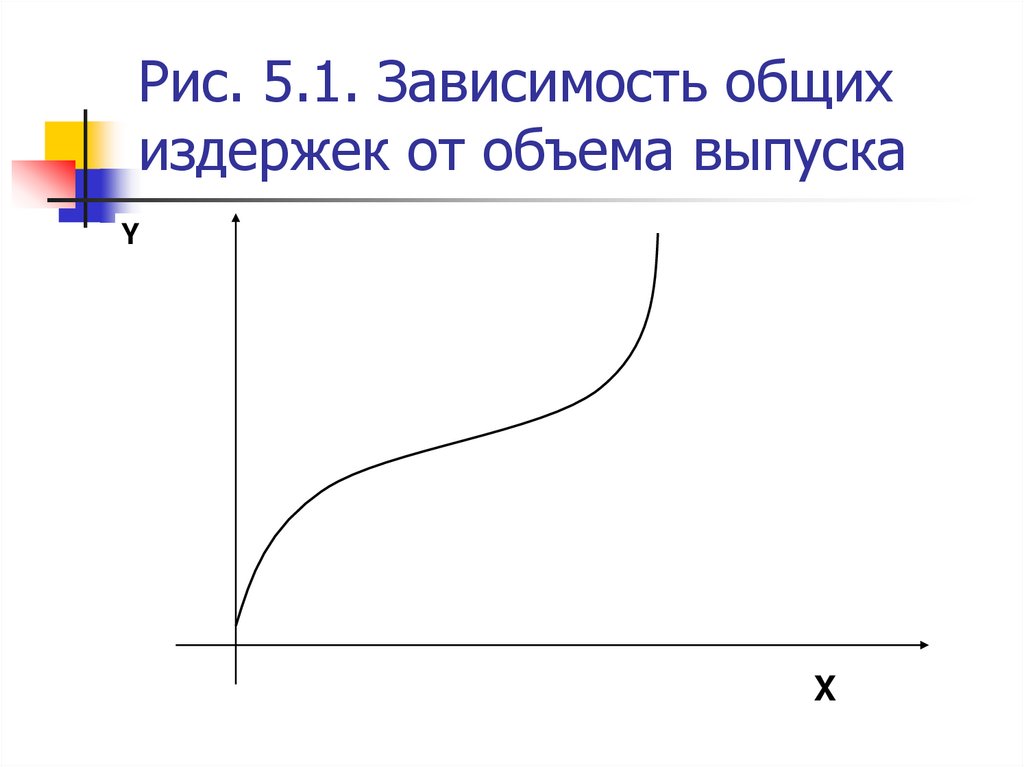
6. Рис. 5.1. Зависимость общих издержек от объема выпуска
YX
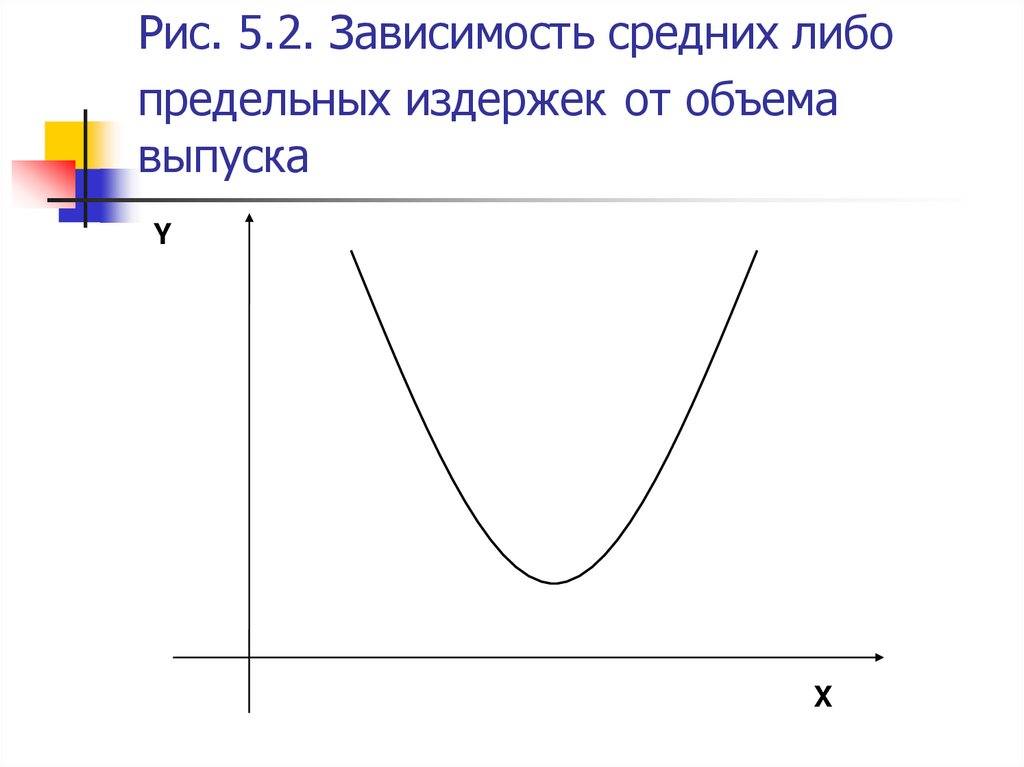
7. Рис. 5.2. Зависимость средних либо предельных издержек от объема выпуска
YX
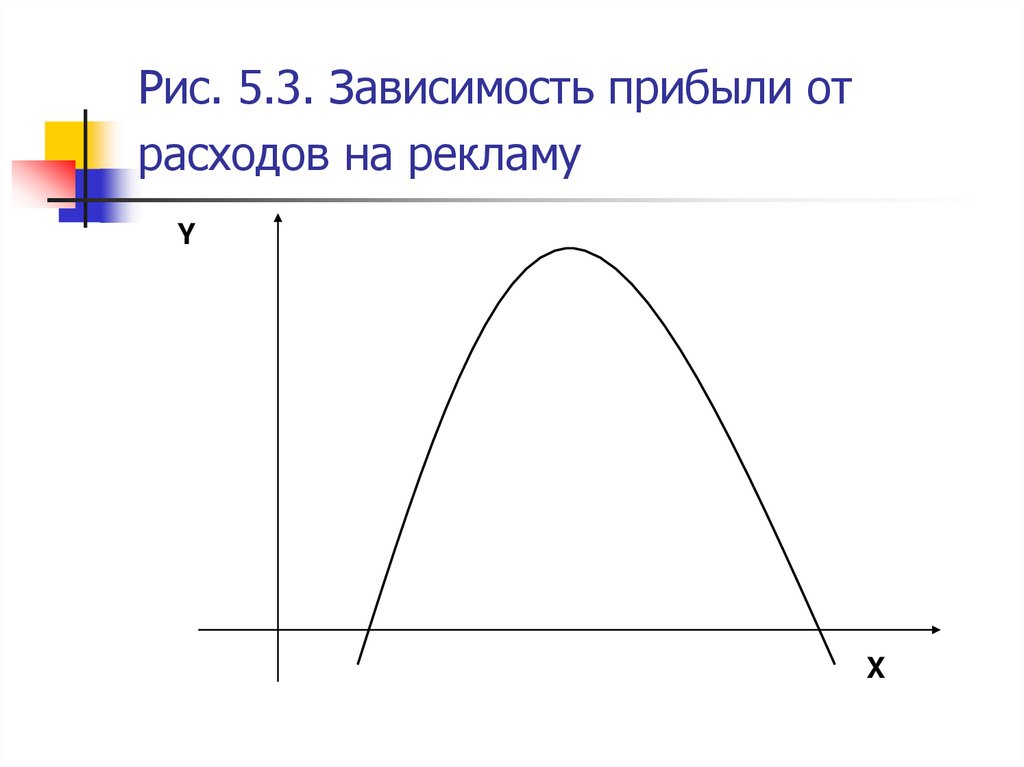
8. Рис. 5.3. Зависимость прибыли от расходов на рекламу
YX
9. Замена
Z1 XZ2 X
2
Zm X
m
...
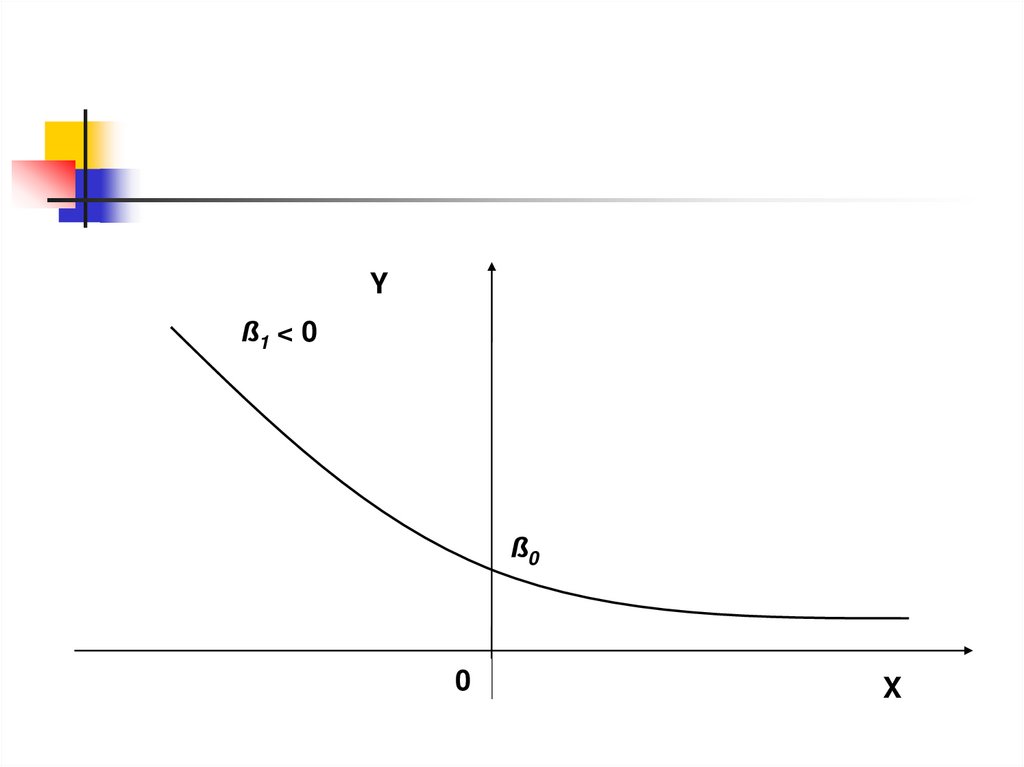
10. Тогда получим модель:
Y 0 1Z1 2 Z 2... m Z m
11. Зависимость гиперболического типа
1Y 0 1
X
12. Рис. 5.4. Зависимость средних фиксированных издержек от объема выпускаемой продукции
Yß0 > 0
ß1 > 0
ß0
X
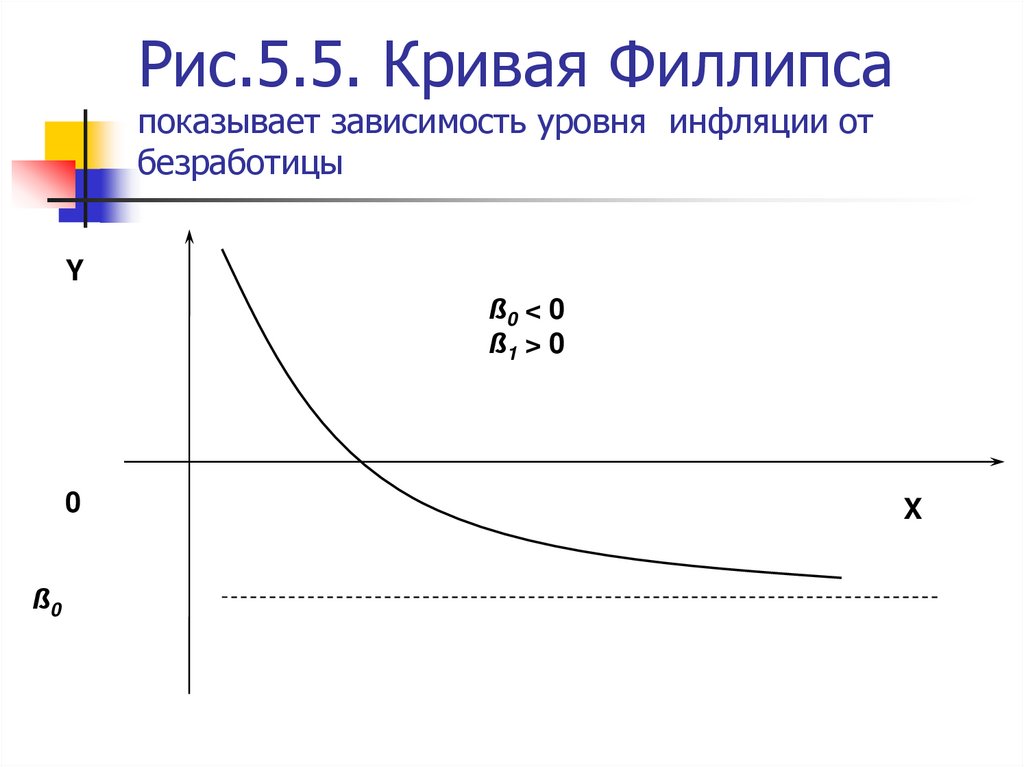
13. Рис.5.5. Кривая Филлипса показывает зависимость уровня инфляции от безработицы
Yß0 < 0
ß1 > 0
0
ß0
X
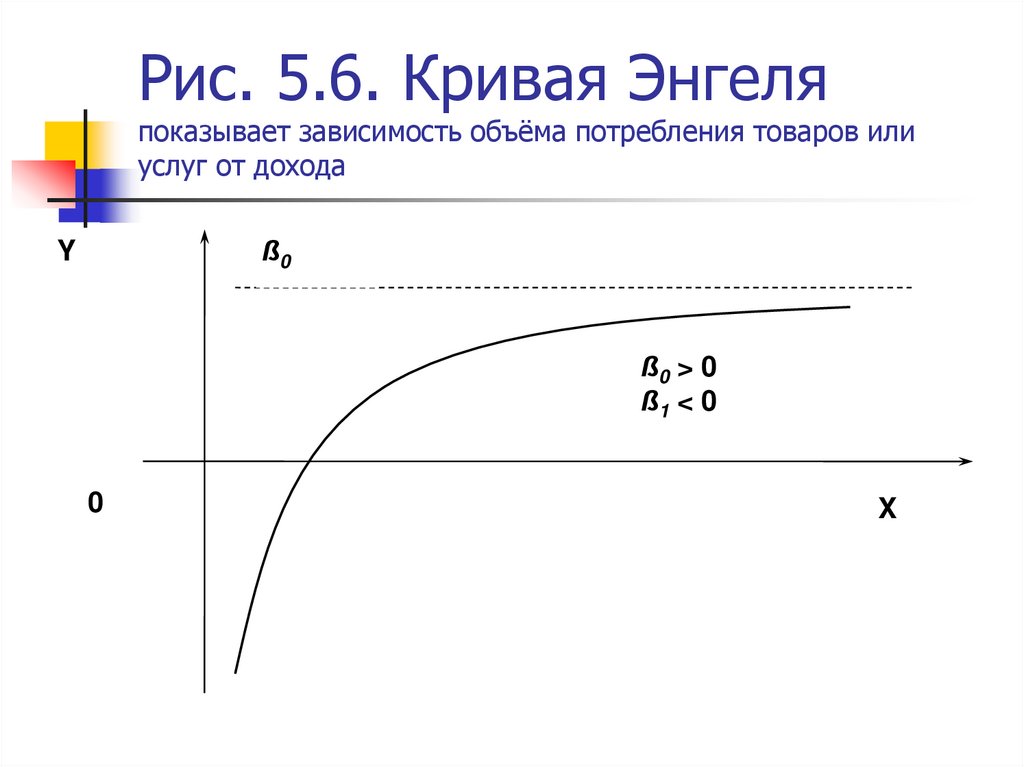
14. Рис. 5.6. Кривая Энгеля показывает зависимость объёма потребления товаров или услуг от дохода
ß0Y
ß0 > 0
ß1 < 0
0
X
15. Преобразование
1Z
X
16.
Y 0 1Z17. Логарифмическая зависимость (линейно-логарифимическая)
Логарифмическаязависимость (линейнологарифимическая)
Y 0 1 ln X
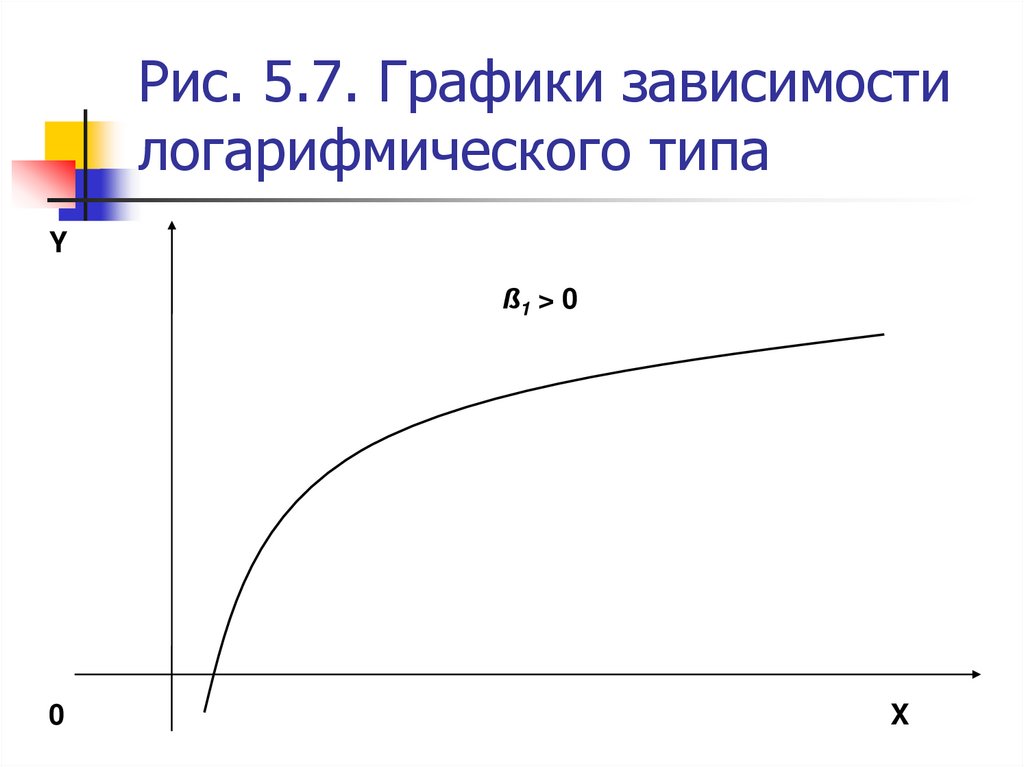
18. Рис. 5.7. Графики зависимости логарифмического типа
Yß1 > 0
0
X
19.
Yß1 < 0
0
X
20. Преобразование
Z ln X21.
GNP 0 1 ln M22.
23. Зависимости степенного типа
1Y 0 X
24.
ln Y ln 0 1 ln Xln
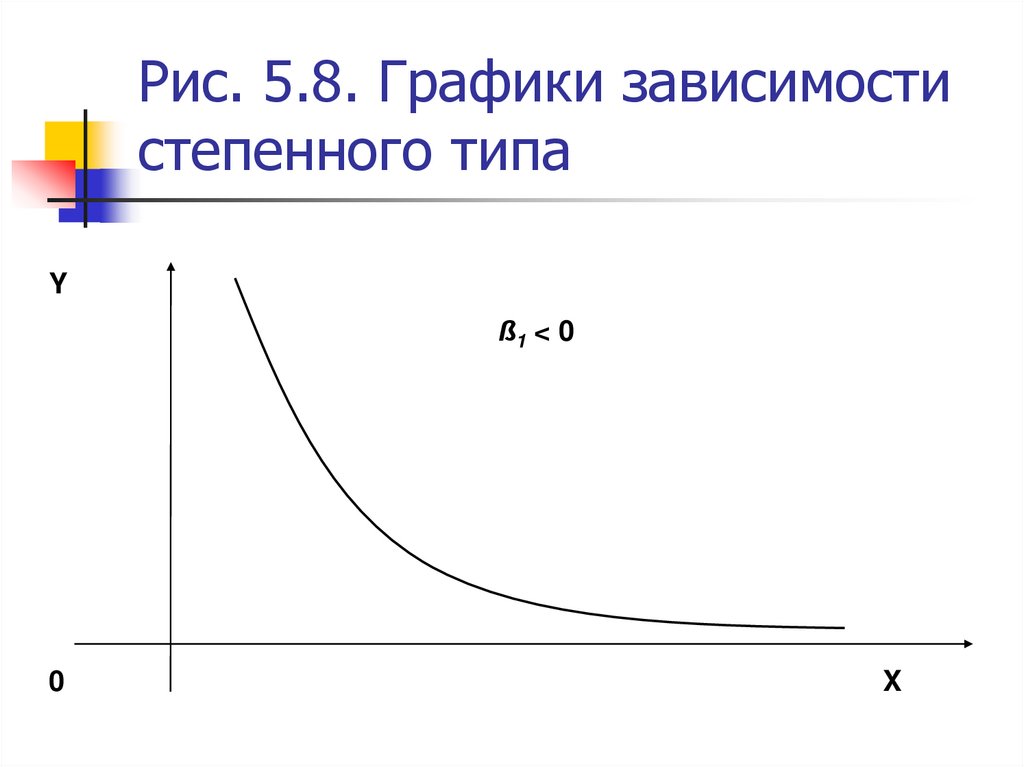
25.
26. Рис. 5.8. Графики зависимости степенного типа
Yß1 < 0
0
X
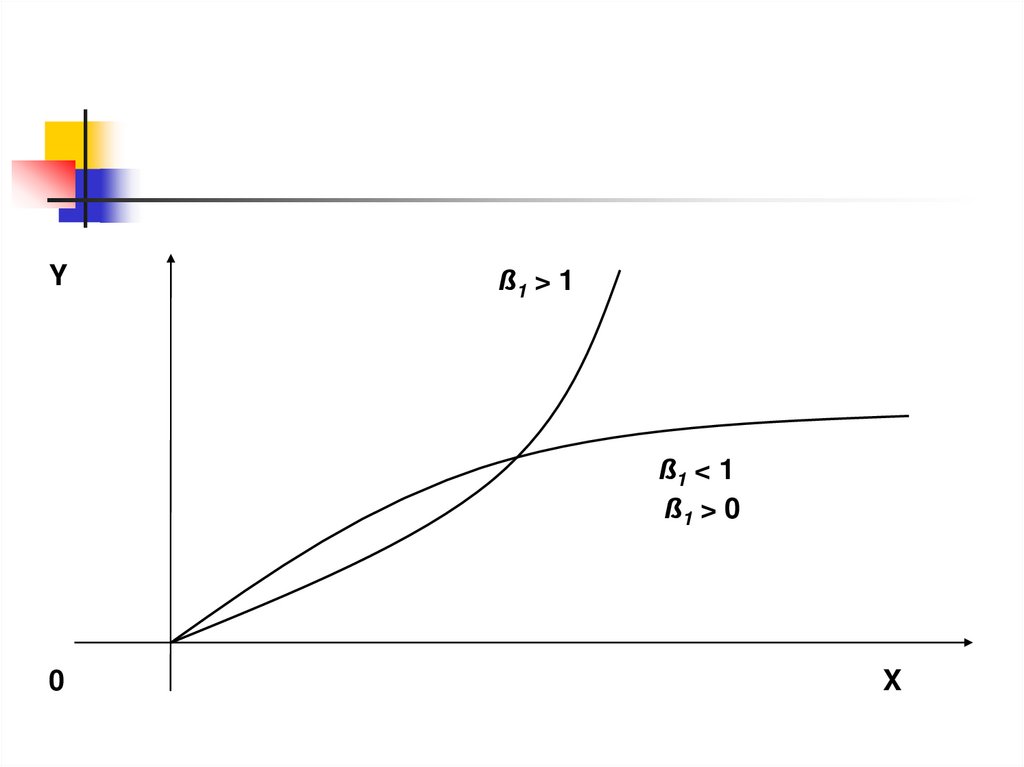
27.
Yß1 > 1
ß1 < 1
ß1 > 0
0
X
28. Функция Кобба-Дугласа
Y AK L29.
ln Y ln A ln Kln L ln
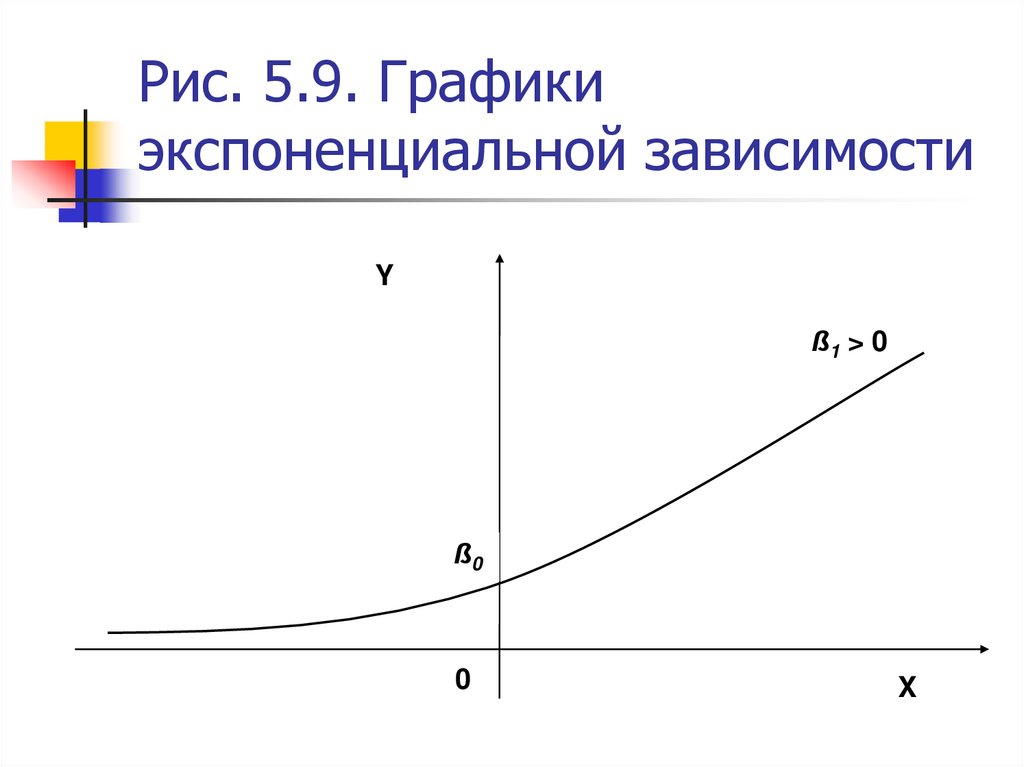
30. Зависимость показательного (экспоненциального) типа
Y 0e1 X
31. Рис. 5.9. Графики экспоненциальной зависимости
Yß1 > 0
ß0
0
X
32.
Yß1 < 0
ß0
0
X
33.
ln Y ln 0 1 X34. Замена
Y ln Y*
35.
36.
37.
38.
некорректно сравнивать, используя SSE илиR^2, так как зависимые переменные разные
39.
можно сравнивать, используя SSE или R^2,так как зависимые переменные одинаковые
40.
Различают два класса нелинейныхрегрессий:
1. Регрессии, нелинейные относительно
включенных в анализ объясняющих
переменных, но линейные по
оцениваемым параметрам
Например:
- полиномы различных степеней;
- равносторонняя гипербола;
- линейно-логарифмическая функция.
41.
Различают два класса нелинейныхрегрессий:
2. Регрессии, нелинейные по
оцениваемым параметрам
Например:
- степенная;
- показательная;
- экспоненциальная.
42.
Регрессии, нелинейные по включеннымпеременным, но линейные по
параметрам
Регрессии, нелинейные по включенным
переменным, но линейные по
параметрам, приводятся к линейному
виду простой заменой переменных
(подстановкой), а дальнейшая оценка
параметров производится с помощью
метода наименьших квадратов.
43.
Регрессии, нелинейные по оцениваемымпараметрам
Регрессии, нелинейные по оцениваемым
параметрам, делятся на два типа:
- нелинейные модели, внутренне линейные
(приводятся к линейному виду с помощью
соответствующих преобразований,
например, логарифмированием) и
- нелинейные модели, внутренне
нелинейные (к линейному виду не
приводятся).


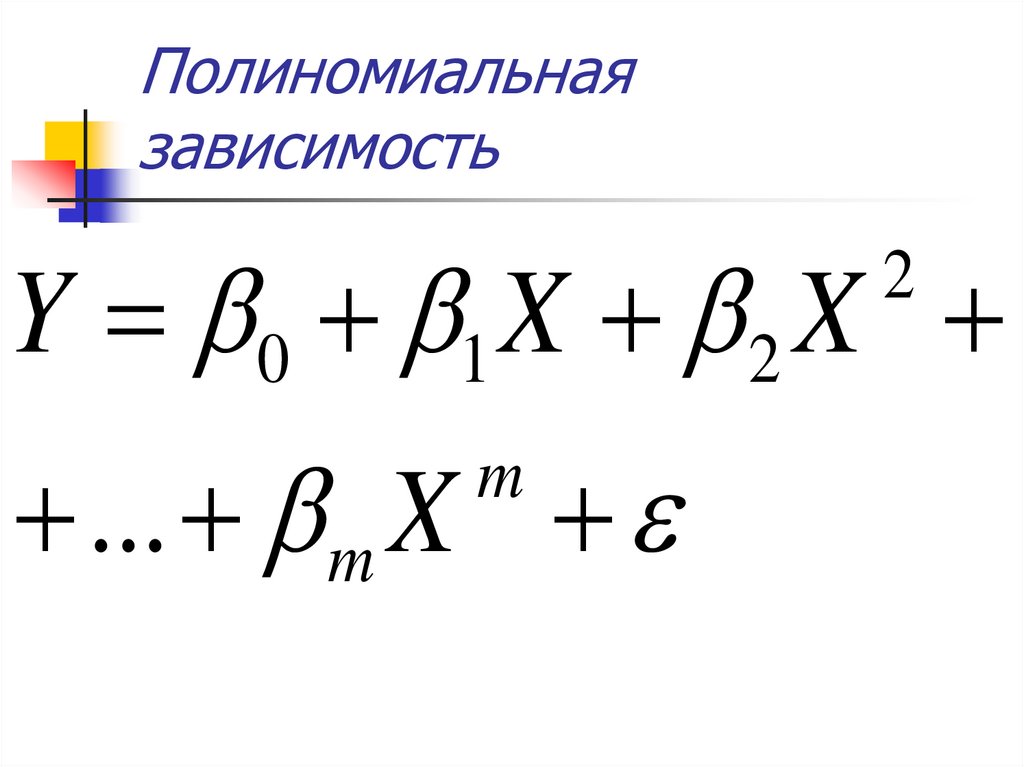

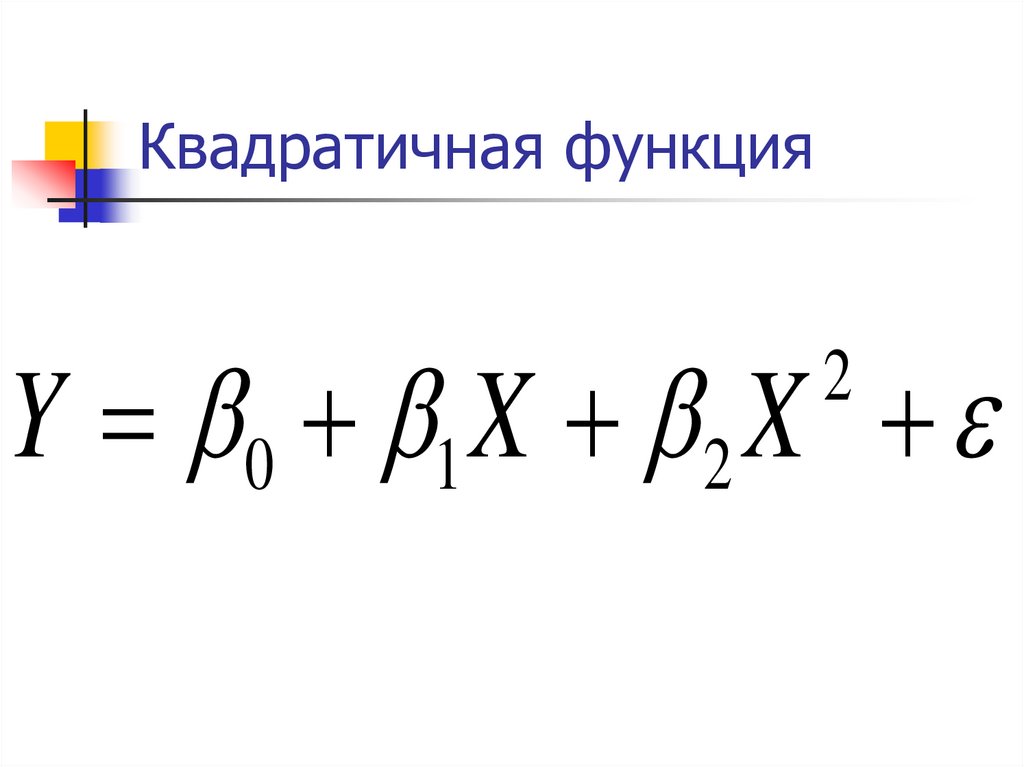


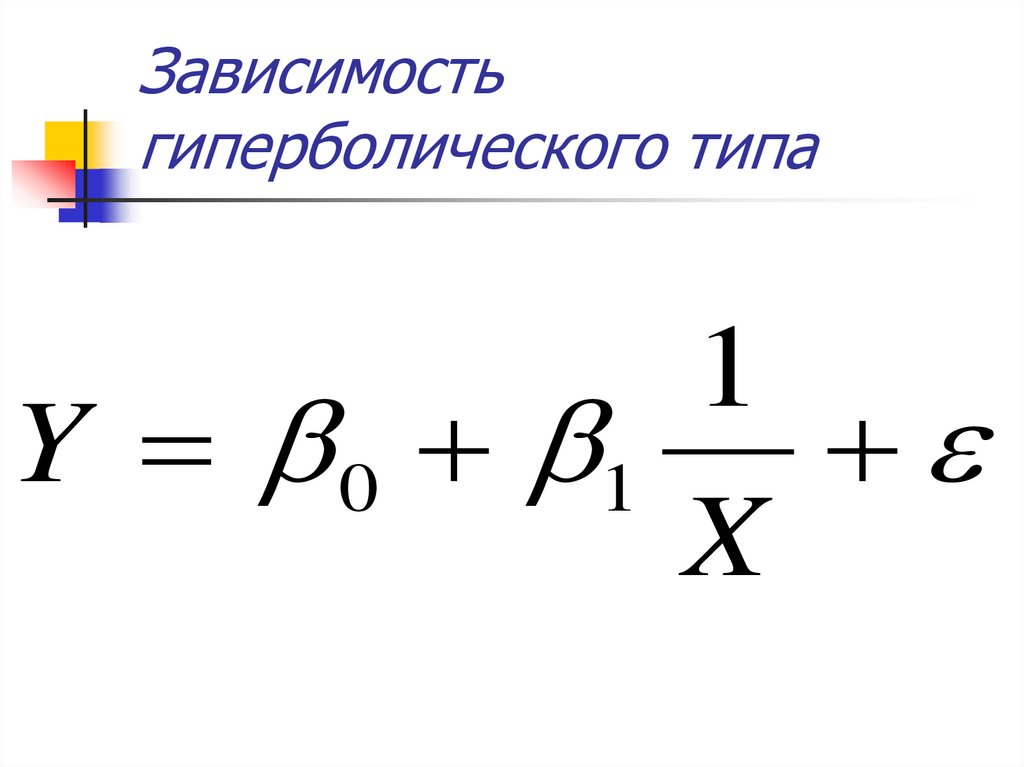



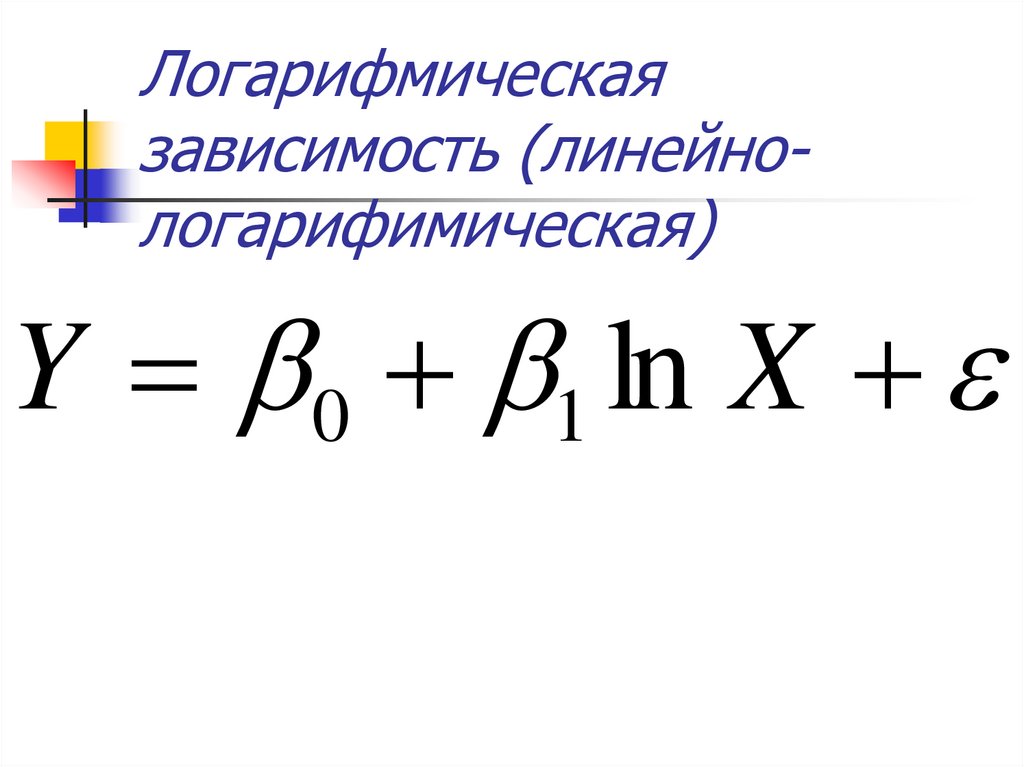

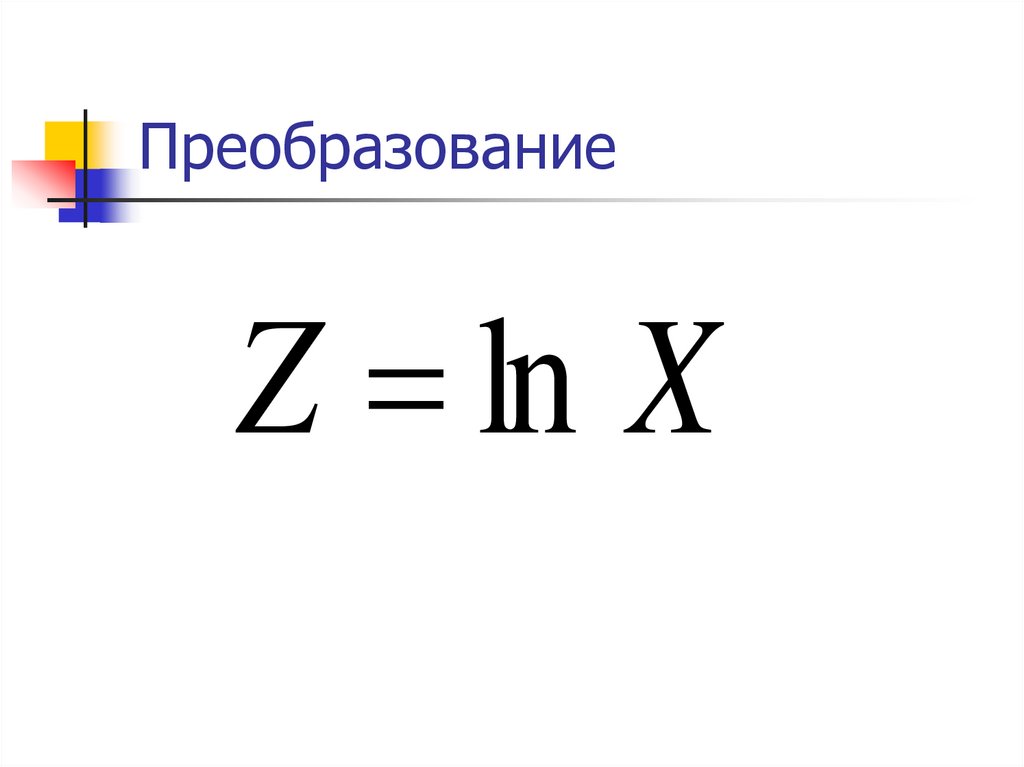
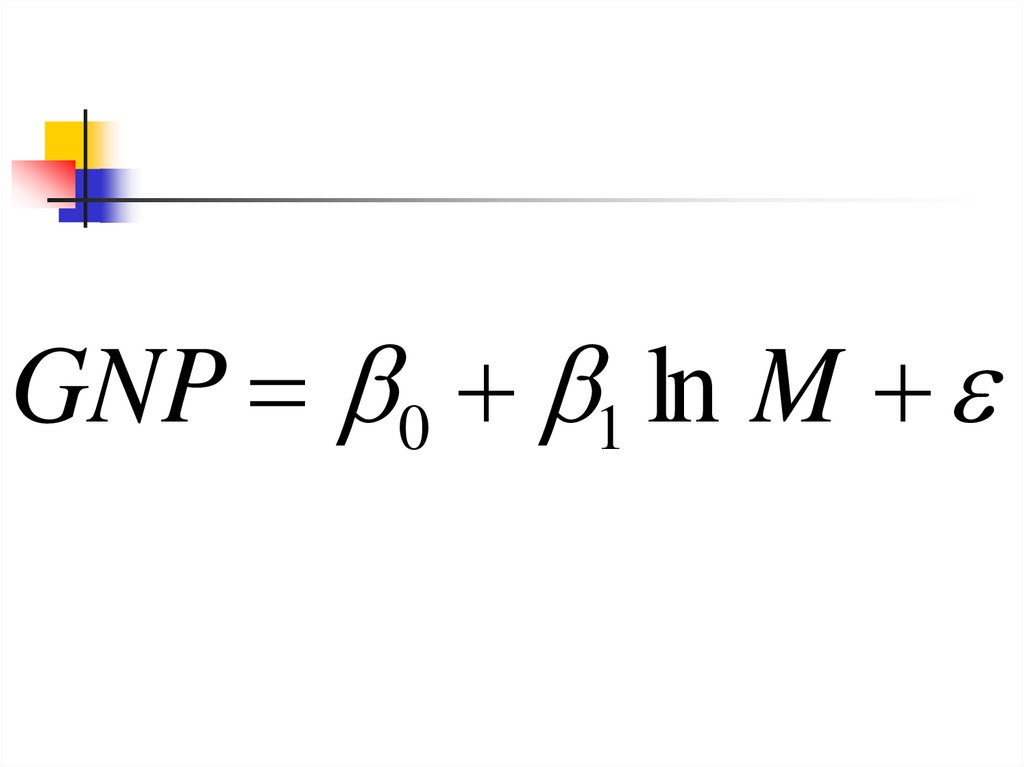

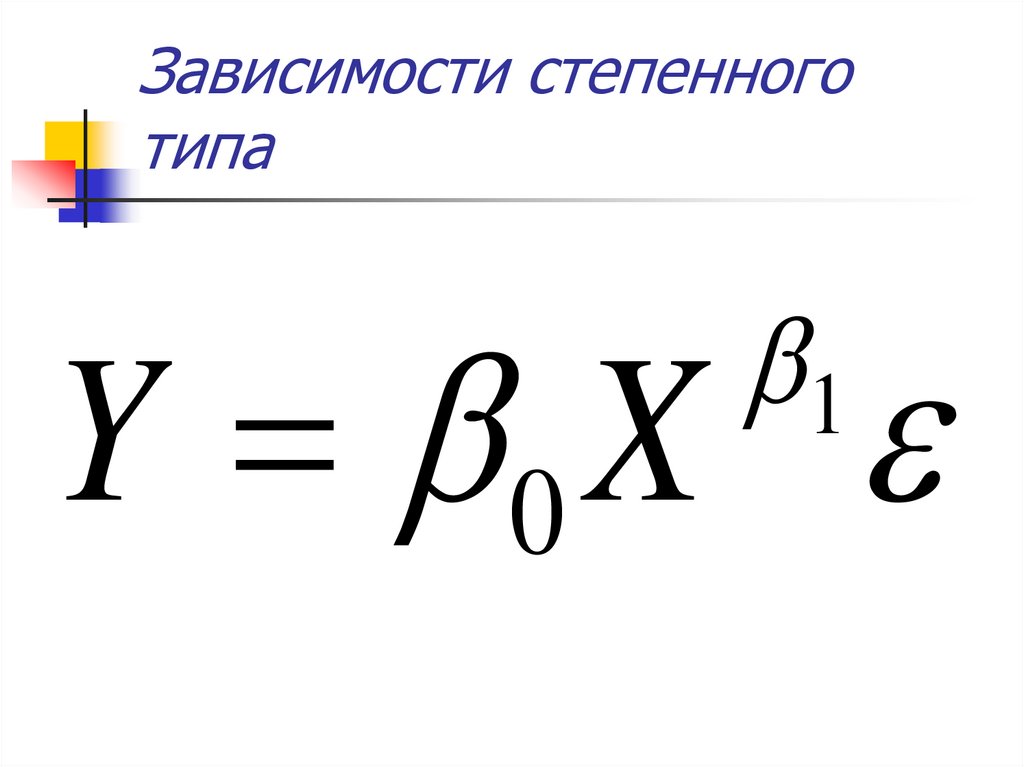





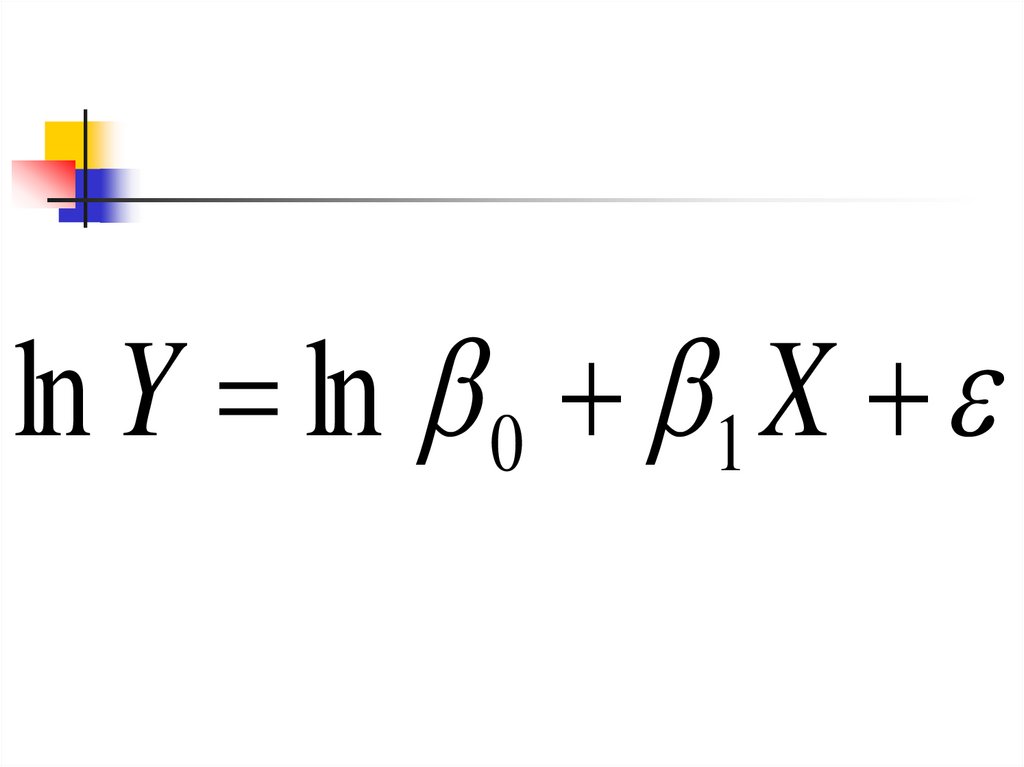











 mathematics
mathematics








