Similar presentations:
Эконометрики, как наука. Математические методы в экономике
1.
ФГБОУ ВПО «Челябинский государственный университет»Институт экономики отраслей, бизнеса и администрирования
Кафедра экономики отраслей и рынков
Эконометрика
Курс лекций
Автор: канд. экон. наук Е.А. Бирюкова
Челябинск, 2018
1
2.
Список литературыБигильдеева, Т. Б. Эконометрика: учебное пособие /
Т. Б. Бигильдеева, Е. А. Постников .— Челябинск.
Доугерти, К. (Кристофер). Введение в эконометрику: учебник для студентов вузов.
Эконометрика: учебник / И. И. Елисеева [и др.];
под ред. И. И. Елисеевой .— 2-е изд., перераб. и доп. — М.
Магнус, Я. Р. Эконометрика: начальный курс :
учебник / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий .— 8-е изд. — М.
Замков, О. О. Математические методы в экономике:
Учебник / О. О. Замков, А. В. Толстопятенко, Ю. Н. Черемных; — М.
Бородич, С. А. Эконометрика: учебное пособие / С. А. Бородич .— Минск.
Орлов, А. И. Эконометрика:
Учебник для вузов / А. И. Орлов .— 2-е изд., перераб. и доп. — М.
2
3.
Рекомендуемые сайтыдля поиска статистических данных
1 www.moex.ru
2. www.gks.ru
3. www.rbc.ru
4. www.cbr.ru
5. www.skrin.ru
6. www.finam.ru
……………………
Journal of Econometrics (Швеция),
Econometric Reviews (США),
Econometrica (США),
Sankhya. Indian Journal of Statistics.
Ser.D. Quantitative Economics (Индия),
Publications Econometriques (Франция)
3
4.
Разделы дисциплины№ темы
Наименование разделов, тем дисциплины
1
Предмет и метод эконометрики
2
Экономические показатели как случайные величины.
Показатели связи, используемые в эконометрике
3
Парный регрессионный анализ
4
Множественный регрессионный анализ
5
Регрессионные модели с переменной
(использование фиктивных переменных)
6
Специфика построения динамических регрессионных
моделей
7
Гетероскедастичность в регрессионных моделях
8
Эконометрические
модели
одновременных уравнений
в
виде
структурой
системы
4
5.
Задачи курса1. Получение и систематизирование знания в области
эконометрического анализа
2. Практическое применение эконометрических
методов и моделей
3.Использование пакетов прикладных программ в
эконометрическом анализе
5
6.
Определение эконометрикиТермин «эконометрика» был впервые введен бухгалтером П.
Цьемпой (Австро-Венгрия, 1910 г.) («эконометрия» – у
Цьемпы).
Цьемпа считал, что если к данным бухгалтерского учета
применить методы алгебры и геометрии, то будет получено
новое, более глубокое представление о результатах
хозяйственной деятельности.
Концепция не прижилась, но название «эконометрика»
оказалось весьма удачным для определения нового направления
в экономической науке, которое выделилось в 1930-х г.
6
7.
Определение эконометрикиТермин эконометрика впервые был введен Р. Фришем в 1926
году и в дословном переводе означает «экономические
измерения» или «измерения в экономике».
Создание «Эконометрического общества».
Наряду с широким пониманием, существует узкая трактовка
эконометрики как совокупность методов анализа связей между
различными экономическими показателями (факторами) на
основании реальных статистических данных с использованием
аппарата теории вероятностей и математической статистики.
7
8.
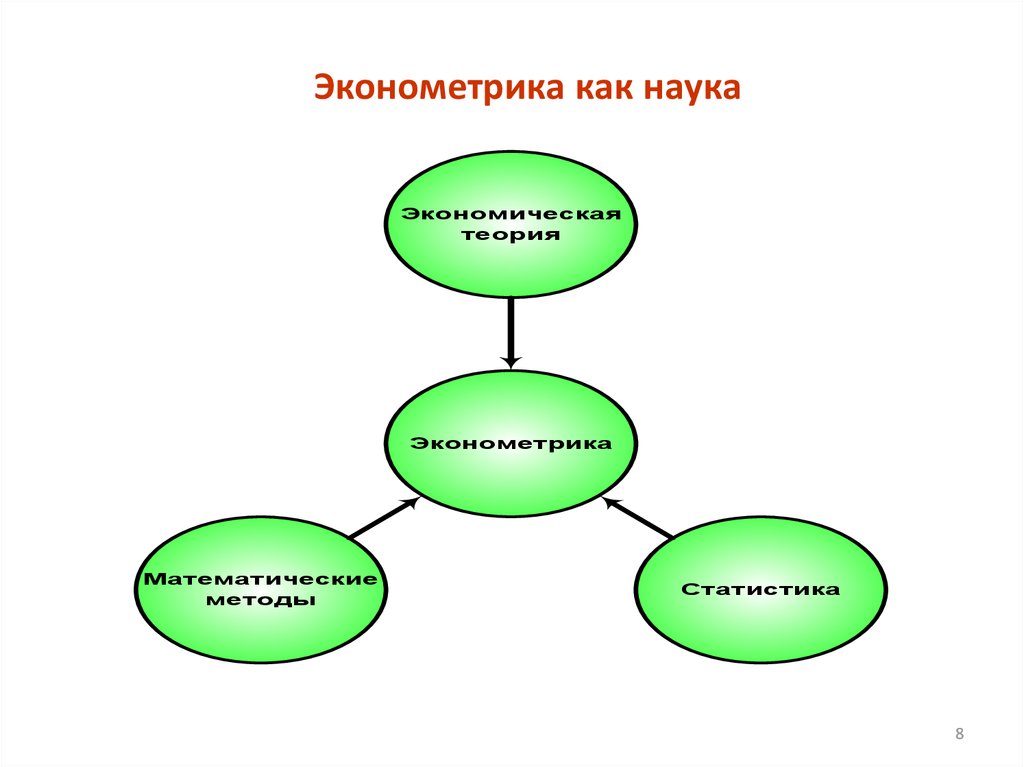
Эконометрика как наукаЭкономическая
теория
Эконометрика
Математические
методы
Статистика
8
9. Цели и задачи эконометрики
Задача эконометрики состоит в выявлении связеймежду количественными характеристиками
экономических объектов в целях построения
математических правил прогноза (вычисления
приближённых значений) недоступных для
наблюдения количественных характеристик объектов
по наблюдённым или заданным значениям других
количественных характеристик объектов.
Эмпирическим материалом для построения правил
прогноза служат результаты наблюдений за
изучаемыми экономическими объектами (статистика).
9
10.
История эконометрических исследований1. Политическая арифметика. ( У. Петти, Ч. Давенант, Г.
Кинг) Расчет национального дохода.
У. Петти
10
11.
История эконометрических исследований2. Статистическая теория. (Гальтон, К. Пирсон, Ф. Эджворт,
Дж.Э. Юл, Г. Хукер)
Связь между уровнем бедности и формами помощи бедным.
Связь между уровнем брачности и благосостоянием,
в котором использовалось несколько индикаторов благосостояния,
Временные ряды.
Ф. Эджворт
11
12.
История эконометрических исследований3. Г. Мур «Законы заработной платы: эссе по статистической
экономике».
Анализ рынка труда.
Проверка теории производительности Дж. Кларка.
Стратегия
объединения
пролетариата.
4.
Теории по
цикличности
экономики.
К. Жугляр. - 7-11-летние циклы инвестиций.
С. Китчин - 3-5-летнюю периодичность обновления оборотных средств.
С. Кузнец - 15-20-летние циклы в строительстве.
Н. Кондратьев - «длинные волны» продолжительностью 45-60 лет.
12
13.
1314.
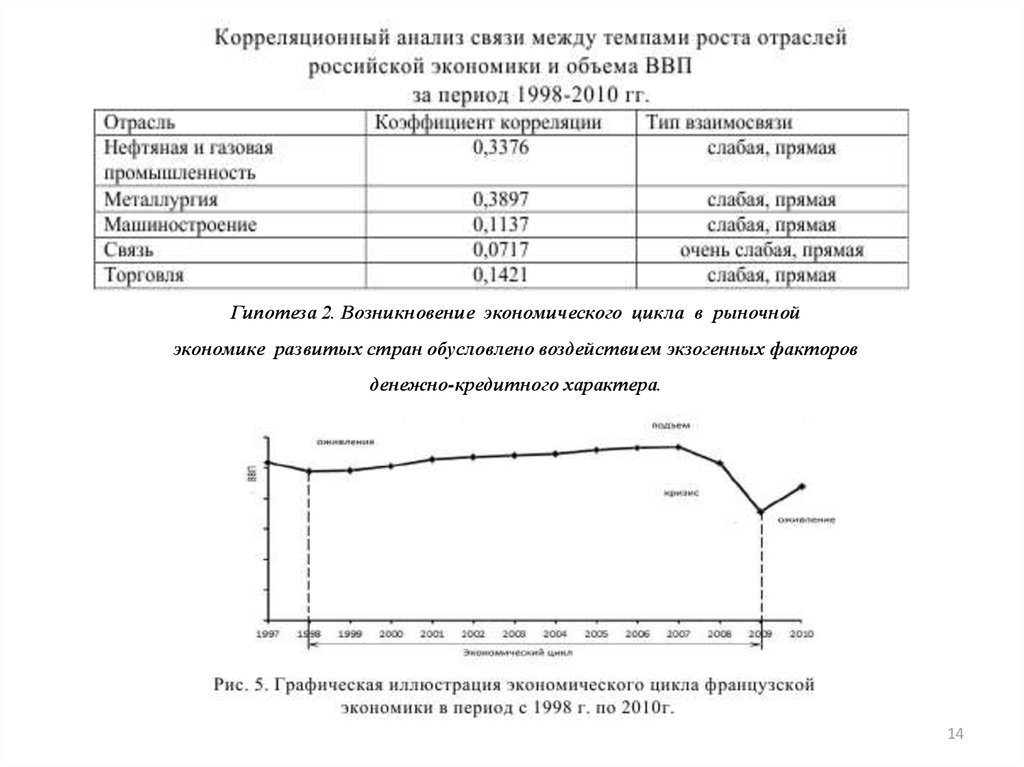
Гипотеза 2. Возникновение экономического цикла в рыночнойэкономике развитых стран обусловлено воздействием экзогенных факторов
денежно-кредитного характера.
14
15.
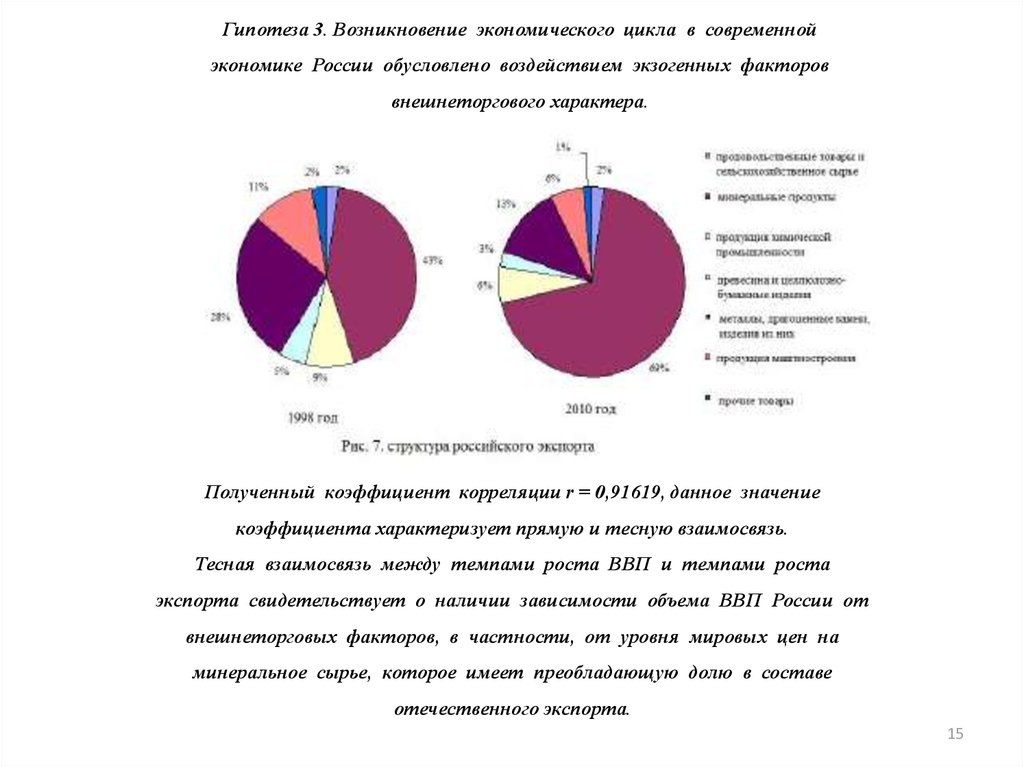
Гипотеза 3. Возникновение экономического цикла в современнойэкономике России обусловлено воздействием экзогенных факторов
внешнеторгового характера.
Полученный коэффициент корреляции r = 0,91619, данное значение
коэффициента характеризует прямую и тесную взаимосвязь.
Тесная взаимосвязь между темпами роста ВВП и темпами роста
экспорта свидетельствует о наличии зависимости объема ВВП России от
внешнеторговых факторов, в частности, от уровня мировых цен на
минеральное сырье, которое имеет преобладающую долю в составе
отечественного экспорта.
15
16.
История эконометрических исследований5. Макроэкономический анализ.
Межотраслевой баланс В. В. Леонтьева.
6.Ч. Кобб и П. Дуглас «Теория производства».
Влияние затрачиваемого капитала и труда на объем
выпускаемой продукции в обрабатывающей промышленности США.
Впервые производственная функция была рассчитана в 1920-е годы для
обрабатывающей промышленности США в виде равенства
16
17.
Наиболее известныеэконометрические исследования
1) модели потребительского и сберегательного
потребления;
2) модели взаимосвязи риска и доходности ценных
бумаг;
3) модели предложения труда;
4) макроэкономические модели (модель роста);
5) модели инвестиций;
6) маркетинговые модели;
7) модели валютных курсов и валютных кризисов и
17
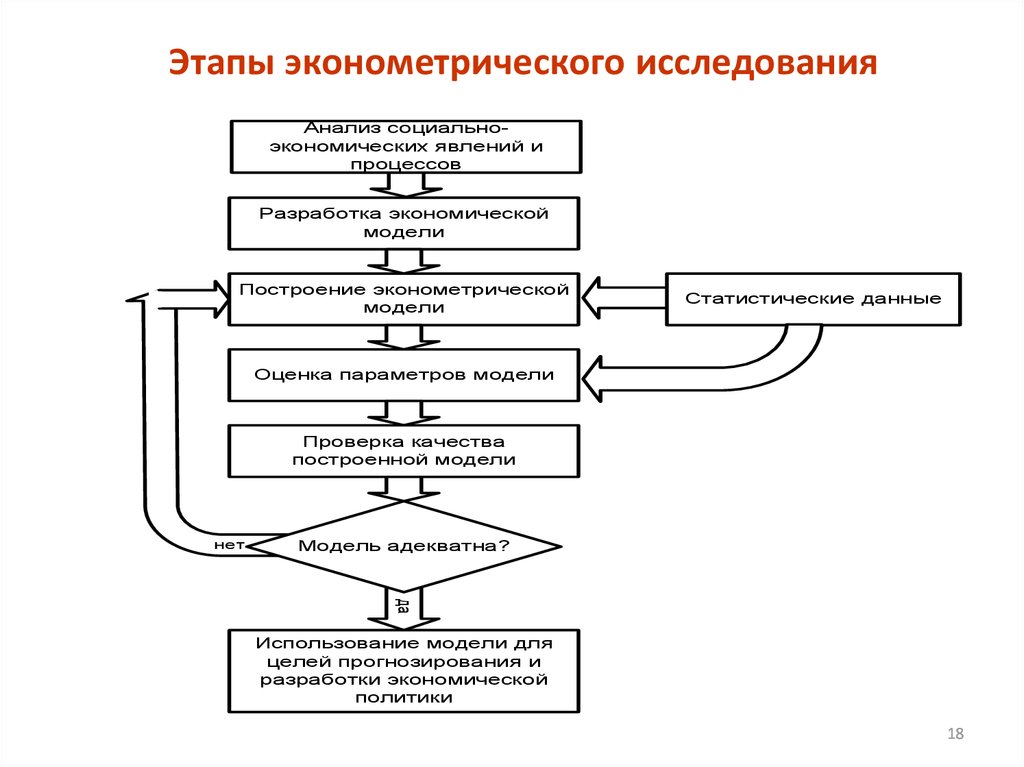
18. Этапы эконометрического исследования
Анализ социальноэкономических явлений ипроцессов
Разработка экономической
модели
Построение эконометрической
модели
Статистические данные
Оценка параметров модели
Проверка качества
построенной модели
нет
Модель адекватна?
да
Использование модели для
целей прогнозирования и
разработки экономической
политики
18
19.
Этапы эконометрического исследованияПодходы к формированию эконометрической модели
«сверху вниз»
«снизу вверх»
19
20.
Спецификация моделиКлассификация переменных
Определение. Эндогенной (зависимой) переменной
называется такая переменная, значение которой
формируется внутри модели в результате
взаимодействия с другими переменными.(y)
Определение. Экзогенной (независимой) переменной
называется переменная, значение которой формируется
вне модели.(x)
20
21.
Классификация статистических данных1. Перекрестные данные или пространственные данные
2.Временные ряды
3.Панельные данные.
Перекрестные (пространственные) данные – это данные по
какому-либо экономическому показателю, полученные для
однотипных объектов и относящиеся к одному периоду
времени.
Например:
данные о расходах разных семей в зависимости от дохода и
состава семьи;
данные о зарплате в зависимости от возраста, стажа,
образования и пр. различных сотрудников;
сведения об объеме производства, количестве работников,
сумме уплаченных налогов по нескольким однотипным
фирмам на один и тот же момент времени.
21
22.
Классификация статистических данныхВременные ряды – данные об одном объекте, процессе за
несколько последовательных моментов времени.
Например:
ежеквартальные (ежемесячные, годовые и пр.) данные по
инфляции или средней заработной плате, или национальному
доходу;
ежедневный курс валют;
котировки ГКО на бирже.
Панельные данные – занимают промежуточное положение: они
отражают наблюдения по большому количеству объектов,
показателей за несколько моментов времени.
Например:
финансовые показатели работы нескольких крупных паевых
инвестиционных фондов за несколько месяцев;
суммы уплаченных налогов нефтяными компаниями за последние
22
несколько лет.
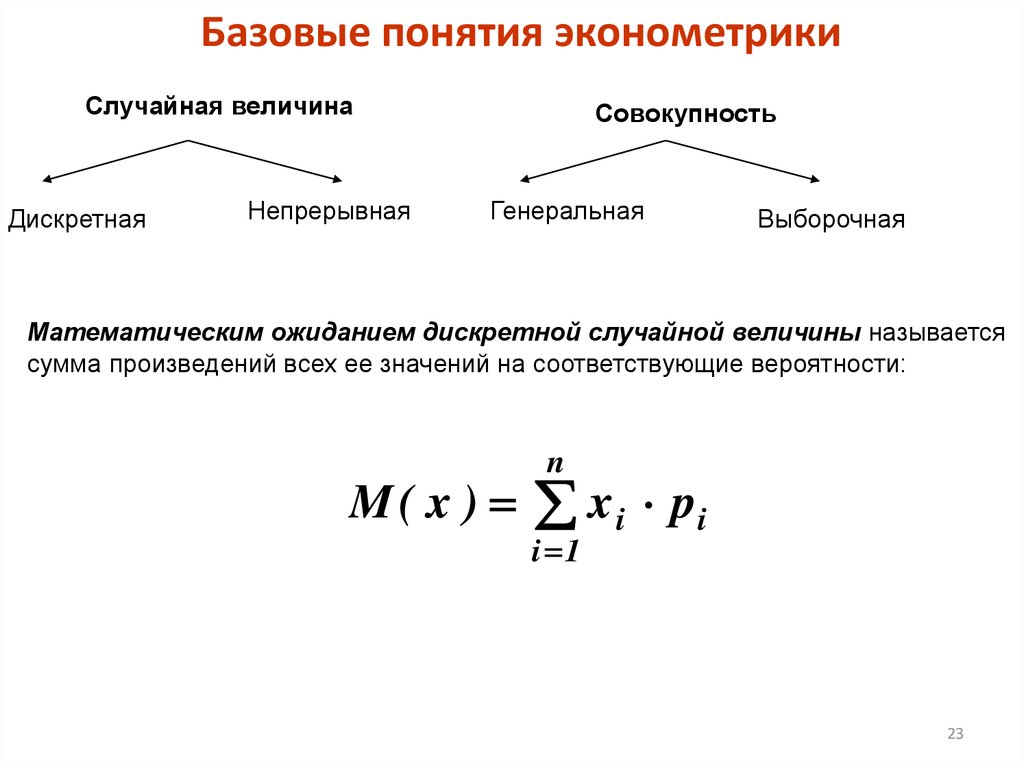
23.
Базовые понятия эконометрикиСлучайная величина
Дискретная
Непрерывная
Совокупность
Генеральная
Выборочная
Математическим ожиданием дискретной случайной величины называется
сумма произведений всех ее значений на соответствующие вероятности:
n
M ( x ) x i pi
i 1
23
24.
Базовые понятия эконометрикиТеоретическая
(генеральная)
дисперсия
случайной
величины
определяется как математическое ожидание квадрата отклонения
случайной
относительно ее математического ожидания
D( x ) M x m x
2
Выборочная дисперсия (вариация) представляет собой среднее
арифметическое квадратов отклонений случайной величины от
среднего значения: (ДИСПР(х))
.
.
1 n
2
var( x ) x i x
n i 1
Для разных выборок, взятых из одной и той же генеральной совокупности,
выборочные средние и выборочные дисперсии будут различны (выборочные
характеристики – случайные величины)
24
25.
Базовые понятия эконометрикиВыборочное среднее (СРЗНАЧ(х))
n
1
x xi
n i 1
Для разных выборок, взятых из одной и той же генеральной совокупности,
выборочные средние и выборочные дисперсии будут различны (выборочные
характеристики – случайные величины)
25
26.
Базовые понятия эконометрикиvar( x )
Выборочная дисперсия
является смещенной оценкой генеральной дисперсии.
В качестве несмещенной оценки этой дисперсии используется уточненная величина
(исправленная дисперсия): (ДИСП(х))
n
n
1
2
2
S
var( x )
xi x
n 1 оценка дисперсии
n 1генеральной
i 1
несмещенная
S2
совокупности;
S
несмещенная
n
xi
i
оценка
стандартного
отклонения
генеральной
совокупности;(СТАНДОТКЛОН(х))
число
измерений
в
выборке;
i - е значение измеренного показателя в выборке;
порядковый номер измерения.
26
27. Базовые понятия эконометрики
• Ковариация – абсолютный показатель связи двухпоказателей. Характеризует направление линейной связи
двух показателей. (Ковар(x,y))
Анализ данных – Ковариация( парный коэффициент)
n
1
xi x yi y
cov x, y
n 1 i 1
cov x, y x y x y
• Коэффициент корреляции – относительный показатель
связи , который характеризует силу и направление
линейной связи двух признаков и изменяется в пределах
от –1 до 1. (Коррел(x,y), Пирсон (x,y))
rx , y
cov x, y
sx s y
27
28.
ЗАДАНИЕ 1Произвести статистическую выборку 2 параметров
экономического характера, объем выборки 10 единиц, с
предполагаемой взаимосвязью между ними.
Определить количественные показатели линейной взаимосвязи
между этими параметрами.
Выводы
28
29.
Базовые понятия эконометрикикоэффициент частной корреляции x и y при условии постоянства z
Анализ данных - Корреляция
rx , y / z
rx , y rx , z ry , z
(1 rx , z ) (1 ry , z )
2
2
коэффициент полной корреляции
R
rx2, y 2rx , y rx , z ry , z ry2, z
1 rx2, y
29
30. Типы эконометрических оценок
•Точечная оценка. Представляет собой конкретное число,которое используется в качестве характеристики
случайной величины. Она не дает точного представления
о распределении показателя, однако определяет
их наиболее вероятные значения.
• Интервальная оценка. Представляет собой интервал,
в котором с известной вероятностью находится истинное
значение исследуемого признака.
30
31.
Точечная оценкаОсновных свойства точечных оценок:
Несмещенность;
Эффективность;
Состоятельность;
Достаточность
31
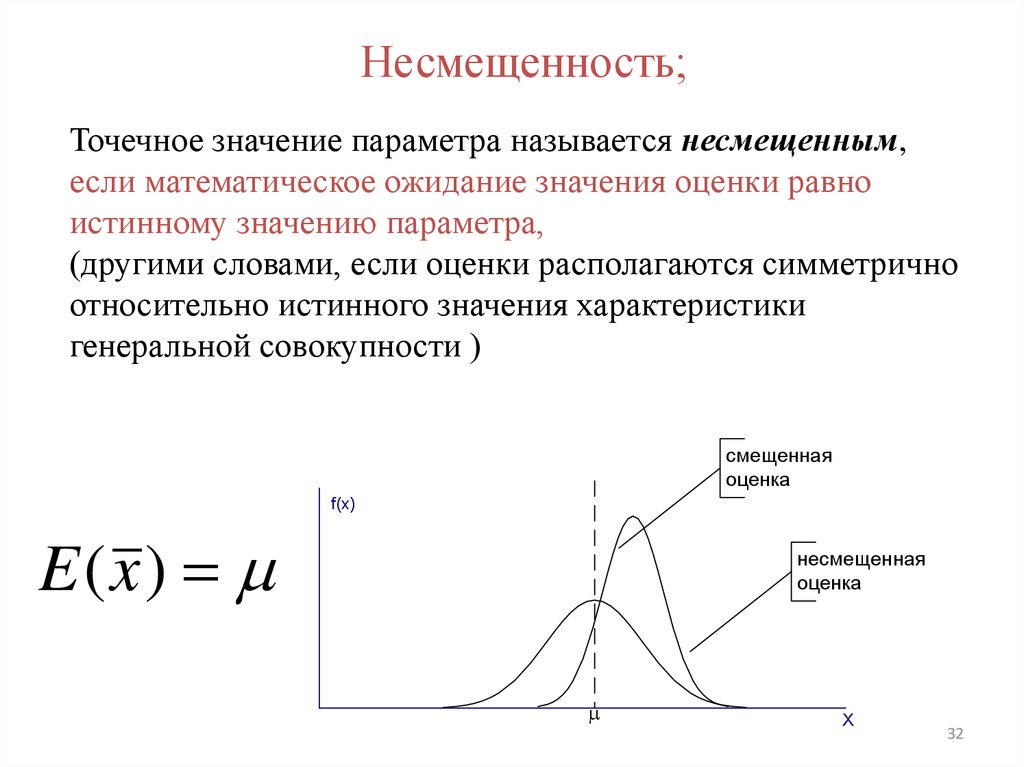
32.
Несмещенность;Точечное значение параметра называется несмещенным,
если математическое ожидание значения оценки равно
истинному значению параметра,
(другими словами, если оценки располагаются симметрично
относительно истинного значения характеристики
генеральной совокупности )
смещенная
оценка
f(x)
E (x )
несмещенная
оценка
X
32
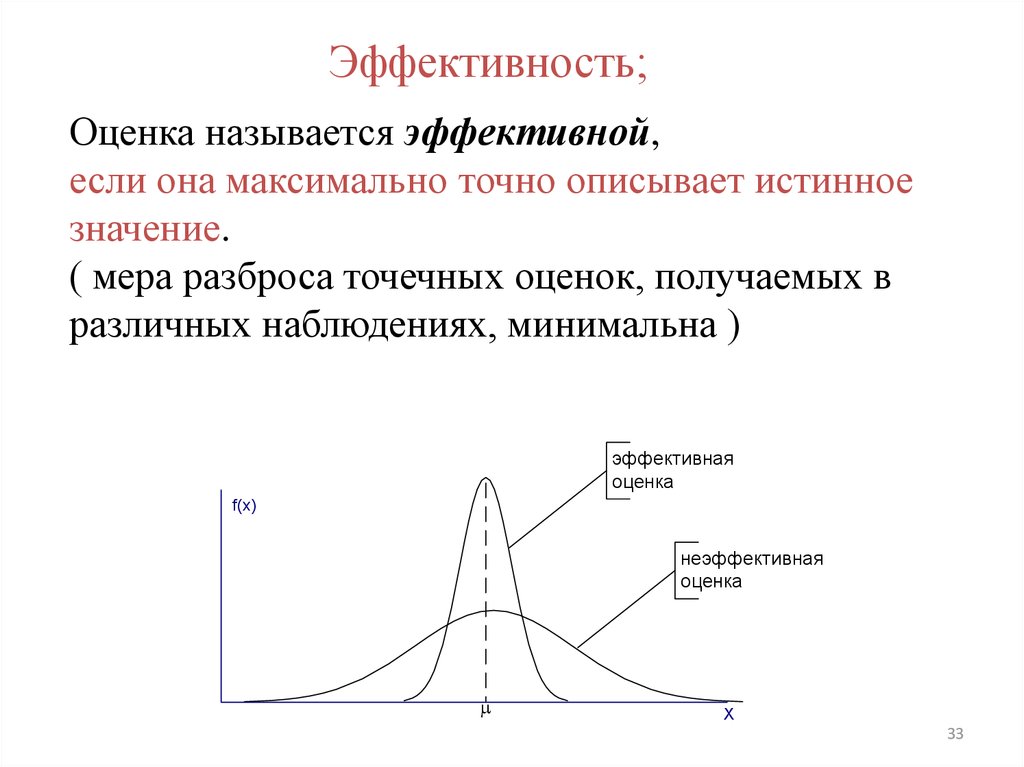
33.
Эффективность;Оценка называется эффективной,
если она максимально точно описывает истинное
значение.
( мера разброса точечных оценок, получаемых в
различных наблюдениях, минимальна )
эффективная
оценка
f(x)
неэффективная
оценка
X
33
34.
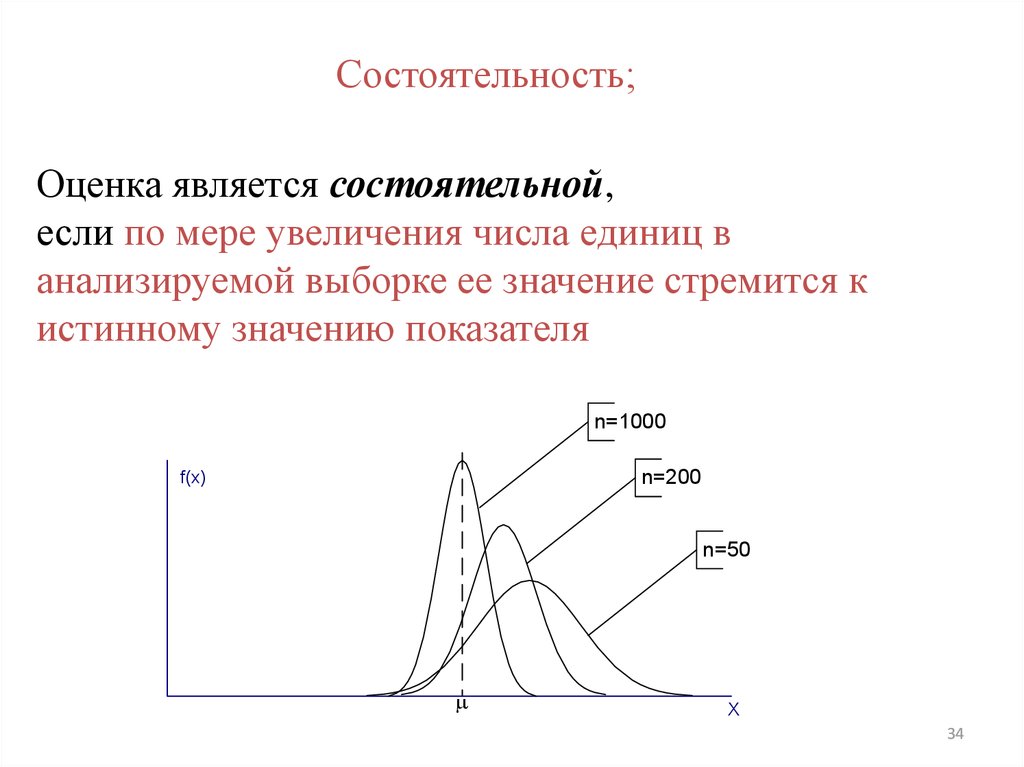
Состоятельность;Оценка является состоятельной,
если по мере увеличения числа единиц в
анализируемой выборке ее значение стремится к
истинному значению показателя
n=1000
n=200
f(x)
n=50
X
34
35.
ДостаточностьПод достаточностью понимают свойство точечной
оценки, согласно которому для ее проведения
используется максимум информации.
При наличии перечисленных свойств оценки
получаются качественные и дают хороший прогноз
35
36.
Интервальная оценкаИнтервальная оценка - интервал, в котором с известной
вероятностью находится истинное значение исследуемого
признака.
Такой интервал называется доверительным, а соответствующая
ему вероятность – доверительной вероятностью (p).
Наряду с доверительной вероятностью (p) используют термин
уровень значимости (α=1-p) – вероятность допущения
исследователем ошибок.
В практическом статистическом анализе большую ценность
представляет именно интервальная оценка.
36
37.
Интервальная оценкаСтандартный уровень значимости (α=1-p)
0, 1
0, 01
0, 05
37
38.
Интервальная оценкадоверительный интервал – интервалов, в которых с
известной вероятностью находится изучаемая переменная.
Величина интервала прямо пропорциональна
дисперсии рассматриваемой случайной величины и
обратно зависима от требуемого уровня
значимости.
38
39.
Проверка статистических гипотезСтатистическая гипотеза - некоторое предположение о
законе распределения случайной величины или о параметрах
этого закона, формулируемое на основе выборки
Н0.
Гипотезу, утверждающую, что различие между сравниваемыми характеристиками
отсутствует, называют нулевой (основной)
НА.
Наряду с основной гипотезой рассматривают альтернативную
гипотезу.
И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная
гипотеза.
39
40.
Проверка статистических гипотезСтатистический критерий — строгое математическое правило, по которому
принимается или отвергается та или иная статистическая гипотеза с
известным уровнем значимости.
1 способ проверки гипотез
1. Стандартным уровням значимости соответствуют табличные,
критические значения tкрит (приложение).
2. Если наблюдаемое значение критерия tрасч > tкрит , то гипотеза
нулевая отвергается на заданном уровне значимости. . Исследуемый
показатель статистически значим.
40
41.
Проверка статистических гипотезtкрит = СТЬЮДРАСПОБР(уровень значимости; степень свободы)
степень свободы = n-k-1
41
42.
Проверка статистических гипотез2 способ проверки гипотез
1. Наблюдаемому значению критерия соответствует определенный
уровень значимости значимостьt
2. Если значимостьt меньше заданного стандартного уровня
значимости, то нулевая гипотеза отвергается.
3. .Исследуемый показатель статистически значим.
Значимость t =СТЬЮДРАСП(t, степень свободы, 2)
степень свободы = n-k-1
42
43. Статистическая значимость коэффициента корреляции (Критерий Стьюдента)
Проверка гипотезы H0: r = 01. Формируем случайную величину
r2
n 2
t расч1
2
1 r
t расч 2
r2
n
2
1 r
где n – количество наблюдений в выборке.
Формула 1 применяется при выборках не более 100 единиц.
Случайная величина tрасч подчиняется закону распределения вероятностей
Стьюдента (приложение).
2. Расчетное значение tрасч сравнивается с критическим
значением tкрит при n-2 степенях свободы и требуемом уровне
значимости (0,05 или 0,01, 0,1).
Если tрасч > tкрит
коэффициент корреляции значимо
отличается от 0 и связь между анализируемыми признаками
статистически значима.
43
44.
ЗАДАНИЕ 2По ранее выбранным статистическим данным (задание 1)
определить статистическую значимость полученного
коэффициента корреляции для различных стандартных
уровней значимости.
44
45. Классификация эконометрических моделей
В зависимости от цели исследования и спецификиэкономической модели:
факторные (регрессионные) статические модели:
y f x1 , x2 , , xm ε
динамические модели:
y f t , x t
модель системы одновременных уравнений:
y1 f x1 , x2 , , xm ε
y f x , x , , x ε
2
1
2
m
y m f x1 , x2 , , xm ε
В зависимости от количества изучаемых факторов:
парная эконометрическая модель (одна факторная переменная)
множественная эконометрическая модель (более одной факторной
переменной)
45
46. Парный регрессионный анализ
Регрессионная модель – это эконометрическая модель,описывающая зависимость между двумя факторами.
y f x
Уравнение линейной регрессии
yˆ f ( x) a0 a1 x
где a0 и a1 – оценки коэффициентов регрессии
регрессионную модель можно представить в виде:
y yˆ
где yˆ – объясненная на основе построенной модели составляющая
y,
а ε –случайная составляющая, ошибка.
46
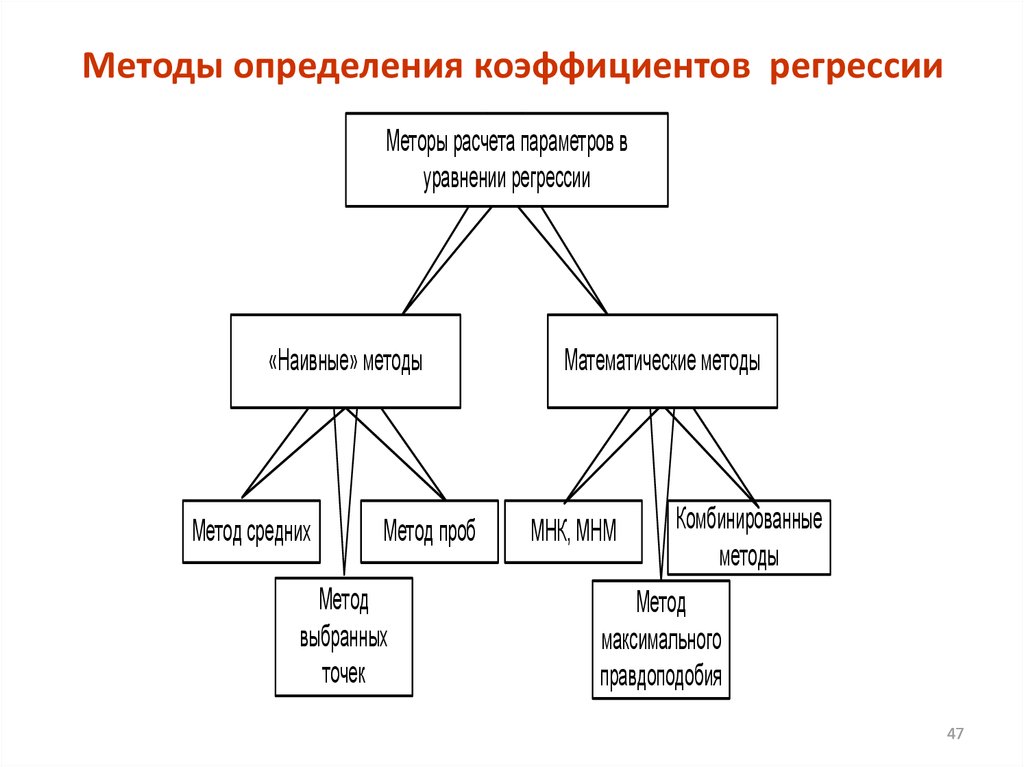
47. Методы определения коэффициентов регрессии
Меторы расчета параметров вуравнении регрессии
«Наивные» методы
Метод средних
Метод проб
Метод
выбранных
точек
Математические методы
МНК, МНМ
Комбинированные
методы
Метод
максимального
правдоподобия
47
48.
Математические методыСмысл математических методов можно определить как
решение
задачи
минимизации
функционала
F,
формируемого на основе суммирования отклонений
эмпирических данных от результата расчета по
регрессионной модели:
n
n
i 1
i 1
F g ( yi yˆi ) g (ei )
где g() – функция, определяющая аналитическую форму измерения разброса
фактических данных от модели.
48
49.
Математические методыНаиболее распространены два вида функции g():
g ( yi yˆi ) ( yi yˆi )
2
метод наименьших квадратов (МНК)
g ( yi yˆi ) yi yˆi
методе наименьших модулей (МНМ)
49
50.
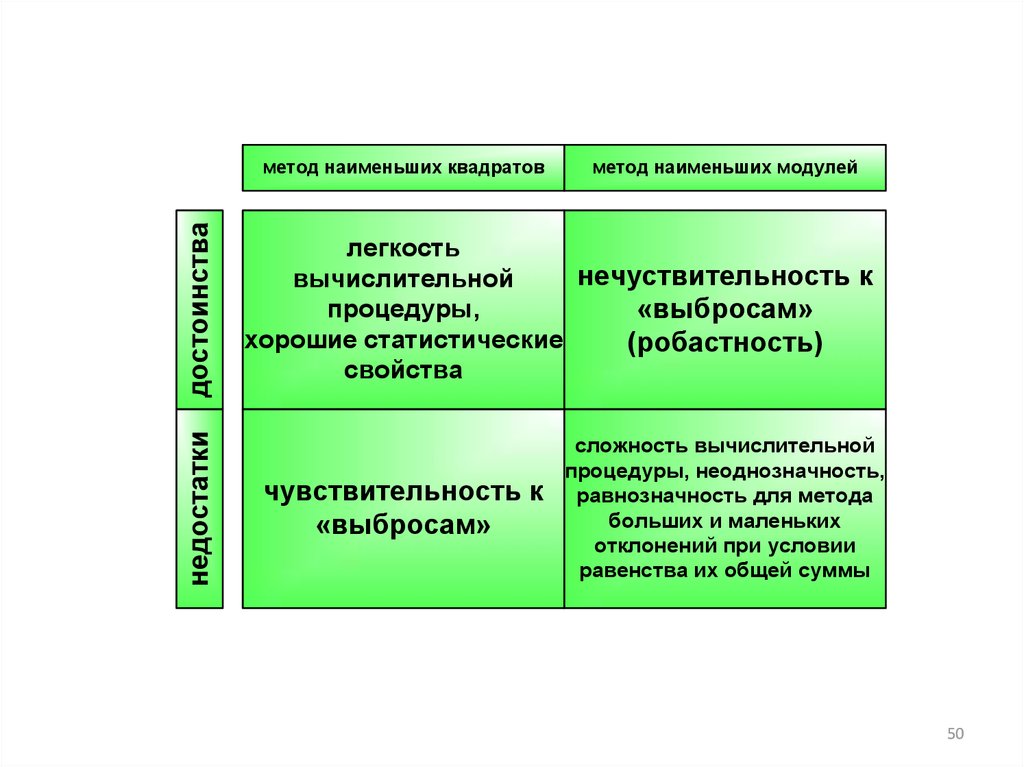
недостаткидостоинства
метод наименьших квадратов
метод наименьших модулей
легкость
нечуствительность к
вычислительной
процедуры,
«выбросам»
хорошие статистические
(робастность)
свойства
чувствительность к
«выбросам»
сложность вычислительной
процедуры, неоднозначность,
равнозначность для метода
больших и маленьких
отклонений при условии
равенства их общей суммы
50
51.
функция ХубераДля совмещения достоинств этих методов разработана более слож
кусочно заданная :
yi yˆi 2 , yi yˆi c
2
ˆ
ˆ
g ( yi yi ) 2c yi yi c , yi yˆi ñ
2
ˆ
2
c
y
y
c
, yi yˆi ñ
i
i
где с – параметр, показывающий границу, начиная с которой в
качестве меры отклонения используется модуль (при меньших – квадрат),
чем он больше, тем сильнее чувствительность .
51
52.
Метод наименьших квадратовУсловия применения (предпосылки) МНК
(теорема Гаусса – Маркова).
Для получения по МНК наилучших результатов (при этом оценки коэффициентов
обладают свойствами состоятельности, несмещенности и эффективности)
необходимо выполнение ряда предпосылок
1. Случайное отклонение имеет нулевое математическое ожидание.
Данное условие означает, что случайное отклонение в среднем не оказывает
влияния на зависимую переменную.
2. Дисперсия случайного отклонения постоянна.
Из данного условия следует, что несмотря на то, что при каждом конкретном
наблюдении случайное отклонение ei может быть различным, но не должно
быть причин, вызывающих большую ошибку
52
53.
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
Для получения по МНК наилучших результатов (при этом оценки
коэффициентов обладают свойствами состоятельности,
несмещенности и эффективности)
необходимо выполнение ряда предпосылок.
53
54.
Метод наименьших квадратовУсловия применения (предпосылки) МНК
(теорема Гаусса – Маркова).
1.Математическое ожидание случайного отклонения равно 0 для
M(ε)=0
всех наблюдений:
2.Дисперсия случайных отклонений постоянна:
s const
2
ε
3. Случайные отклонения независимы друг от
друга:
reie j 0 i, j
4 Модель линейна относительно параметров
54
55.
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
Для получения по МНК наилучших результатов (при этом оценки
коэффициентов обладают свойствами состоятельности, несмещенности и
эффективности)
необходимо выполнение ряда предпосылок
1. Математическое ожидание случайного отклонения равно 0
для всех наблюдений:
M(ε)=0
Ошибка не имеет систематического смещения.
55
56.
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
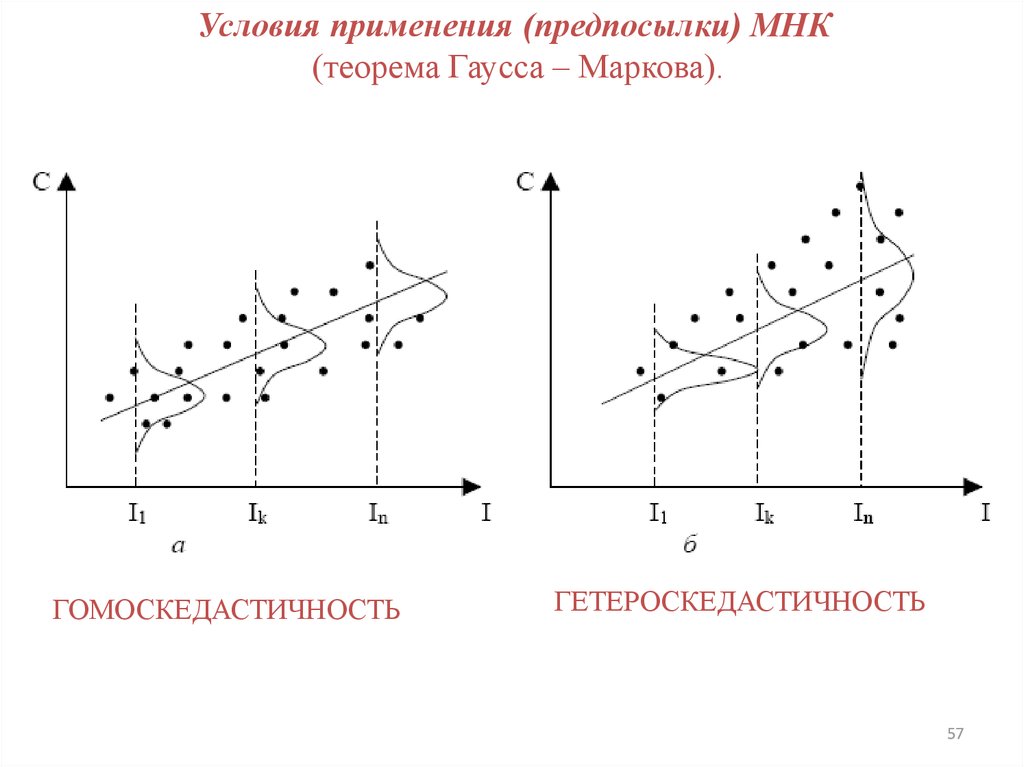
2. Дисперсия случайных отклонений постоянна: для всех
наблюдений (гомоскедастичность)
s const
2
ε
Условие независимости
дисперсии случайной
составляющей
ГОМОСКЕДАСТИЧНОСТЬ
Условие зависимости дисперсии
случайной составляющей от
номера наблюдения
ГЕТЕРОСКЕДАСТИЧНОСТЬ
56
57.
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
ГОМОСКЕДАСТИЧНОСТЬ
ГЕТЕРОСКЕДАСТИЧНОСТЬ
57
58.
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
3. Случайные отклонения независимы друг от друга:
r i j 0 i, j
Некоррелированность ошибок в разных наблюдениях
58
59.
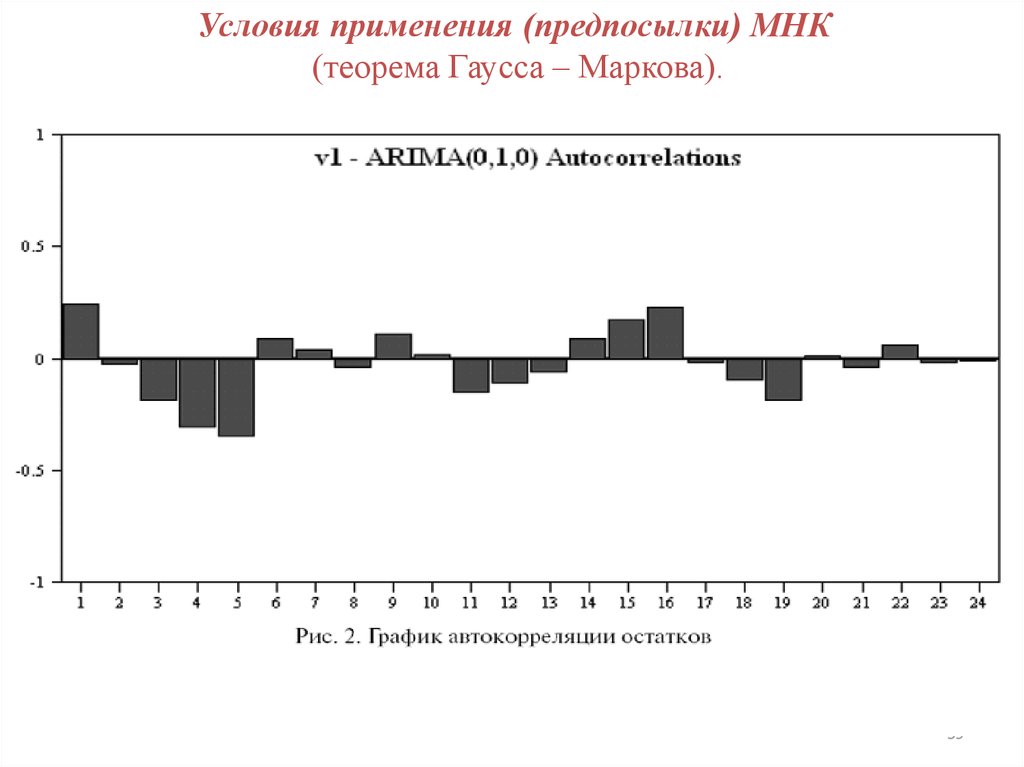
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
59
60.
Условия применения (предпосылки) МНК(теорема Гаусса – Маркова).
4. Модель линейна относительно параметров
теорема Гаусса – Маркова
Если условия 1-4 регрессионного анализа выполняются, то
оценки, сделанные с помощью МНК, являются
наилучшими линейными несмещенными оценками
коэффициентов регрессии.
60
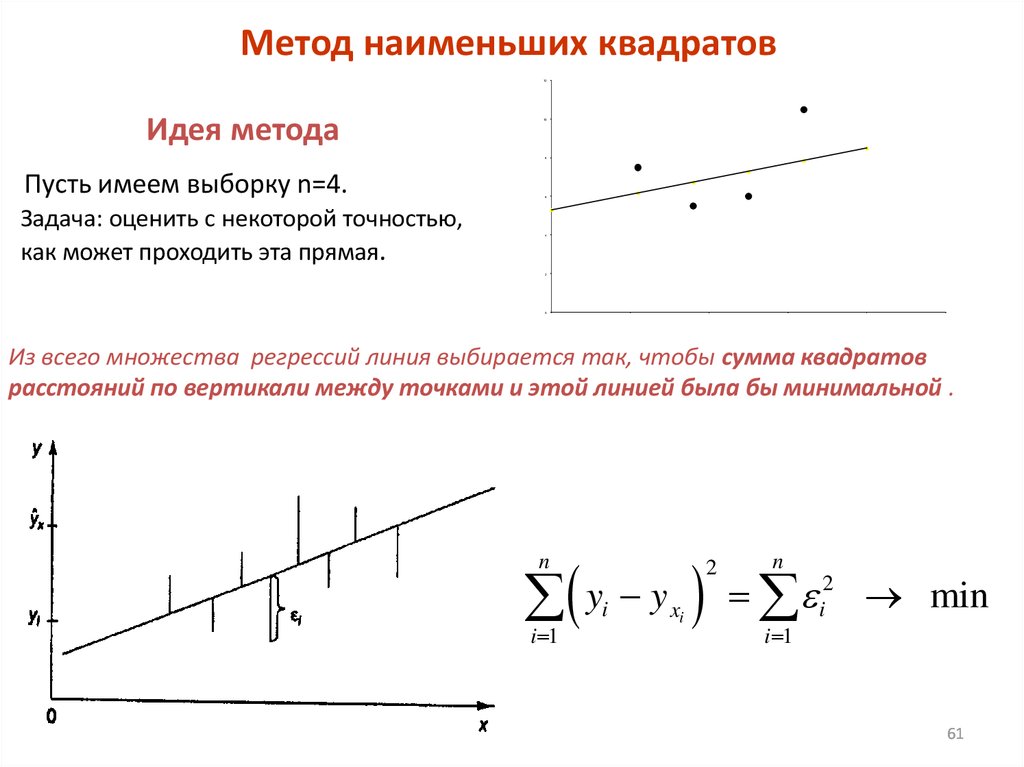
61. Метод наименьших квадратов
12Идея метода
10
8
Пусть имеем выборку n=4.
Задача: оценить с некоторой точностью,
как может проходить эта прямая.
6
4
2
0
0
5
10
15
20
25
Из всего множества регрессий линия выбирается так, чтобы сумма квадратов
расстояний по вертикали между точками и этой линией была бы минимальной .
n
i 1
yi y xi
2
n
i2 min
i 1
61
62.
Метод наименьших квадратовКоэффициенты линии регрессии
yˆ f ( x) a0 a1 x
Угловой
коэффициент
наклона
Коэффициент
отрезка
sy
xy x y cov( x, y )
r
a1 2
x, y
2
2
sx
sx
x x
a y a x
1
0
Для нахождения коэффициентов а1 и а0 служат функции НАКЛОН
и ОТРЕЗОК. категории «Статистические»
62
63.
Метод наименьших квадратовФункция ЛИНЕЙН- функция, которая рассчитывает все
основные характеристики линейной регрессии
Коэффициент а1
Коэффициент а0
Стандартная ошибка m а1
Стандартная ошибка m а0
Коэффициент детерминации
Среднеквадратическое отклонение у
F – статистика
Степени свободы п-2
Регрессионная сумма квадратов
Остаточная сумма квадратов
63
64.
ЗАДАНИЕ 3По выбранным самостоятельно статистическим данным с
помощью функции ЛИНЕЙН () построить и графически
отобразить линейную парную регрессию без свободного члена.
Оценить адекватность модели с помощью коэффициента
детерминации и критерия Фишера.
64
65.
Метод наименьших квадратовВажно, чтобы регрессионная сумма (объясненная
регрессией) была намного больше остаточной (не
объясненная регрессией, вызванная случайными
факторами).
65
66.
Пример применения МНКX
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
Y
1,91
2,76
2,67
4,03
4,12
2,81
6,53
6,24
9,03
6,87
9,09
7,08
7,79
8,75
11,19
10,15
10,52
10,89
10,59
13,40
ỹ
2,17
2,72
3,26
3,80
4,34
4,88
5,42
5,97
6,51
7,05
7,59
8,13
8,68
9,22
9,76
10,30
10,84
11,38
11,93
12,47
е
-0,26
0,04
-0,59
0,23
-0,22
-2,07
1,11
0,27
2,52
-0,18
1,50
-1,05
-0,89
-0,47
1,43
-0,15
-0,32
-0,49
-1,34
0,93
e 2
0,07
0,00
0,35
0,05
0,05
4,30
1,22
0,07
6,36
0,03
2,24
1,11
0,78
0,22
2,05
0,02
0,10
0,24
1,78
0,87
σ(y)
1,20
1,19
1,17
1,16
1,15
1,15
1,14
1,14
1,13
1,13
1,13
1,13
1,14
1,14
1,15
1,15
1,16
1,17
1,19
1,20
X-стаж работы сотрудника;
Y- часовая оплата труда.
Модель: Y=a0+a1X+e
Σxi=210; Σyi=146.42;
Σxi2=2870; Σxiyi=1897.66
20 1897.66 210 146.42
1.63
20 2870 44100
1
a 0 20 155.42 1.63 210 0.54
21.93
2
u 20 2 1.10
a1
66
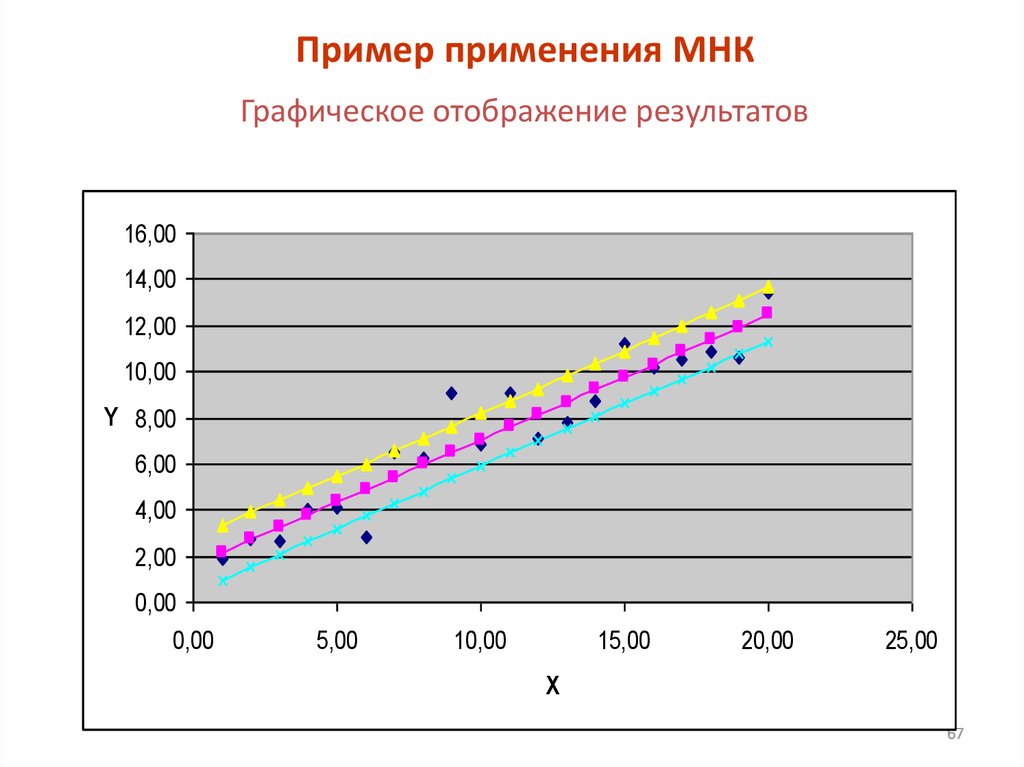
67.
Пример применения МНКГрафическое отображение результатов
16,00
14,00
12,00
10,00
Y 8,00
6,00
4,00
2,00
0,00
0,00
5,00
10,00
15,00
20,00
25,00
X
67
68.
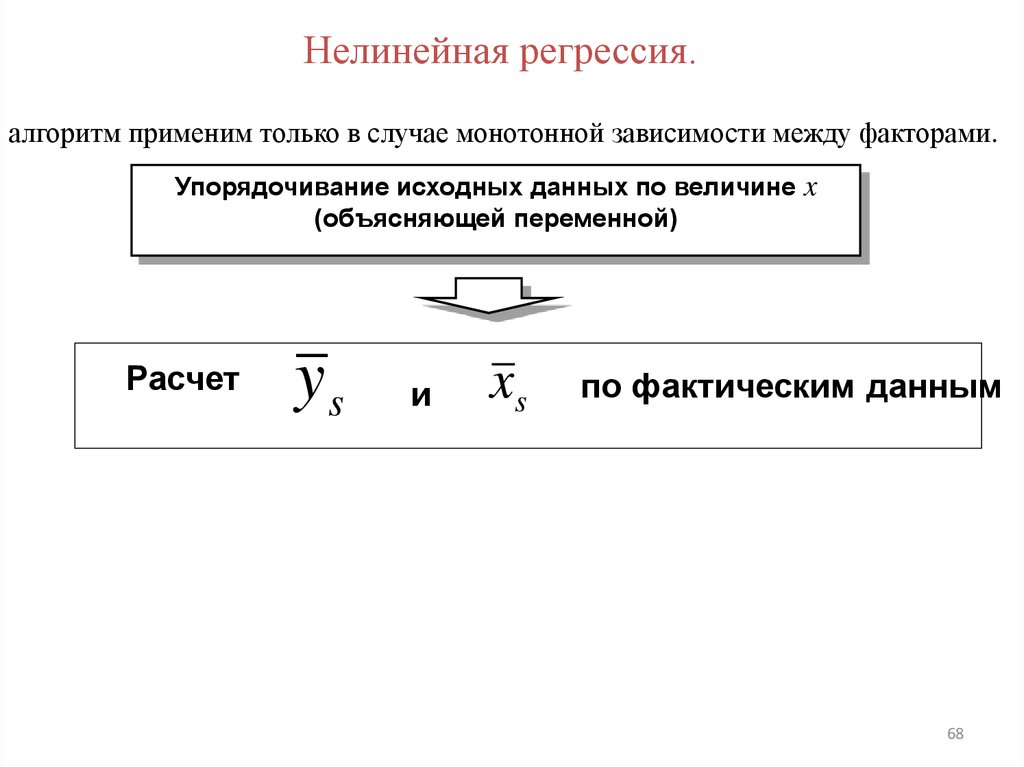
Нелинейная регрессия.алгоритм применим только в случае монотонной зависимости между факторами.
Упорядочивание исходных данных по величине x
(объясняющей переменной)
Расчет
ys
и
xs
по фактическим данным
68
69.
Нелинейная регрессия.Предполагаема
я форма
модели
Уравнение
линейная
y α 0 α1 x ε
показательная
y α0 α1 ε
x
степенная
гиперболическая
(1)
гиперболическая
(2)
y α 0 x α1 ε
α1
y α0 ε
x
1
y
α 0 α, 1 x ε
x
y
,
гиперболическая
α 0 α1 x ε
(3)
логарифмическ
ая
y α0 α1 ln x ε
xs
x1 x n
2
ys
y1 y n
2
x1 xn
2
y1 y n
x1 xn
y1 y n
2 x1 x n
x1 x n
y1 y n
2
x1 xn
2
2 y1 y n
y1 y n
2 x1 x n
x1 x n
2 y1 y n
y1 y n
x1 xn
y1 y n
2
69
70.
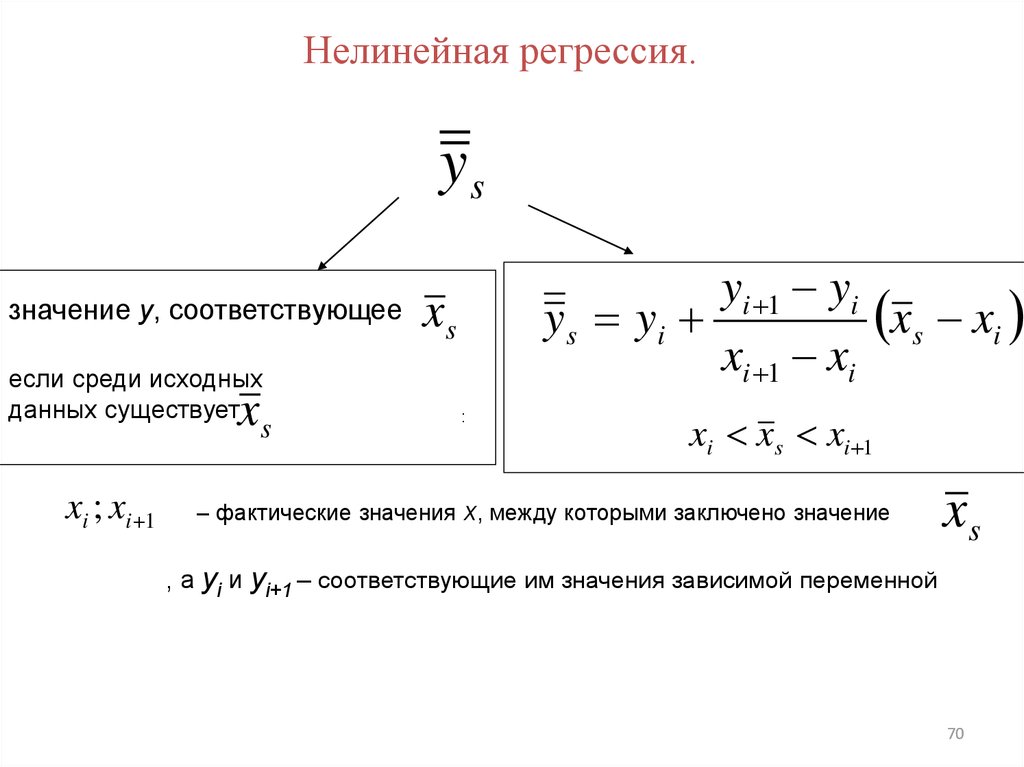
Нелинейная регрессия.ys
значение y, соответствующее
если среди исходных
данных существует
xs
xi ; xi 1
yi 1 yi
xs xi
y s yi
xi 1 xi
xs
:
xi xs xi 1
– фактические значения x, между которыми заключено значение
xs
, а yi и yi+1 – соответствующие им значения зависимой переменной
70
71.
Нелинейная регрессия.Расчет разницы и выбор формы, которой
соответствует наименьшая разница
ys ys
min
71
72.
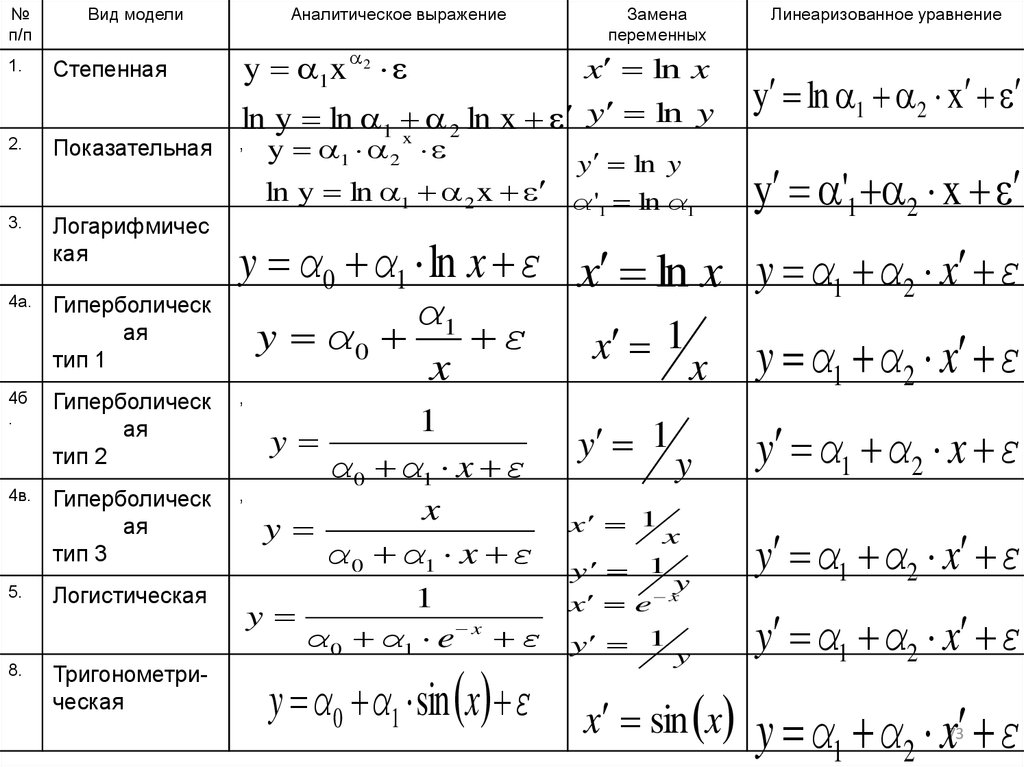
Расчет параметров нелинейных регрессионных моделейОсновное требование – уравнение регрессии должно быть либо
линейно относительно параметров, либо преобразуемо в такое
уравнение (это преобразование называется линеаризацией)
В случае линеаризации происходит замена переменных в уравнении
регрессии с тем, чтобы привести его к линейному виду.
Линеаризованы могут быть функции с числом параметров, равным
числу параметров в соответствующей линейной модели (для парной
регрессии – с двумя параметрами),
72
73.
№п/п
Вид модели
1.
Степенная
2.
Показательная
3.
Логарифмичес
кая
4а.
Гиперболическ
ая
тип 1
4б
.
4в.
5.
8.
Аналитическое выражение
y 1x 2
x ln x
y ln y
ln y ln 1
ln
x
2
, y x
1
2
y ln y
ln y ln 1 2 x α ' ln α
1
α1
y α0
ε
x
,
Гиперболическ
ая
тип 3
,
Тригонометрическая
1
Линеаризованное уравнение
y ln 1 2 x
y '1 2 x
y α0 α1 ln x ε x ln x y α1 α2 x ε
Гиперболическ
ая
тип 2
Логистическая
Замена
переменных
1
y
α 0 α1 x ε
x
y
α 0 α1 x ε
y
1
α 0 α1 e x ε
y α 0 α1 sin x ε
x 1
y 1
x
y
x 1
x
y 1
y
x
x e
y 1
y
x sin x
y α1 α2 x ε
y α1 α2 x ε
y α1 α2 x ε
y α1 α2 x ε
y α1 α2 x ε
73
74.
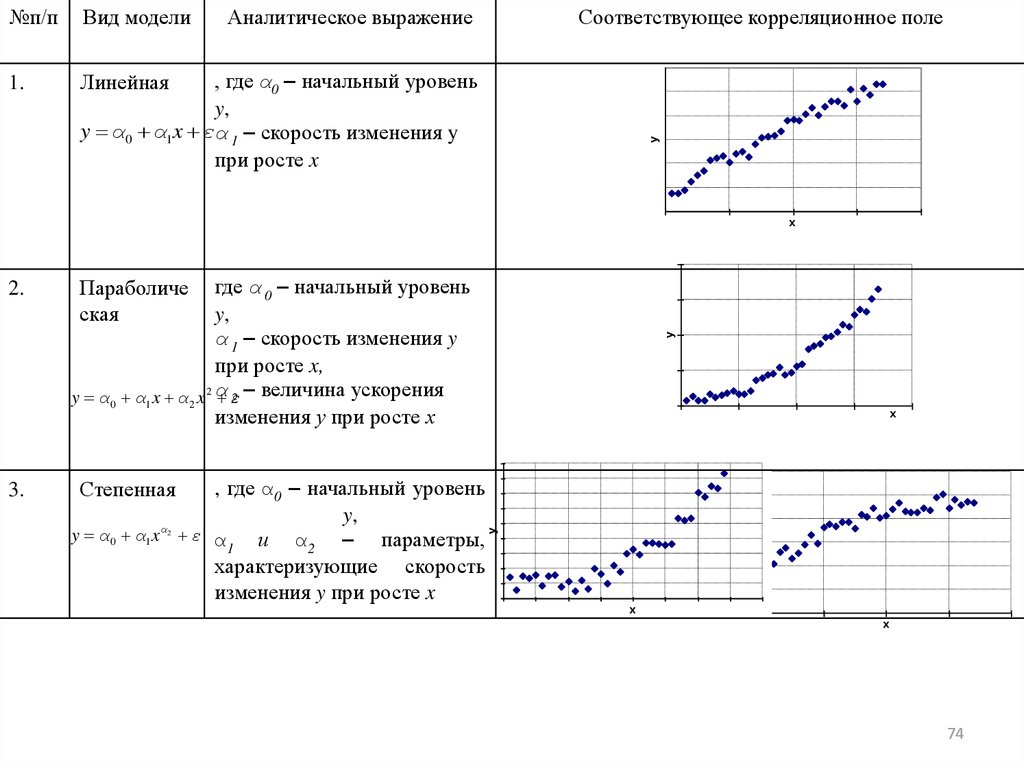
№п/пВид модели
1.
Линейная
Аналитическое выражение
Соответствующее корреляционное поле
y
, где α0 – начальный уровень
y,
y α0 α1 x εα 1 – скорость изменения y
при росте x
x
y
x
, где α0 – начальный уровень
y,
α
y α 0 α1 x ε α
и α2 – параметры,
1
характеризующие скорость
изменения y при росте x
Степенная
2
y
3.
где α 0 – начальный уровень
y,
α 1 – скорость изменения y
при росте x,
2 – величина ускорения
y α 0 α1 x α 2 x 2 α
ε
изменения у при росте х
Параболиче
ская
y
2.
x
x
74
75.
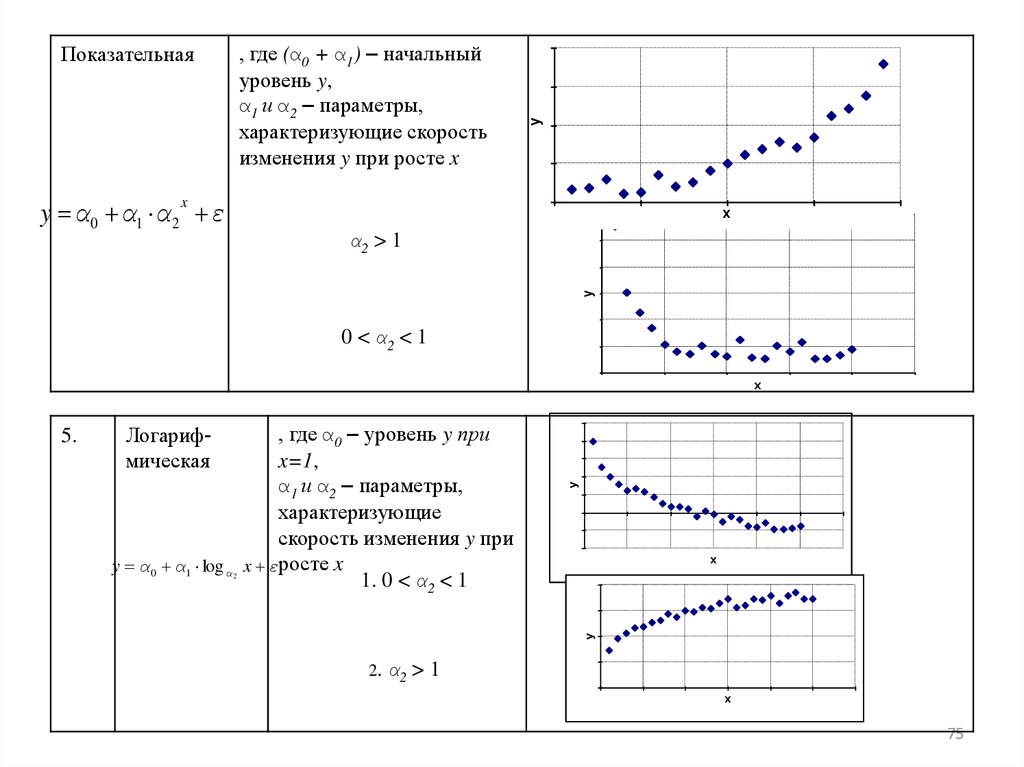
y α0 α1 α 2 εy
, где (α0 + α1) – начальный
уровень y,
α1 и α2 – параметры,
характеризующие скорость
изменения y при росте x
Показательная
x
x
y
α2 > 1
0 < α2 < 1
x
, где α0 – уровень y при
x=1,
α1 и α2 – параметры,
характеризующие
скорость изменения y при
y α 0 α1 log α x εросте x
1. 0 < α2 < 1
y
Логарифмическая
x
2
y
5.
2. α2
>1
x
75
76.
y α0Тригонометричес
кая
y
, где α0 – уровень y при x ∞,
α1 –скорость уменьшения y при
росте x
α2 – предельное значение х,
начиная с которого начинает
убывать y
x
α1
ε
α2 x
, где α0 – значение ряда, вокруг
которого осуществляется
колебательный процесс
α1 – амплитуда колебания y,
α2 – скорость изменения y
y α 0 α1 sin α 2 x ε
y
Гиперболическая
x
76
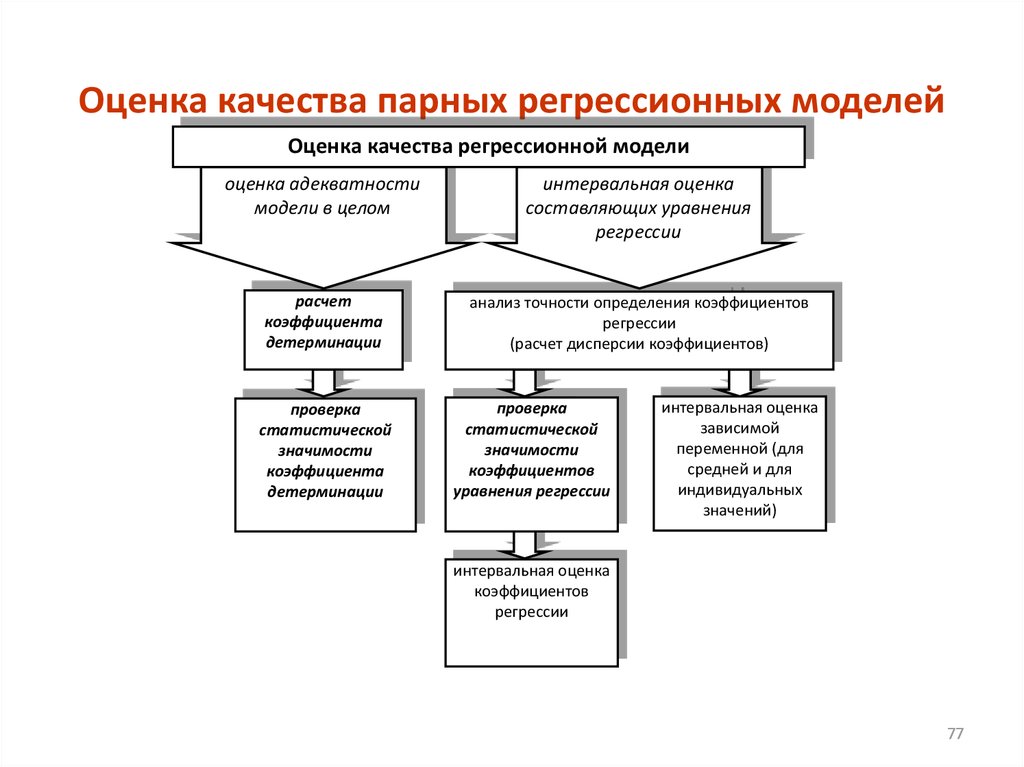
77. Оценка качества парных регрессионных моделей
Оценка качества регрессионной моделиоценка адекватности
модели в целом
интервальная оценка
составляющих уравнения
регрессии
расчет
коэффициента
детерминации
анализ точности определения коэффициентов
регрессии
(расчет дисперсии коэффициентов)
проверка
статистической
значимости
коэффициента
детерминации
проверка
статистической
значимости
коэффициентов
уравнения регрессии
интервальная оценка
зависимой
переменной (для
средней и для
индивидуальных
значений)
интервальная оценка
коэффициентов
регрессии
77
78.
ЗАДАНИЕ 4По
исходным
данным
экономического
характера
проанализировать выбор оптимального типа эконометрической
модели :
линейная
a a х
y
0
1
нелинейная вида
y a
0
a1 x
нелинейная вида.
a1
y a0 x
78
79.
Оценка качества парных регрессионных моделейВ оценке качества парных регрессионных моделей можно
выделить следующие основные этапы
:
Анализ адекватности модели в целом
Анализ точности определения (дисперсии и стандартные ошибки) оценок
коэффициентов регрессии
Проверка статистической значимости коэффициентов регрессионного
уравнения
Интервальная оценка коэффициентов регрессионного уравнения при
заданном уровне значимости
Определение доверительных интервалов для зависимой переменной
79
80. Оценка качества парных регрессионных моделей
1. Для определения адекватностикоэффициент детерминации R2.
1 n
s
( yˆ i y) 2
n 1 i 1
модели
в
целом
2
yˆ
R
2
s y2
n
1
( yi y ) 2
n 1 i 1
используется
s
2
yˆ
s
2
y
Если R2 =1, то такая модель называется «абсолютно хорошей». Это означает,
что выбранный регрессор полностью объясняет поведение эндогенной
переменной.
Если R2 =0, то такую модель называют «абсолютно плохой». В этом случае
весь диапазон изменения эндогенной переменной объясняется влиянием
случайного возмущения, а выбранный регрессор не оказывает влияния, не
объясняет поведение эндогенной переменной.
80
81. Оценка качества парных регрессионных моделей Статистическая значимость коэффициента детерминации
2. Проверка статистической гипотезы о равенстве нулю R2: (H0: R2=0).Внимание! Формулируется гипотеза о равенстве нулю R2, т.е гипотеза о том,
что модель плохая.
Для проверки гипотезы H0: R2=0:
2.1. Формируем случайную величину с известным законом
распределения
2
R
F
n 2
2
1 R
1 способ проверки
2.2. Вычисляется по данным выборки значение Fрасч.
2.3. Находится по таблице значение Fкрит(Pдоверит., k, n-k-1).
Fкрит = FРАСПОБР(α, k, n-k-1)
81
82.
Оценка качества парных регрессионных моделейСтатистическая значимость коэффициента
детерминации
Для проверки гипотезы H0: R2=0:
2.4. Сравниваются значения Fкрит и Fрасч
Если Fрасч ≤ Fкрит,
то гипотеза не отвергается. Значит модель имеет плохое качество
спецификации. Т.е. выбранный регрессор не объясняет поведение
эндогенной переменной.
2 способ проверки
1. Наблюдаемому значению критерия соответствует определенный уровень
значимости
значимостьF=FРАСП(Fрасч;k;n-k-1)
2. Если значимостьF меньше заданного стандартного уровня значимости,
исследуемый показатель статистически значим.
82
83.
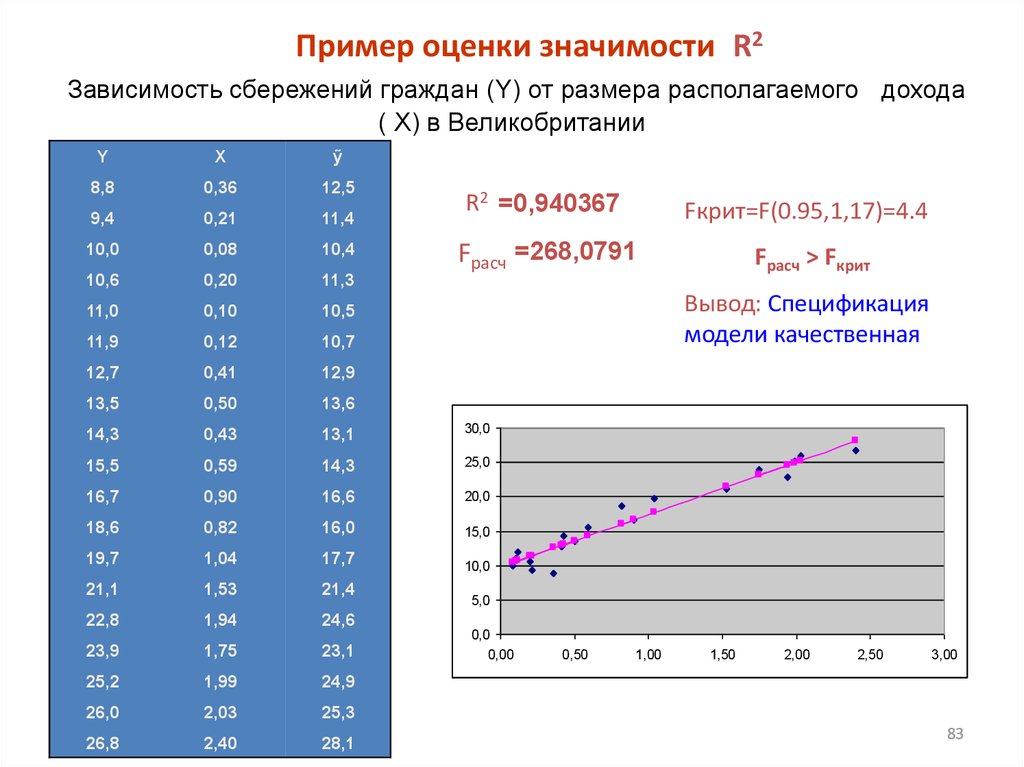
Пример оценки значимости R2Зависимость сбережений граждан (Y) от размера располагаемого дохода
( X) в Великобритании
Y
X
ỹ
8,8
0,36
12,5
9,4
0,21
11,4
10,0
0,08
10,4
10,6
0,20
11,3
11,0
0,10
10,5
11,9
0,12
10,7
12,7
0,41
12,9
13,5
0,50
13,6
14,3
0,43
13,1
30,0
15,5
0,59
14,3
25,0
16,7
0,90
16,6
20,0
18,6
0,82
16,0
15,0
19,7
1,04
17,7
10,0
21,1
1,53
21,4
22,8
1,94
24,6
23,9
1,75
23,1
25,2
1,99
24,9
26,0
2,03
25,3
26,8
2,40
28,1
R2 =0,940367
Fкрит=F(0.95,1,17)=4.4
Fрасч =268,0791
Fрасч > Fкрит
Вывод: Спецификация
модели качественная
5,0
0,0
0,00
0,50
1,00
1,50
2,00
2,50
3,00
83
84.
2. Анализ точности определения оценок регрессииОсуществляется путем вычисления
дисперсий коэффициентов регрессии.
Для линейной регрессионной модели
y a0 a1 x e
значения выборочных дисперсий будут равны
s
2
a1
s e2
2
x
x
i
s a20
se2 xi2
n xi x
2
x 2 sa21
оценки коэффициентов будут тем точнее,
чем меньше значение необъясненной дисперсии.
84
85.
Оценка качества парных регрессионных моделей3. Оценка статистической значимости коэффициента регрессии
Гипотеза о равенстве коэффициента регрессии 0.
Для коэффициента a1 такая гипотеза будет иметь вид:
H0 : a1 = 0
H1 : a1 ≠ 0
Для проверки этой гипотезы пользуются t-статистикой для каждого коэффициента:
t
a1
sa1
Правило «грубой» оценки статистической значимости
коэффициентов регрессионного уравнения
№п/п
Значения t
Описание значимости
коэффициента
Доверительная
вероятность
1.
t 1
практически незначим
меньше 0,7
2.
относительно (слабо) значим
от 0,7 до 0,95
3.
1 t 2
2 t 3
существенно значим
от 0,95 до 0,99
4.
3 t
гарантированно значим
больше 0,99
85
86.
3. Оценка статистической значимости коэффициента регрессииСтандартный, табличный способ
2 способ проверки гипотез
1. Стандартным уровням значимости соответствуют табличные,
критические значения tкрит (приложение).
2. Если наблюдаемое значение критерия tрасч > tкрит , то гипотеза
нулевая отвергается на заданном уровне значимости. . Исследуемый
показатель статистически значим.
tкрит = СТЬЮДРАСПОБР(уровень значимости; степень свободы)
степень свободы = n-k-1
86
87.
3. Оценка статистической значимости коэффициента регрессииСтандартный, табличный способ
3 способ проверки гипотез
1. Наблюдаемому значению критерия соответствует определенный
уровень значимости значимостьt
2. Если значимостьt меньше заданного стандартного уровня
значимости, то нулевая гипотеза отвергается.
3. .Исследуемый показатель статистически значим.
Значимость t =СТЬЮДРАСП(t, степень свободы, 2)
87
88. 4.Интервальная оценка коэффициентов регрессионного уравнения при заданном уровне значимости
Интервальная оценка коэффициентов регрессионного уравненияосуществляется для того, чтобы получить более полное представление о
характере регрессионной зависимости между переменными. Ее
результатом будут доверительные интервалы для каждого коэффициента:
Доверительный интервал определяет границы, в которых будет
находиться значение теоретического коэффициента регрессии с уровнем
значимости α.
для a1 –
a1 tα
s
;
a
t
s
a
1
α
a
1
1
; n 2
; n 2
2
2
для a0 –
a0 tα
s
;
a
t
s
a
0
α
a
0
0
; n 2
; n 2
2
2
Уровень значимости α определяется исходя из требуемой точности.
88
89.
5. Определение доверительных интервалов для зависимой переменнойПозволяет решить две задачи:
во-первых, провести интервальную оценку математического ожидания
зависимой переменной для конкретного значения независимой переменной и
заданного уровня значимости,
и, во-вторых, определить границы, за пределами которых может оказаться не
более чем α-ая доля индивидуальных значений зависимой переменной для
конкретного значения независимой переменной.
89
90.
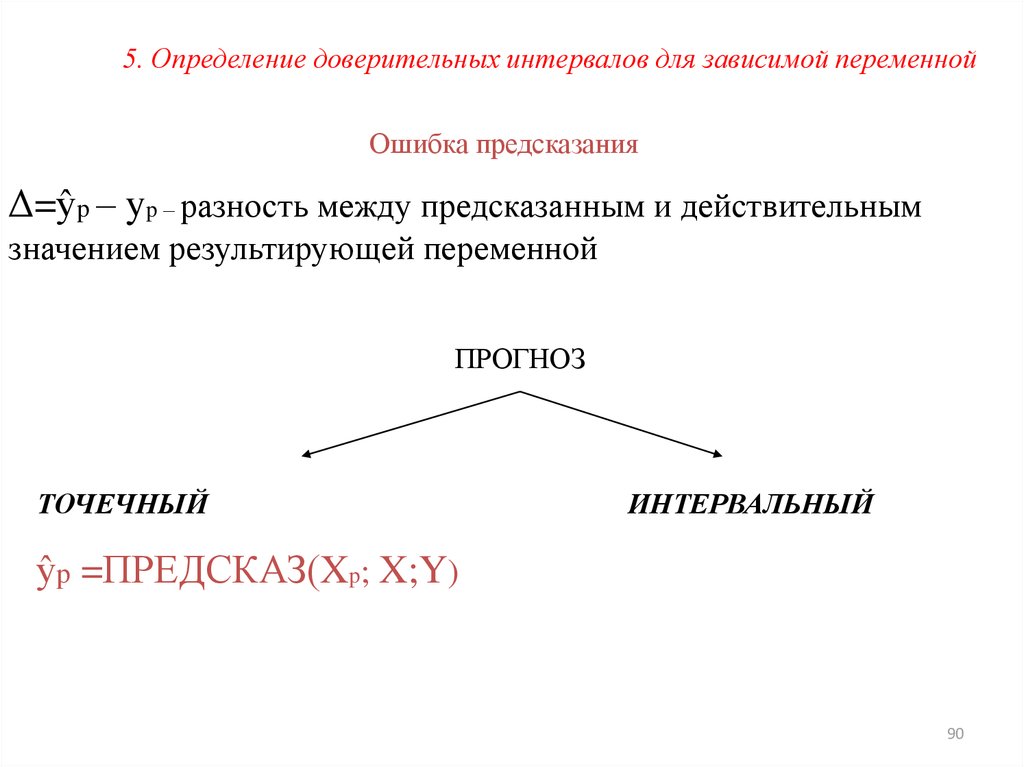
5. Определение доверительных интервалов для зависимой переменнойОшибка предсказания
Δ=ŷp – yp – разность между предсказанным и действительным
значением результирующей переменной
ПРОГНОЗ
ТОЧЕЧНЫЙ
ИНТЕРВАЛЬНЫЙ
ŷp =ПРЕДСКАЗ(Xp; X;Y)
90
91.
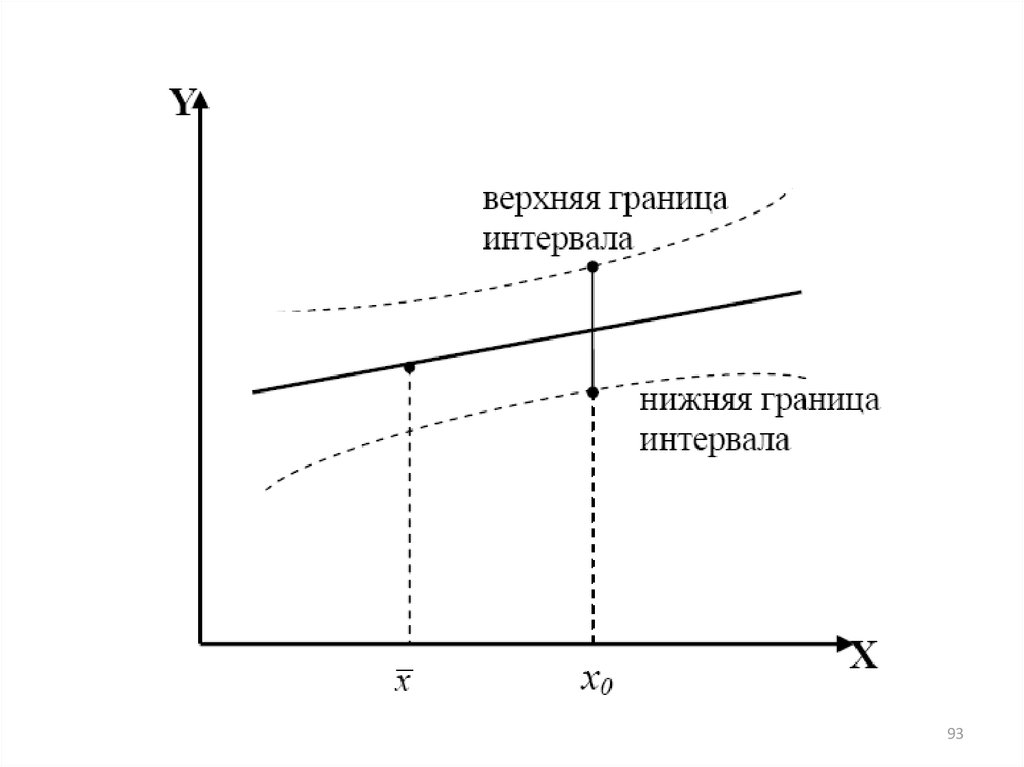
Расчет доверительных интервалов для зависимой переменнойинтервальной оценкой прогнозного значения y p :
y p y y p y p y ,
p
где
y my tтабл , а my
p
p
p
–
средняя
ошибка
прогнозируемого
p
индивидуального значения:
1 xp x
my Sост 1
.
2
p
n
n x
2
(1.16)
91
92.
Расчет доверительных интервалов для зависимой переменнойГДЕ
2
y
y
x
0,1257
2
0, 021 ошибка регрессии
1 Sост
- стандартная
n 2
8 2
Sост=CTOYX(Y, X)
2
x
2
- дисперсия
x
3
tтабл
2
= ДИСПР(X)
= СТЬЮДРАСПОБР(уровень значимости; степень свободы)
92
93.
9394.
6. Средняя ошибка аппроксимацииЧтобы иметь общее суждение о качестве модели из относительных
отклонений по каждому наблюдению, определяют среднюю ошибку
аппроксимации:
y yx
1
A
100%
n
y
Средняя ошибка аппроксимации не должна превышать 8–10%.
94
95.
ЗАДАНИЕ 5По выбранным статистическим данным с помощью функции
ЛИНЕЙН () построить и графически отобразить линейную
парную
регрессию
со
свободным
членом.
Оценить
статистическую значимость коэффициента наклона 3
способами для стандартного уровня значимости 5%.
95
96.
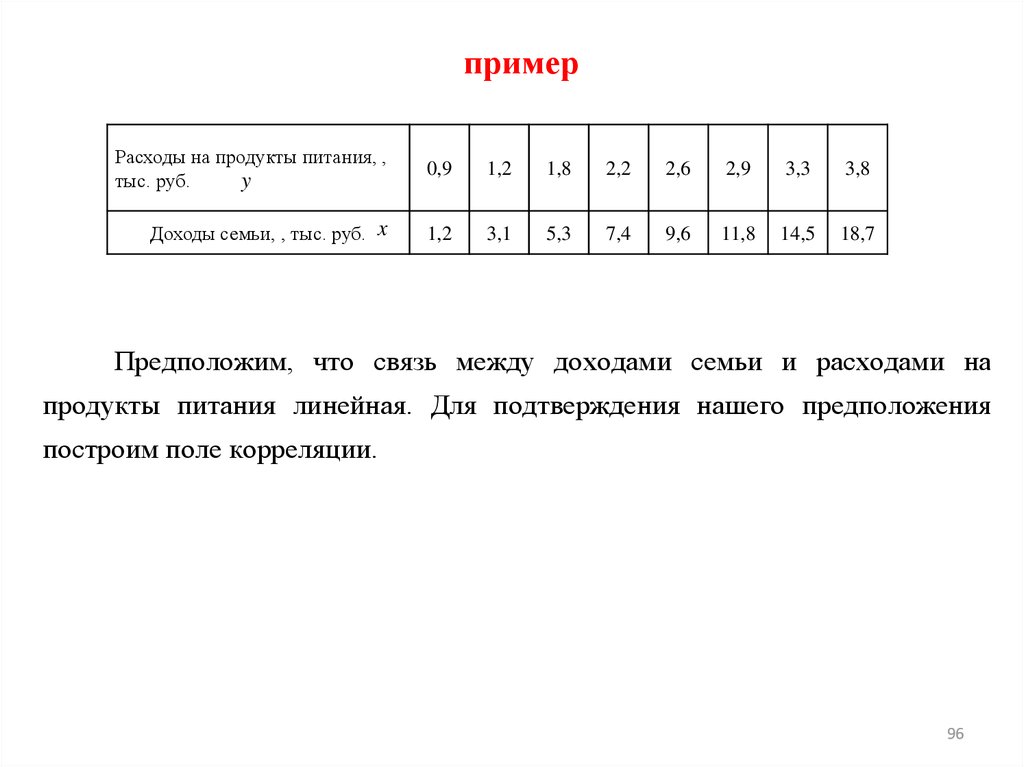
примерРасходы на продукты питания, ,
y
тыс. руб.
0,9
1,2
1,8
2,2
2,6
2,9
3,3
3,8
Доходы семьи, , тыс. руб. x
1,2
3,1
5,3
7,4
9,6
11,8
14,5
18,7
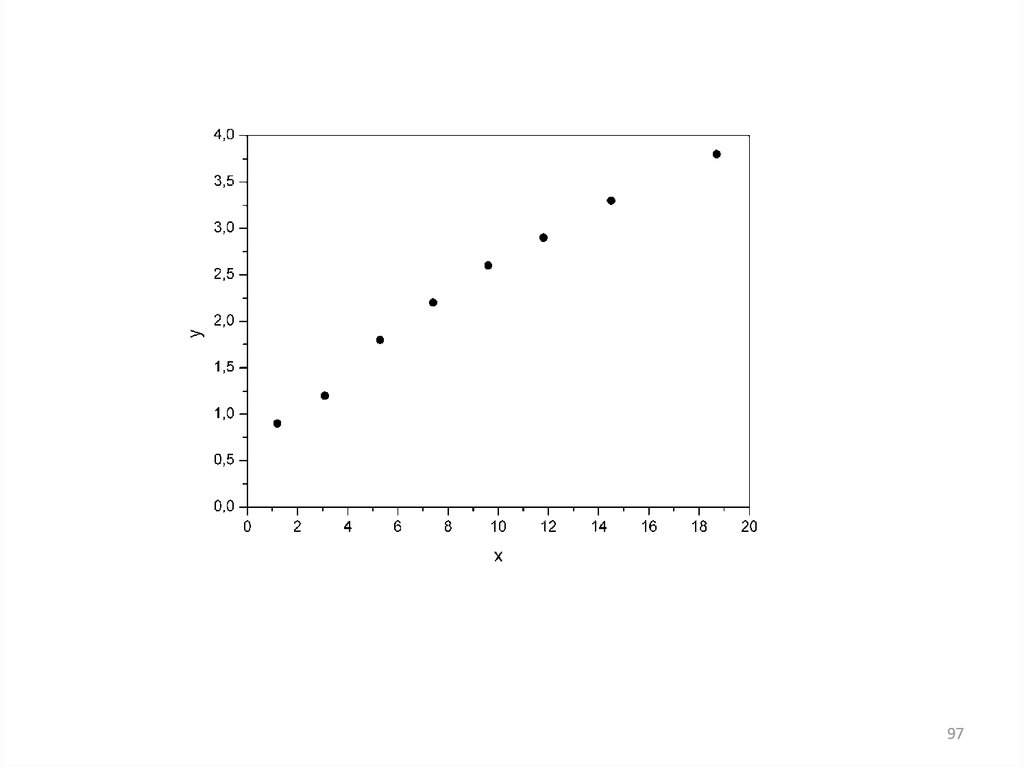
Предположим, что связь между доходами семьи и расходами на
продукты питания линейная. Для подтверждения нашего предположения
построим поле корреляции.
96
97.
9798.
11
2
3
4
5
6
7
8
Итого
Среднее
значение
2
yx
y yx
y y
6
0,81
1,44
3,24
4,84
6,76
8,41
10,89
14,44
50,83
7
1,038
1,357
1,726
2,079
2,449
2,818
3,272
3,978
18,717
8
–0,138
–0,157
0,074
0,121
0,151
0,082
0,028
–0,178
–0,017
9
0,0190
0,0246
0,0055
0,0146
0,0228
0,0067
0,0008
0,0317
0,1257
10
15,33
13,08
4,11
5,50
5,81
2,83
0,85
4,68
52,19
110,66
6,35
2,34
–
0,0157
6,52
–
–
–
–
–
–
–
–
–
–
–
–
x
y
x y
x
2
1,2
3,1
5,3
7,4
9,6
11,8
14,5
18,7
71,6
3
0,9
1,2
1,8
2,2
2,6
2,9
3,3
3,8
18,7
4
1,08
3,72
9,54
16,28
24,96
34,22
47,85
71,06
208,71
5
1,44
9,61
28,09
54,76
92,16
139,24
210,25
349,69
885,24
8,95
2,34
26,09
–
–
5,53 0,935
30,56 0,874
2
y
2
x
2
Ai , %
98
99.
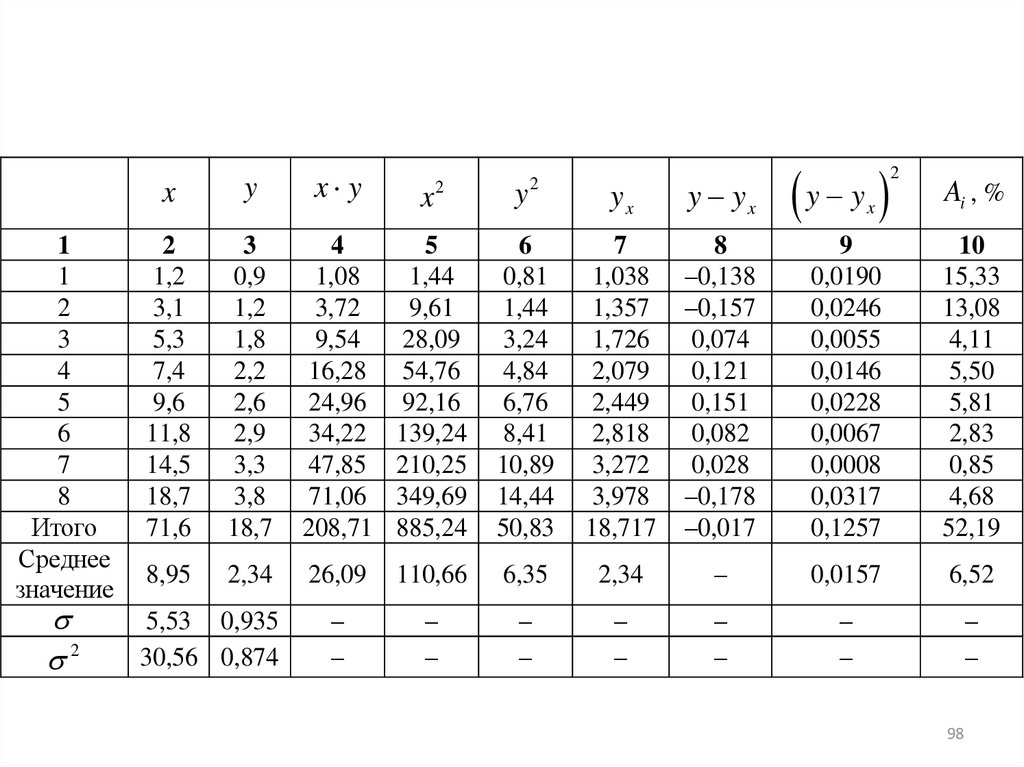
Рассчитаем параметры линейного уравнения парной регрессииyx a b x
b
cov x, y
2
x
x y x y
x2 x 2
26,09 8,95 2,34
0,168
30,56
a y b x 2,34 0,168 8,95 0,836
Получили уравнение:
y x 0,836 0,168 x . Т.е. с увеличением
дохода семьи на 1000 руб. расходы на питание увеличиваются на 168 руб.
99
100.
уравнение линейной регрессии всегда дополняется показателемтесноты связи – линейным коэффициентом корреляции rxy :
x
5,53
rxy b
0,168
0,994 .
y
0,935
Оценим качество уравнения регрессии в целом с помощью F -критерия
Фишера. Сосчитаем фактическое значение F -критерия:
F
rxy2
1 rxy2
n 2
0,987
6 455,54 .
1 0,987
Табличное значение ( k1 1 , k2 n 2 6 ,
0,05 ): Fтабл 5,99 .
Так как Fфакт Fтабл , то признается статистическая значимость уравнения в
целом.
100
101.
Для оценки статистической значимости коэффициентов регрессии икорреляции рассчитаем t -критерий Стьюдента
0,168
18,065 ,
Фактические значения t -статистик: tb
0,0093
0,836
0,994
ta
8,574 , tr
21,376 . Табличное значение t 0,0975
0,0465
критерия Стьюдента при 0,05 и числе степеней свободы n 2 6
есть tтабл 2,447 . Так как tb tтабл , ta t табл и tr tтабл , то признаем
статистическую значимость параметров регрессии и показателя тесноты
101
102.
И, наконец, найдем прогнозное значение результативного фактора y pпри значении признака-фактора, составляющем 110% от среднего уровня
x p 1,1 x 1,1 8,95 9,845 , т.е. найдем расходы на питание, если доходы
семьи составят 9,85 тыс. руб.
y p 0,836 0,168 9,845 2, 490 (тыс. руб.)
Значит, если доходы семьи составят 9,845 тыс. руб., то расходы на
питание будут 2,490 тыс. руб.
Найдем доверительный интервал прогноза. Ошибка прогноза
my
p
1
Sост 1
n
xp x
2
n x2
1 9,845 8,95 2
0,021 1
0,154 ,
8
8 30,56
а доверительный интервал ( y p y y p y p y ):
p
p
2,113 y p 2,867 .
Т.е. прогноз является статистически надежным.
102
103.
103104.
Пакет EXCEL1.Загрузка надстройки «Пакет анализа»
2. Нажмите кнопку Microsoft Office
3. Щелкните Параметры Excel, а затем выберите категорию Надстройки.
2. В списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3. В списке Доступные надстройки выберите Пакет анализа и нажмите кнопку ОК.
4. Выполните инструкции программы установки, если это необходимо.
5. В диалоговом окне Анализ данных выберите название нужного инструмента (регрессия)
анализа и нажмите кнопку ОК.
6. Для выбранного инструмента укажите в диалоговом окне нужные параметры анализа.
Пример реализации в Excel
По данным проведенного опроса восьми групп семей известны данные связи расходов
населения на продукты питания с уровнем доходов семьи.
Расходы на продукты
питания, y , тыс. руб.
Доходы семьи, x , тыс. руб.
0,9
1,2
1,8
2,2
2,6
2,9
3,3
3,8
1,2
3,1
5,3
7,4
9,6
11,8 14,5 18,7
104
105.
Пакет EXCEL(офис 2003)
1. Excel
2. Сервис
Надстройки
3. Анализ данных
4. Регрессия
105
106.
19
7
5
3
Индекс РТС ВВП
Y
X1
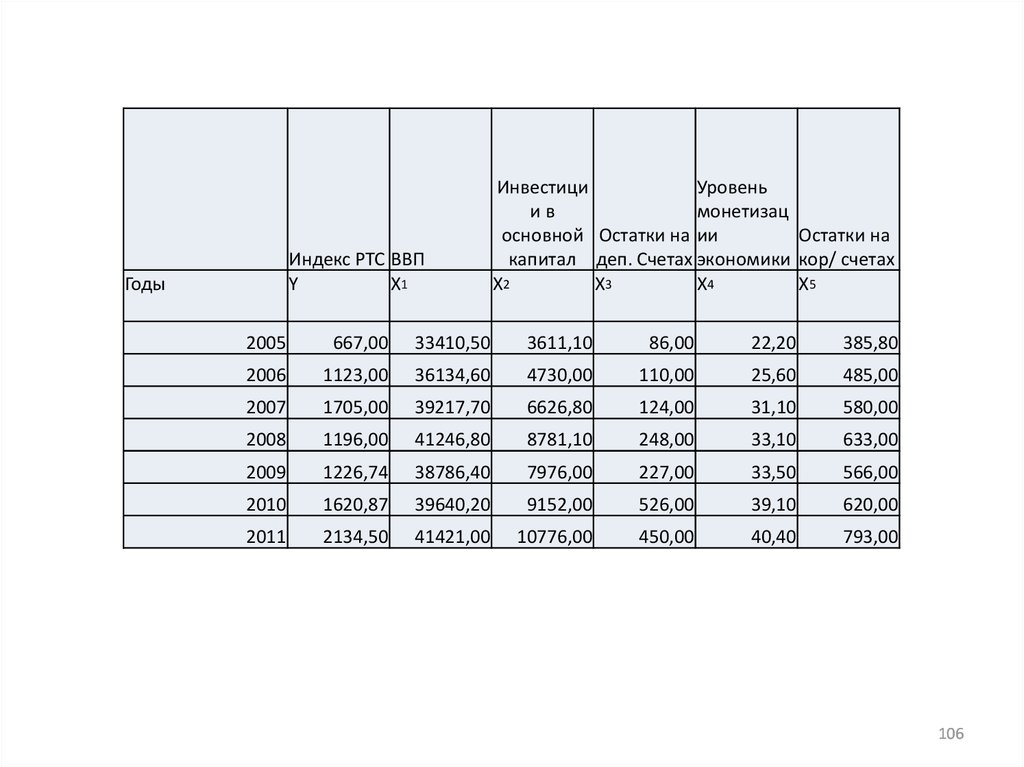
Годы
Инвестици
Уровень
ив
монетизац
основной Остатки на ии
Остатки на
капитал деп. Счетах экономики кор/ счетах
X2
X3
X4
X5
2005
667,00
33410,50
3611,10
86,00
22,20
385,80
2006
1123,00
36134,60
4730,00
110,00
25,60
485,00
2007
1705,00
39217,70
6626,80
124,00
31,10
580,00
2008
1196,00
41246,80
8781,10
248,00
33,10
633,00
2009
1226,74
38786,40
7976,00
227,00
33,50
566,00
2010
1620,87
39640,20
9152,00
526,00
39,10
620,00
2011
2134,50
41421,00
10776,00
450,00
40,40
793,00
106
107.
ВЫВОД ИТОГОВРегрессионная статистика
Множественный R
R-квадрат
Нормированный
R-квадрат
Стандартная
ошибка
Наблюдения
0,997711
0,995427
0,972565
78,9934
7
Дисперсионный анализ
df
Регрессия
Остаток
Итого
Y-пересечение
Переменная X 1
Переменная X 2
Переменная X 3
Переменная X 4
Переменная X 5
5
1
6
SS
1358412
6239,957
1364652
Коэффицие Стандарт
нты
ная ошибка
-3129,78
1290,498
-0,00251
0,045717
-0,45396
0,087086
-0,8439
0,671823
150,2883
30,08599
5,756647
0,89834
MS
271682,3
6239,957
Значимост
F
ьF
43,53914
0,114534
tстатисти
ка
P-Значение
-2,42525
0,248975
-0,055
0,96502
-5,21278
0,120661
-1,25613
0,428034
4,995293
0,125781
6,408092
0,098551
Нижние
Верхние
95%
95%
-19527,1
13267,55
-0,5834
0,578375
-1,56049
0,652571
-9,38022
7,692422
-231,99
532,5671
-5,65785
17,17114
Нижние
Верхние
95,0%
95,0%
-19527,1
13267,55
-0,5834
0,578375
-1,56049
0,652571
-9,38022
7,692422
-231,99
532,5671
-5,65785
17,17114
107
108.
Коэффициенты эластичностиДля регрессионной модели актуален вопрос о том, какова сила влияния различных
факторов на значение зависимой переменной.
Коэффициент эластичности показывает,
на сколько процентов изменится в среднем результат,
если фактор изменится на 1%.
x
Э f x
y
108
109.
Вид функцииy a b x
b
y a
x
y a xb
Средний коэффициент эластичности,
b x
a b x
b
a x b
b
109
110.
ЗАДАНИЕ 6По исходным данным экономического характера построить с
помощью инструмента Регрессия пакета «Анализ данных»
регрессионную зависимость. Сделать выводы по полученной
аналитике. Как изменится результирующая переменная y, если х
изменить на 10% в сторону увеличения?
110
111.
Множественная регрессияy x a b1 x1 b2 x2 ... bm xm
МНК
y y
i
i
xi
2
min
111
112.
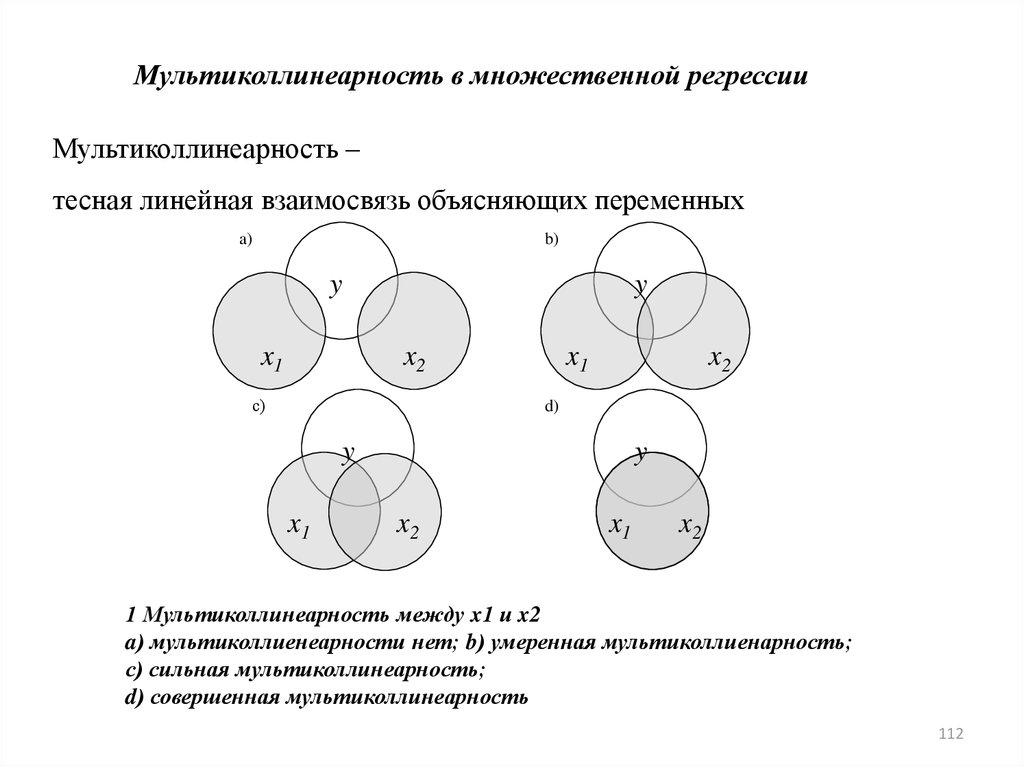
Мультиколлинеарность в множественной регрессииМультиколлинеарность –
тесная линейная взаимосвязь объясняющих переменных
a)
b)
y
y
x1
x2
с)
x1
x2
d)
y
x1
y
x2
x1
x2
1 Мультиколлинеарность между x1 и x2
a) мультиколлиенеарности нет; b) умеренная мультиколлиенарность;
с) сильная мультиколлинеарность;
d) совершенная мультиколлинеарность
112
113.
Последствия мультиколлинеарности:высокие значения дисперсии оценок коэффициентов и ухудшение точности их
интервальных оценок
чувствительность оценок коэффициентов к изменениям исходных данных
сложность оценки влияния каждой из объясняющих переменных на объясняемую
получение неверного знака у коэффициента перед объясняющей переменной
113
114.
Метод обнаружения мультиколлинеарностиНа первом этапе построения модели составляется матрица корреляции размером
(m+1) x (m+1), где m – общее число всех возможных независимых переменных (факторов).
В нее помещаются коэффициенты корреляции между факторами и результативным
признаком, а также попарно между всеми факторами. В ячейке rij указывается
коэффициент корреляции между i-м и j-м фактором. Эта матрица будет симметричной
относительно главной диагонали, причем на диагонали будут значения, равные 1:
rx1 x2 rx1 xm rx1 y
rx1 x1 rx1 x2 rx1 xm rx1 y 1
rx2 xm rx2 y
rx2 x1 rx2 x2 rx2 xm rx2 y rx2 x1 1
r
rxm x2 rxm xm rxm y rxm x1 rxm x2 1
rxm y
x m x1
ryx
1 ryx2 ryxm ryy ryx1 ryx2 ryxm 1
После этого в модель включаются факторы, для которых значение rij по модулю
варьируется в пределах от 0,4 до 0.8.
Анализ данных - Корреляция
114
115.
Методы устранения мультиколлинеарности:
исключение коррелированных переменных из модели
проведение нового наблюдения
изменение спецификации модели
использование предварительной информации о значениях
параметров
преобразования переменных
115
116.
ЗАДАНИЕ 7Сделать статистическую выборку 2 факторов и результирующего
признака экономического характера. С помощью инструмента
«Корреляция» определить целесообразность включения в модель
каждого фактора. Построить уравнения зависимости каждого
фактора от результирующего признака, а также уравнение
множественной регрессии. Какая регрессия из 3 более
достоверна?(R*R).
116
117.
ГетероскедастичностьГетероскедастичность – это различие в дисперсиях случайных отклонений при
различных значениях зависимой переменной.
Наличие гетероскедастичности фактически означает невыполнение одной из
предпосылок применения МНК (условие постоянства дисперсий).
117
118.
ГетероскедастичностьПоследствия гетероскедастичности:
неэффективность оценок
признание статистической значимости незначимых переменных
сужение доверительных интервалов относительно их действительных значений
Методы обнаружения гетероскедастичности:
графический анализ остатков
тест ранговой корреляции Спирмена
тест Парка
тест Глейзера
тест Голдфельда – Квандта
тест Уайта
118
119.
ГетероскедастичностьТест Голдфельда-Квандта
Исходная совокупность упорядочивается по мере возрастания значений независимой переменной.
Исходная совокупность делится на 3 части размерами p, n-2p, p.
Для первой и третьей подвыборок строят отдельно регрессионные модели в Excel
(Пакет анализа «Регрессия»)
Расчет ошибок и суммы квадратов отклонений:
p
S e
2
1
i 1
2
i
S32
n
2
e
i
i n p 1
119
120.
ГетероскедастичностьРасчет F-статистики по формуле:
если S3 > S1, то
если S1 > S3, то
S1
F
S3
S3
F
S1
F > Fα;ν1;ν2
ν1=ν2=p-m-1
нет
да
гетероскедастичность есть
гетероскедастичности нет
Рекомендуемые значения p для выборок различных размеров
n
p
30
11
60
22
120
121.
ЗАДАНИЕ 8Проверить гипотезу об отсутствии гетероскедастичности для
построенной модели множественной регрессии (тест Г-К).
121
122.
АвтокорреляцияАвтокорреляция остатков означает наличие корреляции между остатками текущих
и предыдущих (последующих) наблюдений
Вообще под автокорреляцией i-го порядка понимают зависимость между et и et-i.
Причины возникновения автокорреляции:
ошибки спецификации
инерционность экономических законов
временные лаги в равновесных моделях
сглаживание данных
122
123.
Автокорреляцияr i j 0 i, j
Отсутствие автокорреляции
Методы обнаружения автокорреляции:
графический метод
метод рядов
критерий Дарбина-Уотсона
123
124.
критерий Дарбина-УотсонаT
DW
2
e
e
t t 1
t 2
T
et
2
t 1
Доказано, что статистика Дарбина-Уотсона связана с коэффициентом
корреляции между соседними отклонениями по формуле:
DW 2 1 ret et 1
№п/п
Значения DW
Вывод о наличии автокорреляции
Значения ret et 1
1
близко к 0
близко к 1
сильная положительная
автокорреляция
2
близко к 2
близко к 0
автокорреляция отсутствует
3
близко к 4
близко к –1
сильная отрицательная
автокорреляция
124
125.
Ограничения регрессионного анализа1.
Использование регрессионной модели для прогнозирования вне границ
изменения наблюдаемых данных. Прогнозирование на основе
регрессионных моделей может осуществляться только на основе
экстраполяции, в противном случае возможны серьезные ошибки.
2.
Смешение понятий причинно-следственной и регрессионной
зависимости. По наличию статистической связи нельзя делать вывод о
том, что взаимосвязанные явления влияют друг на друга.
3.
Перенесение прошлых тенденций в ряде динамики на будущее.
Поскольку исторические условия в прошлом и будущем различаются.
4.
Выявление нереальных (ошибочных) связей. Для проведения
регрессионного анализа и трактовки его результатов необходима
теоретическая гипотеза о взаимосвязи исследуемых переменных.
125
126. Множественная регрессионная модель
• Стандартная форма нормальных уравнений длявычисления коэффициентов линии регрессии
n
n
n
n
yi
a1 x1i a 2 x 2i a m x mi
na0
i 1
i 1
i 1
i 1
n
n
n
n
n
2
a0 x1i a1 x1i a 2 x1i x 2i a m x1i x mi yi x1i
i 1
i 1
i 1
i 1
i 1
n
n
n
n
n
2
a0 x 2i a1 x1i x 2i a 2 x 2i a m x 2i x ni yi x 2i
i 1
i 1
i 1
i 1
i 1
n
n
n
n
n
2
a
x mi a1 x1i x mi a 2 x 2i x mi a m x mi yi x mi
0
i 1
i 1
i 1
i 1
i 1
126
127. Регрессионные модели с переменной структурой
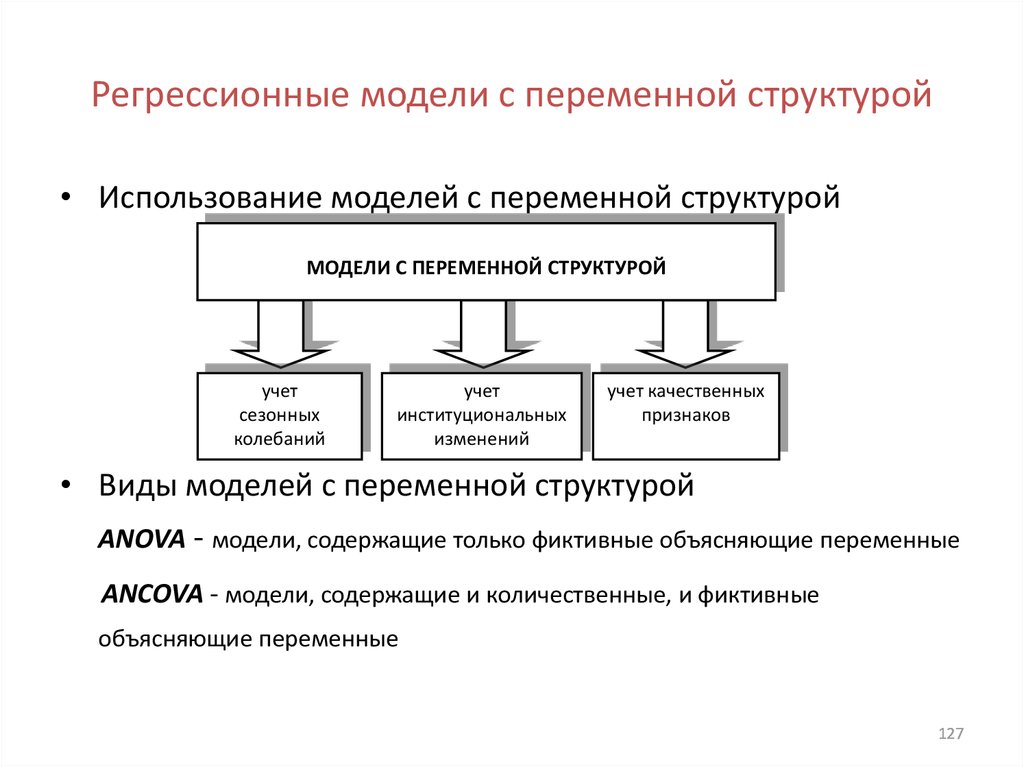
• Использование моделей с переменной структуройМОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
учет
сезонных
колебаний
учет
институциональных
изменений
учет качественных
признаков
• Виды моделей с переменной структурой
ANOVA - модели, содержащие только фиктивные объясняющие переменные
ANCOVA - модели, содержащие и количественные, и фиктивные
объясняющие переменные
127
128.
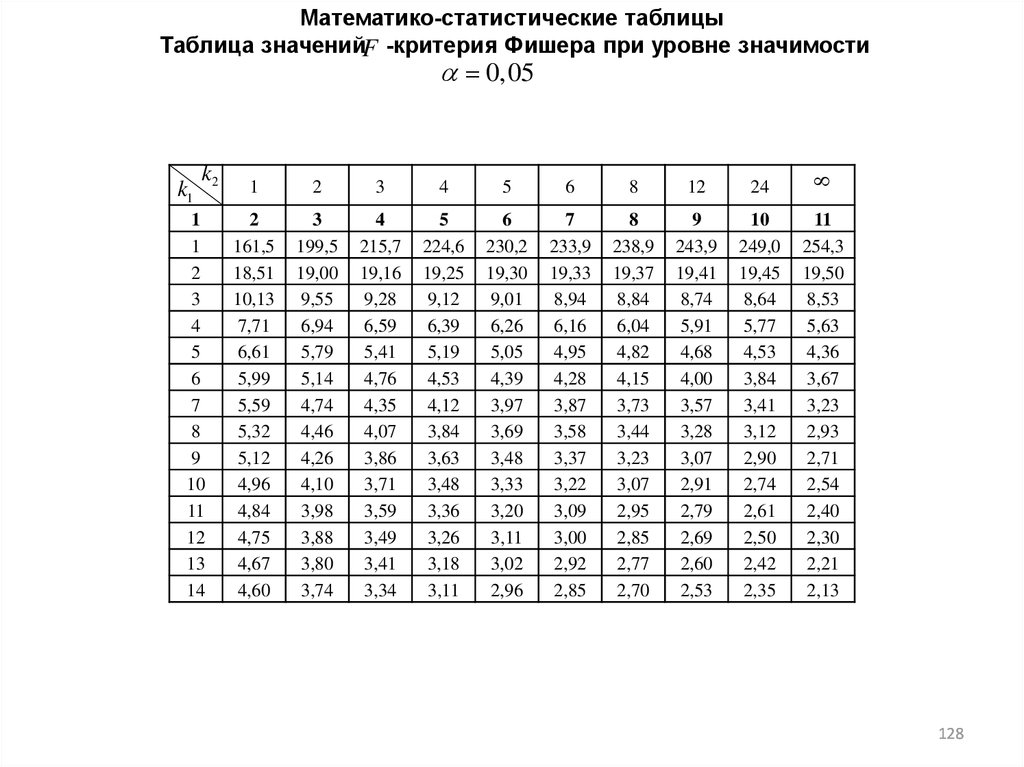
Математико-статистические таблицыТаблица значенийF -критерия Фишера при уровне значимости
0,05
k1
k2
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
8
12
24
2
161,5
18,51
10,13
7,71
6,61
5,99
5,59
5,32
5,12
4,96
4,84
4,75
4,67
4,60
3
199,5
19,00
9,55
6,94
5,79
5,14
4,74
4,46
4,26
4,10
3,98
3,88
3,80
3,74
4
215,7
19,16
9,28
6,59
5,41
4,76
4,35
4,07
3,86
3,71
3,59
3,49
3,41
3,34
5
224,6
19,25
9,12
6,39
5,19
4,53
4,12
3,84
3,63
3,48
3,36
3,26
3,18
3,11
6
230,2
19,30
9,01
6,26
5,05
4,39
3,97
3,69
3,48
3,33
3,20
3,11
3,02
2,96
7
233,9
19,33
8,94
6,16
4,95
4,28
3,87
3,58
3,37
3,22
3,09
3,00
2,92
2,85
8
238,9
19,37
8,84
6,04
4,82
4,15
3,73
3,44
3,23
3,07
2,95
2,85
2,77
2,70
9
243,9
19,41
8,74
5,91
4,68
4,00
3,57
3,28
3,07
2,91
2,79
2,69
2,60
2,53
10
249,0
19,45
8,64
5,77
4,53
3,84
3,41
3,12
2,90
2,74
2,61
2,50
2,42
2,35
11
254,3
19,50
8,53
5,63
4,36
3,67
3,23
2,93
2,71
2,54
2,40
2,30
2,21
2,13
128
129.
Критические значенияt
-критерия
Стьюдента при уровне значимости 0,10, 0,05, 0,01 (двухсторонний)
Число
степене
й
свободы
d.f.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
00,10
0,05
0,01
6,3138
2,9200
2,3534
2,1318
2,0150
1,9432
1,8946
1,8595
1,8331
1,8125
1,7959
1,7823
1,7709
1,7613
1,7530
1,7459
1,7396
12,706
4,3027
3,1825
2,7764
2,5706
2,4469
2,3646
2,3060
2,2622
2,2281
2,2010
2,1788
2,1604
2,1448
2,1315
2,1199
2,1098
63,657
9,9248
5,8409
4,5041
4,0321
3,7074
3,4995
3,3554
3,2498
3,1693
3,1058
3,0545
3,0123
2,9768
2,9467
2,9208
2,8982
Число
степене
й
свободы
d.f.
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
00,10
0,05
0,01
1,7341
1,7291
1,7247
1,7207
1,7171
1,7139
1,7109
1,7081
1,7056
1,7033
1,7011
1,6991
1,6973
1,6839
1,6707
1,6577
1,6449
2,1009
2,0930
2,0860
2,0796
2,0739
2,0687
2,0639
2,0595
2,0555
2,0518
2,0484
2,0452
2,0423
2,0211
2,0003
1,9799
1,9600
2,8784
2,8609
2,8453
2,8314
2,8188
2,8073
2,7969
2,7874
2,7787
2,7707
2,7633
2,7564
2,7500
2,7045
2,6603
2,6174
2,5758
129
130. Задание по эконометрике для студентов заочного отделения Института экономики отраслей, бизнеса и администрирования
Проведите эконометрическое исследование1. Поиск статистических данных по выбранной Вами тематике.
Минимальный объем выборки составляет 7 периодов для одного
объекта исследования или, соответственно, 7 объектов анализа для
одного периода исследования (например, 1 год). Обязательно
отобразить статистические данные в домашней контрольной работе, а
также источник информации. (сайт, литература и т.д.)
2. 2. Разработка эконометрической модели с минимум 2 факторами
(регрессорами) и определение параметров в Excel. Отразить
результаты в печатном виде.
3. Ваши выводы по оценке качества построенной модели: а) уравнение
регрессии; б) коэффициент детерминации; в) статистическая
значимость коэффициента детерминации; г) статистическая значимость
каждого коэффициента уравнения.
130

































































































 mathematics
mathematics economics
economics








