Similar presentations:
Эконометрика. Методы исследования в эконометрике
1.
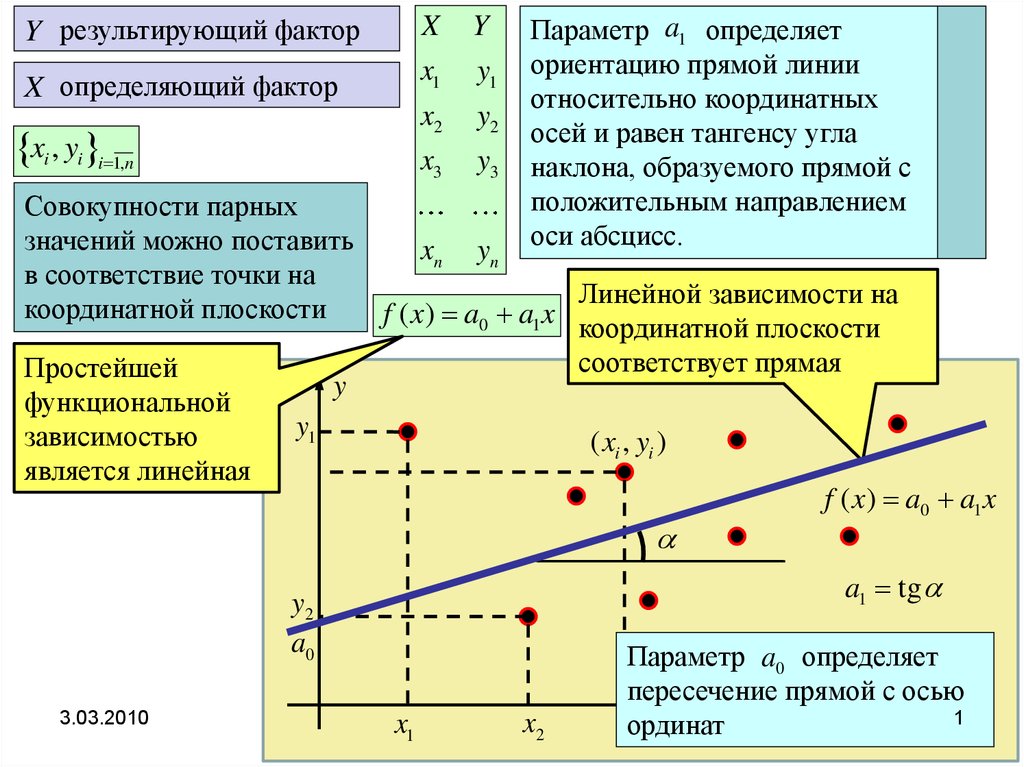
Y результирующий факторX
Y
X определяющий фактор
x1
y1
xi , yi i 1,n
x2
y2
x3
y3
xn
yn
Совокупности парных
значений можно поставить
в соответствие точки на
координатной плоскости
Простейшей
функциональной
зависимостью
является линейная
y
a1 определяет
Параметр
Задача
эконометрики:
для исследуемых
ориентацию
прямой
факторов
линии по
имеющимся для
относительно
координатных
них данным
построить
осей
и равен
и оценить
тангенсу угла
функциональную
наклона,
образуемого
зависимость
прямой с
положительным направлением
y f ( x)
оси абсцисс.
Линейной зависимости на
f ( x) a0 a1 x координатной плоскости
соответствует прямая
y1
( xi , yi )
a1 tg
y2
a0
3.03.2010
f ( x) a0 a1 x
x1
Р. Мунипов
x
2
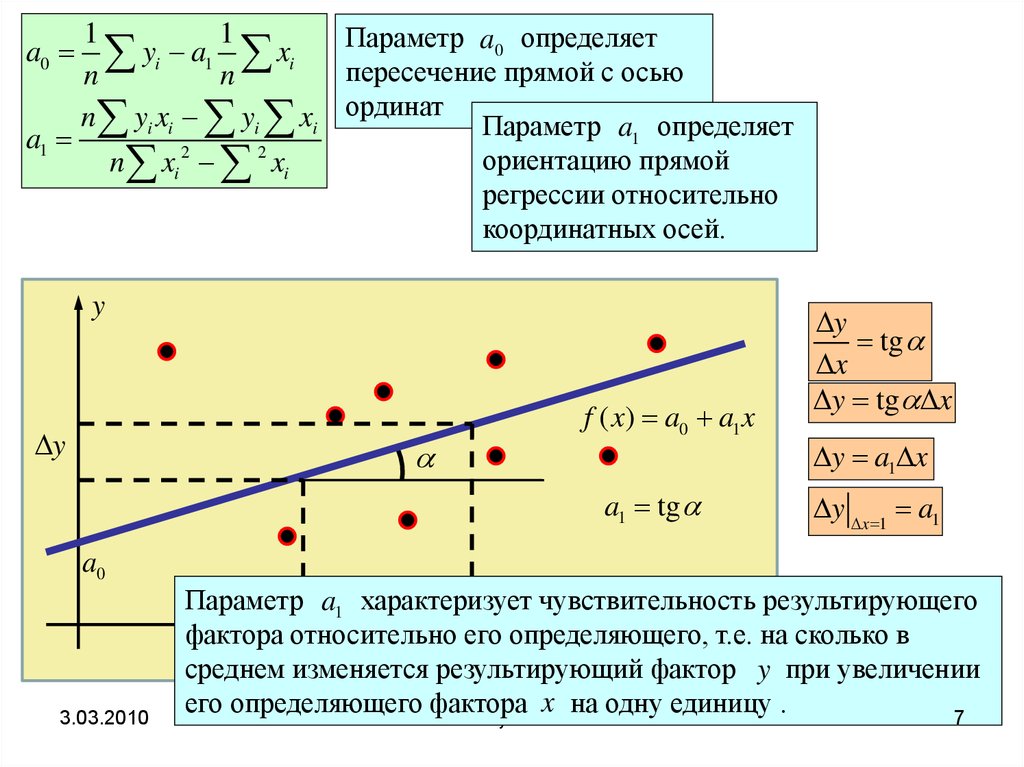
Параметр a0 определяет
x
пересечение прямой с осью
1
ординат
2.
Очевидно, прямая должнапроходить к данным точкам на
наименьшем удалении от них.
Такую прямую можно найти
изменяя её параметры a0 и a1
e1 y1 (a0 a1 x1 )
e2 y2 (a0 a1 x2 )
Изменение параметра a0
влечёт параллельный перенос
прямой относительно её
исходного положения
Отклонения
точек от
прямой
Изменение параметра a1
изменяет ориентацию прямой
линии относительно
координатных осей
ei yi (a0 a1 xi )
f ( x) a0 a1 x
y
en yn (a0 a1 xn )
y1
( xi , yi )
ei
e1
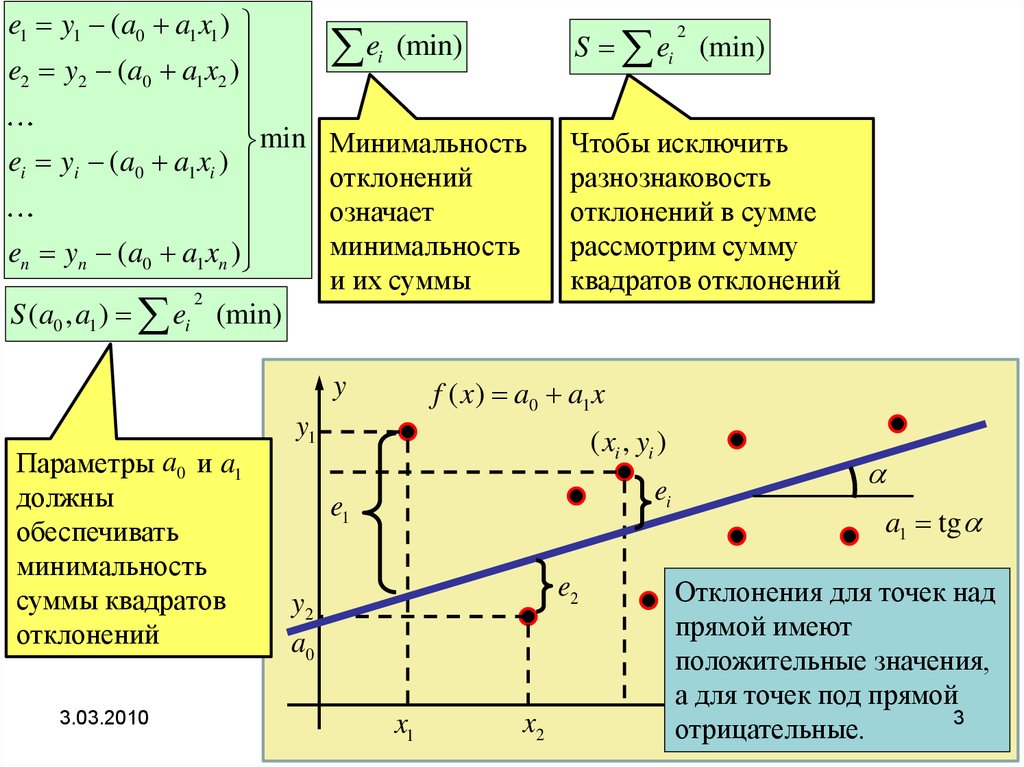
Параметры a0 и a1
должны
обеспечивать
минимальность
отклонений
3.03.2010
e2
y2
a0
x1
Р. Мунипов
x
2
a1 tg
Требование – прямая должна
проходить к данным точкам на
наименьшем удалении от них
x
означает, что отклонения
2
должны быть минимальными.
3.
e1 y1 (a0 a1 x1 )e2 y2 (a0 a1 x2 )
min
ei yi (a0 a1 xi )
en yn (a0 a1 xn )
S (a0 , a1 ) ei (min)
2
ei (min)
S ei (min)
Минимальность
отклонений
означает
минимальность
и их суммы
Чтобы исключить
разнознаковость
отклонений в сумме
рассмотрим сумму
квадратов отклонений
2
f ( x) a0 a1 x
y
y1
Параметры a0 и a1
должны
обеспечивать
минимальность
суммы квадратов
отклонений
3.03.2010
( xi , yi )
ei
e1
e2
y2
a0
x1
Р. Мунипов
x
2
a1 tg
Отклонения для точек над
прямой имеют
положительные значения,
x
а для точек под прямой
3
отрицательные.
4.
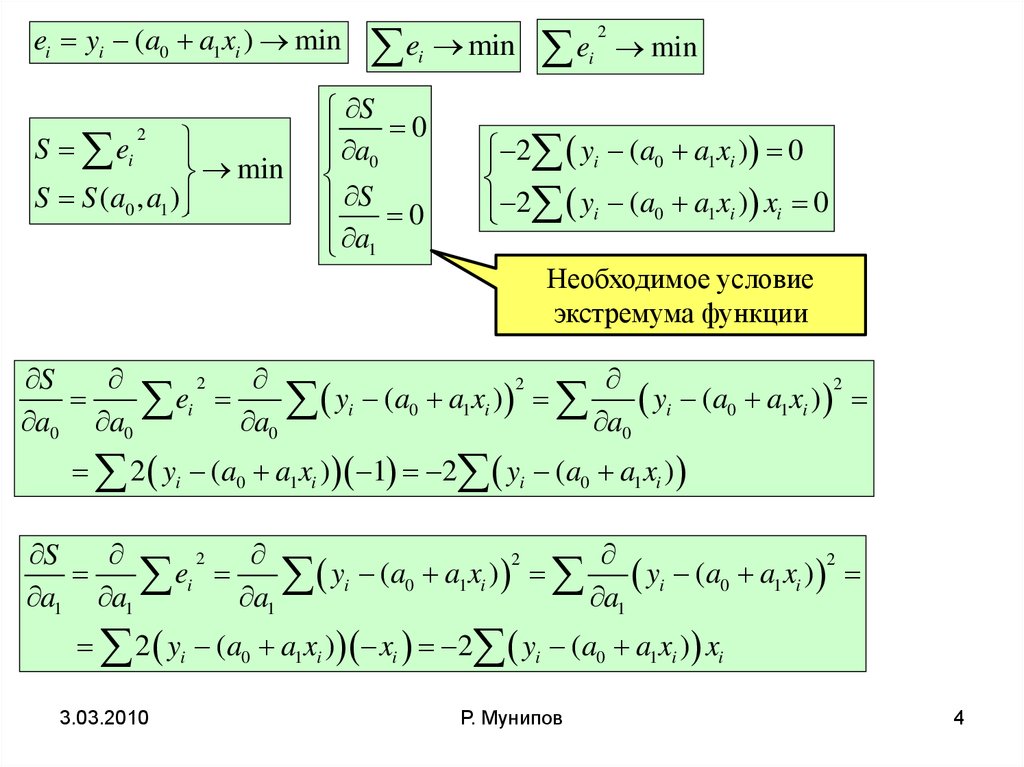
ei yi (a0 a1 xi ) minS ei
min
S S (a0 , a1 )
2
ei min
S
a 0
0
S 0
a1
e
i
2
min
2 yi (a0 a1 xi ) 0
2 yi (a0 a1 xi ) xi 0
Необходимое условие
экстремума функции
2
S
2
2
e
y
(
a
a
x
)
y
(
a
a
x
)
i 0 1i i 0 1i
i
a0 a0
a0
a0
2 yi (a0 a1 xi ) 1 2 yi (a0 a1 xi )
2
S
2
2
e
y
(
a
a
x
)
y
(
a
a
x
)
i
i
0
1 i
i
0
1 i
a1 a1
a1
a1
2 yi (a0 a1 xi ) xi 2 yi (a0 a1 xi ) xi
3.03.2010
Р. Мунипов
4
5.
yi (a0 a1 xi ) 0yi (a0 a1 xi ) xi 0
y (a
i
0
yi na0 a1 xi 0
2
yi xi a0 xi a1 xi 0
a1 xi ) y1 a0 a1 x1
y2 a0 a1 x2
y3 a0 a1 x3
yn a0 a1 xn
yi na0 a1 xi
na0
a0 xi
a1 xi
a1 xi 2
yi
yi xi
2
y
(
a
a
x
)
x
y
x
a
x
a
x
i 0 1i i 11 01 11
y2 x2 a0 x2 a1 x2 2
y3 x3 a0 x3 a1 x32
yn xn a0 xn a1 xn 2
yi xi a0 xi a1 xi 2
3.03.2010
Р. Мунипов
5
6.
a1 xina0
a0 xi
yi
yi xi
a1 xi 2
Система уравнений
определения параметров
линейной регрессии
Линейная регрессия есть прямая
на координатной плоскости,
проходящая на наименьшем
удалении от заданных точек.
na0 yi a1 xi
1
1
a0 yi a1 xi
n
n
1
1
2
y
a
x
i 1 i xi a1 xi yi xi
n
n
y a x x a n x
i
1
i
i
1
2
i
n yi xi
y x a x a n x n y x
a n x x n y x y x
n y x y x
a
n x x
2
i
i
1
2
1
2
i
1
i
Выражения для параметров
линейной регрессии
i i
2
i
i
i i
1
2
i
3.03.2010
i i
i
2
i
i
i
i
Р. Мунипов
1
1
a0 yi a1 xi
n
n
n yi xi yi xi
a1
n xi 2 2 xi
6
7.
11
Параметр a0 определяет
a0 yi a1 xi
пересечение прямой с осью
n
n
n yi xi yi xi ординат Параметр a определяет
1
a1
2
2
ориентацию прямой
n xi xi
регрессии относительно
координатных осей.
y
y
f ( x) a0 a1 x
a1 tg
a0
3.03.2010
y
tg
x
y tg x
y a1 x
y x 1 a1
x
x
Параметр a1 характеризует
чувствительность
результирующего
фактора относительно его определяющего, т.е. на сколько в
среднем изменяется результирующий фактор y при увеличении
x на одну единицу .
его определяющего фактора
Р. Мунипов
7
8.
11
a0 yi a1 xi
n
n
a0 y a1 x
f ( x) y a1 x a1 x
f ( x) y a1 ( x x )
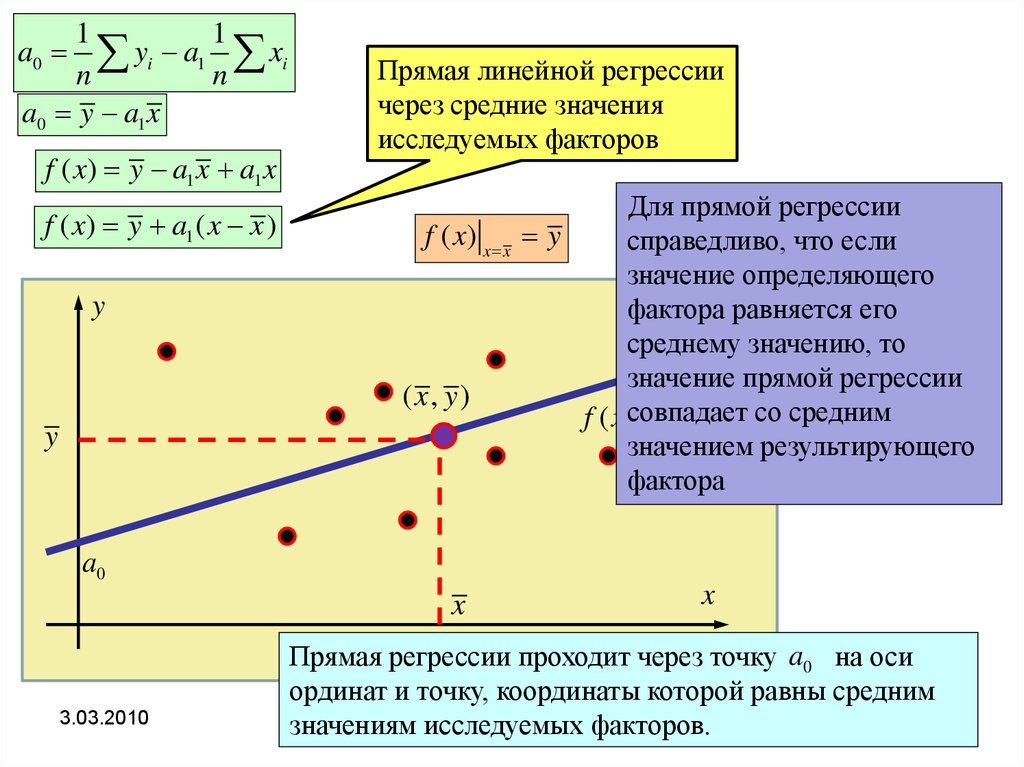
Прямая линейной регрессии
через средние значения
исследуемых факторов
f ( x) x x
y
(x, y)
y
a0
x
3.03.2010
Для прямой регрессии
y
справедливо, что если
значение определяющего
фактора равняется его
среднему значению, то
значение прямой регрессии
f ( x)совпадает
a0 a1 xсо средним
значением результирующего
фактора
x
Прямая регрессии проходит через точку a0 на оси
ординат и точку, координаты которой равны средним
Р. Мунипов факторов.
значениям исследуемых
8
9.
S (a0 , a1 ) ei (min)2
a0
a1 xi
na0
a0 xi
yi
yi xi
a1
a1 xi 2
1
1
y
a
xi
i
1
n
n
n yi xi yi xi
n xi 2 2 xi
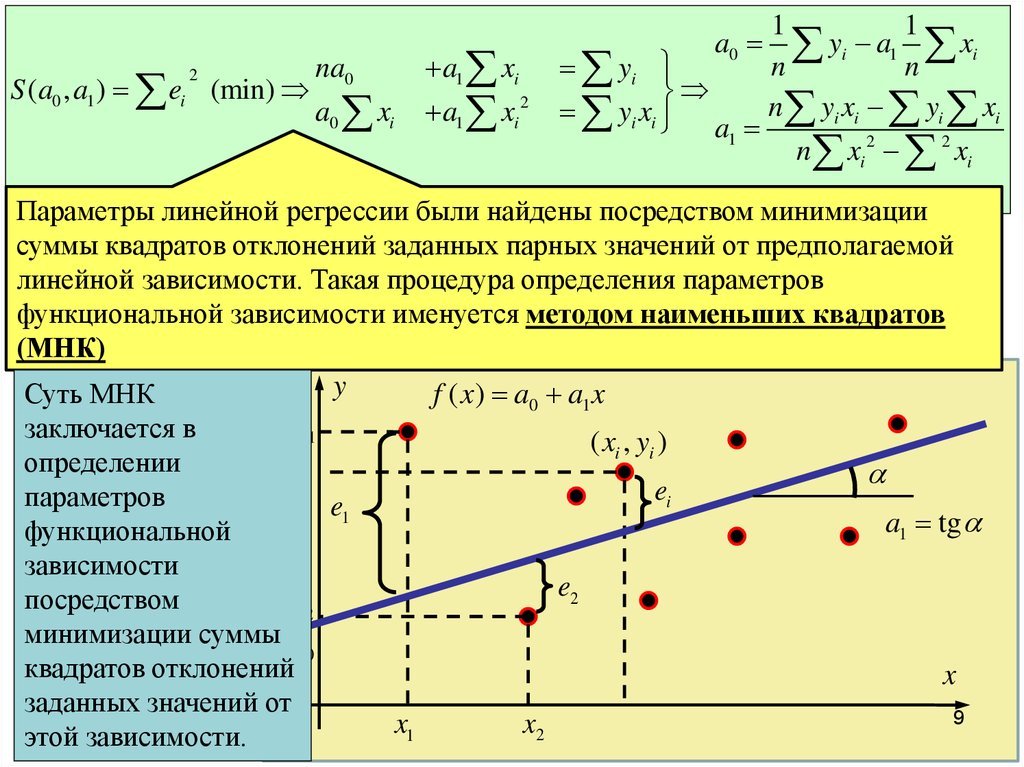
Параметры линейной регрессии были найдены посредством минимизации
суммы квадратов отклонений заданных парных значений от предполагаемой
линейной зависимости. Такая процедура определения параметров
функциональной зависимости именуется методом наименьших квадратов
(МНК)
y
Суть МНК
y1
заключается в
определении
параметров
e1
функциональной
зависимости
посредством
y2
минимизации суммы a
0
квадратов отклонений
заданных
значений от
3.03.2010
этой зависимости.
f ( x) a0 a1 x
( xi , yi )
ei
a1 tg
e2
x
x1
Р. Мунипов
x
2
9
10.
xi , yi i 1,nf ( x) a0 a1x
na0
ei yi (a0 a1xi ) a0 xi
a1 xi
a1 xi 2
yi
yi xi
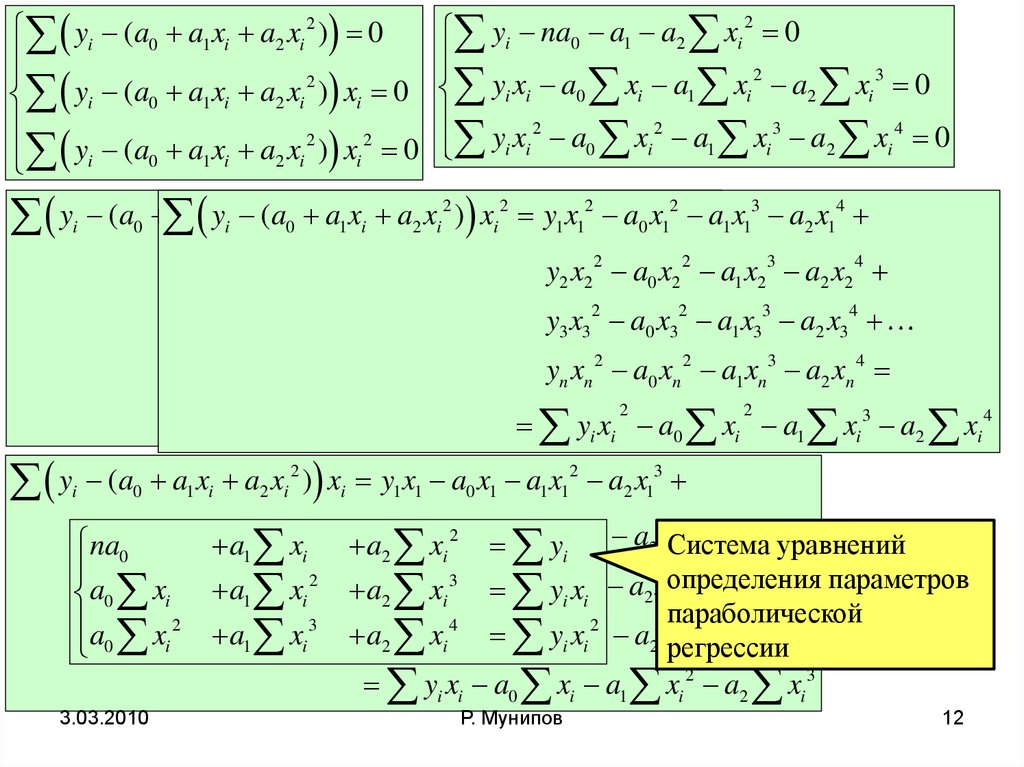
Для заданных парных значений можно
найти линейную зависимость наименее
отличающуюся от этих данных
f ( x) a0 a1 x
Может оказаться, что лучшей линий
наиболее приближенной к данным
значениям будет кривая, в качестве
которой можно взять параболическую
кривую – параболическую регрессию
y
ei yi (a0 a1xi a2 xi 2 ) min
x
f ( x) a0 a1x a2 x 2
3.03.2010
S ei
min
S S (a0 , a1 , a2 )
Р. Мунипов
2
10
11.
SНеобходимое
S yi (a0 a1 xi a2 xi )
0
min a
условие
0
S S (a0 , a1 , a2 )
экстремума
S
0
функции
2 yi (a0 a1 xi a2 xi 2 ) 0
a1
S
2
2 yi (a0 a1 xi a2 xi ) xi 0
0
a2
2
2
2 yi (a0 a1 xi a2 xi ) xi 0
S
2 2
2 2
yi (a0 a1 xi a2 xi )
yi (a0 a1xi a2 xi )
a0 a0
a0
2
2
2 yi (a0 a1 xi a2 xi 2 ) 1 2 yi (a0 a1 xi a2 xi 2 )
S
2 2
2 2
yi (a0 a1 xi a2 xi )
yi (a0 a1xi a2 xi )
a1 a1
a1
2 yi (a0 a1 xi a2 xi 2 ) xi 2 yi (a0 a1xi a2 xi 2 ) xi
S
2 2
2 2
y
(
a
a
x
a
x
)
y
(
a
a
x
a
x
i
0
1 i
2 i
i
0
1 i
2 i )
a2 a2
a2
2 yi (a0 a1 xi a2 xi 2 ) xi 2 2 yi (a0 a1 xi a2 xi 2 ) xi 2
3.03.2010
Р. Мунипов
11
12.
yi (a0 a1 xi a2 xi 2 ) 02
yi (a0 a1 xi a2 xi ) xi 0
2
2
yi (a0 a1 xi a2 xi ) xi 0
yi na0 a1 a2 xi 2 0
2
3
yi xi a0 xi a1 xi a2 xi 0
2
2
3
4
y
x
a
x
a
x
a
x
i i
0 i
1 i
2 i 0
y (a a x y a(ax ) a xy aa x )a x
i
0
1 i i
2
2 i0
2
1 i1
20 i
2
1 i1
ay21xx1122 a0 x12 a1x13 a2 x14
y2 a0 a1 x2 ay2 x2 2
a0 x2 2 a1 x23 a2 x2 4
y3 a0 a1 x3 ay23 x32
a0 x32 a1 x33 a2 x34
yn a0 a1 xn yan2 xn 2 a0 xn 2 a1 xn 3 a2 xn 4
2
2
3
4
yi na0 a 1 xyii x i 2a2
a0 x
i xi a1 xi a2 xi
y (a
i
2
2
3
a
x
a
x
)
x
y
x
a
x
a
x
a
x
0
1 i
2 i
i
1 1
0 1
1 1
2 1
na0
a0 xi
2
a
x
0 i
3.03.2010
a1 xi
a1 xi 2
a1 xi 3
2
3
2 a x a x
y
x
a
x
2 x
2
0 2 y1 2
2 Система
2
уравнений
a2
i
i
3
параметров
y3 x3xi 3 a0 x3
ay1ix3i 2 a2 xопределения
a2
3
параболической
4
22
3
a2
yn xxn i a0 xn
ay1i xin a2 xрегрессии
n
yi xi a0 xi a1 xi 2 a2 xi 3
Р. Мунипов
12
13.
f ( x) a0 a1 xna0
a0 xi
a1 xi
a1 xi
2
yi
yi xi
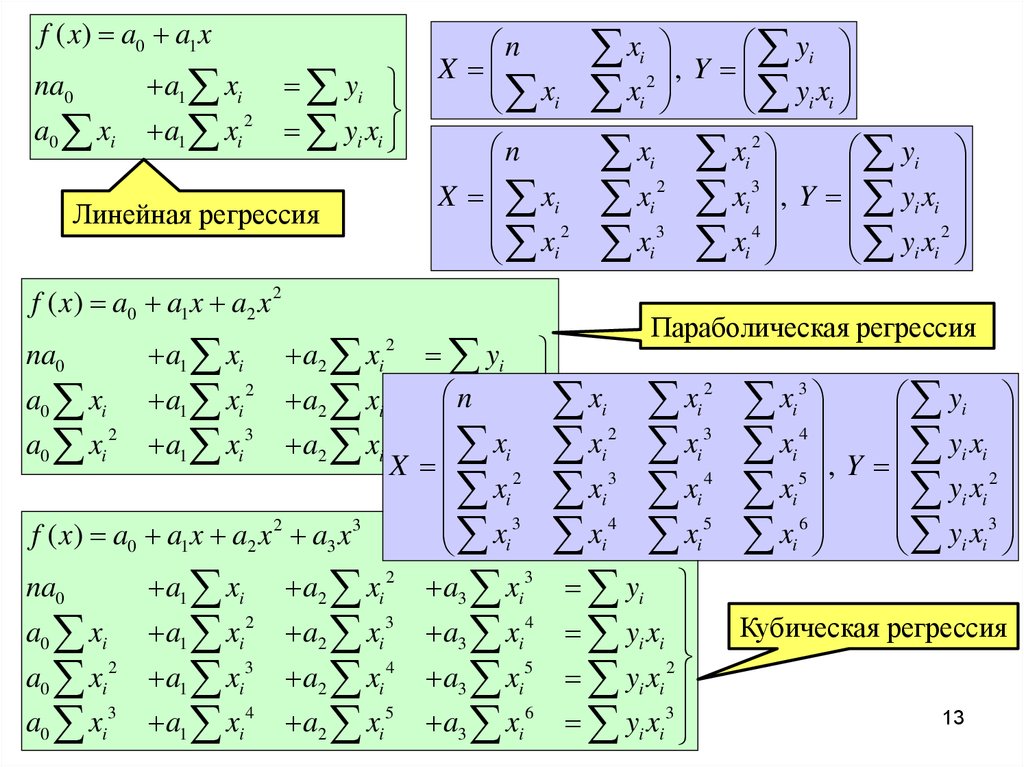
Линейная регрессия
f ( x) a0 a1 x a2 x 2
a2 xi
n
X xi
xi 2
x , Y y
y x
x
y
x x
x
x
,
Y
y x
y x
x x
i
i
2
i
i i
2
i
i
2
i
3
i
3
i
i
i
4
i
i
i
2
i
Параболическая регрессия
yi
yi
n yi xi xi xi 2 xi 3
a0 xi a1 xi 2 a2 xi 3
2
3
4
2
y
x
x
x
x
x
a0 xi 2 a1 xi 3 a2 xi 4
y
x
i i i i i i , Y i i
X
xi 2 xi 3 xi 4 xi 5
yi xi 2
3
3
4
5
6
2
3
y
x
x
x
x
x
f ( x) a0 a1 x a2 x a3 x
i
i
i
i
i
i
na0
a1 xi a2 xi 2 a3 xi 3 yi
Кубическая регрессия
a0 xi a1 xi 2 a2 xi 3 a3 xi 4 yi xi
a0 xi 2 a1 xi 3 a2 xi 4 a3 xi 5 yi xi 2
3.03.2010
Мунипов
13
a0
xi 3 a1 xi 4 a2 xi 5 a3Р.
xi 6 yi xi 3
na0
a1 xi
n
X
xi
2
14.
f ( x) a0 a1 x a2 x2
n
a1 xi
i 1
a0 xi
i 1
i 1
n
k
a1 xi
n
xi
X xi 2
xk
3.03.2010
i
4
i 1
k 1
i 1
x
x
x
a2 xi
n
a2 xi
i 1
i
x
x
x
2
i
2
i
3
k 1
x
i
n
ak xi k 1
n
ak xi k 2
i 1
k 2
n
ak xi 2 k
i 1
Полиномиальная
регрессия
yi
yi xi
yi xi 2
k
yi xi
yi
k 1
y
x
i
i i
2
k 2
,
Y
y
x
ii
i
k
2k
y
x
x
Р.
Мунипов
i
i i
x
x
x
k
i
3
i
i
ak xi k
i 1
n
3
i 1
n
a0 xi
a1 xi
a2 xi
3
i 1
n
2
n
i 1
n
2
i 1
n
2
i 1
n
a0 xi
j 0
a2 xi
i 1
n
ak x a j x j
n
a1 xi
na0
k
k
4
i
k 2
x
i
14
15.
Наибольшую практическую значимость в прикладном эконометрическоманализе имеет линейная регрессия. Регрессии второго (параболическая),
третьего (кубическая) и более высокого порядков менее применимы в силу
значительного роста степеней.
Вместе с тем, все регрессии преобразуют дискретно заданные значения в
непрерывную зависимость. Однако, линейная регрессия устанавливает
постоянный средний темп роста результирующего фактора относительного
определяющего, параболическая регрессия устанавливает переменный
линейный темп роста, но постоянные его темп изменения, кубическая –
переменный нелинейный темп роста и линейный его темп изменения.
Регрессии четвертого и более высоких порядков в прикладном
эконометрическом анализе почти не применяются в силу отсутствия должной
экономической интерпретации.
3.03.2010
Р. Мунипов
15
16.
xi , yi i 1,nf ( x) a0 a1
1
f ( x) a0 a1
x
1
x
1
ei yi a0 a1
xi
1
a1
xi
na0
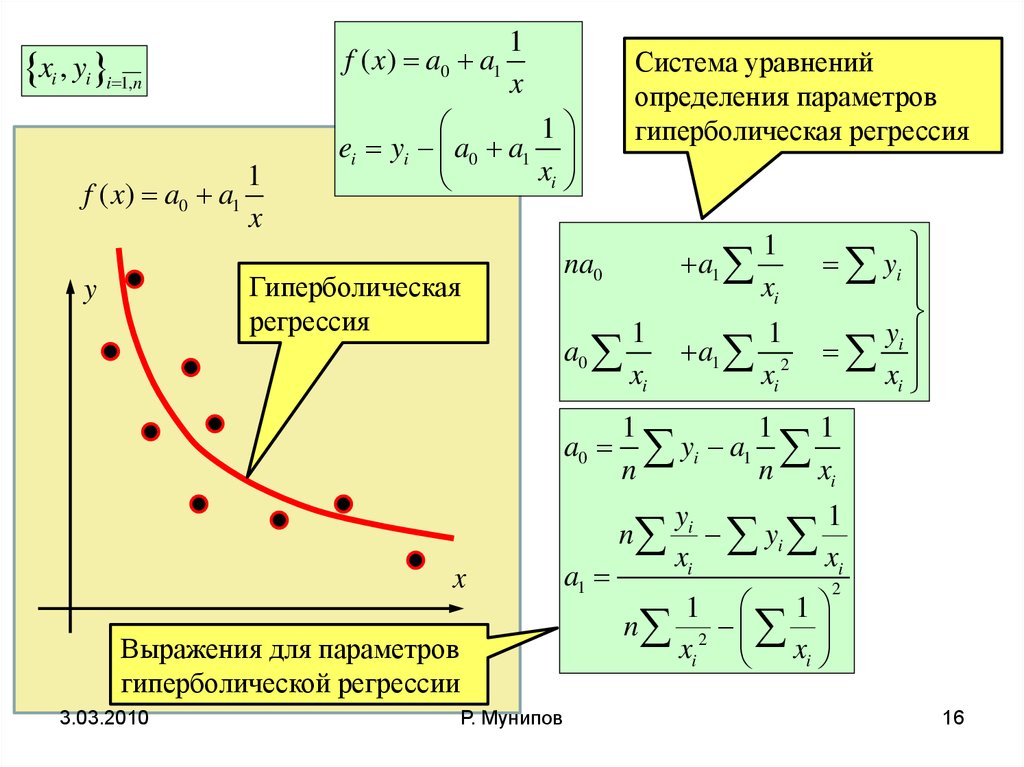
Гиперболическая
регрессия
y
Система уравнений
определения параметров
гиперболическая регрессия
a0
1
xi
a1
1
xi 2
yi
yi
xi
1
1
1
a0 yi a1
n
n xi
x
Выражения для параметров
гиперболической регрессии
3.03.2010
Р. Мунипов
a1
n
yi
1
yi
xi
xi
1 1
n 2
xi xi
2
16
17.
YX (1)
X (2)
X (k )
y1
x1(1)
x1(2)
x1( k )
y2
x2 (1)
x2 (2)
x2 ( k )
y3
x3(1)
x3(2)
x3( k )
yn
xn (1)
xn (2)
xn ( k )
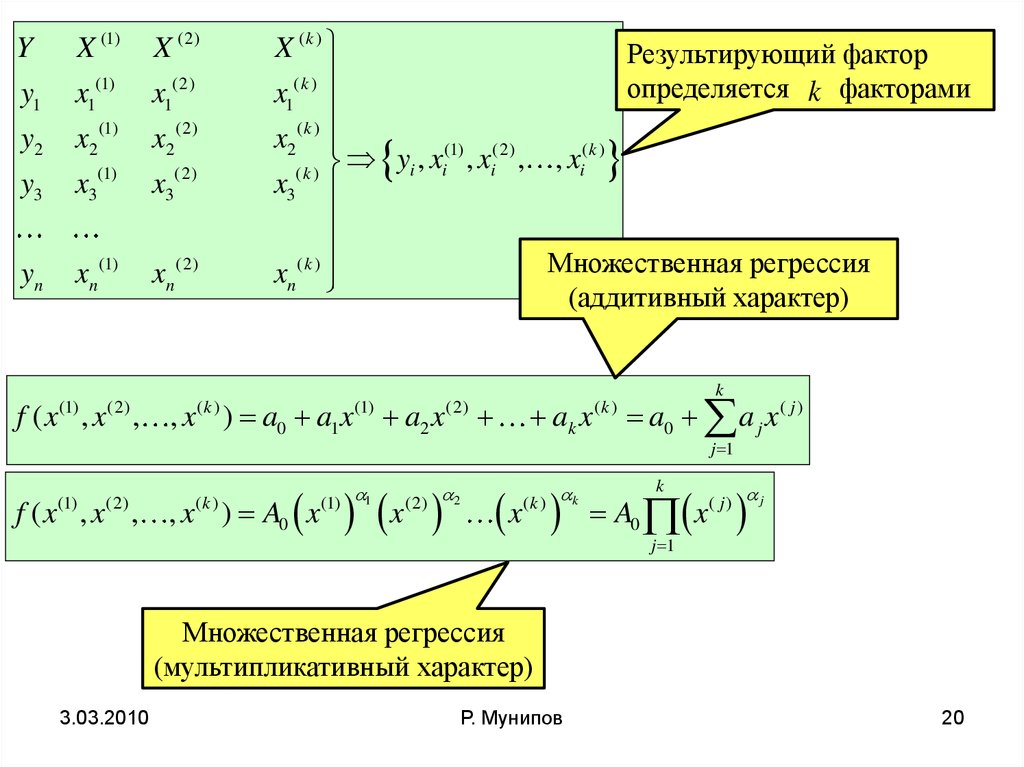
Результирующий фактор
определяется k факторами
Множественная регрессия
f ( x , x , , x ) a0 a1x a2 x
(1)
(2)
(k )
(1)
ei yi a0 a1 xi a2 xi
(1)
(2)
(2)
ak xi
(k )
ak x
k
(k )
a0 a j x ( j )
j 1
k
( j)
yi a0 a j xi
j 1
Отклонения в множественной регрессии
3.03.2010
Р. Мунипов
17
18.
kf ( x Параметры
, x , , x a) множественной
a0 a1 x a2 x регрессии
ak xопределяют
a0 a j x ( j )
j
j 1
чувствительность результирующего фактора относительно
n
n
n
n
(1)
(2)
(k )
соответствующего
определяющего.
Этот
параметр
показывает
на
na0
a xi
a2 xi
ak xi
yi
сколько в 1среднем
изменяется
результирующий
фактор
при
i 1
i 1
i 1
i 1
n увеличенииn определяющегоn на одну единицу, при
n условии, чтоn
(1)
(1) (1)
(1) (2)
(1) ( k )
(1)
a0 другие
xi
факторы
a1 xi постоянные.
xi
a2 xi xi
ak xi xi
yi xi
i 1
i 1
i 1
i 1
i 1
n
n
n
n
n
a0 xi (2) a1 xi (2) xi (1) a2 xi (2) xi (2) ak xi (2) xi ( k ) yi xi (2)
i 1
i 1
i 1
i 1
i 1
n
n
n
n
(1)
(2)
(k )
n
x
x
x
y
i
i
i
in
n
n
n
n
i 1
i 1
i 1
i 1
(k )
( k ) (1)
( k ) (2)
( k ) ( k )
a0 xin
a1
xi
n a2 xi xi
n ak xi xi n yi x i ( k )
n xi
(1)
(1) (1)
(1)
(2)
(1) (ik )1
(1)
i 1
i
1
i
1
i
1
x
x
x
x
x
x
x
y
x
i
i
i
i
i
i
i
i i
i 1
i 1
i 1
i 1
i 1
n
n
n
n
n
X
(2)
(2) (1)
(2) (2)
(2) ( k ) , Y
(2)
xi xi
xi xi
xi xi
xi
yi xi
i 1
i 1
i 1
i 1
i 1
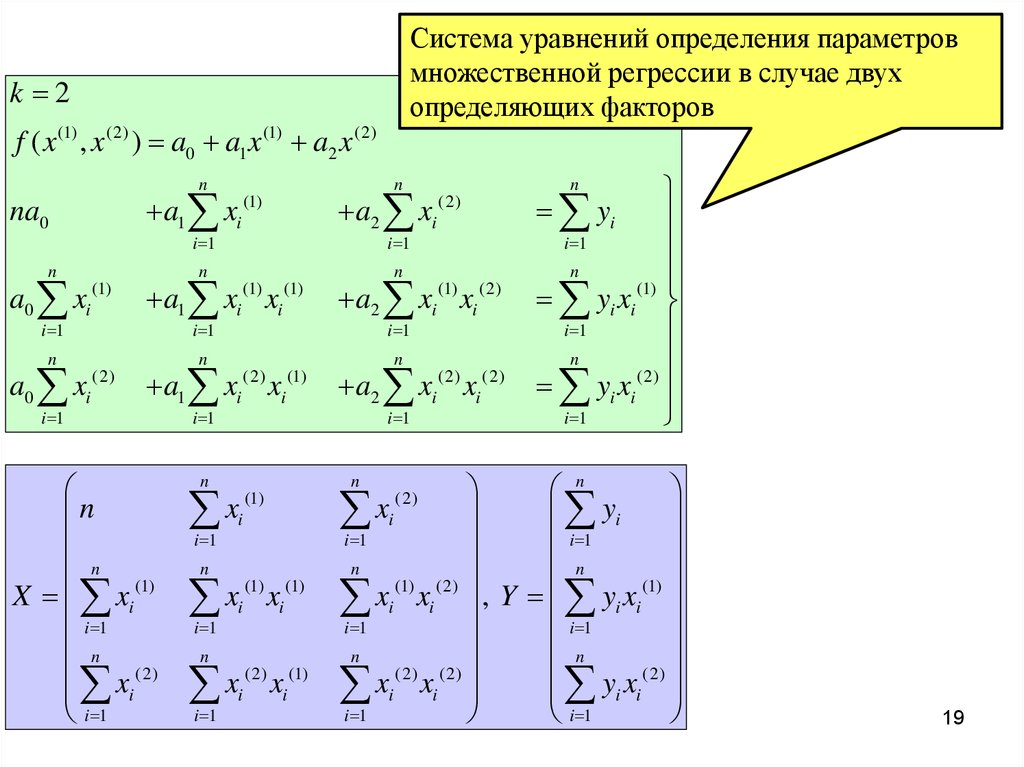
определения
Система уравнений
параметров множественной
регрессии
n
n
n
n
n
( k ) (1)
( k ) (2)
(k ) (k )
x (k )
y x (k )
x
x
x
x
x
x
i
i
i
i
i
i
i
i i
3.03.2010
Р. Мунипов
18
i 1
i 1
i 1
i 1
i 1
(1)
(2)
(k )
(1)
(2)
(k )
19.
Система уравнений определения параметровмножественной регрессии в случае двух
определяющих факторов
k 2
f ( x (1) , x (2) ) a0 a1 x (1) a2 x (2)
n
a1 xi
na0
n
(1)
i 1
n
i 1
a1 xi xi
(1)
a1 xi xi
n
n (1)
X xi
i 1
n (2)
xi
i 1
3.03.2010
(2)
n
(1)
i 1
n
x
i 1
(1) (1)
x
i xi
i 1
n
i 1
i 1
n
x
y
i
i
i 1
i 1
n
n
(1) (2)
(1)
xi xi , Y yi xi
i 1
i 1
n
n
(2) (2)
(2)
xi xi
yi xi
i 1
i 1
Р. Мунипов
(2)
n
i
a2 xi (2) xi (2)
yi
n
(1)
i
x
a2 xi (1) xi (2)
i 1
n
(2)
i 1
n
(1)
yi xi
i 1
n
(2)
yi xi
i 1
n
(2)
i 1
n
(1)
i 1
a0 xi
a2 xi
i 1
n
a0 xi
n
(1)
(2)
xi (1)
19
20.
YX (1)
X (2)
y1
x1(1)
x1(2)
y2
x2 (1)
x2 (2)
y3
x3(1)
x3(2)
yn
xn (1)
xn (2)
X (k )
Результирующий фактор
определяется k факторами
x1( k )
x2 ( k )
(1)
(2)
(k )
y
,
x
,
x
,
,
x
i
i
i
i
(k )
x3
(k )
Множественная регрессия
xn
(аддитивный характер)
f ( x , x , , x ) a0 a1x a2 x
(1)
(2)
(k )
f ( x , x , , x ) A0 x
(1)
(2)
(k )
(1)
x
(1) 1
(2)
(2) 2
ak x
x
( k ) k
k
(k )
a0 a j x ( j )
j 1
A0 x
k
j 1
( j) j
Множественная регрессия
(мультипликативный характер)
3.03.2010
Р. Мунипов
20
21.
f A0 xx
(1) 1
ln f ln A0 x
x
(2) 2
(1) 1
ln f ln A0 ln x
x
(k ) k
(2) 2
(1) 1
x
ln x
Параметры A0 и j неизвестны
( k ) k
(2) 2
ln x
ln f ln A0 1 ln x (1) 2 ln x (2)
k
ln x
( k ) k
Есть множественная регрессия
аддитивного характера
относительно неизвестных
величин ln A0 , 1 , 2 , , k
3.03.2010
Р. Мунипов
По свойству логарифмов,
логарифм произведения
равен сумме логарифмов
(k )
По свойству логарифмов,
степень в логарифме есть
сомножитель перед
логарифмом
21
22.
n1 ln xi
n 0
n
2 ln xi
(1)
i 1
y f (x , x ,
(1)
n
0 ln xi
1 ln xi ln xi
(1)
i 1
1 ln xi ln xi
(2)
i 1
3.03.2010
0 ln A0 ,
1 ln xi
i 1
A0 e 0
2 ln xi (1) ln xi (2)
n
(1)
2 ln xi (2) ln xi (2)
i 1
n
(k )
n
(k )
x
( k ) k
i 1
i 1
n
(2) 2
n
(1)
n
(2)
x
(1) 1
i 1
n
0 ln xi
, x ) A0 x
(k )
n
(1)
i 1
0 ln xi
(2)
i 1
ln xi
(1)
2 ln xi ( k ) ln xi (2)
i 1
Р. Мунипов
i 1
n
ln yi
i 1
n
k ln xi (1) ln xi ( k )
i 1
n
(1)
ln yi ln xi
i 1
n
k ln xi (2) ln xi ( k )
i 1
n
ln yi ln xi (2)
i 1
n
(k )
(k )
k ln xi ln xi
i 1
n
22
ln yi ln xi ( k )
i 1
(2)
n
k ln xi ( k )
23.
Столбец свободных членовn
в системе уравнений
ln yi
i 1
n
Матрица коэффициентов при
(1)
ln yi ln xi
неизвестных в системе уравнений
i 1
определения параметров
n
Y
(2)
множественной регрессии
ln
y
ln
x
i
i
мультипликативного характера
i 1
n
n
n
n
ln y ln x ( k )
(1)
(2)
(k )
i
in
ln
x
ln
x
ln
x
i
i
i
i 1
i 1
i 1
i 1
n
n
n
n
(1)
(1)
(1)
(1)
(2)
(1)
(k )
ln
x
ln
x
ln
x
ln
x
ln
x
ln
x
ln
x
i
i
i
i
i
i
i
i 1
i 1
i 1
i 1
n
n
n
n
X
(2)
(2)
(1)
(2)
(2)
(2)
(k)
ln xi ln xi
ln xi ln xi
ln xi ln xi
ln xi
i 1
i 1
i 1
i 1
n
n
n
n
(k )
(1)
(k )
(2)
(k )
(k )
ln x ( k )
ln
x
ln
x
ln
x
ln
x
ln
x
ln
x
i
i
i
i
i
i
i
3.03.2010
Р.
Мунипов
23
i 1
i 1
i 1
i 1
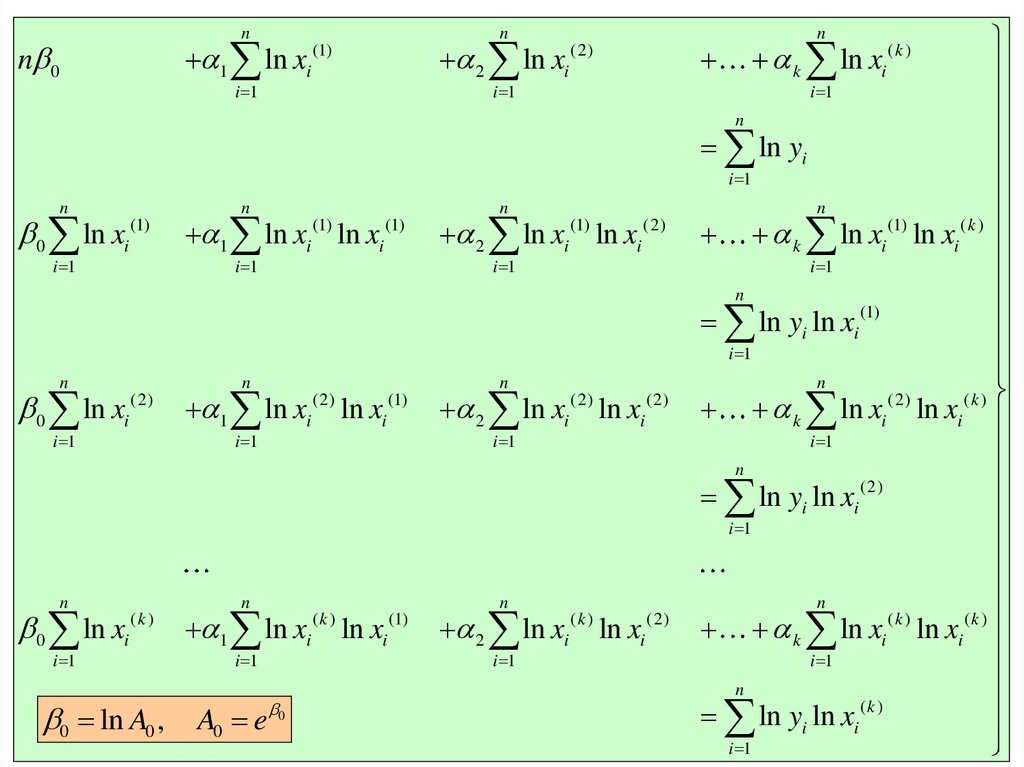
24.
k 2y f ( x , x ) A0 x
(1)
(2)
x
(1) 1
(2) 2
n
1 ln xi
n 0
n
2 ln xi
(1)
i 1
n
0 ln xi
i 1
1 ln xi ln xi
(1)
n
(1)
i 1
n
0 ln xi
i 1
n
(1)
i 1
1 ln xi ln xi
(2)
i 1
2 ln xi (1) ln xi (2)
i 1
n
(2)
n
(1)
2 ln xi (2) ln xi (2)
i 1
i 1
n
ln yi ln xi (1)
i 1
n
(2)
ln yi ln xi
i 1
n
(2)
ln yi
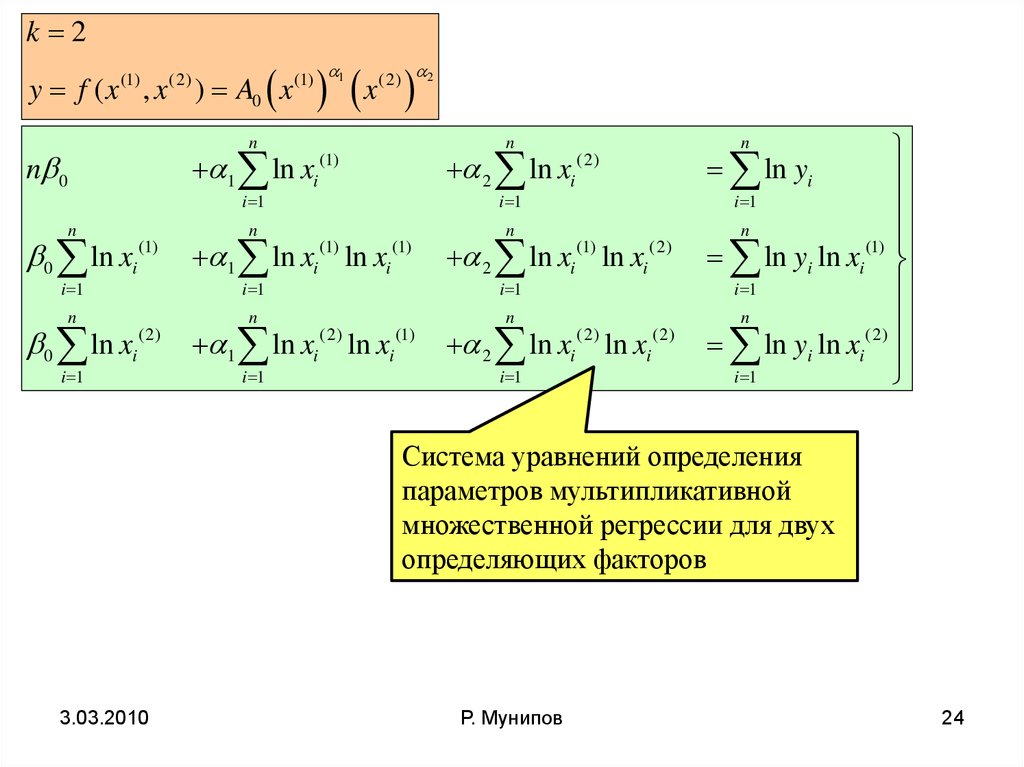
Система уравнений определения
параметров мультипликативной
множественной регрессии для двух
определяющих факторов
3.03.2010
Р. Мунипов
24
25.
В математической экономике рассматривается производственная функция,определяющая зависимость производимой продукции от факторов её
обеспечивающих.
Рассмотрим мультипликативную производственную функцию от двух
факторов, основных фондов K и трудовых затрат L
Y AK 1 L 2
где Y есть выпуск продукции, параметр A – коэффициент приведения или
коэффициент технической оснащенности экономики, 1 , 2 коэффициенты
эластичности по фондам и труду соответственно, которые показывают на
сколько в среднем процентов увеличится выпуск продукции при увеличении
соответствующего фактора производства на один процент. Можно показать,
что коэффициенты эластичности удовлетворяют неравенствам,
0 1 1
0 2 1
3.03.2010
Р. Мунипов
25
26.
Типы экономик1 2
2 1
Экономика называется трудосберегающей, когда
эластичность по фондам больше эластичности по труду.
Суть такой экономики в том, что наибольшую значимость
для прироста выпуска продукции имеют фонды
Экономика называется фондосберегающей, когда
эластичность по труду больше эластичности по фондам.
Суть такой экономики в том, что наибольшую значимость
для прироста выпуска продукции имеет труд
Экономика называется прогрессивной: увеличение факторов
1 2 1 производства на один процент влечёт увеличение выпуска
продукции более чем на один процент
1 2 1
Экономика называется регрессивной: увеличение факторов
производства на один процент влечёт увеличение выпуска
продукции менее чем на один процент
1 2 1
Экономика называется экономикой Дугласа-Коба:
увеличение факторов производства на один процент влечёт
увеличение выпуска продукции на один процент
3.03.2010
Р. Мунипов
26
27.
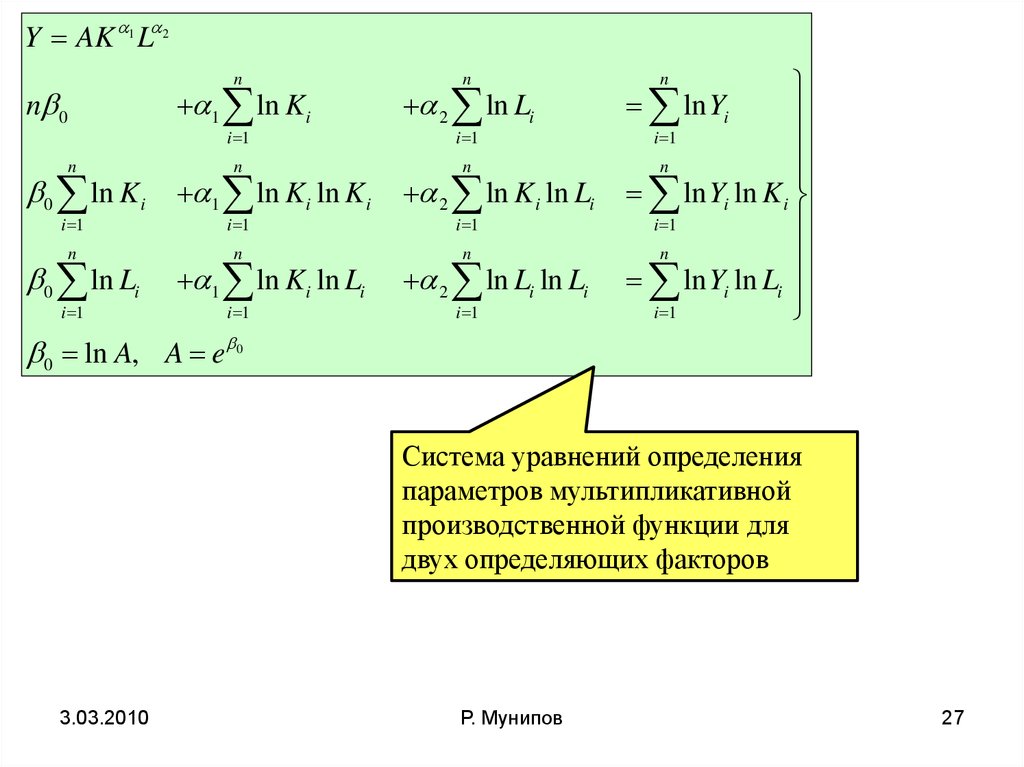
Y AK 1 L 2n
1 ln K i
n 0
i 1
n
0 ln K i
i 1
n
0 ln Li
i 1
n
1 ln K i ln K i
i 1
n
1 ln K i ln Li
i 1
0 ln A, A e
n
2 ln Li
i 1
n
2 ln K i ln Li
i 1
n
2 ln Li ln Li
i 1
i 1
n
ln Yi ln K i
i 1
n
ln Yi ln Li
i 1
n
ln Yi
0
Система уравнений определения
параметров мультипликативной
производственной функции для
двух определяющих факторов
3.03.2010
Р. Мунипов
27
28.
xi i 1,nx
( )
n1
xi ( ) n1 x
( ) ( )
i 1
x
( )
n2
xi
i 1
( )
n2 x
n1
x
i 1
i
n1
x
Среднее значение – есть величина,
сумма расстояний которой на
числовой оси до заданных значений
справа и слева от неё одинакова
n1
( ) ( xi ( ) x )
i 1
( )
n2
( xi ( ) x )
i 1
n1 n2 n
3.03.2010
i 1
x
Сумма расстояний для точек
справа от среднего, таких
точек n1
Сумма расстояний для точек
слева от среднего, таких
точек n2
Р. Мунипов
( )
i
n1
i 1
( )
i
n2 ( )
n1 x xi n2 x
i 1
n2
n1 x xi ( ) n2 x
i 1
( )
n2
xi ( ) n1 n2 x
i 1
x nx
i
1
x xi
n
Определяющее
выражение для среднего
(средне арифметического)
28
29.
1x xi
n
x
x x C
xi i 1,n
i
i
1
1
x xi
x xi
n
n
i 1, n
1
1
1
xi xi C ( x1 C
n
n
n
x2 C
x3 C
1
1
xn C ) ( xi nC ) xi C x C
n
n
Для среднего справедливо: если к элементам
совокупности прибавить одну и ту же величину, то
среднее значение увеличится на эту же величину.
xi i 1,n
1
x xi
n
3.03.2010
x x C
i
i
i 1,n
x x C
Р. Мунипов
29
30.
xxi i 1,n
*
i
xi x
i 1,n
1
1
x xi
x * xi*
n
n
1
1
1
*
*
x xi xi x ( x1 x
n
n
n
x2 x
x3 x
1
1
xn x ) ( xi nx ) xi x x x 0
n
n
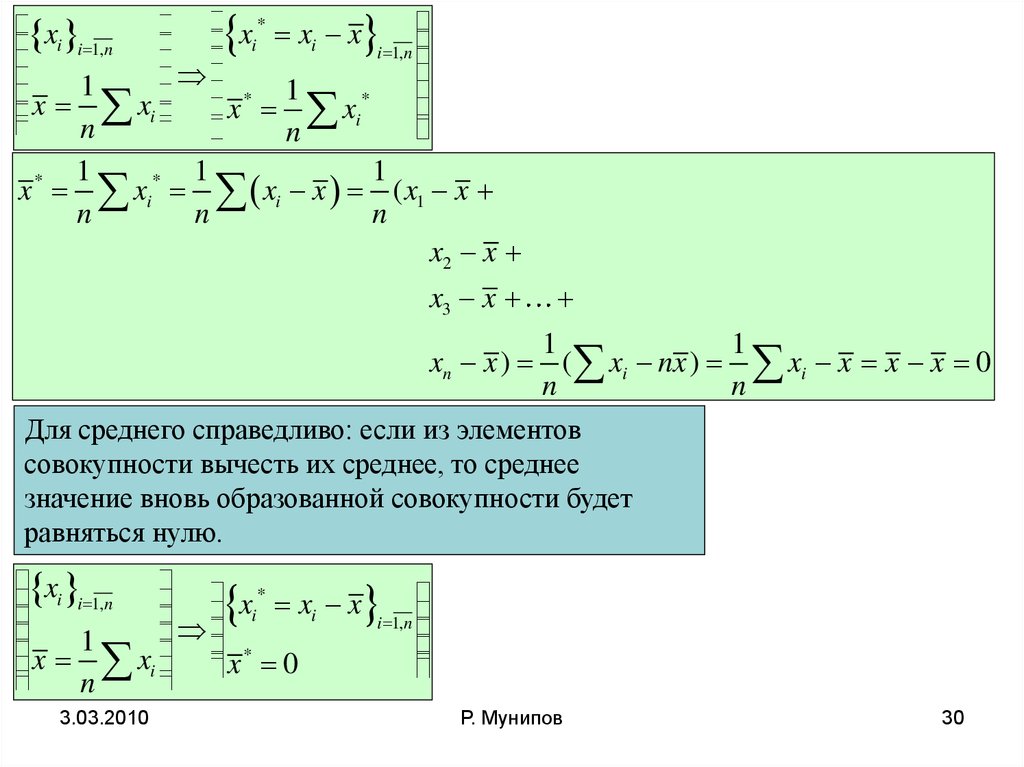
Для среднего справедливо: если из элементов
совокупности вычесть их среднее, то среднее
значение вновь образованной совокупности будет
равняться нулю.
xi i 1,n
x
1
xi
n
3.03.2010
x
i
*
xi x
i 1,n
x* 0
Р. Мунипов
30
31.
xi i 1,n1
x xi
n
ei xi x i 1,n
e x x ( x
i
i
1
Отклонения значений
совокупности от их
среднего значения
x
x2 x
x3 x
xn x ) xi nx xi n
1
xi xi xi 0
n
Для среднего справедливо: сумма отклонений
значений совокупности от их среднего равна нулю.
xi i 1,n
1
x xi
n
ei xi x i 1,n
e 0
i
В силу разно знаковости
отклонений их сумма, для
значений
совокупности слева и
3.03.2010
справа от среднего, равна нулю
x
x
ei
( )
ei
Р. Мунипов
ei
0
( )
( )
ei
0
( )
31
32.
1x xi
n
x
x Cx
xi i 1,n
i
i
i 1,n
1
1
x xi
x xi
n
n
1
1
1
xi Cxi C xi Cx
n
n
n
Для среднего справедливо: если элементы
совокупности умножить на одну и ту же величину, то
среднее значение умножится на эту же величину.
xi i 1,n
1
x xi
n
3.03.2010
x Cx
i
i
i 1,n
x Cx
Р. Мунипов
32
33.
xi
x
(C )
( B)
i
i 1, n1
( A)
x
x
( A)
i
i 1, n2
i 1, n3
1 n2 ( B )
1 n3 (C )
1 n1 ( A)
( B)
(C )
x xi
x xi
xi
n2 i 1
n3 i 1
n1 i 1
x ( A)
x (C )
x ( B)
x
x
n1x ( A) n2 x ( B ) n3 x (C )
x
n1 n2 n3
nj
k
x
n
j 1
wj
x ( j) wj x ( j)
nj
k
n
j 1
j
3.03.2010
j 1
j
k
nj
n j x ( j)
k
n
j 1
k
k
j 1
x
k
1
j 1
j
Выражение для
генеральной средней
через средние значения в
группах
количество групп
количество значений в j группе
x ( j ) среднее значение в j группе
Вес j группыР. Мунипов
33
34.
xi i 1,nxi i 1,n 1
1 n
1 n 1
xn xi
xn 1
xi
n i 1
n 1 i 1
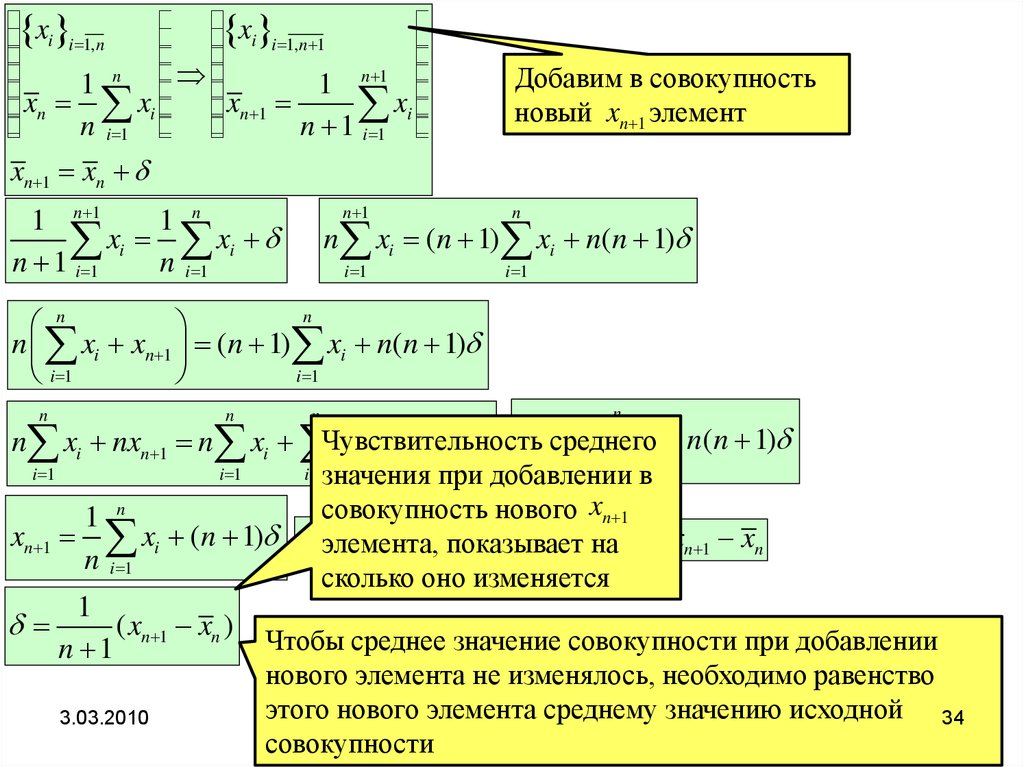
Добавим в совокупность
новый xn 1 элемент
xn 1 xn
1 n 1
1 n
xi xi
n 1 i 1
n i 1
n 1
n
i 1
i 1
n xi (n 1) xi n(n 1)
n
n
n xi xn 1 (n 1) xi n(n 1)
i 1
i 1
n
n
n
n
n xi nxn 1 n xi Чувствительность
xi n(n 1) nxnсреднего
1 xi n( n 1)
i 1 в
i 1
i 1
i 1значения при добавлении
совокупность нового xn 1
1 n
1) (n на
xn 1 xi (n 1) xnэлемента,
1) xn 1 xn
1 xn ( nпоказывает
n i 1
сколько оно изменяется
1
( xn 1 xn )
Чтобы среднее значение совокупности при добавлении
n 1
нового элемента не изменялось, необходимо равенство
этого нового элемента
среднему значению исходной 34
3.03.2010
Р. Мунипов
совокупности
35.
xi i 1,nx
x
ei xi x (min) ei (min)
Var ( x) ei 2 (min)
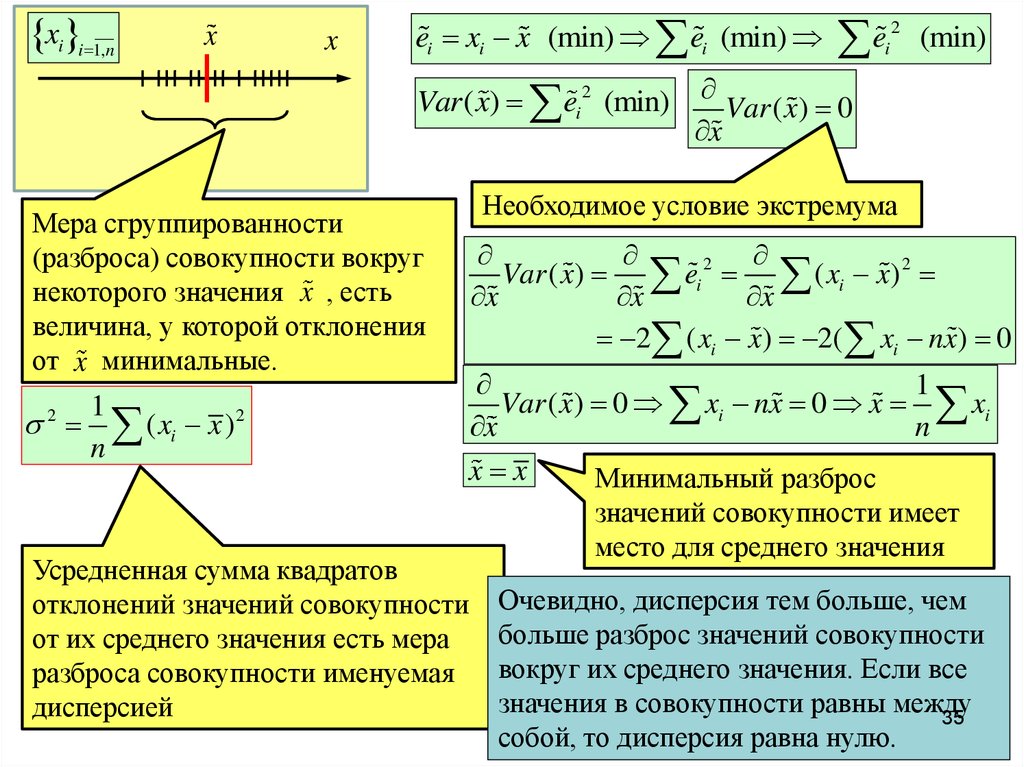
Мера сгруппированности
(разброса) совокупности вокруг
некоторого значения x , есть
величина, у которой отклонения
от x минимальные.
2
1
2
(
x
x
)
i
n
e
2
i
(min)
Var ( x) 0
x
Необходимое условие экстремума
Var ( x) ei 2 ( xi x) 2
x
x
x
2 ( xi x) 2( xi nx) 0
1
Var ( x) 0 xi nx 0 x xi
x
n
x x
Минимальный разброс
значений совокупности имеет
место для среднего значения
Усредненная сумма квадратов
отклонений значений совокупности Очевидно, дисперсия тем больше, чем
больше разброс значений совокупности
от их среднего значения есть мера
вокруг их среднего значения. Если все
разброса совокупности именуемая
значения в совокупности равны между
дисперсией
3.03.2010
Р. Мунипов
35
собой, то дисперсия равна нулю.
36.
x x Cxi i 1,n
1
2 ( xi x )2
n
2
i
i
i 1,n
1
x xi
x x C
n
1
1
2 ( xi x )2
2
2
( xi x )
n
n
1
1
1
2
2
2
2
(
x
x
)
(
x
C
x
C
)
(
x
x
)
i
i
i
n
n
n
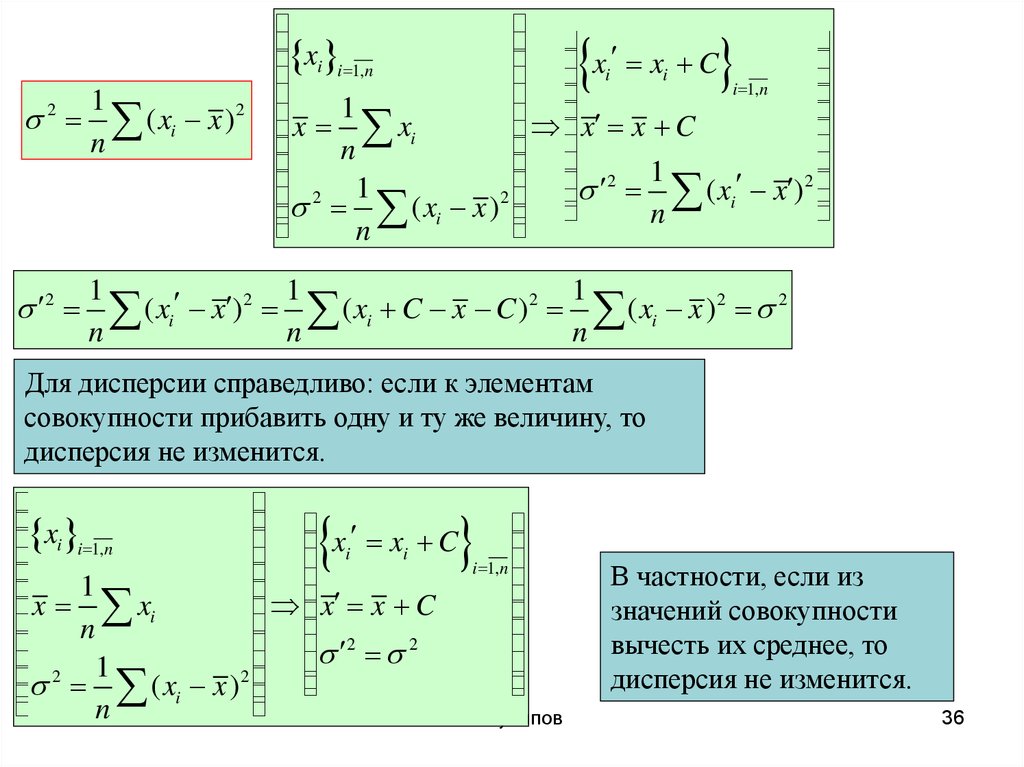
Для дисперсии справедливо: если к элементам
совокупности прибавить одну и ту же величину, то
дисперсия не изменится.
xi i 1,n
x x C
i
i
1
x xi
x x C
n
2
2
1
2
( xi x )2
n
3.03.2010
i 1,n
Р. Мунипов
В частности, если из
значений совокупности
вычесть их среднее, то
дисперсия не изменится.
36
37.
x Cxxi i 1,n
1
2 ( xi x )2
n
2
i
i
i 1,n
1
x xi
x Cx
n
1
1
2 ( xi x ) 2
2
2
( xi x )
n
n
1
1
2
2
2 1
2
2 2
(
x
x
)
(
Cx
Cx
)
C
(
x
x
)
C
i
i
i
n
n
n
Для дисперсии справедливо: если элементы
совокупности умножить на одну и ту же величину, то
дисперсия умножится на квадрат этой величины.
xi i 1,n
xi Cxi
i 1,n
В частности, если значения
совокупности поделить на одну
и ту же величину, то дисперсия
поделится на квадрат этой
величины.
1
xi
x Cx
n
2
2 2
C
1
2
2
( xi x )
n
3.03.2010
Р. Мунипов
x
37
38.
Кореньиз дисперсии,
именуемый
*
xi квадратный
xi xi (СКО),
i 1,n
средне квадратическим
отклонением
i 1,n
1 мера сгруппированности
также
есть
x xi
x* x
совокупности
вокруг среднего значения.
n
1
СКО имеет
соответствующую
1 размерность
*2 ( xi* x * )2
2
2
совокупности
( xi x )
n
размерности
n
1
2 ( xi x )2
n
1
2
2
(
x
x
)
i
n
2
*2
1
1 xi x
1 1
1 2
*
* 2
2
( xi x ) 2 ( xi x ) 2 1
n
n n
Для дисперсии справедливо: если элементы
совокупности поделить на СКО, то дисперсия вновь
образованной совокупности будет равна единице.
xi i 1,n
x
i
*
xi
1
xi
x* x
n
*2
1
1
2
2
( xi x )
n
3.03.2010
i 1,n
x
Р. Мунипов
38
39.
1( xi x )2
n
1
1
1
2 ( xi x ) 2 ( xi 2 x 2 2 xxi ) ( x12 x 2 2 xx1
n
n
n
x2 2 x 2 2 xx2
2
x32 x 2 2 xx3
xn 2 x 2 2 xxn )
1
2
2
x
nx
2 x xi
i
n
2
1
1 2
1
2
x
nx
2
x
xi
i
n
n
n
1
1
2
2
x
x
2
x
x
xi 2 x 2
i
n
n
2
1
1
1
2 xi 2 x 2 xi 2 xi x 2 x 2
n
n
n
3.03.2010
Р. Мунипов
Дисперсию
совокупности можно
исчислить как разность
среднего квадратов и
квадрата среднего
x
i
2
n 2 nx 2
39
40.
xi 1, n1
x ( A)
x
x
(C )
(B)
( A)
i
1 n1 ( A)
xi
n1 i 1
i
x (B)
i
i 1, n2
1 n2 ( B )
xi
n2 i 2
x (C )
i 1, n3
1 n3 ( C )
xi
n3 i 1
n1
n2
n3
i 1
i 1
i 1
( A)2 ( xi ( A) x ( A) ) 2 ( B )2 ( xi ( B ) x ( B ) ) 2 (C )2 ( xi (C ) x ( C ) )2
x ( A)
x (C )
x ( B)
x
( A)2
( B )2
2
x x
1
3
nj
3
( j)
n
x
j
j 1
j 1
(C )2
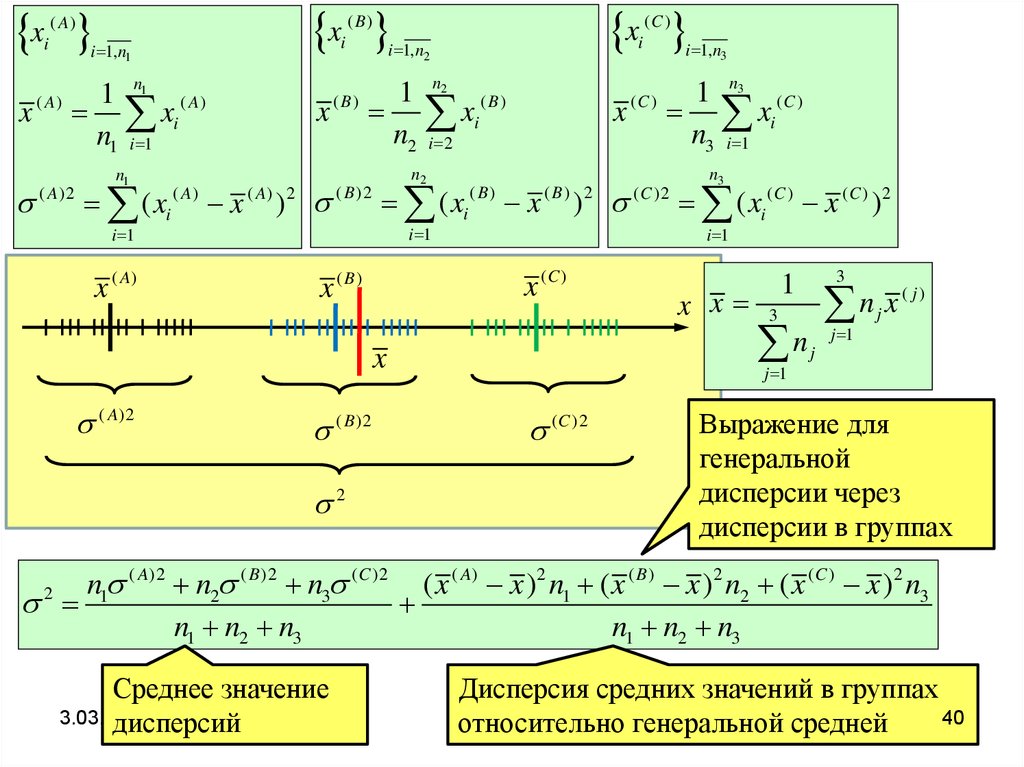
Выражение для
генеральной
дисперсии через
дисперсии в группах
( A)2
( B )2
( C )2
( A)
2
( B)
2
(C )
2
n
n
n
(
x
x
)
n
(
x
x
)
n
(
x
x
)
n3
2
3
1
2
2 1
n1 n2 n3
n1 n2 n3
Среднее значение
3.03.2010
дисперсий
Дисперсия средних значений в группах
Р. Мунипов
40
относительно
генеральной средней
41.
n1 ( A)2 n2 ( B )2 n3 (C )2 ( x ( A) x )2 n1 ( x ( B) x )2 n2 ( x ( C ) x )2 n3n1 n2 n3
n1 n2 n3
2
n
j 1
k
n
j
j 1
j
j 1
j
j
( j)
k
nj
(x
3
n
x )2 n j
( j)
x )2 n j
j 1
k
(x
k
n
( j)
j
1
j 1
n x
k
j 1
( j )2
3
1
j 1
k
1
n
j
k
n
( j )2
j
j 1
1
2
x
n
3
j 1
3
1
2
j 1
j
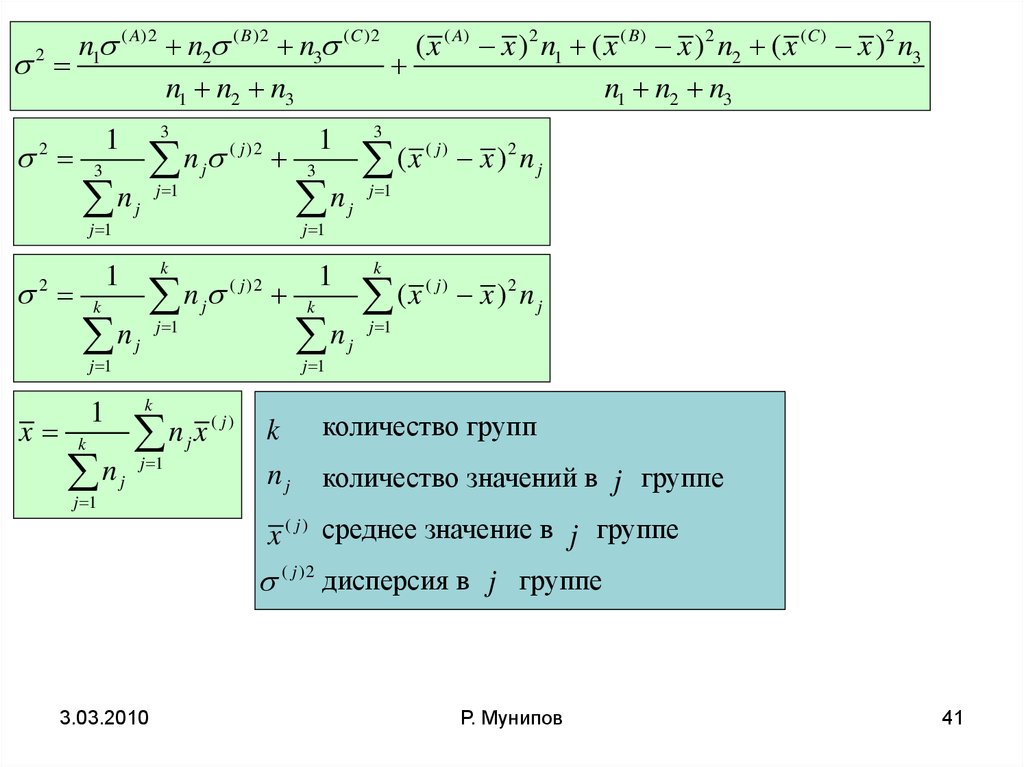
количество групп
количество значений в j группе
x ( j ) среднее значение в j группе
( j )2 дисперсия в j группе
3.03.2010
Р. Мунипов
41
42.
k1
2
n
k
n
j 1
j 1
( j )2
j
j
k
1
(x
k
n
j 1
j 1
k
w j
j 1
wj
nj
j 1
(x
j 1
( j)
Межгрупповая дисперсия есть
дисперсия средних значений в
группах относительно генеральной
средней
2
2
2
x
x ) wj
2
2 внутригрупповая дисперсия
x 2 межгрупповая дисперсия
Вес j группы
k
n
k
( j )2
x )2 n j
j
Внутригрупповая
дисперсия есть среднее
значение дисперсий в
группах
2
( j)
j
Генеральная дисперсия есть
сумма внутригрупповой и
межгрупповой дисперсий
3.03.2010
Р. Мунипов
42
43.
x2
2
n
j 1
x
( j )2
n
j 0
k
j 1
j
k
1
2
(x
k
n
j 1
x2
2
0 2 1
2
k
1
2
2
j 1
( j)
x ) 2 n j 0 ( A)
x
1
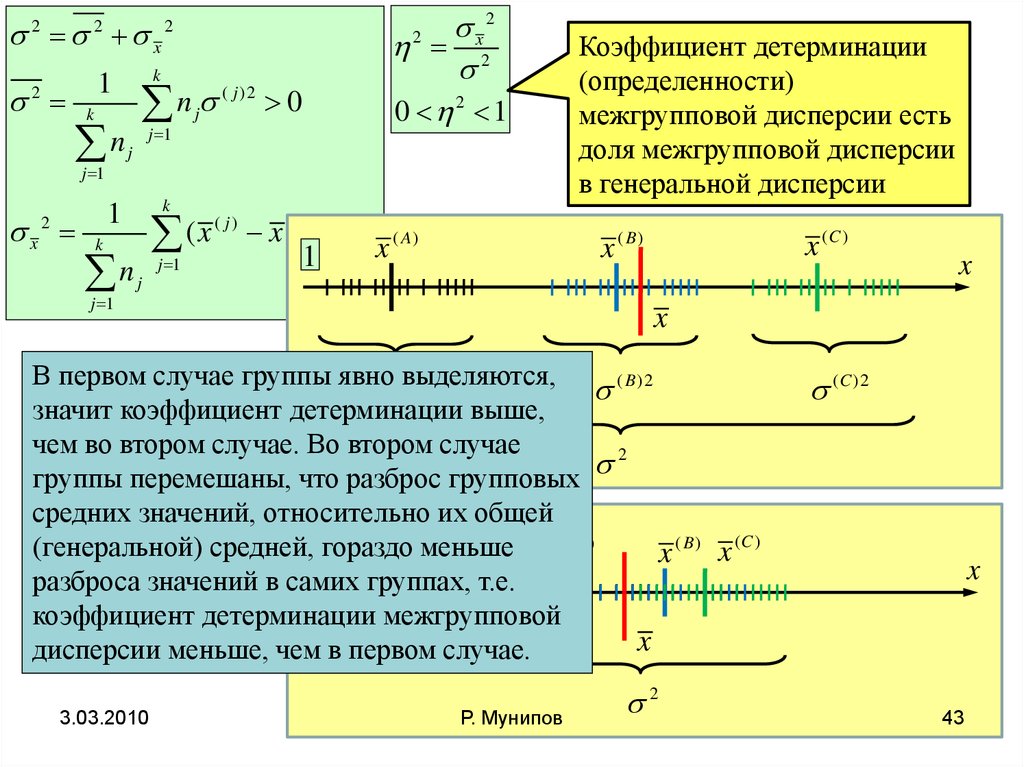
Коэффициент детерминации
(определенности)
межгрупповой дисперсии есть
доля межгрупповой дисперсии
в генеральной дисперсии
x (C )
x ( B)
j
x
В первом случае группы явно
( A)2выделяются, ( B )2
значит коэффициент детерминации выше,
чем во втором случае. Во втором случае
2
группы перемешаны, что разброс групповых
средних значений, относительно их общей
(C )
(генеральной) средней,2 гораздо меньше x ( A)
x ( B) x
разброса значений в самих группах, т.е.
коэффициент детерминации межгрупповой
x
дисперсии меньше, чем в первом случае.
3.03.2010
x
Р. Мунипов
2
(C )2
x
43
44.
xi i 1,nxn
n
1
xi
n i 1
xi i 1,n 1
1 n 1
xn 1
xi
n 1 i 1
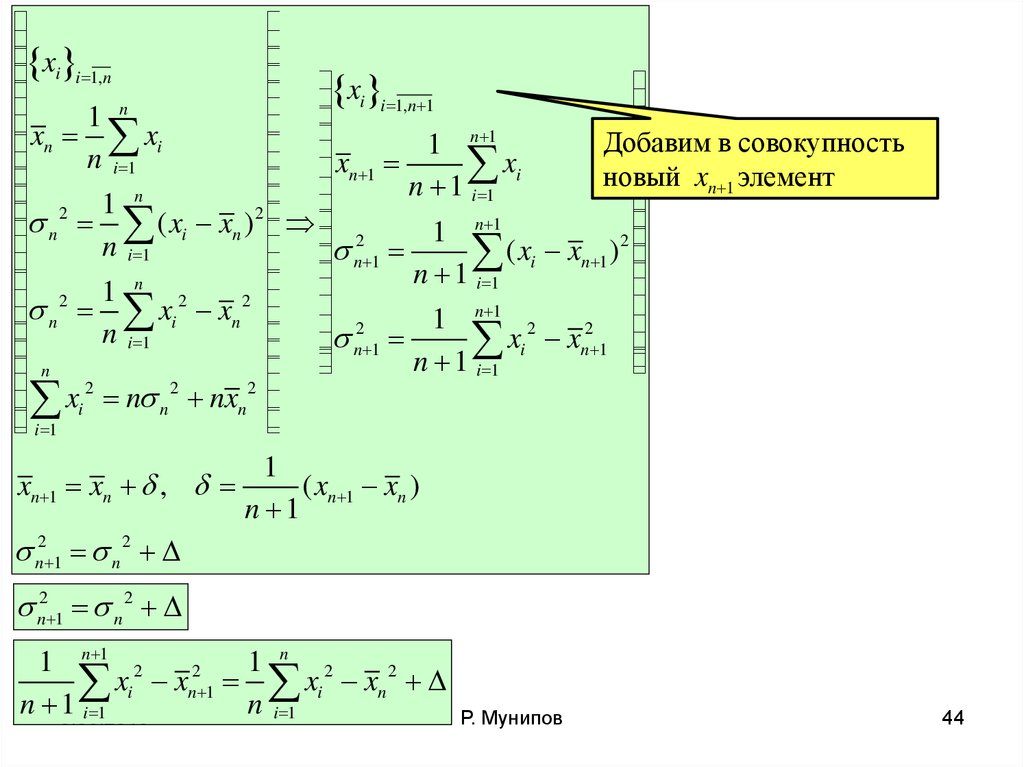
Добавим в совокупность
новый xn 1 элемент
1 n
n 1
n ( xi xn ) 2 2
1
2
n i 1
n 1
(
x
x
)
i n 1
n 1 i 1
n
1
n 1
n 2 xi 2 xn 2
1
2
2
2
n i 1
n 1
x
x
i
n 1
n
1
i 1
n
2
2
2
xi n n nxn
2
i 1
xn 1 xn ,
1
( xn 1 xn )
n 1
n2 1 n 2
n2 1 n 2
1 n 1 2
1 n 2
2
2
x
x
x
x
i
n 1
i
n
n 3.03.2010
1 i 1
n i 1
Р. Мунипов
44
45.
1 n 1 21 n 2
2
2
x
x
x
x
i
n 1
i
n
n 1 i 1
n i 1
n 1
n
n xi n(n 1) x
2
2
n 1
i 1
(n 1) xi 2 n(n 1) xn 2 n(n 1)
i 1
n
n 2
2
2
n xi xn 1 n(n 1) xn 1 (n 1) xi 2 n(n 1) xn 2 n(n 1)
i 1
i 1
n
n xi nx
2
i 1
2
n 1
nx
n
2
n 1
n(n 1) x
n(n 1) nx
n(n 1) nx
2
n 1
2
i 1
i 1
n
2
n 1
2
n 1
n
n xi xi 2 n(n 1) xn 2 n(n 1)
n(n 1) x
2
n 1
xi 2 n(n 1) xn 2 n(n 1)
i 1
n(n 1) x
2
n 1
n
xi 2 n(n 1) xn 2
i 1
xi 2 n(n 1) xn2 1 xn 2
n
i 1
n(n 1) nxn2 1 n n 2 nxn2 n(n 1) xn2 1 xn 2
(n 1)
xn2 1 n 2 xn2 (n 1) xn2 1 Р. Мунипов
xn 2
3.03.2010
45
46.
(n 1) xn2 1 n 2 xn2 (n 1) xn2 1 xn 2(n 1) xn2 1 n 2 xn2 (n 1)( xn 1 xn )( xn 1 xn )
(n 1) xn2 1 n 2 xn2 (n 1) ( 2 xn )
(n 1) x
2
n 1
n
2
1
xn 1 xn
x (n 1)
( xn 1 xn )
2 xn
n 1
n 1
2
n
xn 1 xn
(n 1) x n x ( xn 1 xn )
2 xn
n 1
xn 1 xn 2nxn 2 xn
2
2
2
(n 1) xn 1 n xn ( xn 1 xn )
n 1
xn 1 xn 2nxn
2
2
2
(n 1) xn 1 n xn ( xn 1 xn )
n 1
(n 1) 2 (n 1) xn2 1 (n 1) n 2 (n 1) xn2 ( xn 1 xn ) xn 1 xn 2nxn
2
n 1
2
2
n
(n 1)2 (n 1) xn2 1 (n 1) n 2 (n 1) xn2 ( xn 1 xn )( xn 1 xn ) 2nxn ( xn 1 xn )
(n 1)2 (n 1) xn2 1 (n 1) n 2 (n 1) xn2 ( xn2 1 xn2 ) 2nxn ( xn 1 xn )
(n 1)2 nxn2 1 xn2 1 (n 1) n 2 (n 1) xn2 xn2 1 xn2 2nxn ( xn 1 xn )
Р. Мунипов
(n 1)2 nxn2 1 (n 1) n 2 (n 1) xn2 xn2 2nxn ( xn 1 xn )
3.03.2010
46
47.
(n 1)2 nxn2 1 (n 1) n 2 (n 1) xn2 xn2 2nxn ( xn 1 xn )(n 1)2 nxn2 1 (n 1) n 2 nxn2 xn2 xn2 2nxn 1xn 2nxn2
(n 1)2 nxn2 1 2nxn 1xn nxn2 (n 1) n 2
(n 1) 2 n xn2 1 2 xn 1 xn xn2 (n 1) n 2
(n 1)2 n xn 1 xn (n 1) n 2
2
n
1
2
2
x
x
n 1
n
n
(n 1)2
n 1
1
xn 1 xn
2
n
n
n 1 n 1
1
n 2
n2
n 1
2
Чувствительность
дисперсии при добавлении
в совокупность нового xn 1
элемента, показывает на
сколько оно изменяется
Значение нового элемента
не изменяющего дисперсии
n2 1 n 2
1
n 1 2
xˆn 1 xn
2
(1,2)
ˆ
0 n
x
x
n
n
n 1
n
n
n 1 n 1
2
3.03.2010
Р. Мунипов
47
48.
n1
2
2
x
x
n 1
n
n
(n 1)2
n 1
n
n 1 2
2
x
x
n
n
2 n 1
(n 1)
n
n
n 1 2
n 1 2
x xn
n xn 1 xn
n
2 n 1
(n 1)
n
n
n
n 1 2
n 1 2
xn 1 xn
n xn 1 xn
n
2
(n 1)
n
n
n
(1)
(2)
ˆ
ˆ
x
x
x
x
n 1
n 1
n 1
n 1
2
(n 1)
3.03.2010
Р. Мунипов
48
49.
n(1)
(2)
ˆ
ˆ
x
x
x
x
n 1
n 1
n 1
n 1
2
(n 1)
xˆn(1) 1 xn
n 1 2
n
n
xˆn(2) 1 xn
n 1 2
n
n
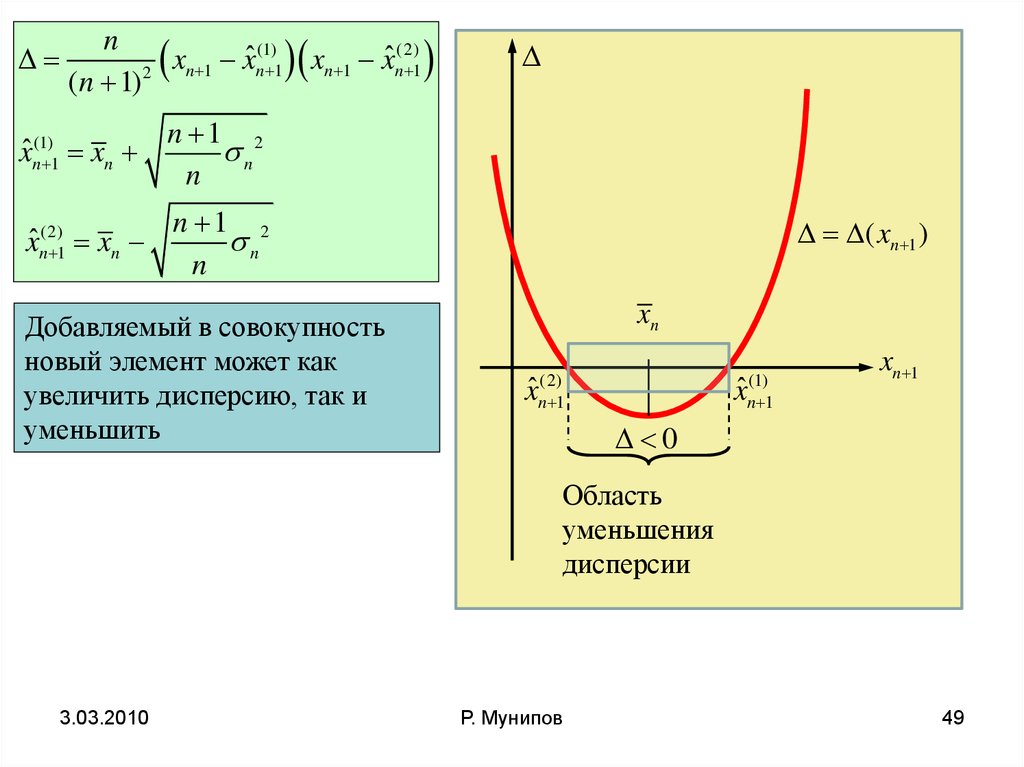
Добавляемый в совокупность
новый элемент может как
увеличить дисперсию, так и
уменьшить
( xn 1 )
xn
xˆ
xˆ
(2)
n 1
(1)
n 1
xn 1
0
Область
уменьшения
дисперсии
3.03.2010
Р. Мунипов
49
50.
* xi xxi
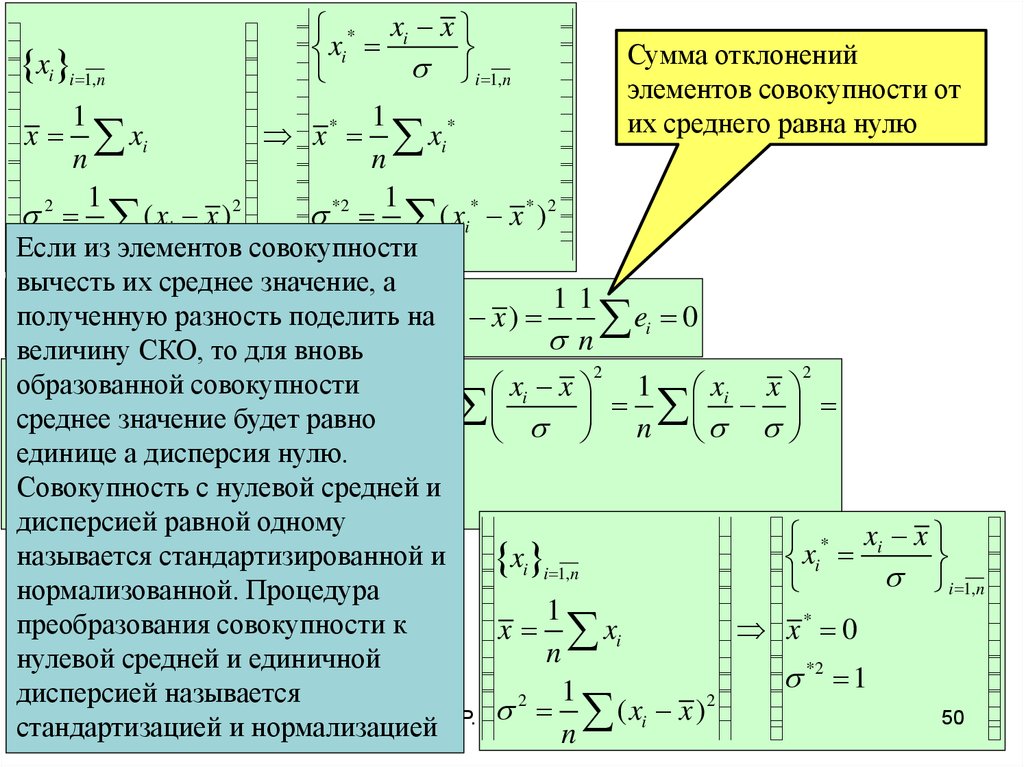
Сумма отклонений
xi i 1,n
i 1,n
элементов совокупности от
1
1
их среднего равна нулю
x xi
x * xi*
n
n
1
1
2 ( xi x ) 2
*2 ( xi* x * ) 2
n элементов совокупности
n
Если из
вычесть их среднее значение, а
1
1 xi x 1 1
11
*
поделить
на
xполученную
xi* разность
(
x
x
)
ei 0
i
n
n то для
вновь
n
n
величину
СКО,
2
2
образованной
совокупности
1
1
1
x
x
1
x
x
i
i
*2
2
* 2
среднее
значение
( xi* x * )будет
(
x
)
i
равно
n
n
n n
единице а дисперсия нулю.
1 1
1 2
2
Совокупность
с
нулевой
средней
(
x
x
)
1 и
i
2
2
n
дисперсией
равной одному
* xi x
называется стандартизированной и
xi
xi i 1,n
Общий
множитель
вынесли
i 1,n
нормализованной. Процедура
за знак суммы
1
преобразования
совокупности к
x xi
x* 0
n
нулевой средней и единичной
*2
1
1
дисперсией называется
2
2
(x x )
3.03.2010
50
стандартизацией
и нормализацией Р. Муниповn i
51.
1x
xi
n
2 1 ( x x ) 2
x n i
xi , yi i 1,n :
y 1 y
i
n
1
y2 ( yi y ) 2
n
y
ei( x ) xi x
( xi , yi )
ei( y ) yi y
y
x
x
ei( x ) xi x
1
( xi x )( yi y ) ( xi x )( yi y ) cov( X ,Y )
( y)
n
ei yi y
Усреднённая сумма
произведений отклонений
парных значений факторов
от их средних есть величина
именуемая
ковариацией.
3.03.2010
Ковариаций двух факторов характеризует
сгруппированность парных значений этих
факторов относительно их средних. Чем
компактнее располагаются парные значения к
одному
из средних значений, тем меньше 51
Р. Мунипов
величина ковариации
52.
1cov( X ,Y ) ( xi x )( yi y )
n
cov( X , X )
1
( xi x )2 x 2
n
Ковариация совокупности с самой собой равна дисперсии этой совокупности.
1
Y X
y x cov( X , Y ) Y X n ( xi x )( yi y )
i
i
1
xi , yi i 1,n : 1
( xi x )( xi x )
x n xi
n
1
y x
( xi x )( xi x )
n
Выражение для
1
2
(
x
x
)(
x
x
)
i
i
x
ковариации двух
n
совокупностей, одна
2
cov(
X
,
Y
)
x
из которых линейно
Y X
зависит от другой
3.03.2010
Р. Мунипов
52
53.
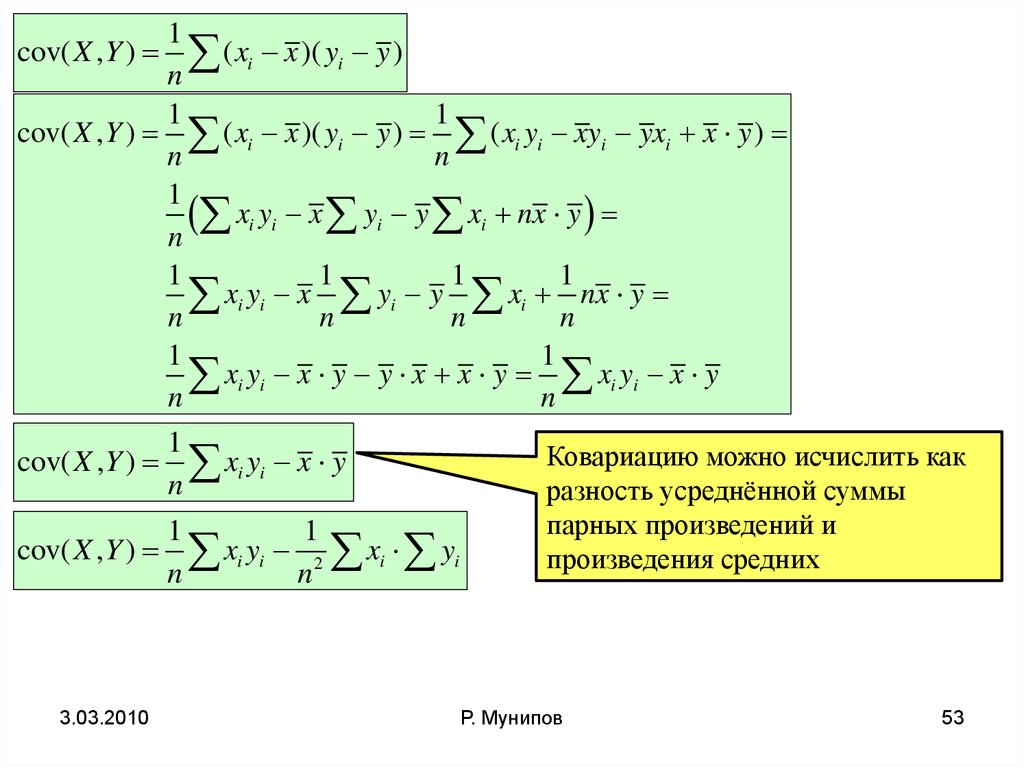
1cov( X ,Y ) ( xi x )( yi y )
n
1
1
cov( X , Y ) ( xi x )( yi y ) ( xi yi xyi yxi x y )
n
n
1
xi yi x yi y xi nx y
n
1
1
1
1
x
y
x
y
y
x
nx y
i i
i
i
n
n
n
n
1
1
x
y
x
y
y
x
x
y
xi yi x y
i i
n
n
cov( X , Y )
1
xi yi x y
n
1
1
cov( X ,Y ) xi yi 2 xi yi
n
n
3.03.2010
Ковариацию можно исчислить как
разность усреднённой суммы
парных произведений и
произведения средних
Р. Мунипов
53
54.
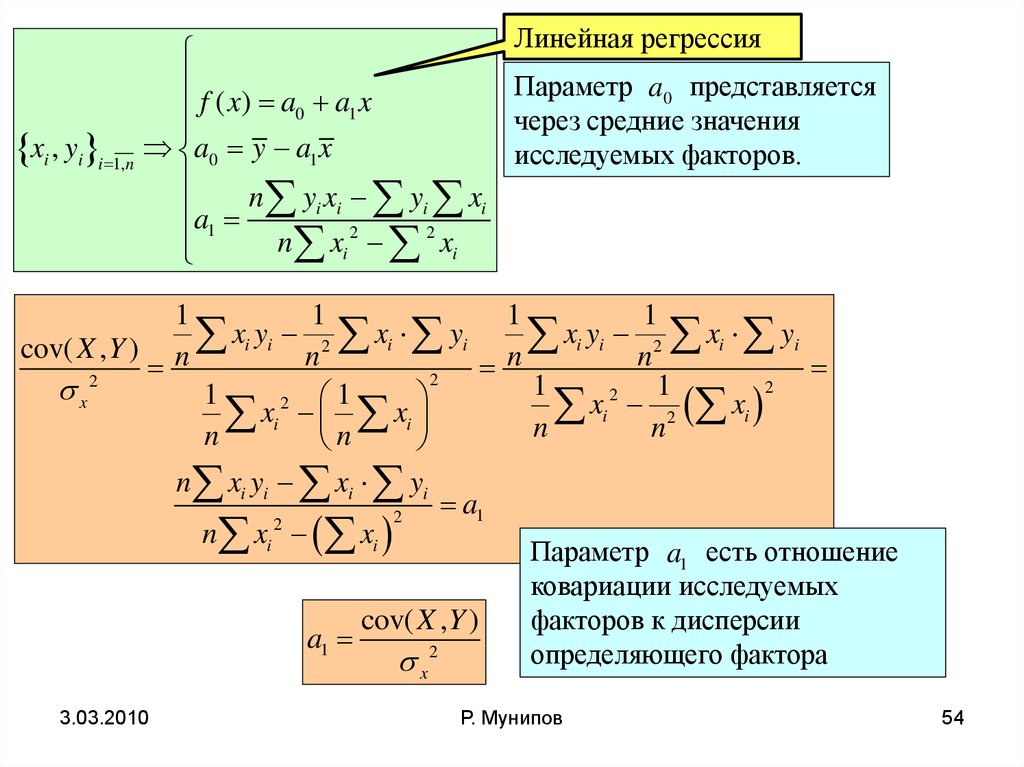
Линейная регрессияПараметр a0 представляется
f
(
x
)
a
a
x
0
1
через средние значения
xi , yi i 1,n a0 y a1x
исследуемых факторов.
a n yi xi yi xi
1
n xi 2 2 xi
1
1
1
1
x
y
x
y
x
y
x y
cov( X , Y ) n i i n 2 i i n i i n 2 i i
2
2
2
1
1
x
2
1
1
2
x
i 2 xi
xi xi
n
n
n
n
n xi yi xi yi
n xi xi
2
a1
3.03.2010
2
a1
cov( X , Y )
x2
Параметр a1 есть отношение
ковариации исследуемых
факторов к дисперсии
определяющего фактора
Р. Мунипов
54
55.
11
a0 yi a1 xi
f ( x) a0 a1 x
n
n
2
xi , yi i 1,n ei yi f ( xi ) S ei (min)
n yi xi yi xi
e (min)
a1
i
n xi 2 2 xi
a0 y a1 x
f ( x) y a1 ( x x )
cov( X , Y )
a
2
ei yi y a1 ( xi x )
1
x
y
S ei yi f ( xi )
2
3.03.2010
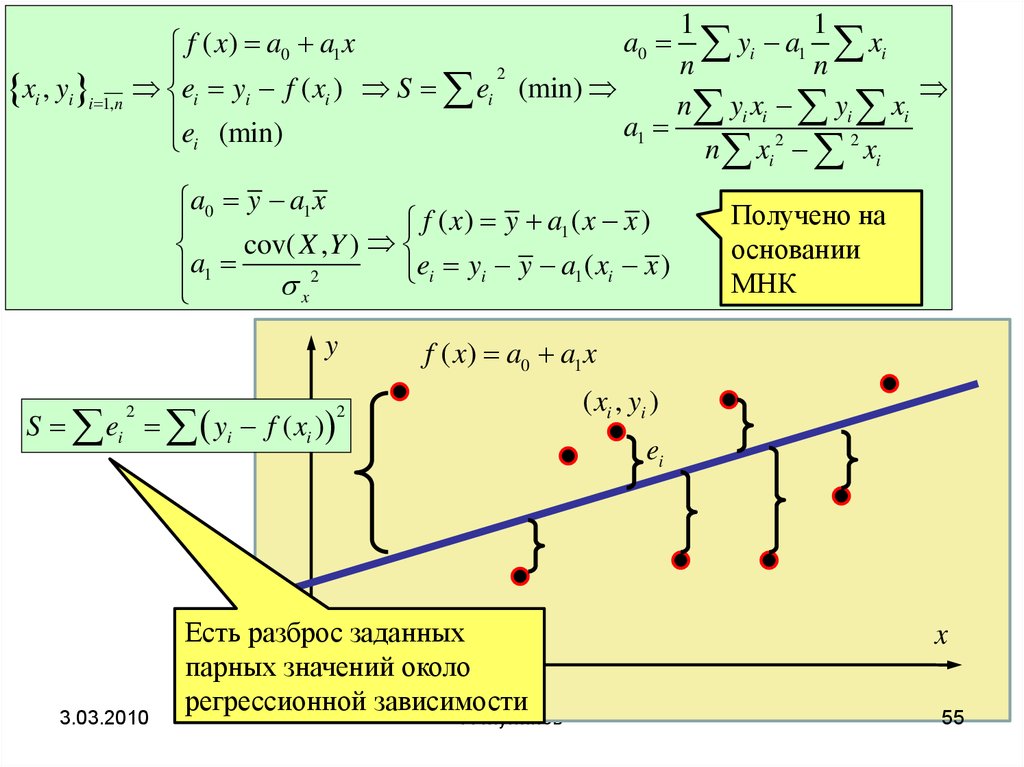
Получено на
основании
МНК
f ( x) a0 a1 x
( xi , yi )
2
ei
Есть разброс заданных
парных значений около
регрессионной зависимости
Р. Мунипов
x
55
56.
f ( x) y a ( x x )1
2
2
x
,
y
e
y
y
a
(
x
x
)
S ei yi f ( xi )
i i i 1,n i i
1
i
cov( X , Y )
a1
x2
S yi y a1 ( xi x ) ( yi y ) 2 a12 ( xi x ) 2 2a1 ( xi x )( yi y )
1
2
x 22
(
x
x
)
y()x x ) 2 n 2
( yi y ) an12 ( xi i x )2 2a1 ( xi x )( y i
i
x
2 ,Y )
2
2
n y 2 a 12 n2 x 21 2a(1nycov(
X
y
)
(
y
y
)
n
i
i
y
y
n
2
( xi x )( yi y ) n cov( X , Y )
cov( X , Y ) 1 2
cov( X , Y )
, Y
n y 2 cov(
2
cov(
X
)
X
,
x ( xi x )( y2i y )
2Y )
x
x
n
2
2
2
2
cov(
X
,
Y
)
cov(
X
,
Y
)
cov(
X
,
Y
)
2
2
2
n y
n y
x 2
2
2
2
2
x
x
x
2
cov( X , Y )
n y 2 1
2 2
3.03.2010
x
y
Р. Мунипов
56
57.
2cov( X , Y )
S n y 2 1
2 2
x
y
S n y 2 1 cor( X ,Y )
2
cor( X ,Y )
cov( X ,Y )
x 2 y 2
Коэффициент корреляции
1
1
y f (x )
y f ( x ) 1 cor( X ,Y )
n
n
1 cor( X ,Y )
Rˆ 1 cor( X ,Y )
y f ( x )
i
i
2
n y 1 cor( X ,Y )
2
2
i
2
p
i
2
y
2
2
2
i
y
2
2
i
2
p2
2
p2 y 2 Rˆ 2
Коэффициент обусловленности
линейной регрессии
3.03.2010
Р. Мунипов
Дисперсия
сгруппированность парных
значений вокруг линейной
регрессии
57
58.
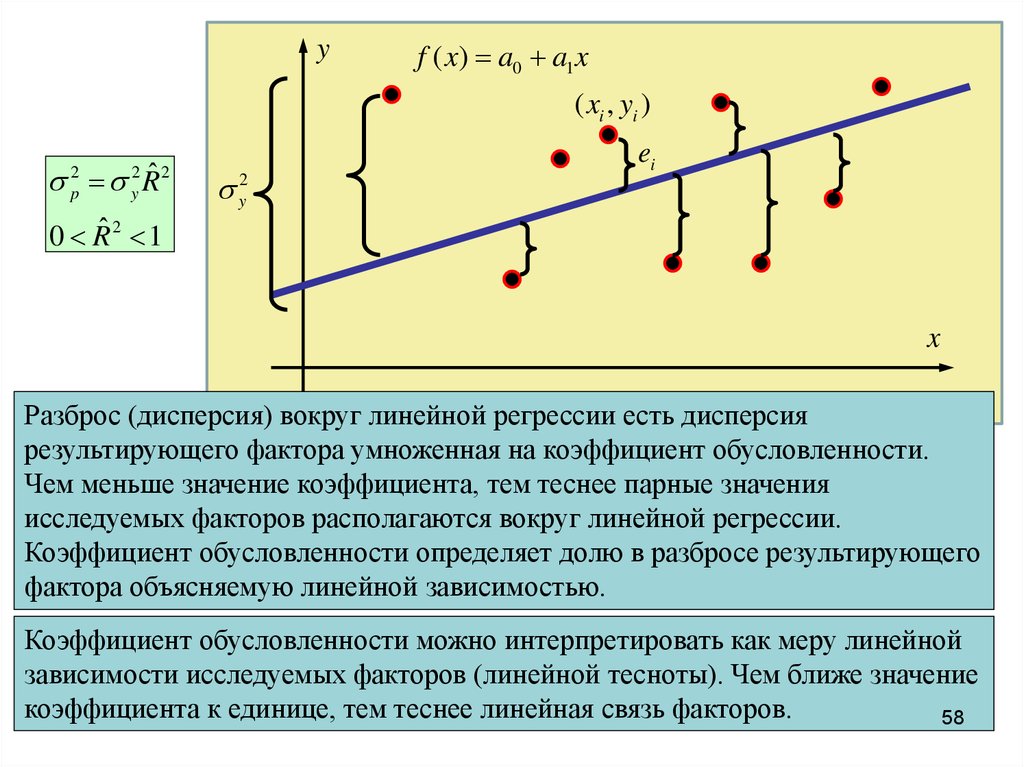
yf ( x) a0 a1 x
( xi , yi )
Rˆ
2
p
2
y
2
y2
ei
0 Rˆ 2 1
x
Разброс (дисперсия) вокруг линейной регрессии есть дисперсия
результирующего фактора умноженная на коэффициент обусловленности.
Чем меньше значение коэффициента, тем теснее парные значения
исследуемых факторов располагаются вокруг линейной регрессии.
Коэффициент обусловленности определяет долю в разбросе результирующего
фактора объясняемую линейной зависимостью.
Коэффициент обусловленности можно интерпретировать как меру линейной
зависимости исследуемых факторов (линейной тесноты). Чем ближе значение
коэффициента
к единице, тем теснееР. линейная
связь факторов.
3.03.2010
Мунипов
58
59.
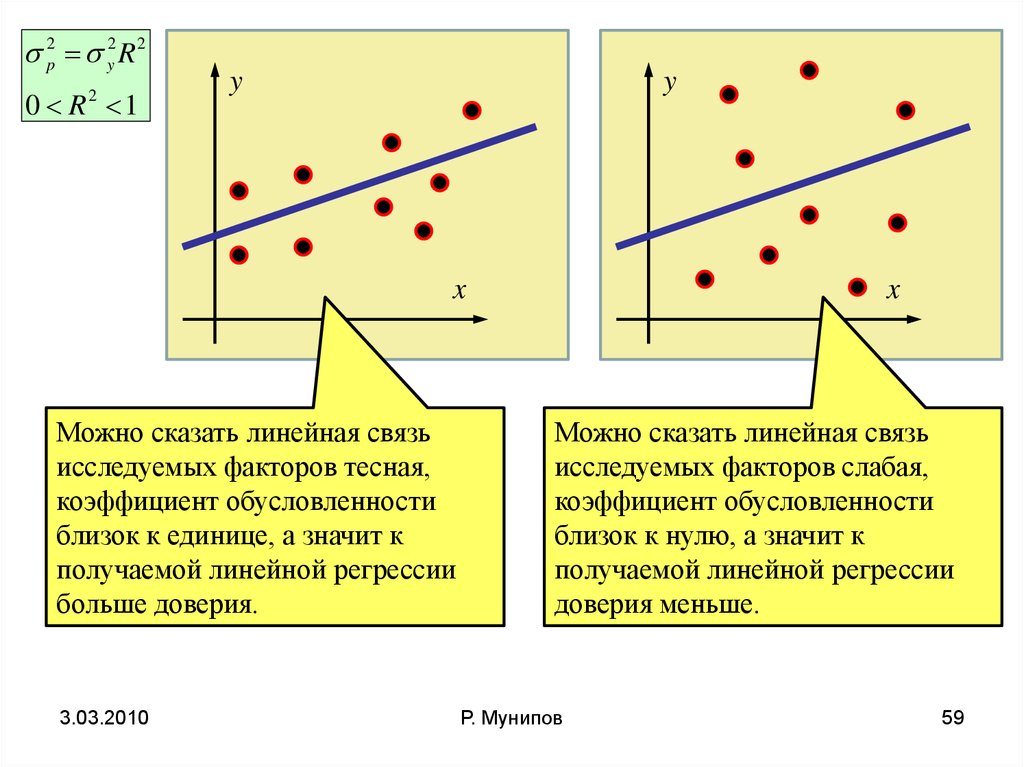
p2 y2 R 20 R 1
2
y
y
x
Можно сказать линейная связь
исследуемых факторов тесная,
коэффициент обусловленности
близок к единице, а значит к
получаемой линейной регрессии
больше доверия.
3.03.2010
x
Можно сказать линейная связь
исследуемых факторов слабая,
коэффициент обусловленности
близок к нулю, а значит к
получаемой линейной регрессии
доверия меньше.
Р. Мунипов
59
60.
p2 y 2 1 cor( X , Y )2
1 cor( X , Y ) 1
cor( X ,Y )
cov( X ,Y )
x 2 y 2
cor( X ,Y )
( x x )( y y )
(x x ) ( y y)
i
i
2
i
2
i
Коэффициент корреляции есть мера линейной зависимости исследуемых
факторов (линейной тесноты). Чем ближе абсолютное значение
коэффициента к единице, тем теснее линейная связь факторов.
y
cor1
y
x
3.03.2010
cor2
x
Р. Мунипов
cor1 cor2
60
61.
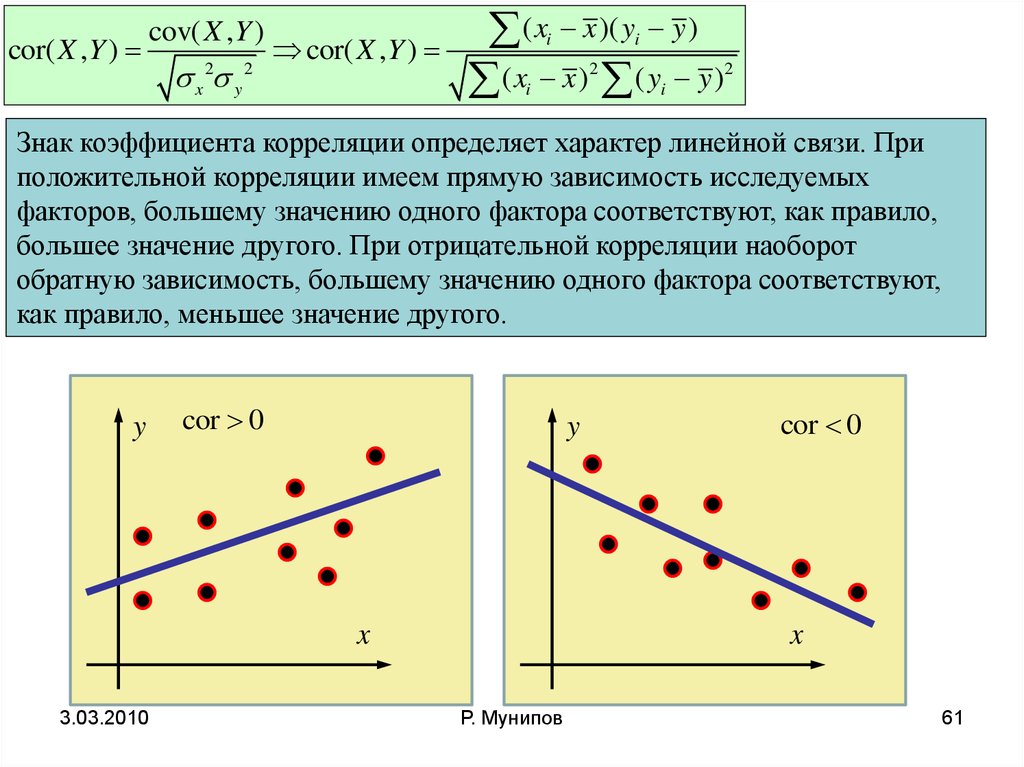
cor( X ,Y )cov( X ,Y )
x 2 y 2
cor( X ,Y )
( x x )( y y )
(x x ) ( y y)
i
i
2
i
2
i
Знак коэффициента корреляции определяет характер линейной связи. При
положительной корреляции имеем прямую зависимость исследуемых
факторов, большему значению одного фактора соответствуют, как правило,
большее значение другого. При отрицательной корреляции наоборот
обратную зависимость, большему значению одного фактора соответствуют,
как правило, меньшее значение другого.
y
cor 0
y
x
3.03.2010
cor 0
x
Р. Мунипов
61































 mathematics
mathematics