Метод наименьших квадратов

1. Метод наименьших квадратов.

В математической статистике методы получения наилучшего
приближения к исходным данным в виде
аппроксимирующей функции получили название
регрессионного анализа.
Основными задачами регрессионного анализа являются
установление зависимости между переменными и оценка
(прогноз) значений зависимой переменной.
В экономических исследованиях часто заданному значению
одной переменной может соответствовать множество
значений другой переменной.
Другими словами, каждому значению одной переменной
соответствует условное распределение другой переменной.
Зависимость, при которой каждому значению одной
переменной соответствует условное математическое
ожидание другой называется регрессионной:
M(Y|X) = f(X)

2. Метод наименьших квадратов.

Уравнение парной регрессии.
yt = a0 + a1xt + ut
(7.1)
Постановка задачи.
Дано: выборка наблюдений за поведением переменных yt и xt.
Найти: 1. Оценки значений параметров a0 и a1.
2. Оценки точности σ(a0) и σ(a1).
3. Оценка рассеяния случайного возмущения σu.
4. Оценку точности прогнозирования σ(y(x0)).
Принятые обозначения:
Выборка:
y1 x 1
y2 x 2
……….
yn x n
Система уравнений
наблюдений.
y1 = a0 + a1x1 + u1
yt = a0 + a1x2 + u2
……………………
yn = a0 + a1xn + un
Вектор Y
Матрица X
y
1
y
Y 2
...
y
n
1 x1
1 x2
X
... ...
1 x
n

3. Метод наименьших квадратов

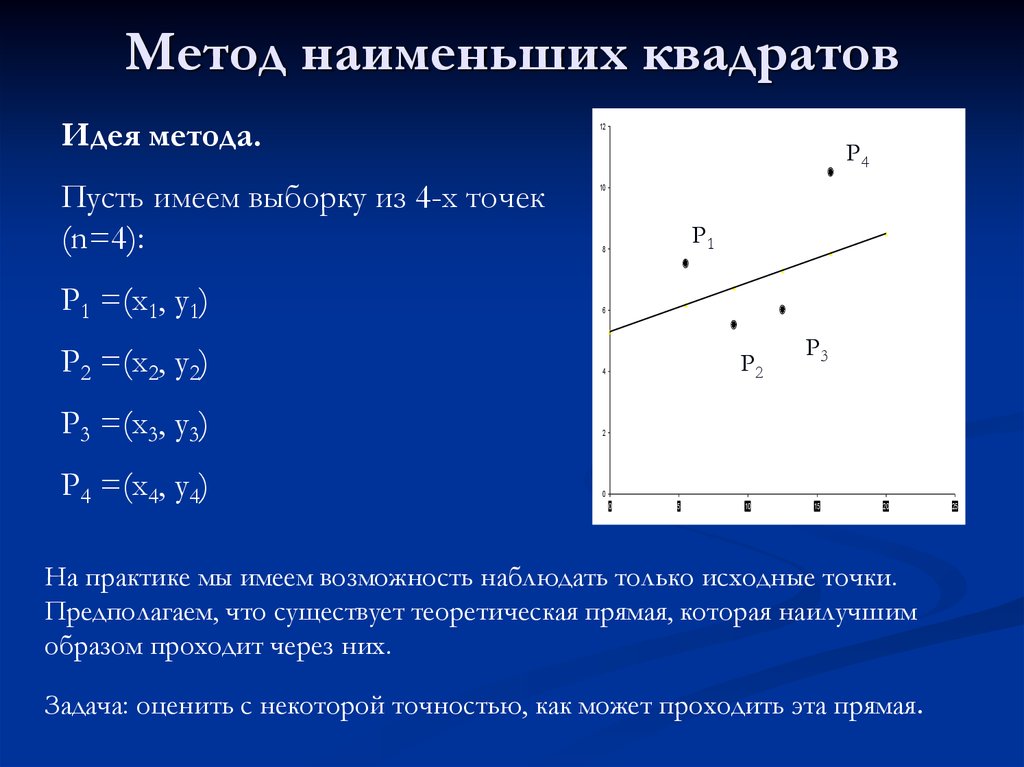
Идея метода.
Пусть имеем выборку из 4-х точек
(n=4):
P1 =(x1, y1)
P2 =(x2, y2)
P3 =(x3, y3)
P4 =(x4, y4)
12
P4
10
P1
8
6
P2
4
P3
2
0
0
5
10
15
20
На практике мы имеем возможность наблюдать только исходные точки.
Предполагаем, что существует теоретическая прямая, которая наилучшим
образом проходит через них.
Задача: оценить с некоторой точностью, как может проходить эта прямая.
25

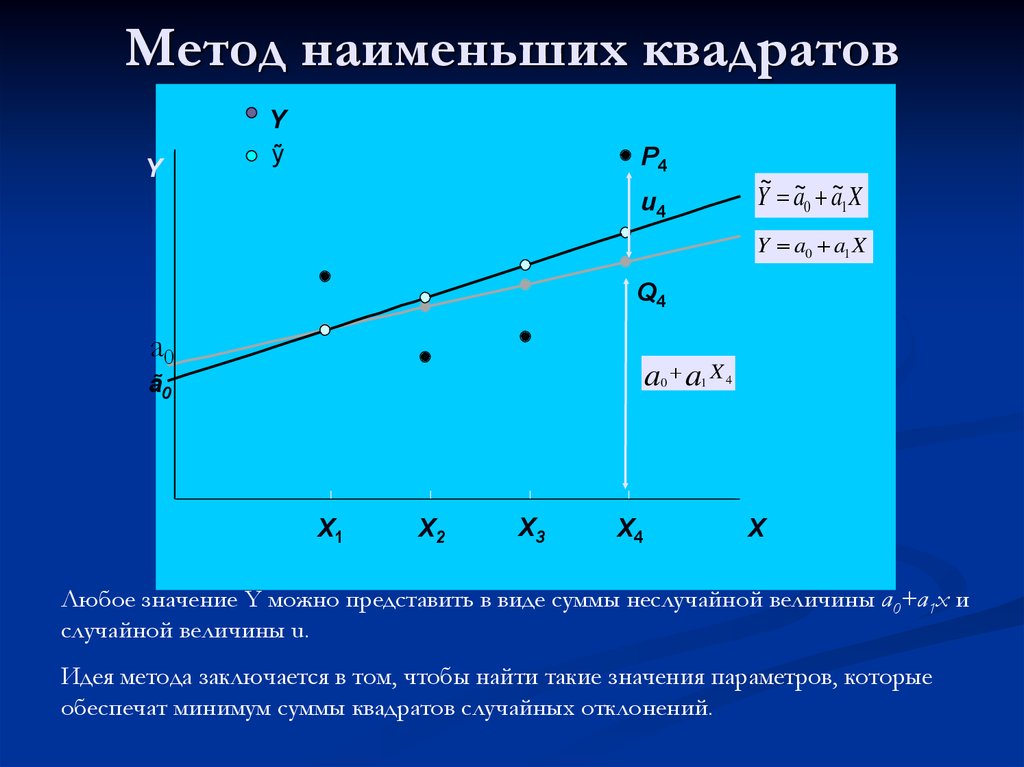
4. Метод наименьших квадратов

Y
Y
ỹ
P4
~
Y a~0 a~1 X
u4
Y a0 a1 X
Q4
a0
a a X
ã0
0
X1
X2
X3
X4
1
4
X
Любое значение Y можно представить в виде суммы неслучайной величины a0+a1x и
случайной величины u.
Идея метода заключается в том, чтобы найти такие значения параметров, которые
обеспечат минимум суммы квадратов случайных отклонений.

5. Реализация метода наименьших квадратов

Итак, оценки параметров модели парной регрессии согласно МНК
будем искать из условия:
S=Σui2=Σ(yi-ã0+ã1xi)2=min
Условиями минимума функции являются равенство нулю первых
производных и положительность вторых производных по ã0 и ã1.
S
2
a0
S
2
a1
y a~ a~ xi 1 0
i
0
1
y a~ a~ xi x 0
i
0
1
при этом:
S 1 0
~
a
S x 0
~
a
2
2
0
2
2
2
1
i
(7.2)
i
Система уравнений (7.2) называется
системой нормальных уравнений
для вычисления оценок параметров
модели (7.1)

6. Реализация метода наименьших квадратов

Упростим систему нормальных уравнений (7.2)
~0 a~1 xi y
na
i
0
1
(7.3)
i
x a a x x y
2
i
i
i
Для решения системы (7.3) выразим из первого уравнения ã0,
подставим его во второе уравнение.
1
n
1
xi n
Или
a~
0
y a~ x
7.4
y a~ x x a x y
i
1
i
i
1
i
2
i
1
x y a~ x n x a~
2
i
1
i
i
i
1
i
i
n xi y
i
Откуда получаем :
a~ x x x n x y x y
n x y x y
~
7.5
a n
x x x
2
1
i
i
i
1
i
i
i
i
i
2
i
i
i
i
i
i

7. Реализация метода наименьших квадратов

Вычислив с помощью (7.5) оценку ã1, с помощью выражения
(7.4) получим значение оценки параметра ã0.
1
1
Cov( x, y )
x y y
x y xi y x y
x
x
i
i yi
i
i
n 1
n 1
1
1
1
x
y
x
y
y
x
x
x
x
i yi
i
i yi
i yi
i
n 1
n 1
n
1
1
1
2
2
2
2
2
2
( x) (n 1) xi x n 1 ( xi 2 xi x x ) n 1 xi 2 x xi x
1
1
2
2
2 1
n
x
x
x
x
i
i
i xi
n 1
n 1
n
Тогда выражение (7.5) можно записать в виде:
a
1
Cov( x, y )
2
( x)
(7.6)

8. Реализация метода наименьших квадратов

Вопрос. Как связано полученное решение со
случайными возмущениями?
Cov( x, y ) Cov( x, a0 a1 x u )
Cov( x, a0) Cov( x, a1 x) Cov( x, u )
2
a1 ( x) Cov( x, u )
Подставляя (7.7) в (7.6) получим выражение:
Cov( x, u )
~
a a
( x)
1
1
2
Условие несмещенности оценки параметра ã1
~) a
M (a
1
1
1
2
( x)
Cov( x, u )
(7.7)

9. Характеристики точности уравнения парной регрессии

Вычислим дисперсии параметров уравнения регрессии и
дисперсию прогнозирования эндогенной переменной.
1. Дисперсия параметра ã1
1
x
(
y
)
y
x
i
i
Cov
(
x
,
y
)
2
2
~
2 (n 1)
(
)
a 1 2 ( x) 1
2
(n 1) xi x
x ( y x)
x
a
a
2 xi
2
xi
0
1
ui
i
2
2
x
x
x
x
i
i
2
2
( xi x ) (u i )
1
2
2
~
(
)
(7.8)
a1
u n 2 ( x)
2 2
xi x

10. Характеристики точности уравнения парной регрессии

Дисперсия параметра ã0
2
( y)
2
1
n
2
1
u
(
)
y
i n
2
n
y
i
2
Дисперсия σ2(ã1) известна (7.8), необходимо вычислить
дисперсию y.
y a~ x
a~ ~
Cov y , a 0
2
2
0
1
2
( y) x
2
(a~ ) 2 xCov y, ~a
2
1
1
1
(7.9)
В результате получаем:
2
2 1
x
2 ~
2
u
a0
n n
( x)
2
(7.10)

11. Характеристики точности уравнения парной регрессии

Дисперсия прогноза эндогенной переменной.
~
~
a a x u
~
x a
a ~
~ 2Cov a
~ , u 2 xCov a
~ ,u
2 xCov a , a
2
~y
2
2
2
0
1
2
0
1
0
1
(7.11)
2
u
0
1
Ковариации между случайными возмущениями и оценками
параметров равны нулю, т.к. эти переменные независимые.
~0 a~1 Cov y a~1 x, a~1 Cov y, a~1 xCov a~1 , a 1 x
Cov a
2
a~
1
(7.12)
Подставляя в (7.11) (7.10), (7,8) и (7,12), получаем:
2
1 x x 2
(~
y ) u 1
2
n n
( x)
2
(7.13)

12. Пример применения МНК

X
Y
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
1,91
2,76
2,67
4,03
4,12
2,81
6,53
6,24
9,03
6,87
9,09
7,08
7,79
8,75
11,19
10,15
10,52
10,89
10,59
13,40
ỹ
2,17
2,72
3,26
3,80
4,34
4,88
5,42
5,97
6,51
7,05
7,59
8,13
8,68
9,22
9,76
10,30
10,84
11,38
11,93
12,47
U
-0,26
0,04
-0,59
0,23
-0,22
-2,07
1,11
0,27
2,52
-0,18
1,50
-1,05
-0,89
-0,47
1,43
-0,15
-0,32
-0,49
-1,34
0,93
U2
0,07
0,00
0,35
0,05
0,05
4,30
1,22
0,07
6,36
0,03
2,24
1,11
0,78
0,22
2,05
0,02
0,10
0,24
1,78
0,87
σ(y)
1,20
1,19
1,17
1,16
1,15
1,15
1,14
1,14
1,13
1,13
1,13
1,13
1,14
1,14
1,15
1,15
1,16
1,17
1,19
1,20
X-стаж работы сотрудника;
Y- часовая оплата труда.
Модель: Yt=a0+a1Xt+Ut
Σxi=210; Σyi=146.42;
Σxi2=2870; Σxiyi=1897.66
20 1897.66 210 146.42
~
1.63
a
20 2870 44100
1
~
155.42 1.63 210 0.54
a
1
0
20
21.93
2
~
u 20 2 1.10

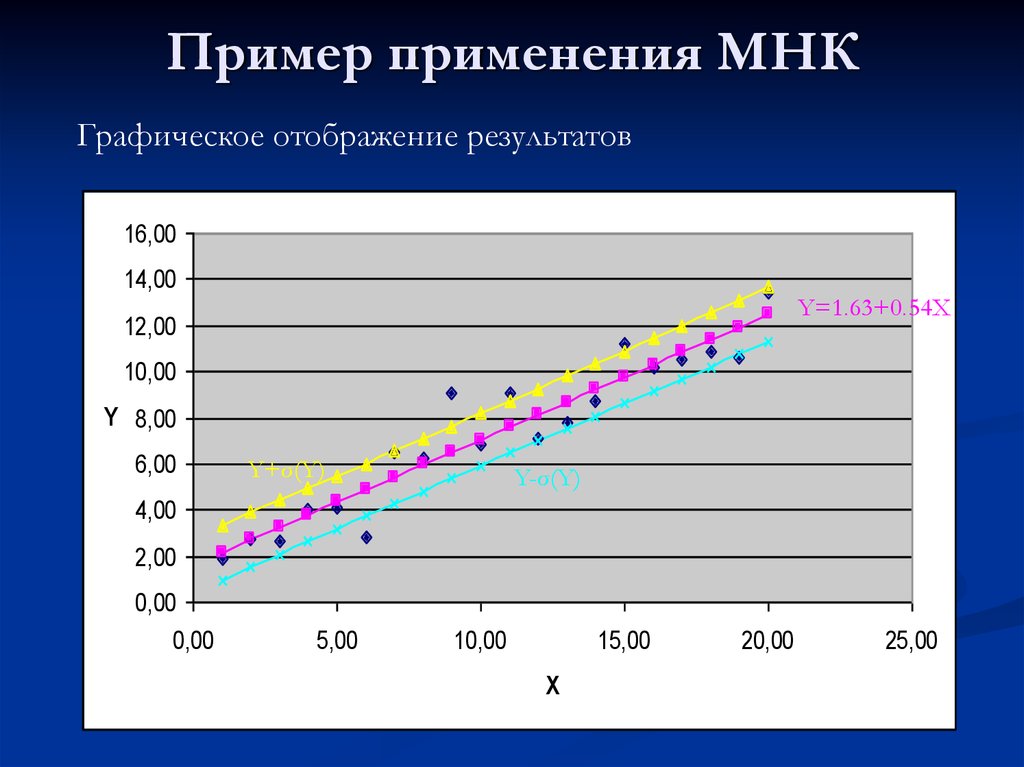
13. Пример применения МНК

Графическое отображение результатов
16,00
14,00
Y=1.63+0.54X
12,00
10,00
Y 8,00
6,00
Y+σ(Y)
Y-σ(Y)
4,00
2,00
0,00
0,00
5,00
10,00
15,00
X
20,00
25,00