Метод наименьших квадратов

1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

2.

Истинная модель парной линейной
регрессии Y = а + b*X + e.
Для ее оценки используется выборка:
(Y1, X1)
………
(Yn, Xn)
Получается выборочное уравнение
регрессии
Y a b*X

3.

Для элемента (Yi, Xi) выборки, i = 1, …,
n, можно записать:
a
b
*
X
Y
i
i
e Y Y
i
i
i
a
b
*
Yi
Xi ei

4. Как оцениваются по выборке коэффициенты регрессии?

5.

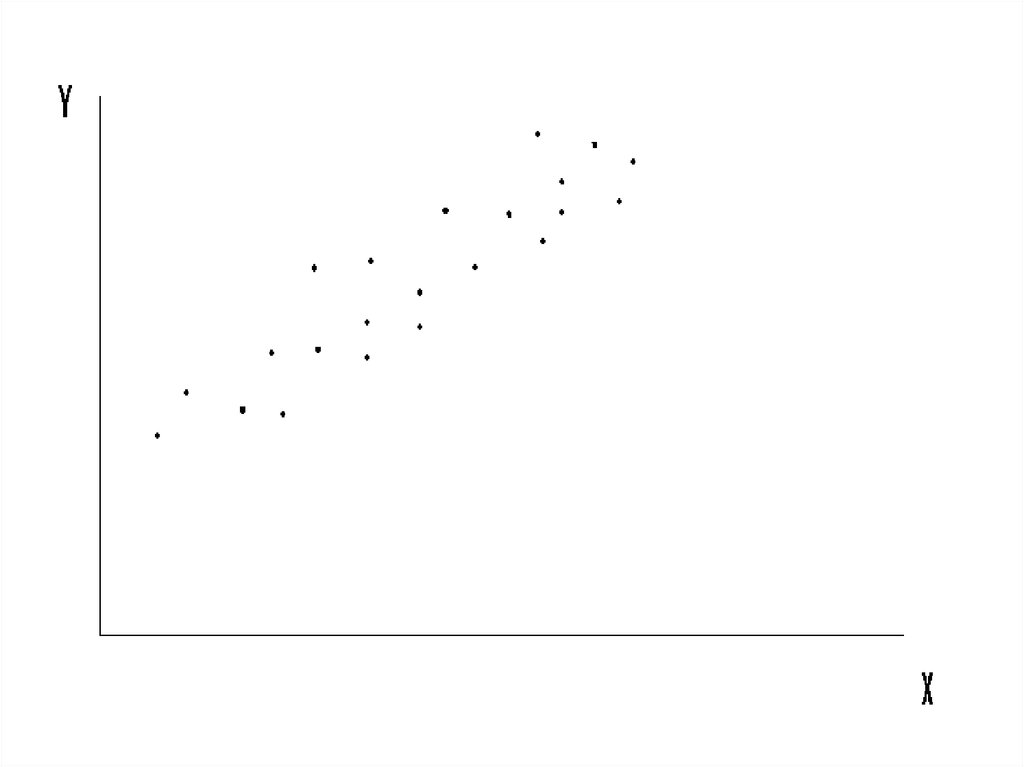
Выборка (Yi, Xi), по которой мы должны
оценить теоретическую модель
Y = a + b*X + e,
графически представляется в виде
«облачка» точек:

6.

7.

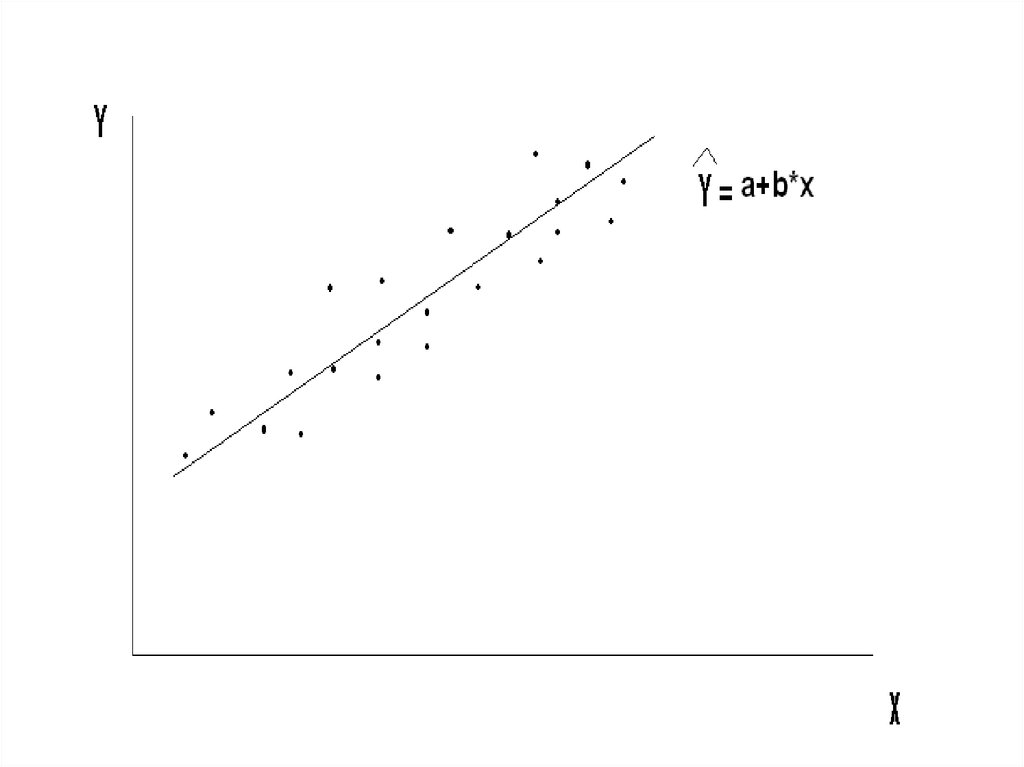
По этим точкам мы хотим получить
такое выборочное уравнение
Y a b*X
(т. е. оценки a и b), которое как
можно точнее представляло бы
истинную линию регрессии

8. Интуиция подсказывает:

Чем лучше оцененная прямая
регрессии представляет выборку,
тем точнее она приближает
истинную прямую регрессии.

9.

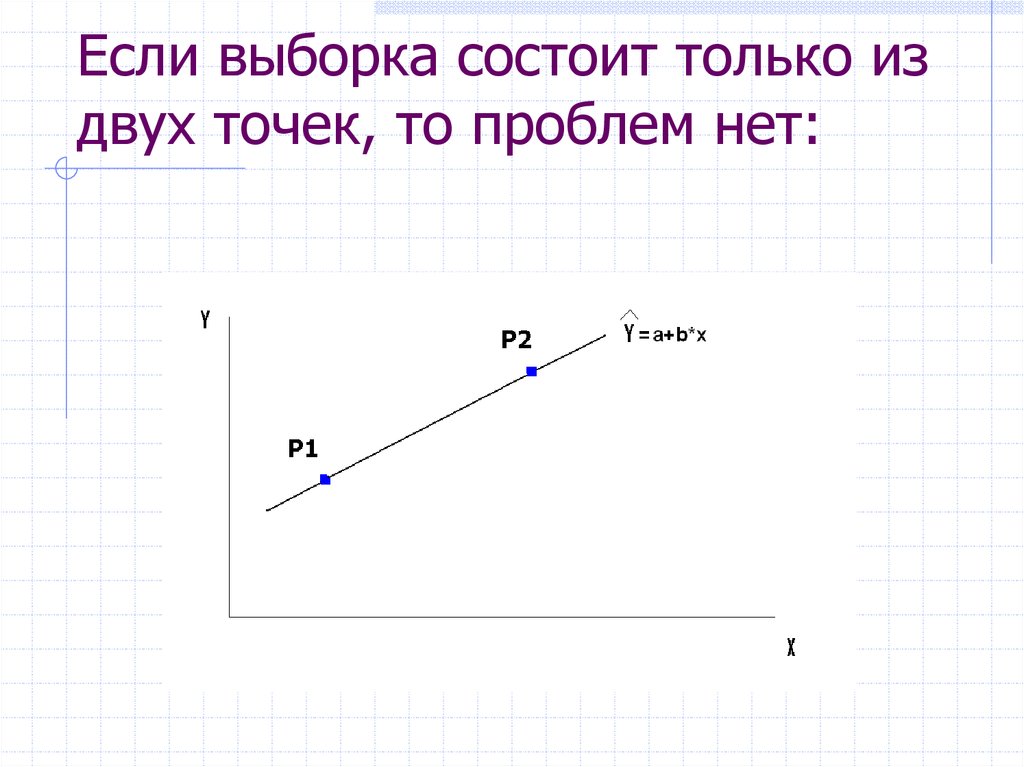
10. Если выборка состоит только из двух точек, то проблем нет:

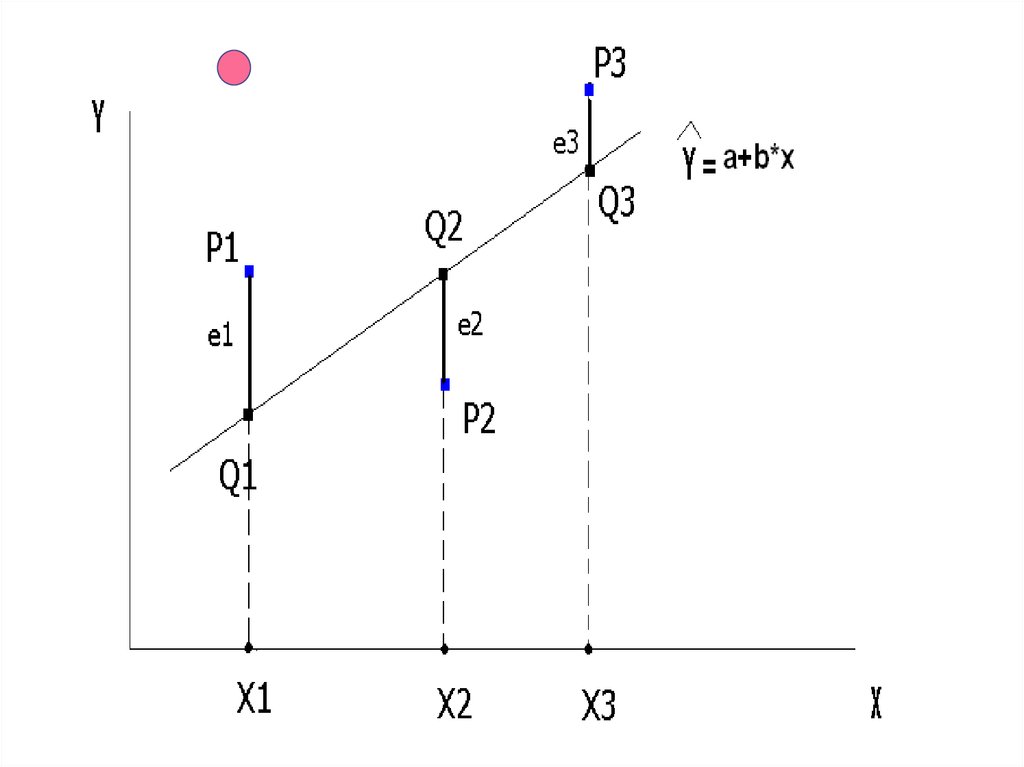
11. Если точек больше двух:

12.

13.

Точки выборки
P1 = (X1, Y1), P2 = (X2, Y2), P3 = (X3, Y3)
моделируются (оцениваются) точками линии
регрессии
Q1 = (X1, Ŷ1), Q2 = (X2, Ŷ2 ), Q3 = (X3, Ŷ3 ).
Точность моделирования Yi для каждого Xi
определяется величиной ошибки
ei = Yi - Ŷ1.
Хотелось бы, чтобы выборочное уравнение
Ŷ = a + b*X с наименьшими ошибками моделировало
бы сразу все выборочные значения Yi, i =1, …, n.

14. Принцип метода наименьших квадратов

Для данной выборки (X1, Y1), …, (Xn, Yn)
параметры a и b рассчитываются
таким образом, чтобы получить
минимальное значение суммы
квадратов остатков:
n
2
min
e
i 1
i

15.

Или
Yi Yi
n
min
i 1
2
Yi Yi S
n
i 1
2

16. Решаем систему уравнений:    

Решаем систему уравнений:
S
0
a
S
0
b

17. После преобразований получаем систему нормальных уравнений для коэффициентов регрессии

n
n
i 1
i 1
n * a Y i b * X i 0
n
n
n
i 1
i 1
a * X i X i *Y i a * X i 0
i 1
2

18.

Решение этой системы дает значения
для оценок параметров уравнения регрессии a и b:
b
xy x y
x x
2
2
a y b x

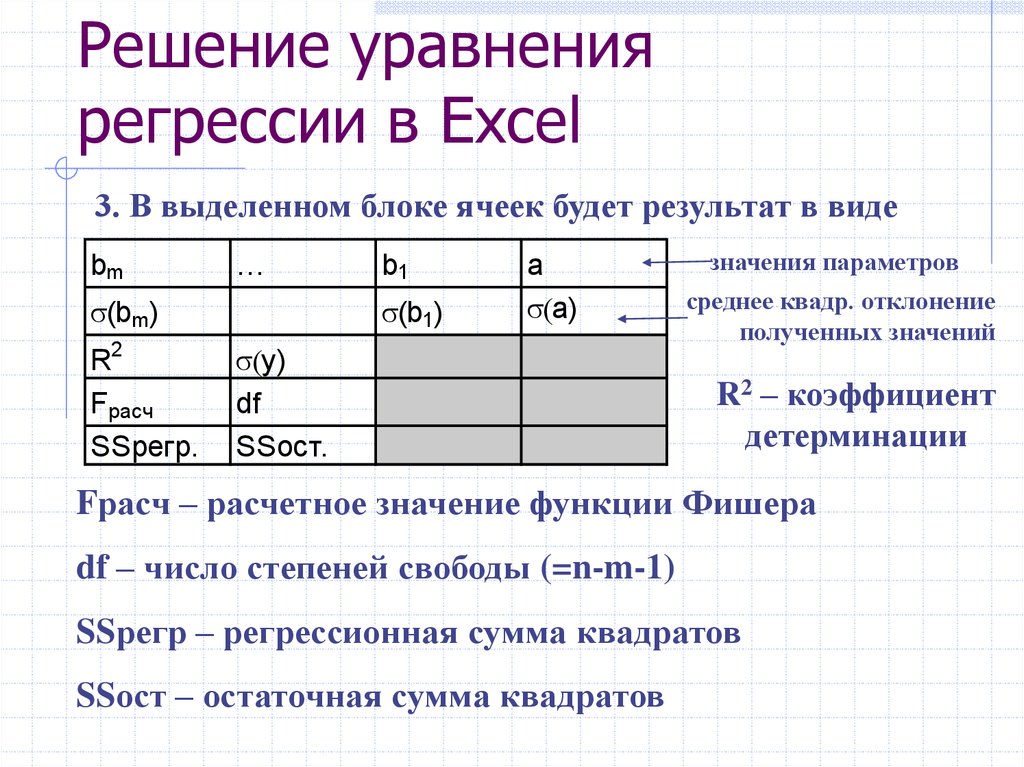
19. Решение уравнения регрессии в Excel

1. На листе Excel выделяют блок ячеек в котором
- строк всегда 5
- столбцов–(m+1), где m – число независимых
переменных
2. Вводят функцию: ЛИНЕЙН(…)<Shift>+<Ctrl>+<Enter>
Константа: =1, если параметр а присутствует в уравнении
=0, если уравнение имеет вид у=b*x
Статистика: =1, если необходима оценка достоверности
=0, если оценка не нужна

20. Решение уравнения регрессии в Excel

3. В выделенном блоке ячеек будет результат в виде
bm
…
(bm )
R2
Fрасч
SSрегр.
b1
(b1)
a
a)
y)
df
SSост.
значения параметров
среднее квадр. отклонение
полученных значений
R2 – коэффициент
детерминации
Fрасч – расчетное значение функции Фишера
df – число степеней свободы (=n-m-1)
SSрегр – регрессионная сумма квадратов
SSост – остаточная сумма квадратов

21.

Коэффициент детерминации показывает,
насколько хорошо в выборке изменения Y
объяснены изменениями Х. Т. е., насколько
хорошо выборочная модель регрессии
объясняет поведение Y в выборке.
Изменения фактора Y измеряются его
дисперсией 2(Y).

22. Коэффициент детерминации:

R
2
2
r
yx
- часть дисперсии Y, объясненная
уравнением регрессии, т. е.
изменениями в выборке фактора Х.

23. Еще одно дополнение к R2

Мы знаем, что 0 ≤ R2 ≤ 1.
Однако, если модель регрессии не
имеет свободного члена,
например,
Y = b*x + e, то
возможны отрицательные
значения R2.
Это также недостаток R2.

24. Статистические свойства МНК-оценок коэффициентов регрессии. ТЕОРЕМА ГАУССА-МАРКОВА

25.

Почему при оценке параметров модели a
и b минимизируется именно
n
e
i 1
2
i
?
Потому что при выполнении некоторых
условий оценки a и b, полученные по МНК,
оказываются очень хорошими:
несмещенными, эффективными,
состоятельными.

26. Каких условий?

МНК-оценки a и b являются
случайными величинами, свойства
которых существенным образом
зависят от свойств случайного члена
e модели регрессии.

27. Условия Гаусса-Маркова

1. Математическое ожиданиет значений остатков e
равно 0:
М(ei) = 0 для всех наблюдений хi
2. Значение дисперсии ошибки является постоянной
величиной σei2 = σ2 = const для всех наблюдений Xi
(условие гомоскедастичности)
3. Значения e, для разных значений хi независимы
между собой
(отсутствие автокорреляции в остатках)
4. Значения хi и ei для одного и того же наблюдения
независимы между собой
σXi, ei = 0 для всех
наблюдений
5. Модель является линейной относительно параметров

28. Условия Гаусса-Маркова

Для уравнения множественной регрессии:
6. Факторы xi независимы между собой в том
смысле, что их выборочные парные линейные
коэффициенты корреляции не превышают
некоторого порога p:
rx j xi p (условие отсутствия
мультиколлинеарности)
7. Остатки являются нормально распределенной
случайной величиной, т.е. подчиняются закону
нормального распределения.

29.

Модель, удовлетворяющая предпосылкам
МНК (1)-(7), называется классической
нормальной моделью регрессии,
если не выполняется только условие (7), то
модель – классическая модель регрессии.

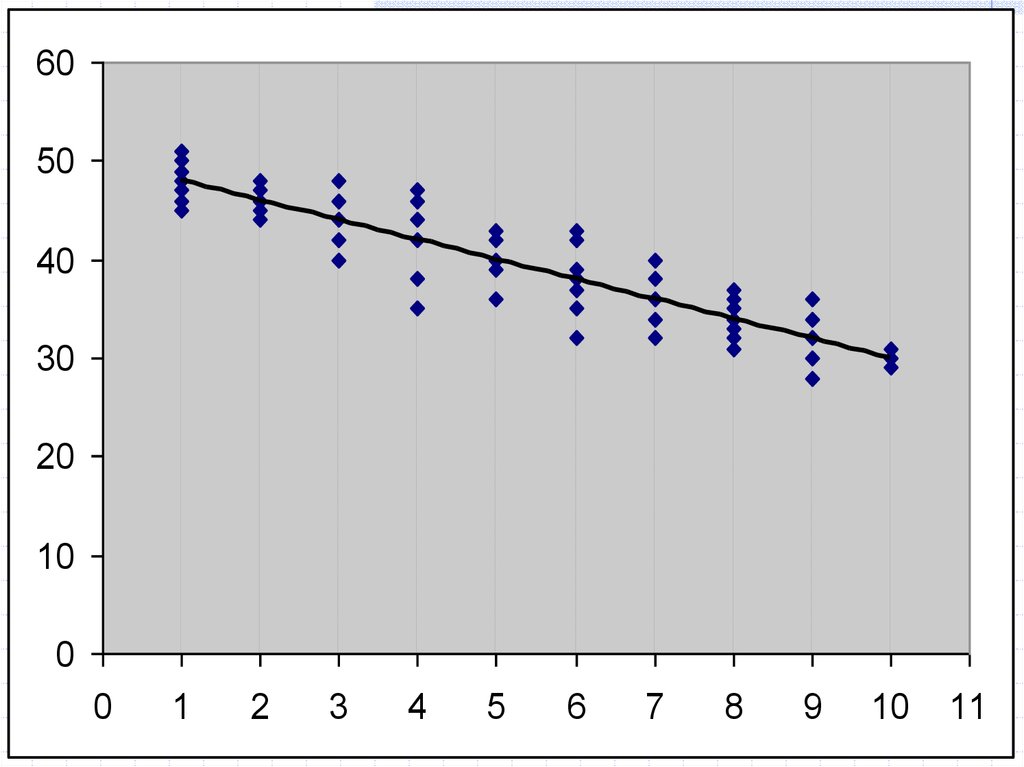
30.

60
50
40
30
20
10
0
0
1
2
3
4
5
6
7
8
9
10
11

31.

Если 1-е условие Г-М не
выполняется, МНК дает
смещенную оценку для b.

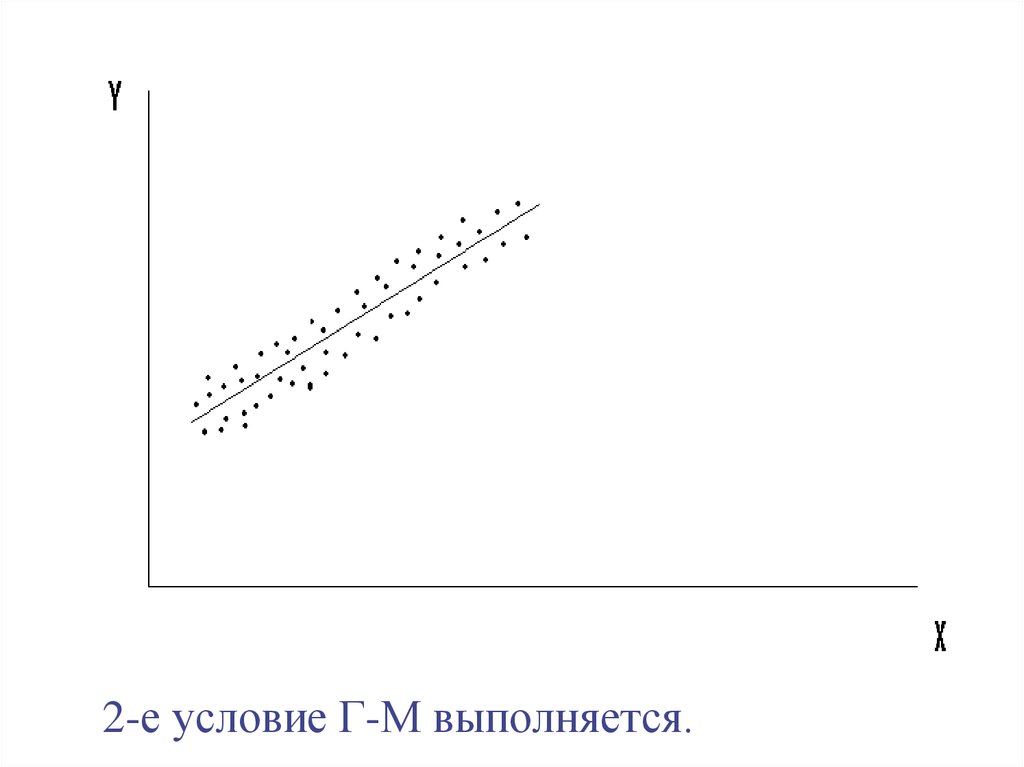
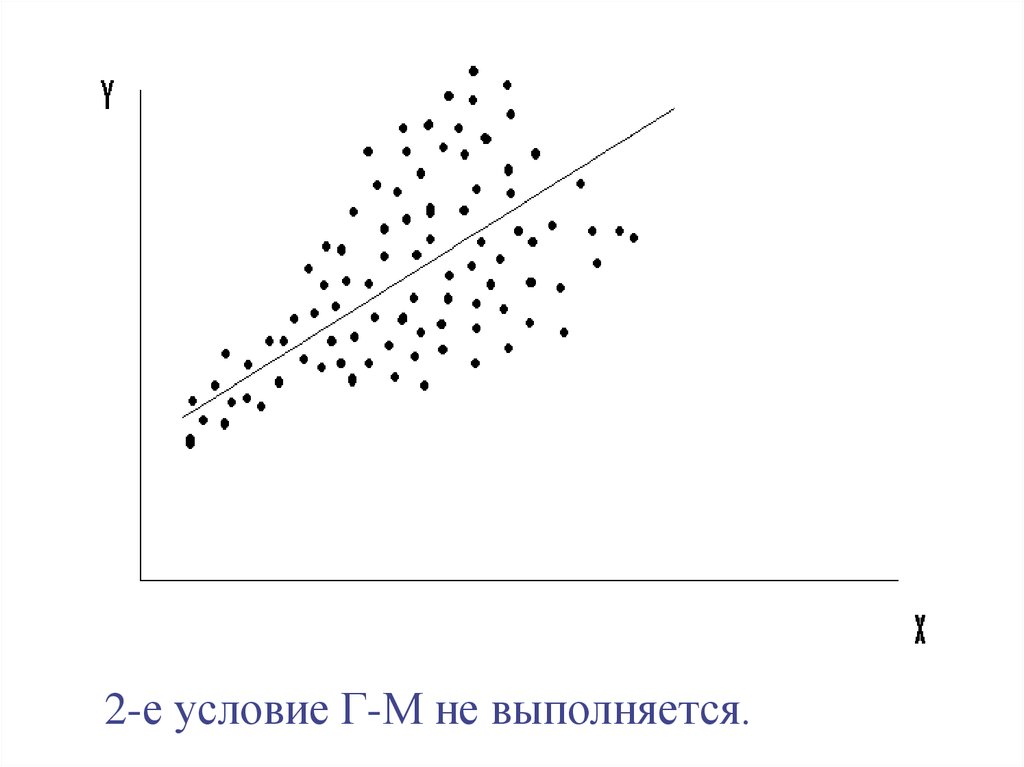
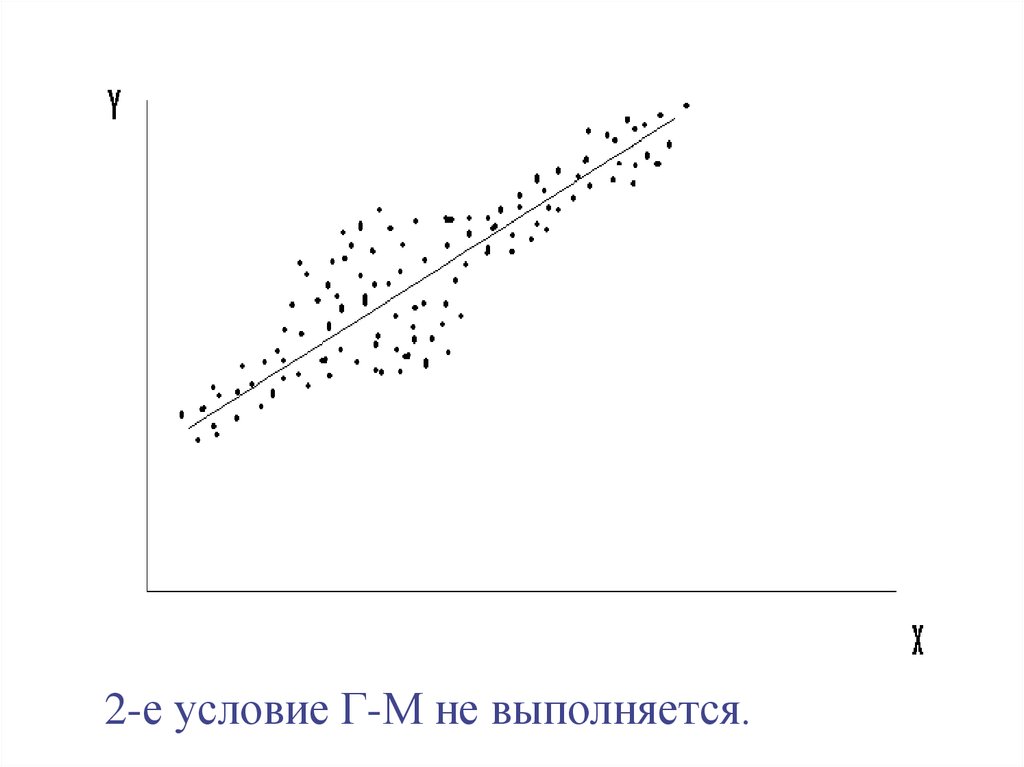
32. 2. σei2 = σ2 = const для всех наблюдений Xi

Условие гомоскедастичности ошибок.
Когда оно не выполняется, говорят о
гетероскедастичности ошибок.

33.

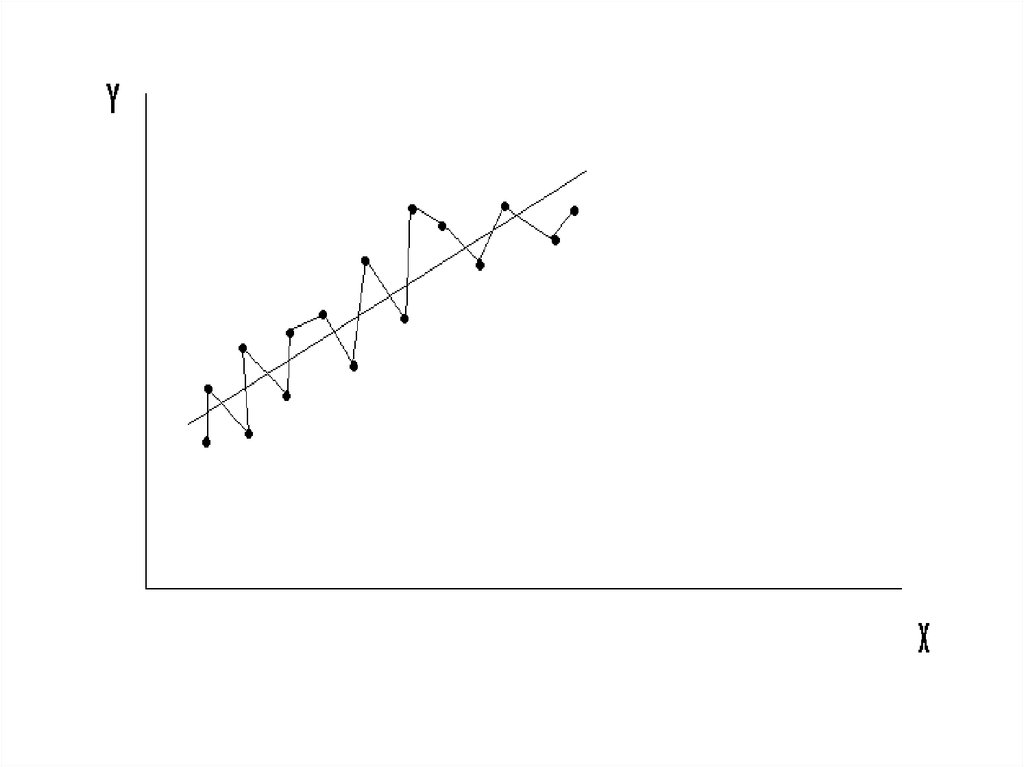
2-е условие Г-М выполняется.

34.

2-е условие Г-М не выполняется.

35.

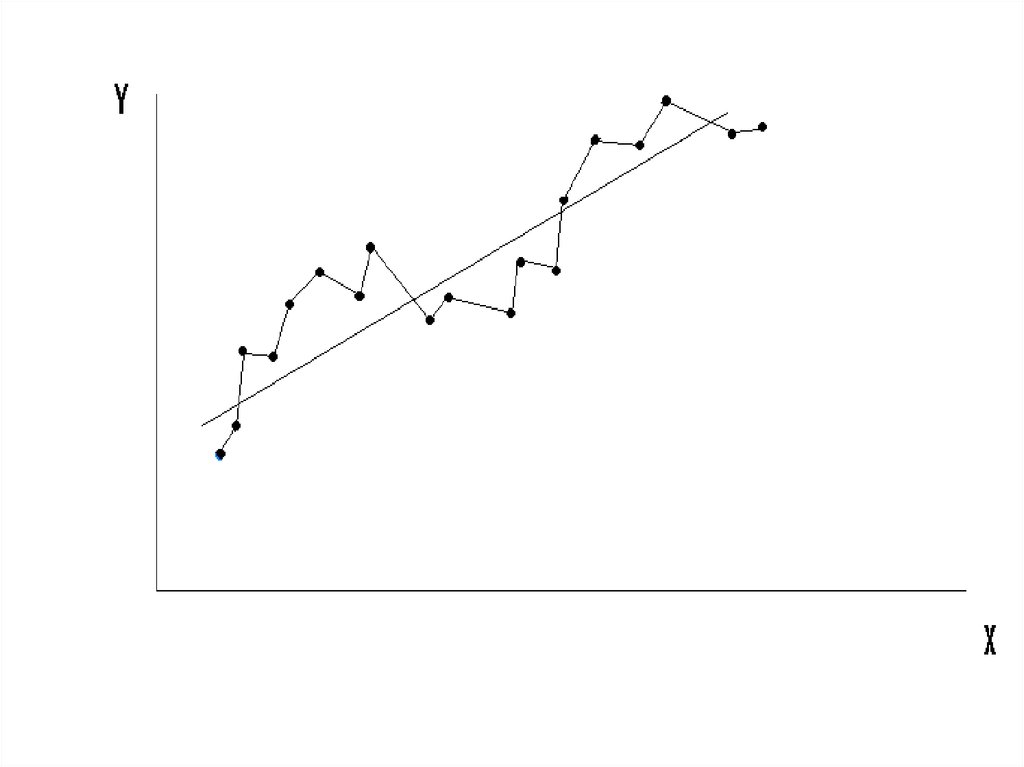
2-е условие Г-М не выполняется.

36. 3. σei, ej = 0 для всех Xi и Xj, i  j .

3. σei, ej = 0 для всех Xi и Xj, i j .
Условие некоррелированности ошибок для
разных наблюдений.
Это условие часто нарушается, когда данные
являются временными рядами, из-за
наличия в динамике экономических
показателей различных регулярных
колебаний.
При невыполнении (3) говорят об
автокоррелированности остатков.

37.

38.

39. 4. σXi, ei = 0 для всех наблюдений.

Случайный член распределен
независимо от объясняющей
переменной.
Это всегда выполняется, если
объясняющие переменные не
являются случайными величинами.

40. Дополнительное условие: 7. Случайный член, i=1, …, n, имеет нормальное распределение, ei ~ N(0, e2)

Дополнительное условие:
7. Случайный член, i=1, …, n,
имеет нормальное
распределение,
ei ~ N(0, e2)

41.

Это условие не нужно для обеспечения
хороших свойств оценок a и b.
Но оно позволяет корректно проводить
проверку гипотез о коэффициентах
регрессии.
Реальность предположения о
нормальности ei обеспечивается
Центральной предельной теоремой.

42. Теорема Гаусса-Маркова

Если предпосылки МНК соблюдаются, то оценки,
полученные по МНК, обладают следующими
свойствами:
1. Оценки параметров являются несмещенными, т.е.
М(bi)= bi и М(а)= а. Это вытекает из того, что М(еi)=
0 и говорит об отсутствии систематической ошибки в
определении положения линии регрессии
2. Оценки параметров состоятельны, т.к. дисперсия
оценок параметров при возрастании числа n
наблюдений стремится к нулю. Т.е. При увеличении
объема выборки надежность оценок возрастает.
3. Оценки параметров эффективны, т.е. Они имеют
наименьшую дисперсию по сравнению с другими
оценками данных параметров.

43. F-критерий Фишера

H0 – гипотеза о статистической незначимости
уравнения регрессии и показателя тесноты
связи: b=0, ryx=0
2
R
F
(n m 1)
2
1 R
Если Fрасч Fтабл , то отвергается гипотеза H0 и
признается значимость и надежность
полученных оценок параметров a и b

44. t-статистика Стьюдента

H0 – гипотеза о статистической незначимости
оценок параметров уравнения регрессии и
показателя тесноты связи: a=b=ryx=0
b
a
r
tb
; ta
; tr
mb
ma
mr
где mb , ma , mr – случайные ошибки
параметров линейной регрессии и
коэффициента корреляции

45. Формулы для расчета случайных ошибок:

mb
ma
mr
^ 2
(
y
y)
(n m 1) ( x x )
^ 2
(
y
y
)
2
2
x
(n m 1) n ( x x )
1 r
2
yx
n m 1
2

46. Расчет доверительного интервала прогноза

где
a a a
b b b
a tтаблma , b tтаблmb
Если в границы доверительного интервала попадает ноль,
т.е. нижняя граница отрицательна, а верхняя
положительна, то оцениваемый параметр принимается
нулевым, т.к. он не может одновременно принимать и
положительное и отрицательное значение.

47. Расчет прогнозного значения

Прогнозное значение yp определяется путем
подстановки в уравнение регрессии
соответствующего (прогнозного) значения xp.
Вычисляется средняя стандартная ошибка прогноза:
( y y)
^ 2
my p
^
1 (xp x)
1
2
n m 1
n (x x)
2
и строится доверительный интервал прогноза:
y y p tтабл my
^
^
p
^
p