Similar presentations:
Метод наименьших квадратов
1.
1. Спецификация линейной модели парнойрегрессии.
2. Оценки параметров линейной регрессии.
Метод наименьших квадратов (МНК).
3. Предпосылки МНК и свойства МНК-оценок.
4. Интервалы прогноза по линейному
уравнению регрессии.
5. Нелинейная парная регрессия, ее
линеаризация и применение.
2.
1 вопросСуть регрессионного анализа
Корреляционный
анализ
Регрессионный
анализ
• X и Y равноценны, не делятся на
независимую и зависимую
• Измеряют наличие и силу
взаимосвязи между X и Y, основной
мерой является коэффициент
корреляции
• X и Y не равноценны, изменение
независимой X служит причиной
для изменения зависимой Y
• Анализируют как X влияет на Y «в
среднем» и определяют функцию
регрессии Y на X.
3.
Цель регрессионного анализаТермин «регрессия» был введен Фрэнсисом Гальтоном в конце 19 века.
Основная цель – оценка функциональной зависимости
между независимыми переменными X и условным
математическим ожиданием (средним значением)
зависимой переменной Y
4.
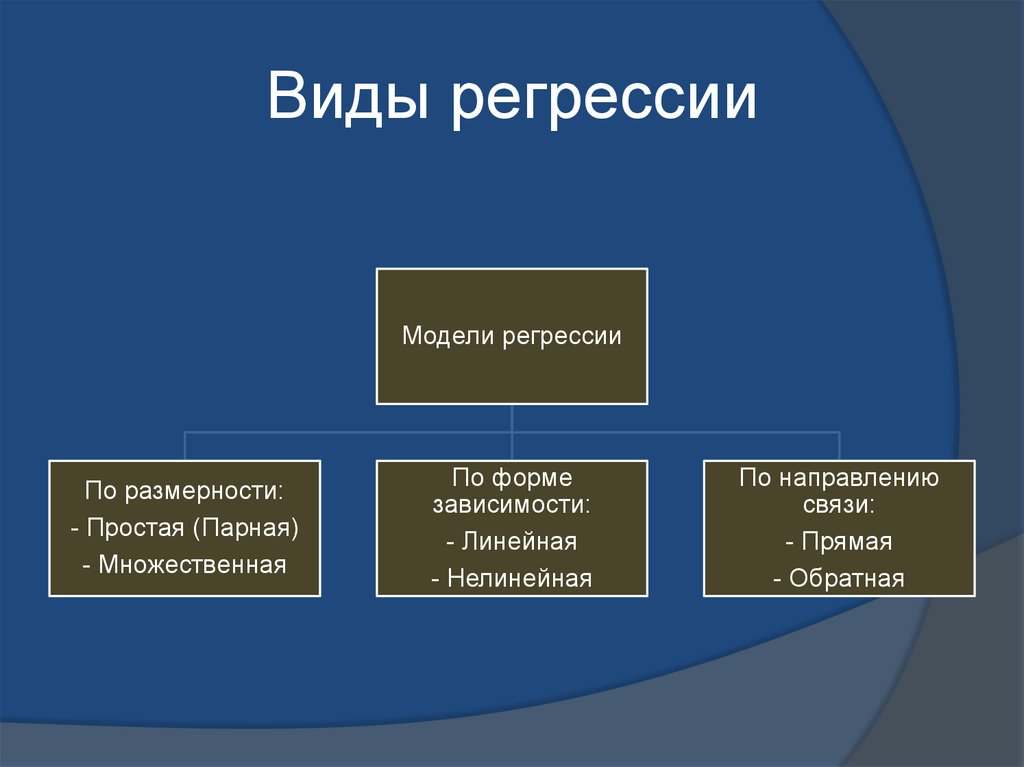
Виды регрессииМодели регрессии
По размерности:
- Простая (Парная)
- Множественная
По форме
зависимости:
- Линейная
- Нелинейная
По направлению
связи:
- Прямая
- Обратная
5.
Простая (парная) регрессия представляет собой модель, где среднеезначение зависимой переменной Y рассматривается как функция
одной независимой переменной X:
Yx f (x)
Множественная регрессия представляет собой модель, где среднее
значение зависимой переменной Y рассматривается как функция
нескольких независимых переменных X1, X2, …, :
Yx f ( x1, x2 ,..., xm )
6.
Определяется состав переменных иматематическая функция для отражения
связи между ними.
7.
Yi Yxi iYi - фактическое значение зависимой
переменной Y
Yxi - теоретическое (среднее) значение
зависимой переменной Y, найденное из
уравнения регрессии
εi - случайная величина (остаток регрессии)
8.
Yxi a b xiYxi - теоретическое (среднее) значение зависимой переменной Y,
найденное из уравнения регрессии
b - эмпирический коэффициент регрессии
а- эмпирический свободный коэффициент
В конкретном случае:
Yi a b xi ei
ei – оценка теоретического случайного отклонения ε
9.
Yi xi iα – свободный коэффициент
β - коэффициент регрессии
εi – случайное отклонение (возмущение)
Случайное отклонение включает влияние не учтенных в модели
факторов, случайных ошибок и особенностей измерения. Источники его
присутствия в модели: спецификация модели, выборочный характер
исходных данных, особенности измерения переменных.
10.
Ошибкиспецификации
Ошибки выборки
Ошибки измерения
• Неправильный
выбор
математической
функции
• Недоучет
существенного
фактора
• Неоднородные
статистические
данные
• Неправильный
выбор временного
интервала
информации
• Преднамеренные
ошибки в
отчетности
• Непреднамеренные
ошибки из-за
сокрытия
информации
11.
Графическийметод
• Основан на визуальном анализе
поля корреляции
Аналитический
метод
• Основан на изучении материальной
природы взаимосвязи
Эксперименталь
ный метод
• Основан на сравнении величины
остаточной дисперсии,
рассчитанной при разных моделях
12.
YY
0
X
0
X
Yx a b x Yx a b x c x
2
13.
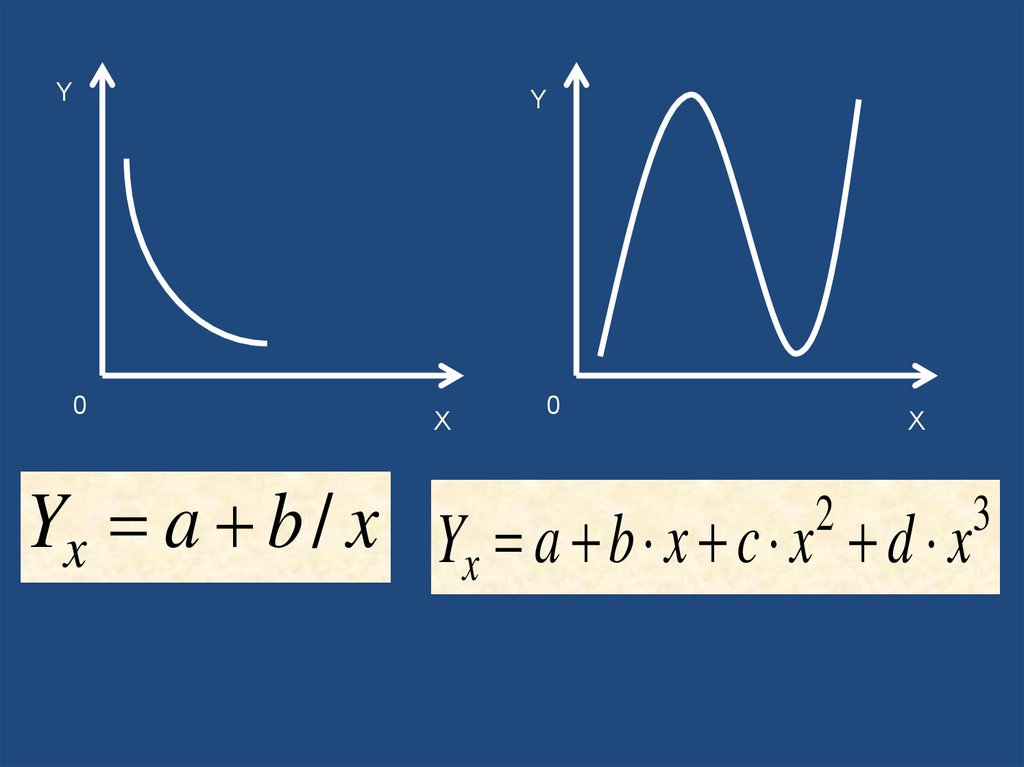
Y0
Y
X
0
X
Yx a b / x Yx a b x c x2 d x3
14.
YY
0
Yx a x
X
b
0
Yx a b
X
x
15.
2 вопросПостроение линейной регрессии сводится к оценке ее
параметров – a и b
Классический подход к оцениванию параметров основан
на методе наименьших квадратов
Из множества линий на графике выбирается та, для
которой минимальна сумма квадратов расстояний по
вертикали между точками наблюдений и этой линией
16.
YYi
εi
Yxi
Yxi a b xi
0
X
17.
Суть метода наименьших квадратов(МНК) - оценки параметров таковы, что
сумма квадратов отклонений фактических
значений зависимой переменной Y от
расчетных (теоретических) Yx
минимальна:
n
( yi yxi )
i 1
2
min
18.
S ( yi y x i ) ( y a b x) ;2
2
dS
2 y 2 n a 2 b x 0;
da
dS
2
2 y x 2 a x 2 b x 0.
db
19.
n a b x y,2
a x b x y x
a y b x,
b
y x y x
x (x)
2
2










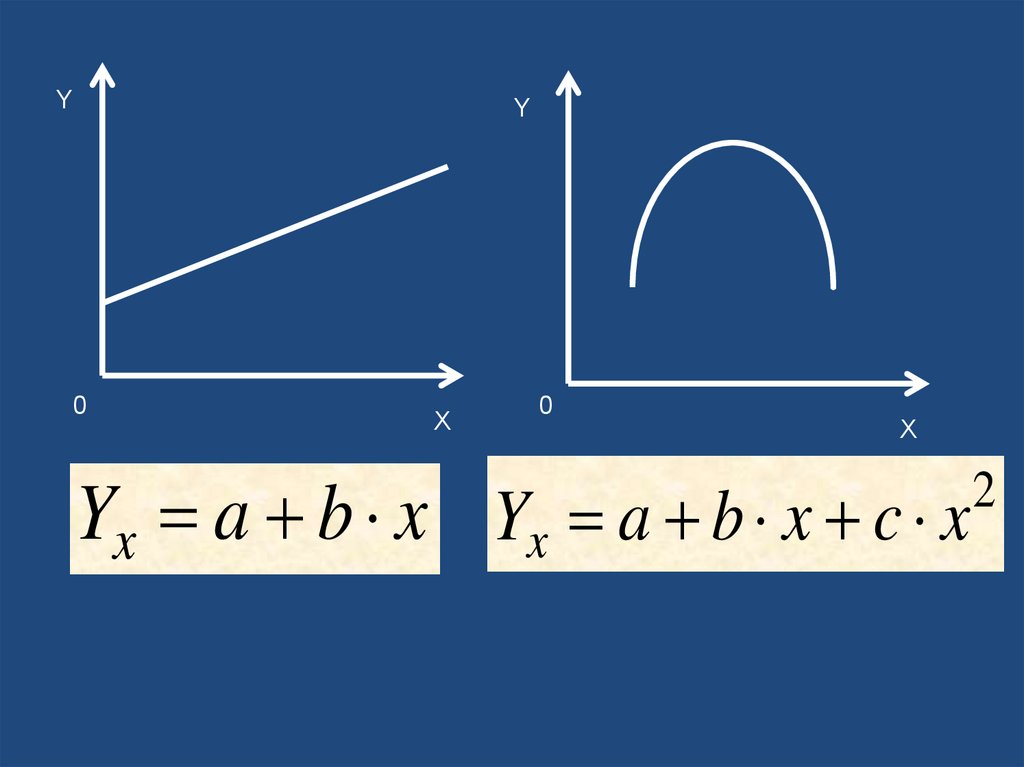
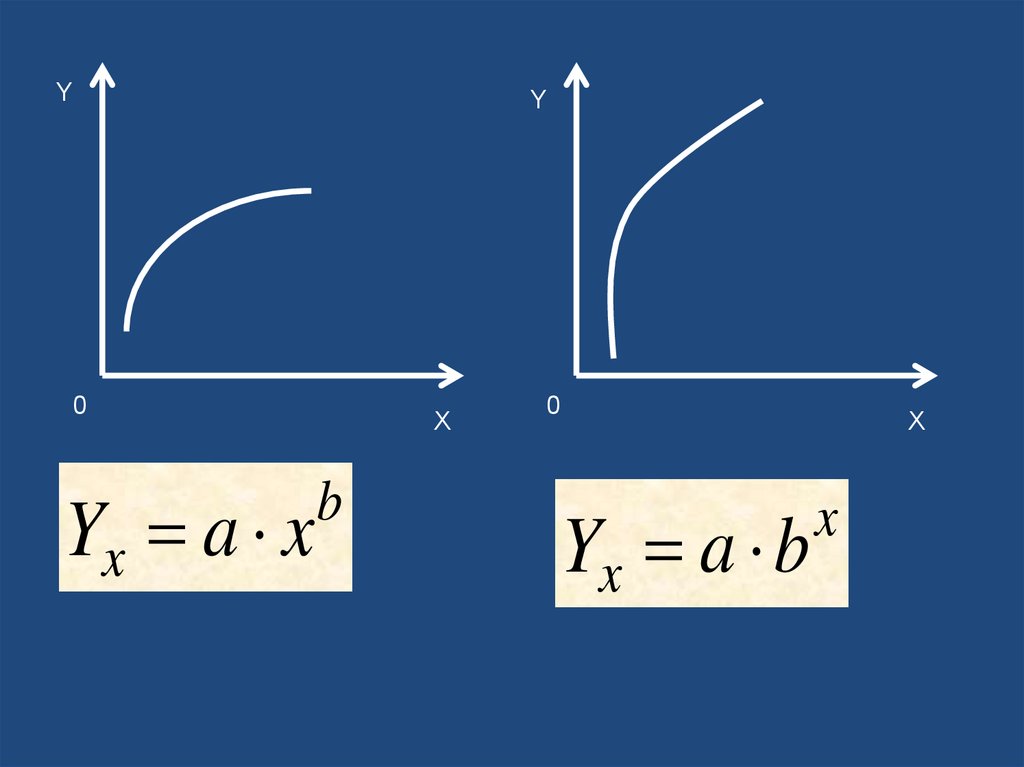




 mathematics
mathematics








