Similar presentations:
Предпосылки метода наименьших квадратов. Обобщенный МНК
1. Лекция № 3. Предпосылки метода наименьших квадратов. Обобщенный МНК
Вопросы• 1. Предпосылки МНК и способы
проверки их выполнения.
• 2. Свойства оценок, полученных с
помощью МНК.
• 3. Обобщенный МНК.
1
2.
1. При оценке параметров уравнениярегрессии с помощью МНК делаются
определенные предпосылки
относительно случайной
составляющей ε.
В модели
у = а + b1x1 + b2x2 +…+ bpxp + ε
случайная составляющая ε
представляет собой ненаблюдаемую
величину.
2
3.
После получения оценок параметровмодели можно получить оценки ε,
вычисляя разности фактических и
теоретических
значений
результативного признака у. Так как
они
не
являются
реальными
случайными остатками, их можно
считать
некоторой
выборочной
реализацией неизвестного остатка
заданного уравнения, т.е. εi .
3
4.
При изменении спецификации модели,добавлении в нее новых наблюдений
выборочные
остатки
εi
могут
меняться.
Поэтому
в
задачу
регрессионного анализа входит не
только построение самой модели, но и
исследование случайных отклонений
εi, т.е. остаточных величин.
4
5.
Проверяястатистическую
достоверность
коэффициентов
регрессии
и
корреляции,
мы
останавливались
на
t-критерии
Стьюдента, F-критерии Фишера. При
этом
делались
предположения
относительно поведения остатков εi -
5
6.
этонезависимые
случайные
величины; их среднее значение равно
0; они имеют постоянную дисперсию
и подчиняются нормальному закону
распределения. Эти предположения
являются условиями теоремы ГауссаМаркова.
6
7.
2.Статистические
проверки
параметров регрессии, показателей
корреляции
основаны
на
непроверяемых
предпосылках
распределения
случайной
составляющей εi. Они носят лишь
предварительный характер. Уже после
построения
уравнения
регрессии
проводится проверка наличия у
оценок εi тех свойств, которые
изначально предполагались.
7
8.
• Речь идет о том, что оценкипараметров регрессии должны быть
несмещенными, состоятельными и
эффективными. Эти свойства
оценок, полученных по МНК, имеют
чрезвычайно важное практическое
значение в использовании
результатов регрессии и корреляции.
8
9.
• Напомним, что несмещенностьоценки означает, что ее
математическое ожидание равно
оцениваемому параметру, а
математическое ожидание остатков
равно нулю. Следовательно, при
большом числе выборочных
оцениваний остатки не будут
накапливаться и найденный
параметр регрессии bi
9
10.
можно рассматривать как среднеезначение из возможного большого
количества несмещенных оценок.
Несмещенные оценки можно
сравнивать по разным
исследованиям.
10
11.
Эффективность оценок означает, чтоони характеризуются наименьшей
дисперсией. В практических
исследованиях это означает
возможность перехода от точечного
оценивания к интервальному.
11
12.
Степень реалистичностидоверительных интервалов
параметров регрессии
обеспечивается, если оценки будут
не только несмещенными и
эффективными, но и
состоятельными. Состоятельность
оценок характеризует увеличение их
точности с увеличением объема
выборки.
12
13.
Большой практический интереспредставляют те результаты
регрессии, для которых
доверительный интервал
ожидаемого значения параметра
регрессии bi имеет предел значений
вероятности, равный единице. То
есть вероятность получения оценки
на заданном расстоянии от
истинного значения параметра
близка к единице.
13
14.
Указанные критерии оценок(несмещенность, состоятельность,
эффективность) обязательно
учитываются при разных способах
оценивания.
МНК строит оценки регрессии на
основе минимизации суммы
квадратов остатков. Поэтому очень
важно исследовать их поведение.
14
15.
Условия, необходимые для получениянесмещенных, состоятельных и
эффективных оценок, представляют
собой предпосылки МНК,
соблюдение которых желательно
для получения достоверных
результатов регрессии.
15
16.
Исследования остатков εiпредполагают проверку наличия
следующих пяти предпосылок МНК:
1) случайный характер остатков;
2) нулевая средняя величина остатков,
не зависящая от хi;
3) гомоскедастичность – дисперсия
каждого отклонения εi одинакова для
всех значений х;
16
17.
4) отсутствие автокорреляцииостатков. Значения остатков εi
распределены независимо друг от
друга;
5) остатки подчиняются нормальному
распределению.
Если хотя бы одна предпосылка не
выполняется, следует корректировать модель.
17
18.
• Для проверки первой предпосылкистроится график зависимости
остатков εi от теоретических значений
результативного признака .
Если все значения остатков εi
размещаются в горизонтальной
полосе, то остатки представляют
собой случайные величины и МНК
оправдан, теоретические значения у х
хорошо аппроксимируют фактические
значения у (рис. 1).
18
19.
*Рис.1. Зависимость случайных остатков εi от
теоретических значений ŷх
19
20.
• Если же зависимость остатков εi от у хпроявляется в том, что:
а) остатки εi не случайны;
б) остатки не имеют постоянной
дисперсии;
в) остатки носят систематический
характер, то нужно либо применять
другую функцию, либо вводить
дополнительную информацию и
заново строить уравнение регрессии
до тех пор, пока остатки εi не будут
случайными величинами.
20
21.
*Рис. 2. Зависимость случайных остатков
εi от теоретических значений ŷх
21
22.
• Вторая предпосылка МНКотносительно нулевой средней
величины остатков означает, что
y y 0.
x
Это выполнимо для линейных моделей
и моделей, нелинейных относительно
включаемых переменных.
22
23.
А для моделей, нелинейныхотносительно оцениваемых
параметров и приводимых к
линейному виду с помощью
логарифмирования, средняя ошибка
равна нулю для логарифмов
исходных данных.
23
24.
Так, для модели видаy ax x ... x имеем , ln y ln y x 0 .
Кроме того, несмещенность оценок
коэффициентов регрессии, полученных
МНК, зависит также от независимости
случайных остатков от величин х, что
также исследуется в рамках
соблюдения второй предпосылки МНК.
С этой целью строится график
зависимости случайных остатков ε от
факторов хi, включенных в регрессию.
b1
1
b2
2
bp
p
24
25.
• Если остатки на графикерасположены в виде горизонтальной
полосы, то они независимы от
значений хj. Если же график
показывает наличие указанной
зависимости, то модель неадекватна
(рис. 2).
25
26.
• *Рис. 3. Зависимость случайных остатков
εi от величины фактора хj .
26
27.
Причины неадекватности могут бытьразные: 1) нарушение третьей
предпосылки МНК (дисперсия
остатков не постоянна для каждого
значения фактора хj);
2) неправильная спецификация
модели, и в нее необходимо ввести
дополнительные члены от хj,
например, хj2, или преобразовать
значения у. Скопление точек в
определенных участках значений
фактора хj говорит о наличии
систематической погрешности
модели.
27
28.
Предпосылка о нормальномраспределении остатков позволяет
проводить проверку параметров
регрессии и корреляции с помощью
критериев t, F. Вместе с тем оценки
регрессии, найденные с
применением МНК, обладают
хорошими свойствами даже при
отсутствии нормального
распределения остатков, т.е. при
нарушении пятой предпосылки МНК.
28
29.
Для получения состоятельных оценокпараметров регрессии по МНК
совершенно необходимо
соблюдение третьей и четвертой
предпосылок.
В соответствии с третьей
предпосылкой МНК требуется, чтобы
дисперсия остатков была
гомоскедастичной. Это значит, что
для каждого значения фактора хj
остатки εi имеют одинаковую
дисперсию. В противном случае
имеем гетероскедастичность.
29
30.
Наличие гетероскедастичности можнонаглядно видеть из поля корреляции
(рис. 4).
30
31.
3132.
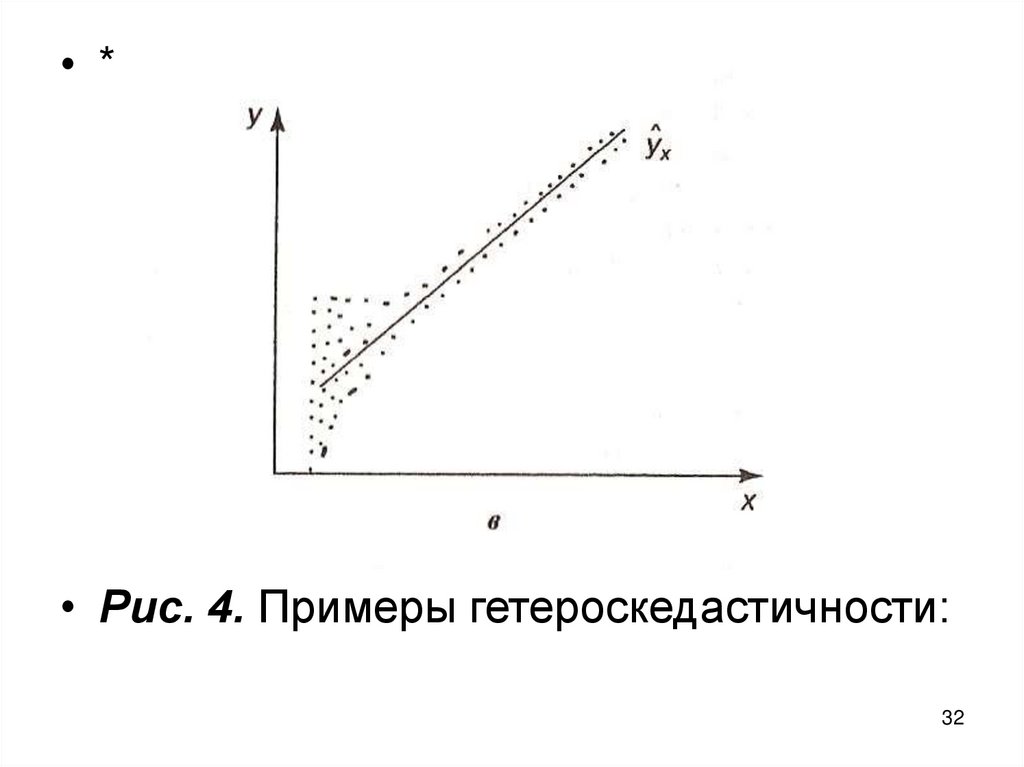
• *• Рис. 4. Примеры гетероскедастичности:
32
33.
а) дисперсия остатков растет по мереувеличения х;
б) дисперсия остатков достигает
максимальной величины при средних
значениях переменной х и уменьшается
при минимальных и максимальных
значениях х;
в) максимальная дисперсия остатков при
малых значениях х и дисперсия
остатков однородна по мере
увеличения значений х.
33
34.
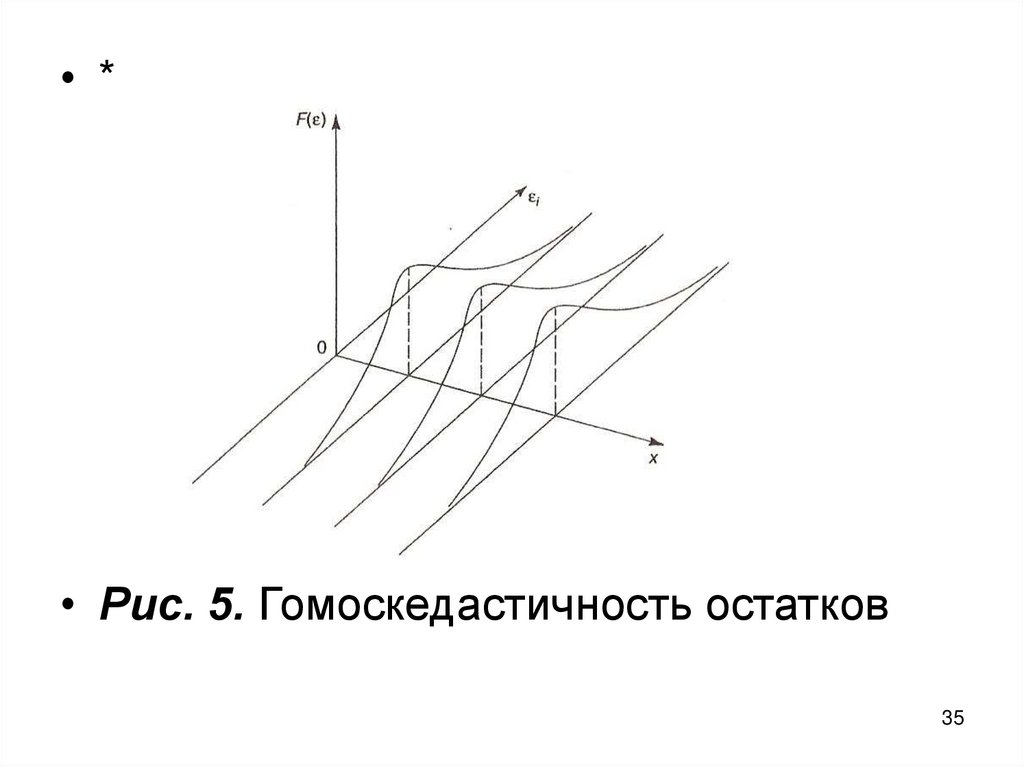
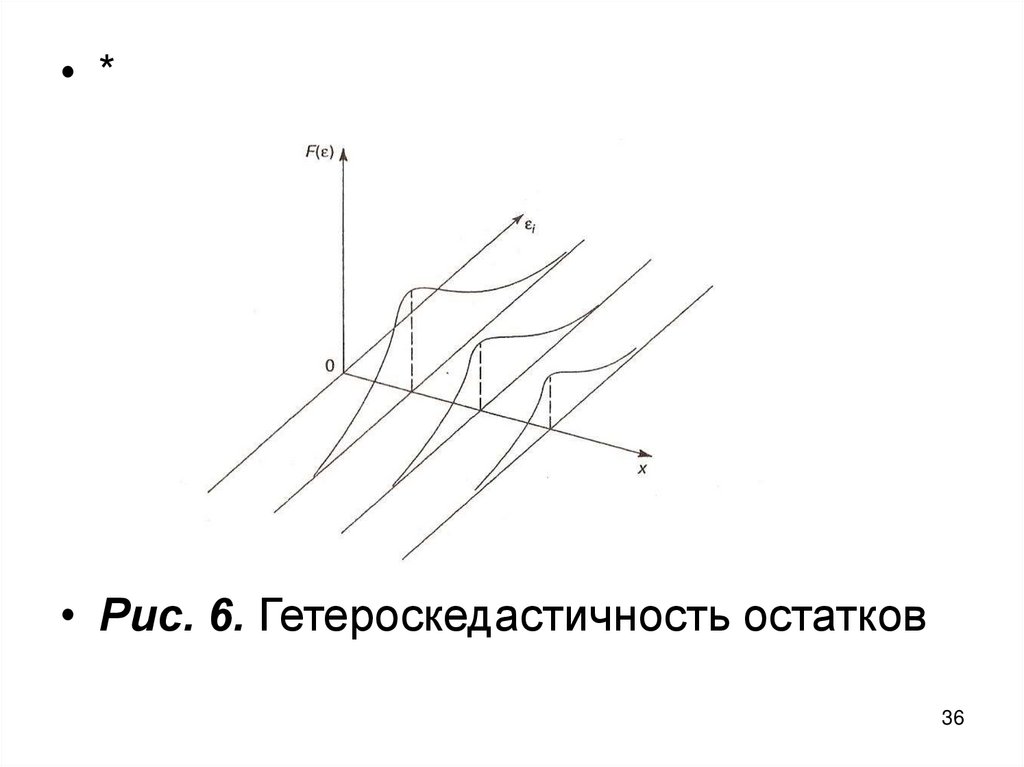
В случае гомоскедастичности длякаждого значения хi распределения
остатков одинаковы, а в случае
гетероскедастичности при переходе
от одного значения хi к другому
меняется диапазон варьирования
остатков.
34
35.
• *• Рис. 5. Гомоскедастичность остатков
35
36.
• *• Рис. 6. Гетероскедастичность остатков
36
37.
Наличие гомоскедастичности илигетероскедастичности можно видеть и
по рассмотренному выше графику
зависимости остатков εi от
теоретических значений
результативного признака ŷх. Так, для
рисунка 4а) зависимость остатков от ŷх
представлена на рис. 7.
37
38.
*Рис. 7. Гетероскедастичность: большая
дисперсия εi для больших значений ŷх.
38
39.
Соответственно для зависимостей,изображенных на полях корреляции
рис. 4 б) и в), гетероскедастичность
остатков представлена на рис. 8 и 9.
39
40.
*• Рис. 8. Гетероскедастичность,
соответствующая полю корреляции рис.
4б)
40
41.
*Рис. 9. Гетероскедастичность,
соответствующая полю корреляции рис.
4в)
41
42.
Наличие гетероскедастичностиможет в отдельных случаях
привести к смещенности оценок
коэффициентов регрессии, хотя
несмещенность этих оценок
зависит в основном от
соблюдения второй
предпосылки МНК.
Гетероскедастичность будет
сказываться на уменьшении
эффективности оценок bi.
42
43.
Практически при нарушениигомоскедастичности мы имеем
неравенства:
, i j ,
2
i
2
j
2
и можно записать
Ki .
2
i
2
При этом величина Ki может меняться
при переходе от одного значения
фактора xi к другому.
43
44.
Это означает, что сумма квадратовотклонений для зависимости
y x a bx
при наличии гетероскедастичности
должна иметь вид:
S гетеро
1
Ki
2
y a bx .
i
i
44
45.
При минимизации этой суммыквадратов отдельные ее слагаемые
взвешиваются: наблюдениям с
наибольшей дисперсией придается
пропорционально меньший вес.
Иными словами, для учета
систематического влияния
неоднородных элементов Ki вклад
каждой пары xi c yi в сумму
квадратов остатков должен быть
дисконтирован.
45
46.
Задача состоит в том, чтобыопределить величину Ki и внести
поправку в исходные переменные.
С этой целью рекомендуется
использовать обобщенный метод
наименьших квадратов, который
эквивалентен обыкновенному МНК,
примененному к преобразованным
данным.
46
47.
3. Обобщенный МНК применяется принарушении гомоскедастичности и
наличии автокорреляции ошибок.
ОМНК применяется к
преобразованным данным и
позволяет получать оценки,
обладающие не только свойством
несмещенности, но и имеющие
наименьшие выборочные
дисперсии. Остановимся на
использовании ОМНК для
корректировки
гетероскедастичности.
47
48.
Как и раньше, будем предполагать, чтосреднее значение остатков равно
нулю, а дисперсия не остается
постоянной для разных значений
фактора, а изменяется
пропорционально величине Ki , т.е.
Ki ,
2
i
2
где -i дисперсия ошибки при
конкретном i-м значении фактора;
2
48
49.
σ2 - постоянная дисперсия ошибки присоблюдении предпосылки о
гомоскедастичности остатков;
Ki – коэффициент
пропорциональности, меняющийся с
изменением величины фактора, что и
обусловливает неоднородность
дисперсии.
49
50.
В общем виде для уравненияyi a bxi i
при
Ki
2
i
2
модель примет вид:
yi xi Ki i .
50
51.
В ней остаточные величиныгетероскедастичны. Предполагая в
них отсутствие автокорреляции,
можно перейти к уравнению с
гомоскедастичными остатками,
поделив все переменные,
зафиксированные в ходе i-го
наблюдения, на Ki .
Тогда дисперсия остатков будет
величиной постоянной, т.е.
2
i
= σ2.
51
52.
Таким образом, от регрессии у по х мыперейдем к регрессии на новых
переменных:
y
х
K
и
K
.
Уравнение регрессии примет вид:
yi
xi
i .
Ki
Ki
Ki
52
53.
Исходные данные для данногоуравнения будут иметь вид:
y
y1
K1
y2
K2
...
yn
Kn
x
x1
K1
x2
K2
...
xn
Kn
53
54.
По отношению к обычной регрессииуравнение с новыми,
преобразованными, переменными
представляет собой взвешенную
регрессию, в которой переменные х
и у взяты с весами
1
.
K
54
55.
Оценка параметров нового уравненияс преобразованными переменными
приводит к взвешенному методу
наименьших квадратов, для которого
необходимо минимизировать сумму
квадратов отклонений вида
2
1
S yi a bxi .
Ki
55
56.
Соответственно получим следующуюсистему нормальных уравнений:
yi
xi
1
a
b
,
K
Ki
Ki
i
yx
2
x
x
i
i
i
i
a b .
K i
Ki
Ki
56
57.
Если преобразованные переменные хи у взять в отклонениях от средних
уровней, то коэффициент регрессии
b можно определить как
b
1
xy
K
.
1 2
x
K
57
58.
При обычном применении МНК дляпеременных в отклонениях от
средних уровней коэффициент
регрессии определяется по формуле
b
x
xy
2
.
58
59.
Таким образом, при использованииобобщенного МНК с целью
корректировки гетероскедастичности
коэффициент регрессии b
представляет собой взвешенную
величину по отношению к обычному
МНК с весами 1/K.
59
60.
Рассмотрим данный подход дляуравнения множественной
регрессии.
Пусть рассматривается модель вида
y = a + b1x1 + b2x2 + ε,
для которой дисперсия остатков
оказалась пропорциональной K2i ,
где Ki – коэффициент
пропорциональности, принимающий
различные значения для
соответствующих i значений
60
факторов х1 и х2.
61.
Так какK ,
рассматриваемая модель примет вид
2
i
2
2
i
yi a b1 x1i b2 x2i Ki i ,
где ошибки гетероскедастичны.
61
62.
Для перехода к новому уравнению сгомоскедастичными остатками
разделим все члены исходного
уравнения на коэффициент
пропорциональности K.
Тогда
yi a
x1i
x2 i
b1 b2 i .
Ki Ki
Ki
Ki
62
63.
• Это уравнение не содержитсвободного члена. Вместе с тем,
найдя переменные в новом
преобразованном виде и применяя к
ним обычный МНК, получим иную
спецификацию модели:
yi
x1i
x2i
A b1 b2 i .
Ki
Ki
Ki
63
64.
Параметры такой модели зависят отконцепции, принятой для
коэффициентов
пропорциональности Ki. В
эконометрических исследованиях
довольно часто выдвигается
гипотеза, что остатки εi
пропорциональны значениям
фактора.
64
65.
Так, если в уравненииy a b1 x1 b2 x2 ... bp x p E
предположить, что Е = εх1, т.е. K = x1 и
x ,
2
i
2 2
1
то ОМНК предполагает оценку
параметров следующего
трансформированного уравнения:
xp
x2
y
b1 b2
... b p
.
x1
x1
x1
65
66.
Если предположить, что ошибкипропорциональны xp, то модель
примет вид:
x p 1
x1
y
bp b1 ... bp 1 .
xp
xp
xp
66
67.
Применение в этом случаеобобщенного МНК приводит к тому,
что наблюдения с меньшими
значениями преобразованных
переменных x/K имеют при
определении параметров регрессии
относительно больший вес, чем с
первоначальными переменными.
67
68.
Вместе с тем следует иметь в виду, чтоновые преобразованные
переменные получают новое
экономическое содержание и их
регрессия имеет иной смысл, чем
регрессия по исходным данным.
68






















































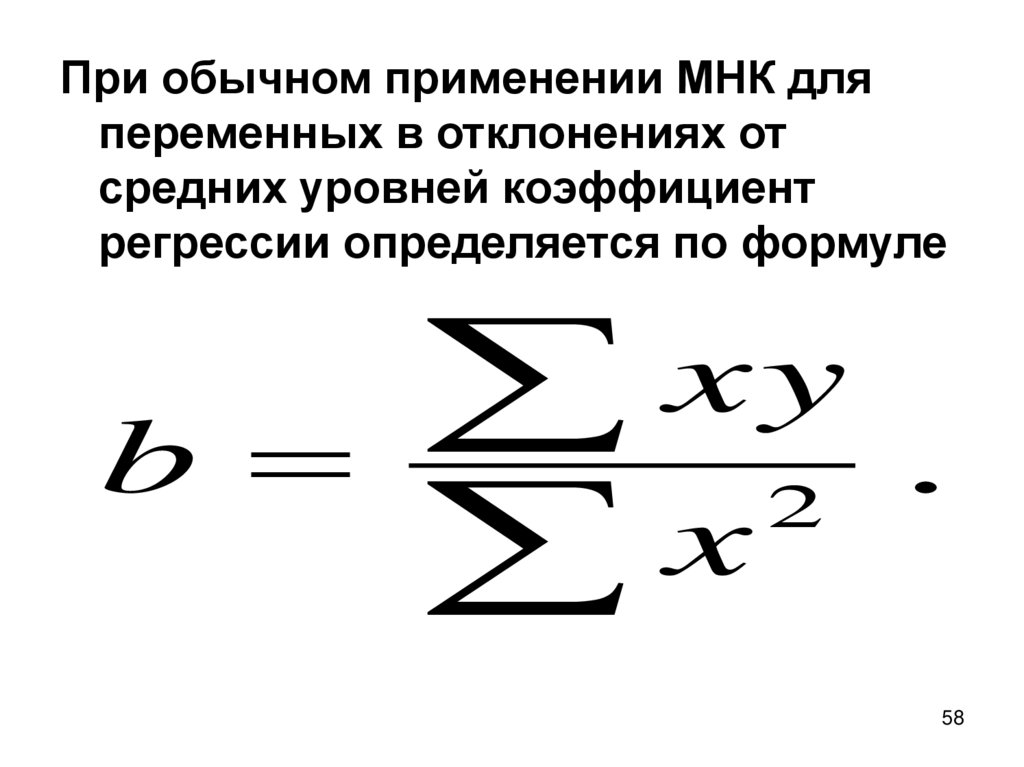










 mathematics
mathematics








