Предпосылки метода наименьших квадратов

1. Предпосылки метода наименьших квадратов

2. Исследование остаточных величин.

В задачу регрессионного
анализа входит не только
построение самой модели, но и
исследование случайных
отклонений, т.е. остаточных
величин.

3.

Оценки параметров регрессии должны
отвечать определенным критериям:
Несмещенность оценки (математическое
ожидание остатков равно нулю).
Эффективность (оценки имеют
наименьшую дисперсию).
Состоятельность (дисперсия оценок
параметров при возрастании числа
наблюдений стремится к нулю)

4.

Указанные критерии оценок
(несмещенность, состоятельность,
эффективность) обязательно учитываются
при разных способах оценивания.
Так как метод наименьших квадратов строит
оценки регрессии на основе минимизации
суммы квадратов остатков, то очень важно
исследовать поведение остаточных величин
регрессии i.

5.

Исследование остатков i предполагают
проверку наличия следующих пяти
предпосылок МНК (теорема ГауссаМаркова):
I. случайный характер остатков;
II. нулевая средняя величина остатков, не
зависящих от x;
III. гомоскедастичность – дисперсия
каждого отклонения одинаковая для всех
значений x;
IV. отсутствие автокорреляции остатков.
Значения остатков распределены
независимо друг от друга;
V. остатки подчиняются нормальному
распределению.

6.

Если распределение случайных
остатков не соответствует
некоторым предпосылкам
МНК, то следует
корректировать модель.

7.

I.
Прежде всего, проверяется
случайный характер остатков первая предпосылка МНК.
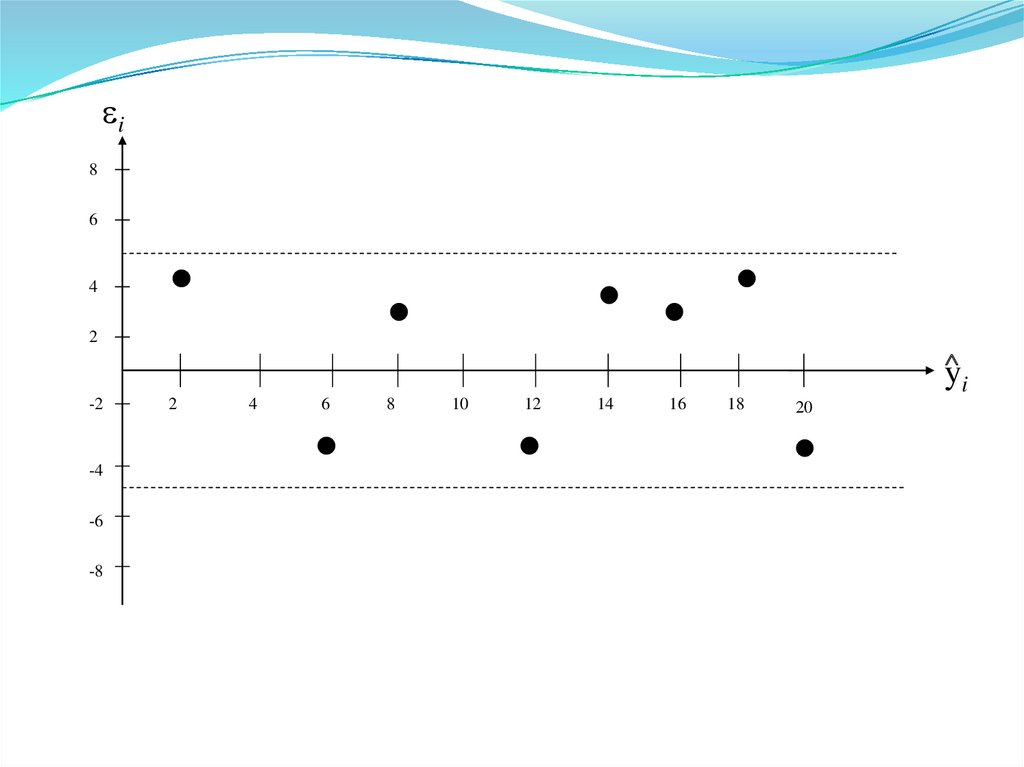
С этой целью строится график
зависимости остатков i от
теоретических значений
результативного признака y .

8.

i
8
6
4
2
yi
-2
-4
-6
-8
2
4
6
8
10
12
14
16
18
20

9.

Если на графике получена горизонтальная полоса (из
точек, как показано на рис.), то остатки i
представляют собой случайные величины и МНК
оправдан, теоретические значения y аппроксимируют
фактические значения y.
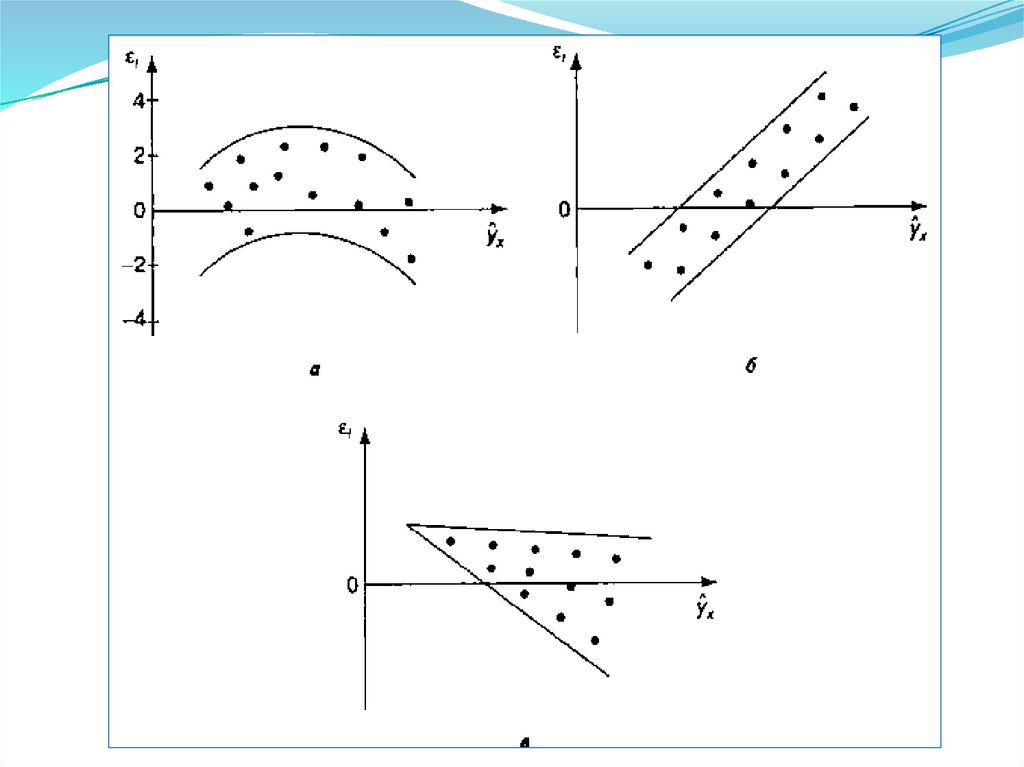
Возможны следующие случаи: если i зависит от y , то:
остатки не случайны (рис. а);
остатки не имеют постоянной дисперсии (рис. в);
остатки носят систематический характер (рис. б).

10.

11.

В этих случаях необходимо либо
применять другую функцию, либо
вводить дополнительную
информацию и заново строить
уравнение регрессии до тех пор,
пока остатки не будут случайными
величинами.

12.

II. Вторая предпосылка МНК
относительно нулевой средней
величины остатков означает, что
( у уˆ x ) 0.
• Это означает, что случайное отклонение в среднем не
оказывает влияния на зависимую переменную. В каждом
конкретном наблюдении случайный член может быть либо
положительным, либо отрицательным, но он не должен
иметь систематического смещения.
• Если ошибка имеет не нулевое среднее значение, то
оценки по МНК окажутся смещенными.

13.

III. В соответствии с третьей предпосылкой
МНК требуется, чтобы дисперсия
остатков была гомоскедастичной. Это
значит, что для каждого значения
фактора остатки должны иметь
одинаковую дисперсию.
D const
2
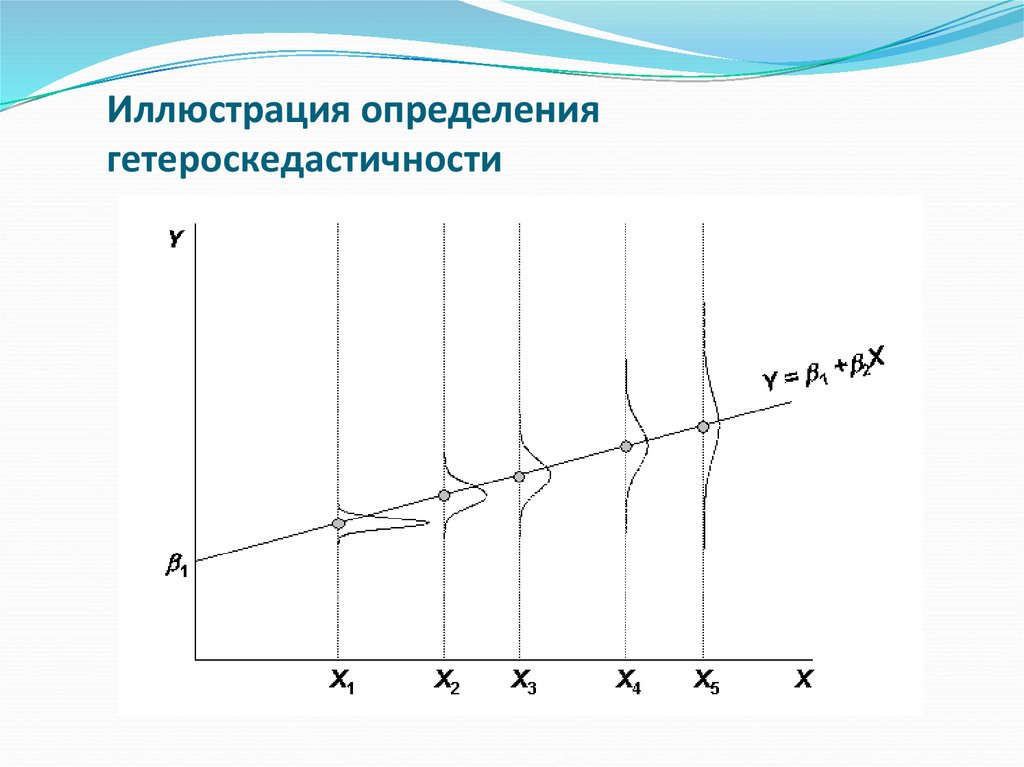
Если это условие не соблюдается, то
имеет место гетероскедастичность.
Наличие гетероскедастичности можно наглядно
видеть из графика зависимости остатков от
теоретических значений результативного признака.

14. Иллюстрация определения гетероскедастичности

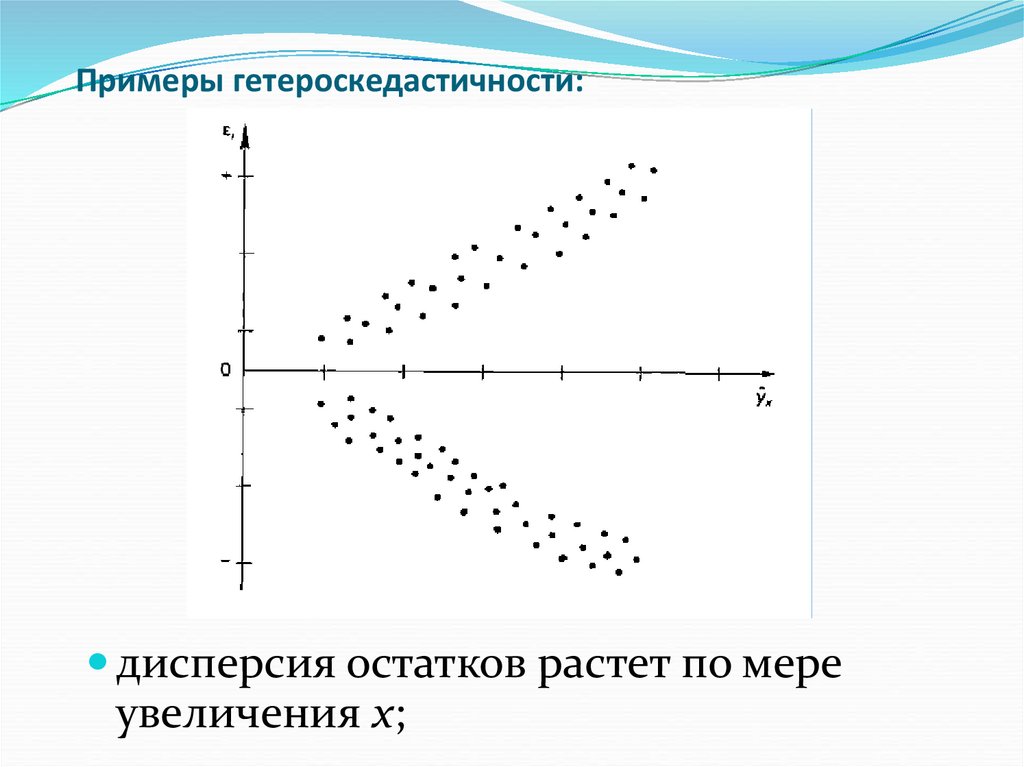
15. Примеры гетероскедастичности:

дисперсия остатков растет по мере
увеличения x;

16.

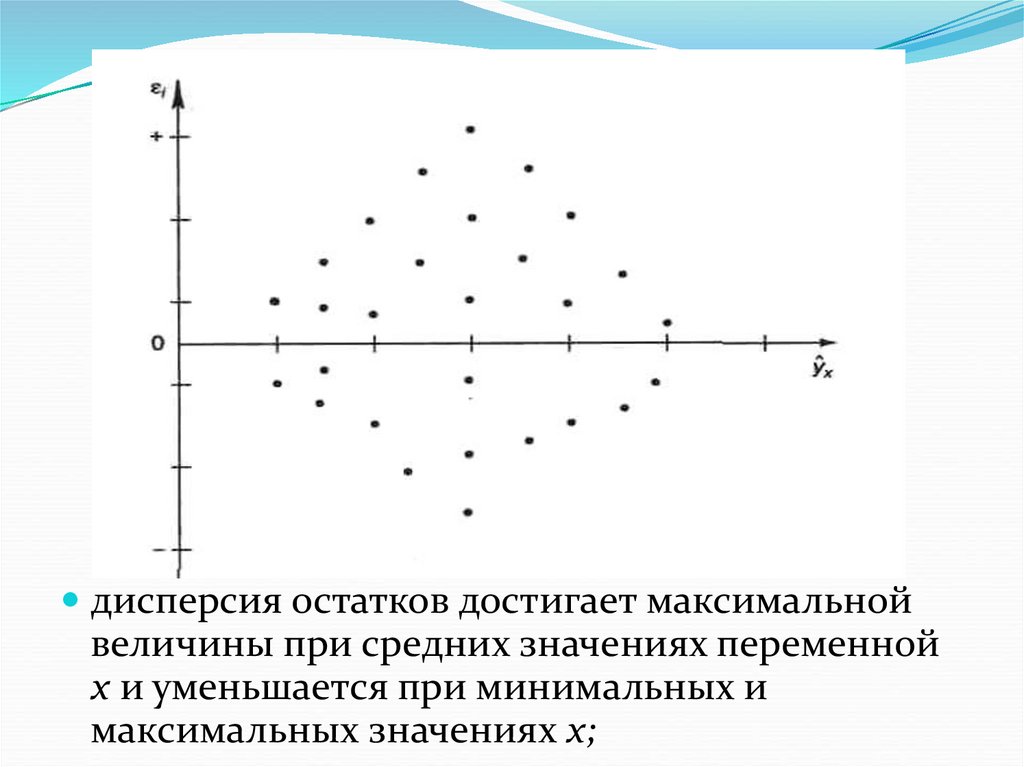
дисперсия остатков достигает максимальной
величины при средних значениях переменной
х и уменьшается при минимальных и
максимальных значениях х;

17.

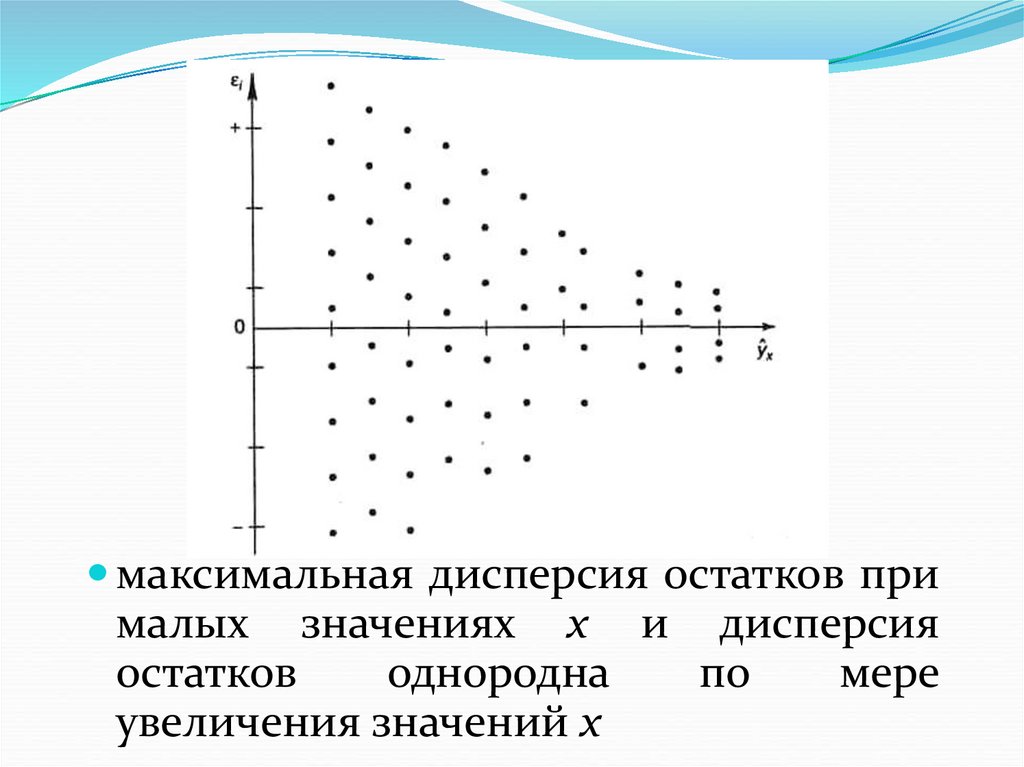
максимальная дисперсия остатков при
малых значениях х и дисперсия
остатков
однородна
по
мере
увеличения значений х

18. Метод Гольдфельда — Квандта

При малом объеме выборки, что
наиболее характерно для
эконометрических исследований,
для оценки гетероскедастичности
может использоваться метод
Гольдфельда — Квандта.

19. Метод Гольдфельда — Квандта

1. Упорядочение n наблюдений по мере
возрастания переменной у.
2. Исключение из рассмотрения С
центральных наблюдений; при этом
(n - С): 2 > р, где р — число
оцениваемых параметров.

20. Метод Гольдфельда — Квандта

3. Разделение совокупности из (n – C) наблюдений
на две группы (соответственно с малыми и
большими значениями фактора x) и определение
по каждой из групп уравнений регрессии.
4. Определение остаточной суммы квадратов для
первой (S1) и второй (S2) групп и нахождение их
отношения:
R S1 : S 2

21. Метод Гольдфельда — Квандта

При выполнении нулевой гипотезы о
гомоскедастичности отношение R
будет удовлетворять F -критерию с
(n-C-2p):2 степенями свободы для
каждой остаточной группы квадратов.
Чем больше величина превышает
табличное значение F-критерия, тем
более нарушена предпосылка о
равенстве дисперсий остаточных
величин.

22. Пример использования метода Гольдфельда — Квандта

Поступление доходов в бюджет
Санкт-Петербурга (у — млрд руб.) в
зависимости от численности
работающих на крупных и средних
предприятиях (х -тыс. чел.)
экономики районов за 1994 г.

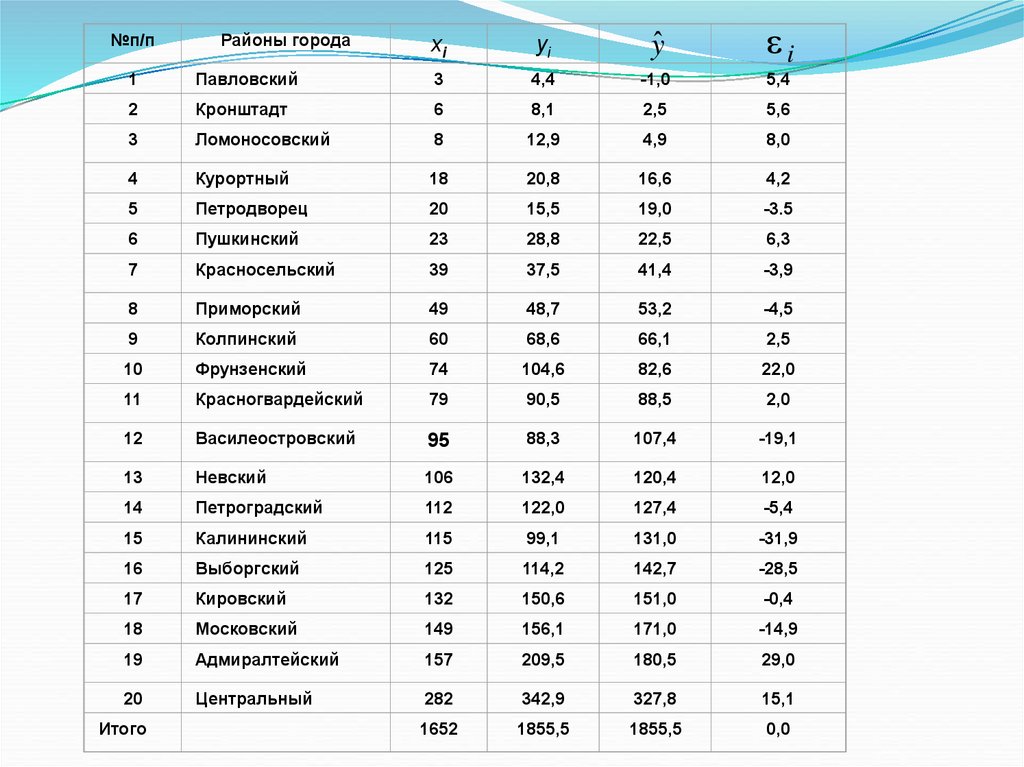
23.

№п/п
Районы города
xi
yi
ŷ
i
1
Павловский
3
4,4
-1,0
5,4
2
Кронштадт
6
8,1
2,5
5,6
3
Ломоносовский
8
12,9
4,9
8,0
4
Курортный
18
20,8
16,6
4,2
5
Петродворец
20
15,5
19,0
-3.5
6
Пушкинский
23
28,8
22,5
6,3
7
Красносельский
39
37,5
41,4
-3,9
8
Приморский
49
48,7
53,2
-4,5
9
Колпинский
60
68,6
66,1
2,5
10
Фрунзенский
74
104,6
82,6
22,0
11
Красногвардейский
79
90,5
88,5
2,0
12
Василеостровский
95
88,3
107,4
-19,1
13
Невский
106
132,4
120,4
12,0
14
Петроградский
112
122,0
127,4
-5,4
15
Калининский
115
99,1
131,0
-31,9
16
Выборгский
125
114,2
142,7
-28,5
17
Кировский
132
150,6
151,0
-0,4
18
Московский
149
156,1
171,0
-14,9
19
Адмиралтейский
157
209,5
180,5
29,0
20
Центральный
282
342,9
327,8
15,1
1652
1855,5
1855,5
0,0
Итого

24.

В соответствии с уравнением
yˆ x 4,565 1,178 x
r 0,9828, F 510,7
найдены теоретические значения
отклонения от их фактических
значений y , т. е. i .
ŷ x
и

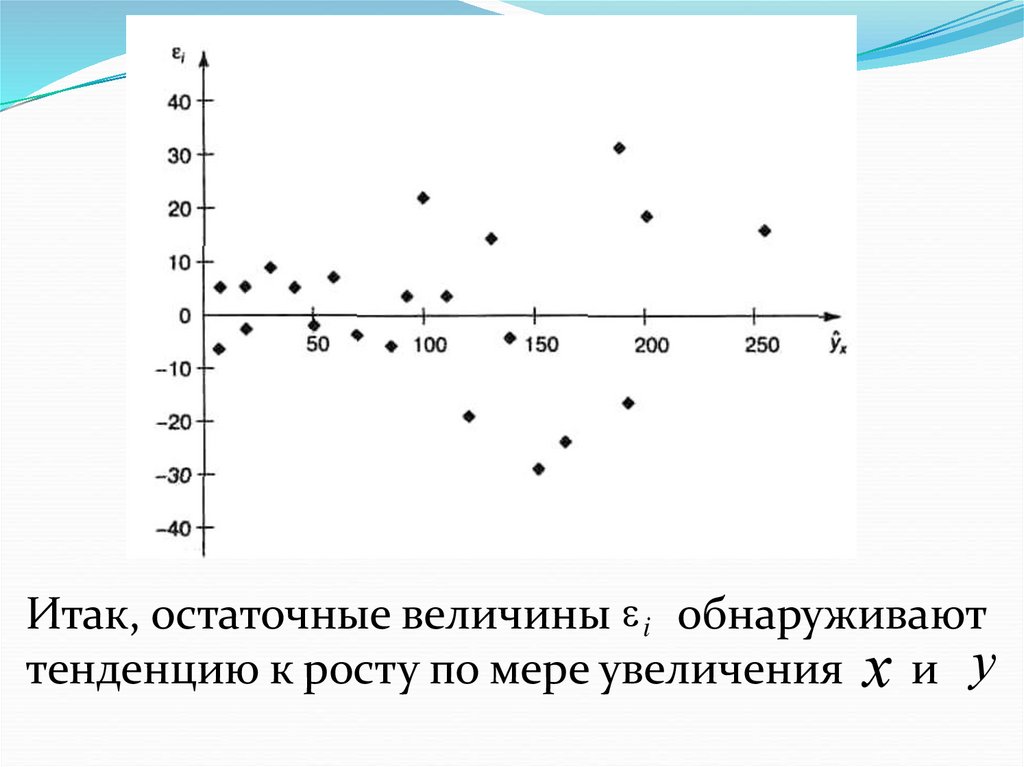
25.

Итак, остаточные величины i обнаруживают
тенденцию к росту по мере увеличения x и y

26.

Этот вывод подтверждается и по критерию
Гольдфельда – Квандта.
Для его применения необходимо
определить сначала число исключаемых
центральных наблюдений C.
При n=20 берем C=4 (при n=60 C= 16 , при
n=30 C=8). Тогда в каждой группе будет по 8
наблюдений 20 4 : 2 . Результаты расчетов
представлены в таблице.

27.

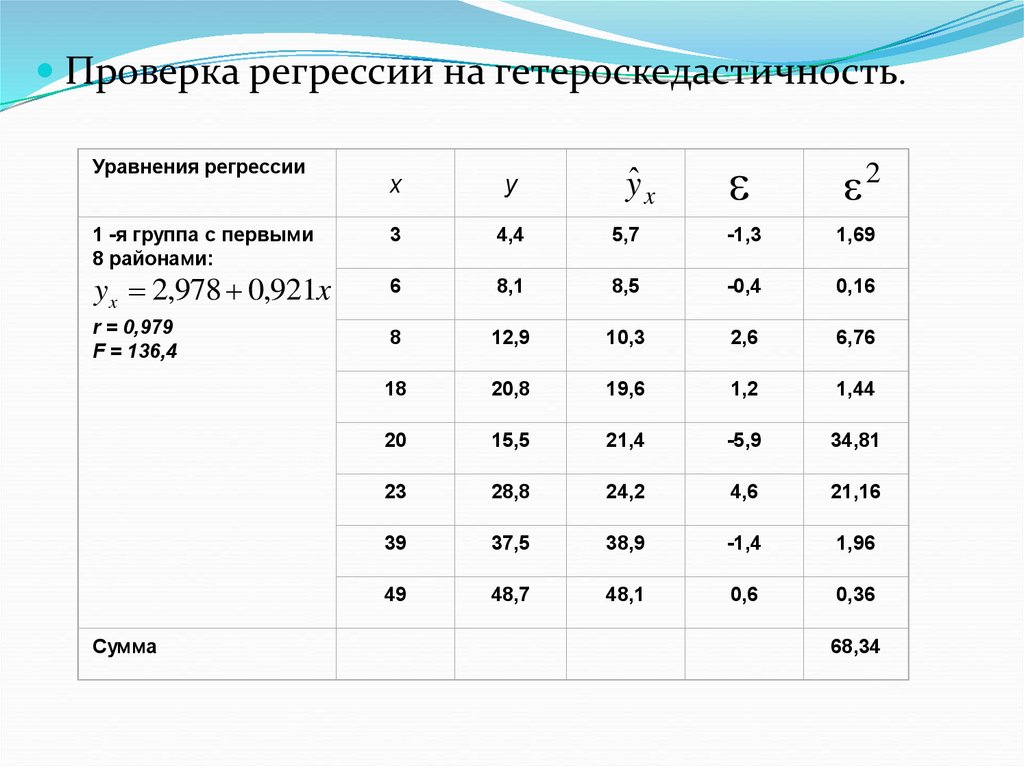
Проверка регрессии на гетероскедастичность.
Уравнения регрессии
ŷ x
2
x
y
3
4,4
5,7
-1,3
1,69
y x 2,978 0,921x
6
8,1
8,5
-0,4
0,16
r = 0,979
F = 136,4
8
12,9
10,3
2,6
6,76
18
20,8
19,6
1,2
1,44
20
15,5
21,4
-5,9
34,81
23
28,8
24,2
4,6
21,16
39
37,5
38,9
-1,4
1,96
49
48,7
48,1
0,6
0,36
1 -я группа с первыми
8 районами:
Сумма
68,34

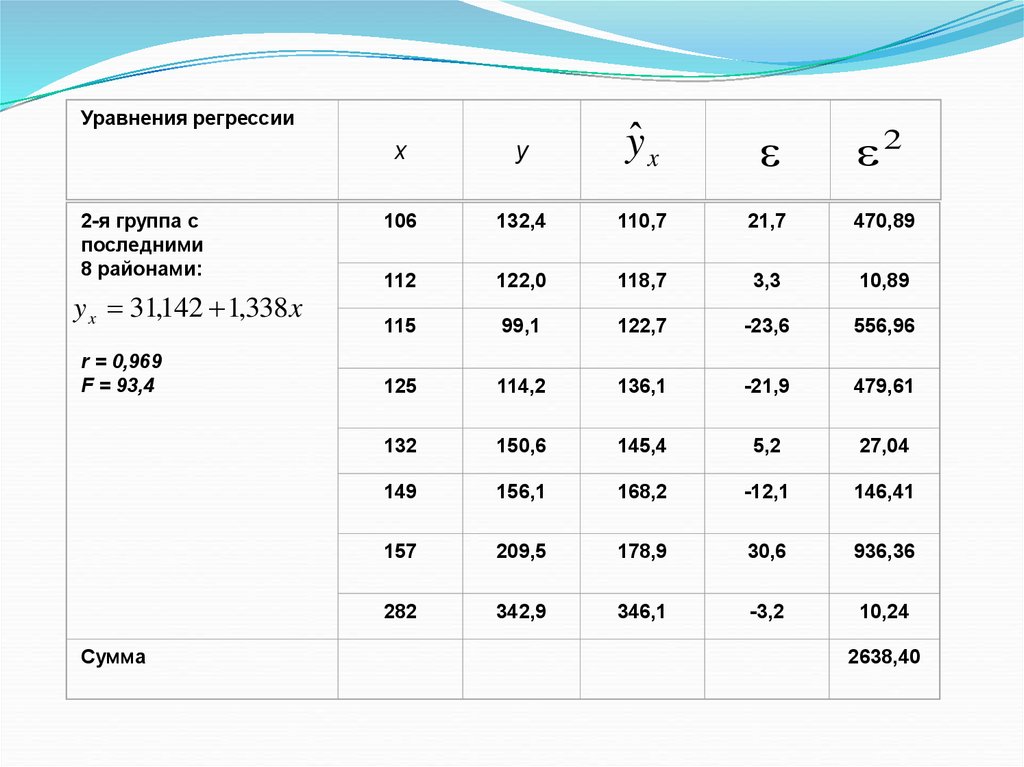
28.

Уравнения регрессии
2-я группа с
последними
8 районами:
y x 31,142 1,338 x
r = 0,969
F = 93,4
Сумма
x
y
ŷ x
2
106
132,4
110,7
21,7
470,89
112
122,0
118,7
3,3
10,89
115
99,1
122,7
-23,6
556,96
125
114,2
136,1
-21,9
479,61
132
150,6
145,4
5,2
27,04
149
156,1
168,2
-12,1
146,41
157
209,5
178,9
30,6
936,36
282
342,9
346,1
-3,2
10,24
2638,40

29.

Величина
R 2638,4 : 68,34 19,3 , что
превышает табличное значение – Fкритерия 4,28 при 5 %-ном уровне
значимости для числа степеней
свободы 6 для каждой остаточной
суммы квадратов 20 4 2 2 : 2 ,
подтверждая тем самым наличие
гетероскедастичности.

30.

IV.Четвертая предпосылка
МНК - отсутствие
автокорреляции остатков,
т. е. значения остатков i
распределены независимо
друг от друга.

31.

Автокорреляция остатков означает наличие
корреляции между остатками текущих и
предыдущих (последующих) наблюдений.
Коэффициент корреляции между i и j ,
где i - остатки текущих наблюдений, j остатки предыдущих наблюдений
(например, j = i - 1), может быть определен по
формуле:
r i j
cov( i , j )
i j
i j i j
i j
.

32.

V.
При использовании F-критерия
Фишера и t-критерия Стьюдента
делаются предположения
относительно поведения остатков
–остатки представляют собой
независимые случайные величины с
нулевым средним; они имеют
одинаковую (постоянную)
дисперсию и подчиняются
нормальному распределению.

33.

Наряду с предпосылками МНК
должны соблюдаться определенные
требования относительно
переменных, включаемых в модель:
соотношение 1 фактор на 6-7
наблюдений;
факторы должны быть свободны
от мультиколлинеарности.

34. Обобщенный метод наименьших квадратов

35. Обобщенный метод наименьших квадратов

При нарушении гомоскедастичности и наличии
автокорреляции остатков рекомендуется вместо
традиционного МНК использовать обобщенный
МНК. Его для случая устранения
гетероскедастичности часто называют методом
взвешенных наименьших квадратов.
2
Метод применим, если известны дисперсии для
i
каждого наблюдения.
Основан на делении каждого наблюдаемого значения
на соответствующее ему стандартное отклонение
остатков.

36. Метод взвешенных наименьших квадратов. Случай парной регрессии

i
yi a bxi i
yi
xi i
1
a b
i
i
i i
yi
xi
1
i
yi ,
zi ,
xi ,
i
i
i
i
i
yi
azi bxi
i
Получили уравнение регрессии без свободного
члена, но с дополнительной объясняющей
переменной z и с «преобразованным»
остатком . Можно показать, что для него
выполняются условия Гаусса-Маркова 1 – 5.

37. Метод взвешенных наименьших квадратов. Случай парной регрессии

На практике, значения дисперсии остатков, как
правило, не известны. Для применения метода ВНК
необходимо сделать реалистичные предположения об
этих значениях. Например:
2
Дисперсии i пропорциональны xi:
2i 2 xi , i 1, n
2
Дисперсии i пропорциональны xi2:
2i 2 xi2 , i 1, n

38. Метод взвешенных наименьших квадратов. Случай парной регрессии

Гипотеза о пропорциональности остатков
величине фактора может иметь реальное
основание: при обработке недостаточно
однородной совокупности, включающей
как крупные, так и мелкие предприятия,
большим объемным значения фактора
может соответствовать большая дисперсия
результативного признака и большая
дисперсия остаточных величин.