Similar presentations:
Приближение функций. Метод наименьших квадратов
1.
Приближение функцийМетод наименьших
квадратов
2.
План1. Постановка
– логарифмическая
– обратнопропорциональная
– дробно-линейная
– дробно-рациональная
задачи
2. Понятие о методе
наименьших
квадратов
4. Общий алгоритм
3. Приближающие
МНК
функции
5. Погрешность МНК
–
–
–
–
линейная
квадратичная
степенная
показательная
3.
Постановка задачиСуществует много Основная задача состоит в
методов анализа
восстановлении функции
и обработки
по ее значениям в
данных,
нескольких точках.
полученных в
Это часть более основной
ходе
проблемы естествознания:
эксперимента.
как найти существующую
закономерность по
разрозненным фактам.
4.
Постановка задачиПусть в результате измерений в процессе
опыта получена таблица некоторой
зависимости f(x):
x
x1
x2
…
xi
…
xn
f(x)
y1
y2
…
yi
…
yn
Нужно найти формулу, выражающую эту
зависимость аналитически.
5.
Метод наименьших квадратовПоставим задачу так, чтобы с самого начала
учитывался характер исходной функции, т.е.
надо найти функцию заданного вида y = F(x),
которая в узловых точках принимает как можно
более близкие значения к значениям из
таблицы, но не обязательно совпадает с ними.
Практически вид приближающей функции F
устанавливают следующим образом: по
таблице строится точечный график функции f,
а затем проводится плавная кривая, по
возможности наилучшим образом отражающая
характер расположения точек.
6.
Методнаименьших
квадратов
y
Y=F(x)
В узловых точках функции f(x) и
F(x) будут отличаться на
величину
i f x i F xi
Отклонения εi могут принимать
положительные или
отрицательные значения.
Чтобы эти знаки не учитывать,
возведем каждое отклонение
в квадрат и просуммируем
квадраты отклонений по всем
узлам:
x
Q i2 f x i F x i
n
n
i 1
i 1
2
7.
Метод наименьших квадратовСпособ построения приближающей
функции F(x) из условия минимума
величины Q называется методом
наименьших квадратов (МНК).
В качестве приближающих функций в
зависимости от характера точечного
графика функции f часто используют
следующие функции:
8.
Приближающие функции1.
y ax b
5.
1
y
ax b
2.
y ax bx c
6.
y a * ln x b
3.
y ax
m
7.
1
y a b
x
4.
y ae
mx
8.
x
y
ax b
2
9.
Когда вид приближающей функции (1-8)установлен, задача сводится только к
отысканию параметров a,b,m,c.
Рассмотрим метод их нахождения в
общем виде на примере функции с
тремя параметрами:
y F x, a, b, c
10.
Сумма квадратов отклонений Q в этомслучае
a,b,c
F
,
a
,
b
,
c
y
i
xi
n
2
i 1
является функцией трех переменных
(параметров a, b, c). Задача сводится к
отысканию ее минимума. Используем
необходимое условие экстремума
0,
0,
0
a
b
c
11.
n2 y i F xi, a, b, c F a/ xi, a, b, c 0,
i 1
n
2 y i F xi, a, b, c F b/ xi, a, b, c 0,
i 1
n
2 y F x , a, b, c F / x , a, b, c 0.
i
i
c i
i 1
y i F xi,a,b,c a,b,c
n
2
i 1
Решив эту систему трех уравнений с тремя
неизвестными относительно параметров a, b, c, мы
и получим конкретный вид искомой функции
F(x, a, b, c).
Изменение количества параметров не изменит
самого подхода, а приведет лишь к изменению
количества уравнений в системе.
12.
Нахождениеприближающих функций
различных видов
Линейная функция
(линейная регрессия).
13.
y ax bЧастные производные:
( y ax b) x 0
i
i
i
i
( y ax b) 0
i
i
i
F
F
x,
1.
a
b
y a 2 b 0
xi
xi
i xi
yi a xi nb 0
Разделим каждое уравнение на n:
1
2
1
1
a * n xi b * n xi n xi yi
1
a * 1
b yi
n xi
n
14.
Обозначим:1
1
1
1
2
M 2 , xi M x , xi y M xy , y M y
x
i
i
i
x n
n
n
n
Тогда система имеет вид:
M x 2 a M x b M xy
M x a b M y
1
2
1
1
a
*
b
*
xi yi
x
x
i
i
n
n
n
1
a * 1
b
yi
n xi
n
Коэффициенты этой системы – числа, которые
легко вычисляются в каждой конкретной
задаче по формулам через значения и из
исходной таблицы. Решив последнюю
систему, получаем конкретный вид линейной
функции y=ax+b.
15.
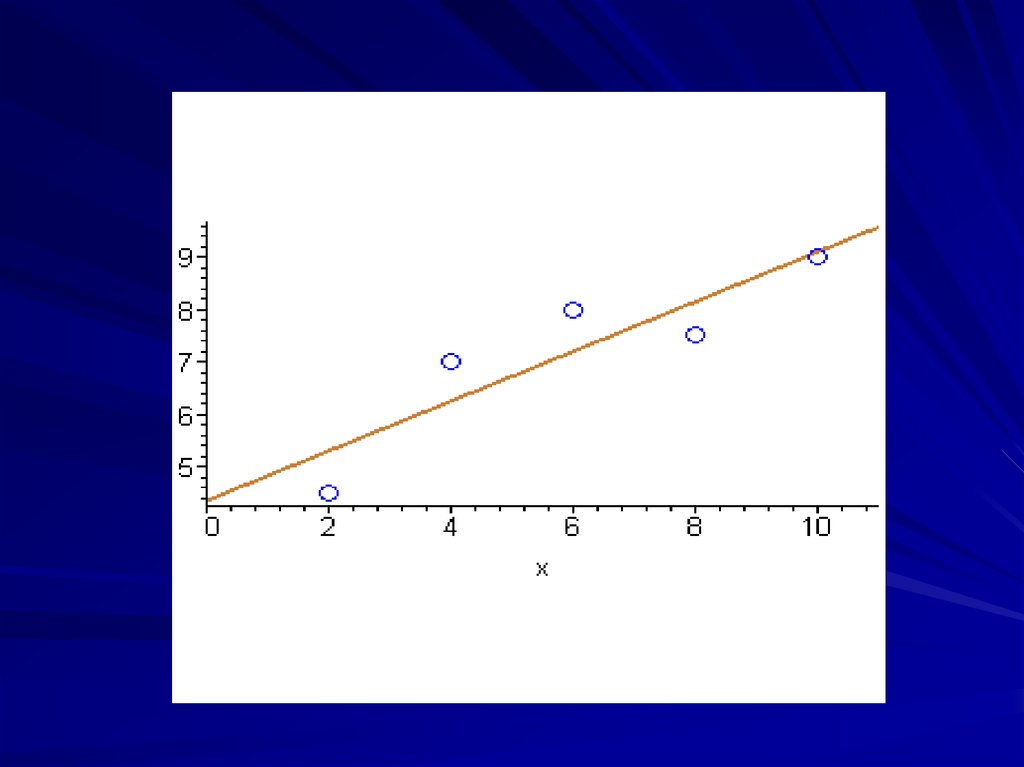
Пример 1. Данные опыта приведены втаблице:
x
f(x)
2
4,5
4
7,0
6
8,0
8 10
7,5 9,0
Полагая, что х и у
связаны линейной
зависимостью
у=ах+b, найти а и b.
y
10
8
6
4
2
0
y
0
5
10
15
16.
S2
xi
yi
xi
xiyi
2
4,5
4
9
4
7
16
28
6
8
36
48
8
7,5
64
60
10
9
100
90
30
36
220
235
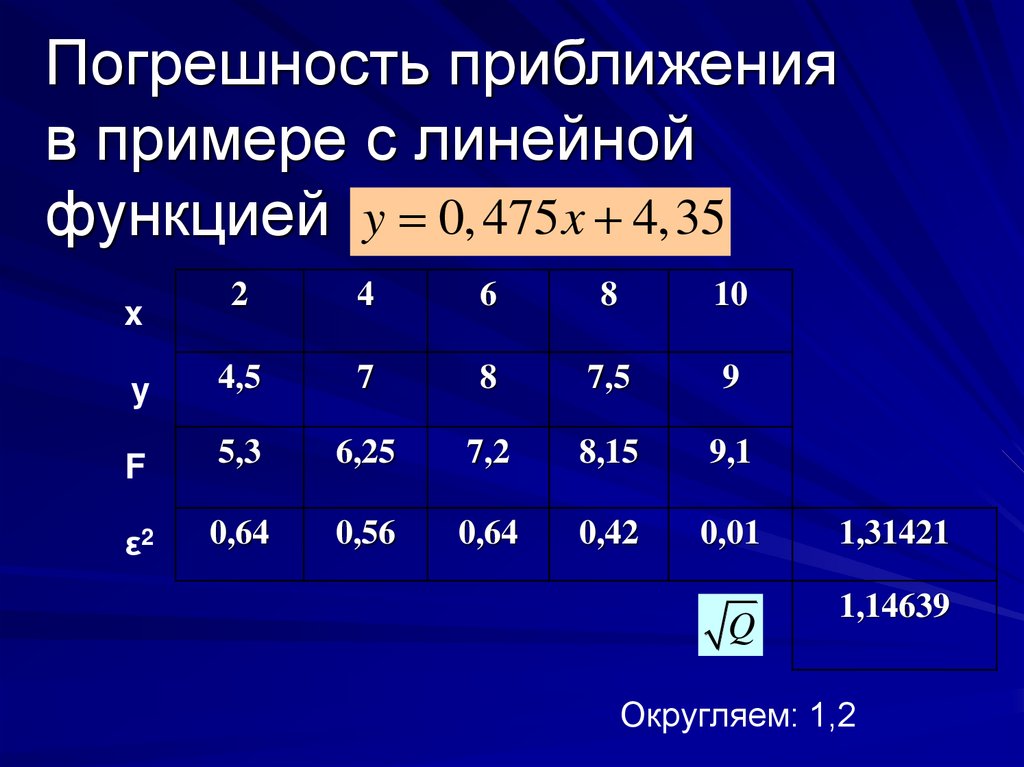
y 0, 475 x 4,35
M x 2 a M x b M xy
M x a b M y
1
M x2 220 44
5
1
M xy 235 47
5
44 a 6 b 47
6 a b 7.2
a 0, 475
b 4,35
17.
18.
Квадратичная регрессия(параболическая функция)
В этом случае приближенная функция имеет вид:
F x,a,b,c ax2 bx c
Составим систему
2
2
y
c
0
ax
bx
x
i
i
i
i
2
yi axi bxi c xi 0
2
y axi bxi c 0
i
F
F
2 F
x ;
x;
1
a
b
c
19.
После несложных преобразований и введения новыхпеременных:
1
1
1
3
2
4
M x 4 n xi ; M x 3 n xi ; M x 2 y n xi y i ;
получим:
M 4 * a M 3 * b M 2 * c M 2y
x
x
x
x
M x 3 * a M x 2 * b M x * c M xy
M 2 * a M * b c M y
x
x
Решение последней системы дает значения a, b, c для
приближенной функции в виде параболы.
20.
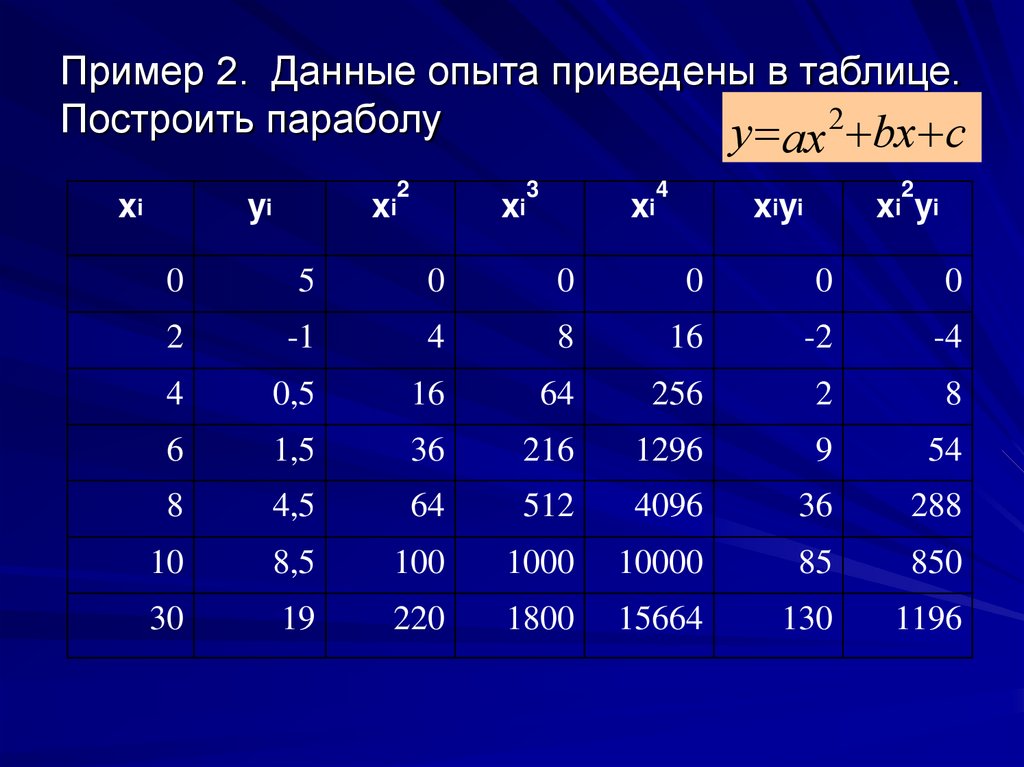
Пример 2. Данные опыта приведены в таблице.2
Построить параболу
y ax bx c
xi
yi
xi
2
xi
3
xi
4
2
xiyi
xi yi
0
5
0
0
0
0
0
2
-1
4
8
16
-2
-4
4
0,5
16
64
256
2
8
6
1,5
36
216
1296
9
54
8
4,5
64
512
4096
36
288
10
8,5
100
1000
10000
85
850
30
19
220
1800
15664
130
1196
21.
Из системы найдем a,b,c.15664a 1500b 220c 1196
1500a 220b 30c 130
220a 30b 6c 19
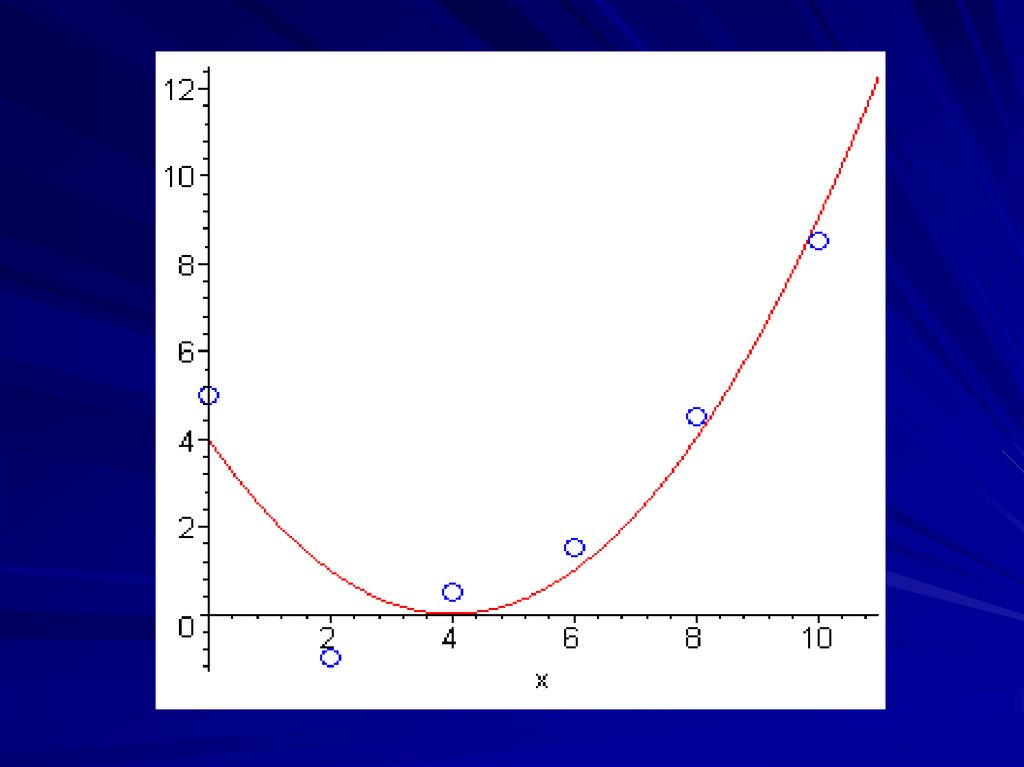
Решив систему, получим a=0,25; b=-2; c=4.
y 0,25 x 2 2 x 4
22.
23.
Степенная функция(геометрическая регрессия)
Покажем, что нахождение приближенных
функций с двумя параметрами F(x, a, b)
в виде элементарных функций (3) – (8)
может быть сведено к нахождению
параметров линейной функции.
Будем искать функцию в виде:
F x, a, m a x
m
24.
F x, a, m a xm
Предположим, что любые xi>0 и yi>0.
Прологарифмируем F:
ln F ln a m ln x
Т. к. F – приближающая функция для f, то ln F –
приближающая функция для ln f . Введем новую
переменную =lnx. Тогда ln F функция от u.
Обозначим (*)
m A; ln a B.
Тогда
(u, A, B) Au B
т. е. задача свелась к отысканию приближающей
функции в виде линейной.
25.
Практически при нахожденииприближающей степенной функции
необходимо выполнить следующие
действия:
1. По исходной таблице составить новую,
прологарифмировав значения х и у.
2. По новой таблице найти параметры А
и В для линейной функции.
3. Используя введенные обозначения (*),
найти а и m и подставить в исходное
выражение для степенной функции.
26.
Показательная функцияF x, a , m a e , a 0
mx
Прологарифмируем это равенство
ln F ln a m x
Обозначения те же (*):
m A; ln a B.
ln F Ax B
Т. о., алгоритм построения приближающей функции
следующий:
Прологарифмировать значения функции у в
исходной таблице.
Для новой таблицы с исходными значениями xi и
новыми yi найти параметры А и В.
Используя введенное обозначение (*) найти а и m,
подставить их в формулу показательной функции.
27.
Логарифмическая функцияF x, a, b a ln x b
Для перехода к линейной функции
достаточно сделать подстановку:
u ln x
Практически: в исходной таблице
логарифмируем значения xi, по новым
значениям аргумента и исходным
значениям yi находятся параметры а и
b, которые подставляют в выражение
для функции.
28.
ГиперболаF x, a , b
a
b
x
Выполнив подстановку:
получим: (u, a, b) au b
Практический алгоритм: в исходной
таблице значения аргумента следует
заменить обратными числами и найти
для новой таблицы приближающую
функцию в виде линейной. Полученные
параметры а и b подставить в исходную
формулу.
1
u
x
29.
1Дробно – линейная функция F x, a, b ax b
Перепишем равенство следующим образом:
1
ax b
F x, a , b
Отсюда следует, что для нахождения
параметров а и b необходимо в исходной
таблице значения xi оставить прежние, а
значения yi заменить обратными числами,
после чего по полученной таблице найти
приближенную функцию.
30.
Дробно-рациональная функция1
b
a
F x, a , b
x
Выполнив подстановку:
получим: Ф u, a, b bu a
В исходной таблице значения х и у
заменяем обратными величинами:
1
u
x
1 1
и
x y
по новой таблице строим функцию
вида (u , a, b) bu a.
Найденные значения а и b будут
искомыми.
31.
Общий алгоритм построенияуравнения регрессии
1. Составление таблицы значений аргумента и
соответствующих значений функции.
2. Выбор вида приближающего уравнения.
3. Преобразование данных к линейному типу
зависимости.
4. Получение параметров уравнения регрессии.
5. Обратное преобразование данных и
вычисление суммы квадратов отклонений.
6. Вывод результата.
32.
Погрешность МНКВ узловых точках функции f(x) и F(x) будут
отличаться на величину i f xi F xi
Возведем каждое отклонение εi в квадрат и
просуммируем квадраты отклонений по всем
2
узлам:
n
n
2
Q i f xi F xi
i 1
i 1
В качестве погрешности берем





























 mathematics
mathematics








