Similar presentations:
Метод наименьших квадратов
1. Метод наименьших квадратов
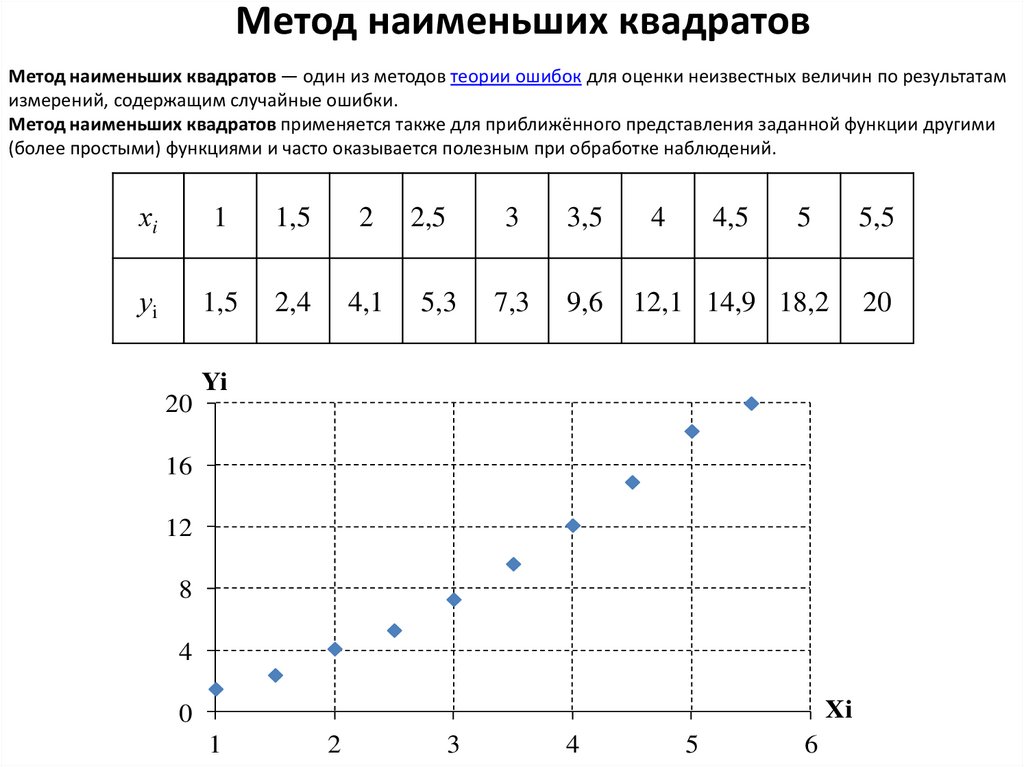
Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатамизмерений, содержащим случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими
(более простыми) функциями и часто оказывается полезным при обработке наблюдений.
хi
1
1,5
2
2,5
3
3,5
4
5
5,5
уi
1,5
2,4
4,1
5,3
7,3
9,6
12,1 14,9 18,2
20
20
4,5
Yi
16
12
8
4
Xi
0
1
2
3
4
5
6
2.
Необходимо построить функцию, которая быпроходила наиболее близко к указанным точкам
y f x, a, b, c a bx cx 2
Q y y y a bx cx
2
2
2
Q yi a bxi cxi
i 1
i 1
n
n
n
n
2
Q a, b, c yi y xi , a, b, c yi
i 1
i 1
2
2
a bxi cxi2
xi , yi – координаты заданных точек (данные из таблицы)
n – количество заданных точек
Q – квадратичная невязка (погрешность)
n
xi x1 x2 ... xn 1 xn
i 1
n
yi y1 y2 ... yn 1 yn
i 1
2
3.
nQ a, b, c yi
i 1
a bxi cxi2
2
Для отыскания 3 неизвестных необходимо получить СЛАУ.
Воспользуемся свойством, что производная от константы (в.ч. и частная) равна 0!
Для получения СЛАУ достаточно взять частные производные функции Q по всем
неизвестным константам. При этом полученная СЛАУ как раз таки и позволит
определить значения констант в сглаживающей функции.
n
n
n
2
дQ
2
an
b
x
c
x
i
i yi ,
2
y
a
bx
cx
0,
i
i
i
i 1
i 1
i 1
дa
i
1
n
n
n
n
n
дQ
2
3
2
a
x
b
x
c
x
2 yi a bxi cxi xi 0,
i
i
i y i xi ,
i 1
i 1
i 1
i 1
i 1
дb
n
n
n
n
n
дQ
2
3
4
2
2 yi a bxi cxi2 xi2 0. a xi b xi c xi y i xi .
i 1
дc
i 1
i 1
i 1
i 1
n
4.
nn
n
2
дQ
2
an
b
x
c
x
i
i yi ,
2
y
a
bx
cx
0,
i
i
i
i 1
i 1
i 1
дa
i 1
n
n
n
n
n
дQ
2
3
2
a
x
b
x
c
x
2 yi a bxi cxi xi 0,
i
i
i y i xi ,
i 1
i 1
i 1
i 1
i 1
дb
n
n
n
n
n
дQ
2
3
4
2
2 yi a bxi cxi2 xi2 0. a xi b xi c xi y i xi .
i 1
дc
i 1
i 1
i 1
i 1
n
5.
№ п/п1
2
3
4
5
6
7
8
9
10
Сумма
X
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
32,5
Y
1,5
2,4
4,1
5,3
7,3
9,6
12,1
14,9
18,2
20
95,4
X2
1
2,25
4
6,25
9
12,3
16
20,3
25
30,3
126,25
X3
1
3,38
8
15,6
27
42,9
64
91,1
125
166
544,375
X4
1
5,06
16
39,1
81
150
256
410
625
915
2498,31
X×Y
1,5
3,6
8,2
13,3
21,9
33,6
48,4
67,1
91
110
398,5
X2×Y
1,5
5,4
16,4
33,1
65,7
118
194
302
455
605
1795,05
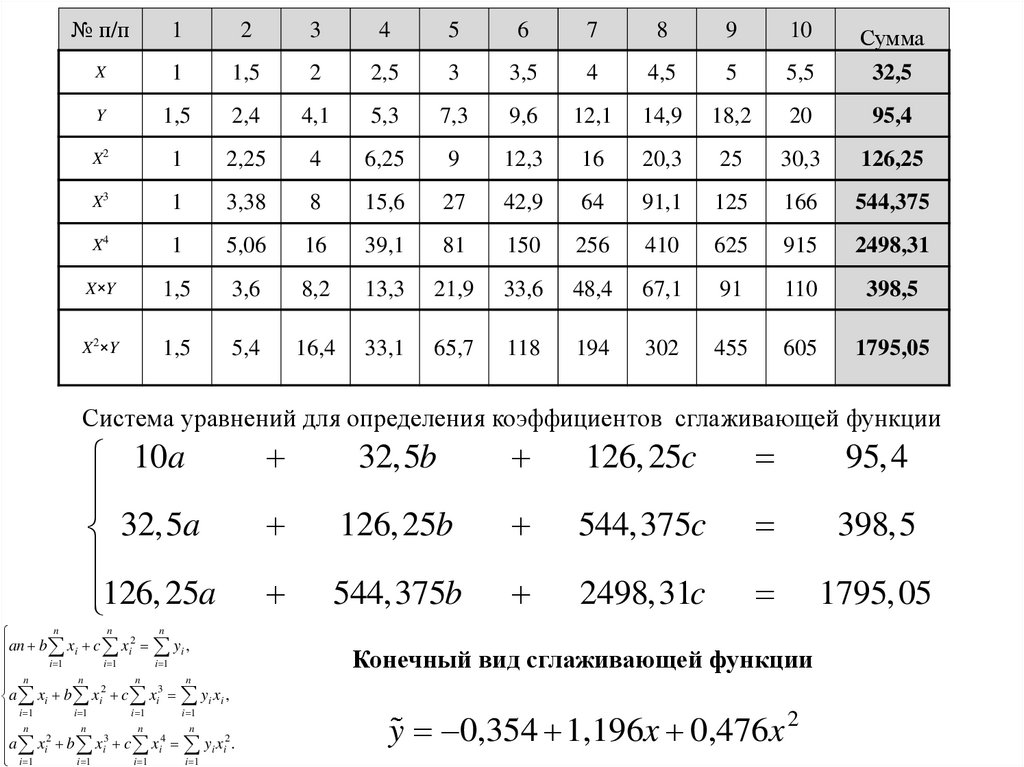
Система уравнений для определения коэффициентов сглаживающей функции
10a
32,5a
126, 25a
n
n
n
2
an
b
x
c
x
yi ,
i
i
i 1
i 1
i 1
n
n
n
n
2
3
a
x
b
x
c
x
i
i i y i xi ,
i
1
i 1
i 1
i 1
n
n
n
n
a xi2 b xi3 c xi4 y i xi2 .
i 1
i 1
i 1
i 1
32,5b
126, 25c
95, 4
126, 25b
544,375c
398,5
544,375b
2498,31c
1795, 05
Конечный вид сглаживающей функции
y 0,354 1,196x 0,476x 2
6.
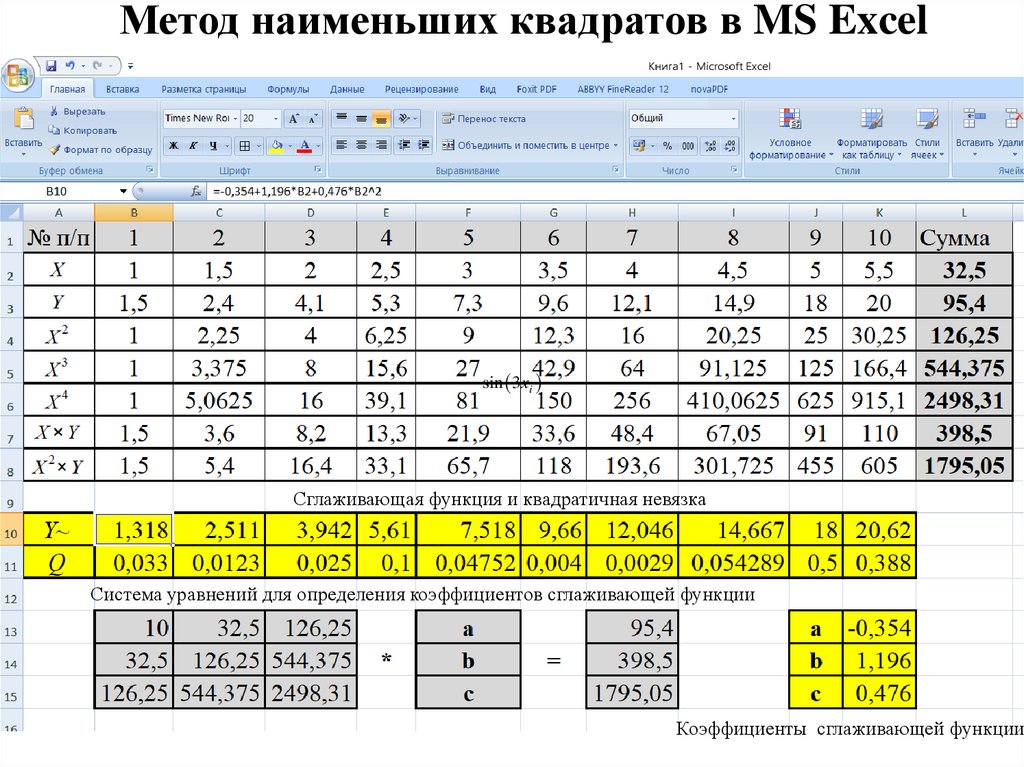
Метод наименьших квадратов в MS Excelsin 3xi
Сглаживающая функция и квадратичная невязка
Система уравнений для определения коэффициентов сглаживающей функции
Коэффициенты сглаживающей функции
7.
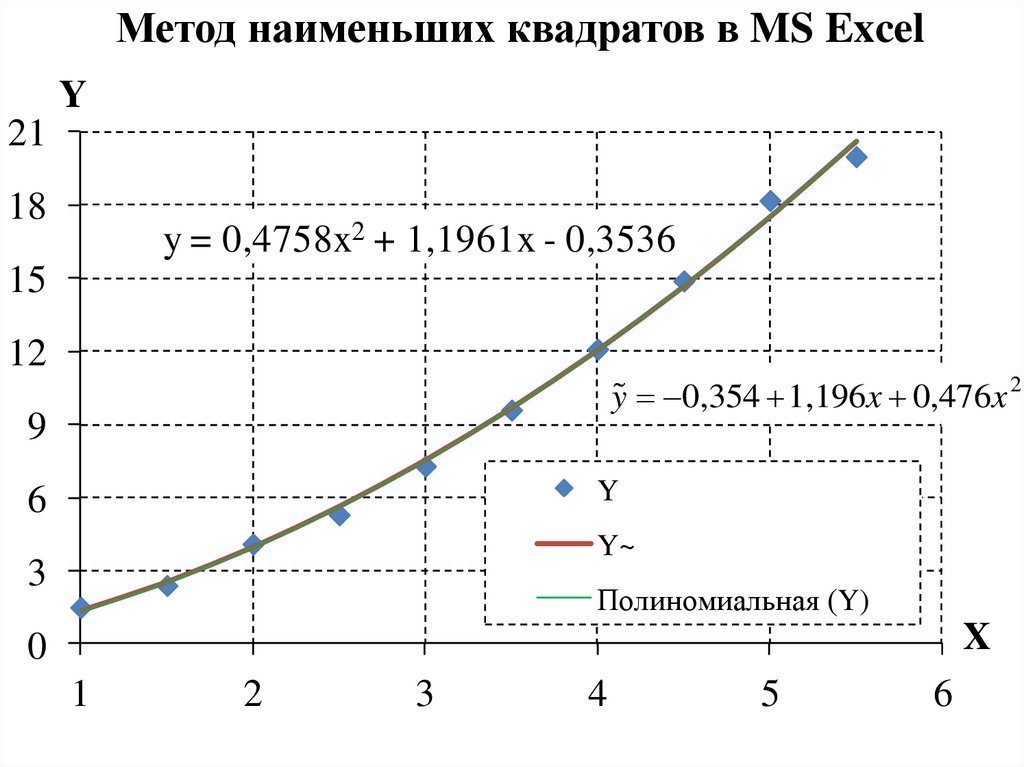
Метод наименьших квадратов в MS ExcelY
21
18
y = 0,4758x2 + 1,1961x - 0,3536
15
12
y 0,354 1,196x 0,476x 2
9
Y
6
Y~
3
Полиномиальная (Y)
X
0
1
2
3
4
5
6
8.
Что делать если сглаживающая функция не полином?y a0 a1 sin x a2 sin 2 x a3 sin 3x
y a0 a1 cos 0,1 x a2 cos 0, 2 x a3 cos 0,3 x
y a0 a1 ln x a 2 ln 2 x a3 ln 3 x
y a0 a1 sin x a 2 sin 2 x a3 sin 3 x
.....
Q y y y y a0 , a1 , a 2 ,..., x
2
Q
0,
a0
y e
a0 a1x a2 x 2 a3 x 3 a4 x 4 a5 x 5
Q
0,
a1
Q
0,....
a 2
2
Получить и решить
СЛАУ
Воспользоваться свойствами экспоненты
y ln a0 a1x a 2 x 2 a3 x 3 a 4 x 4 a5 x 5
свойствами
Воспользоваться
логарифма
9.
y a0 a1 sin x a2 sin 2 x a3 sin 3xQ y y y a0 a1 sin x a2 sin 2 x a3 sin 3x
2
n
Q yi a0 a1 sin xi a 2 sin 2 xi a3 sin 3xi
i 1
2
2
n
дQ
2 yi a0 a1 sin xi a 2 sin 2 xi a3 sin 3xi 0
i 1
дa0
n
дQ
2 yi a0 a1 sin xi a 2 sin 2 xi a3 sin 3xi sin xi 0
дa1
i 1
n
дQ
2 yi a0 a1 sin xi a 2 sin 2 xi a3 sin 3xi sin 2 xi 0
дa 2
i 1
n
дQ
дa 2 yi a0 a1 sin xi a 2 sin 2 xi a3 sin 3xi sin 3xi 0
i 1
3
10.
nn
a0 a1 sin xi a 2 sin 2 xi a3 sin 3xi yi
i 1
i 1
n
n
2
a0 sin xi a1 sin xi a 2 sin 2 xi sin xi a3 sin 3xi sin xi yi sin xi
i 1
i 1
n
n
2
a0 sin 2 xi a1 sin xi sin 2 xi a 2 sin 2 xi a3 sin 3xi sin 2 xi yi sin 2 xi
i 1
i n1
n
2
a0 sin 3xi a1 sin xi sin 3xi a 2 sin 2 xi sin 3xi a3 sin 3xi yi sin 3xi
i 1
i 1
При формировании СЛАУ для компактности знак суммы не показан
n
sin x
sin 2 x
sin 3x
sin x
sin 2 x
sin 2 x
sin 2 x sin x
sin 2 x sin x
sin 2 2 x
sin 3x sin x
sin 3x sin 2 x
sin 3x
y
a0
sin 3x sin x a1 y sin x
*
sin 3x sin 2 x a 2 y sin 2 x
2
sin 3x a3 y sin 3x
На каждой позиции стоит сумма sin или их произведений от каждой компоненты
исходных данных, т.е. сначала находятся все sin, а потом идет сложение!
11.
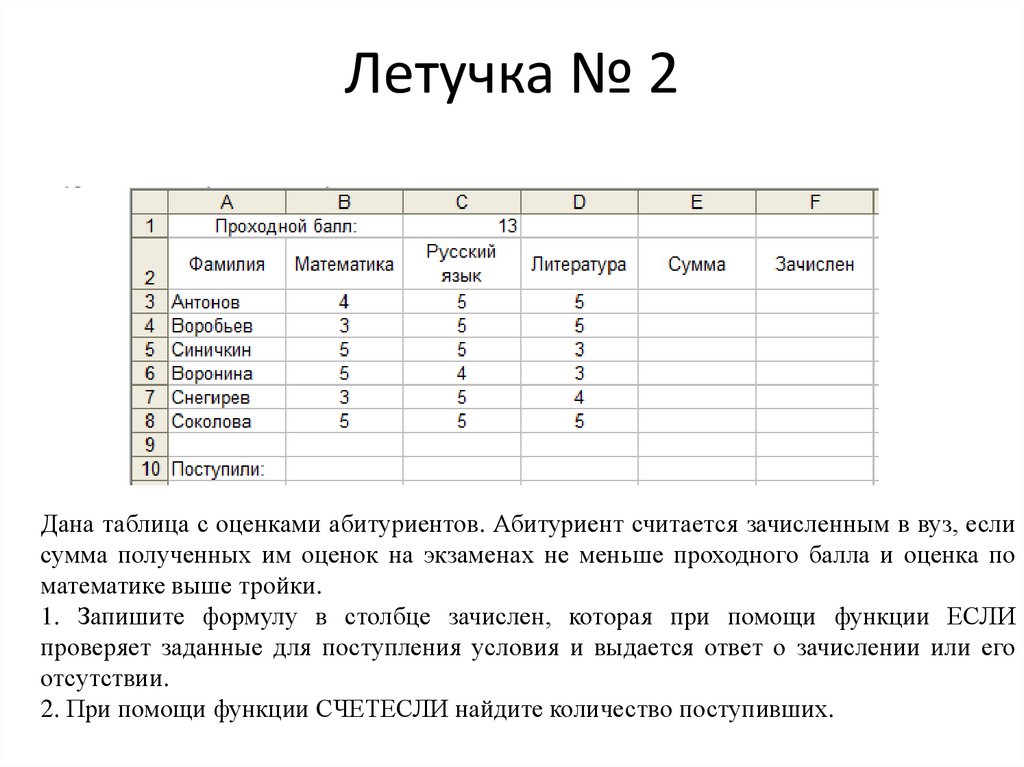
Летучка № 2Дана таблица с оценками абитуриентов. Абитуриент считается зачисленным в вуз, если
сумма полученных им оценок на экзаменах не меньше проходного балла и оценка по
математике выше тройки.
1. Запишите формулу в столбце зачислен, которая при помощи функции ЕСЛИ
проверяет заданные для поступления условия и выдается ответ о зачислении или его
отсутствии.
2. При помощи функции СЧЕТЕСЛИ найдите количество поступивших.






 mathematics
mathematics








