Метод наименьших квадратов (МНК)

1. Метод наименьших квадратов (МНК)

2.

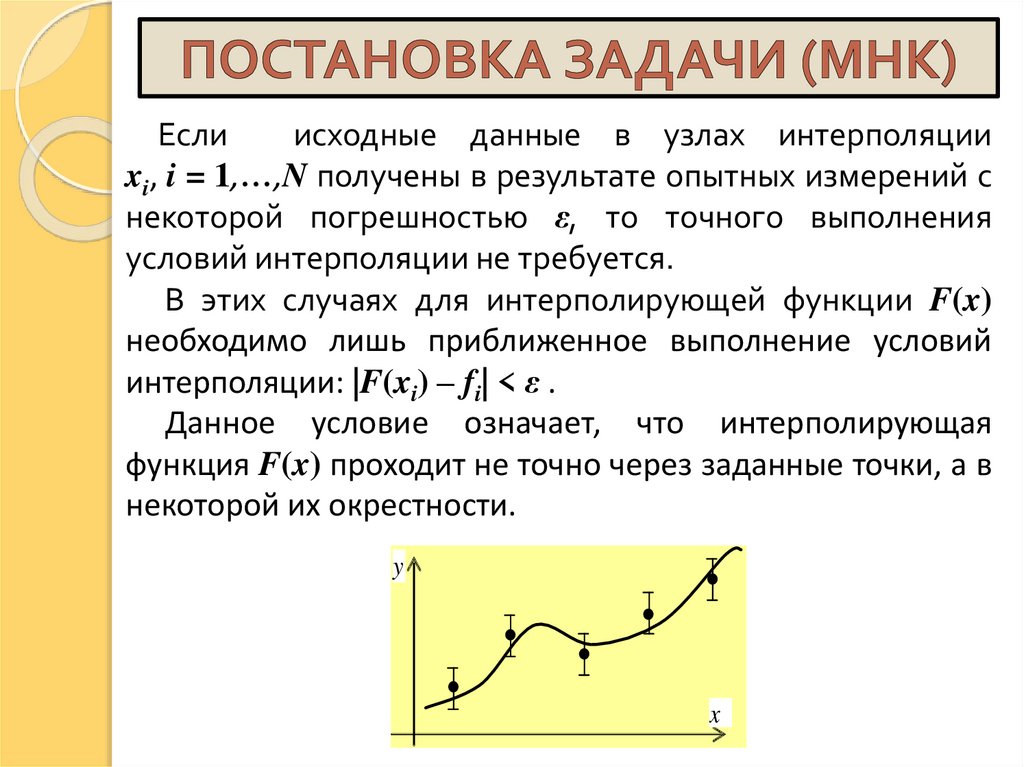
Если
исходные данные в узлах интерполяции
xi, i = 1,…,N получены в результате опытных измерений с
некоторой погрешностью ε, то точного выполнения
условий интерполяции не требуется.
В этих случаях для интерполирующей функции F(x)
необходимо лишь приближенное выполнение условий
интерполяции: |F(xi) – fi| < ε .
Данное условие означает, что интерполирующая
функция F(x) проходит не точно через заданные точки, а в
некоторой их окрестности.
y
x

3.

Будем искать интерполирующую функцию в
виде полинома, например, 3-ей степени:
P3(x)=a1+a2x+a3x2+a4x3
Существует много таких полиномов, каждый из
которых
определяется
своим
набором
коэффициентов (a1, a2, a3, a4).
Суть метода наименьших квадратов (МНК)
состоит в том, что среди всех возможных
полиномов этого вида выбирается тот, который
имеет наименьшую сумму квадратов отклонений
в узлах интерполяции от заданных значений.

4.

В i-й точке полином P3(x) отклоняется от
значения fi на величину (P3(xi)–fi). Суммируя
квадраты отклонений полинома по всем точкам
i=1,…,N, получим функционал квадратов
отклонений:
N
G (a1 , a2 , a3 , a4 )
i 1
N
( P3 ( xi ) f i ) 2
(a1 a2 xi a3 xi2 a4 xi3 f i ) 2
i 1
Найдем минимум этого функционала. Для
этого приравняем к нулю его частные
производные по переменным a1, a2, a3, a4.

5.

Используя стандартные правила дифференцирования,
получим:
G
2
a1
N
(a1 a 2 x i a3 x i2 a 4 x i3 f i ) 0,
i 1
G
2
a 2
N
G
2
a3
x i (a1 a 2 x i a3 x i2 a 4 x i3 f i ) 0,
i 1
N
x i2 (a1 a 2 x i a3 x i2 a 4 x i3 f i ) 0,
G
2
a 4
i 1
N
i 1
x i3 (a1 a 2 x i a3 x i2 a 4 x i3 f i ) 0.

6.

Собирая коэффициенты при неизвестных ai, получим СЛАУ,
которая называется нормальной системой.
N a1
xi a2
x i a1
i 1
i 1
x i2 a1
i 1
xi3 a2
x i3 a1
i 1
x i3 a3
i 1
x i4 a 4
xi4 a3
x i5 a 4
i 1
i
f i xi2 ,
i 1
N
N
i
N
i 1
xi5 a3
f x ,
i 1
N
N
xi4 a2
N
i 1
i 1
N
N
i
N
N
i 1
i 1
i 1
xi2 a2
f,
i 1
i 1
N
N
x i3 a 4
N
N
N
x i2 a3
i 1
i 1
N
N
N
N
x i6 a 4
f i xi3 .
i 1
Решая СЛАУ одним из известных методов,
неизвестные коэффициенты (a1, a2, a3, a4).
находим

7.

Для
заданной
системы
точек
(узлов
интерполяции)
xi, i = 1,…,N построить полином 1-ой степени, имеющий в узлах
интерполяции минимальное отклонение от заданных значений fi.
Полином 1-ой степени представляет собой линейную зависимость
вида: P1(x)=a1+a2x.
1
0.5
Исходные данные
0.5
x 0.7
1
1.2
0.2
f 0.2
0.5
1
Решение
ORIGIN 1
N
N a
1
N
x a
i 2
i 1
Нормальная система
N
i 1
i 1
f
i
i 1
N
x a
N
xi a2 xi fi
i 1
2
i 1

8.

Вычислим коэффициенты при неизвестных a1, a2 и
свободные члены:
N 5
N
N
i
x 1.4
x
i
i 1
N
xi fi 2.44
f 1
i
i 1
i 1
Решим нормальную
матрицы:
5 1.4
A
1.4 4.18
4.18
i 1
N
2
систему
1
b
2.44
методом
обратной
0.04
a A b
0.57
1

9.

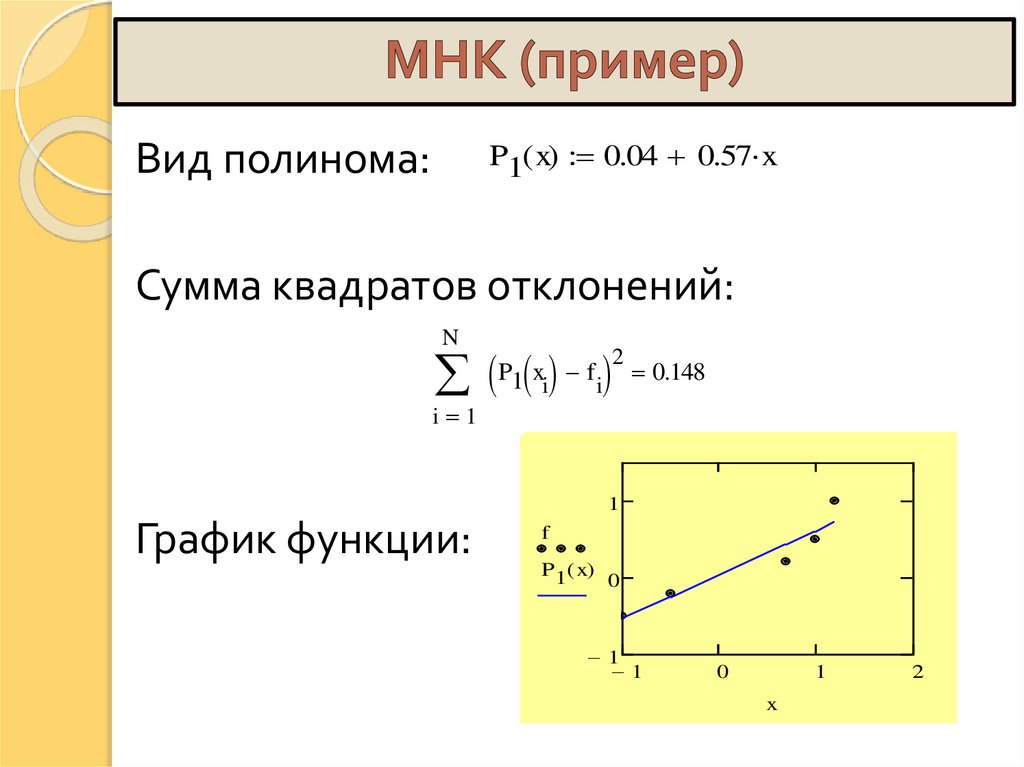
P1( x) 0.04 0.57 x
Вид полинома:
Сумма квадратов отклонений:
N
P1 x f
i
i
2
0.148
i 1
1
График функции:
f
P 1( x)
0
1
1
0
1
x
2

10. Численное интегрирование

11.

Найти значение определенного интеграла
b
I f x dx
a
для функции f(x), заданной на некотором отрезке [a, b].
Исходя из геометрической интерпретации определенного
интеграла, основой методов численного интегрирования является
нахождение площади криволинейной трапеции, ограниченной
подынтегральной функцией f(x), осью x, прямыми x=a и x=b.
y
f(x)
a
b
x

12.

Формулы
приближенного
интегрирования
называются
квадратурными формулами. Простейшей квадратурной формулой
является общая формула прямоугольников, которая вычисляется с
n
помощью приближенного равенства:
In
f i xi xi 1
i 1
где xi, i =0,1,…,n – заданная система точек на отрезке интегрирования
[a, b]; ξi – произвольная точка элементарного промежутка
[xi-1, xi].
Геометрически это означает, что площадь криволинейной
трапеции заменяется на сумму площадей прямоугольников,
основанием которых является i-й интервал [xi-1, xi], а высотой –
значение функции f(ξi ).
Погрешность любой квадратурной формулы определяется
модулем разности между значением, вычисленным по квадратурной
формуле In, и точным значением интеграла I: I I
n
n

13. Квадратурные формулы

Формула левых прямоугольников
Формула правых прямоугольников
Формула средних прямоугольников
Формула трапеций
Формула Симпсона

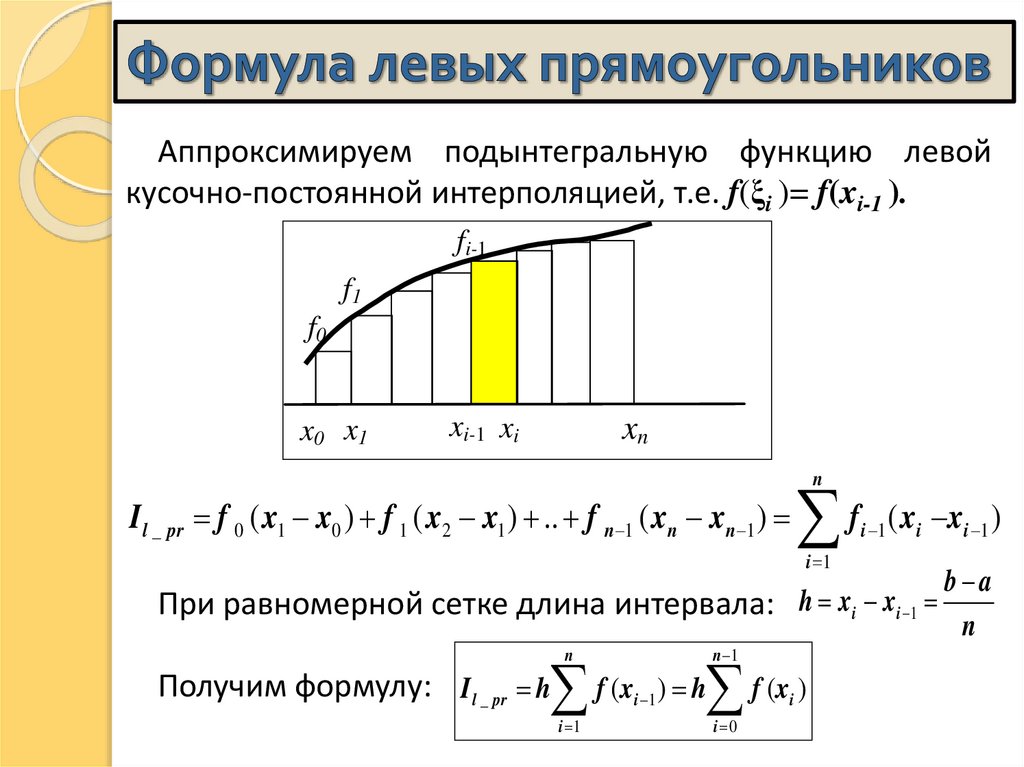
14. Формула левых прямоугольников

Аппроксимируем подынтегральную функцию левой
кусочно-постоянной интерполяцией, т.е. f(ξi )= f(xi-1 ).
fi-1
f1
f0
x0 x1
i
xn
xi-1 xi
n
I l _ pr f 0 ( x1 x0 ) f 1 ( x2 x1 ) .. f n 1 ( xn xn 1 )
f
i 1
i 1
( xi xi 1 )
b a
При равномерной сетке длина интервала: h xi xi 1
n
n 1
n
f (x
Получим формулу: I l _ pr h
i 1
i 1
f (x )
) h
i
i 0

15. Формула левых прямоугольников (пример)

2
Дан определенный интеграл:
4
4
(
5
x
2 x )dx
x
1
Вычислить значение интеграла в пакете MathCad с помощью
оператора интегрирования.
Используя формулу левых прямоугольников при сетке с
количеством отрезков n=10 составить П-Ф и вычислить
приближенное значение интеграла. Оценить погрешность.
ORIGIN 0
f ( x)
4
x
I0
4
5 x 2 x
I( f a b n )
2
f ( x) d x 25.79
1
( b a)
h
n
Il_pr I( f 1 2 10) 22.095
S 0
for i 0 n 1
x a i h
i
i
S S f x
S h S
S
Il_pr I0 3.694

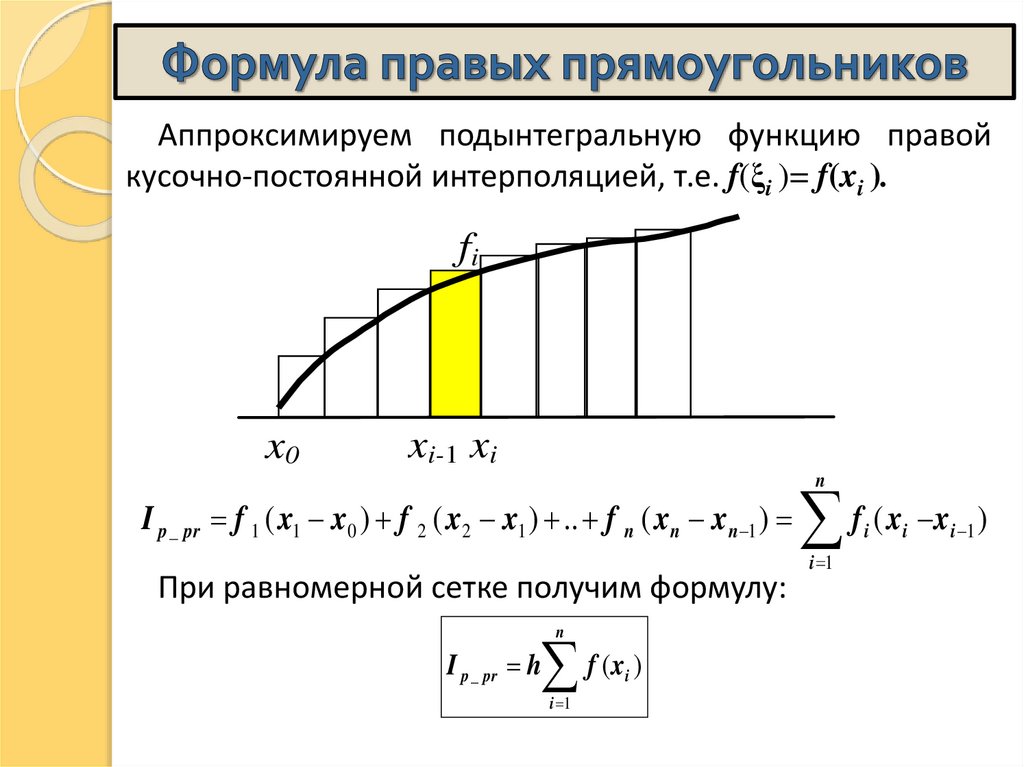
16. Формула правых прямоугольников

Аппроксимируем подынтегральную функцию правой
кусочно-постоянной интерполяцией, т.е. f(ξi )= f(xi ).
fi
x0
xi-1 xi
n
I p _ pr f 1 ( x1 x0 ) f 2 ( x2 x1 ) .. f n ( xn xn 1 )
При равномерной сетке получим формулу:
n
f (x )
I p _ pr h
i
i 1
f ( x x
i
i 1
i
i 1
)

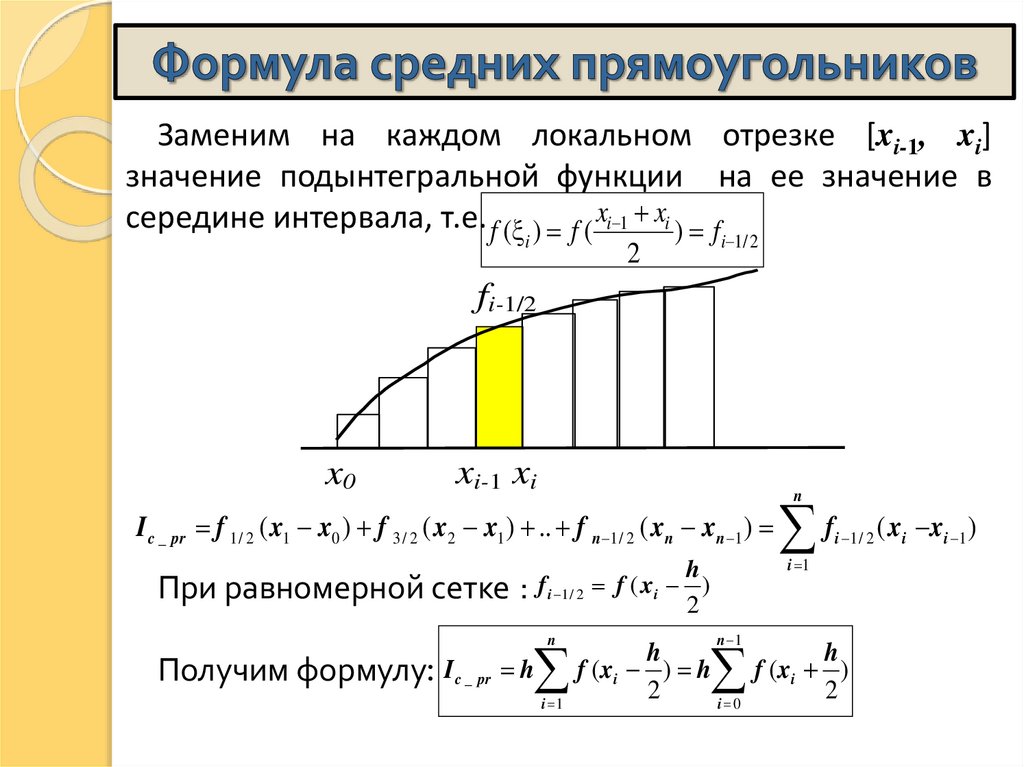
17. Формула средних прямоугольников

Заменим на каждом локальном отрезке [xi-1, xi]
значение подынтегральной функции на ее значение в
середине интервала, т.е. f ( ) f ( xi 1 xi ) f
i
2
i 1/ 2
fi-1/2
x0
xi-1 xi
n
I c _ pr f 1 / 2 ( x1 x0 ) f 3 / 2 ( x2 x1 ) .. f n 1 / 2 ( xn xn 1 )
При равномерной сетке : f i 1 / 2
n
Получим формулу: I c _ pr h
i 1
f
i 1 / 2
i 1
h
f ( xi )
2
n 1
h
h
f (xi ) h
f (xi )
2
2
i 0
( xi xi 1 )

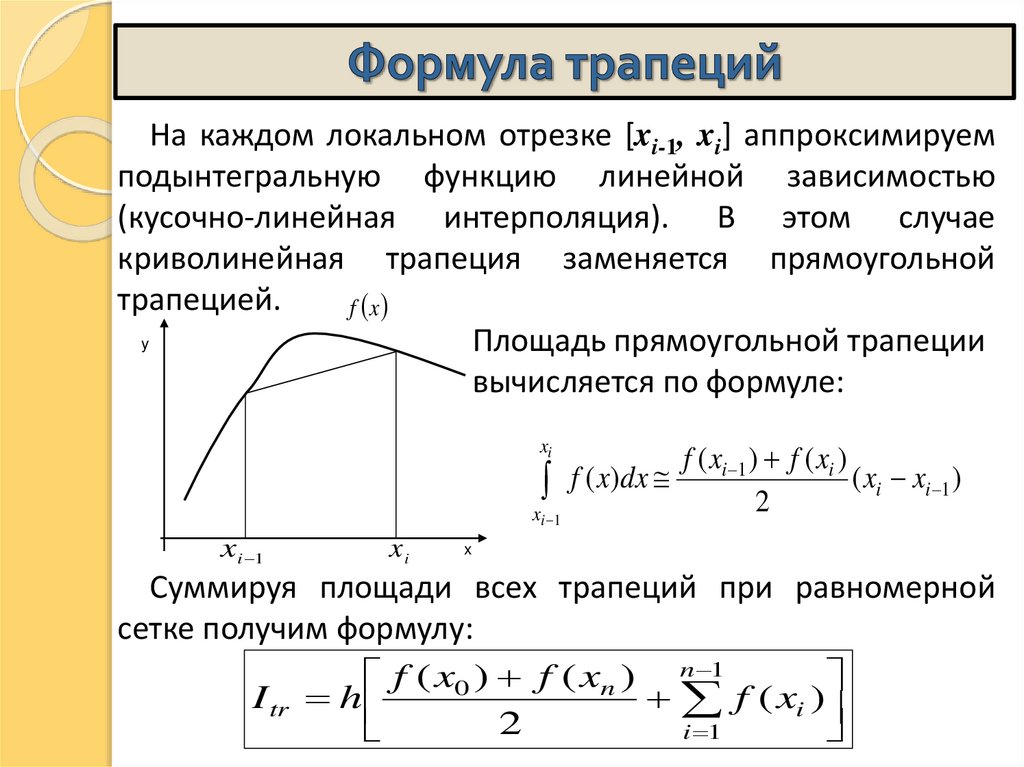
18. Формула трапеций

На каждом локальном отрезке [xi-1, xi] аппроксимируем
подынтегральную функцию линейной зависимостью
(кусочно-линейная интерполяция). В этом случае
криволинейная трапеция заменяется прямоугольной
трапецией.
f x
y
Площадь прямоугольной трапеции
вычисляется по формуле:
xi
xi 1
x i 1
xi
f ( x)dx
f ( xi 1 ) f ( xi )
( xi xi 1 )
2
x
Суммируя площади всех трапеций при равномерной
сетке получим формулу:
f ( x0 ) f ( xn ) n 1
I tr h
f ( xi )
2
i 1

19. Формула Симпсона

На каждом локальном отрезке [xi-1, xi] аппроксимируем
подынтегральную
функцию
кусочно-параболической
зависимостью, т.е. параболой, проходящей через три
точки:
xi 1 , f xi 1
x , f x x , f x
i
, i 12 i 12 , i
xi 1 xi
где xi 1
‒ середина отрезка.
2
2
Интерполируя на каждом отрезке подынтегральную
функцию полиномом Лагранжа второй степени при
равномерной сетке получим формулу:
h n
xi 1 xi
I simp f xi 1 4 f
f xi
6 i 1
2