Similar presentations:
Исследование операций. Симплексный метод
1. Исследование операций
Лекция 22. Симплексный метод
Слайд 2Симплексный метод
- переход от одного опорного плана к
другому
- при этом значение целевой функции
возрастает (при условии, что данная
задача имеет оптимальный план)
3. Простейшая задача
Слайд 3Простейшая задача
Найти максимальное значение функции
F c1x1 c2 x 2 ... cn x n
при условиях:
(1)
bi 0, x j 0 (i 1,..., m; j 1,..., n )
x1 a1,m 1x m 1 ... a1n x n b1 ,
x 2 a 2,m 1x m 1 ... a 2 n x n b 2 ,
(2)
..................................................
x a
m,m 1x m 1 ... a mn x n b m
m
4. В векторной форме
Слайд 4В векторной форме
Найти максимальное значение функции
n
F c jx j
(1)
при условиях:
j 1
x1A1 x 2A2 ... x mAm
x m 1A m 1 ... x n A n A0 (2)
x j 0 ( j 1,..., n )
(3)
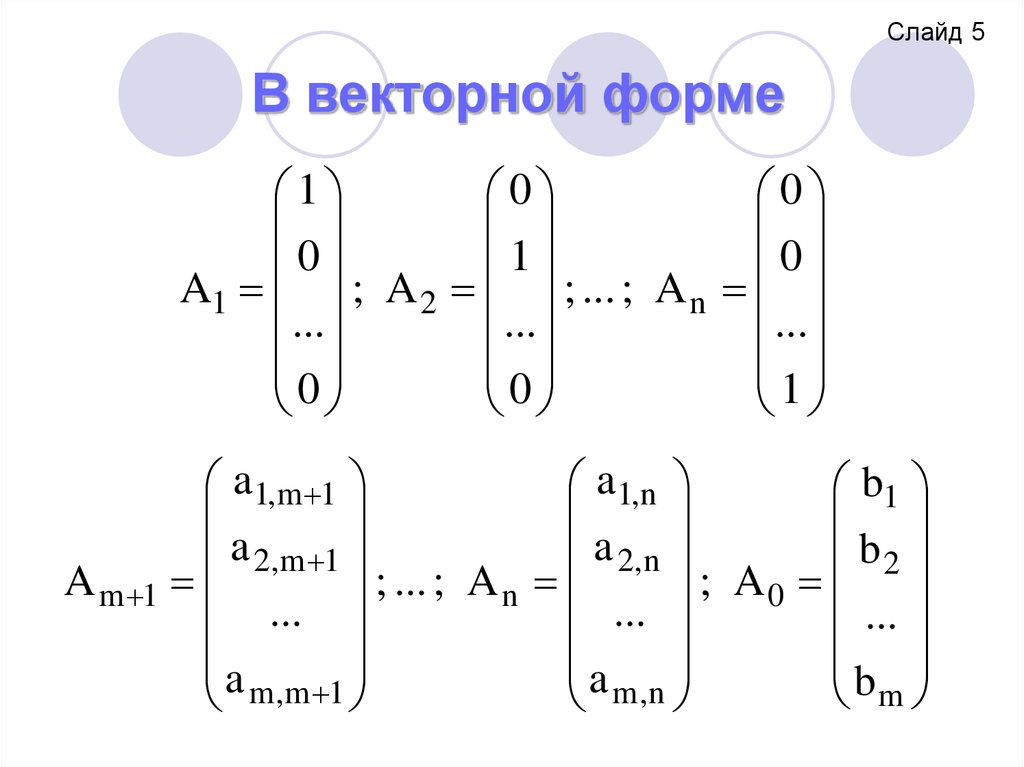
5. В векторной форме
Слайд 5В векторной форме
1
0
0
0
1
0
A1 ; A 2 ; ... ; A n
...
...
...
0
0
1
a1,m 1
a1,n
b1
a 2,m 1
a 2, n
b2
A m 1
; ... ; A n
; A0
...
...
...
b
a
a
m
m,m 1
m ,n
6. Продолжение
Слайд 6Продолжение
b1A1 b 2A 2 ... b m A m A0
Опорный план: X = ( b1, b2, …, bm, 0, …, 0 )
A1, A2 , ..., Am - базис m-мерного пространства
A1, ..., A n , A0 - линейно выражаются через
векторы базиса
m
Пусть
A j x ij A i ( j 0,..., n )
i 1
7. Продолжение
Слайд 7Продолжение
m
Пусть
z j ci x ij ;
i 1
j zj cj
A1, A2 , ..., Am
- единичные
m
x ij a ij ; z j ci a ij
i 1
m
j ci a ij c j
i 1
( j 1,..., n )
8. Теоремы
Слайд 8Теоремы
Теорема 1 (признак оптимальности):
Опорный план X* = ( x1, x2, …, xm, 0, …, 0 )
задачи (1)-(3) является оптимальным, если
j ( j 1,..., n ) j 0
Теорема 2: Если k 0 для некоторого j=k и
среди чисел a ik 0 (i 1,..., m) , то целевая
функция (1) задачи (1)-(3) не ограничена на
множестве ее планов
9. Теоремы
Слайд 9Теоремы
Теорема 3: Если опорный план X задачи (1)-(3)
не вырожден и k 0 , но среди a ik есть
положительные, то существует опорный план
X* такой, что F(X)>F(X)
Теоремы позволяют проверить, является ли
найденный опорный план оптимальным и
нужно ли переходить к новому опорному
плану
10. Этапы:
Слайд 17Этапы:
1) Находим опорный план
2) Составляем симплекс-таблицу
3) Выясняем, есть ли хотя бы одно ∆j < 0
Если нет, то найденный опорный план
оптимален
Если есть, то либо устанавливают
неразрешимость задачи, либо переходят
к новому опорному плану
11. Этапы:
Слайд 18Этапы:
4) Находим направляющие столбец и строку
5) Определяем положительные компоненты
нового опорного
Все эти числа записываем
в новой симплекс-таблице
6) Проверяем найденный опорный план на
оптимальность
Если план не оптимален, то возвращаемся
к этапу 4
Если план оптимален или установлена
неразрешимость, процесс решения задачи
заканчиваем
12. Проблемы
Слайд 16Проблемы
Если задача имеет вырожденные опорные
планы, то на одной из итераций одна или
несколько переменных опорного плана могут
оказаться равными нулю, т.е. при переходе от
одного опорного плана к другому значение
функции может остаться прежним
Возможен случай, когда функция сохраняет
свое значение в течение нескольких
итераций
Возможен возврат к первоначальному базису
(зацикливание)











 mathematics
mathematics








