Similar presentations:
Симплексная таблица и ее преобразование (алгоритм симплекс-метода)
1.
Симплексная таблица и ее преобразование(алгоритм симплекс-метода)
С ( х) (с, х) max
Aх b
х 0
(1)
Пусть система ограничений Ax=b преобразована в
приведенную форму:
x i aij x j хi 0 , i
j
xi0 0, i
(2)
2.
Будем считать, что в приведенной форме (2) базисныевектора расположены первыми по порядку, т.е. 1,2,..., m
В качестве исходного базиса необходимо выбирать
единичный базис, так как в этом случае все вектора
1
1
.
А j A A j E A j EAj A j
Координаты вектора Аj совпадают с координатами его
разложения по базису:
a1 j
1
0
0
a2 j
0
1
0
Аj
a1 j a 2 j ...a mj
...
...
...
0
0
1
a
mj
3.
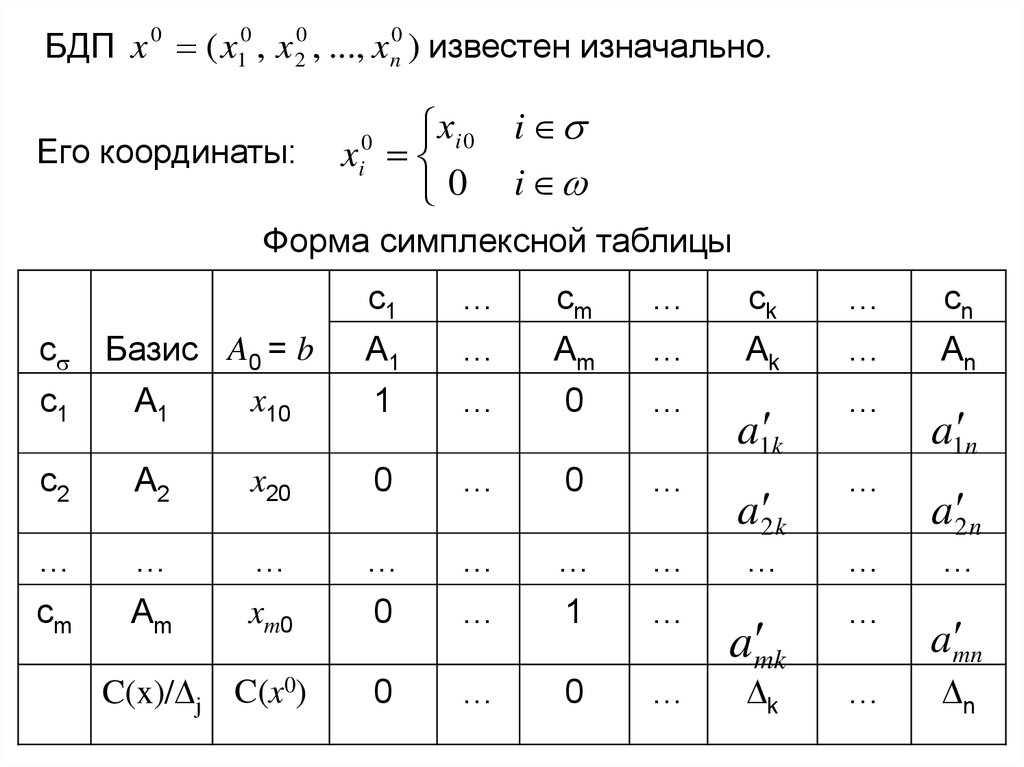
БДП x 0 ( x10 , x 20 , ..., x n0 ) известен изначально.Его координаты:
хi 0
x
0
0
i
i
i
Форма симплексной таблицы
c
c1
Базис A0 = b
x10
A1
c1
A1
1
…
…
…
cm
Am
0
…
…
…
c2
A2
x20
0
…
0
…
…
cm
…
Am
…
xm0
…
0
…
…
…
1
…
…
0
…
0
…
C(x)/ j C(x0)
ck
Ak
a1 k
a 2 k
…
amk
k
…
…
…
…
…
…
…
cn
An
a1 n
a 2 n
…
amn
n
4.
cσ – коэффициенты целевой функции при базисныхпеременных;
А1, А2, …, Аn – векторы-столбцы решаемой задачи;
c1, с2, …, cn – коэффициенты целевой функции;
C(x) – значение целевой функции на плане x;
j – двойственные оценки.
Из симплексной таблицы легко выписывается БДП:
x 0 ( x10 , x 20 , ..., x n0 ) = (x10, x20,…, xm0, 0, 0,…,0)
5.
Значение целевой функции на этом плане вычисляется поформуле:
С ( x 0 ) ci xi0 c1 x10 c2 x20 ... cm xm0
i
Двойственные оценки j вычисляются по формуле:
j ci аij c j ,
j 1, n
i
Переход к новому БДП осуществляется при помощи двух
правил.
Правило 1. Определение номера вектора, вводимого в
базис.
min j k 0
1 j n
(3)
6.
Правило 2. Определение номера вектора, выводимого избазиса.
Необходимо определить номер r выводимого из базиса
вектора Ar , r . Новый носитель плана будет выглядеть
так: нов = k \ r .
xi0 xr0
min
0 а
аik
ik ark
(4)
(предполагаем, что минимум достигается при i=r) .
Номер выводимого вектора определяется с помощью
симплекс-таблицы:
0
r
xr 0
x
ark
ark
(5)
7.
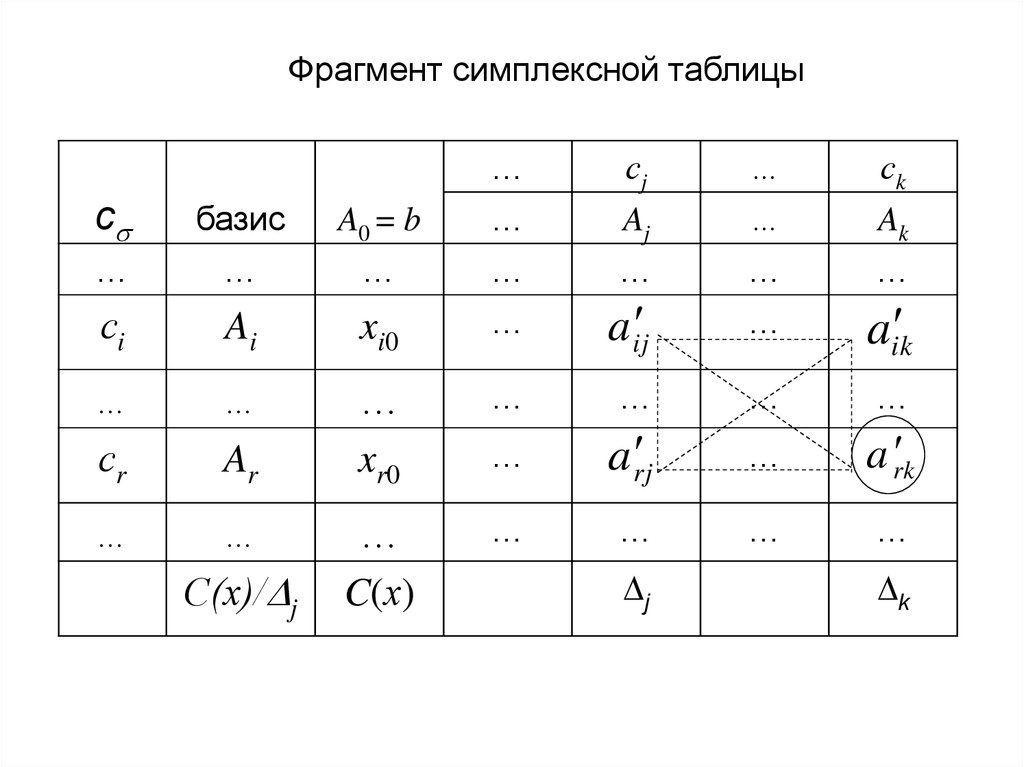
Опр.Элемент
, стоящий на пересечении вектора,
a rk
вводимого в базис, и вектора, выводимого из
базиса, называется ведущим (или разрешающим)
элементом симплексной таблицы.
8.
Фрагмент симплексной таблицыA0 = b
…
базис
…
…
…
…
…
сi
Ai
xi0
…
a ij
…
…
…
сr
…
Ar
…
xr0
…
…
…
…
…
a rj
…
a rk
…
…
C(х)/ j
…
C(х)
…
…
…
…
c
сj
Aj
…
…
сk
Ak
…
…
j
aik
k
9.
Формулы пересчета элементов симплекс-таблицыпри переходе к новому базису:
нов
а rj
аik , j 0, n, j k , i , i r
аij аij
а rk
а rj
нов
а kj
, j 0, n
а rk
1 i k
нов
аik ik
0 i k
ik - символ Кронекера
(6)
10.
Координаты нового плана вычисляются по формулам:нов
х
x
i
0
i
0
x нов xr 0 ,
k 0
ark
xr 0
aik , i , i k
ark
(7)
i k
Новые двойственные оценки:
нов
j
a rj
j
k
a rk
(8)
11.
Значение целевой функции на новом плане равноС( х
нов
xr 0
) C(x )
k
ark
0
(9)
Теорема.
Для нового базисного допустимого плана имеет место
неравенство
С(хнов)
С(х0),
т.е.
полученный
путем
преобразований план не хуже, чем план, имеющийся на
предыдущей итерации.
12.
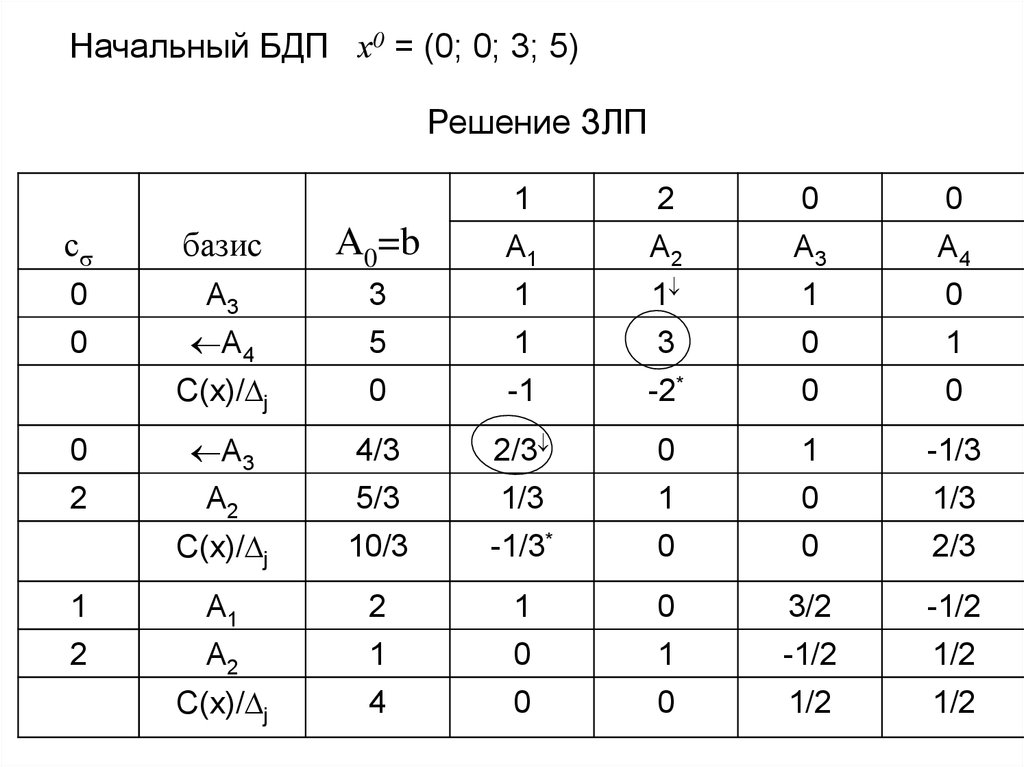
Пример.С ( X ) x1 2 x 2 max
x1 x 2 3
x1 3 x 2 5
x ,x 0
1 2
Приведем ЗЛП к каноническому виду путем введения
дополнительных переменных:
С ( X ) x1 2 x 2 max
x1 x 2 x3 3
x 3x x 5
2
4
1
x1 , x 2 , x3 , x 4 0.
13.
Начальный БДП х0 = (0; 0; 3; 5)Решение ЗЛП
1
2
0
0
с
базис
A0=b
A1
A2
A3
A4
0
A3
3
1
1
1
0
0
A4
5
1
3
0
1
C(х)/ j
0
-1
-2*
0
0
0
A3
4/3
2/3
0
1
-1/3
2
A2
5/3
1/3
1
0
1/3
C(х)/ j
10/3
-1/3*
0
0
2/3
1
A1
2
1
0
3/2
-1/2
2
A2
1
0
1
-1/2
1/2
C(х)/ j
4
0
0
1/2
1/2
14.
Выполнив преобразования симплекс-таблицы,получаем оптимальный план хопт = (2; 1; 0; 0) и значение
целевой функции на этом плане С(хопт) = 4.











 mathematics
mathematics








