Симплекс-метод

1. Симплекс-метод

Впервые симплексный метод был предложен
американским ученым Дж. Данцигом в 1949
году, однако еще в 1939 году идеи метода были
разработаны
российским
ученым
А.В.
Канторовичем.
СМ решения задачи ЛП основан на переходе от
одного допустимого решения к другому, при
котором значение ЦФ возрастает.
Указанный переход возможен, если известно
какое-нибудь допустимое решение.

2.

Из линейной алгебры известно:
Равенства называются линейно независимыми, если
никакое из них нельзя получить из других путем умножения
на какие-то коэффициенты и суммирования, т.е. никакое из
них не является следствием остальных.
В линейной алгебре доказывается, что максимальное число
линейно
независимых
равенств,
связывающих
n
переменных x1 …xn, равно n .
В линейной алгебре доказывается, что систему из r
независимых равенств с n переменными всегда можно
разрешить относительно каких-то r
переменных
(называемых базовыми) и выразить через них остальные nr переменных (называемых свободными). Свободным
переменным можно придавать какие угодно значения.
Теорема1 Любому допустимому решению задачи ЛП
соответствует по крайней мере хотя бы одна угловая
точка многоугольника решений, и наоборот, любой
угловой точке многогранника решений соответствует
допустимое базисное решение.

3.

Для реализации СМ необходимо 3 основных
момента:
Необходимо отыскать способ отыскания
исходного допустимого решения.
Должен быть описан механизм перехода от
одного допустимого решения к другому (к
другой вершине многоугольника).
Должен быть сформулирован критерий, с
помощью которого можно проверить на
оптимальность: остановить процесс поиска или
идти дальше.

4.

Рассмотрим задачу ЛП в стандартной форме
n
F c j x j
j 1
при
max
выполнении условий:
n
,
i
1
,
m
a
x
b
ij
j
i
j 1
x 0, j 1, n
j

5. Алгоритм решения задачи :

1.
Стандартная задача ЛП сводится к основной
задаче.
F= c1x1+…+cnxn max
a11x1+…+a1nxn+xn+1=b1
a11x1+…+a1nxn
….
am1x1+…+amnxn+
xj 0 j=1,n
+xn+2=b2
xn+m=bm

6. Определяется начальное допустимое решение

2.
Определяется начальное допустимое решение
Для этого запишем систему ограничений в векторной
форме
x1A1+x2A2+…+ xnAn+xn+1An+1+…+ xn+mAn+m =A0 , где
0
b1
a11
a1n
1
0
b2
0
a 21
a
2n
... An m A0
A1
A
...
A
n
1
...
n
...
...
...
...
1
a
0
b
m1
m
amn
An+1…An+m – линейно-независимые векторы m – мерного пространства
первоначальное допустимое решение: x0=(0,…0,b1…bm).

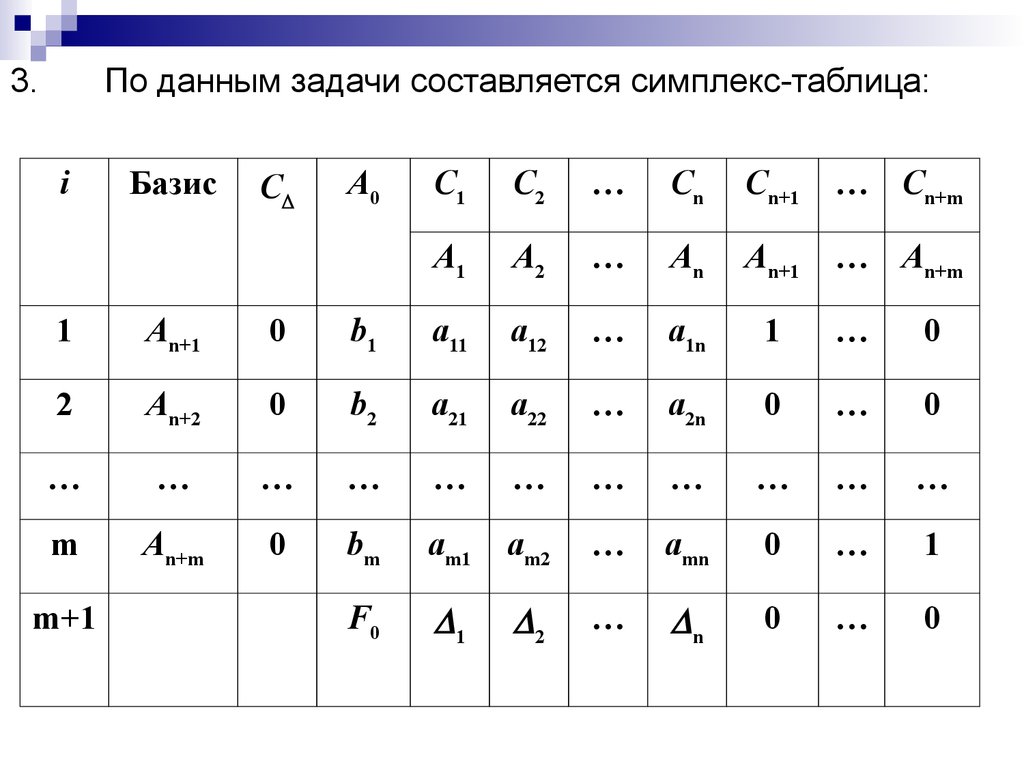
7. По данным задачи составляется симплекс-таблица:

3.
По данным задачи составляется симплекс-таблица:
i
Базис
C
A0
C1
C2
…
Cn
Cn+1
… Cn+m
A1
A2
…
An
An+1
… An+m
1
An+1
0
b1
a11
a12
…
a1n
1
…
0
2
An+2
0
b2
a21
a22
…
a2n
0
…
0
…
…
…
…
…
…
…
…
…
…
…
m
An+m
0
bm
am1
am2
…
amn
0
…
1
F0
1
2
…
n
0
…
0
m+1

8.

В (m+1) –й строке в столбцах векторов A j
записываются значения
∆j =
m
c a
i 1
i ij
cj
( j 1, n)
сiaij- значение целевой функции, если вместо
неизвестных подставить коэффициенты
разложения j – го вектора по векторам базиса. Δназывают оценками плана.
Значение F0 равно скалярному произведению
m
вектора А0 на вектор C∆
ci bi
F0=
i 1

9.

4.
Полученное допустимое решение проверяется на
оптимальность (в случае максимизации).
Используются теоремы:
Теорема2 Если для некоторого опорного плана x*
выполняются неравенства Δj ≥0, то этот план
оптимальный .
Теорема3 Если для опорного плана Х задачи ЛП
существует хотя бы один элемент j , для которого Δj
< 0 и среди коэффициентов разложения j-го вектора
есть хотя бы один аij >0, то существует такой
опорный план Х’, для которого F(x’)>F(x).
Если хотя бы для одной отрицательной оценки ∆j < 0.
коэффициенты разложения aij
соответствующего
вектора неположительные, то линейная функция не
ограничена
на
многограннике
решений,
и
следовательно, задача не имеет решения.

10.

Наличие оптимальности проверяется по
следующему признаку:
Согласно теорем выясняется, имеется
ли хотя бы одно отрицательное ∆j (ЦФ
исследуется на максимум). Если нет, то
найденное
решение
является
оптимальным.
Если же среди чисел ∆j имеются
отрицательные,
то
либо
устанавливается
неразрешимость
задачи, либо переходят к новому
допустимому решению.

11.

В случае исследования целевой функции на минимум
допустимое решение является оптимальным, если все
разности ∆j ≤ 0 . Если хотя бы одно ∆j>0 , тогда в базис
включается вектор, соответствующий этой оценке, и
вычисляется новое допустимое решение, при котором
линейная целевая функция будет принимать меньшее
значение.
Если положительных элементов в последней строке
симплекс-таблицы, несколько, то в базис должен быть
включен вектор, которому соответствует максимальный
положительный ∆j .> 0.
Если имеется несколько одинаковых максимальных
значений ∆j , то из соответствующих им векторов
включается в базис вектор, которому соответствует
минимальное Сj .
Если хотя бы для одной положительной оценки ∆ j> 0.
коэффициенты разложения aij
соответствующего
вектора неположительные, то линейная функция не
ограничена
на
многограннике
решений,
и
следовательно, задача не имеет решения.

12.

5.
Находится
направляющий
столбец
и
направляющая строка.
Направляющий
столбец
определяется
наибольшим
по
абсолютной
величине
отрицательным числом ∆j , а направляющая
строка
–
минимальным
отношением
компонент
столбца
вектора
А0
к
положительным компонентам направляющего
столбца
Выбор
максимального
по
модулю
отрицательного
элемента
∆j
означает
включение в базис переменной, увеличение
которой приводит к максимальному росту ЦФ

13.

6.
Определяются положительные компоненты нового
допустимого решения и коэффициенты разложения
векторов Aj по векторам нового базиса и числа F0 ∆j
по следующим формулам:
bi (br / a rk ) aik , при i r
bi
при i r
br / a rk
aij (arj / ark ) aik , при i r
arj
при i r
arj / ark
где k – номер направляющего столбца (вектор Ak вводится в
базис), r – номер направляющей строки (Ar исключается из
базиса).

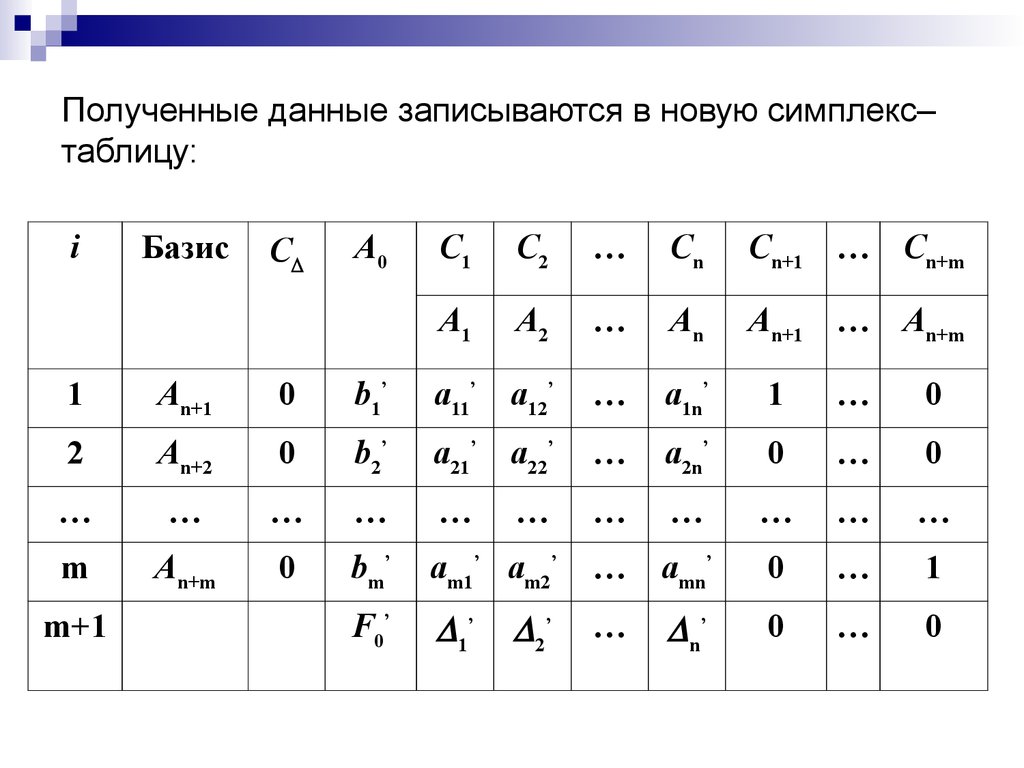
14. Полученные данные записываются в новую симплекс–таблицу:

Полученные данные записываются в новую симплекс–
таблицу:
i
Базис
C
A0
C1
C2
…
Cn
Cn+1 … Cn+m
A1
A2
…
An
An+1 … An+m
1
An+1
0
b1’
a11’
a12’
…
a1n’
1
…
0
2
An+2
0
b2’
a21’ a22’
…
a2n’
0
…
0
…
…
…
…
…
…
…
…
…
…
…
m
An+m
0
bm’
am1’ am2’
…
amn’
0
…
1
F0’
1’
…
n’
0
…
0
m+1
2’

15.

Проверяют найденное допустимое
решение на оптимальность
Если решение не является оптимальным
то возвращаются к п.5 ,
если оптимальное или установлена
неразрешимость
задачи
процесс
решения заканчивается.
7.

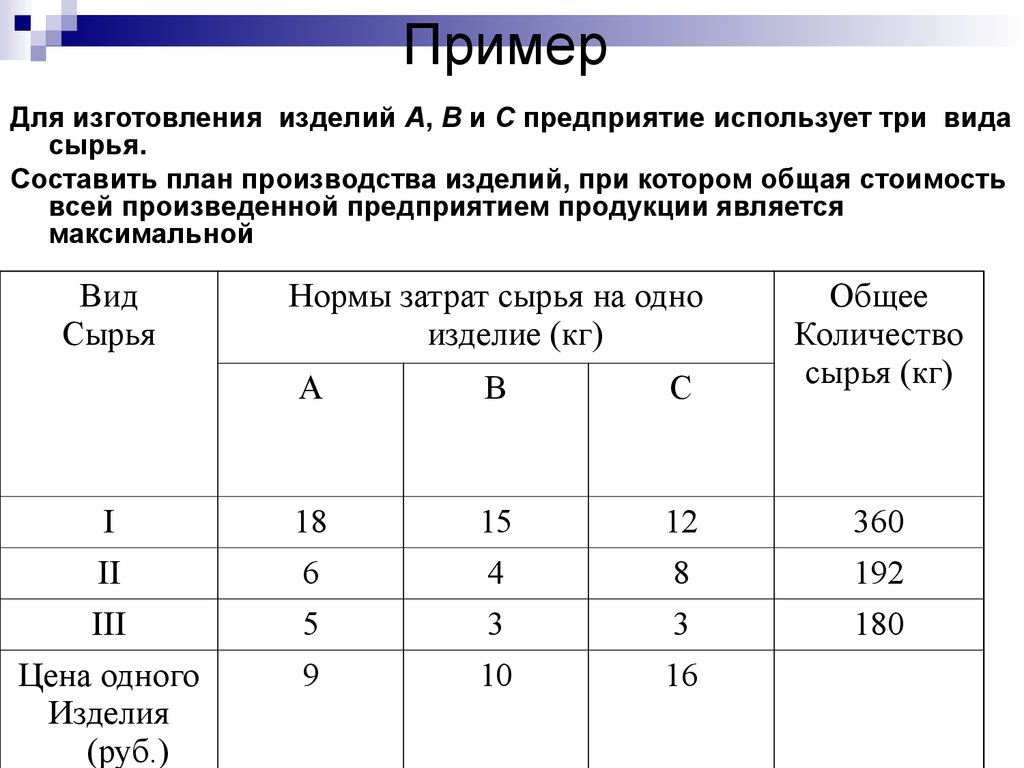
16. Пример

Для изготовления изделий A, B и C предприятие использует три вида
сырья.
Составить план производства изделий, при котором общая стоимость
всей произведенной предприятием продукции является
максимальной
Вид
Сырья
Нормы затрат сырья на одно
изделие (кг)
A
B
C
Общее
Количество
сырья (кг)
I
II
III
18
6
5
15
4
3
12
8
3
360
192
180
Цена одного
Изделия
(руб.)
9
10
16

17. Составим математическую модель задачи.

18 x1 15 x 2 12 x 3 360
6 x1 4 x 2 8 x 3 192
5 x1 3 x 2 3 x 3 180
x 0, x 0, x 0
2
3
1
F 9 x 10 x2 16 x3
1
max

18. Запишем эту задачу в форме основной задачи линейного программирования.

18 x 15 x 12 x
1
2
3
6 x1 4 x 2 8 x3
5x 3x 3x
1
2
3
x4 360
x5 192
x6 180

19. Полученную систему уравнений запишем в векторной форме:

x1 A1 x2 A2 x3 A3 x4 A4 x5 A5 x6 A6 A0 ,
где
18
15
12
1
0
0
360
A1 6 ; A2 4 ; A3 8 ; A4 0 ; A5 1 ; A6 0 ; A0 192 .
5
3
3
0
0
1
180

20.

Среди векторов имеются три единичных вектора ,
которые образуют базис трехмерного векторного
пространства.
A4 , A5 , A6
Исходное решение задачи
0, 0, 0, 360, 192, 180
X1

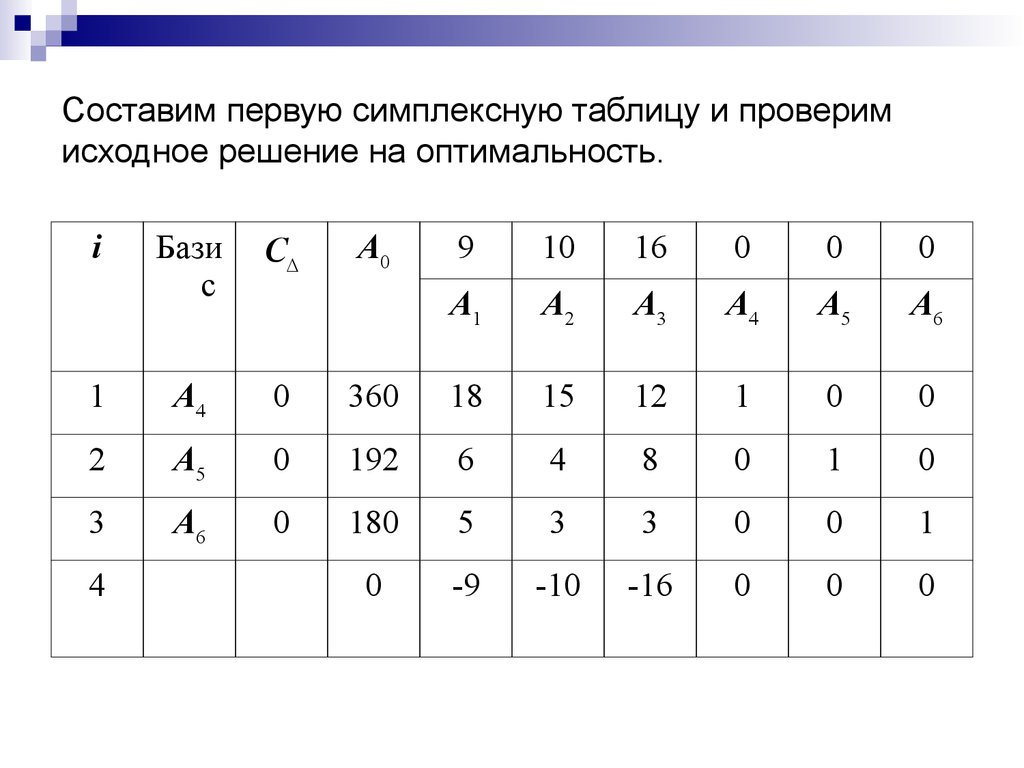
21. Составим первую симплексную таблицу и проверим исходное решение на оптимальность.

i
Бази
с
C
1
A4
0
2
A5
3
A6
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
360
18
15
12
1
0
0
0
192
6
4
8
0
1
0
0
180
5
3
3
0
0
1
0
-9
-10
-16
0
0
0

22. Значения, стоящие в четвертой строке симплексной таблицы вычисляются следующим образом:

,
c
0 360 0 192 0 180 0
A
0
F0
,
c
c1 0 18 0 6 0 5 9 9
A
1
1
,
c
A
2 c 2 0 15 0 4 0 3 10 10
2
,
3 c A3 c 3 0 12 0 8 0 3 16 16

23.

Исходное решение не является оптимальным, т.к. в 4-й
строке таблицы имеются три отрицательных числа:
-9, -10, -16.
В базис будем вводить вектор A3, т.к. максимальное по
абсолютной величине отрицательное число (-16) стоит в
4-й строке этого вектора .
Определим вектор, исключаемый из базиса.
b a для a 0, т.е.
min 360 12; 192 8; 180 3 192 8.
min
i
i3
i3
Следовательно, вектор A5 исключается из базиса.

24.

i
Бази
с
C
1
A4
0
2
A5
3
A6
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
360
18
15
12
1
0
0
0
192
6
4
8
0
1
0
0
180
5
3
3
0
0
1
0
-9
-10
-16
0
0
0

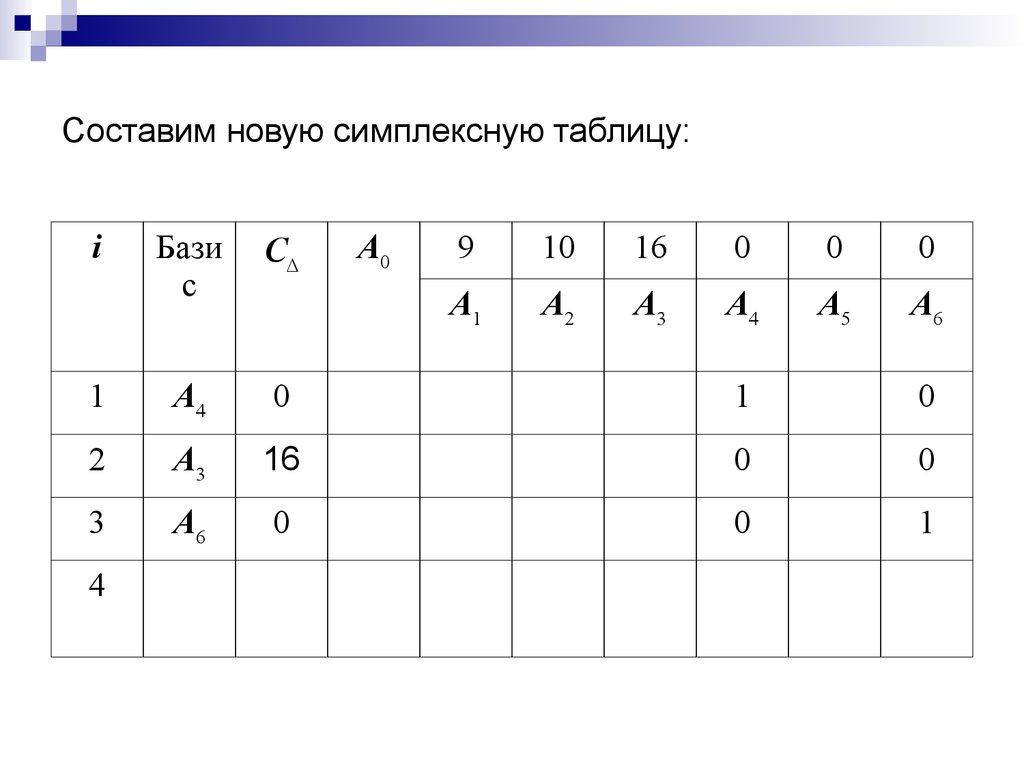
25. Составим новую симплексную таблицу:

i
Бази
с
C
1
A4
0
1
0
2
A3
16
0
0
3
A6
0
0
1
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6

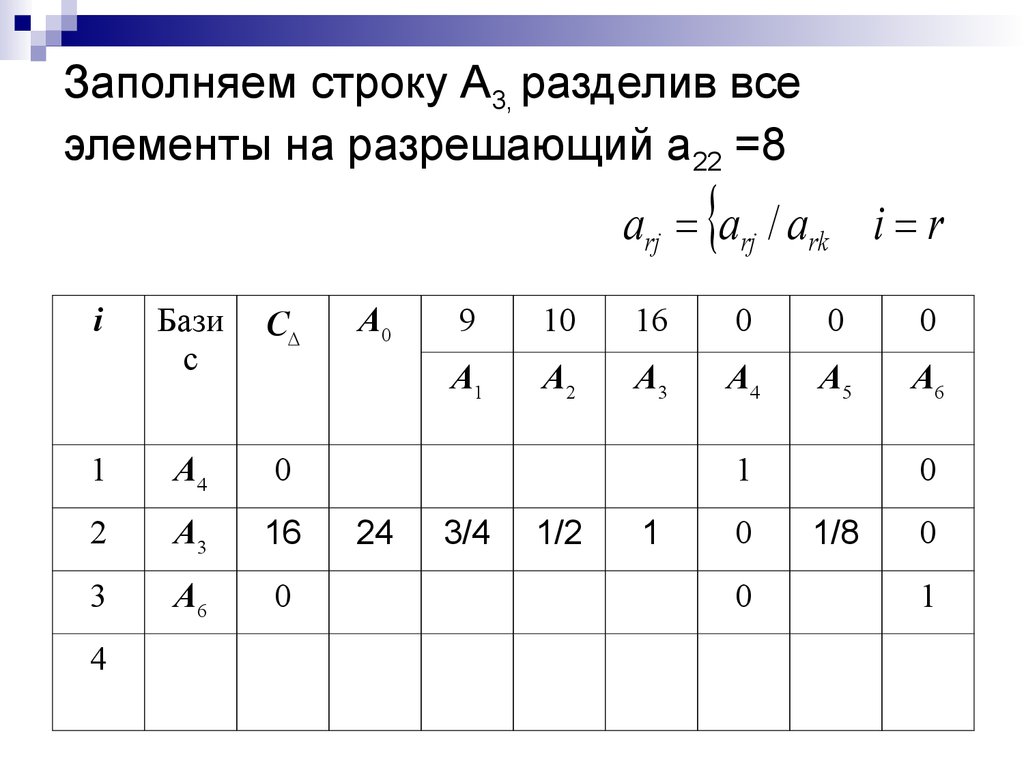
26. Заполняем строку A3, разделив все элементы на разрешающий а22 =8

arj arj / ark i r
i
Бази
с
C
1
A4
0
2
A3
16
3
A6
0
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
1
24
3/4
1/2
1
0
0
0
1/8
0
1

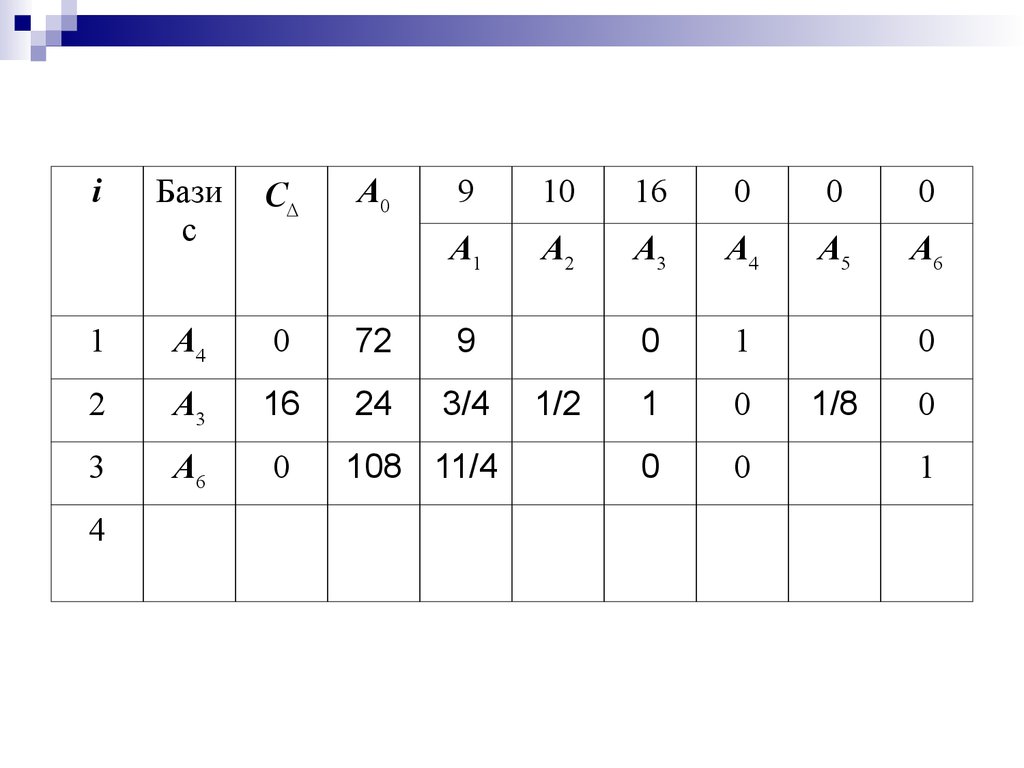
27. Вычисление остальных элементов таблицы производим по рекуррентным формулам:

b bi br a rk a , при i r
'
aij aij a rj a rk a , при i r,
'
i
ik
ik
где k - номер направляющего столбца,
r - номер направляющей строки.
В нашем случае k=3 r=2

28. Тогда компоненты вектора A0 находятся

192
12 72
b b1 b2 a 23 a 360
8
'
b3 b3 b2 a 23 a 180 24 3 108
'
1
13
33

29.

i
Бази
с
C
1
A4
0
72
2
A3
16
24
3
A6
0
108
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
0
1
1
0
0
0
3/4
1/2
0
1/8
0
1

30. Вычислим компоненты вектора A1:

a
a
21
23 a 18 6 8 12 9
a a11
'
5 6 8 3 11 4
a
a
21
23 a
a31 a31
'
11
13
33

31.

i
Бази
с
C
1
A4
0
72
9
2
A3
16
24
3/4
3
A6
0
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
0
1
1
0
0
0
108 11/4
1/2
0
1/8
0
1

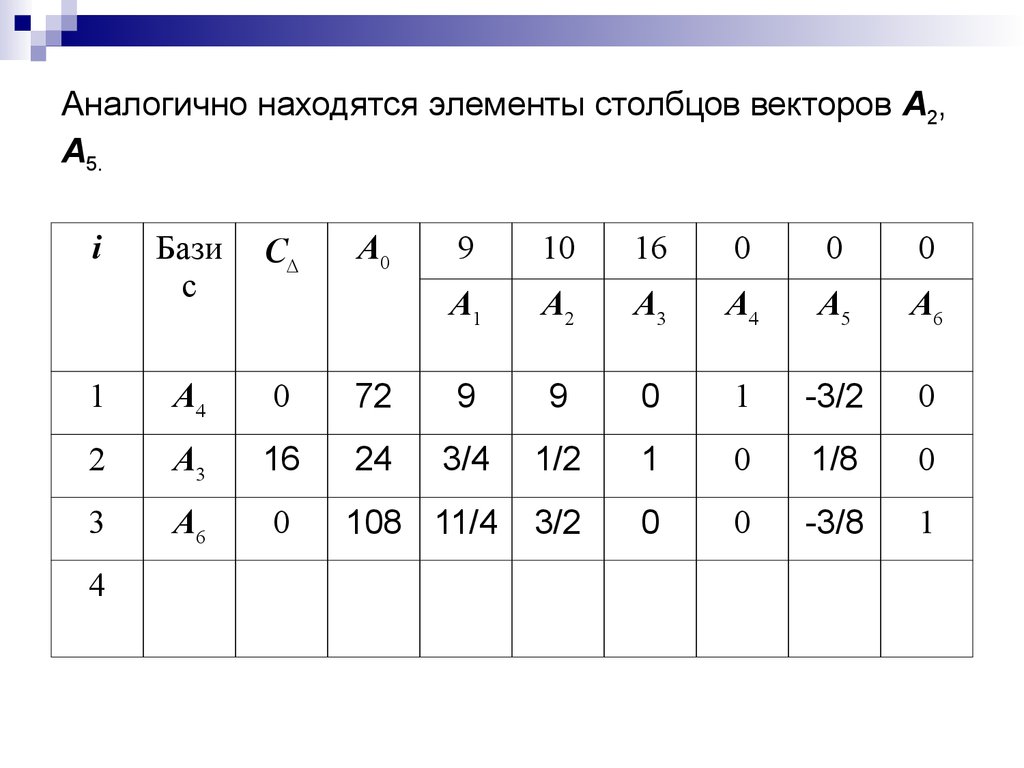
32. Аналогично находятся элементы столбцов векторов A2, A5.

i
Бази
с
C
1
A4
0
2
A3
16
3
A6
0
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
72
9
9
0
1
-3/2
0
24
3/4
1/2
1
0
1/8
0
108 11/4
3/2
0
0
-3/8
1

33. Теперь заполним четвертую строку симплексной таблицы.

F 0 c , A0 0 72 16 24 0 108 384
1 c , A1 c1 0 9 16 3 4 0 11 4 9 3
2 c , A2 c2 16 1 2 10 2
5 c , A5 c5 16 1 8 0 2

34.

i
Базис
C
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
1
A4
0
72
9
9
0
1
-3/2
0
2
A3
16
24
3/4
1/2
1
0
1/8
0
3
A6
0
108 11/4
3/2
0
0
-3/8
1
384
-2
0
0
2
0
4
3
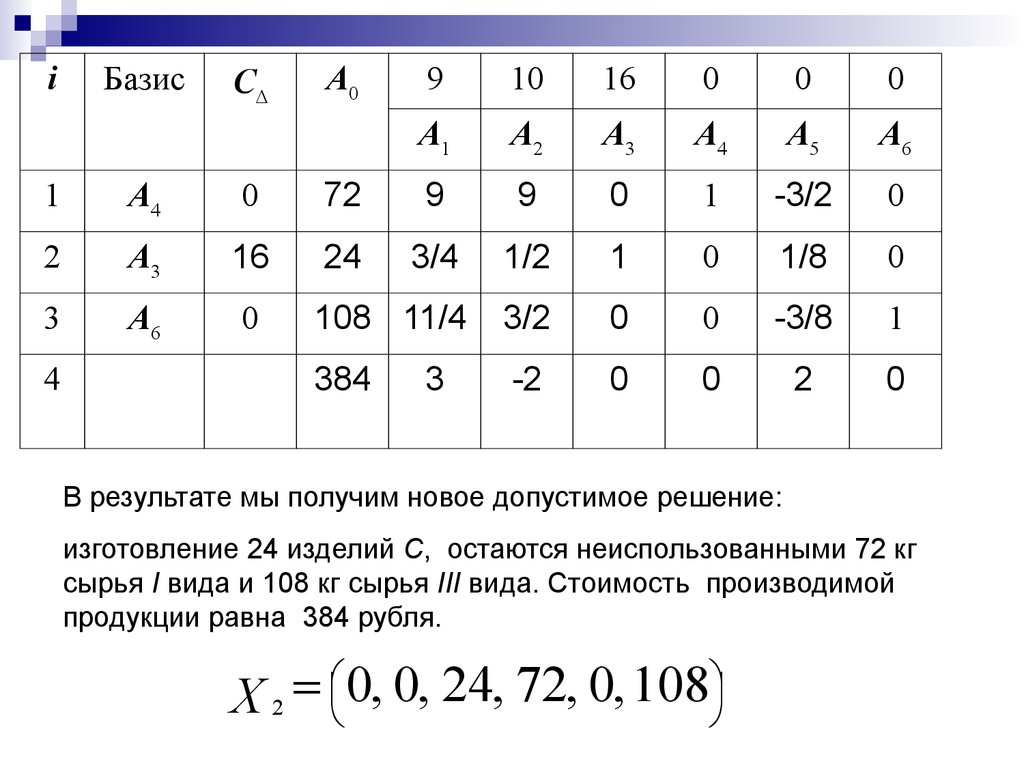
В результате мы получим новое допустимое решение:
изготовление 24 изделий C, остаются неиспользованными 72 кг
сырья I вида и 108 кг сырья III вида. Стоимость производимой
продукции равна 384 рубля.
0, 0, 24, 72, 0, 108
X2

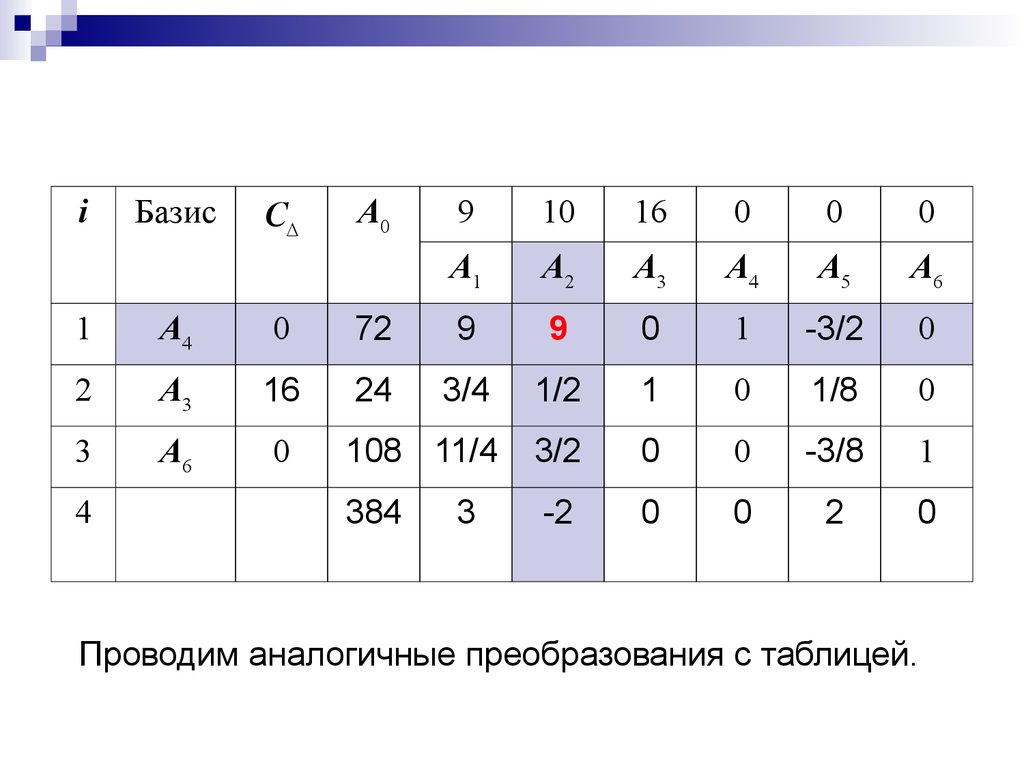
35. Решение X2 не является оптимальным, т.к. в 4-ой строке последней симплекс–таблице в столбце вектора A2 стоит отрицательное число –2.

В базис вводится вектор A2,
Для определения направляющей строки найдем
72
min 72 9, 24 2 1, 108 2 3
8
9
Следовательно, исключению из базиса подлежит вектор A4,

36.

i
Базис
C
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
1
A4
0
72
9
9
0
1
-3/2
0
2
A3
16
24
3/4
1/2
1
0
1/8
0
3
A6
0
108 11/4
3/2
0
0
-3/8
1
384
-2
0
0
2
0
4
3
Проводим аналогичные преобразования с таблицей.

37.

i
Бази
с
C
1
A2
10
2
A3
3
A6
4
A0
9
10
16
0
0
0
A1
A2
A3
A4
A5
A6
8
1
1
0
1/9
-1/6
0
16
20
1/4
0
1
-1/18 5/24
0
0
96
5/4
0
0
11/16 -1/8
1
400
5
0
0
2/9
5/3
В результате получаем новое оптимальное решение
X 3 0, 8,
20,
0, 0, 96
0

38. Ответ

Это решение соответствует плану выпуска
продукции, включающего изготовление 8
изделий B и 20 изделий C.
При этом сырье I и II видов используется
полностью и остается неиспользованным
96 кг сырья III вида.
Стоимость производимой продукции равна 400
рублей.

39. Вопросы

1.
2.
3.
4.
5.
6.
7.
В чем смысл симплекс-метода?
Что необходимо для реализации СМ?
Теорема о соответствии допустимых решений
задачи и многоугольника решений.
С чего начинается решение задачи СМ?
Как определяется начальное допустимое
решение (опорный план)?
Что такое оценка плана?
Теоремы, позволяющие проверить решение
на оптимальность (при максимизации).

40.

8.
9.
10.
11.
12.
Что
меняется
при
определении
минимального решения?
Как определяется направляющий столбец?
Как определяется направляющая строка?
Как рассчитать следующую симплекстаблицу?
Когда задача не имеет решения?