Similar presentations:
Симплекс метод
1.
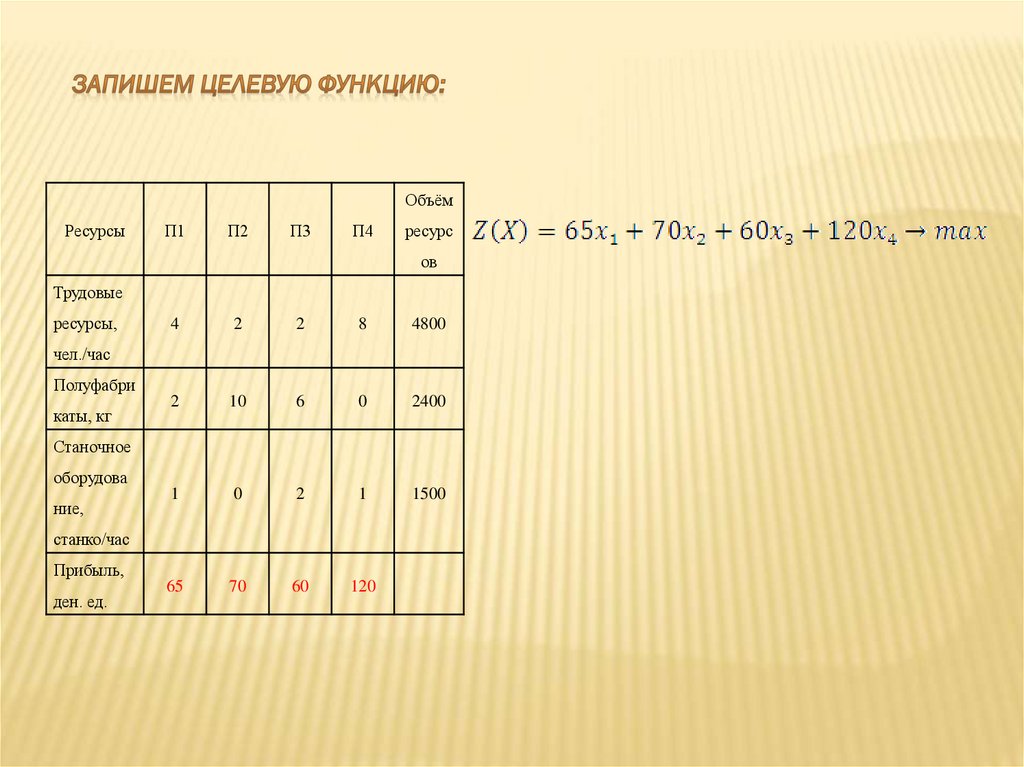
Пусть некоторое предприятие планирует выпустить 4 вида продукции (П1-П4).Причём сбыт любого количества обеспечен. Для изготовления продукции используются
трудовые ресурсы, полуфабрикаты (сырье) и станочное оборудование. Общий объём
ресурсов в расчёте на неделю, расход каждого ресурса на единицу, выпускаемой
продукции и прибыль, получаемая за единицу продукции известны
Требуется построить план производства продукции, для получения максимальной
прибыли.
Ресурсы
Объём
П1
П2
П3
П4
4
2
2
8
4800
2
10
6
0
2400
1
0
2
1
1500
65
70
60
120
ресурсов
Трудовые
ресурсы,
чел./час
Полуфабрика
ты, кг
Станочное
оборудование
, станко/час
Прибыль,
ден. ед.
2.
РесурсыОбъём
П1
П2
П3
П4
4
2
2
8
4800
2
10
6
0
2400
1
0
2
1
1500
65
70
60
120
ресурсов
Трудовые
ресурсы,
чел./час
Полуфабрикат
ы, кг
Станочное
оборудование,
станко/час
Прибыль, ден.
ед.
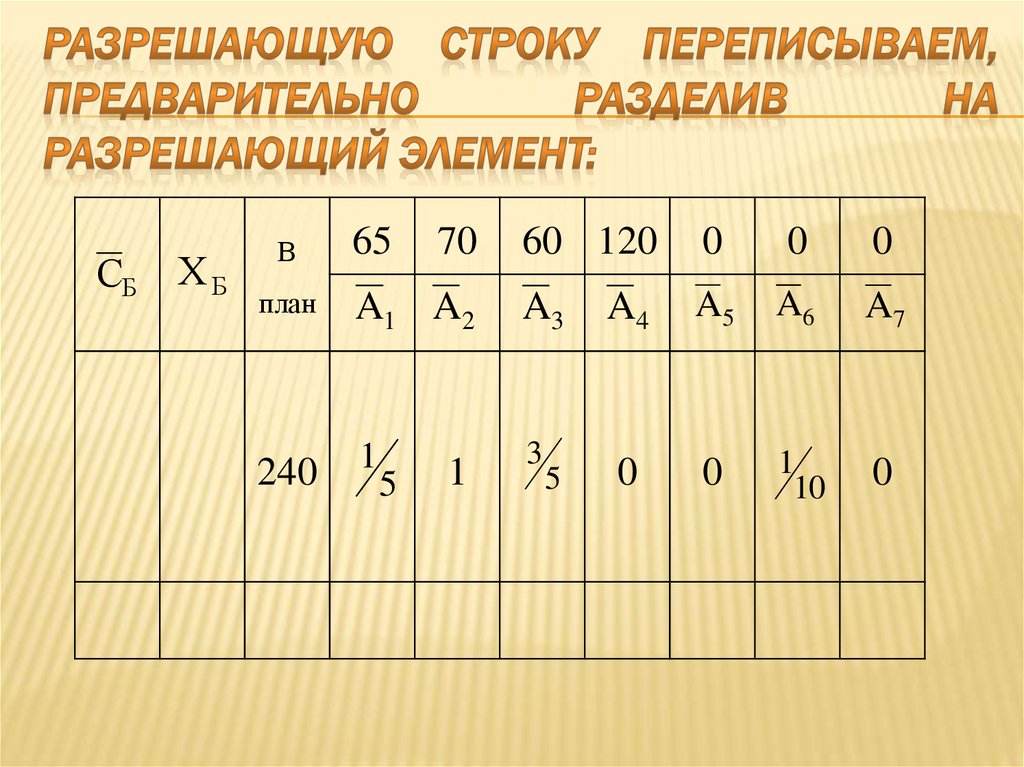
3.
ОбъёмРесурсы
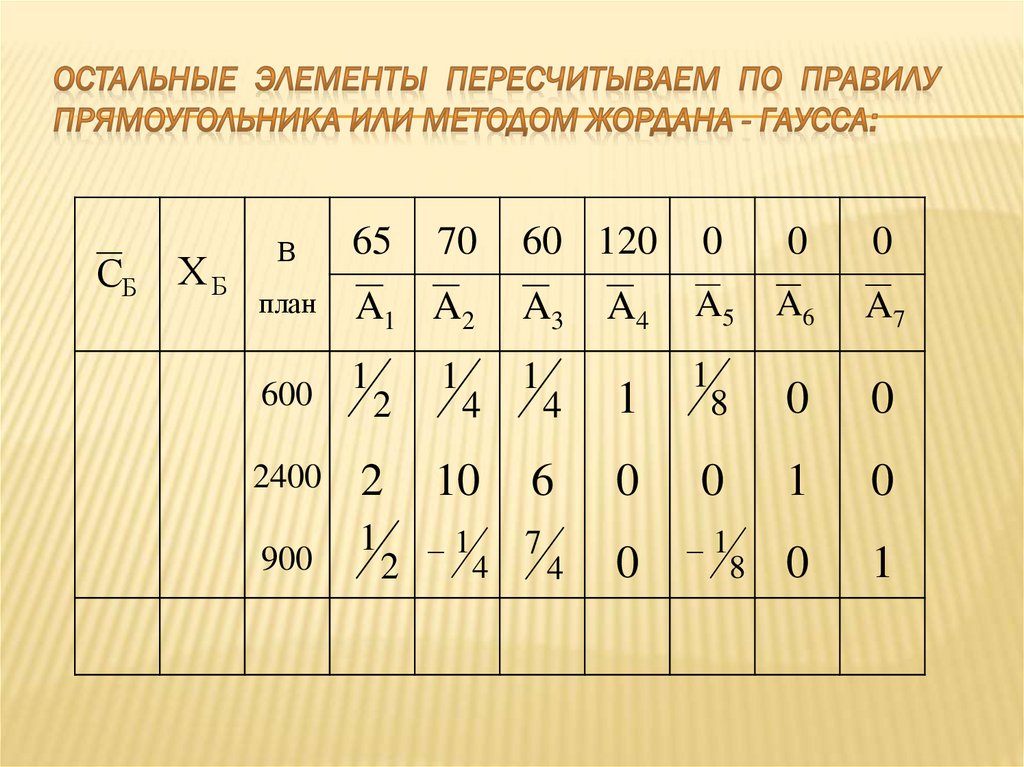
П1
П2
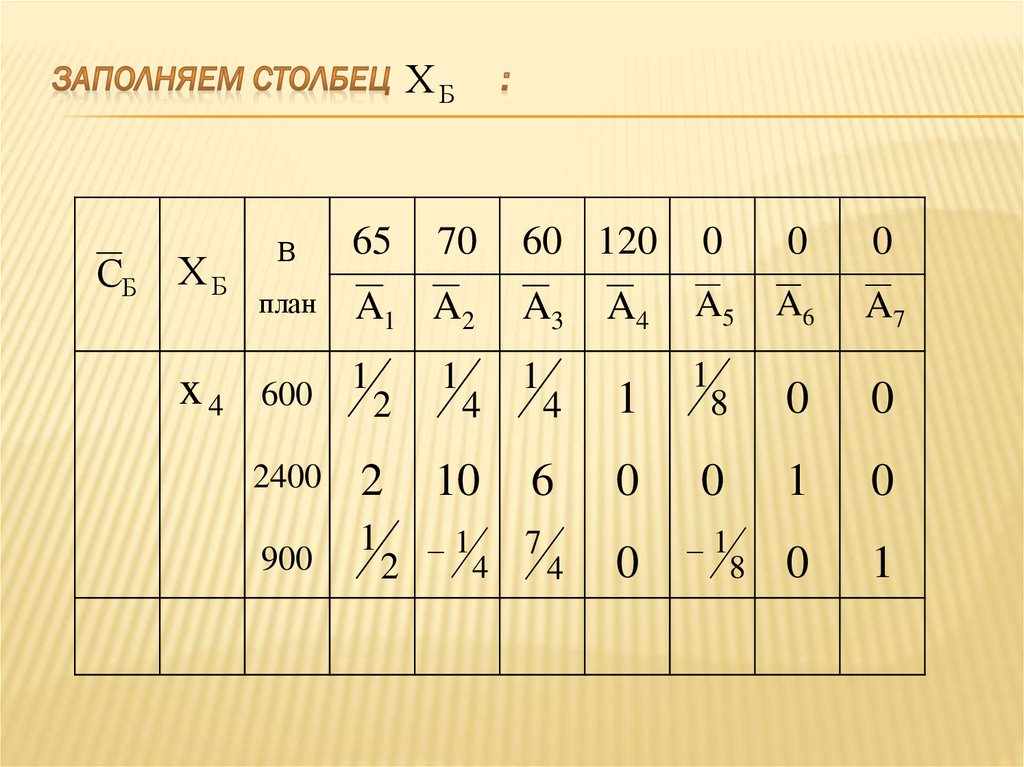
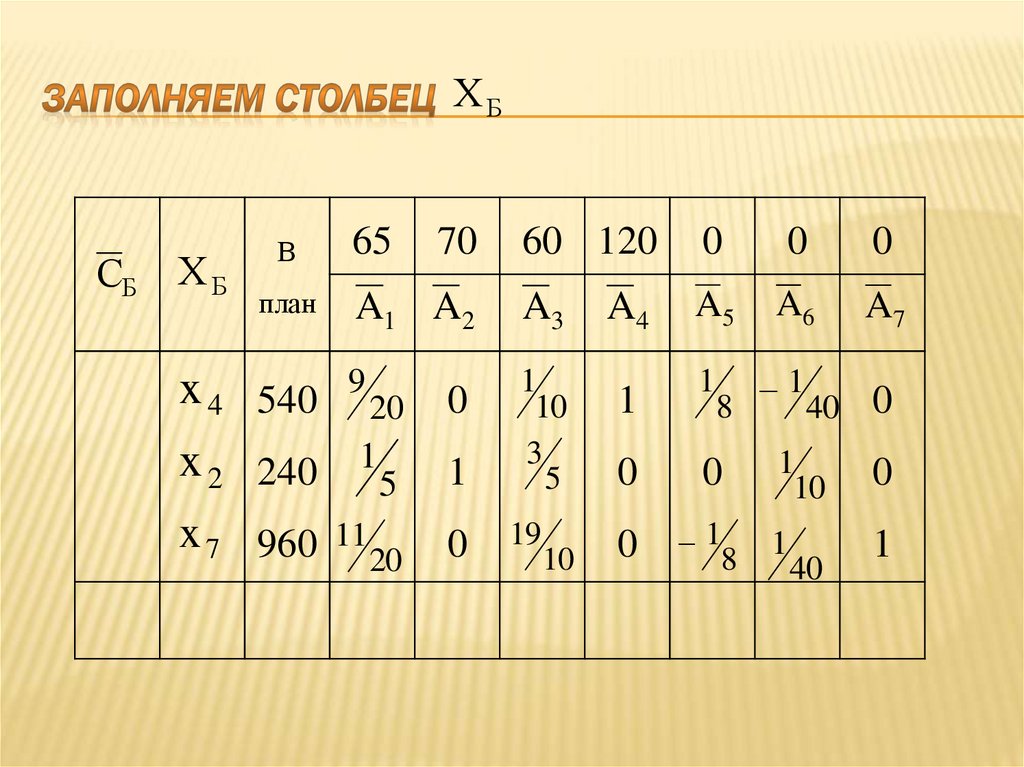
П3
П4
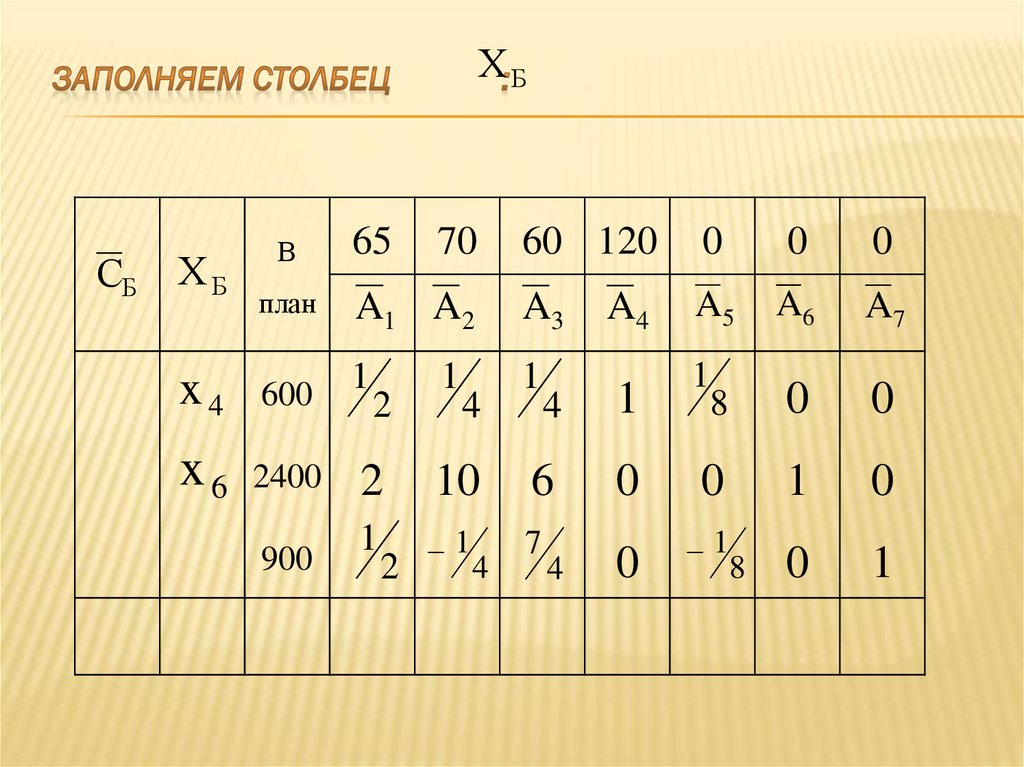
ресурс
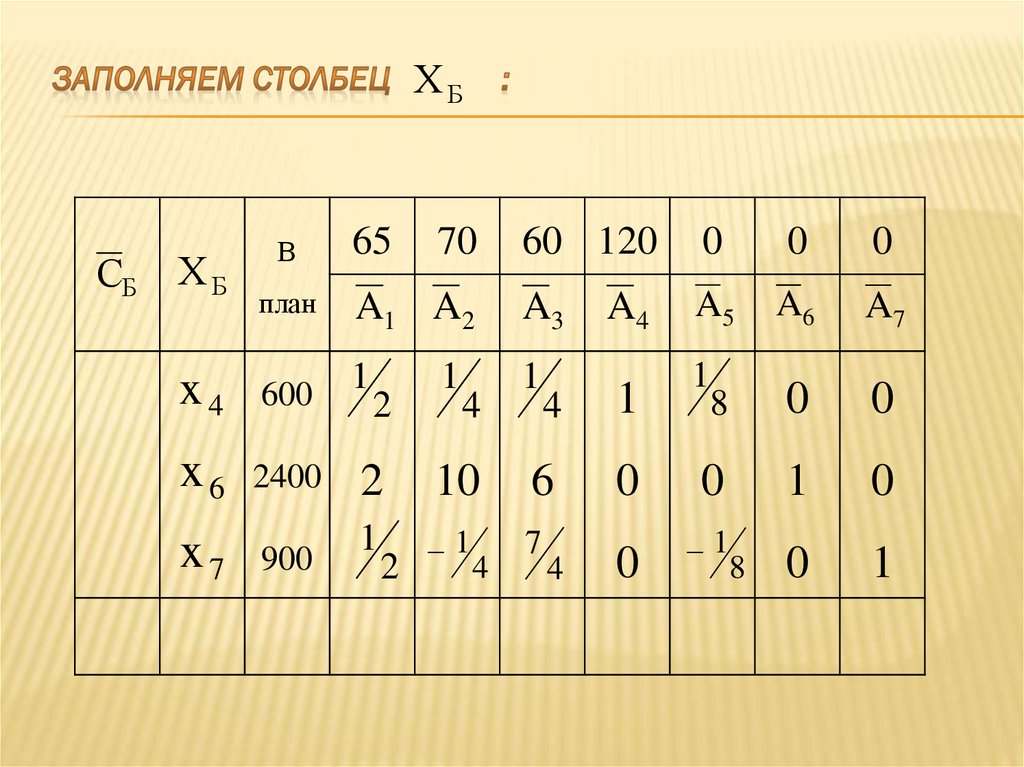
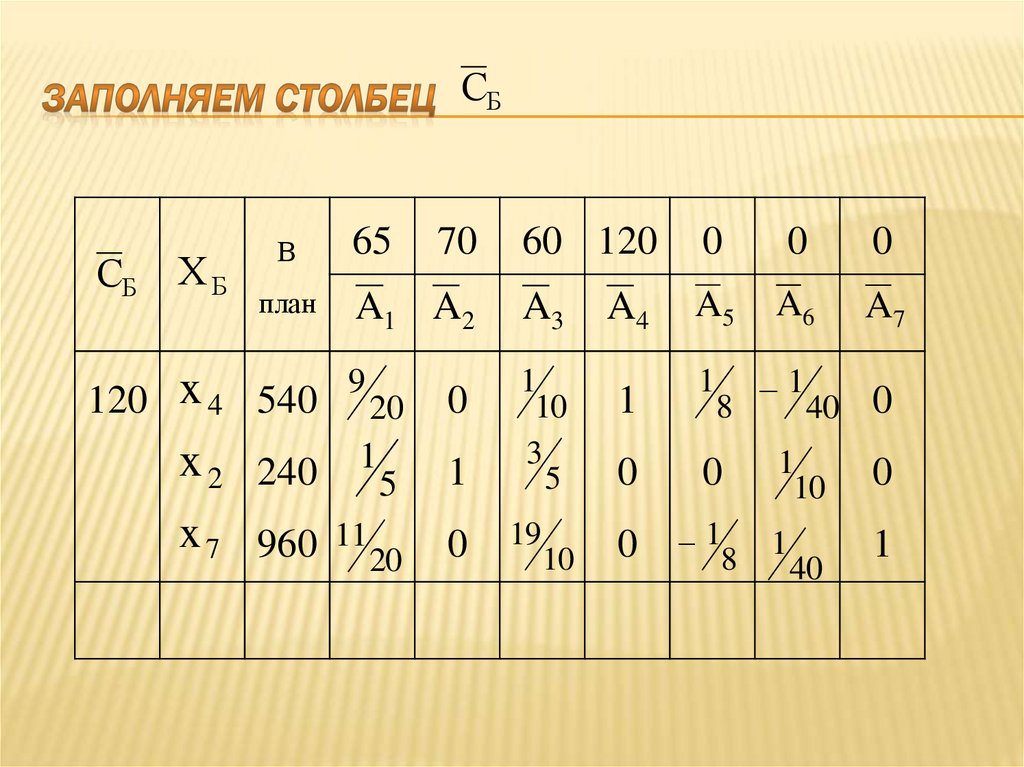
ов
Трудовые
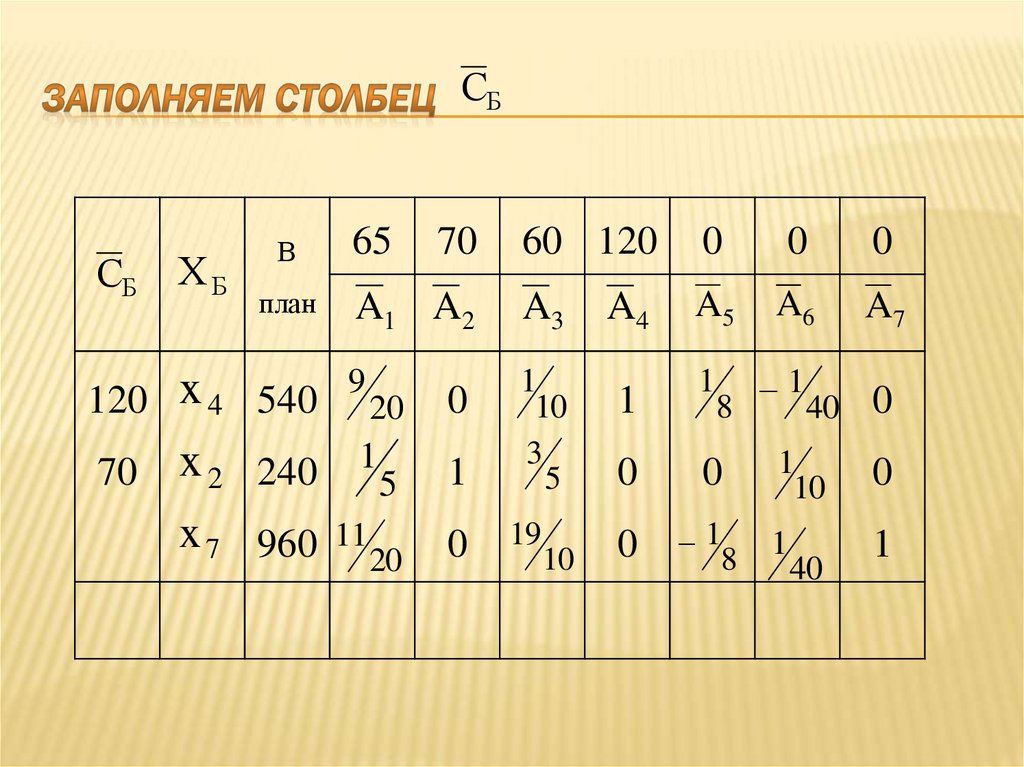
ресурсы,
4
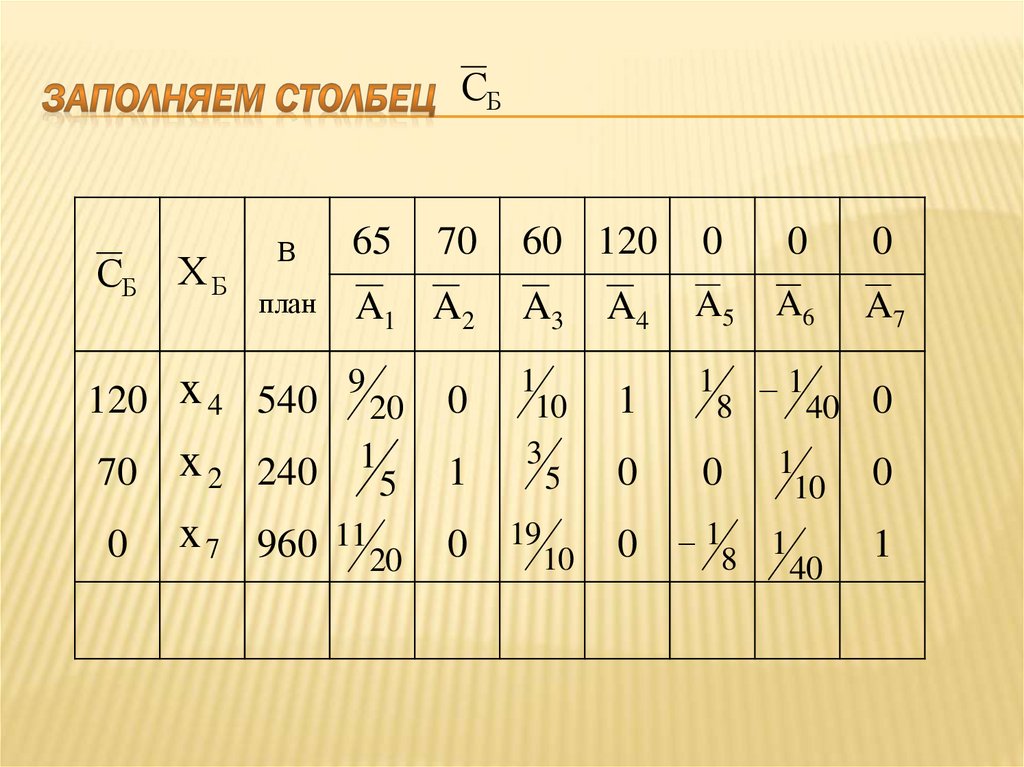
2
2
8
4800
2
10
6
0
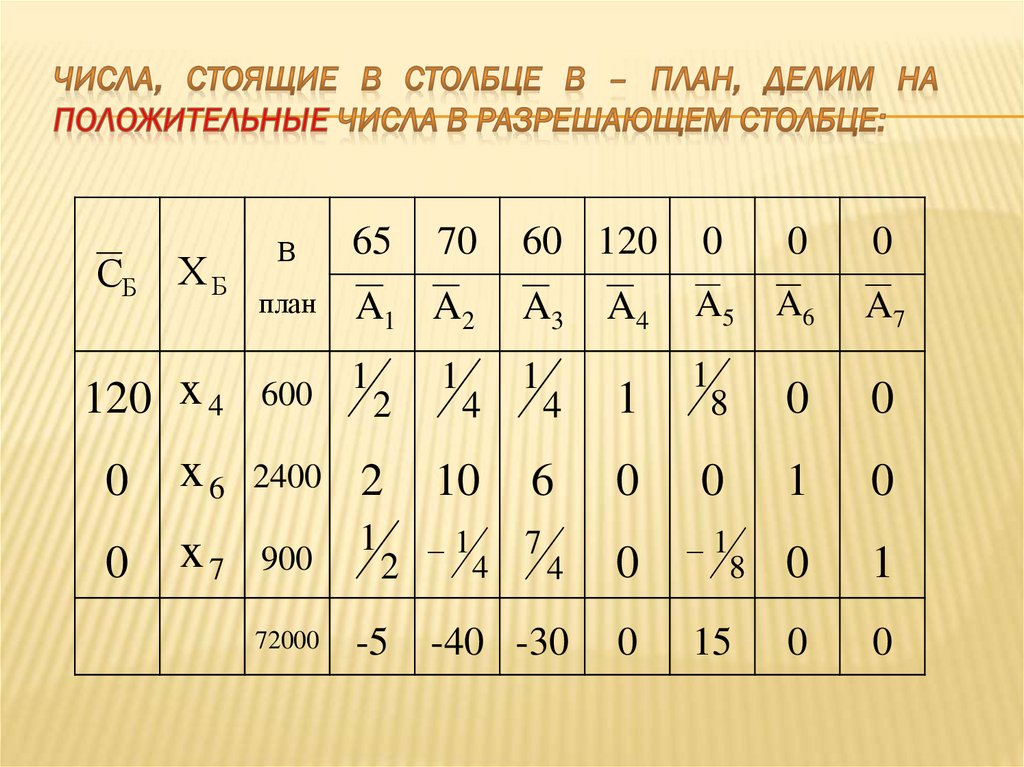
2400
1
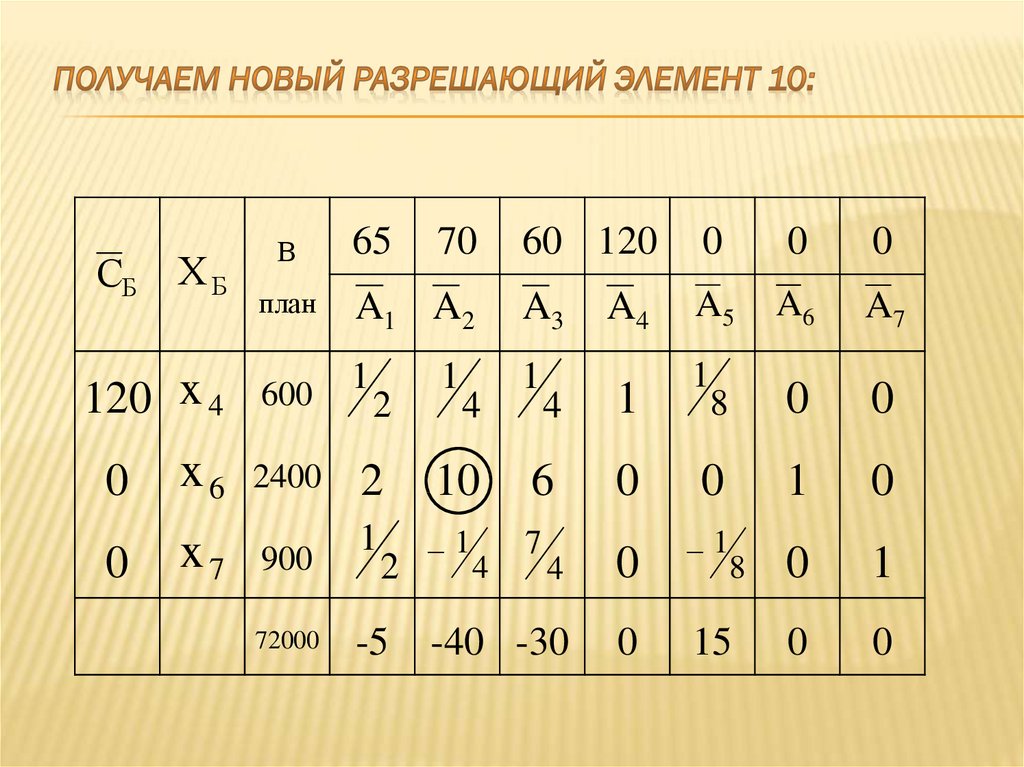
0
2
1
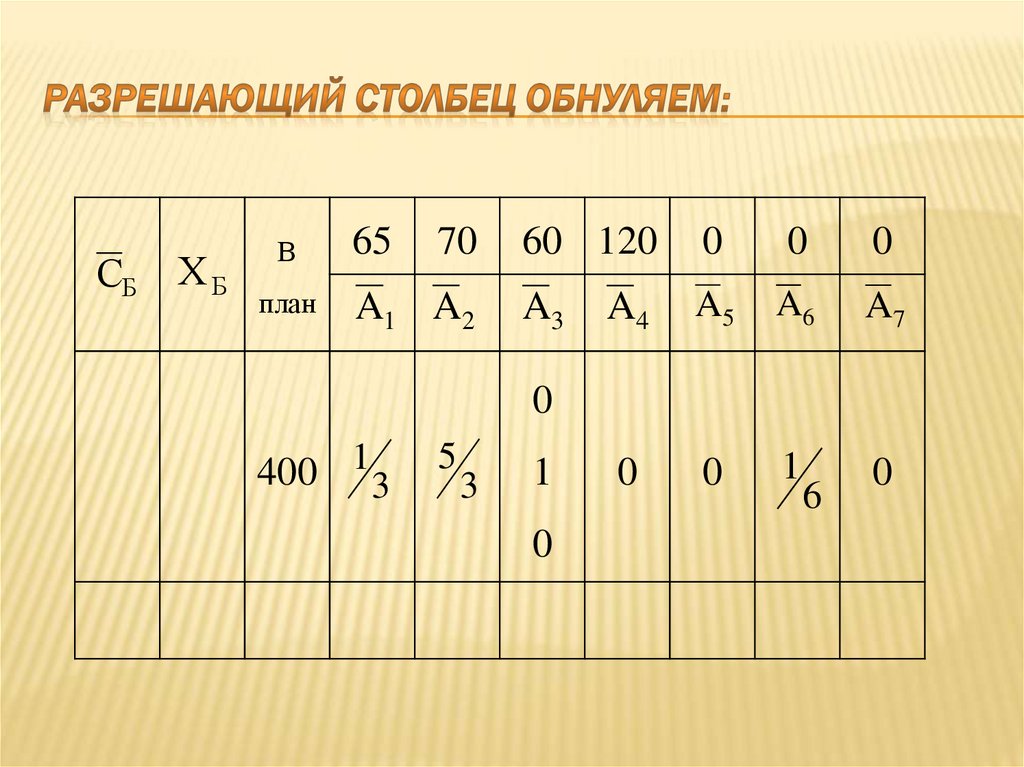
1500
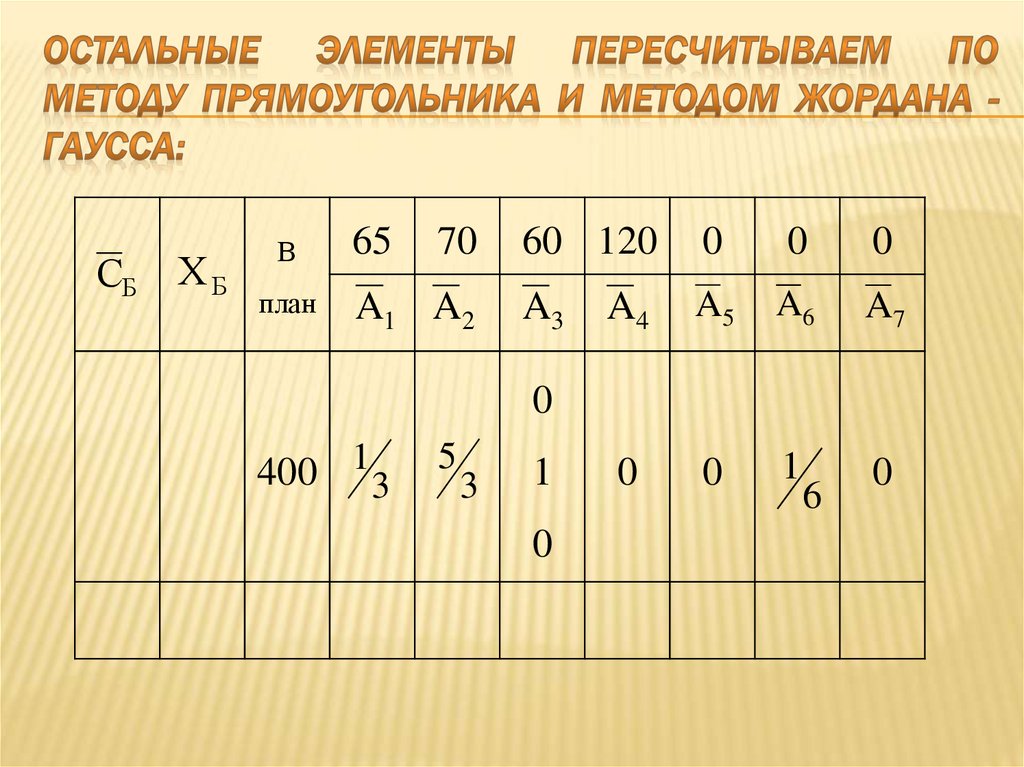
65
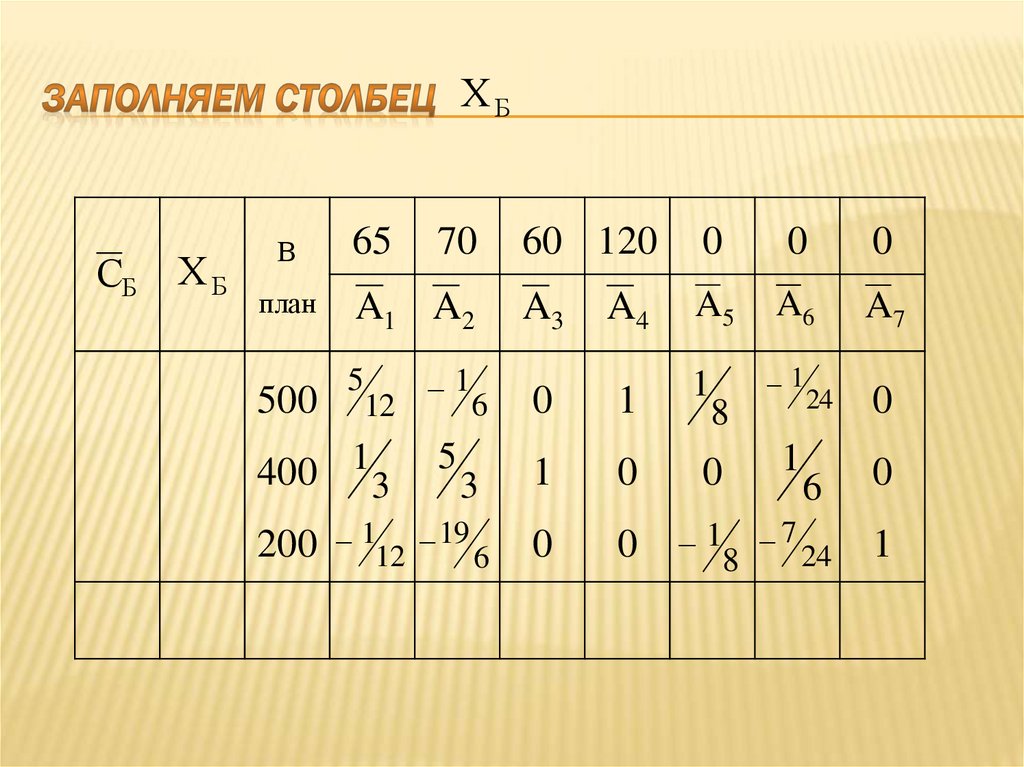
70
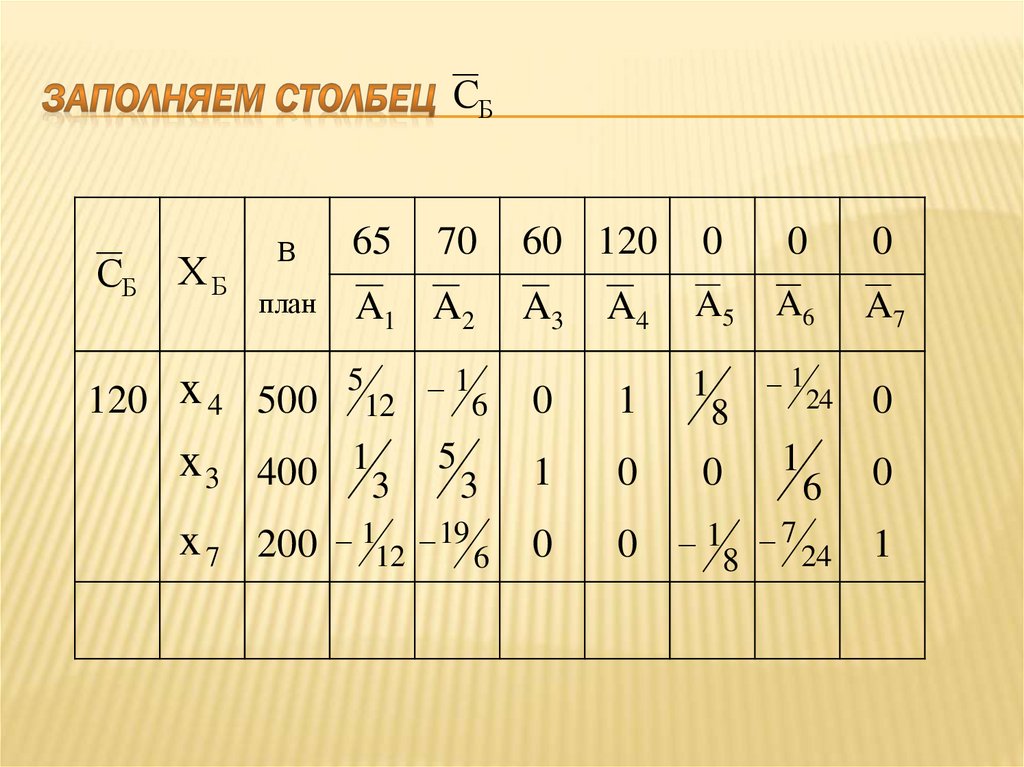
60
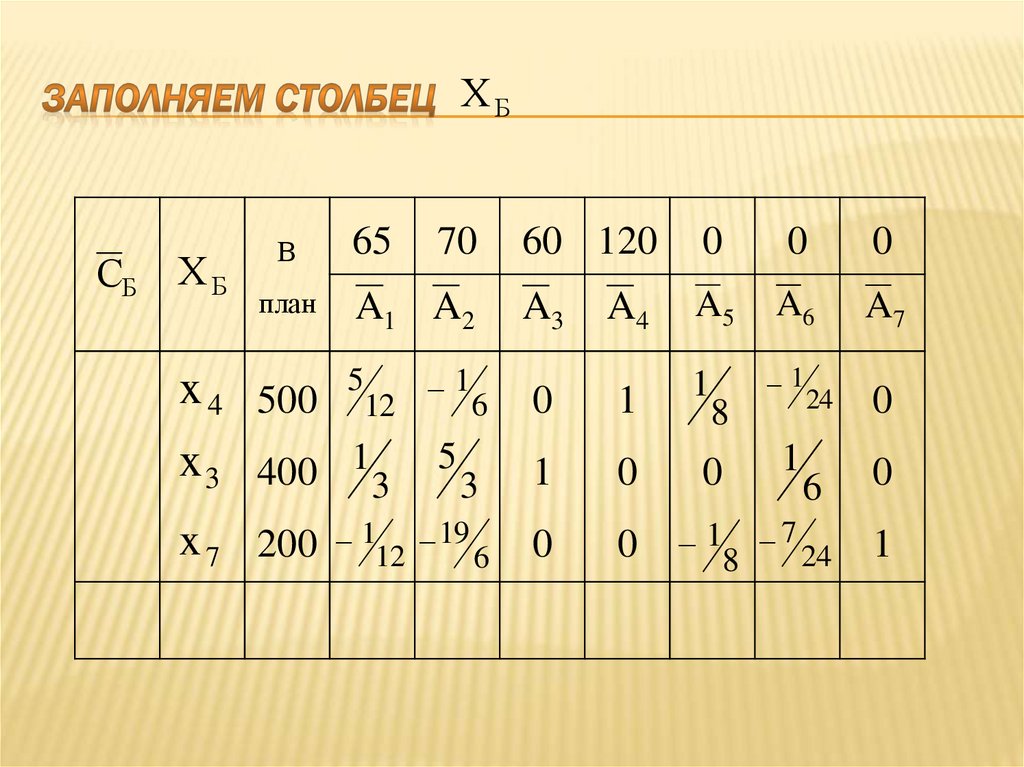
120
чел./час
Полуфабри
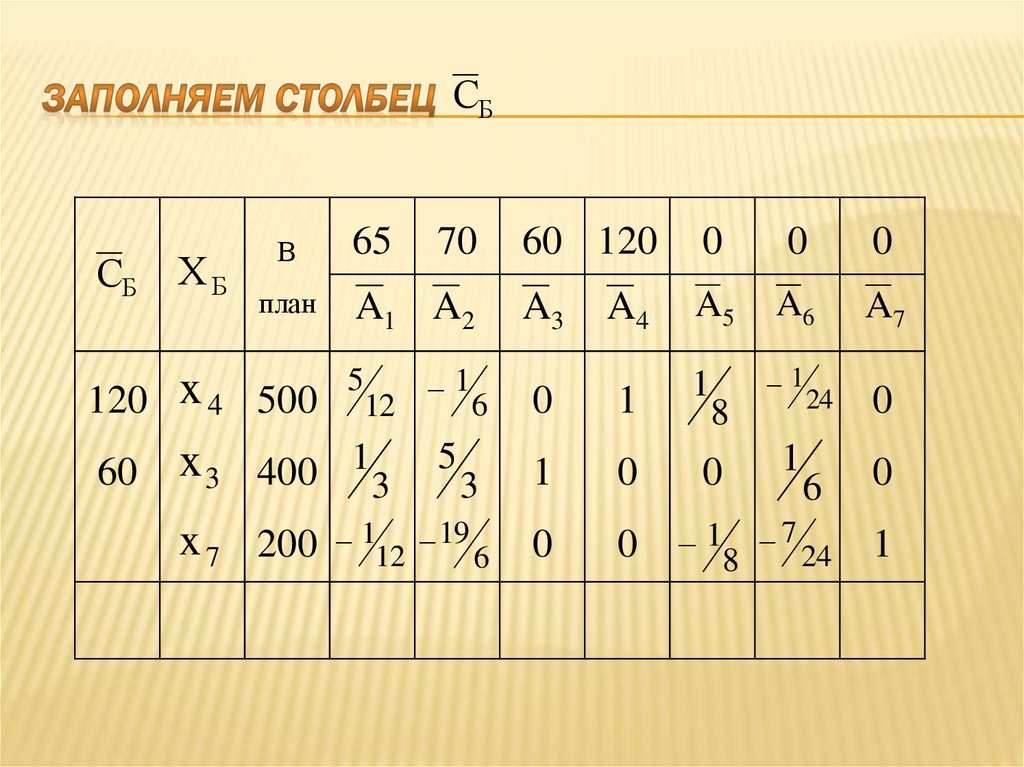
каты, кг
Станочное
оборудова
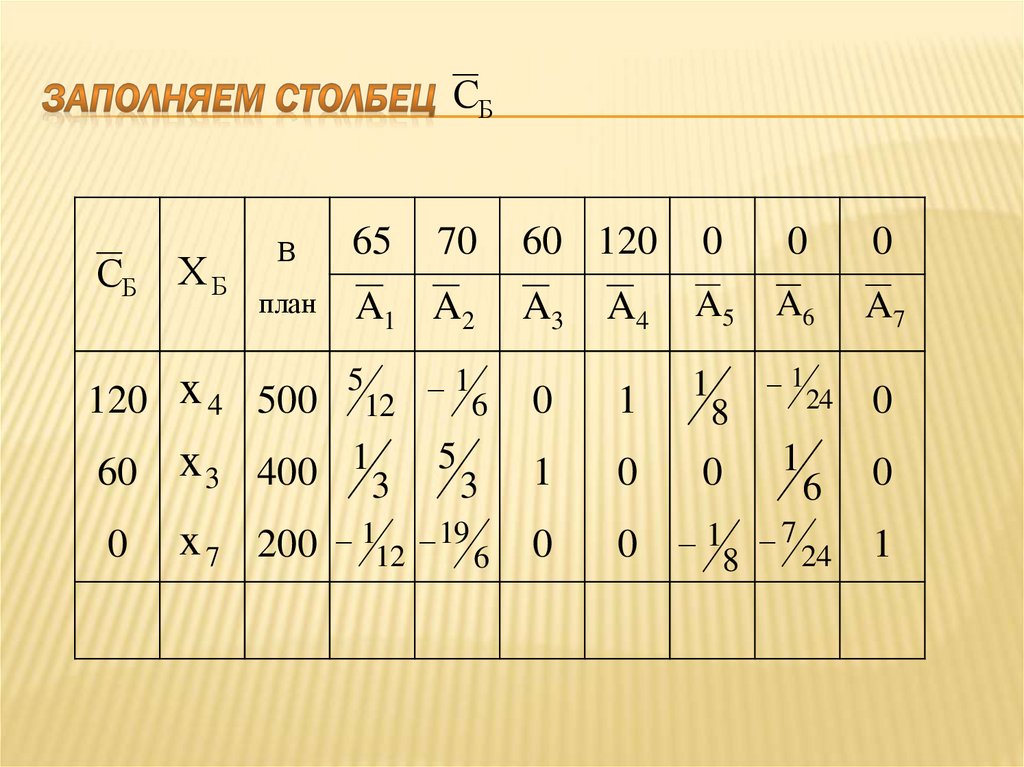
ние,
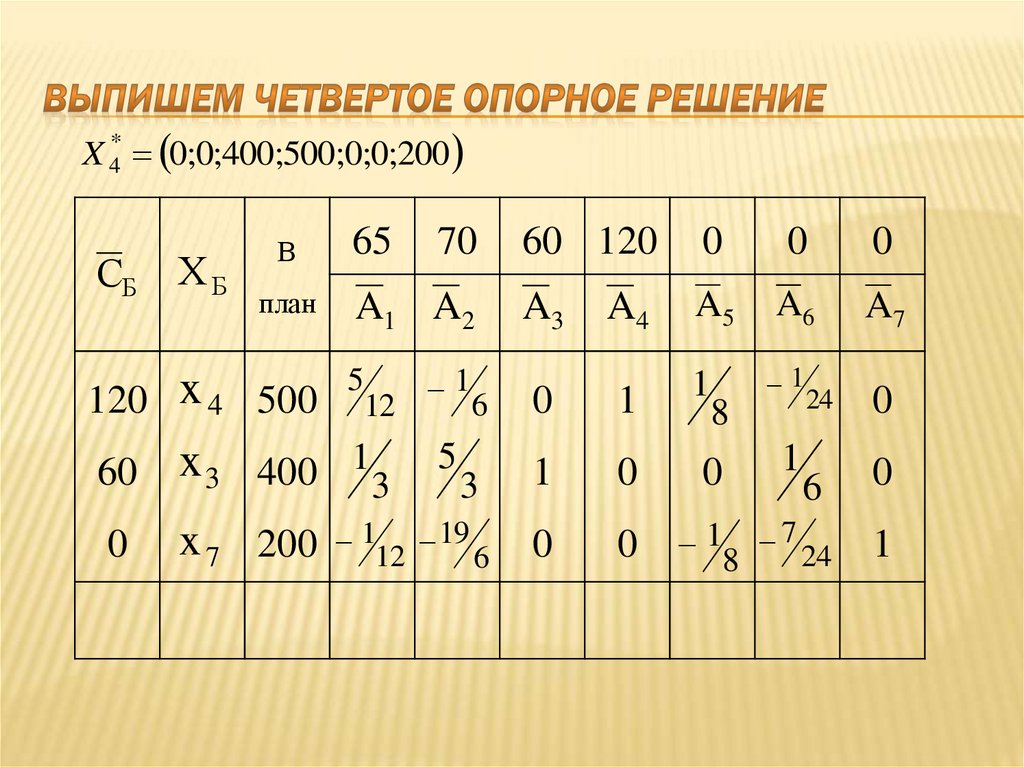
станко/час
Прибыль,
ден. ед.
4.
ОбъёмРесурсы
П1
П2
П3
П4
ресурс
ов
Трудовые
ресурсы,
4
2
2
8
4800
2
10
6
0
2400
1
0
2
1
1500
65
70
60
120
чел./час
Полуфабри
каты, кг
Станочное
оборудова
ние,
станко/час
Прибыль,
ден. ед.
5.
Графический метод для решения не подходит.Приведём задачу к каноническому виду.
6.
В канонической форме целевая функция должна стремиться к max.Если в системе ограничений хотя бы одно выражение содержит в своей правой
части
отрицательное значение,
то данное неравенство (уравнение)
необходимо умножить на (-1).
7.
В системе ограничений от неравенств переходим к равенствам.Для этого, в первое неравенство системы добавляем переменную
5, а в
целевую функцию вводим её с коэффициентом 0.
При этом знак
в первом неравенстве заменяем на знак
.
x
8.
В системе ограничений от неравенств переходим к равенствам.Для этого, во второе неравенство системы добавляем переменную x 6 , а в
целевую функцию вводим её с коэффициентом 0.
При этом знак
во втором неравенстве заменяем на знак
.
9.
В системе ограничений от неравенств переходим к равенствам.Для этого, в третье неравенство системы добавляем переменную x 7 , а в
целевую функцию вводим её с коэффициентом 0.
При этом знак
третьем неравенстве заменяем на знак
.
10. Строим симплекс – таблицу:
СБХБ
В
план
A1 A2
A3
A4
A5
A6
A7
11. Заполняем верхнюю строку, выписав коэффициенты при неизвестных в целевой функции:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A5
A6
A7
A4
12. Заполняем первую строку, выписав коэффициенты при неизвестных из первого уравнения системы ограничений:
СБХБ
В
план
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
4
2
8
1
0
0
2
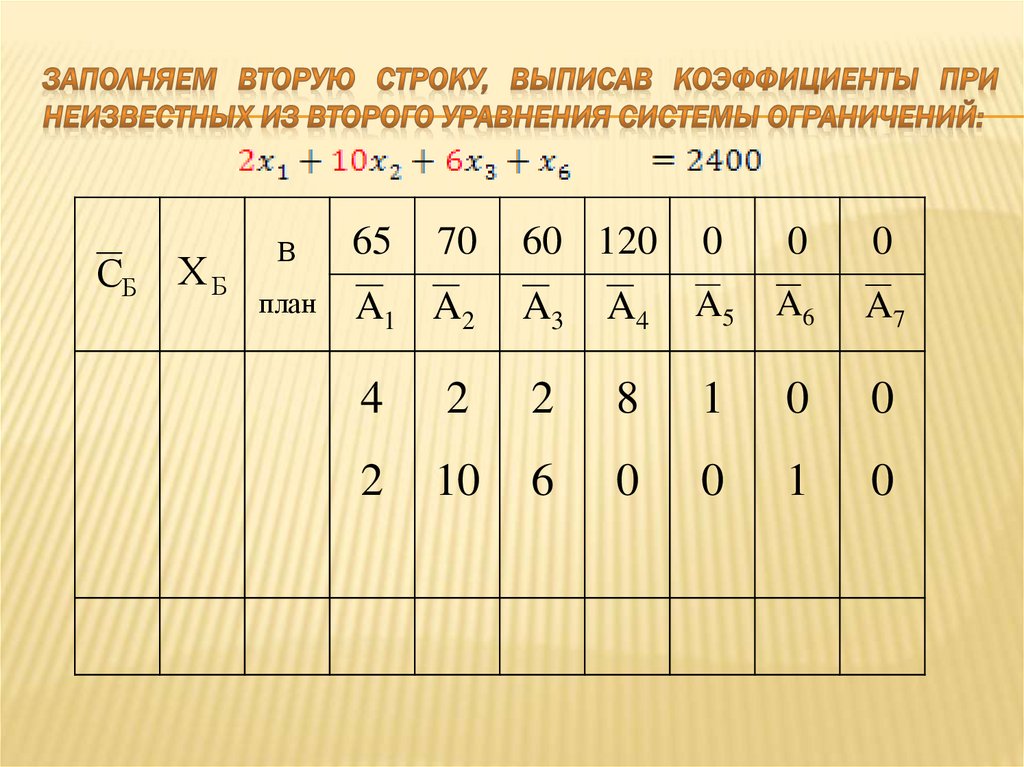
13. Заполняем вторую строку, выписав коэффициенты при неизвестных из второго уравнения системы ограничений:
СБХБ
В
план
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
4
2
2
8
1
0
0
2
10
6
0
0
1
0
14. Заполняем третью строку, выписав коэффициенты при неизвестных из третьего уравнения системы ограничений:
СБХБ
В
план
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
4
2
2
8
1
0
0
2
10
6
0
0
1
0
1
0
2
1
0
0
1
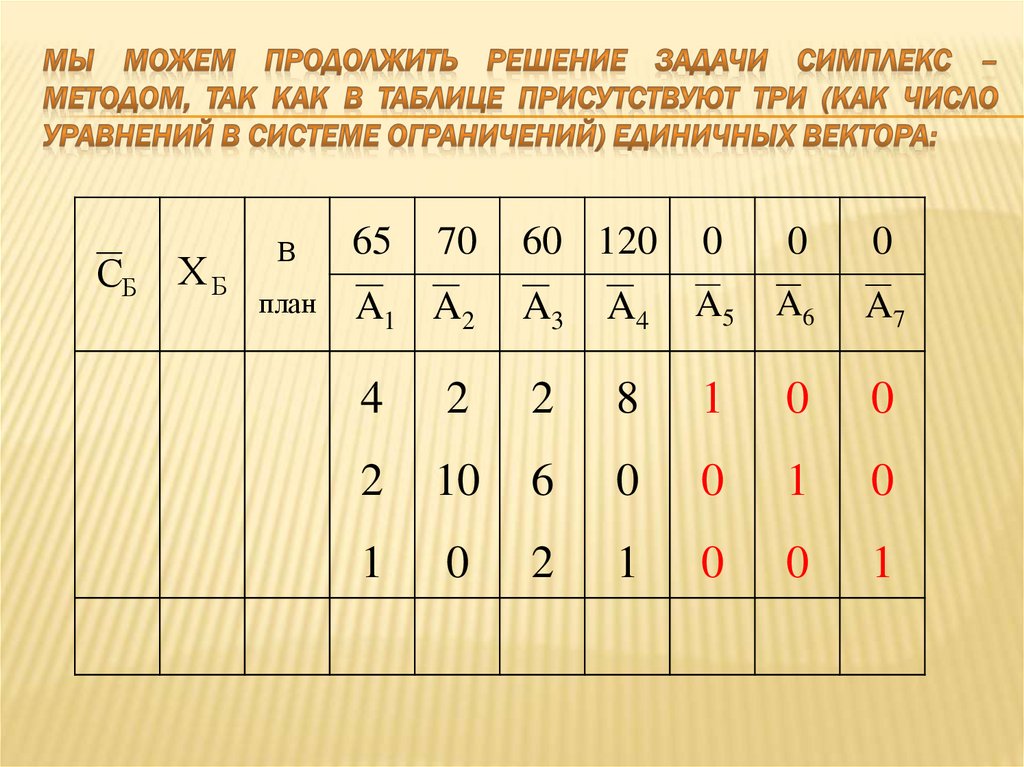
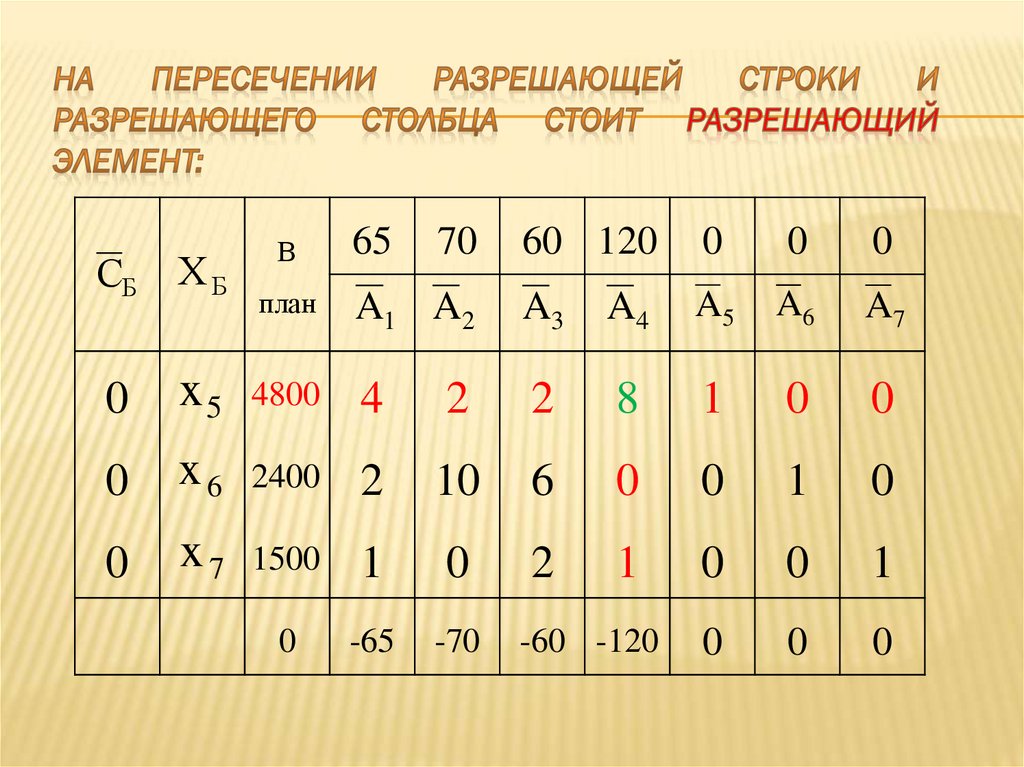
15. Мы можем продолжить решение задачи симплекс – методом, так как в таблице присутствуют три (как число уравнений в системе
СБХБ
В
план
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
4
2
2
8
1
0
0
2
10
6
0
0
1
0
1
0
2
1
0
0
1
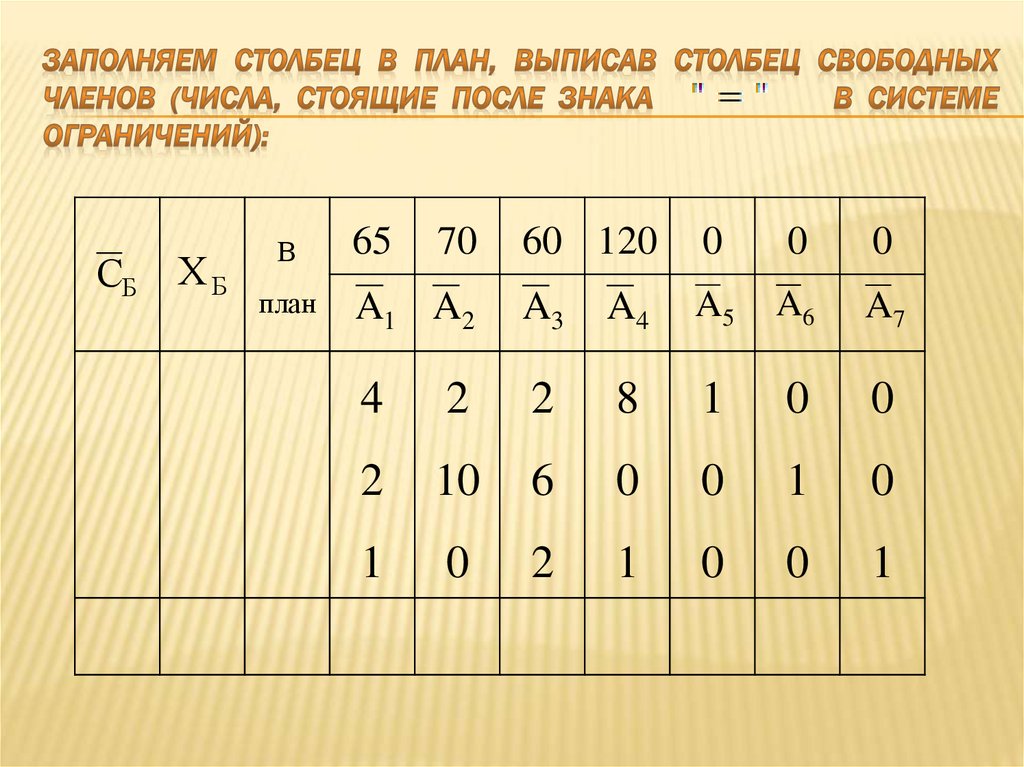
16. Заполняем столбец В план, выписав столбец свободных членов (числа, стоящие после знака в системе ограничений):
СБХБ
В
план
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
4
2
2
8
1
0
0
2
10
6
0
0
1
0
1
0
2
1
0
0
1
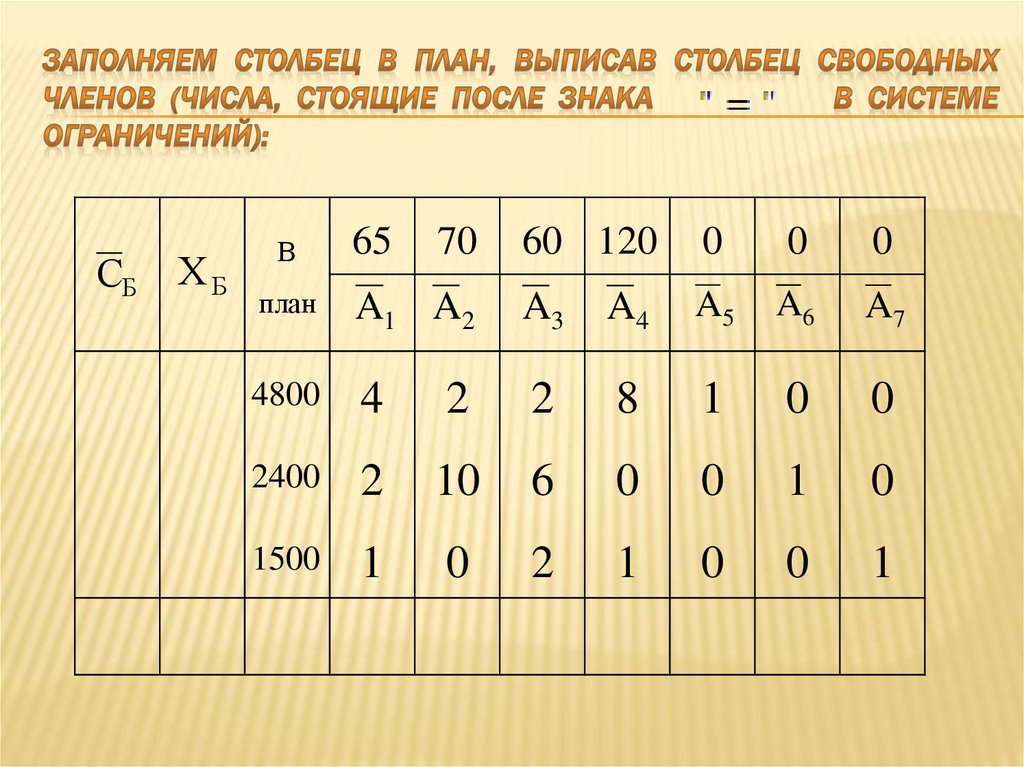
17. Заполняем столбец В план, выписав столбец свободных членов (числа, стоящие после знака в системе ограничений):
СБХБ
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
4800
4
2
2
8
1
0
0
2400
2
10
6
0
0
1
0
1500
1
0
2
1
0
0
1
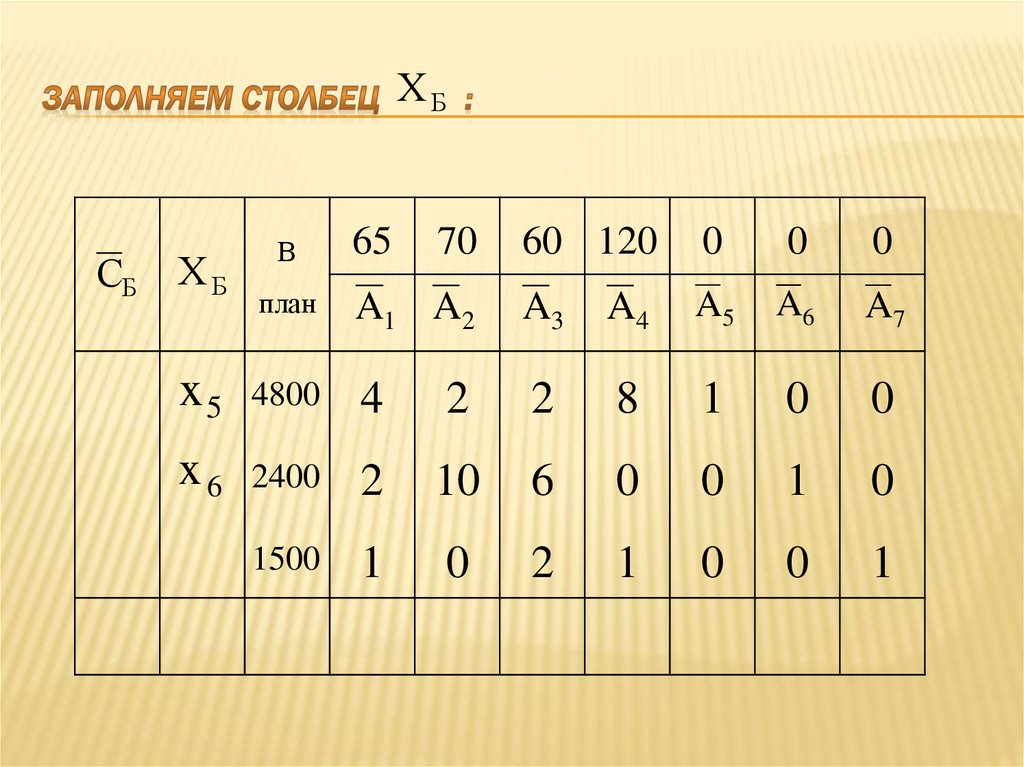
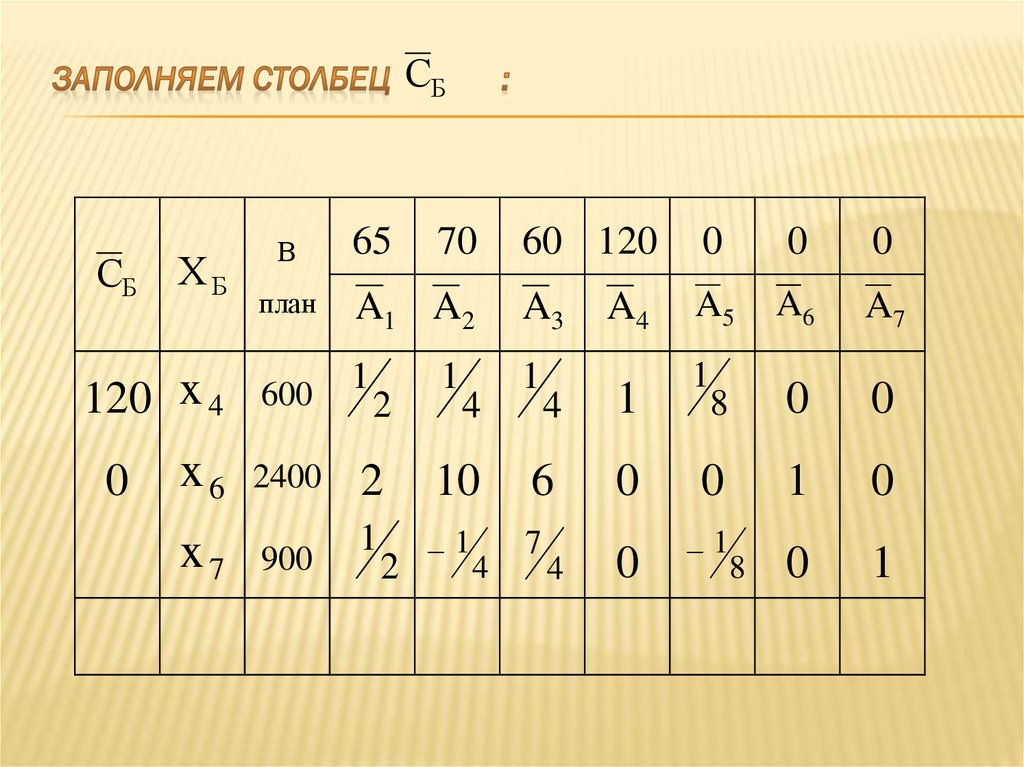
18. Заполняем столбец :
ХБСБ
ХБ
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
4800
4
2
2
8
1
0
0
2400
2
10
6
0
0
1
0
1500
1
0
2
1
0
0
1
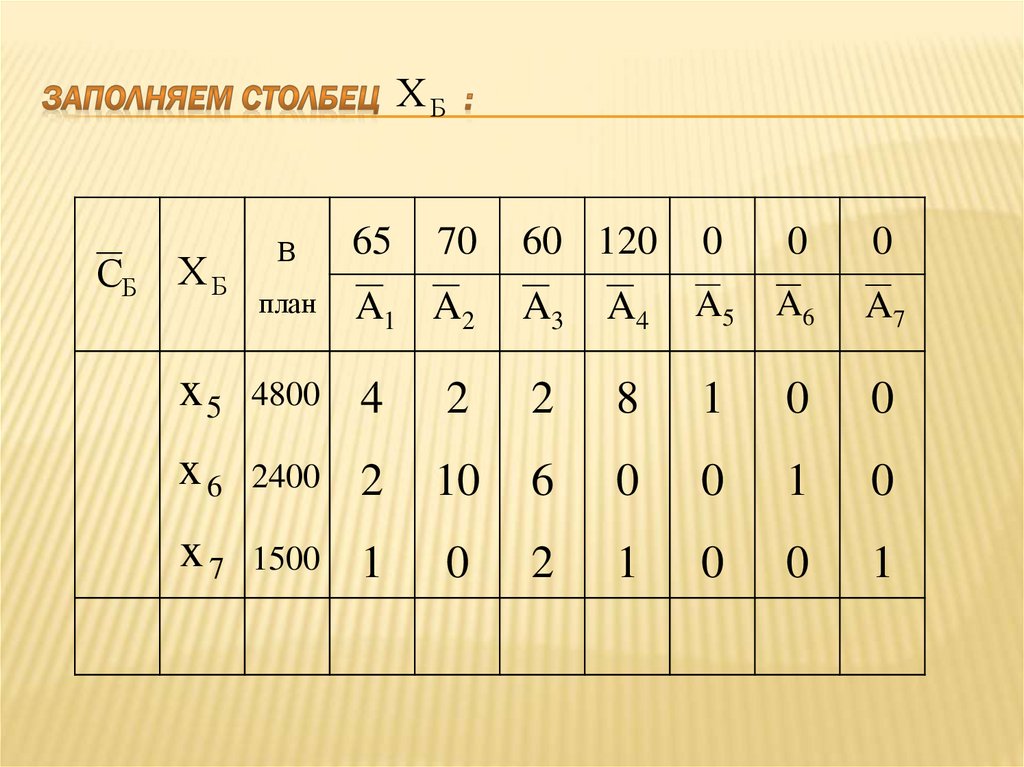
19. Заполняем столбец :
ХБСБ
ХБ
x5
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
4800
4
2
2
8
1
0
0
2400
2
10
6
0
0
1
0
1500
1
0
2
1
0
0
1
20. Заполняем столбец :
ХБСБ
ХБ
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
x6
2400
2
10
6
0
0
1
0
1500
1
0
2
1
0
0
1
21. Заполняем столбец :
ХБСБ
ХБ
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
x6
2400
2
10
6
0
0
1
0
x7
1500
1
0
2
1
0
0
1
22. Заполняем столбец ( - коэффициенты в целевой функции при базисных переменных ):
СБ СБСБ
ХБ
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
x6
2400
2
10
6
0
0
1
0
x7
1500
1
0
2
1
0
0
1
23. Заполняем столбец :
СБСБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
x6
2400
2
10
6
0
0
1
0
x7
1500
1
0
2
1
0
0
1
24. Заполняем столбец :
СБСБ
ХБ
0
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
x6
2400
2
10
6
0
0
1
0
x7
1500
1
0
2
1
0
0
1
25. Заполняем столбец :
СБСБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
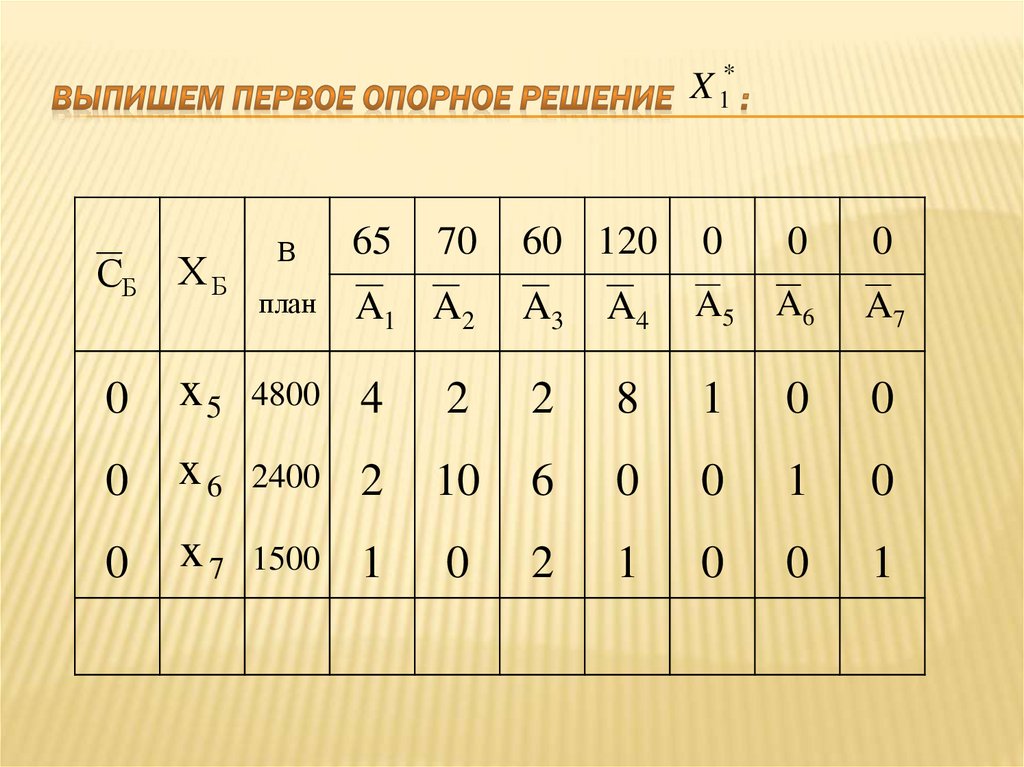
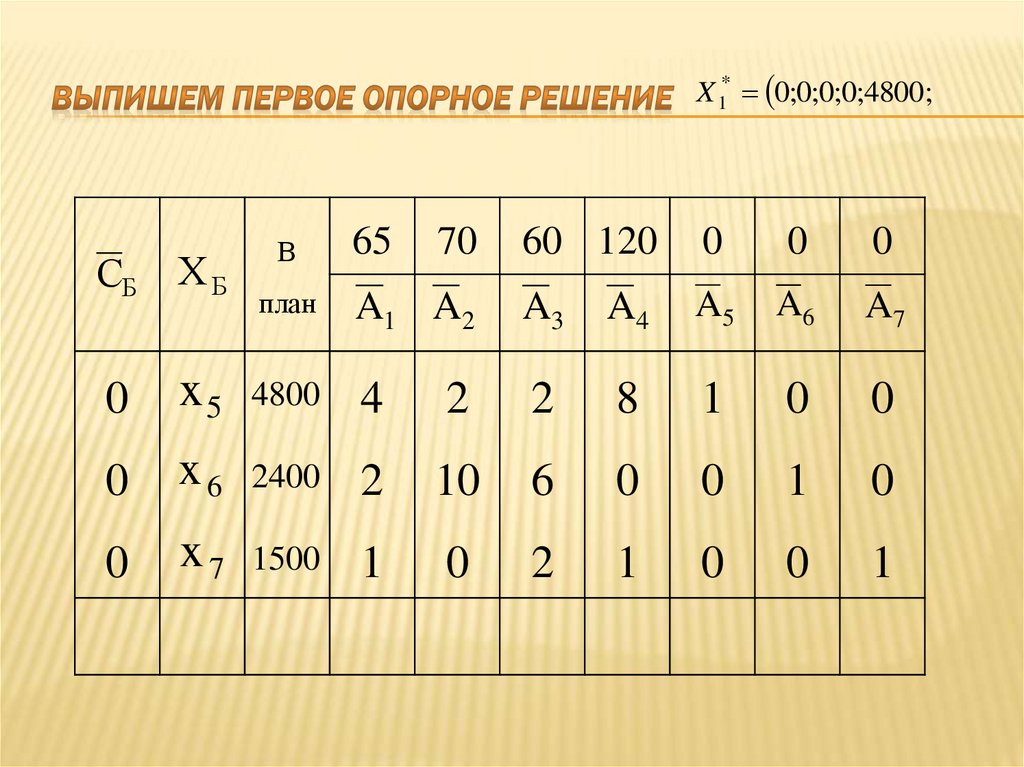
26. Выпишем первое опорное решение :
X 1*СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
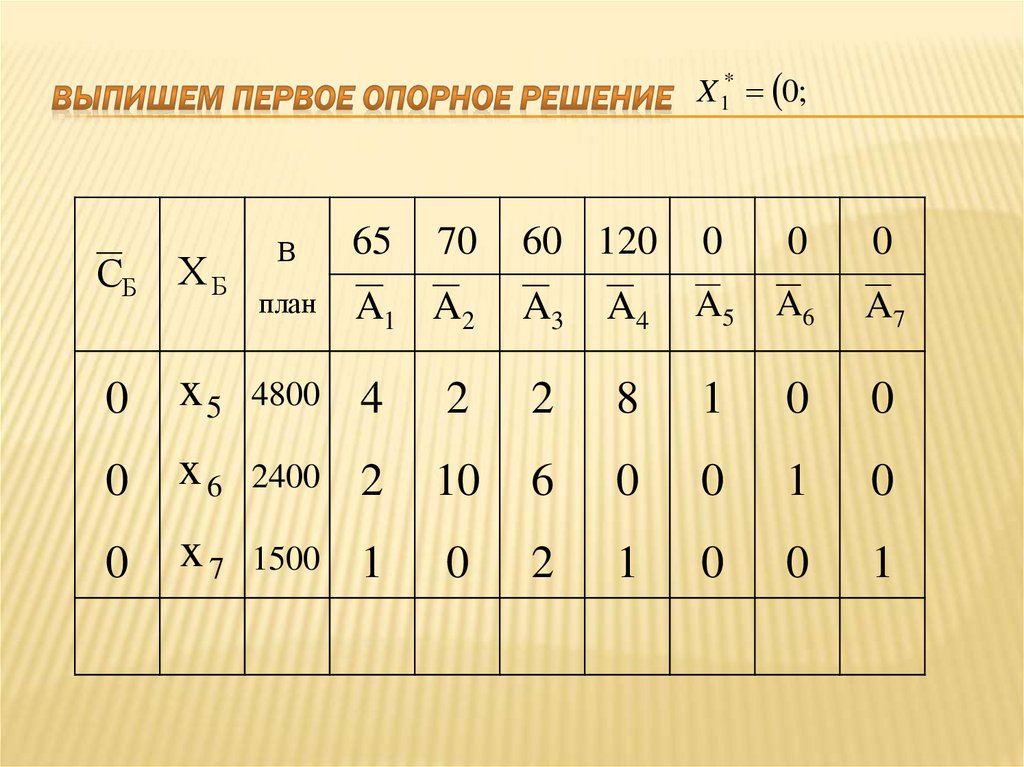
27. Выпишем первое опорное решение
X 1* 0;СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
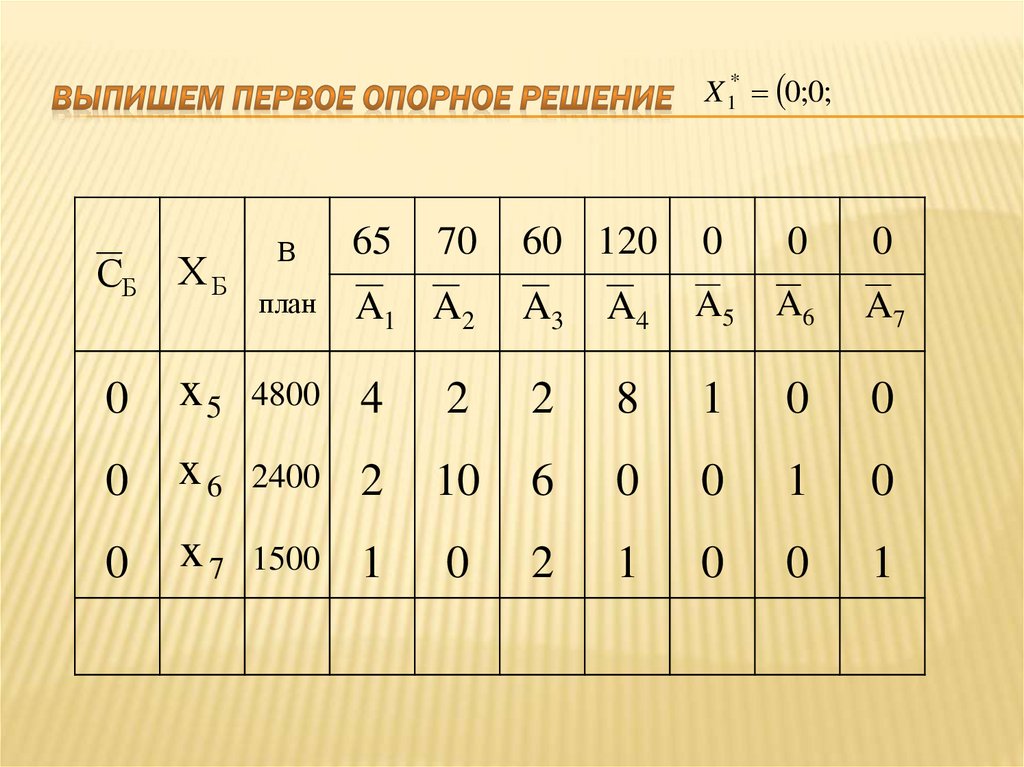
28. Выпишем первое опорное решение
X 1* 0;0;СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
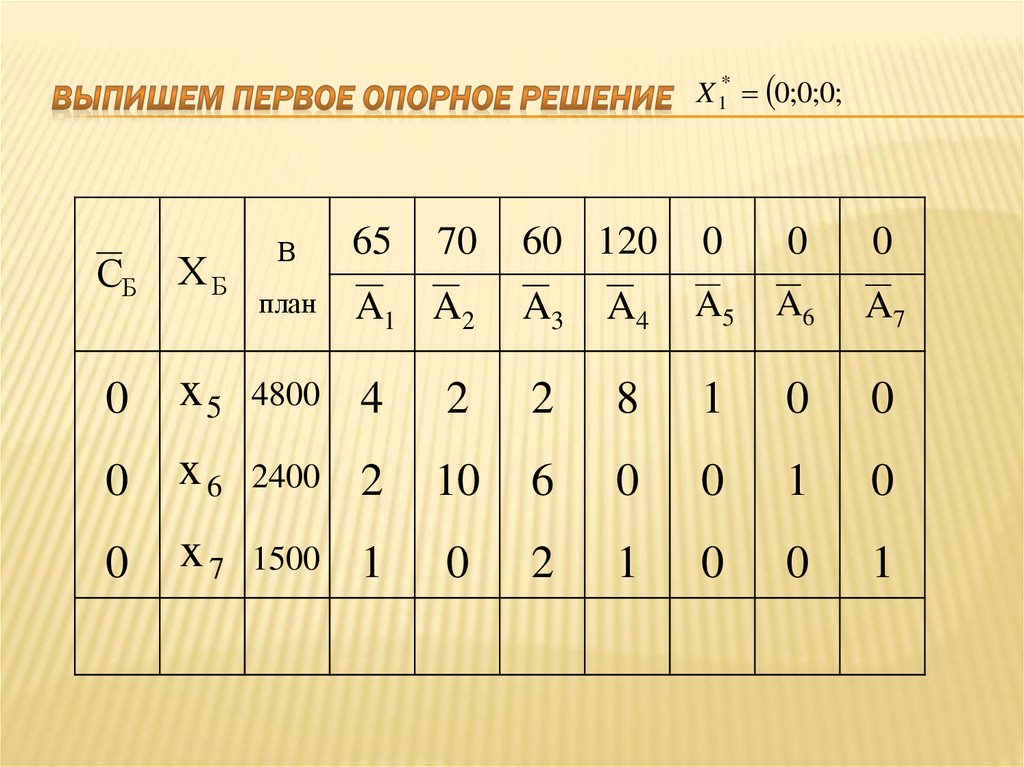
29. Выпишем первое опорное решение
X 1* 0;0;0;СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
30. Выпишем первое опорное решение
X 1* 0;0;0;0;СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
31. Выпишем первое опорное решение
X 1* 0;0;0;0;4800;СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
32. Выпишем первое опорное решение
X 1* 0;0;0;0;4800;2400;СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
33. Выпишем первое опорное решение
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
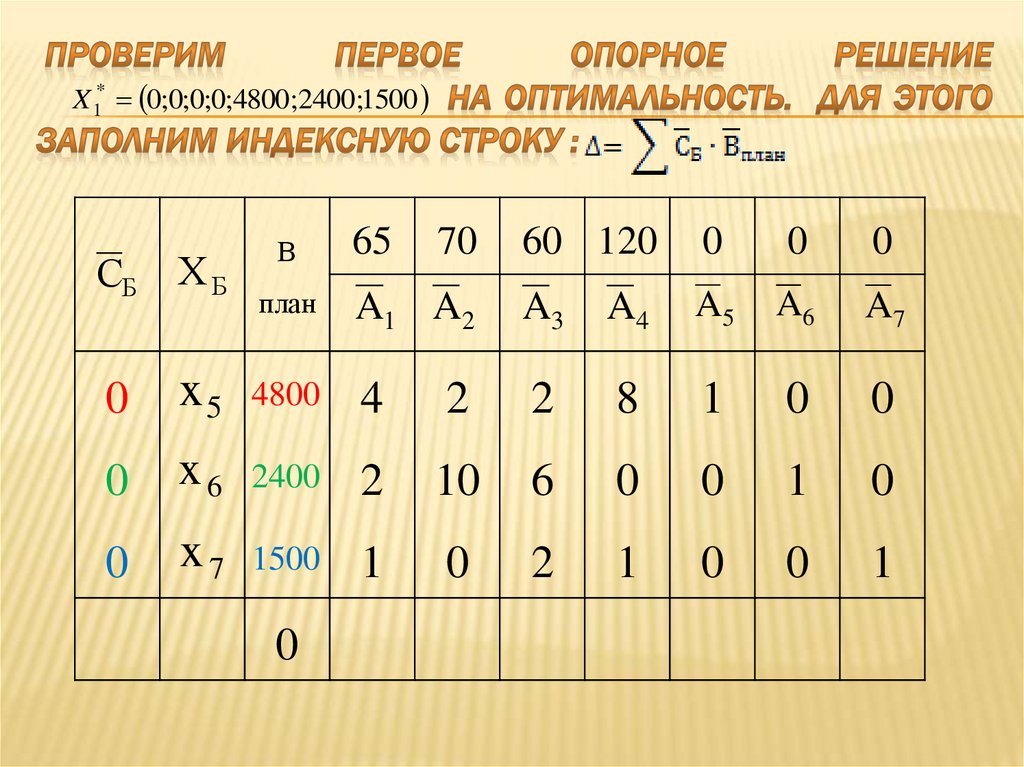
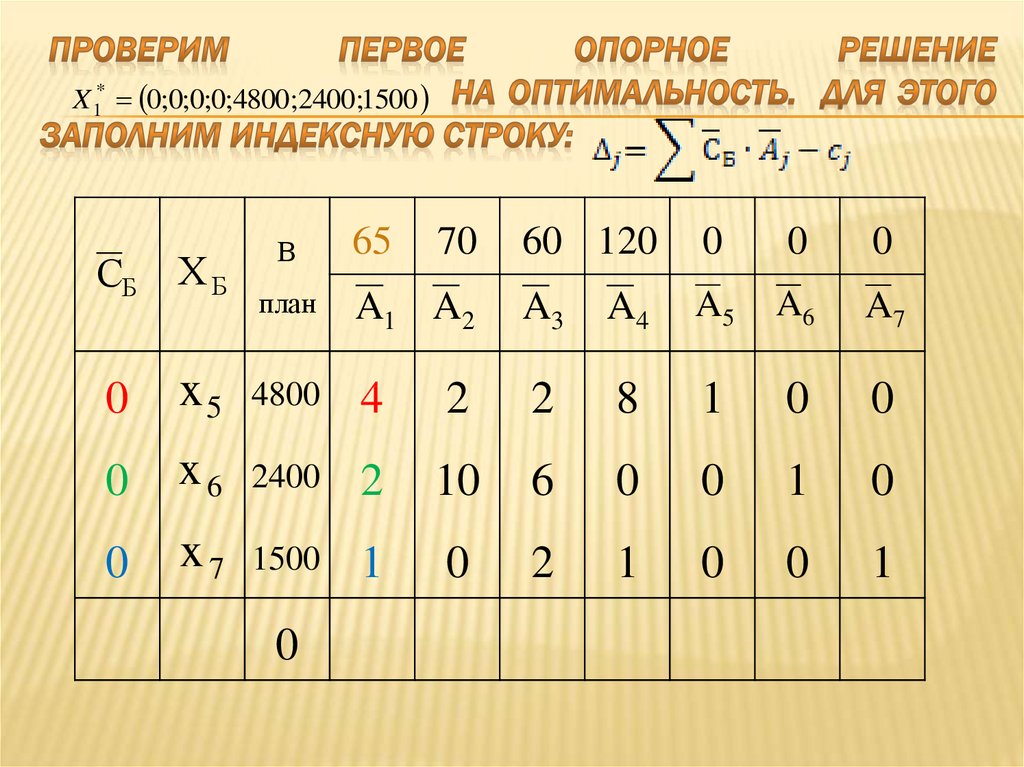
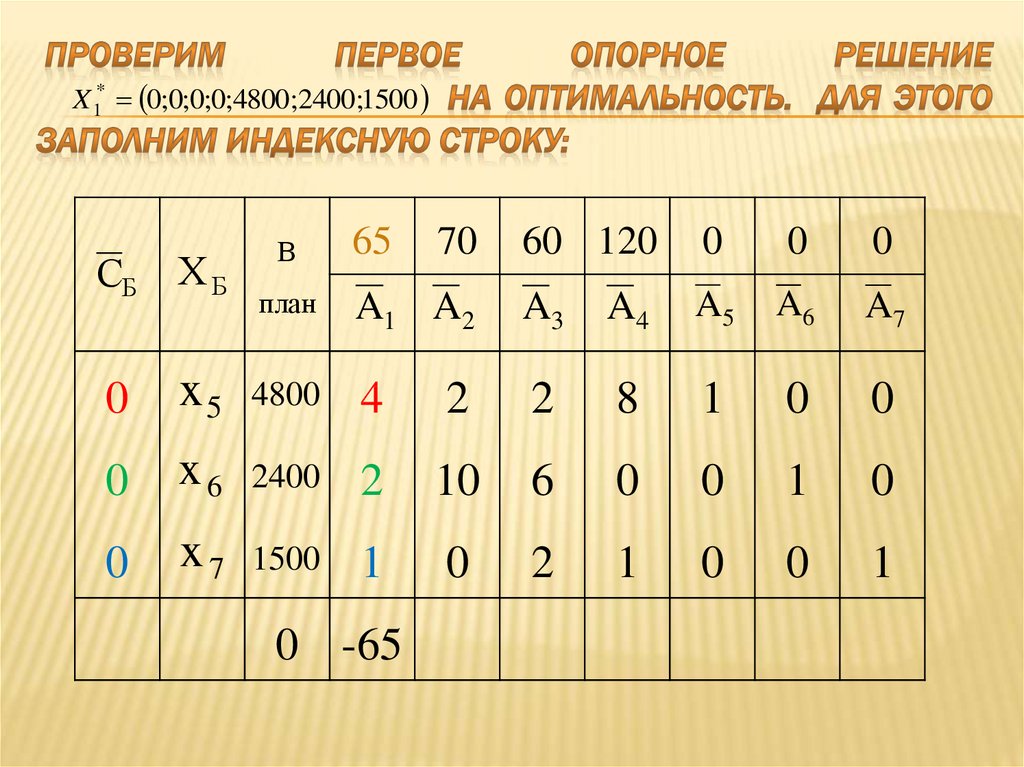
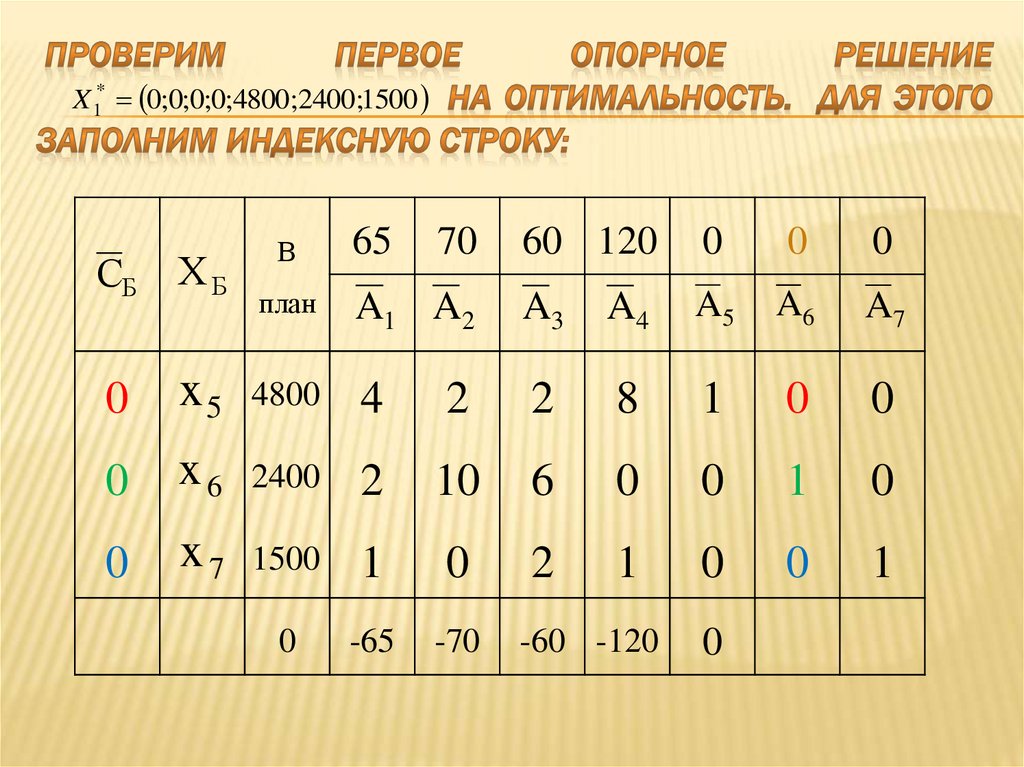
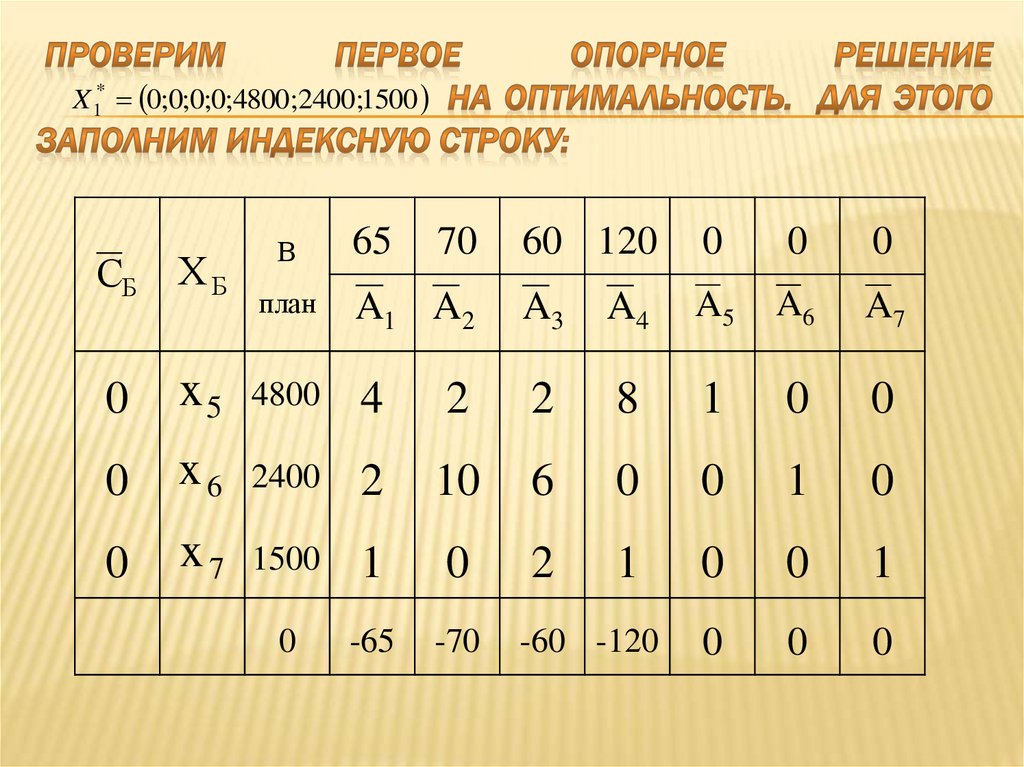
34. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
35. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку :
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
36. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
37. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0 -65
38. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0 -65
39. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65 -70
40. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65 -70
41. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
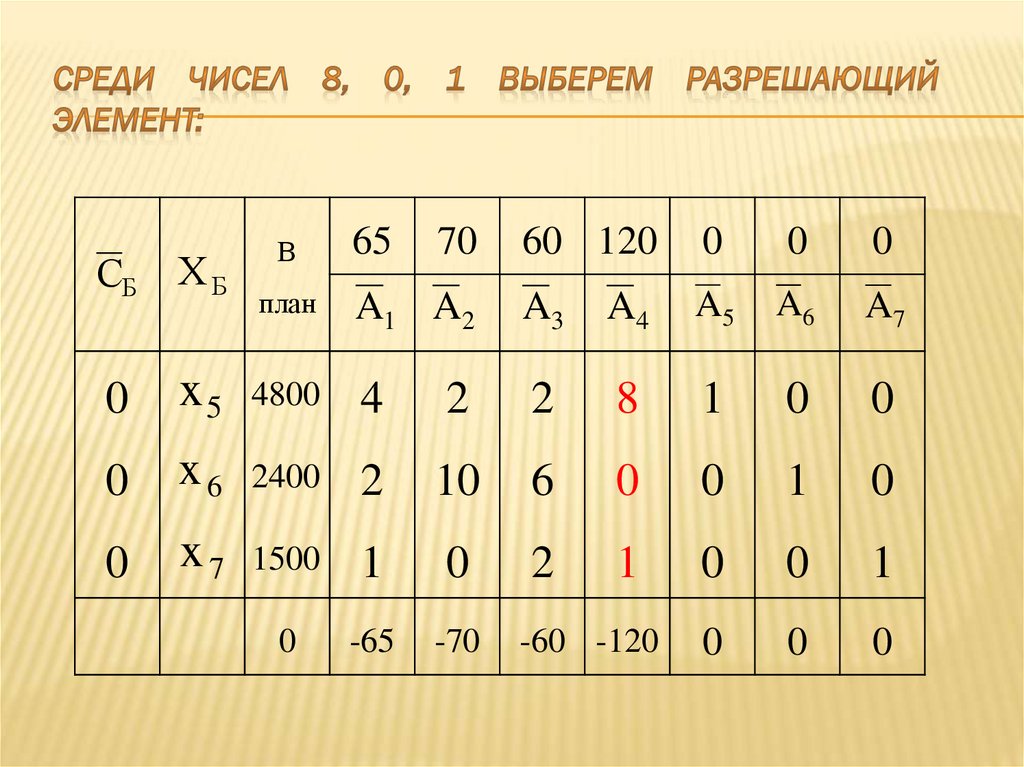
-65 -70 -60
42. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65 -70 -60
43. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
-60 -120
44. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
-60 -120
45. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
-60 -120
0
46. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
-60 -120
0
47. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
-60 -120
48. Проверим первое опорное решение на оптимальность. Для этого заполним индексную строку:
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
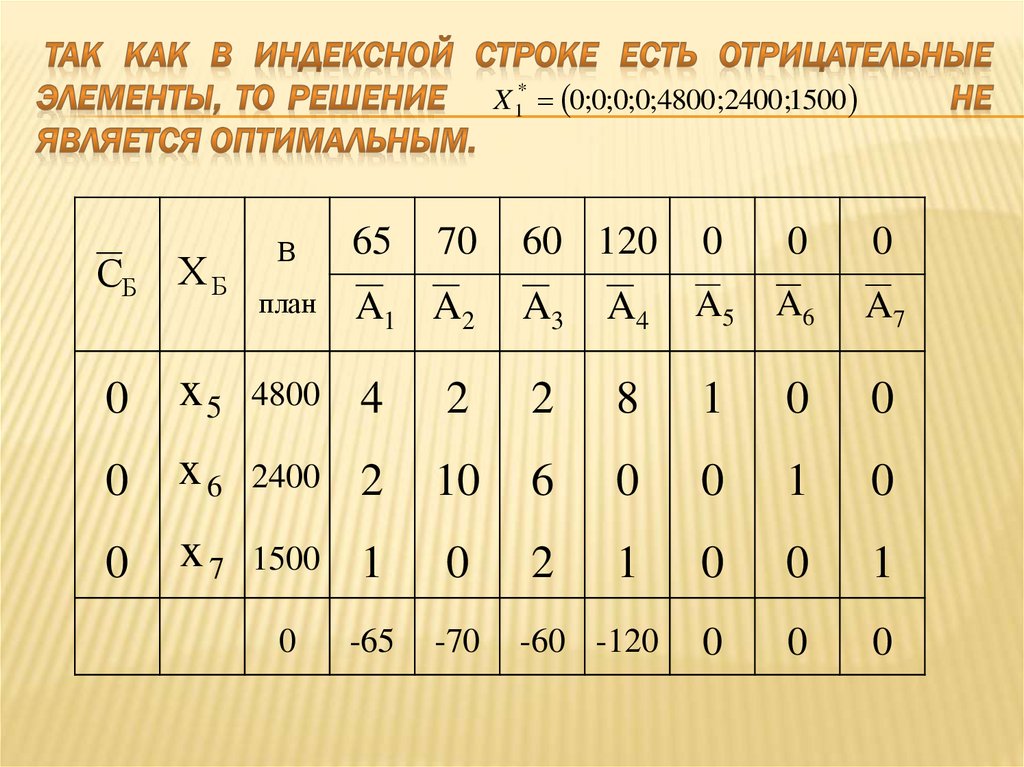
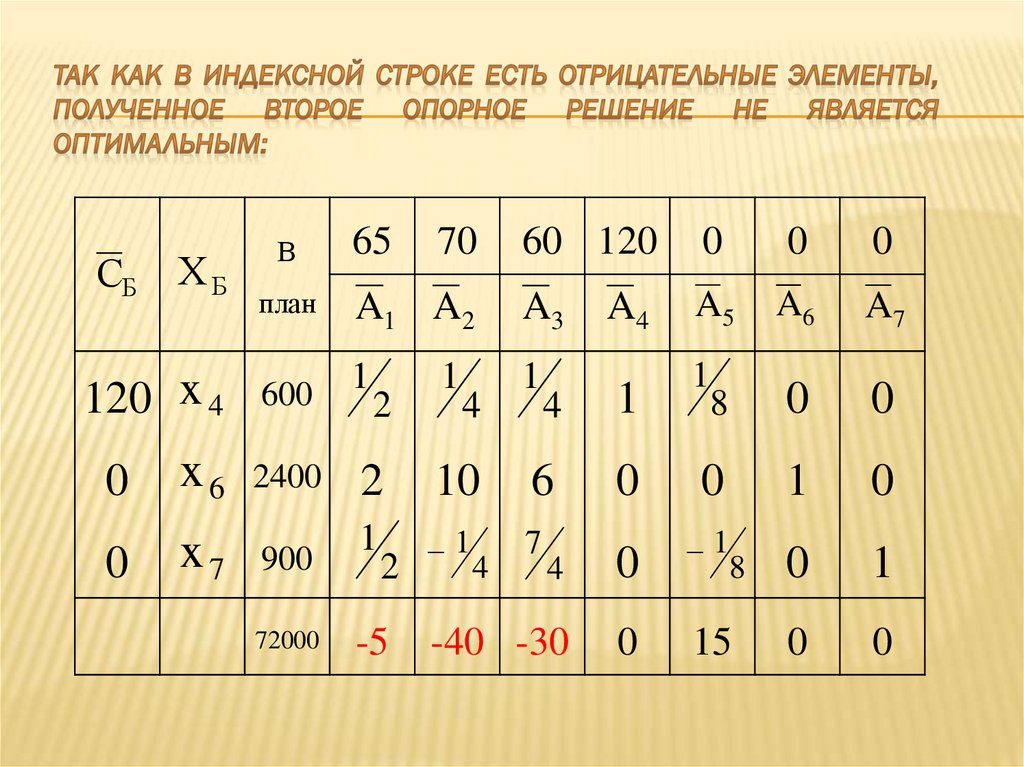
49. Так как в индексной строке есть отрицательные элементы, то решение не является оптимальным.
X 1* 0;0;0;0;4800;2400;1500СБ
ХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
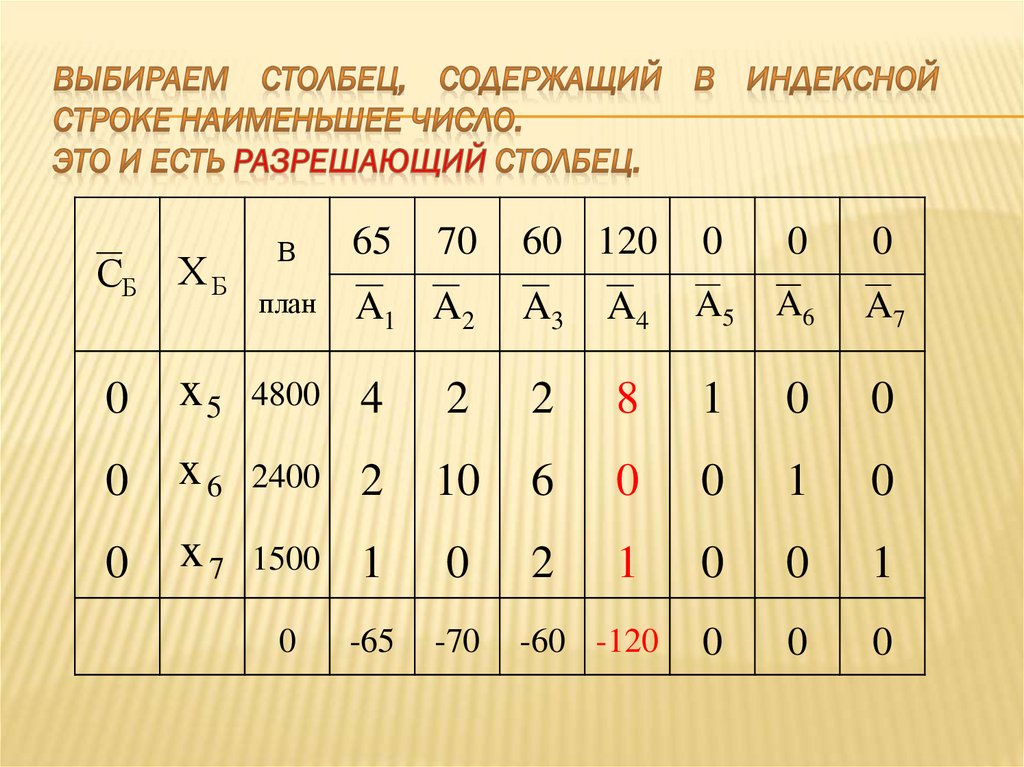
-65
-70
0
0
0
-60 -120
50.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
51.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
52.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
53.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
54.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
55.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
56.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
57.
СБХБ
0
В
65
70
60 120
0
0
0
план
A1 A2
A3
A4
A5
A6
A7
x5
4800
4
2
2
8
1
0
0
0
x6
2400
2
10
6
0
0
1
0
0
x7
1500
1
0
2
1
0
0
1
0
-65
-70
0
0
0
-60 -120
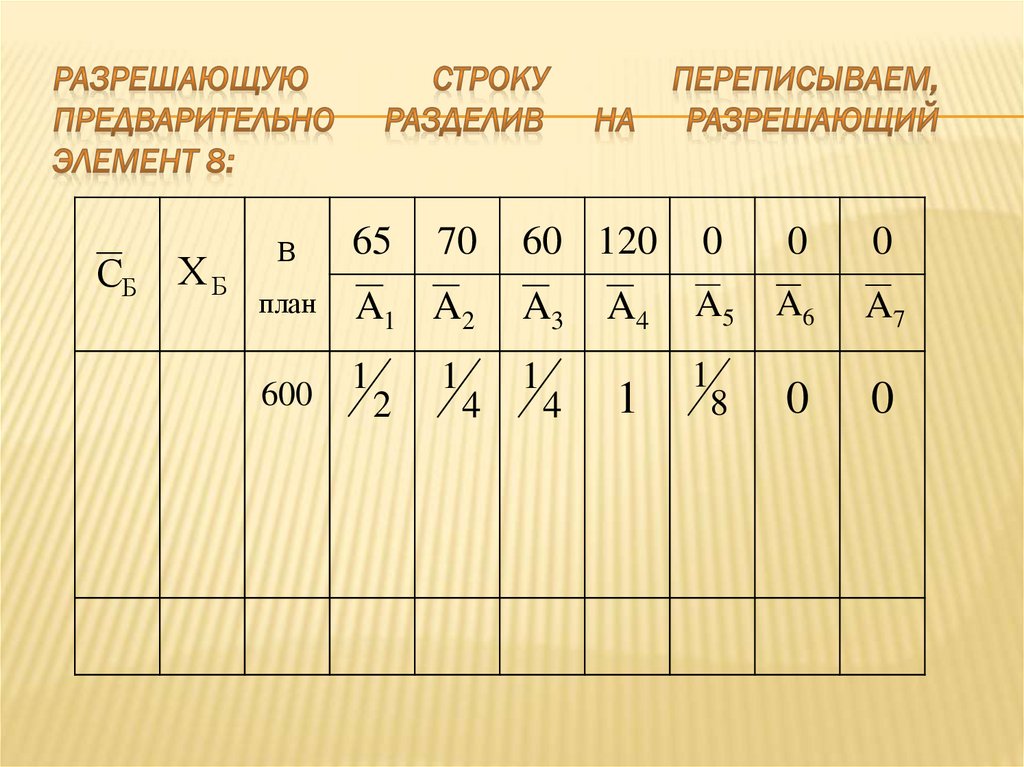
58. Строим новую симплекс – таблицу:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A5
A6
A7
A4
59.
СБХБ
В
план
600
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
1
0
0
2
70
1
4
4
A4
1
1
8
60.
СБХБ
В
план
600
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
1
0
0
2
70
1
4
4
A4
1
0
0
1
8
61.
СБХБ
В
план
600
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
1
0
0
2
70
1
4
4
A4
1
0
0
1
8
62.
СБХБ
60 120
0
0
0
A1 A2
A3
A5
A6
A7
600
1
1
8
0
0
2400
2
1
В
план
900
65
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
63.
ХБСБ
ХБ
60 120
0
0
0
A1 A2
A3
A5
A6
A7
600
1
1
8
0
0
2400
2
1
В
план
900
65
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
64.
ХБСБ
ХБ
x4
60 120
0
0
0
A1 A2
A3
A5
A6
A7
600
1
1
8
0
0
2400
2
1
В
план
900
65
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
65.
ХБСБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
x4
600
1
x6
2400
2
1
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
66.
ХБСБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
x4
600
1
x6
2400
2
1
x7
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
67.
СБСБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
x4
600
1
x6
2400
2
1
x7
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
68.
СБСБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
x6
2400
2
1
x7
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
69.
СБСБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
x6
2400
2
1
0
x7
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
70.
СБСБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
71.
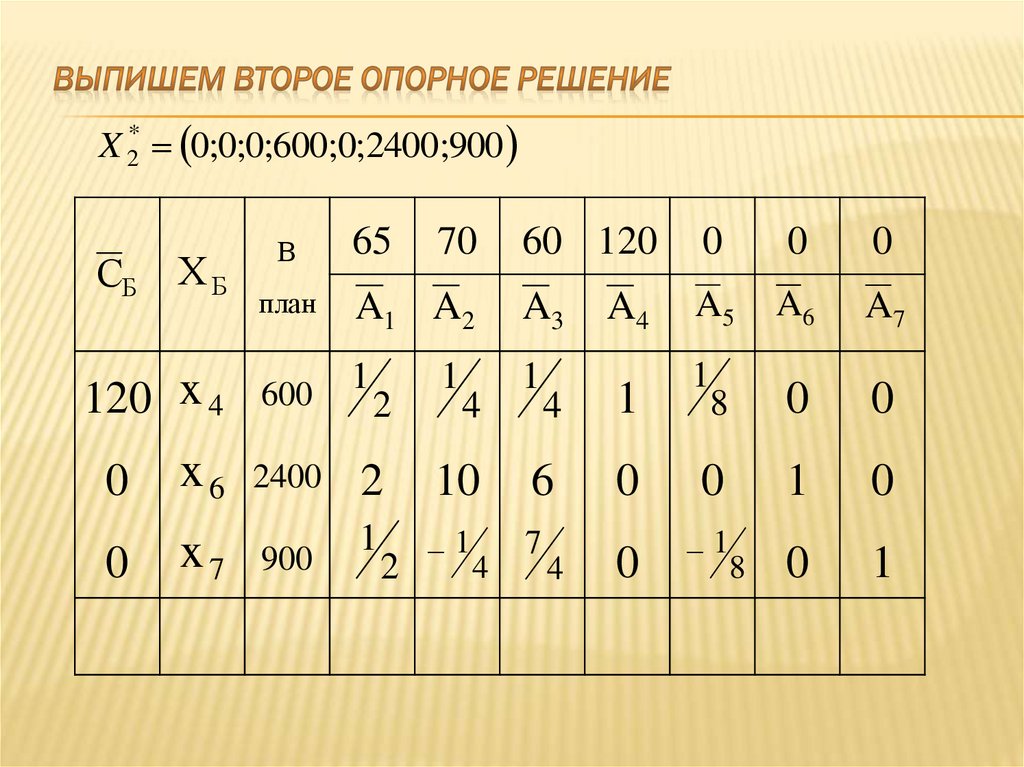
X 2* 0;0;0;600;0;2400;900СБ
ХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
72.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
2
2
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
0
1
8
0
1
4
4
4
73.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
74.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
75.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
76.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
77.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
78.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
79.
СБХБ
В
план
65
60 120
0
0
0
A1 A2
A3
A5
A6
A7
1
8
0
0
120 x 4
600
1
0
x6
2400
2
0
x7
1
900
72000
2
2
-5
70
1
A4
1
4
1
10
6
0
0
1
0
1
7
4
0
1
8
0
1
-40 -30
0
15
0
0
4
4
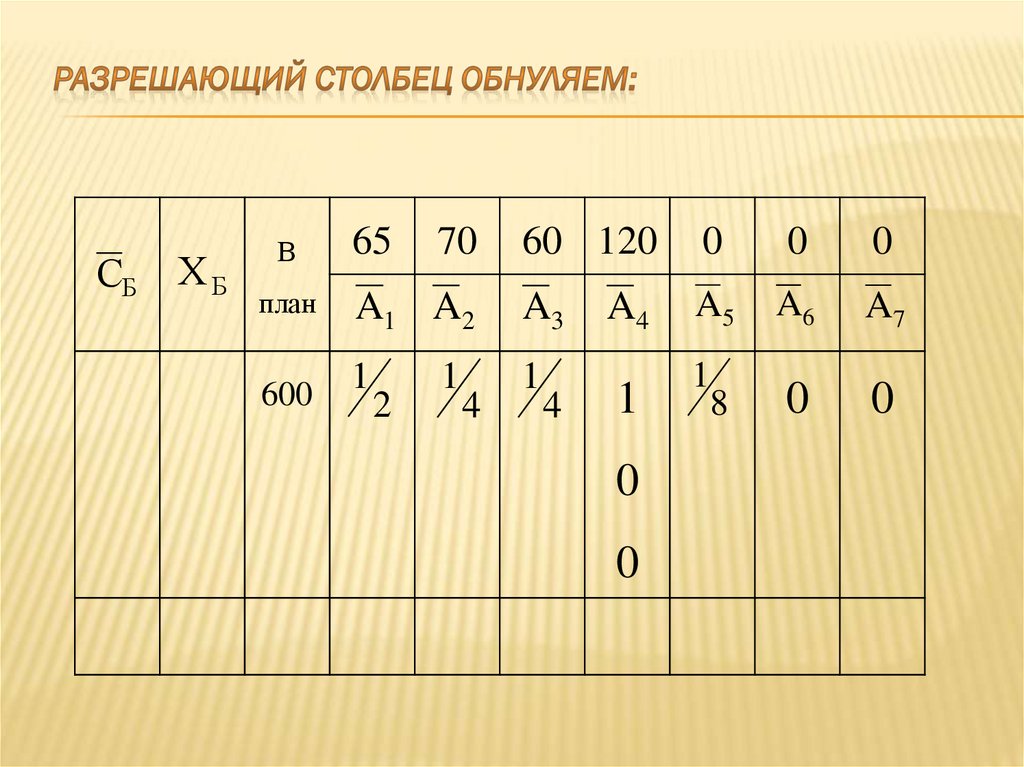
80. Строим новую симплекс – таблицу:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A5
A6
A7
A4
81. Разрешающую строку переписываем, предварительно разделив на разрешающий элемент:
СБХБ
В
план
240
65
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
1
3
0
0
1
10
0
5
70
1
5
82. Разрешающий столбец обнуляем:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
0
0
1
10
0
0
240
1
5
1
0
3
5
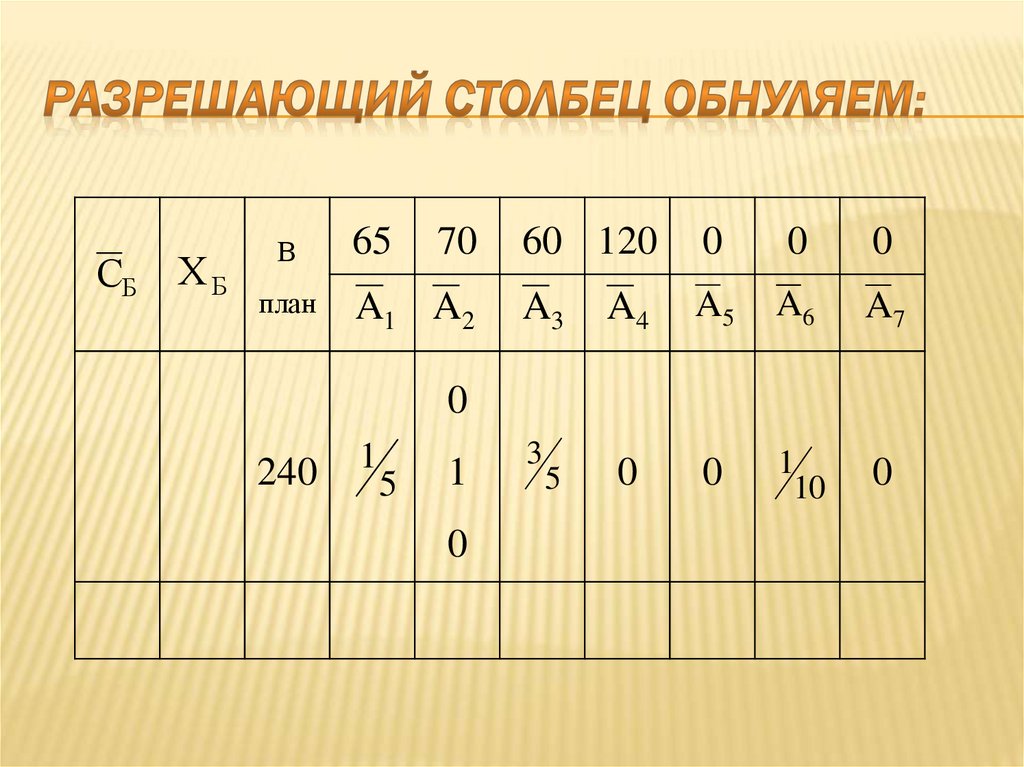
83. Остальные элементы таблицы пересчитываем по методу прямоугольника или методом жордана - гаусса:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
0
0
1
10
0
0
240
1
5
1
0
3
5
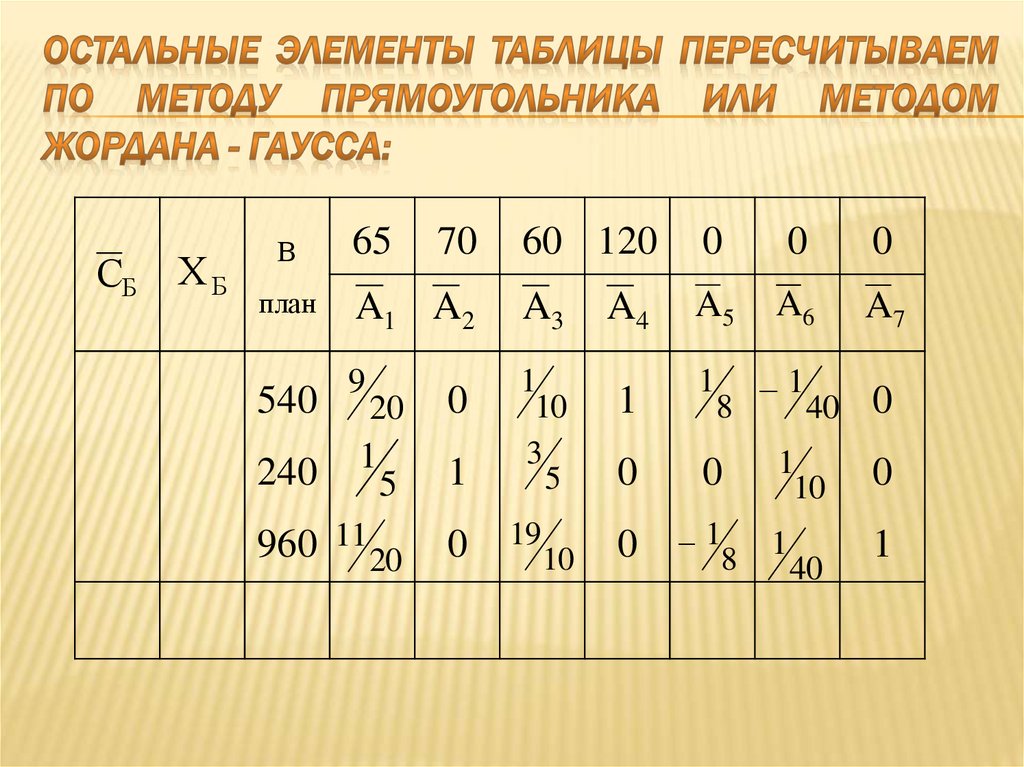
84. Остальные элементы таблицы пересчитываем по методу прямоугольника или методом жордана - гаусса:
СБХБ
В
план
540
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
9
1
10
3
5
1
1
0
0
0
1
8
20
0
1
5
1
960 11 20
0
240
19
10
1
8
40 0
1
10
0
1
1
40
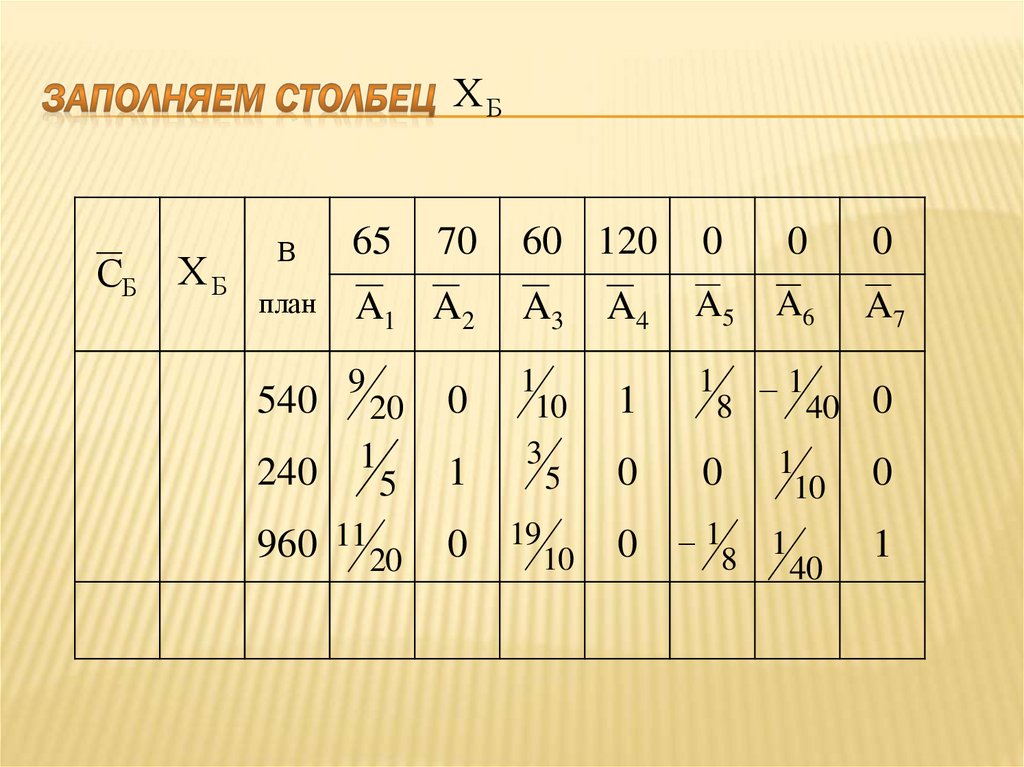
85. Заполняем столбец
ХБСБ
ХБ
В
план
540
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
9
1
10
3
5
1
1
0
0
0
1
8
20
0
1
5
1
960 11 20
0
240
19
10
1
8
40 0
1
10
0
1
1
40
86. Заполняем столбец
ХБСБ
ХБ
В
план
x 4 540
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
9
1
10
3
5
1
1
0
0
0
1
8
20
0
1
5
1
960 11 20
0
240
19
10
1
8
40 0
1
10
0
1
1
40
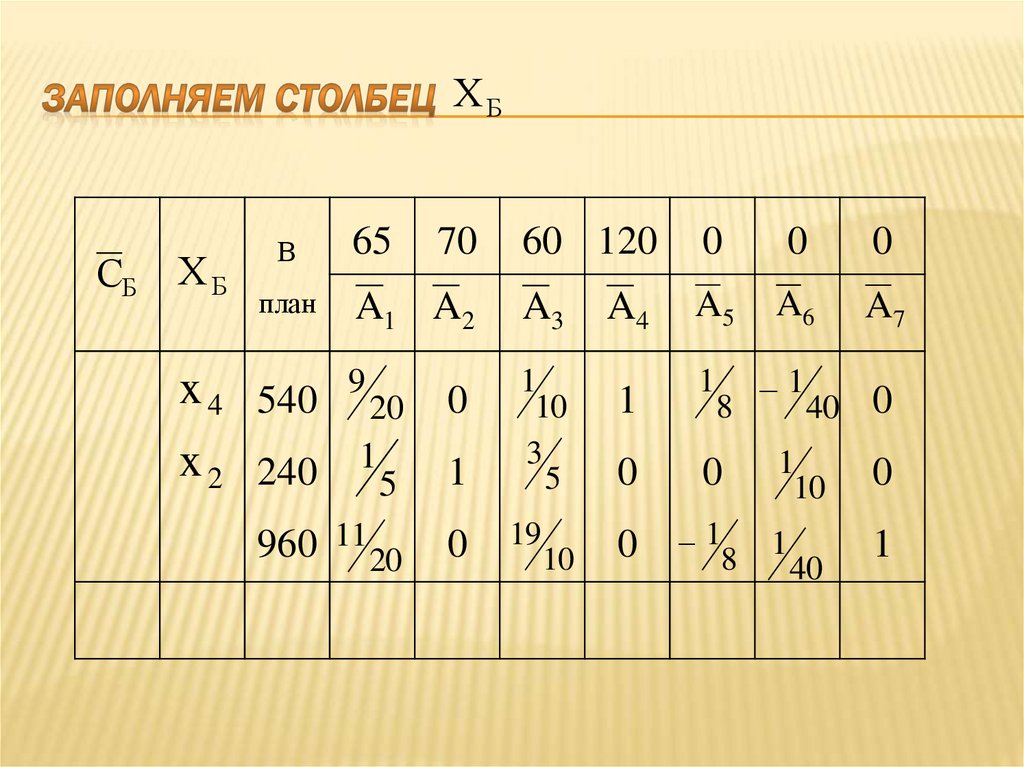
87. Заполняем столбец
ХБСБ
ХБ
В
план
x 4 540
x 2 240
65
70
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
9
1
10
3
5
1
1
0
0
0
1
8
20
0
1
5
1
960 11 20
0
19
10
1
8
40 0
1
10
0
1
1
40
88. Заполняем столбец
ХБСБ
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
x 4 540
x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
89. Заполняем столбец
СБСБ
60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
x 4 540
x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
90. Заполняем столбец
СБ60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
СБ
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
91. Заполняем столбец
СБ60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
СБ
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
92. Заполняем столбец
СБ60 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
СБ
0
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
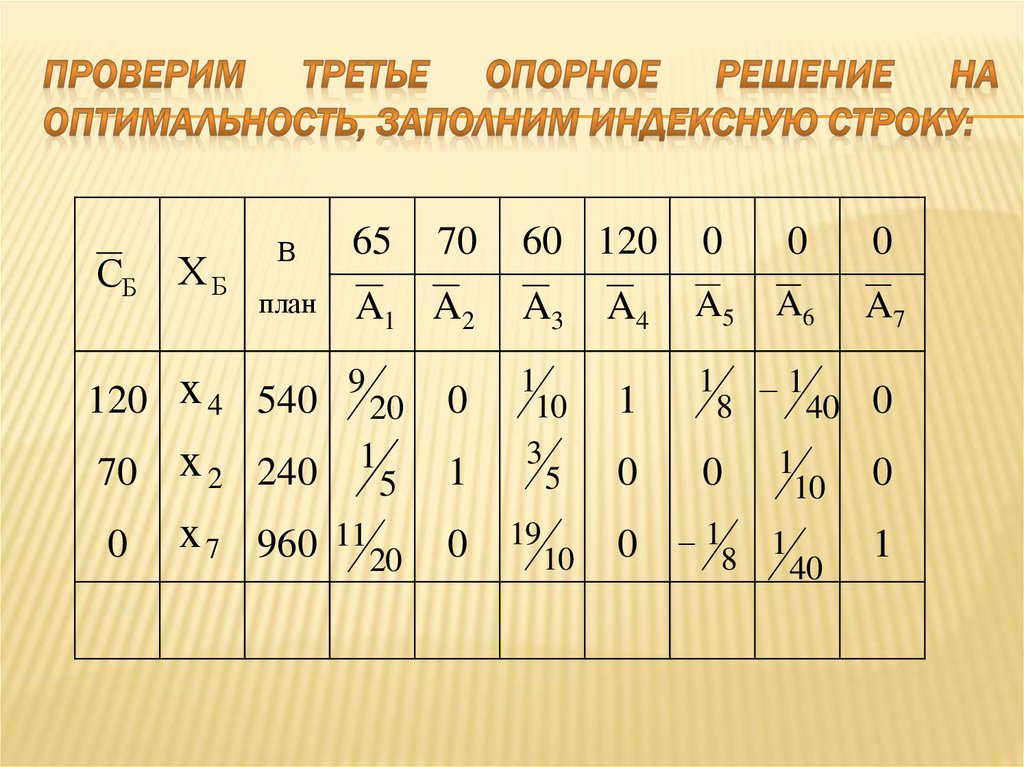
93. Выпишем третье опорное решение
X 3* 0;240;0;540;0;0;96060 120
0
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
СБ
0
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
94. проверим третье опорное решение на оптимальность, заполним индексную строку:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
СБ
0
ХБ
В
план
65
70
20
0
1
5
1
20
0
19
10
1
8
40 0
1
10
0
1
1
40
95. проверим третье опорное решение на оптимальность, заполним индексную строку:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
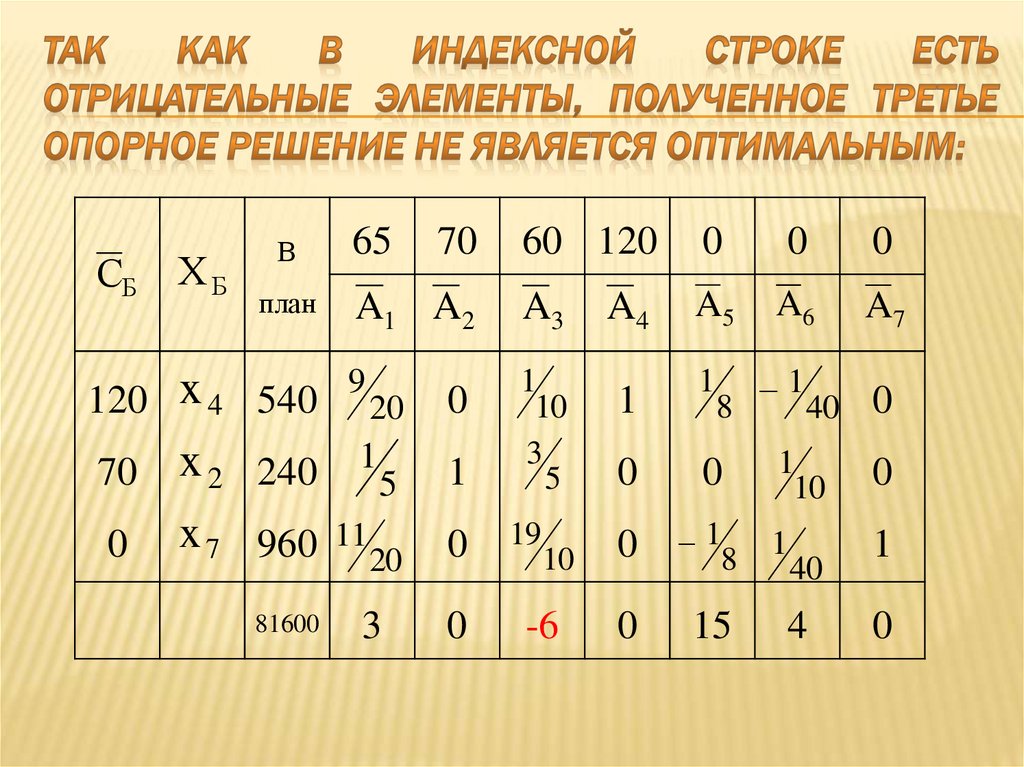
96. Так как в индексной строке есть отрицательные элементы, полученное третье опорное решение не является оптимальным:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
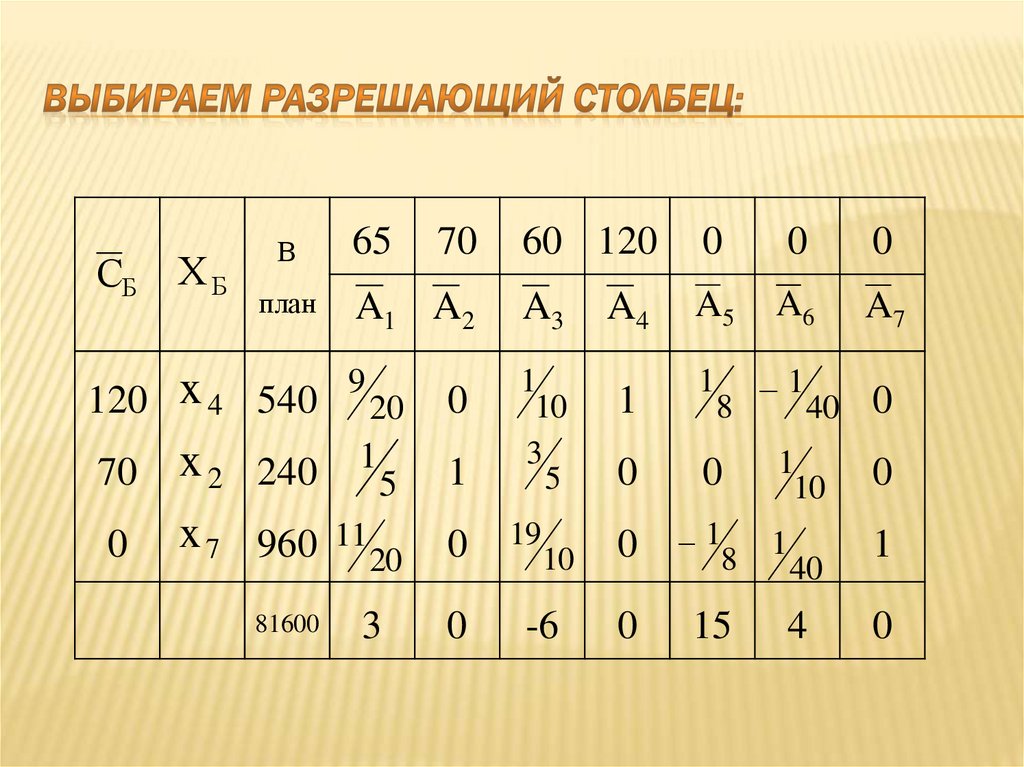
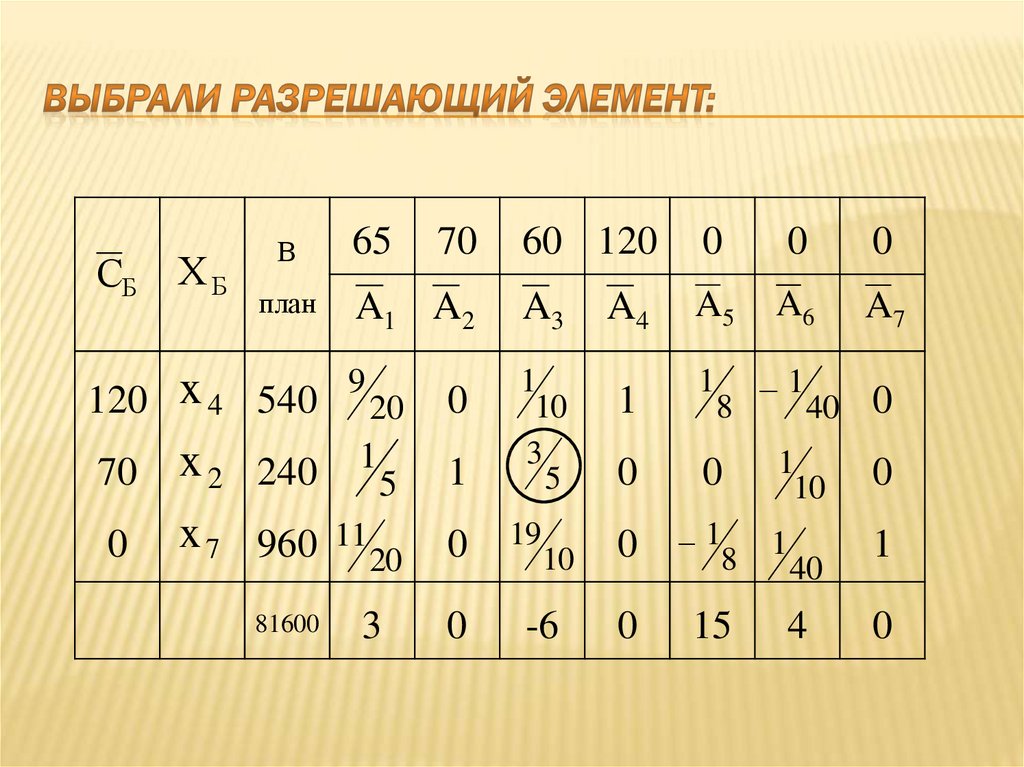
97. Выбираем разрешающий столбец:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
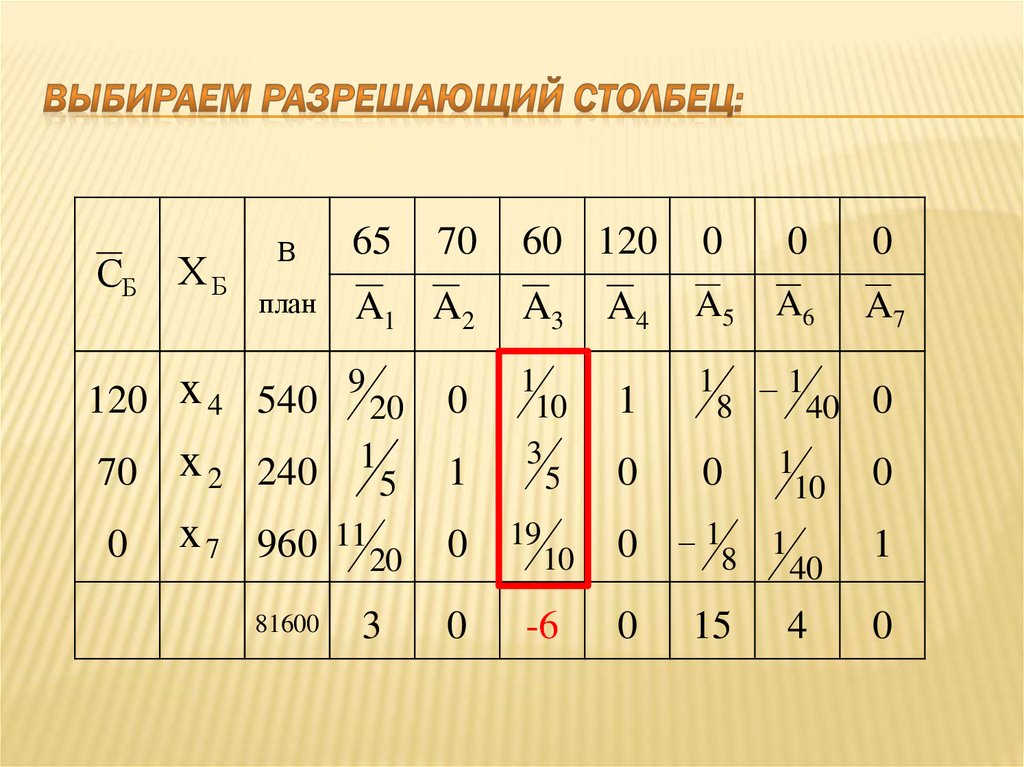
98. Выбираем разрешающий столбец:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
99. Выбираем разрешающую строку:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
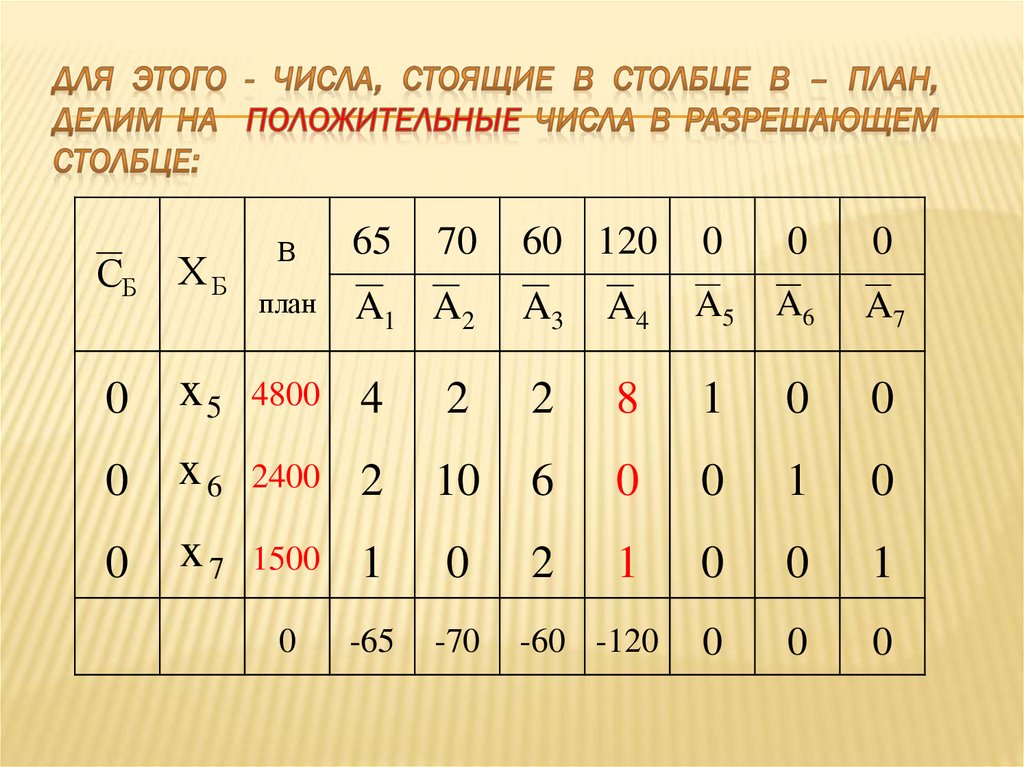
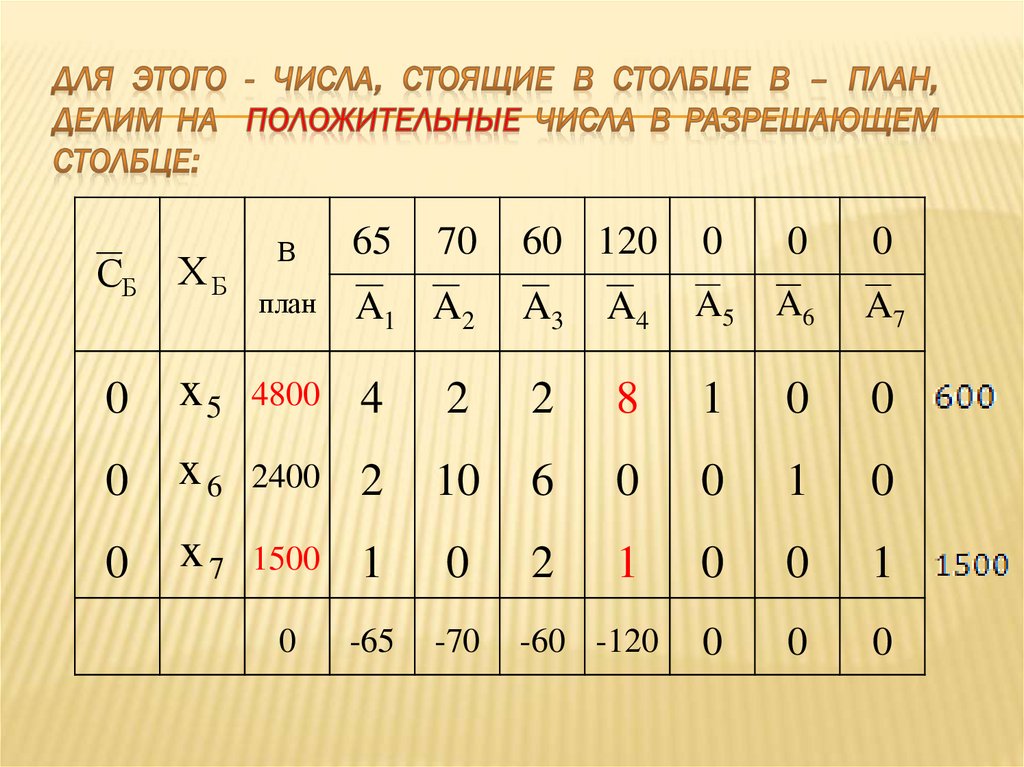
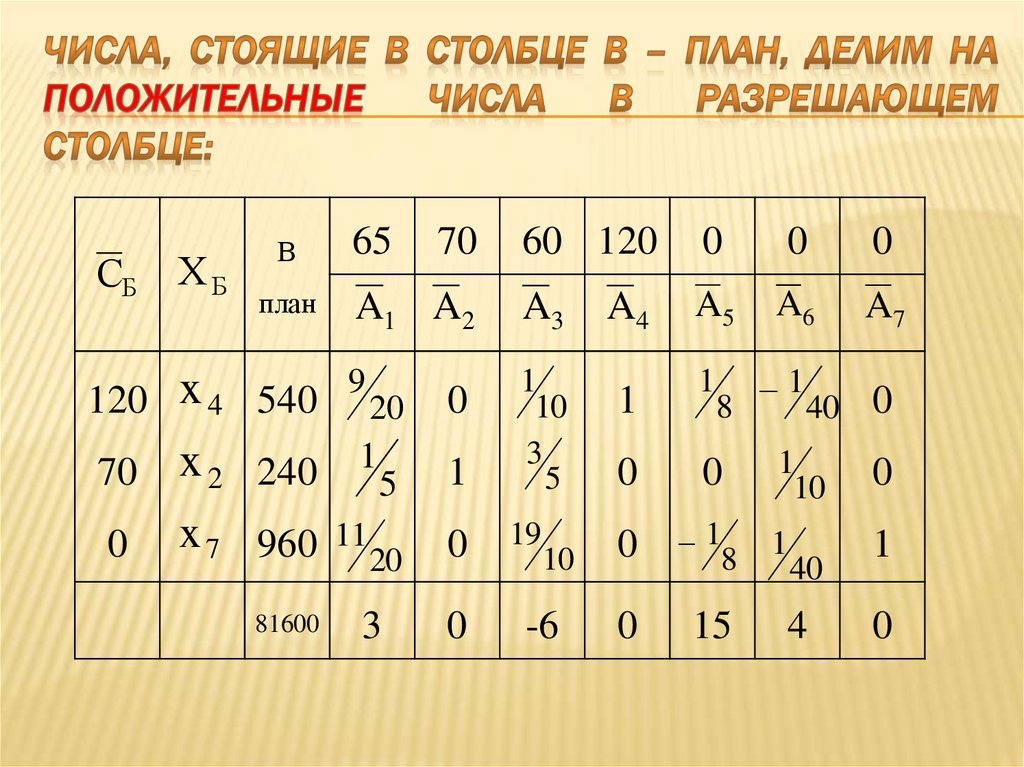
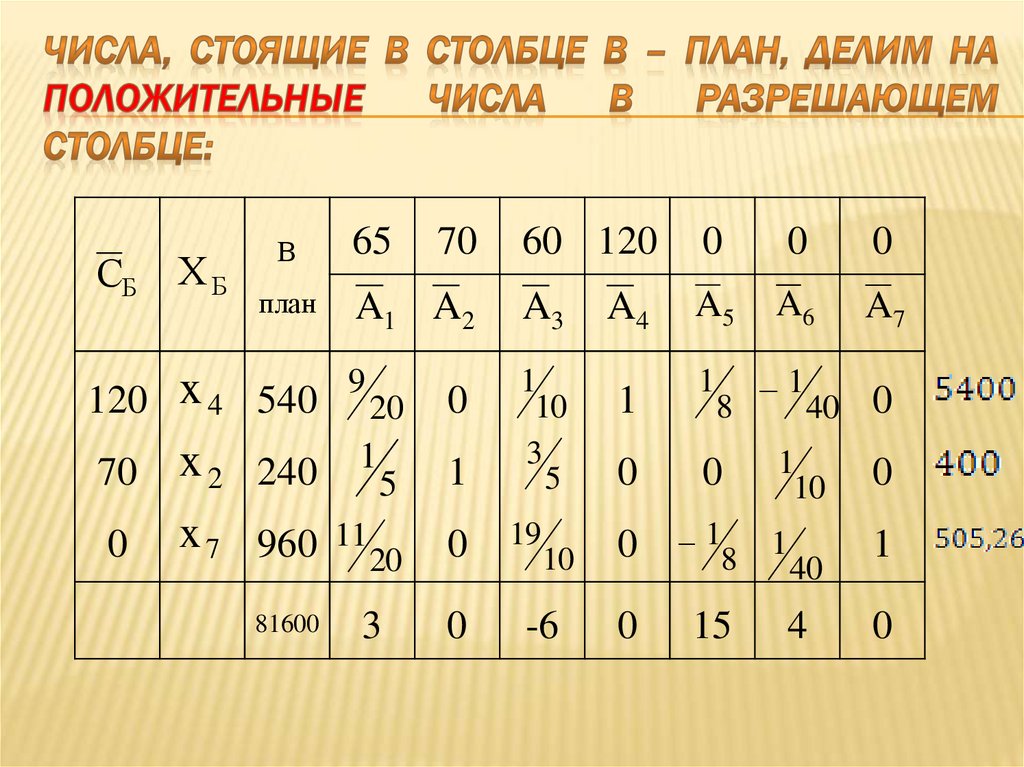
100. числа, стоящие в столбце В – план, делим на положительные числа в разрешающем столбце:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
101. числа, стоящие в столбце В – план, делим на положительные числа в разрешающем столбце:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
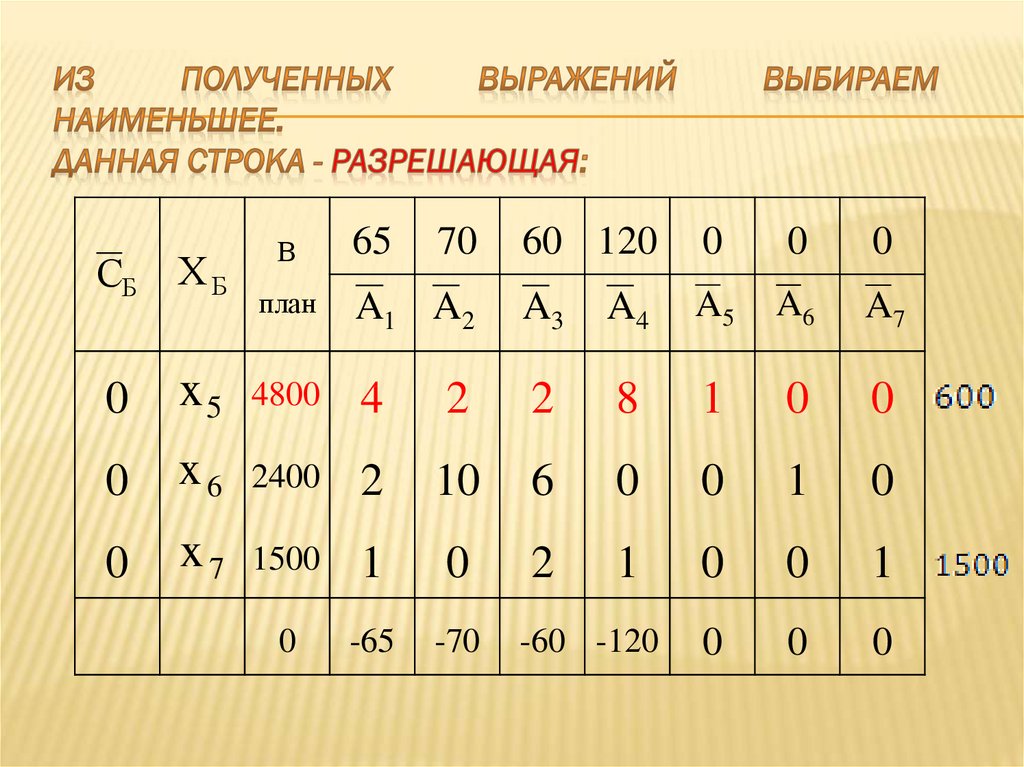
102. Выбрали разрешающий элемент:
60 1200
0
0
A1 A2
A3
A4
A5
A6
A7
120 x 4 540
70 x 2 240
9
1
10
3
5
1
1
0
0
x 7 960
11
0
1
8
0
15
СБ
0
ХБ
В
план
81600
65
70
20
0
1
5
1
20
0
3
0
19
10
-6
1
8
40 0
1
10
0
1
1
40
4
0
103. Строим новую симплекс – таблицу:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A5
A6
A7
A4
104. Разрешающую строку переписываем, предварительно разделив на разрешающий элемент:
СБХБ
В
план
65
70
A1 A2
400 1 3
5
3
60 120
0
0
0
A3
A4
A5
A6
A7
1
0
0
1
0
6
105. Разрешающий столбец обнуляем:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
0
0
1
0
0
400 1 3
5
3
1
0
6
106. Остальные элементы пересчитываем по методу прямоугольника и методом жордана - гаусса:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
0
0
1
0
0
400 1 3
5
3
1
0
6
107. Остальные элементы пересчитываем по методу прямоугольника и методом жордана - гаусса:
СБХБ
В
65
70
план
A1 A2
500
5
1
6
12
400 1 3 5 3
200 112 19 6
60 120
0
0
0
A3
A4
A5
A6
A7
0
1
1
1
0
0
0
0
8
1
1
24
0
6
0
1 7 24
8
1
108. Заполняем столбец
ХБСБ
ХБ
В
65
70
план
A1 A2
500
5
1
6
12
400 1 3 5 3
200 112 19 6
60 120
0
0
0
A3
A4
A5
A6
A7
0
1
1
1
0
0
0
0
8
1
1
24
0
6
0
1 7 24
8
1
109. Заполняем столбец
ХБСБ
ХБ
В
план
x 4 500
65
70
A1 A2
5
1
6
12
400 1 3 5 3
200 112 19 6
60 120
0
0
0
A3
A4
A5
A6
A7
0
1
1
1
0
0
0
0
8
1
1
24
0
6
0
1 7 24
8
1
110. Заполняем столбец
ХБСБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
x 4 500 512 16 0
x 3 400 13 5 3 1
200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
111. Заполняем столбец
ХБСБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
x 4 500 512 16 0
x 3 400 13 5 3 1
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
112. Заполняем столбец
СБСБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
x 4 500 512 16 0
x 3 400 13 5 3 1
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
113. Заполняем столбец
СБСБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
x 3 400 13 5 3 1
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
114. Заполняем столбец
СБСБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
60 x 3 400 1 3 5 3 1
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
115. Заполняем столбец
СБСБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
60 x 3 400 1 3 5 3 1
0
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
116. Выпишем четвертое опорное решение
X 4* 0;0;400;500;0;0;200СБ
ХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
60 x 3 400 1 3 5 3 1
0
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
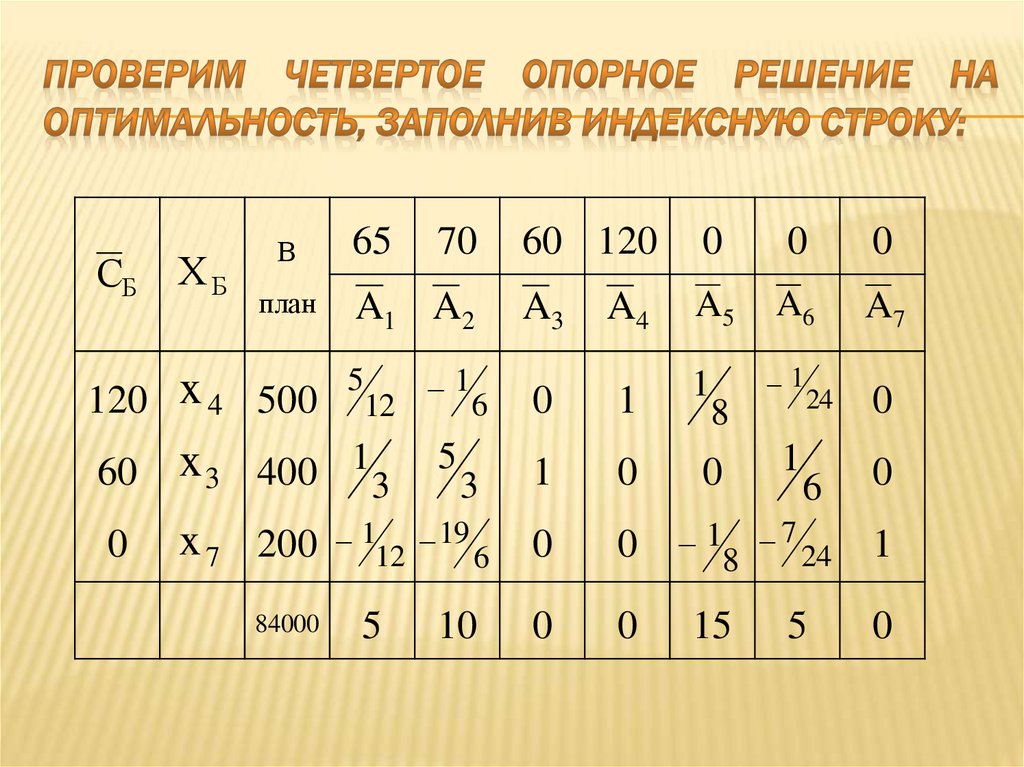
117. проверим четвертое опорное решение на оптимальность, заполнив индексную строку:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
60 x 3 400 1 3 5 3 1
0
x 7 200
1 19
12
6
0
0
8
1
1
24
0
6
0
1 7 24
8
1
118. проверим четвертое опорное решение на оптимальность, заполнив индексную строку:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
60 x 3 400 1 3 5 3 1
0
x 7 200
84000
1 19
12
6
5
10
0
0
0
0
8
1
1
24
0
6
0
1 7 24
8
1
15
5
0
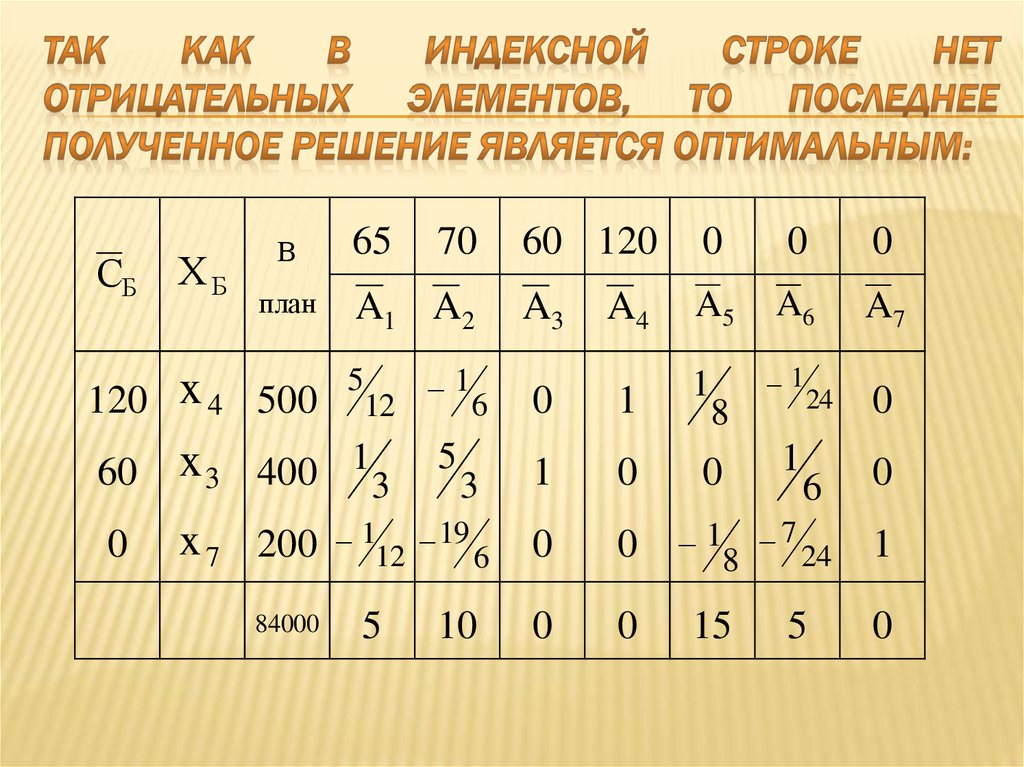
119. Так как в индексной строке нет отрицательных элементов, то последнее полученное решение является оптимальным:
СБХБ
В
план
65
70
A1 A2
60 120
0
0
0
A3
A4
A5
A6
A7
1
1
0
0
5
1
x
120
4 500
6 0
12
60 x 3 400 1 3 5 3 1
0
x 7 200
84000
1 19
12
6
5
10
0
0
0
0
8
1
1
24
0
6
0
1 7 24
8
1
15
5
0
120.
Последнее опорное решение X 4* 0;0;400;500;0;0;200Значение целевой функции возьмем из последней таблицы
4 84000
Ответ: max Z X 84000 при
X 0;0;400;500






















































 mathematics
mathematics








