Similar presentations:
Двойственный симплекс-метод
1. Двойственный симплекс-метод
2. Введение
Рассмотрим следующую задачу линейногопрограммирования (ЗЛП):
min ( 2 x1 + 4 x2 )
3 x1 + x2 ³ 3
4 x1 + 3x2 ³ 6
x1 + 2 x2 £ 3
x1,2 ³ 0
3.
Приведем рассматриваемую ЗЛП к каноническомувиду:
max ( -2 x1 - 4 x2 )
max ( -2 x1 - 4 x2 )
3 x1 + x2 - S1 = 3
-3 x1 - x2 + S1 = -3
4 x1 + 3 x2 - S 2 = 6
-4 x1 - 3 x2 + S 2 = -6
x1 + 2 x2 - S3 = 3
x1 + 2 x2 - S3 = 3
x j ³ 0, j = 1, 2,
x j ³ 0, j = 1, 2,
S j ³ 0, j = 1,3
Si ³ 0, i = 1,3
4.
Рассмотрим расширеннуюæ -3 -1 1 0 0 -3 ö
ç
÷
матрицу системы
P (0) = ç -4 -3 0 1 0 -6 ÷
ç1 2 0 0 1 3÷
линейных уравнений:
è
ø
(0)
P
Матрица
содержит единичную подматрицу
порядка 3 и следовательно, определяет базисное
решение
X N = ( -3; -6;3) ;
( 0)
N
системы уравнений, причем
C N ( 0) = ( 0;0;0 )
( 0)
= ( 3; 4;5 )
5.
Так как элементы (n+1=6)-го столбца матрицы(0)
системы P не являются неотрицательными, то
она не является К-матрицей ЗЛП.
Вычислим
(0)
симплекс-разности матрицы P :
(
)
D (j0) = C N ( 0) , a (j0) - C j = -C j ³ 0; j = 1,5
(0)
P
Так как все симплекс-разности матрицы
являются
неотрицательными, то базисное решение
X N = ( -3; -6;3) ;
( 0)
N
( 0)
= ( 3; 4;5 )
не являющееся допустимым решением ЗЛП,
является «лучшим», чем оптимальное решение.
6. В чем отличие двойственного симплекс-метода от обычного??
В чем отличие двойственного симплексметода от обычного??При решении задачи симплекс-методом текущее
базисное решение является допустимым, но
неоптимальным. Эти соображения позволяют
построить метод решения определенного класса
ЗЛП. В этом методе, называемом ДВОЙСТВЕННЫМ
СИМПЛЕКС-МЕТОДОМ, на каждой итерации
обеспечивается выполнение условия оптимальности
текущего базисного решения, не являющегося
допустимым. Критерием окончания процесса
итераций является получение допустимого решения.
7.
КЗЛП имеет вид:n
f ( x) = c j x j max
(1)
j =1
n
a
j =1
ij
x j = bi , i = 1, m
x j ³ 0 , j = 1, n, bi ³ 0
(2)
(3)
или в екторно - матричной форме
f ( x) = (с, x ) max
(4)
Ax = b
(5)
x ³ 0,
b³0
(6)
8. Р-матрица. Определение
Р-матрицей КЗЛП (1) –(3) называетсярасширенная матрица системы линейных уравнений,
равносильной системе (2), содержащую единичную
подматрицу порядка m на месте n первых столбцов,
все симплекс-разности которой неотрицательны.
Очевидно, что всякая P-матрица ЗЛП ( 1)
определяет некоторое базисное решение системы
уравнений (2).
Базисное решение системы линейных уравнений
, определяемое
Р-матрицей, называется
( 1)
псевдопланом ЗЛП.
9. Условие перехода от одной Р-матрицы ЗЛП к другой
( s)Пусть известна Р-матрица P , определяющая
псевдоплан
( S)
( S)
( S)
XN
=b ; N
( s)
( s +1)
P
Условия перехода от матрицы
к матрице P
составляют содержание следующей теоремы:
10. Теорема 1:
( s)lой
строке матрицы P
есть хотя бы один отрицательный элемент. Тогда
с помощью одного шага метода Жордана-Гаусса
( s +1)
можно построить новую Р-матрицу
, P
выбрав направляющий элемент из условия:
Пусть bl( S ) < 0 и в
q ( S)
D (KS )
D (KS )
=
= min
-alK 1£ j £ n -alK
aij <0
( S)
( s)
b
P
Замечание: Если в матрице
не l < 0 , то
определяемый ею псевдоплан является
решением ЗЛП.
11. Теорема 2:
( S)( s)
Пусть bl < 0 и в lой
строке матрицы P
нет ни
одного отрицательного элемента. Тогда множество
планов Р ЗЛП (1) - (3) пусто.
12. Теорема 3:
( s)s +1
P
При переходе от матрицы
к матрице P ( )
целевая функция изменяется в соответствии с
формулой:
(
)
(
)
f X N ( S +1) = f X N ( S ) + q ( ) bl(
откуда следует, что
S
(
S)
(
= f X N( S)
)
(
)
f X N ( S +1) £ f X N ( S )
D (K ) ( S )
+
bl
-alK
S
) т.к. b
( S)
l
<0
( S)
a
< 0. Из последнего неравенства следует, что
И lK
при переходе от одного псевдоплана к другому
значению функции f ( x ) не возрастает.
13. Алгоритм Р-метода
(0)P
Будем считать, что известна исходная Р- матрица
задачи линейного программирования,
определяющая исходный псевдоплан:
(
X N ( S ) = b1( ) , b2( ) ,K , bm( )
N
( S)
(
0
0
0
)
= N1( ) , N 2( ) ,K , N m( )
0
0
0
)
В методе последовательного уточнения
оценок
( 1)
( 2)
( S)
последовательно строят Р-матрицы P , P ,K , P ,K
задачи линейного программирования, пока не
получат Р-матрицу ЗЛП, определяющую ее
оптимальный план.
14.
Рассмотрим алгоритм S-ой итерации методапоследовательного уточнения оценок. В начале S-ой
итерации имеем Р-матрицу P ( s -1) задачи линейного
программирования, определяющую псевдоплан
XN
( S -1)
l
=b
( S -1)
; N
( S -1)
l
S -1
S -1
ШАГ 1. Найдем
bl( ) номер
= minbi( ) из условия
1£i £ m
15.
( S -1)ШАГ 2. Еслиbl
XN
³0
( S -1)
=b
, то псевдоплан
( S -1)
; N
( S -1)
является оптимальным опорным планом, а
(
) (
f X N ( S -1) = C N ( S -1) , X N ( S -1)
)
есть оптимальное значение линейной
формы f x , иначе переходим к шагу 3.
( )
16.
( S -1)a
ШАГ 3. Если lj ³ 0; j = 1, n
то задача
линейного программирования не имеет
решения (множество планов Р пусто),
иначе переходим к шагу 4.
( S -1)
ШАГ 4. Вычисляем для столбцов a j
матрицы P ( S -1) ( j ¹ Ni( S -1) , i = 1, 2,K , m )
( S -1)
D
симплекс-разности j
и находим номер
К из условия:
q
( S -1)
( S -1)
DK
= ( S -1)
-alK
ìï D (jS -1)
( S -1)
= min í ( S -1) , alj < 0
1£ j £ n - a
ïî lj
}
üï
ý
ïþ
17.
ШАГ 5. Вычисляем компоненты вектора N ( S -1)( S)
Ni
( S -1)
= Ni
( S)
; i = 1, m; i ¹ l ; N l
=K
ШАГ 6. Производим один шаг метода
Жордана-Гаусса с направляющим
элементом a ( S -1) .
lK
( S)
Вычисляем элементы Р-матрицы P
методом Жордана-Гаусса. Присваиваем
переменной алгоритма S значение S+1 и
переходим к шагу 1.
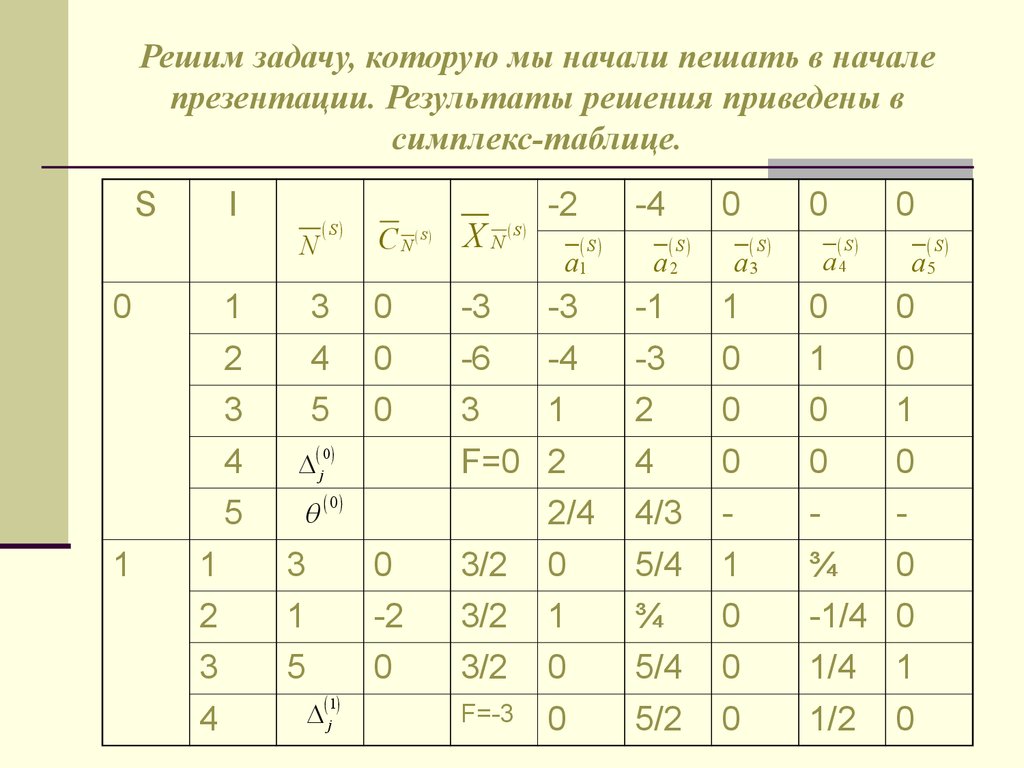
18. Решим задачу, которую мы начали пешать в начале презентации. Результаты решения приведены в симплекс-таблице.
SI
N
0
1
( S)
C N( S)
X N( S)
-2
-4
( S)
a1
0
( S)
0
( S)
a2
0
( S)
( S)
a4
a3
a5
1
3
0
-3
-3
-1
1
0
0
2
4
0
-6
-4
-3
0
1
0
3
5
0
3
1
2
0
0
1
4
D (j0 )
F=0 2
4
0
0
0
5
q ( 0)
2/4
4/3
-
-
0
1
3
0
3/2
0
5/4
1
¾
2
1
-2
3/2
1
¾
0
-1/4 0
3
5
0
3/2
0
5/4
0
1/4
1
F=-3
0
5/2
0
1/2
0
4
D (j )
1
19.
Решим следующую ЗЛП:min f ( x ) = 6 X 1 + 3 X 2
- 3X1 + X 2 ³ 1
2 X1 - 3X 2 ³ 2
X 1, 2 ³ 0
20.
Приводим ЗЛП к каноническому видуmax f ( x ) = (-6 X 1 - 3 X 2 )
3 X 1 - X 2 + S1 = -1
- 2 X 1 + 3 X 2 + S 2 = -2
X j ³ 0,
j = 1,2, Si ³ 0, i = 1,2.
21.
Т.К. расширенная матрицаæ 3 -1 1 0
~ (0) ç
A = ç- 2 3 0 1
ç
è
системы линейных уравнений является Р-матрицей.
-1 ö
÷
- 2÷
÷
ø
Следовательно, к решению данного ЗЛП применим Р-метод.
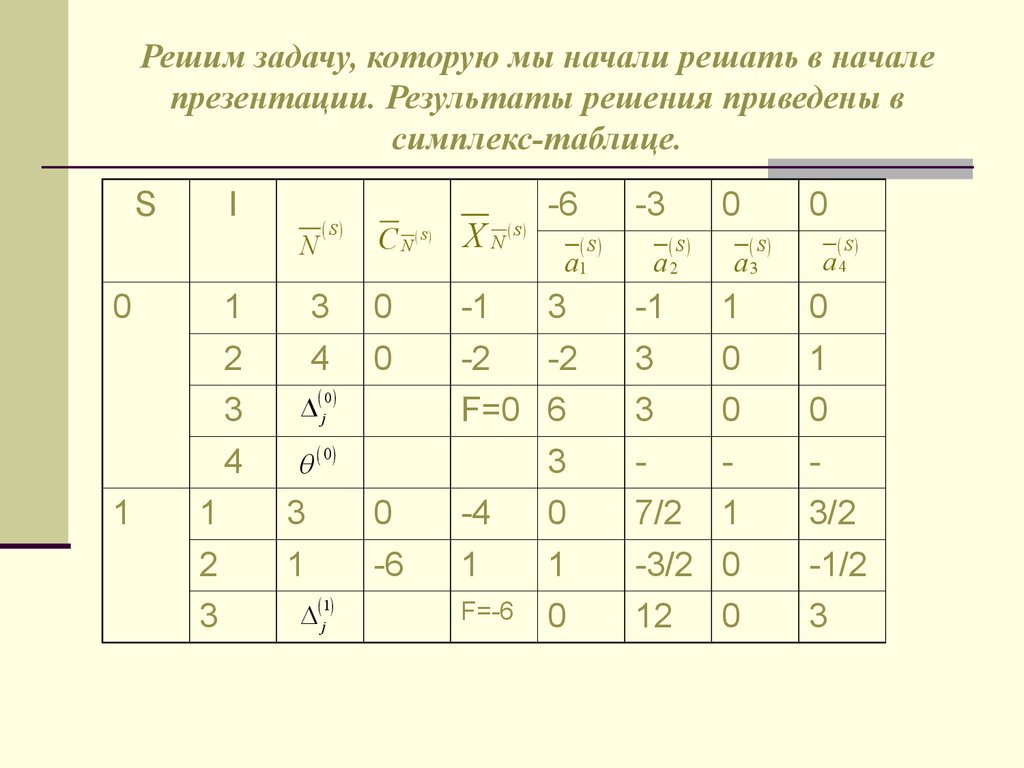
22. Решим задачу, которую мы начали решать в начале презентации. Результаты решения приведены в симплекс-таблице.
SI
N
0
1
( S)
C N( S)
X N( S)
-6
-3
( S)
0
( S)
a1
0
( S)
a2
( S)
a4
a3
1
3
0
-1
3
-1
1
0
2
4
0
-2
-2
3
0
1
3
D (j0)
F=0 6
3
0
0
4
q ( 0)
3
-
-
-
1
3/2
1
3
0
-4
0
7/2
2
1
-6
1
1
-3/2 0
-1/2
F=-6
0
12
3
3
D (j1)
0
23.
Т.К. bl=-4<0, а все a1j>=0, то множество плановЗЛП является пустым множеством.





















 mathematics
mathematics programming
programming








