Similar presentations:
Medical physics
1. Radiation Safety
RadiationSafety
Biomechanics
Существует 230 типов возможных типов
симметрии!
Их делят на семь классов
Решетка с наименьшей симметрией называется
I. триклинной.
Ее элементарная ячейка представляет собой
параллелепипед
1. Основные вектора (a, b, c) имеют разную длину
2. нет ни одной одинаковой пары углов между ними
3. ни какой вращательной или зеркальной симметрии
При инверсии R (x,y,z) заменяется на –R (-x,-y,-z)
может быть с центром инверсии и без него.
2. Radiation Safety
RadiationSafety
Biomechanics
II - тригональная
Ее элементарная ячейка представляет собой
параллелепипед
1. Основные вектора (a, b, c) все вектора равны
2. Все углы между ними равны
имеет симметрию
не изменяется если вращать вокруг наибольшей
диагонали.
3. Radiation Safety
RadiationSafety
Biomechanics
III - моноклинная
Если один из основных векторов, скажем c
направлен под прямым углом к двум другим
будет новая симметрия
вращение на 180 градусов вокруг вектора c .
4. Radiation Safety
RadiationSafety
Biomechanics
IV - Гексагональная
это частный случай моноклинной..
1. Вектора a и b равны и угол между ними 60 градусов
2. вектор c направлен под прямым углом к двум
другим a и b
имеет симметрию
Это приводит к тому, что вращение на 60, 120 и 180
градусов вокруг вектора c приводит к той же самой
решетке.
5. Radiation Safety
RadiationSafety
Biomechanics
V - ромбическая
Ее элементарная ячейка представляет собой
параллелепипед
1. Основные вектора (a, b, c) перпендикулярны
друг другу но не равны
2. Все углы между ними равны 90 градусам
имеет симметрию
Симметрична относительно вращений на180
градусов вокруг всех трех осей.
6. Radiation Safety
RadiationSafety
Biomechanics
VI - тетрагональная
Ее элементарная ячейка представляет собой
параллелепипед
1. Два основные вектора (a и b равны)
2. Все углы равны 90 градусам
имеет более высокую симметрию
7. Radiation Safety
RadiationSafety
Biomechanics
VII - кубическая
Ее элементарная ячейка представляет собой куб
1. Все основные вектора (a и b и c равны)
2. Все углы равны 90 градусам
имеет самую высокую симметрию
8. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризуемости
Физики берут простой пример и его рассматривают
сложные задачи – кому-нибудь другому
Мы тоже начнем с макро - свойства материала
Механика сплошной среды сродни
макроэлектродимике, но сложнее
Почему?
возьмем «объект» и
поместим в какую - нибудь
систему координат
9. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
Мы знаем с Вами такое явление, как
поляризация кристаллов под действием
приложенного электрического поля.
мы допустили, что МСС сродни МЭД
Механика сплошной среды (МСМ) – мы хотим изучить
свойства материалов при приложенных нагрузках, так
давайте начнем из известного Вам явления.
Возьмем кубический кристалл и приложим
электрическое поле по оси х , оно даст
поляризацию Р1, а поле направленное по оси
y – дает Р2.
10. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
Для простоты рассмотрим плоский кристалл
Приложенное поле E дает вектор
поляризации P
Теперь рассмотрим общий случай, пусть
кристалл плоский кристалл будет иметь
произвольную ориентацию по
отношению к выбранной системе
координат. Тогда поле направленное по
оси х будет давать поляризацию с
компонентами по всем трем осям.
P x xx E x yx E y zx E z
P E E E
P E E E
y
yx
x
yy
y
z
zx
x
zy
y
yz
zz
z
z
11. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
Диэлектрические свойства кристалла описывается девятью
величинами
xx
yx
zx
yx
yy
zy
zx
yz
zz
Что произойдет при замене старых осей координат на новые?
Для разных систем координат, коэффициенты будут различны.
Надо выяснить, как должны измениться E и P, ибо описываем
одно и тоже поле, но в новой системе координат. Для новой
системы координат Р1(х) будет линейной комбинацией Р(х), Р(y)
и Р (z)
12. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
тогда
a(
E E E )
b( E E E )
c( E E E )
P
1
x
x
xx
yx
yx
x
yy
y
zx
x
zy
y
y
z
zx
z
yz
z
zz
E a E x b E y c E z
1
Мы получим
1
1
x
1
1
1
Все отразиться только в коэффициентах
Связь между Е и Р можно записать в более компактном виде
P E
i
ij
j
j
Придумано много специальных обозначений, но каждое из них удобно для
специального класса задач. Одно из таких – можно не писать знак суммы, понимая
при этом, когда встречается индекс дважды, значить по нему должно быть
суммирование
13. Radiation Safety
RadiationSafety
Biomechanics
Эллипсоид энергии
Какая энергия требуется для поляризации кристалла?
E )/2
Энергия электрического поля равна на единицу объема (
Работа на перемещение одного заряда на расстояние dx,
2
0
qE dx
x
А в единице объема зарядов N и для их перемещения
потребуется работа в N раз больше.
но qNdx равно изменению дипольного момента единицы
объема dP(x), то работа затраченная на единицу объема равна
E dP
x
x
Для объема равна
Ed P
Поскольку P пропорционально E , то работа затраченная на поляризацию
объема от 0 до P равна
up
1
1
1
E P E i P j ij E i E j
2
2
2 i j
14. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
отсюда следует:
Плотность энергии не зависит от координат, т.е – скаляр
Тензор просуммированный по одному индексу дает вектор, а
по двум индексам - скаляр.
Тензор первого ранга –вектор.
Тензор нулевого ранга - скаляр
Тензор поляризации – симметричен.
Это отражает физические реального кристалла
Можно легко проверить : включили электрическое поле по оси х, включили
электрическе поле по оси y Выключили поле по оси х, выключили поле по
оси y . Полная работа равна нулю и тогда дожны быть равны
xy и
yx
u E
p
xx
2
x
( xy yx ) E x E y yy E y
2
15. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
Для двух компонент получаем красивую картинку
2u E
0
xx
2
x
2 xy E x E y yy E y
2
Для трех компонент получаем
В главных осях его можно описать уравнением:
2u E E E
2
0
aa
•По отношению к главным осям только три не нулевые
компоненты aa , bb и cc .
a
2
bb
d
cc
2
c
16. Radiation Safety
RadiationSafety
Biomechanics
Тензор поляризации
•Какой бы не был сложный кристалл, можно определить три его главные оси.
•У тензора только три компоненты, иначе говоря электрическое поле,
направленное по любой главной оси дает поляризацию только по этой оси.
•Для любой системы координат
xx
yx
zx
yx
yy
zy
zx
yz
zz
•Для системы координат по главным осям
aa 0 0
0 bb
0
0
0 cc
•Если все диагональные элементы равны?
17. Radiation Safety
RadiationSafety
Biomechanics
Тензор инерции
В физике есть много примеров других тензоров
Вам известен момент инерции из курса общей физики
Мы знаем, что момент количества движения L твердого тела,
вращающегося вокруг фиксированной оси, пропорционален
угловой скорости и момента инерции I.
Для вращения тела вокруг одной из осей симметрии L и
параллельны.
Но если моменты инерций относительно трех главных осей
различны, то направления L и не совпадают и можно
воспользоваться рассуждениями, которые мы сделали при
тензора поляризации и записать следующее выражение:
18. Radiation Safety
RadiationSafety
Biomechanics
Тензор инерции
•Для системы координат по главным осям
L I I I
L I I I
L I I I
x
xx
x
yx
y
zx
z
y
yx
x
yy
y
yz
z
z
zx
x
zy
y
zz
z
По аналогии с поляризацией, кинетическая энергия
будет квадратичной формой x ,
y,
z
к.э.
1
2 ij I ij i j
Можно показать, что этот тензор симметричный
I
ij
I
Тензор можно «написать» если известна форма тела
Нужно только выписать полную кинетическую энергию всех частиц тела.
ji
19. Radiation Safety
RadiationSafety
Biomechanics
Тензор инерции
Частица с массой m и скоростью v обладает кинетической энергией
А полная кинетическая энергия равна просто сумме
Но скорость
1
2
mv
2
1
2
mv
2
v связана с угловой скоростью соотношением v r
Кинетическая энергия будет равна
к.э.
2
1
m
2 ( r )
Единственное, что нужно сделать это переписать векторное произведение
через компоненты угловой скорости и координаты радиуса вектора.
2
2
2
2
x
y
z
( r ) ( r ) ( r ) ( r )
( yz z y) ( z x x z) ( x y y x)
2
2
2
20. Radiation Safety
RadiationSafety
Biomechanics
Тензор инерции
•Раскрывая скобки и приводя подобные члены можно видеть, что
I xx m( y z ) m(r x )
2
где
r
2
x
2
y
2
z
2
2
2
Выписав остальные члены получим
m( r x )
2
mxy
2
mxy
mxz
m(r y ) mzy
mzy
m(r z )
2
mxz
2
2
Или в тензорных обозначениях
I
ij
m( r
r r )
2
ij
i
j
2
2
21. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Деформацией называют изменение формы и объема твердого тела по действием
внешних сил или при изменении его температуры.
Возьмем тело в декартовой системе координат.
Оси координат
x , i 1, 2,3
i
Выделим бесконечно малый объем ,
включающий точку P с координатами
Положение точки P задается вектором
r
с координатами
x ,x ,x
1
2
x ,x ,x
1
2
3
3
При приложении внешней силы тело деформируется и точка P переместится в точку
с координатами
/
/
/
x1, x 2, x 3
Смещение точки равно
P
u (r ) r 1 r , u i(r ) x i x i
/
Задание вектора u (r ) Полностью определяет деформацию теле во всех точках
Возьмем точку Q После деформации она перейдет в точку Q1
1
22. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Деформация двух точек связаны между собой
u (r d r ) u (r ) du или
u (r d r ) u (r ) d u
i
i
называется вектором
du
относительного смещения
В дифференциальной форме
Разложив функцию в ряд Тейлора и ограничившись
только линейными членами по dx получим
Вектор
u i
u (r d r ) u (r ) d x
u
i
i
k
Это уравнение однородной линейной деформации
Малые деформации- называют упругими.
dui
A
ik
u i
u k
d xk
A
ik
где
Aik
u i
u k
Тензор относительной деформации
Второго ранга третьей мерности
A
ik
1
k
......
i
23. Radiation Safety
RadiationSafety
Biomechanics
Деформация
его можно представить в виде суммы симметричной и антисимметричной части
1
1
Aik 2 ( Aik Aki) 2 ( Aik Aki) ik ik
ik
ik
1
(
)
2 Aik Aki
Симметричная часть называется тензором деформаций
1
( Aik Aki )
2
ik
ki
антисимметричная часть называется тензором поворота
ik
ki
тензор поворота
Предположим, что тензор деформации равен нулю, тогда
Компоненты тензора
ik
Образуют матрицу
Поскольку он антисимметричный, то он
включает только три независимых компоненты.
32
; ;
23
1
13
31
2
21
12
3
dui d xk
ik
0
0
0
12
21
31
13
23
32
)
24. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Тогда матрица получит вид
(
Если ввести вектор поворота
То можно записать
0
3
2
du dr
3
2
0
3
d u 1 d x 2 d x 3
1
)
1
0
2
d u 2 d x1 d x 3
3
1
d u 3 d x1 d x 2
2
С компонентами
, ,
1
2
1
3
Компоненты тензора поворота описывают только поворот тела в целом
12
1 u 1 u 2
1
(
) rot 3u
3
2 x 2 x1
2
1
1
( u 2 u 3 ) rot 1u
23
1
2 x3 x2
2
31
1 u 3 u 1
1
(
) rot 2u
2
2 x1 x 3
2
В векторном виде
1
rotu
2
25. Radiation Safety
RadiationSafety
Biomechanics
Деформация
тензор деформации
Пусть компоненты тензора поворота равны нулю, в этом
случае относительные смещения полностью определяются
d u i ikd x k
тензором деформации
Тензор деформации, как всякий симметричный
0
тензор можно свести к главным осям, т.е.
11 0 0
существует такая система координат, в которой
0
0 22 0
он имеет диагональный вид
0
0
Деформации запишутся в таком виде
d u 1 11d x1 d u 2 22d x 2
0
0
0
0
0
0
0
33
d u 3 33d x 3
0
0
0
Растяжение или сжатие по трем взаимно перпендикулярным
направления называется чистой деформацией
26. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Изменение объема при деформации
Рассмотрим изменение объема при деформации. Поворота нет.
0
0
0
Его величина до деформации равна
V0
x1 x 2 x 3
После деформации ребра примут значения x i x i d u i
01
0
где d u i ii x i
01
0
0
0
V 0 (1 11 22 33) V 0
Тогда объем будет равен
Относительное изменение объема равно
0
0
0
V 0 V 0
01
V 0
11 22 33 ii
0
0
0
0
Видим, что оно не зависит от выбора координат . След
0
тензора ( ДЭ не зависит от выбора СК
ii
ii
0
27. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Изменение объема при деформации
V 0 V 0
01
V 0
u i
V
ii
divu
V
xi
Изменение Объема Тела при деформации описывается
диагональными компонентами тензора
ik , а
недиагональные компоненты этого тензора описывают
деформацию сдвига - изменение формы рассматриваемого
элемента объема
28. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Геометрические свойства линейных деформаций
1. Точки ЭО тела, находящиеся до деформации в одной
плоскости, после линейной деформации также расположатся
в одной плоскости
Действительно, уравнение плоскости в главных осях имеет вид
a x1 b x 2 c x 3 d 0
0
0
0
После деформации новые координаты точек
плоскости
будут
01
0
0
0
связаны со старыми координатами - так x1 x1
11 x 1
01
0
0
0
Или в общем виде
x i x i ii x i
Тогда новые координаты будут удовлетворят уравнению
a
1 11
0
x
01
1
b
1 22
0
x
01
2
c
1 33
0
x
01
3
d 0
29. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Геометрические свойства линейных деформаций
2. Точки ЭО тела, лежащие на одной прямой до деформации,
после линейной деформации также расположатся на
некоторой прямой.
Это следует из первого свойства. (почему?)
Прямая есть результат пересечения двух плоскостей (ну и что?)
Влияние деформации на точки лежащие на одной прямой
проявиться
В чем?
В повороте прямой на некоторый угол
В растяжении или сжатии этого отрезка
30. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Геометрические свойства линейных деформаций
3. Две параллельные до деформации плоскости, останутся
параллельными и после линейной деформации.
Действительно, зададим уравнения двух плоскостей в объеме
A x1 B x 2 C x 3 0
0
0
0
a x1 b x 2 c x 3 0
0
0
Они параллельны
A B C
a b c
0
Если, что Если, выполняется отношение
a
то
После деформации получим
И они будут параллельны
1 11
0
A
1 11
0
x
x
01
1
01
1
b
1 22
0
B
1 22
0
x
01
x
01
2
2
c
1 33
0
C
1 33
0
x
01
3
x
d 0
01
3
D 0
31. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Геометрические свойства линейных деформаций
4. Две параллельные до деформации прямые, останутся
параллельными и после линейной деформации.
Это следует из третьего свойства. (почему?)
Можно повести рассуждения, как и в первом свойстве и
получим это свойство
32. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Эллипсоид деформации
Рассмотрим в элементе объема сферу единичного радиуса,
центр которой находиться в начале координат.
Уравнение сферы в главных осях имеет вид
1 После деформации получим уравнение
0
x1
2
0
x2
2
0
x3
2
01
x1
2
01
x2
2
01
x3
2
1 110 1 022 1 330
2
2
2
1
Что это за уравнение?
Уравнение сферы переходит в уравнение эллипсоида
И когда это будет сфера?
11 22 33
0
0
0
33. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Температурная деформация
Деформация может происходить и не только под действием
внешних сил, но и в результате изменения его температуры
Пусть в начальный момент времени температура была
После нагрева или остывания температура стала
Происходит только расширение или сжатие
если
T
ik
T
T
0
T
0
T
Почему?
1 То деформацию объема можно записать в виде
d u i ikd x k
T
T
где
T
ik
ik T
Это тензор теплового расширения
Деформация происходит без поворота и происходит по осям
34. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Температурная деформация
В главных осях тензор имеет вид
0
0
0
0
0
0
0
11
0
22
0
33
Очевидно, при температурной деформации сфера переходит в
2
2
2
эллипсоид
01
01
01
x1
0
1
11 T
2
Если тело изотропно, то
Сфера в сферу
x2
0
1
22 T
0
11
2
x3
0
1
33 T
22 33
0
А тензор имеет вид
2
1
0
T
ik
T ik
Вектор относительной деформации d u i Td x i
При однородном нагревании l Tl
35. Radiation Safety
RadiationSafety
Biomechanics
Деформация
Температурная деформация
V
T
ii T ii 3 T
Относительное изменение объема
V
1 V
( ) 3
В дифференциальной форме
V T
Величину 3 называют коэффициентом объемного
теплового расширения Теорема Коши-Гельмгольца
u (r d r ) u (r ) d x d x
i
i
ik
кратко:
поступательное движение,
поворот на угол
,
растяжение – сжатие,
температурная деформация
k
ik
k
ik
Td x k
36. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Силы массовые, объемные и поверхностные.
При линейной деформации не только происходит изменение
формы и объема, но возникают силы упругости (напряжения)
Эти силы действуют внутри деформируемого тела на
границах между его частями.
Можно разделить их на две категории: силы массовые
(объемные) и силы поверхностные.
Массовые силы
Это силы пропорциональные массе m элемента объема
F f m
Здесь
f
- напряженность или плотность массовой силы.
V
37. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Силы массовые, объемные и поверхностные.
В общем случае зависит от координат и времени
Если плотность среды - это предел отношения
элемента массы к его объему V , при V
m
стремящемуся к нулю
lim
V 0
f f (r ,t )
m
V
В пределах однородного элемента объема m V
F f m
Или плотность объемной силы
( сила тяжести)
,
38. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Силы поверхностные.
Если выделить объем в теле, то на него будут действовать
некоторые силы вследствие деформации, смещение одних
участков по отношению к другим.
Молекулярные силы с радиусом действия порядка
10
9
m
Т.е. взаимодействие через поверхность
поверхностные силы – это внутренние силы в деформируемом
теле, которое действует на граничных поверхностям.
Пусть на поверхность действует сила d F
где
(n)
dF
(n)
(n)
по нормали
(n)
dS
напряжение, или плотность поверхностных сил
39. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Нужно составить уравнение движения бесконечно
малого тетраэдра по действием массовых и поверхностных сил
Если плотность известна и известен объем тетраэдра, тогда
нужно обозначить площадь каждой грани как d S i
(i )
Напряжение на площадке
, f - напряженность
массовых сил, v - скорость движения тетраэдра
Уравнение движения будет иметь вид
V
dv
(n)
f dV dS (1)S (2)S (3)S
1
2
3
dt
(n)
В эквивалентном виде
(i )
n
i
(n)
i
ik n k
40. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Это трехмерный тензор второго ранга – тензор напряжений
Любая компонента тензора представляет силу, действующую в
направлении оси i на единичную площадку перпендикулярную
оси k
Диагональные – нормальные напряжения
Недиагональные – касательными напряжениями
Это симметричный тензор.
В случае. Если диагональные элементы равны –p,
то тензор описывает всестороннее равномерное сжатие
ik
ik p
41. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
При всестороннем равномерном сжатии тензор
напряжений можно записать p
ik
ik
Поверхностная сила
По третьему закону Ньютона внутренние силы внутри объема
компенсируются и, следовательно результирующая сила
может быть составлена из сил действующих на поверхности
выделенного объема
Пусть F – результирующая сила, действующая на единицу
объема. Она будет равна результирующей поверхностной
силе.
FdV
dF
V
S
(n)
dS
(n)
S
F dV
i
v
S
n dS
ik k
42. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Поверхностная сила
Здесь интегрирование по объему и ограничивающей его
поверхности. Если ввести
d S ndS
тогда
ik
V Fi dV S ik dSk V xk dV
По теореме Гаусса - Остроградского
aik
S ad S S ak dSk V divadV V xk dV
43. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Это выражение справедливо для произвольного объема, то
результирующая сила, действующая на единицу объема равна
ik
Fi
xk
Это говорит о том, что зная зависимость тензора напряжений
от координат и времени можно вычислить силу действующую
на единицу объема, а следовательно, составить уравнение
движение этого объема или элементов объема.
Термодинамика деформирования
Пусть
Работа внутренних сил
dAv
Работа производимая силами внутренних напряжений
единице объема
- результирующая сила
Пусть
Тогда работа этой силы на перемещении
равна
du
F
44. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
ik
dAv Fi dui
dui
xk
ik
Av d Av dV
dui dV
xk
V
V
Интеграл в правой части можно записать
ui
Av ( ik dui )dSk ik d( )dV
xk
S
V
и
V xk ( ik dui )dV V ik ( xk dui )dV
ik 0
45. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
1 ui uk
Av ik d (
)
2 xk xi
V
dV ik d ik dV
V
Это справедливо для любого V
тогда
Av ik d ik
Если после прекращения действия внешних сил тело
полностью возвращается в исходное состояние – деформация
упругая. Если нет – пластическая.
46. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Основное термодинамическое равенство
Первое начало термодинамики
Приращение внутренней энергии единицы объема тела
равно разности полученного из вне тепла
dEвн
dQv
и производимой силами, внутренних напряжений работы dA
dEвн dQv ik d ik
Это является основным термодинамическим тождеством для
деформируемых тел
v
47. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
При обратимом процессе количество теплоты равно
S v- энтропия
TdSv ,
энтропии единицы объема недеформированного тела
где T- температура тела, а
dEвн TdSv ik d ik
Для всестороннего равномерного сжатия газа или жидкости
тензор напряжений равен p
ik
ik
тогда
V
dEвн TdSv p ik d ik TdSv p d ii TdSv pd
V
и
dEвн TdSv pdV
При V=1
48. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР НАПРЯЖЕНИЙ
Первое начало термодинамики
известно, что
и
Fv Eвн TSv
тогда
dFv dEвн TdSv Sv dT
dFv Sv dT ik d ik
Eвн
Fv
ik (
) Sv (
)T
ik
ik
Компоненты тензора напряжений можно получить
дифференцированием энергии по компонентам тензора
деформаций или из свободной энергии.
49. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
СВОБОДНАЯ ЭНЕРГИЯ ДЕФОРМИРУЕМОГО ТЕЛА
Для решения задач упругости необходимо установить связь
между компонентами тензора деформаций и напряжений
Необходимо найти явную зависимость свободной энергии от
компонент тензора деформаций.
1.
Рассматриваем лишь малые деформации
ik
1
2. Температура постоянная вдоль всего тела
В силу малости
ik
1
свободную энергию представить в виде степенного ряда
С.Э. – скаляр, значит каждый член разложения тоже скаляр –
инвариант по СК
50. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
Из компонент симметричного тензора можно составить три
независимых скаляра:
а) сумма диагональных элементов (линейный инвариант)
ii относительное изменение объема деформируемого тела
б) сумма парных произведений (квадратичный инвариант)
в) определитель матрицы
ik
ik ik ik
2
(кубический инвариант)
51. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
при упругой деформации после прекращения действия
внешней силы тело возвращается в исходное состояние и все
ik
равны нулю
ik 0
при
ik 0
Тогда в разложении свободной энергии должны отсутствовать
линейные по
члены
в противном случае при
ik
будут не равно нулю, значит нет упругой деформации
в разложении свободной энергии будут лишь квадратичные члены
1 2
2
Fv F0 ii ik ....
2
52. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
,
F0
коэффициенты Ламэ;
свободная энергия недеформированного тела
Любая деформация – это сумма деформация чистого сдвига
( без изменения объема)
и деформации всестороннего сжатия или растяжения
(с изменением объема)
тензор деформации можно записать в виде
1
1
ik ( ik ik ll ) ik ll
3
3
53. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
След тензора в круглых скобках равен нулю, следовательно,
он тензор сдвига.
второй член – тензор всестороннего сжатия или растяжения
выражение для свободной энергии имеет следующий вид:
k 2
1
2
Fv F0 ll ( ik ik ll )
2
3
где
k
k
2 2 3
и
1
( ik ik ll ) ik 0
3
модуль всестороннего сжатия
k,
Всегда больше нуля
Модуль сдвига
Fv F0 0
54. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
Для установления связи между тензором напряжений и
тензором деформаций найдем дифференциал свободной
энергии
1
dFv k ll d ii 2 ( ik ik ll )d ik
3
если записать
d ii d ( ik ik ) ik d ik
1
dFv k ik ll 2 ( ik ik ll ) d ik
3
1
ik k ik ll 2 ( ik ik ll )
3
55. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
Можно получить и обратную связь,
т.е. тензора деформаций через тензор напряжений
след тензора напряжений равен
ii k ii ll 3k ll
1
ll ll
3k
1
2 1
ik ik ll 2 ik ik ll
3
3 3k
тогда получаем закон Гука
1
1
1
ik ik ll
( ik ik ll )
9k
2
3
56. Radiation Safety
RadiationSafety
Biomechanics
ЗАКОН ГУКА
из него следует, что
При всестороннем сжатии
ik p ik
1
1 V
k
V p T
ll 3 p
V
1
ii ll
V
3k
V
p
V
k
Можно записать
- коэффициент всестороннего сжатия
Поскольку изменение свободной энергии есть квадратичный
компонент тензора деформаций применима теорема Эйлера
57. Radiation Safety
RadiationSafety
Biomechanics
Однородная деформация
Деформация называется однородной, если все
компоненты тензора деформаций постоянны по всему
объему тела, не зависят от координат.
Возьмем стержень и закрепим один конец к другому приложим силу
S – площадь поперечного сечения
F
p нормальное к S напряжение
S
на боковую поверхность не действуют внешние силы, это
означает, что поверхностная сила равна нулю. Мы имеем:
i( n ) ik nk
nk
проекция нормали на координатную ось k.
Проекция на ось приложения силы равна нулю
n2 0
F
58. Radiation Safety
RadiationSafety
Biomechanics
ОДНОРОДНАЯ ДЕФОРМАЦИЯ
Тогда компоненты тензора напряжений удовлетворяют следующим уравнениям:
11n1 13 n3 0; Имеет решение при 11 0 33 0 21 12 0
21n1 23n3 0; 0
Отличным от нуля только 22
23
32
31n1 33n3 0;
Из граничного условия на торце стержня
nk
2k nk p
Проекция нормали к торцу стержня на ось
n1 n3 0
n2 1
22 p
xk
59. Radiation Safety
RadiationSafety
Biomechanics
Теперь можно найти компоненты тензора деформаций,
используя закон Гука
Все недиагональные компоненты тензора равны нулю
Отлична от нуля только компонента
Для диагональных компонент тензора деформаций получаем:
1 1
1
11 33 ( ) p
3 2 3k
1 1 1
22 ( ) p
3 3k
60. Radiation Safety
RadiationSafety
Biomechanics
Модуль Юнга и коэффициент Пуассона
компонента
22
определяет относительное удлинение вдоль оси
Обратная величина коэффициента при р
x2
называется модулем Юнга (Е)
9k
E
3k
компоненты
имеет размерность давления.
11 , 33
Относительное сжатие и растяжение
Отношение поперечного сжатия к продольному растяжению
Коэффициент Пуассона
11 1 3k 2
22 2 3k
безразмерен
61. Radiation Safety
RadiationSafety
Biomechanics
поскольку
k 0И
0
коэффициент Пуассона может изменяться от -1,
1
деформация чистого сдвига (к=0) до
при чистой деформации
0
2
коэффициент Пуассона не может принимать отрицательные значения
в природе не известны тела, в которых при растяжении
увеличивались бы их поперечные размеры.
Для реальных тел 0 1
2
коэффициент Пуассона близкий к
1
2
у какого материала?
62. Radiation Safety
RadiationSafety
Biomechanics
резина
модуль сдвига мал
Почему?
модуль сдвига
Через модуль всестороннего сжатия k,
и коэффициент Ламэ
можно записать через модуль Юнга и коэффициент Пуассона
E
E
E
k
,
,
3(1 2 )
2(1 2 )
(1 2 )(1 )
относительное изменение объема стержня при
однородном растяжении равно
изменение свободной энергии единицы объема
V
1p
ii
V
3k
1
1 p2
F ik ik
2
2 E
63. Radiation Safety
RadiationSafety
Biomechanics
Неизотермическое деформирование
Пусть в недеформированном состоянии температура равна T0
Нужно
в тензор деформаций включить линейный член,
который должен исчезать при
T T
0
Проведя все те же рассуждения получим тензор напряжений
при неизотермическом деформировании
1
ik 3 k (T T0 ) ik k ik ll 2 ( ik ik ll )
3
Повторяя вывод закона Гука, для тензора деформаций получим
1
1
1
ik (T T0 ) ik ik ll ( ik ik ll )
9k
2
3
64. Radiation Safety
RadiationSafety
Biomechanics
АДИАБАТИЧЕСКИЕ И ИЗОТЕРМИЧЕСКИЕ МОДУЛИ
При постоянной температуре свободная энергия
деформируемого тела определяется выражением
k 2
1
2
Fv F0 ll ( ik ik ll )
2
3
модули
называют изотермическими модулями
Без теплообмена с внешней средой, т.е. при постоянной энтропии
Т.е адиабатически
Нужно определить модули
k ,
а
a
65. Radiation Safety
RadiationSafety
Biomechanics
АДИАБАТИЧЕСКИЕ И ИЗОТЕРМИЧЕСКИЕ МОДУЛИ
изменение температуры деформируемого тела
при адиабатическом деформировании равно
T T 0
3 kT
C
Удельная теплоемкость
ii
C
v
Подставляя эту разность в уравнение
1
ik 3 k (T T0 ) ik k ik ll 2 ( ik ik ll )
3
1
получим
k a ik ll 2 ( ik ik ll )
ik
3
2
2
k
a
9
k T k
C
Но по определению
v
1 V
(
V p
)
S
k
1
k
a
k
a
C
C
v
p
k
a
k
1 V
(
V p
)
T
1
k
v
66. Radiation Safety
RadiationSafety
Biomechanics
АДИАБАТИЧЕСКИЕ И ИЗОТЕРМИЧЕСКИЕ МОДУЛИ
Установим связь между адиабатическими и
изотермическими модулями всестороннего сжатия
Воспользуемся термодинамическим соотношением
V
V
T V
( ) ( )
(
)
S
T
p
p
p
Cp
получим
1
k
1 9 T
k
Cp
2
a
2
T
Можно провести все рассуждения и получим закон Гука тот
же, что и в изотермическом процессе, но с другим модулем
всестороннего сжатия
67. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ РАВНОВЕСИЯ ИЗОТРОПНЫХ ТЕЛ
Получим уравнение равновесия единицы объема
изотропного деформированного тела.
Результирующая поверхностная сила определяется выражением
F
i
ik
xk
Если i - напряженность объемной силы ,
то условие равновесия в соответствии с первым законом Ньютона
f
ik
xk
f
i
0
Заменив модули сдвига и всестороннего сжатия на
коэффициент Пуассона и модуль Юнга запишем тензор
напряжений при неизотермическом деформировании
68. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ РАВНОВЕСИЯ ИЗОТРОПНЫХ ТЕЛ
E
E
ik 1 2 (T T 0) ik 1 ( ik 1 2 ik ll )
Подставляя это выражение в уравнение равновесия
ik
xk
f
i
0
получим
ll
E T
E ik
E
1 2 x i 1 x k (1 )(1 2 ) x i
Используя определение тензора деформаций
1 u i u k
ik 2 ( x x )
k
i
f
i
0
69. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ РАВНОВЕСИЯ ИЗОТРОПНЫХ ТЕЛ
u
x
2
2
k
1
1 T 2(1 )
u
i
2
1 2 x i x i
1 2 x i
E
2
i
f
i
В векторных обозначениях будет иметь вид
1
1
2(1 )
u
grad (divu ) 2
gradT
f
1 2
1 2
E
Используя соотношение
grad (divu ) u rot (rotu )
1
1 2
1 2
grad (divu )
rot (rotu ) gradT
f
1
2(1 )
E
70. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ
Из теоремы Коши Гельмгольца смещение точки тела равно.
u (r d r ) u (r ) d x d x
i
i
k
ik
ik
Если смещение за малое время, в пределе
.
v v d x
i
0i
k
t 0
.
ik
1 v i v k
ik 2 ( d d )
xk xi
.
k
ik
d xk
1 v i v k
ik 2 ( d x d x )
k
i
.
Это тензор скоростей поворота и скоростей деформации
Если компоненты тензора поворота
ik определяют вектор
поворота на угол то
вектор скорости поворота
71. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ
Нетрудно получить следующие выражения
1
rot v i
2
1 dV
divv
V dt
.
v v 0 d r d v dif
Тогда в векторном виде
Если изменяется температура нужно добавить изменение
температуры от времени
T
t
72. Radiation Safety
RadiationSafety
Biomechanics
ДИФФЕРЕНЦИРОВАНИЕ ПО ВРЕМЕНИ
ИНТЕГРАЛА ПО ПОДВИЖНОМУ ОБЪЕМУ
Индивидуальный объем – объем состоящий из одних и тех
же частиц он может изменять как форму. так и величину
Получим формулу дифференцирования по времени функции по
некоторому изменяющемуся со временем объема
f
( dV f
f (r ,t )dV V t
t V
d
dV )
dt
dV d x1d x 2d x 3
Преобразуем второе слагаемое
v i
d x1
d
d x 2d x 3 ....... d dV divv dV
dV d
xi
dt
dt
df
d
( fdivv )dV
f
(
r
,
t
)
dV
dt
V
dt V
73. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
Уравнение непрерывности – закон сохранения массы любого
индивидуального объема среды
В движущейся среде выделим некоторый объем,
M dV
масса вещества в котором равна
Где плотность вещества
V
Масса вещества с течением времени не изменяется
dM d
dV 0
dt
dt V
Масса вещества с течением времени не изменяется
Используя ранее полученную формулу получим
d
d
(
div
)
dV
divv 0 Уравнение непрерывности
v
V dt
dt
74. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
Если координаты
рассматривать как координаты
i
индивидуальной частицы , тогда плотность зависит
иt
i
полную производную по времени можно записать в виде
x
d
vi
dt
t
xi
x
или
d
v
dt t
Тогда уравнение непрерывности имеет вид
div( v) 0
t
Не будем рассматривать уравнение непрерывности,
если есть источники и стоки
75. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
d
divv 0
dt
или
Первый член в первом
выражении характеризует
скорость изменения массы
движущейся индивидуальной
частицы единичного объема.
div( v) 0
t
А первый член во втором
выражении определяет
изменение массы единицы
объема за единицу
времени в фиксированной
точке пространства.
76. Radiation Safety
RadiationSafety
Biomechanics
ИНТЕГРАЛЬНАЯ И ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА
УРАВНЕНИЯ НЕПРЕРЫВНОСТИ
уравнение непрерывности не изменит свой вид, если под
понимать не массовую плотность среды, а количество
вещества (количество молей или число молекул).
ЭТО ПРИ ОТСУТСВИИ СТОКОВ И ИСТОЧНИКОВ
Если внутри объема есть n источников или стоков мощностью
Q i то уравнение непрерывности в интегральной форме будет
n
dV
vdS
Q
i
t
i 1
V
S
Qi Больше 0 - источники, меньше 0 - стоки
Они быть распределены в пространстве с объемной
плотностью
77. Radiation Safety
RadiationSafety
Biomechanics
ИНТЕГРАЛЬНАЯ И ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА
УРАВНЕНИЯ НЕПРЕРЫВНОСТИ
Тогда уравнение непрерывности имеет вид
t V
dV vdS dV
S
Такая форма записи справедлива при непрерывном
распределении источников и стоков
и уравнение можно записать в дифференциальной форме
Для стационарного случая, когда плотность не меняется в
любой фиксированной точке пространства с течением
времени, но зависит от координат, то 0, и div v 0
t
Для жидкости, плотность не зависит от координат и времени
d
0 div v 0 Объем не изменится в величине в
dt
процессе движения
78. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Это уравнение выражает закон сохранения импульса
сплошной среды.
Рассмотрим некоторый индивидуальный объем V в
движущейся среде со скоростью
v
Импульс единицы объема
П vdV
V
v
Пi vi dV Пусть
Импульс всего объема
F F
(V )
F
(S )
V
- результирующая сила, действующая на индивидуальный объем
Индекс V- объемные, S -поверхностные
Тогда изменение импульса - должно равняться результирующей сил
(V )
(S )
dП
F F
dt
dПi
Fi (V ) Fi ( S )
dt
79. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Преобразуем каждый член в отдельности
Дифференцируя по времени интеграл по подвижному объему
для левой части получим:
dПi
d ( vi )
d
dvi
(
vi divv)dV
vi (
divv) dV
dt V
dt
dt
dt
V
Выражение в круглых скобках – уравнение непрерывности
– и равно нулю
dПi
dvi
dV
dt V dt
80. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Если f напряженность массовых сил, то
FiV fi dV
V
Результирующая поверхностных сил
Собирая все вместе, получим
ik
Fi
dV
xk
V
S
dvi
ik
V ( dt fi xk )dV 0
Это равенство выполняется для любого индивидуального объема
тогда
dvi
ik
fi
dt
xk
81. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ.
dvi
ik
fi
dt
xk
Это второй закон Ньютона для единичного объема среды.
Слева – произведение массы индивидуальной частицы на
ее ускорение.
Справа –результирующая массовых и поверхностных сил.
Зная траектории всех индивидуальных частиц можно
сделать преставление о характере движения сплошной
среды.
Это, так называемое, субстанциональное описание в
представлении Лагранжа.
82. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ.
Было бы достаточным знать, как изменяется со временем
скорость в любой фиксированной точке пространства, через
которую с течением времени будут проходить частицы
среды.
Такое описание называется локальным или
представлением Эйлера
Чтобы совершить переход от Лагранжа к Эйлеру нужно
установить связь между полной и частной производной
dvi vi
vi
vk
dt
t
xk
Первое слагаемое – изменение скорости
среды в фиксированной точке пространства
Второе слагаемое – различие скоростей в различных точках
Пространства в фиксированный момент времени.
83. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ.
Уравнение движения можно записать в следующем виде:
v i
t
vk
v i
xk
1 ik
xk
f
i
Это уравнение движения в представлении Эйлера
Физический смысл будет лучше виден, если взять объем среды
и расписать баланс импульса. (делать не будем)
84. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ МОМЕНТА ИМПУЛЬСА СРЕДЫ
Возьмем частицу в сплошной среде, которая
движется со скоростью v
в какой то системе координат.
Момент импульса этой частицы равен
Момент импульса объема равен:
r v
M r v dV
Момент всех сил действующий на частицу
K K
(V )
K
(S )
тогда
V
(V )
(S )
dM
K K
dt
Левую часть запишем в следующем виде
85. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ МОМЕНТА ИМПУЛЬСА СРЕДЫ
dM d
d d
r v dV rv rv (
divv) dV
dt
dt V
dt
dt
V
Учтем, что
dv
d
тогда
rv vv r
dt dt
dv
dM
r dV
dt
dt
V
dM i
dvi
ikl xk
dV
В компонентах
dt
dt
V
ikl
символ Леви-Чивита
86. Radiation Safety
RadiationSafety
Biomechanics
ikl
УРАВНЕНИЕ МОМЕНТА ИМПУЛЬСА СРЕДЫ
символ Леви-Чивита
Этот символ – антисимметричный тензор третьего ранга:
равен нулю если среди индексов есть хотя бы два одинаковых
1 если упорядоченная система индексов получается четным
числом перестановок
-1 если упорядоченная система индексов получается нечетным
числом перестановок
С помощью этого символа проекции векторного произведения
можно записать в следующем виде:
ab ikl ak bl
i
а
Al
roti A A ikl
i
xk
а i-компонента ротора в следующем виде
87. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР ПЛОТНОСТИ ПОТОКА ИМПУЛЬСА
Пусть поток i-компоненты импульса через единичную площадку
перпендикулярную оси k. Тогда можно записать
vi dV Пik dSk
dt V
S
можно получить
Пik vi vk ik
А уравнение движения записать в виде
vi
Пik
fi
t
xk
Изменение импульса единицы объема среды в точке
пространства происходит как вследствие импульса от
соседних частей, так действия внешних массовых сил
88. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ СОХРАНЕНИЯ ВНУТРЕННЕЙ ЭНЕРГИИ
Для индивидуального единичного объема справедливо
термодинамическое равенство
dEvn dQv ik ik
Внутренняя энергия единицы массы
Evn v
v
Второе слагаемое – содержит тензор скоростей деформаций
и может быть записано в следующем виде
vi
1 vi vk
ik (
) ik
2 xk xi
xk
/
ik ik
89. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ СОХРАНЕНИЯ ВНУТРЕННЕЙ ЭНЕРГИИ
Учтена симметрия тензора напряжений и определяет работу
внутренних напряжений в единицу времени в единице объема
Изменение за единицу времени внутренней энергии некоторого
индивидуального объема d
d
E
dt
vn
dV
V
dt
vn
dV
V
Проводя дифференцирование по времени и учитывая уравнение
непрерывности получим d
d vn
d
Evn dV
dV
dt V
dt V
dt
работа внутренних напряжений в единицу времени во всем
объеме
vi
V ik ik dV V ik xk dV
90. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ СОХРАНЕНИЯ ВНУТРЕННЕЙ ЭНЕРГИИ
Если внутри объема нет источников или стоков тепла, то тепло
может поступать только через его поверхность.
Пусть вектор плотности теплового потока будет
величина
характеризует энергию, переносимую за
единицу времени через единичную площадку с
нормалью
за счет теплопроводности среды
q
nq
n
d
QV dV qd S divqdV
S
dt V
V
Таким образом скорость изменения внутренней энергии
индивидуального объема равна ( d vn divq vi )dV 0
ik
V
dt
xk
91. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ СОХРАНЕНИЯ ВНУТРЕННЕЙ ЭНЕРГИИ
d vn
vi
V ( dt divq ik xk )dV 0
Подынтегральное выражение равно нулю и
с учетом непрерывности в представлении Эйлера
В представлении Эйлера
vni
vi
(
v vn ) divq ik
t
xk
Внутренняя энергия единицы объема изменяется вследствие
притока тепла и работы внутренних напряжений
При равномерном сжатии термодинамическое
соотношение имеет вид
1
d vn TdS pdV TdS pd ( )
92. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ СОХРАНЕНИЯ ВНУТРЕННЕЙ ЭНЕРГИИ
тогда уравнение внутренней энергии будет иметь вид:
dS
d 1
T
p ( ) divq pdivv
dt
dt
с учетом непрерывности в представлении Эйлера
S
T ( v S ) divq
t
Очевидно, что уравнение
vni
vi
(
v vn ) divq ik
t
xk
Справедливо для любой деформации
93. Radiation Safety
RadiationSafety
Biomechanics
ВЕКТОР УМОВА
Вектор Умова – вектор плотности потока полной энергии.
Пусть E и ε – полная энергия единицы объема и единицы
массы сплошной среды. Тогда можно записать:
E ( vn kin pot )
Баланс полной энергии вещества в этом объеме при отсутствии
источников и стоков энергии можно записать в виде уравнения
непрерывности
EdV Id S
t V
S
I dS
k
S
k
S – поверхность объема и I – вектор Умова, который
характеризует полную энергию которая переносится за
единицу времени через единичную площадку
перпендикулярную оси k.
94. Radiation Safety
RadiationSafety
Biomechanics
с другой стороны
ВЕКТОР УМОВА
vn kin pot
EdV
(
) dV
t V
t
t
t
t
V
pot
Полагаем, что потенциальная энергия не меняется
t
0
скорость изменения внутренней энергии определяется уравнением
vn
vn qk
vi
vk
ik
t
t
xk
xk
Кинетическая энергия единицы массы
сплошной среды, движущейся со скоростью
v
kin
v 2 vi vi
2
2
95. Radiation Safety
RadiationSafety
Biomechanics
ВЕКТОР УМОВА
изменение кинетической энергии за единицу времени
Определяется законом сохранения импульса
kin
vi
vi 1 ik
vi
vi ( vk
fi )
t
t
xk xk
известно, что сила, действующая на единицу массы сплошной
среды во внешнем поле, связана с градиентом потенциальной
энергии
vi
kin
vi vi
pot
vi
( )
и учтем, что
fi
xk xk 2
xk
xi
получим
EdV
(q k vk vi ik )dV
t V
xk
V
Применяя к правой части теорему Гаусса-Остроградского
96. Radiation Safety
RadiationSafety
Biomechanics
ВЕКТОР УМОВА
имеем
EdV (q v k v i ik )d S k
k
t V
S
Подынтегральное выражение – это компонент вектора Умова и
можно записать в векторном виде
I q v v ,(v ) vi ik
где
v
q вектор плотности потока тепла (зависит от
градиента температуры в изотропной среде)
Описывает перенос полной энергии самой
движущейся средой
97. Radiation Safety
RadiationSafety
Biomechanics
ВЕКТОР УМОВА
(v
Вектор плотности потока энергии, связанный с работой
)k внутренних напряжений в единице объема среды.
Он существует в движущейся среде, но его
направление не совпадает с направлением движения.
Можно получить уравнение сохранения полной энергии для
единицы объема среды которое имеет тот же вид, что и
уравнение непрерывности
divI 0
t
В таком общем виде уравнение сохранения полной энергии для
единицы объема среды применяется крайне редко
проще рассматривать различные виды энергии в отдельности
98. Radiation Safety
RadiationSafety
Biomechanics
ЗАМКНУТАЯ СИСТЕМА УРАВНЕНИЙ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Запишем все уравнения, которые мы рассмотрели:
1. Уравнение непрерывности
2. Уравнение движения
div( v) 0
t
vi
vi
1 ik
vk
fi
t
xk
xk
3. Уравнение сохранения внутренней энергии
vni
vi
(
v vn ) divq ik
t
xk
Чтобы подсчитать количество независимых физических величин
в этих уравнениях запишем связь между компонентами тензора
напряжений, тензора деформаций и вектора смещений
99. Radiation Safety
RadiationSafety
Biomechanics
ЗАМКНУТАЯ СИСТЕМА УРАВНЕНИЙ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
1
ik 3 kT (T T0 ) ik k ik ll 2 ( ik ik ll )
3
dui
1 ui uk
ik (
), vi
2 xk xi
dt
Пять скалярных уравнений содержат восемь независимых
физических величин
, ui , vn , qi .......i 1, 2,3
система не замкнута !!!!
100. Radiation Safety
RadiationSafety
Biomechanics
ЗАМКНУТАЯ СИСТЕМА УРАВНЕНИЙ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Необходимы дополнительные уравнения:
6. Термическое уравнение состояния
Устанавливает связь между давлением, плотностью и
температурой
Для одного моля идеального газа
p p( , T )
p RT
где
R
Газовая постоянная
7. Калорическое уравнение состояния
Устанавливает связь между внутренней энергией, давлением и
температурой
vn vn ( p, T )
101. Radiation Safety
RadiationSafety
Biomechanics
ЗАМКНУТАЯ СИСТЕМА УРАВНЕНИЙ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Закон теплопроводности Фурье устанавливает линейную
зависимость плотности теплового потока от градиента
температуры среды
T
q T ,......qi
xi
- коэффициент теплопроводности вещества среды
Теперь система замкнута
Нужно доказать теорему существования и краевые условия
102. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ ИЗОТРОПНЫХ СРЕД
уравнение теплопроводности принято называть ДУ, описывающее
скорость изменения температуры в любой фиксированной точке
среды и пространственную неоднородность температуры в любой
фиксированный момент времени.
Получим из уравнения сохранения внутренней энергии
Возьмем изотропную среду
divq div( T )
из закона Фурье
103. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ ИЗОТРОПНЫХ СРЕД
d вн dQм 1
dvi
ik
dt
dt
dxk
индекс м – рассматриваем единицу массы среды
dQм dQм dT
dT
c
dt
dT dt
dt
где с – удельная теплоемкость
для покоящейся среды v 0
T
T
t
T
c ( v T ) div( T )
t
c
имеем
-коэффициент температуропроводности
104. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР ВЯЗКИХ НАПРЯЖЕНИЙ
Ньютон рассматривал движение пластинки по поверхности
записал
жидкости
Сила сопротивления жидкости тогда, когда есть
нормальный пластинке градиент скорости движения жидкости
12
vi
12
x2
- сила
- коэффициент сдвиговой вязкости
При деформации могут возникать напряжения,
пропорциональные не самой деформации,
а скорости деформации
По аналогии с тензором упругих напряжений ввести тензор,
зависящий от скорости деформации
105. Radiation Safety
RadiationSafety
Biomechanics
ТЕНЗОР ВЯЗКИХ НАПРЯЖЕНИЙ
1
ik ik ll 2 ( ik ik ll )
3
где
ik
- тензор вязких напряжений
- коэффициент сдвиговой вязкости
- коэффициент объемной вязкости
vi
vi vk 2 vl
ik ik
(
ik
)
xk
xk xi 3 xl
Линейная зависимость тензора вязких напряжений от тензора
скоростей деформации называется законом Навье-Стокса
106. Radiation Safety
RadiationSafety
Biomechanics
МОДЕЛИ СПЛОШНЫХ СРЕД
В общем случае движения сплошной среды в ней должны
складываться упругие и вязкие напряжения
Тензор напряжений будет иметь вид
P
ik
ik
ik 3 k (T T 0) ik
v l
v i v k 2
v l
1
k ik ll 2 ( ik ik ll ) ik
(
ik
)
3
xl
xk xi 3
xl
Среда с кинематической точки зрения характеризуется
пятью коэффициентами
Твердое тело
Деформация подчиняется закону Гука, нет вязких напряжений
k 0, 0, 0, 0
107. Radiation Safety
RadiationSafety
Biomechanics
МОДЕЛИ СПЛОШНЫХ СРЕД
Эти задачи составляют предмет теории упругости: растяжение,
изгиб, кручение стержней, пластинок, оболочек …….
Вторая особенность, твердое тело может быть подвергнуто,
0
как сжатию, так и растяжению
ll
Относительные изменение объема при деформации мало
Если возникает необходимость в учете вязкостных свойств
твердого тела. То нужно сохранить в общем тензоре
напряжений члены, зависящие от скоростей деформации.
Это - предмет науки реологии, которая включает такие
разделы. Как теории пластичности и ползучести.
Деформирование за пределами упругости – прокатка,
штамповка …..)
ll
1
108. Radiation Safety
RadiationSafety
Biomechanics
МОДЕЛИ СПЛОШНЫХ СРЕД
ЖИДКОСТЬ
Характерное свойство жидкости – легкое изменение ее формы
Наклоняя сосуд наблюдаем изменение формы
Среда имеет малый модуль сдвига или равен нулю
следовательно
k 0, 0, 0, 0
Жидкость может быть только сжата
Относительные изменение объема при деформации мало
ll
В большинстве задач полагают
1
ll
0
109. Radiation Safety
RadiationSafety
Biomechanics
МОДЕЛИ СПЛОШНЫХ СРЕД
ГАЗ
Газы, как и жидкости легко изменяют свою форму
Среда имеет малый модуль сдвига или равен нулю
k 0, 0, 0, 0
В отличии от жидкости газы принципиально не могут быть
0
растянуты
ll
Газы сильно изменяют свой объема при изменении давления
ll
1
Для газов и жидкостей при неизменной температуре
Тензор упругих напряжений имеет вид
V
p
ik k ik ll , ll
, ik p ik
V
k
110. Radiation Safety
RadiationSafety
Biomechanics
МОДЕЛИ СПЛОШНЫХ СРЕД
Релаксация напряжений
Деление на твердые тела и жидкости весьма условно
Все зависит от времени действия внешних сил и времени
релаксации внутренних напряжений
После снятия внешних сил и релаксации внутренних
напряжений среда не возвращается в исходное состояние
Среда ведет себя как твердое тело (удар о воду)
p
vn
После снятия внешних сил и релаксации внутренних
напряжений среда не возвращается в исходное
состояние
Рассматривается как маловязкая жидкость, или Ньютоновская
жидкость
p
vn
111. Radiation Safety
RadiationSafety
Biomechanics
МОДЕЛИ СПЛОШНЫХ СРЕД
Релаксация напряжений
Например, битум или смола при быстром воздействии внешней
силы ведут себя. Как твердое тело ( рассыпаются при ударе), а
при длительном действии внешних сил растекаются по
поверхности или принимают форму сосуда – жидкость.
Ползучесть - для твердых тел
Полный тензор напряжений для ньютоновских жидкостей и
газов имеет вид
vi
vi vk 2 vl
Pik p ik ik
(
ik
)
xk
xk xi 3 xl
v l
xl
112. Radiation Safety
RadiationSafety
Biomechanics
УПРУГИЕ ВОЛНЫ
Запишем уравнение движения упругой (невязкой) среды
при отсутствии массовых сил
vi
vi 1 ik
vk
t
xk xk
Будем полагать, что скорости частиц среды, малы по
сравнению самого волнового процесса. Поэтому можно
пренебречь вторым слагаемым левой части.
Рассмотрим плоскую волну, при распространении
которой деформации точек среды зависят только от
одной координаты x1 и времени t.
u u ( x1 , t )
dui
vi
dt
113. Radiation Safety
RadiationSafety
Biomechanics
УПРУГИЕ ВОЛНЫ
Тогда уравнение движения для проекции деформации на ось
x1
ui 1 ik
2
t
xk
2
Выражение для тензора упругих напряжений можно записать
ul
ui uk 2 ul
ik k ik
(
ik
)
xl
xk xi 3 xl
114. Radiation Safety
RadiationSafety
Biomechanics
УПРУГИЕ ВОЛНЫ
u1
2 u1
cl
2
2
t
x1
2
получим
2
4
E (1 )
где c (k )
3
(1 )(1 2 )
Для проекции деформации на оси x2, x3, получим
2
l
1
2
2 u2
u2
2
ct
2
t
x12
E
c
2 (1 )
2
2u3
u3 где
2
ct
2
t
x12
2
t
cl- скорость
Волна представляет две независимые волны:
распространения продольной волны и
- скорость
t
распространение поперечной волны.
c
115. Radiation Safety
RadiationSafety
Biomechanics
УПРУГИЕ ВОЛНЫ
Поперечные волны при прохождении через частицы среды не
изменяют их объем и поэтому называются сдвиговыми волнами
V
divu 0
V
прохождении продольной волны сопровождается адиабатическим
изменением объема и поэтому, это волна сжатия.
Если
u3 u2 0
V u1
0
V
x1
cl
2(1 )
Отношение скоростей распространения волн равно ct
1 2
1
Поскольку коэффициент Пуассона изменяется от 0
2
то отношение скоростей
c
2
l
ct
,
116. Radiation Safety
RadiationSafety
Biomechanics
УПРУГИЕ ВОЛНЫ
Используется в сейсмологии. Пусть две станции приняли сигналы
от продольной волны, а затем поперечной . Пусть промежуток
времени между сигналами на первой станции t
1
Времена прохождения продольной и поперечной волн равны:
l1
tl1
cl
l1
tl1
ct
Измеряемый промежуток времени между сигналами равен
1 1 Определяем расстояние от первой станции
t1 l1 ( )
ct cl
t2ct cl
t1ct cl
Тоже делаем для второй станции l2 c c
l1
l
t
cl ct
Проводя окружности вокруг станций, найдем их пересечение и
найдем точку откуда пришел сигнал. Будет две точки
пересечения, нужна третья станция
117. Radiation Safety
RadiationSafety
Biomechanics
ГИДРОДИНАМИКА
Гидродинамика – раздел механики сплошной среды, в котором
изучается движение жидкостей и газов со скоростями меньше
скорости звука. Это значит, что они несжимаемые.
Идеальная жидкость – не обладает диссипативными свойствами
– лишена вязкости и теплопроводности.
УРАВНЕНИЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
При изотермическом движении идеальной жидкости, тензор
напряжений определяется только гидродинамическим
давлением
и имеет вид:
p
Pik p ik
118. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
Уравнение движения будет иметь следующий вид:
vi
vi
1 p
vk
fi
t
t
xi
это уравнение Эйлера
Уравнение непрерывности будет иметь следующий вид:
div( v) 0
t
Уравнение для внутренней энергии:
получаем
S
0
t
S
( v S ) 0
t
119. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
Уравнение для внутренней энергии единицы массы
жидкости будет иметь следующий вид:
(
вн
t
v вн ) pdivv
S
T ( v S ) 0 Где S- энтропия жидкости
t
энтропия единицы массы идеальной жидкости сохраняется в
процессе движения
dS
0
dt
Тепло не покидает и не попадает из вне .
Полагая равной нулю вязкость, мы устраняем источник
возрастания энтропии
120. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
Система уравнений движения идеальной жидкости это
следующие уравнения:
vi
vi
1 p
vk
fi
t
t
xi
(
вн
t
вн
f ( p, )
v вн ) pdivv
div( v) 0
t
S
T ( v S ) 0
t
Если внешние силы заданы, то неизвестных шесть
v , p, ,
i
Для замыкания системы уравнений нужно добавить
калорическое уравнение, зависимость внутренней энергии от
давления и температуры
f ( p, )
вн
вн
121. Radiation Safety
RadiationSafety
Biomechanics
ИЗЭНТРОПИЧЕСКОЕ ДВИЖЕНИЕ
Рассмотрим случай, когда энтропия не изменяется с течением
времени и одинакова во всех точках текущей жидкости
S S0 const
В этом случае нужны только два первых уравнения
И уравнению движения можно придать другой вид:
Воспользуемся термодинамическими соотношениями
энтальпия равна
поскольку
h
1
h вн pV dh
dS 0
1
dp TdS
То мы имеем dh 1 dp
p Если поле внешних сил потенциально т.е.
f вн
122. Radiation Safety
RadiationSafety
Biomechanics
ИЗЭНТРОПИЧЕСКОЕ ДВИЖЕНИЕ
Уравнение движения имеет вид
v
v v (h пот )
t
Воспользуемся формулой векторного анализа
1 2
v v v v, rotv
2
v
v2
v, rotv ( h пот )
t
2
получим
Взяв rot от обеих частей уравнения получим
rotv rot v, rotv
t
Уравнение Эйлера в форме Громека
123. Radiation Safety
RadiationSafety
Biomechanics
ИЗЭНТРОПИЧЕСКОЕ ДВИЖЕНИЕ
в уравнении присутствуют, только скорости – при заданных
граничных условиях есть решение и оно единственное.
Это кинематика!!
Для отыскания других переменных характеристик течения,
зная скорость вернутся к исходной форме уравнений.
Плотность можно найти - из уравнения непрерывности
Давление – из уравнения движения
1
Если ввести аксиальный вектор rotv
Называемый
2 – обычный вектор
вихревой скоростью, Полярный вектор
уравнение Громека
rot v,
t
(аксиальный вектор, или псевдовектор меняет свое направление
при переходе от правой системы координат к левой (отражение))
124. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ БЕРНУЛЛИ
Движение жидкости, при котором во всем пространстве,
занятом движущейся жидкостью, rotv 0 ,
называется потенциальным
Рассмотрим стационарное движение идеальной жидкости, т.е.
v
0
t
пусть оно будет изоэнтрапическим, тогда будем иметь
v2
0 ( h пот )
2
v2
h пот const
И оно будет выполняться при условии, что
2
это и есть уравнение Бернулли
125. Radiation Safety
RadiationSafety
Biomechanics
УРАВНЕНИЕ БЕРНУЛЛИ
Очевидно, что есть уравнение сохранения полной энергии
единицы массы жидкости
Первое слагаемое – кинетическая энергия, второе –внутренняя
энергия плюс работа сил давления и третье –потенциальная
энергия единицы массы жидкости.
Для несжимаемой жидкости (
const )
p
dh dp d
1
Рассмотрим движение идеальной жидкости в поле силы тяжести
пот gz, f пот , f g
2
v
p
gz const
2
126. Radiation Safety
RadiationSafety
Biomechanics
ЛИНИИ ТОКА. ТРАЕКТОРИИ. ТРУБКИ ТОКА.
Линия тока – это линия. Касательная к которой дает направление
скорости движения жидкости в точке касания в данный момент.
Траектория –это воображаемая линия. Описываемая
индивидуальной частицей жидкости при движении
Если в жидкости взять некоторый замкнутый объем и через все
его точки провести линии тока, то они составят трубку тока.
Можно показать что для каждой линии тока выполняется
уравнение Бернулли.
127. Radiation Safety
RadiationSafety
Biomechanics
ЛИНИИ ТОКА. ТРАЕКТОРИИ. ТРУБКИ ТОКА.
Получить уравнение Бернулли можно всегда, когда нам
удается выразить
p
P
Функция Р называется баротропным потенциалом
Для баротропных движений уравнение Бернулли имеет вид:
Ряд примеров:
v2
P пот const
2
Скорость истечения идеальной несжимаемой жидкости из сосуда
Рассмотрим пример истечения из отверстия в боковой стенке
128. Radiation Safety
RadiationSafety
Biomechanics
Проведем гипотетическую линию тока и выберем две точки на
ней –одну на поверхности жидкости в сосуде (1), вторую внутри
отверстия (2) тогда для этой линии, можно записать уравнение
Бернулли
v12 p0
v22 p0
gz1 gz2
2
2
где p0 атмосферное давление, а скорость
на поверхности равна нулю, тогда
v2 2 gH
что это Вам напоминает?
Такую скорость приобретает тело, падающее в пустоте с высоты Н
129. Radiation Safety
RadiationSafety
Biomechanics
РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ В ТУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
Труба располагается горизонтально, силой тяжести
пренебрегаем. Выбираем линию тока. Выбираем на ней две
точки. Жидкость несжимаемая, тогда
2
1
2
2
v
p1 v
p2
2
2
Там где скорость больше гидростатическое давление меньше и
наоборот.
Непрерывность движения жидкости требует выполнения условия:
Почему судам идущим параллельным
v1S1 v2 S2
курсом запрещается сближаться?
Давление воды между судами будет меньше, чем давление
на противоположный борт.
130. Radiation Safety
RadiationSafety
Biomechanics
КАВИТАЦИЯ
Если увеличить скорость движения в трубе и уменьшить самое
узкое сечение трубы, то можно в этом сечении получить
отрицательное давление!!! Действительно:
2
1
2
max
v
p1 v
pmin
2
2
С учетом непрерывности получим
pmin p1
v
2
max
2
v1S1 vmax Smin
2
min
2
1
S
(1
)
S
Если второй член по модулю будет больше p , т.е. частицы
1
жидкости проходящие сечение трубы с отрицательным
давлением, будут подвергаться растяжению.
131. Radiation Safety
RadiationSafety
Biomechanics
КАВИТАЦИЯ
p1 , т.е. частицы
Если второй член по модулю будет больше
жидкости проходящие сечение трубы с отрицательным
давлением, будут подвергаться растяжению.
Жидкость не может находиться в растянутом состоянии
длительное время, она или вскипит, или в ней появятся
пузырьки газа.
Так или иначе в жидкости выделяются пузырьки,
заполненные паром жидкости или газом.
Возникает нарушение неразрывности жидкости, так
называемая кавитация.
Самостоятельно рассмотрите трубку Пито.
132. Radiation Safety
RadiationSafety
Biomechanics
ТРУБКА ПИТО
При обтекании тупого твердого тела идеальной жидкостью на
нем всегда можно указать точку, в которой скорость жидкости
равна нулю.
Для соответствующей линии тока можно записать уравнение
Бернулли
2( p p )
2
0
p
p
v 0 получим v
2
Можно использовать для измерения скорости движения
жидкости или скорости движения тела в неподвижной
несжимаемой жидкости. Это трубка Пито ( или Прандтля)
Разность давлений p 0 p уравновешивается давлением
столба манометрической жидкости gh
2 gh
ж
v
ж
133. Radiation Safety
RadiationSafety
Biomechanics
ТРУБКА ПИТО
В результате длительного экспериментального и теоретического
изучения в настоящее время выработан стандарт, гарантирующий
процентную точность в оптимальном диапазоне измерений.
Как видно из рисунка, давление в отверстии на боковой
поверхности трубки будет равно давлению вдали от трубки в
невозмущенном потоке лишь на расстоянии 3d от носика
трубки. Причины будут понятны при последующем изучении
движений идеальной жидкости.
Так измеряют скорость полета самолета
134. Radiation Safety
RadiationSafety
Biomechanics
СЖИМАЕМОСТЬ СРЕДЫ
Приближение несжимаемой жидкости упрощает решение задач
гидродинамики. Оно выполняется с высокой точностью для
капельных жидкостей ввиду малых изменений плотности при
значительных изменениях давления. Так вода по одной до двух
атмосфер уменьшает в закрытом объеме свой объем в
отношении 1: 20000. Для газов вызывает уменьшение объема 1:2
( закон Бойля-Мариотта.)
Если бы изменение давления газа, вызываемое движущимся
телом, привело к изменению плотности, то в газе возник бы
волновой процесс , выравнивающий плотность газа по всему
объему со скоростью звука. Поэтому при скорости меньшей
скорости звука не успевает изменяться. При скоростях
приближающихся к скорости звука изменение давления
заметно изменяет плотность газа.
135. Radiation Safety
RadiationSafety
Biomechanics
СЖИМАЕМОСТЬ СРЕДЫ
Если жидкость не сжимаема, то давление в критической точке
2
равно
v
p
0
p
2
const
p p
v v
2 h
2 h
0
Для сжимаемой жидкости.
2
2
0
0
Для адиабатического процесса, записывая уравнение
Бернулли можно получить скорость распространения
продольных волн сжатия равную
p
2
2
2 p
p
const
( )
cl
c
l
V
V
s
V
Скорость звука – волна сжатия-растяжения
136. Radiation Safety
RadiationSafety
Biomechanics
СЖИМАЕМОСТЬ СРЕДЫ
Если соотношение 1
4
v
p
2
И его можно записать в виде
То жидкость не сжимаемая
1
2
v
4c
2
1
l
Если скорость движения жидкости значительно меньше
скорости звука в ней, то ее можно рассматривать как не
сжимаемую жидкость.
например если воздух движется со скоростью 70 м в секунду,
то поправка в давлению в критической точке будет меньше
процента.
137. Radiation Safety
RadiationSafety
Biomechanics
ВИХРЕВОЕ ДВИЖЕНИЕ
Движение жидкости, при котором ее индивидуальные частицы
перемещаются не только поступательно, но и вращаются около
некоторой мгновенной оси, проходящей через эти частицы,
называют вихревым. Это не потенциальное движение жидкости.
Вихревая скорость равна:
W vd r
l
rotvd S 2 d S const
(S )
(S )
Скорость движения идеальной жидкости на поверхности
обтекаемого тела может претерпевать разрыв, что означает
появление вихревого движения
138. Radiation Safety
RadiationSafety
Biomechanics
ВИХРЕВОЕ ДВИЖЕНИЕ
Вихревое движение интересно наблюдать в вихревых кольцах.
Чаще всего их демонстрируют с помощью ящика у которого в
передней стенке есть отверстие, а задняя стенка гибкая.
Ящик наполняют дымом и ударяют рукой по задней стенке.
Кольца могут притягиваться друг к другу, отталкиваться и так далее.
С течение времени вихри затухают вследствие вязкости любой
среды и энергия вихревого процесса переходит в тепло..
139. Radiation Safety
RadiationSafety
Biomechanics
ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ
Потенциальное – без вихревое. Каждая частица перемещается
поступательно, т.е.
rotv 0
v , vx
, vy
, vz
x
y
z
rotv rot 0
Для потенциального движения циркуляция по любому
замкнутому контуру равна нулю
Для баротропного потенциального нестационарного движения
уравнение Эйлера записывается в следующем виде
2
v
v,rotv ( v P пот)
t
2
140. Radiation Safety
RadiationSafety
Biomechanics
ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ
v
P пот const f (t )
t 2
2
тогда
Поскольку нам нужна скорость, а она определяется производными
от потенциала по координатам, то любая функция по времени не
изменит потенциала после замены . f (t ) dt
Получим в правой части 0
Можно положить
f (t ) 0
Это уравнение Бернулли для нестационарного движения
идеальной жидкости.
0, а
Для стационарного движения идеальной жидкости
t
это уравнение Бернулли с постоянной правой частью
независящей ни от координат, ни от времени.
141. Radiation Safety
RadiationSafety
Biomechanics
ИДЕАЛЬНАЯ НЕСЖИМАЕМАЯ ЖИДКОСТЬ
Для идеальной несжимаемой жидкости потенциал скорости
должен удовлетворять уравнению Лапласа
divv 0, v , div 0
При потенциальном движении несжимаемой жидкости нам
необходимо найти только одну скалярную функцию.
При потенциальном движении сжимаемой жидкости нам
необходимо учесть, что потенциал будет функцией не
только координат, но и времени. Это делают через
граничные условия в виде.
vn nv n
un
n
142. Radiation Safety
RadiationSafety
Biomechanics
ФУНКЦИЯ ТОКА
Рассмотрим плоское движение. Зависит только от двух
координат и во всех плоскостях параллельных рассматриваемой
характеристики одинаковые.
Для удобства ввели функцию тока
следующими уравнениями
в соответствии со
vx
, vy
y
x
При потенциальном движении должна удовлетворят
двумерному уравнению Лапласа т.е. функция движения тока
должна быть гармонической
v y
vx
rot z v
0
x y
0 0
x x y y
143. Radiation Safety
RadiationSafety
Biomechanics
СВОЙСТВА ФУНКЦИИ ТОКА
Функция тока обладает рядом свойств:
1. Линии тока – это линии, удовлетворяющие уравнению
const
Из уравнения линии тока имеем
dx
dy
v dx v dy 0
y
x
v v
d 0 const
x
y
dx
dy 0
x
y
2. Если на плоскости между двумя точками на двух различных
линиях тока провести произвольную кривую, то поток жидкости
через эту кривую ( масса жидкости в единицу времени) будет
определяться разностью значений функции тока в этих точках.
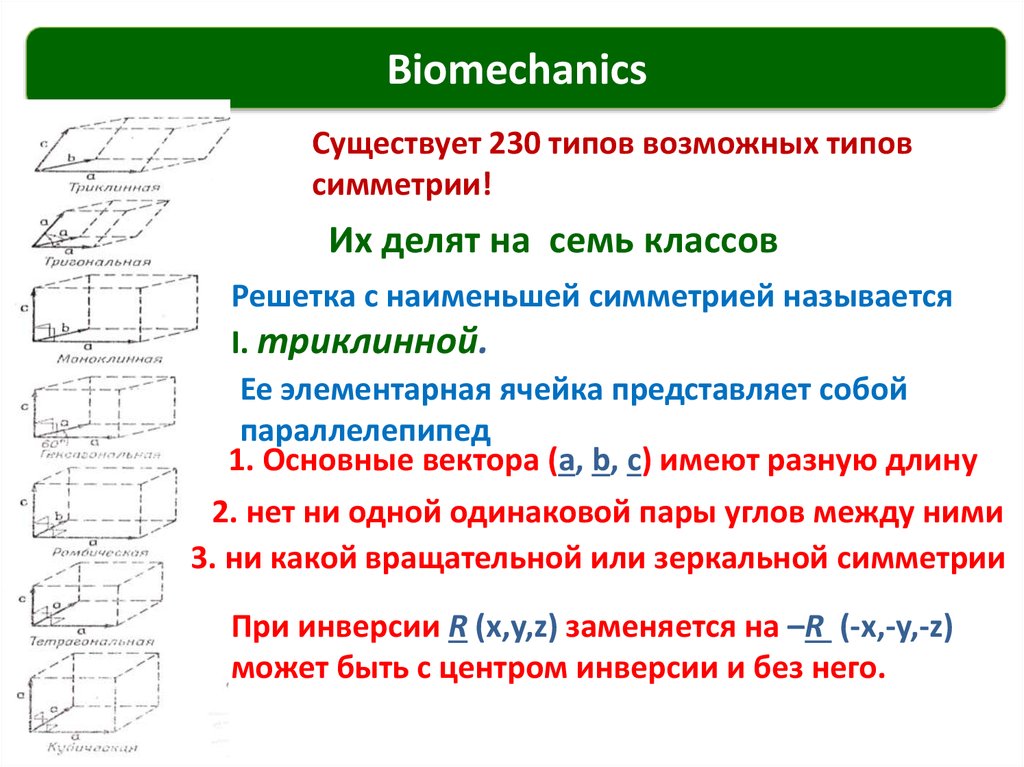
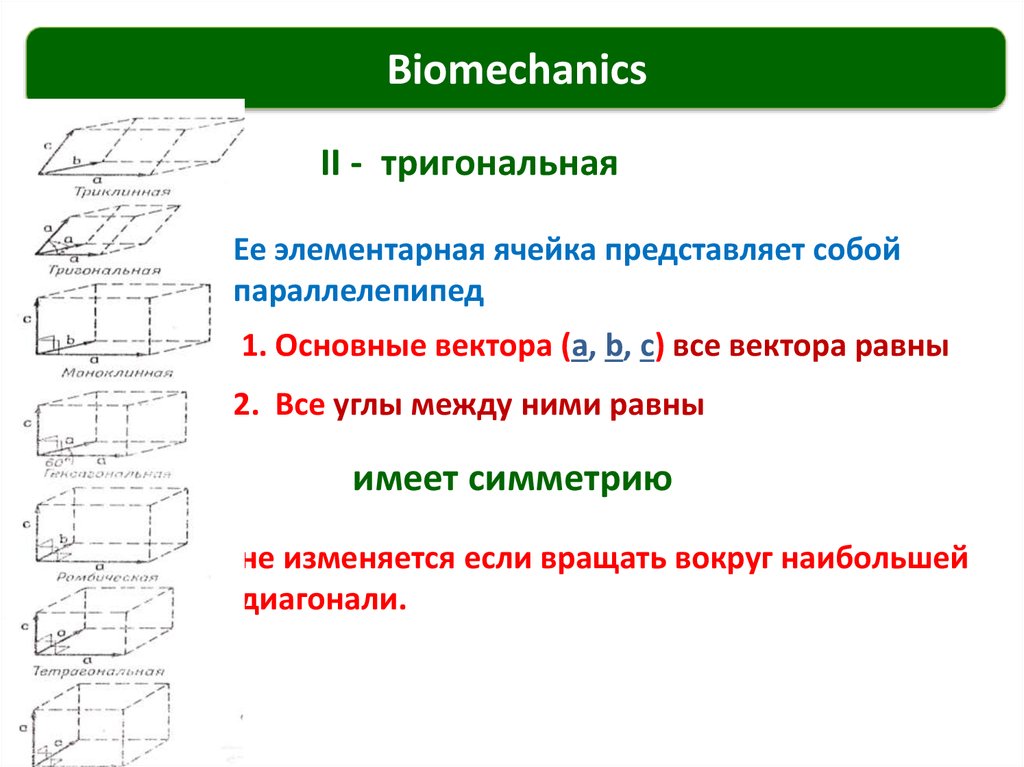






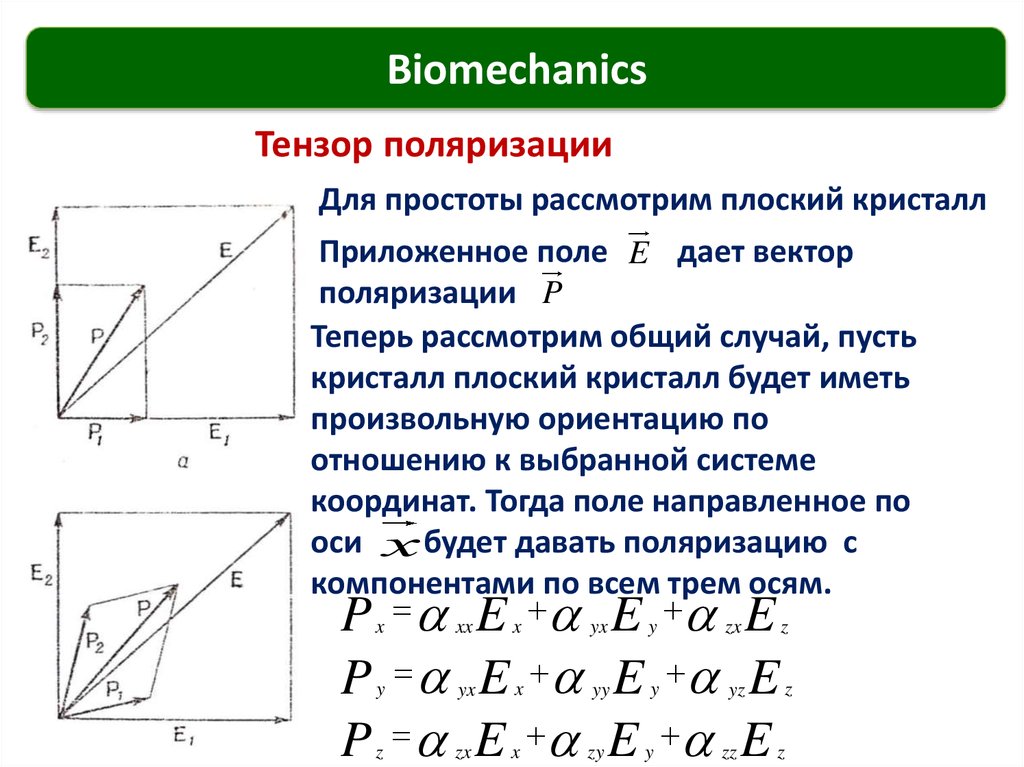










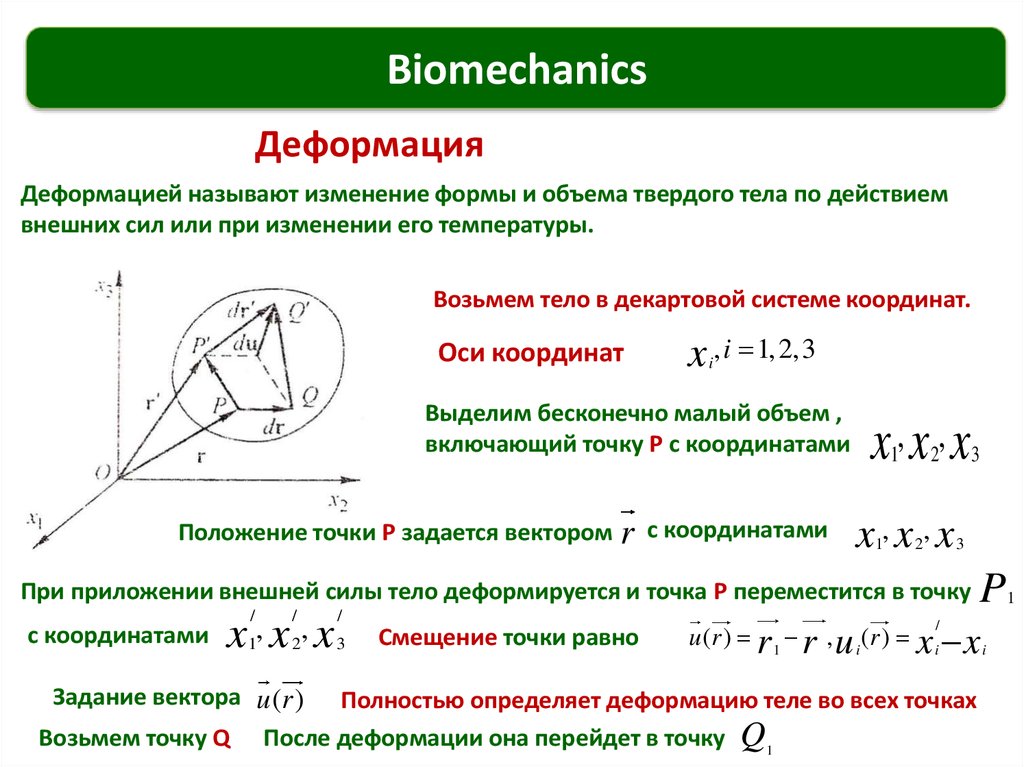





























































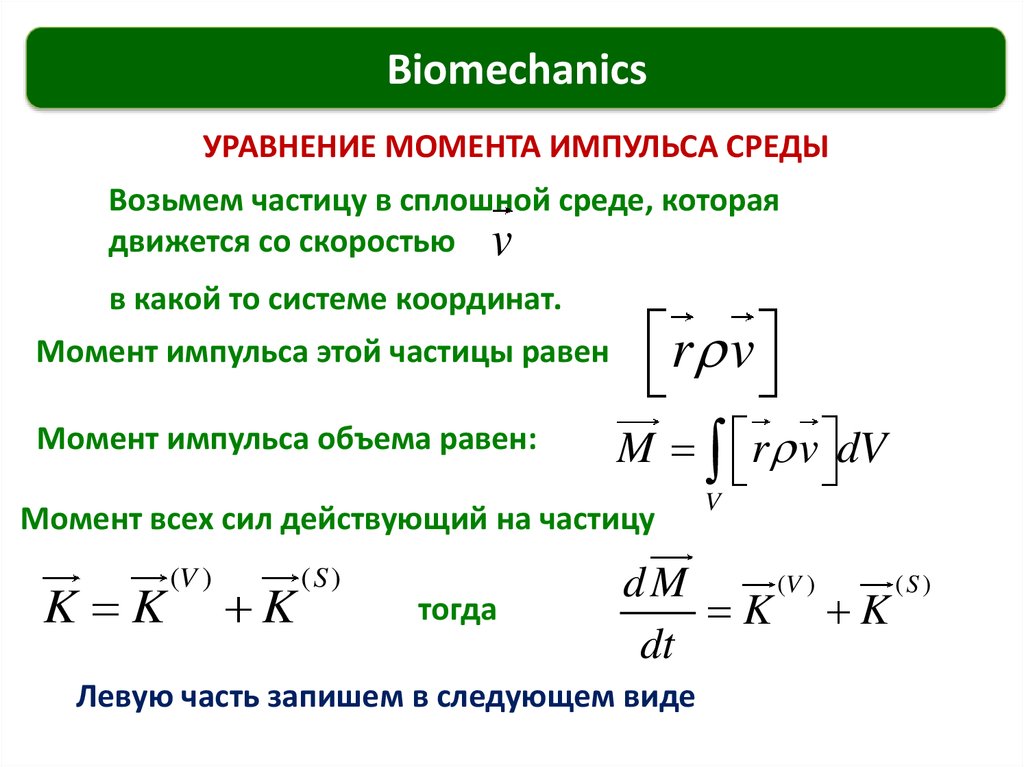
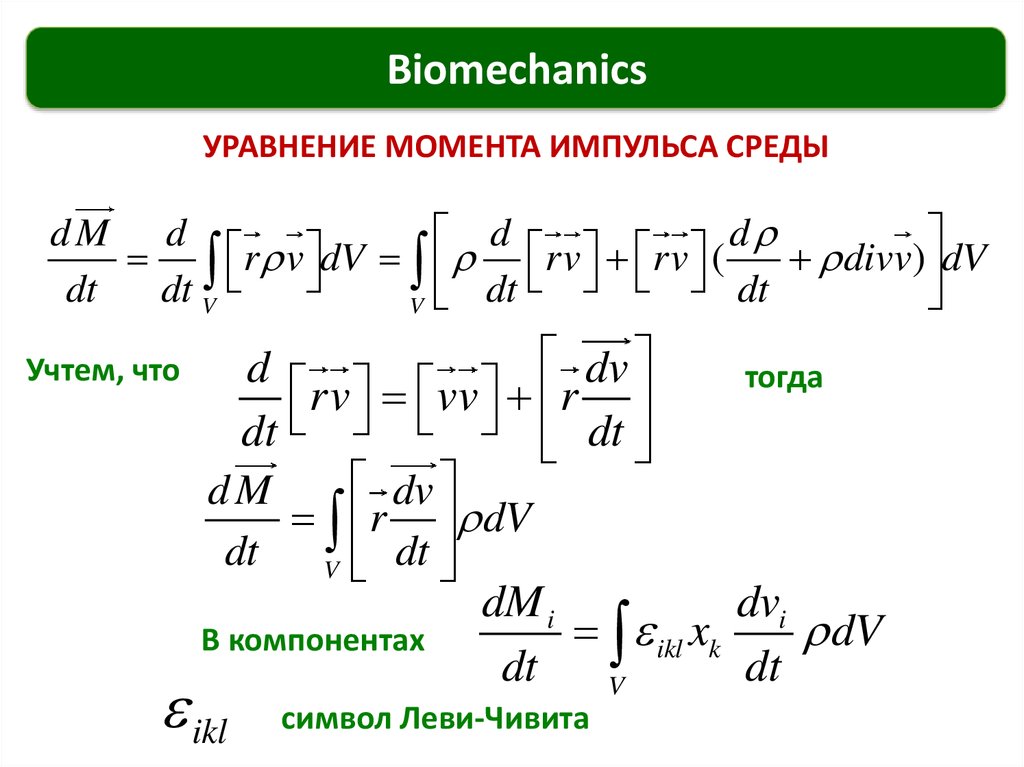




























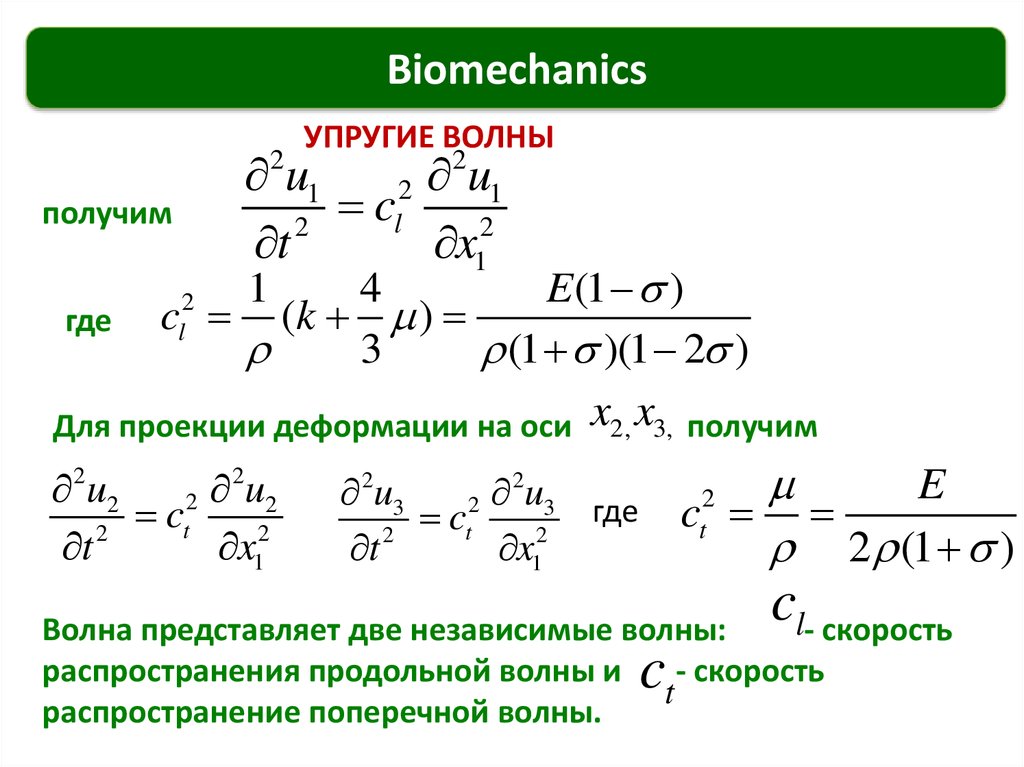

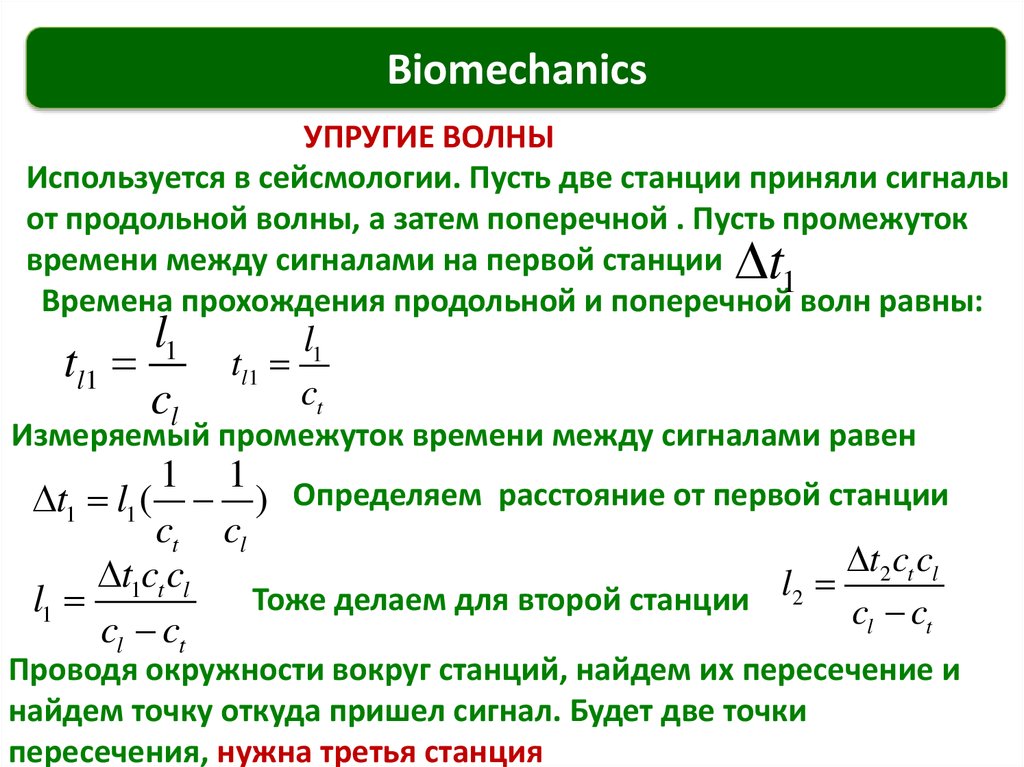
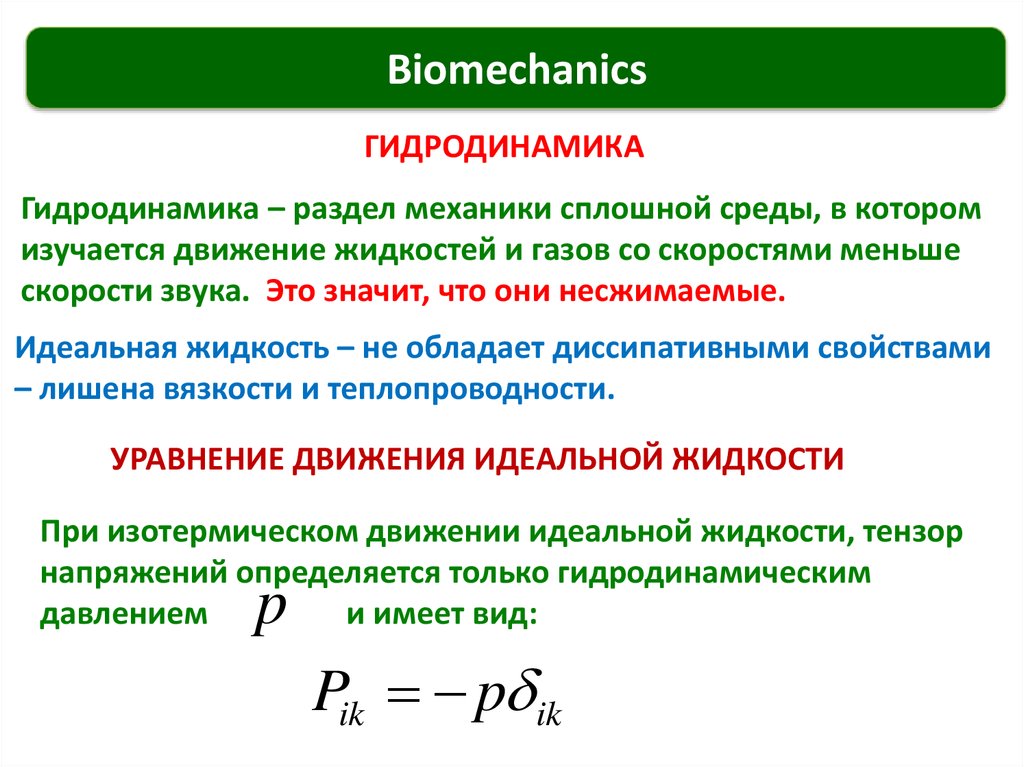
























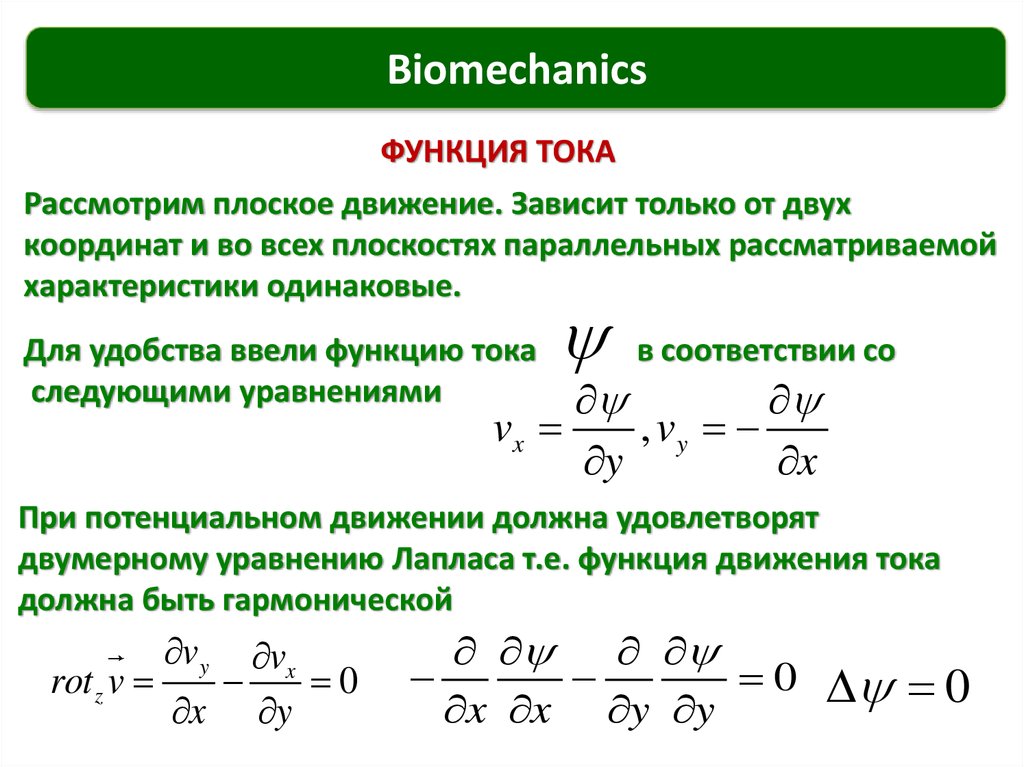

 physics
physics








