Упругие напряжения и обратимые деформации. (Лекция 10)

1.

Лекции 10
Упругие напряжения и обратимые деформации
Тензор напряжений. Тензор деформаций. Закон Гука.
Соотношения Дюамеля-Неймана.
Термодинамическое обоснование уравнений теории
упругости и термоупругости

2.

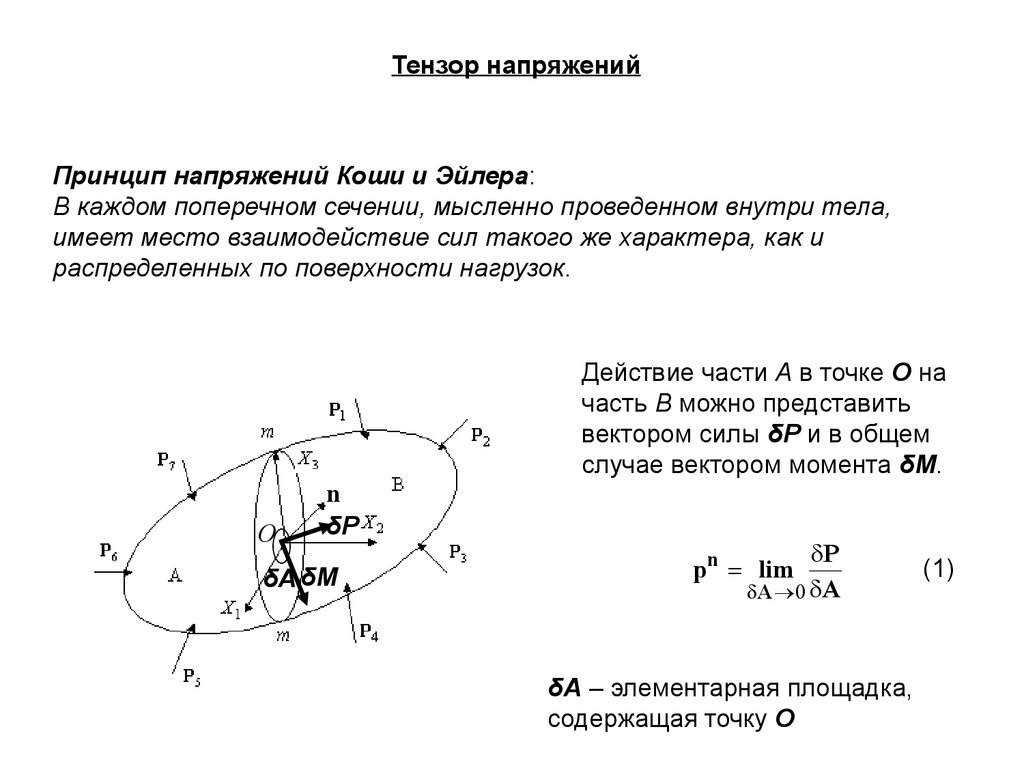
Тензор напряжений
Принцип напряжений Коши и Эйлера:
В каждом поперечном сечении, мысленно проведенном внутри тела,
имеет место взаимодействие сил такого же характера, как и
распределенных по поверхности нагрузок.
Действие части А в точке O на
часть В можно представить
вектором силы δP и в общем
случае вектором момента δM.
O
n
δP
δА δM
P
A 0 A
pn lim
δА – элементарная площадка,
содержащая точку О
(1)

3.

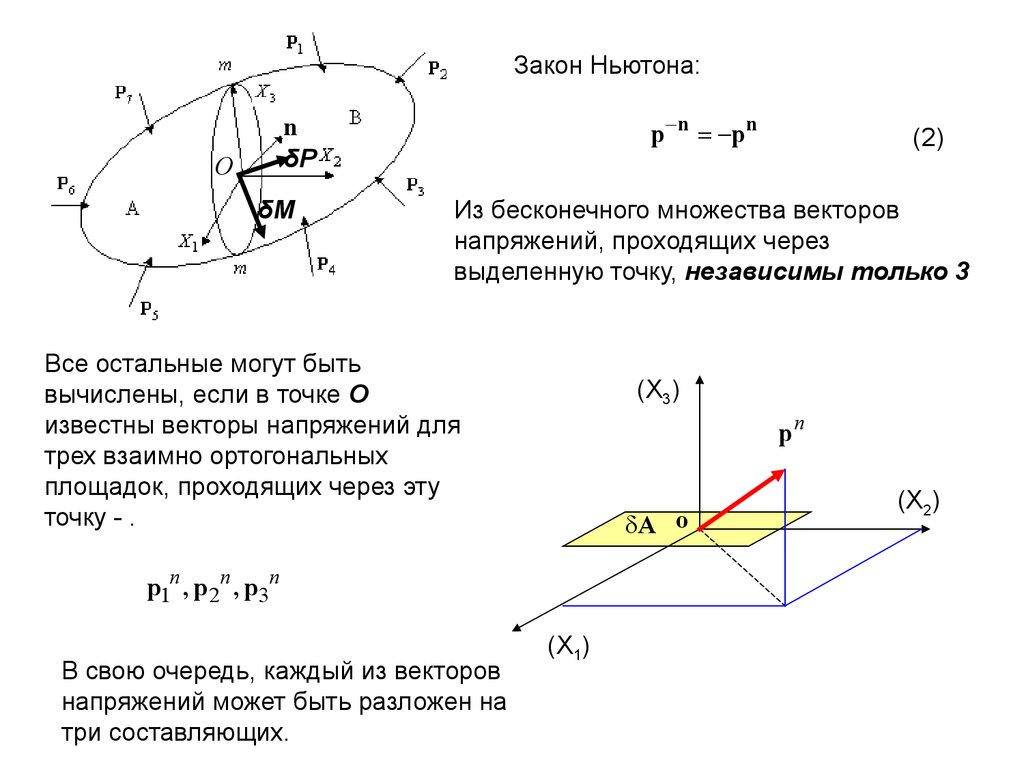
Закон Ньютона:
p n pn
n
δP
O
δM
(2)
Из бесконечного множества векторов
напряжений, проходящих через
выделенную точку, независимы только 3
Все остальные могут быть
вычислены, если в точке О
известны векторы напряжений для
трех взаимно ортогональных
площадок, проходящих через эту
точку - .
(X3)z
pn
A o
p1n , p 2n , p3n
В свою очередь, каждый из векторов
напряжений может быть разложен на
три составляющих.
x
(X1)
(X
y 2)

4.

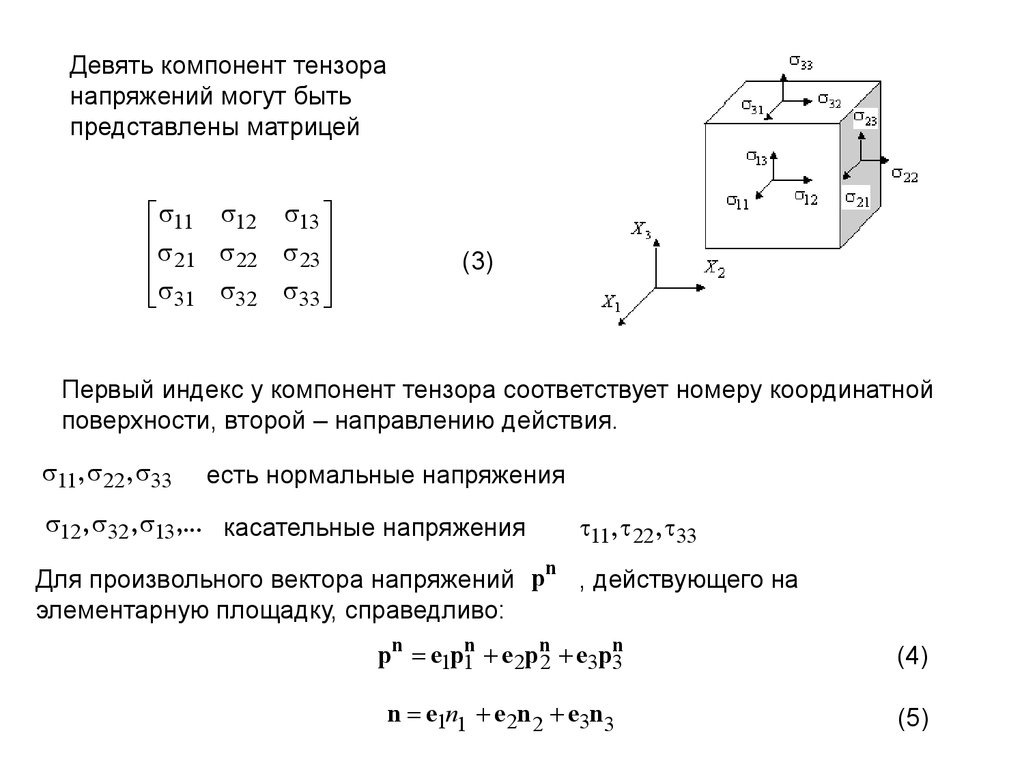
Девять компонент тензора
напряжений могут быть
представлены матрицей
11 12
22
21
31 32
13
23
33
(3)
Первый индекс у компонент тензора соответствует номеру координатной
поверхности, второй – направлению действия.
11 , 22 , 33
есть нормальные напряжения
12 , 32 , 13 ,... касательные напряжения
11 , 22 , 33
n
Для произвольного вектора напряжений p , действующего на
элементарную площадку, справедливо:
pn e1p1n e2pn2 e3pn3
(4)
n e1n1 e 2n 2 e3n3
(5)

5.

Напряженным состоянием в точке называется совокупность напряжений,
действующих по всевозможным площадкам, проведенным через эту точку.
9 компонент тензора напряжений в 3-х взаимноортогональных площадках,
проходящих через выделенную точку, полностью определяют напряженное
состояние в этой точке. Располагая значениями компонент тензора
напряжений ij , i , j 1,2,3
, можно вычислить напряжения на любой
площадке, проходящей через заданную точку.
pn , pn , pn
проекции полного напряжения P n на оси координат
p1n 11n1 12n2 13n3
p 2n 21n1 22n2 23n3
(6)
p3n 31n1 32n2 33n3
n1,n2,n3 – направляющие косинусы нормали
Pj n
3
ij ni ,
j 1,2,3
(7)
или
Pj n ij ni
(8)
i 1
Повторяющийся индекс (i) называется немым (подставным); по нему идет
суммирование. Неповторяющийся индекс (j) называется свободным

6.

Разложение тензора напряжений
Общий случай напряженного состояния можно представить в виде суммы
двух напряженных состояний (такое представление имеет место для любого
тензора!):
0
0 0
(9)
0 0 0 0
Шаровой тензор
0
0 0
0
Девиатор тензора
напряжений
1
11 22 33 p давление
3
s11 s12
S s21 s22
s
31 s32
s13
s23
s33
(11)
sij ij 0 ij
1, i j;
ij
0, i j .
(12)
s11 11 0
(13)
(10)
s12 12
…….

7.

(14)
p S 0 S
1 0 0
0 1 0,
0 0 1
1
2
1
S aij
2
S s ij
S Ss S a
(15)
Sij S ji ,
Sijs S sji ,
i , j 1,2,3
Sij S ji ,
Sija S aji ,
i , j 1,2,3
0
S a S3a
S 2a
a
a
a S 23 S32
S1
,
2
S3a
0
S1a
(16)
S 2a
S1a
0
a
a
a S31 S13
S2
,
2
a
a
a S12 S 21
S3
2
(17)
антисимметричный тензор эквивалентен так называемому аксиальному
вектору с компонентами
S1a , S 2a , S3a

8.

Правило знаков:
Растягивающие нормальные напряжения будем считать
положительными, сжимающие – отрицательными.
Знак касательных напряжений связан с направлениями осей координат:
если внешняя нормаль к данной площадке совпадает с направлением
соответствующей координатной оси, то на этой площадке касательные
напряжения – положительные.

9.

Перемещения и деформации
От приложенной нагрузки тело
деформируется. Точка P переходит в точку
P*, а точка Q – в точку Q*
Полное перемещение:
*
*
PP OP OP
u r R
Вектор перемещений
(18)
u : u1, u2 , u3
Компонента вектора перемещений положительна, если ее направление
совпадает с направлением соответствующей координатной оси
P X1 , X 2 , X 3
P* x1 , x2 , x3
ui xi X i , i 1,2,3
(19)
В результате деформации перемещение точки Q в общем случае не будет
совпадать с перемещением точки P. Эти перемещения будут отличаться на
некоторую малую величину du

10.

du
u r dr u r du
(20)
ui r dr ui r dui
(21)
вектор относительного смещения
Ряд Тейлора:
ui r dr ui r
3
k 1
ui xk 1
ui
u
dxk ui r i dxk
xk
xk
(22)
относительные смещения малы по сравнению с
абсолютными значениями смещений!
Сравниваем (21) и (22):
dui
Aik
ui
dxk Aik dxk
xk
(23)
Тензор относительной деформации точки Q относительно
точки P или тензор дисторсии
Компоненты этого тензора есть функции координат и времени!

11.

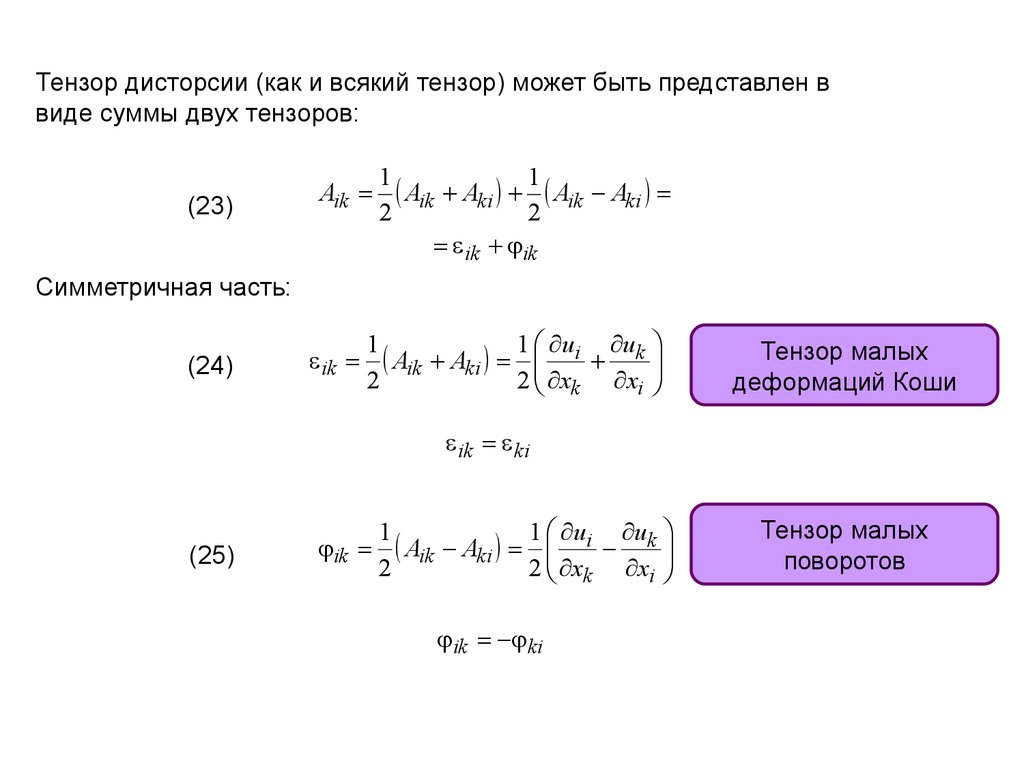
Тензор дисторсии (как и всякий тензор) может быть представлен в
виде суммы двух тензоров:
(23)
Aik
1
Aik Aki 1 Aik Aki
2
2
ik ik
Симметричная часть:
(24)
ik
1
Aik Aki 1 ui uk
2
2 xk xi
Тензор малых
деформаций Коши
ik ki
(25)
ik
1
Aik Aki 1 ui uk
2
2 xk xi
ik ki
Тензор малых
поворотов

12.

Разложение тензора малых деформаций
Как и всякий тензор, тензор деформаций можно представить в виде суммы
двух тензоров:
Шаровой тензор
0
0
0
0
Девиатор тензора
деформаций
0
0
0
0
1
0 , ij0 0 ij
3
0
1
11 22 33
3
e11 e12
e e21 e22
e
31 e32
(27)
e13
e23
e33
(28)
eij ij 0 ij
Тензор малых
деформаций, по
определению,
симметричен!
1, i j;
ij
0, i j .
(29)
e11 11 0
(13)
(26)
12 12
…….

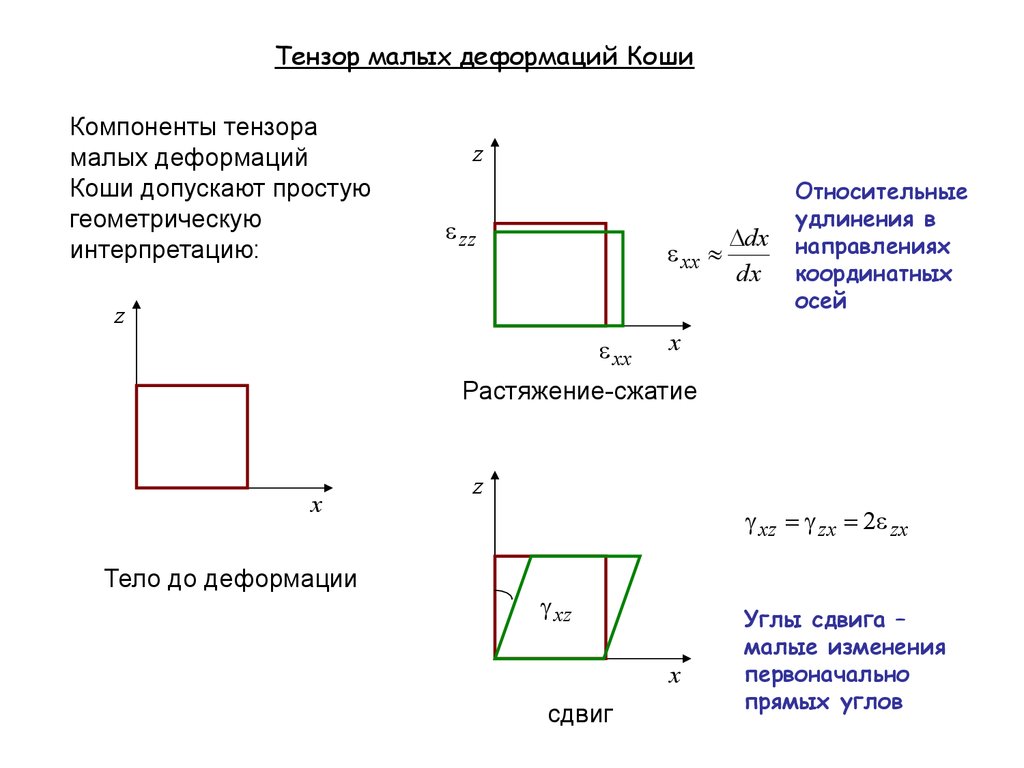
13.

Тензор малых деформаций Коши
Компоненты тензора
малых деформаций
Коши допускают простую
геометрическую
интерпретацию:
z
zz
xx
z
xx
dx
dx
Относительные
удлинения в
направлениях
координатных
осей
x
Растяжение-сжатие
x
Тело до деформации
z
xz zx 2 zx
xz
x
сдвиг
Углы сдвига –
малые изменения
первоначально
прямых углов

14.

Изменение объема при деформации
dx10 , dx20 , dx30
Размеры тела до деформации:
dx3
Его объем:
dx2
dx1
V 0 dx10dx20dx30
(30)
Размеры тела после деформации:
V dx1 x2 dx3
и
dx1 , dx2 , dx3
или: V dx10 dx1 dx20 dx2 dx30 dx3
(31)
Изменение объема:
V V V
0
dx1 dx2 dx3
0 0 0
dx1 dx2 dx3 1
1
1
dx10dx20dx30
dx10
dx20
dx30
(32)
V0 1 11 1 22 1 33 1
V0 11 22 33 11 22 22 33 33 11 11 22 3
I1
I2
I3

15.

(33)
V V0
11 22 33 kk ,
V0
Эта величина относительного
изменения объема не зависит
от выбора системы
координат!
ij 1
V V0
u
kk kk 0 k
V0
xk
u u
u
1 2 3 u
x1 x2 x3
Иначе:
(34)
Если деформация происходит без изменения объема:
0
МЖГ:
kk 0 ;
u 0
v 0,
v
v1
Условие несжимаемости для
деформируемой среды
u
t
u1
u
u
, v 2 2 , v3 3
t
t
t
Компоненты вектора
скорости

16.

Вектор поворота
Пусть
ij 0
Тогда деформация элемента определяется тензором вида:
ik
1
Aik Aki 1 ui uk
2
2 xk xi
0 12
21 0
31 32
или
13
23
0
Это –антисимметричный тензор, включающий только три независимые
величины:
32 23 1
13 31 2
(35)
21 12 3
0
3
2
3
0
1
2
1
0
(36)

17.

Найдем компоненты вектора смещений:
dui ik dxk
du1 3dx2 2dx3
du2 3dx1 1dx3
du3 2dx1 1dx2
или:
du dr
(37)
Векторное произведение
вектора поворота и вектора dr
вектор поворота
1 u u
1
12 1 2 3 rot 3 u
2 x2 x1
2
1 u
u
1
23 2 3 1 rot1 u
2 x3 x2
2
1 u u
1
31 3 1 2 rot 2 u
2 x1 x3
2
1
1
rot u u
2
2
(38)

18.

A grad A
i
A rot A
x1
A1
A1
x
1
A2
x1
A
3
x1
-тензор
j
x2
A2
A1 A2 A3
A
x1 x2 x3
k
x3
A3
-вектор
скаляр
A1
x2
A2
x2
A3
x2
A1
x3
A2
x3
A3
x3

19.

Закон Гука
В технических расчетах деформацию стержня при
растяжении определяют через относительное
удлинение
l l0
l0
Идеальная упругость – однозначная зависимость между силами и
вызванными этими силами перемещениями
Для огромного большинства материалов закон упругости с большой
E
точностью можно считать линейным
E
модуль упругости
Закон Гука
Закон упругости справедлив, пока напряжения не достигнут некоторого
предела, называемого пределом упругости
Для всех материалов, применяемых в технике (кроме резины и
каучукообразных полимеров), модуль упругости весьма высок по сравнению с
пределом упругости, поэтому величина упругой деформации невелика – не
более 1-2 %

20.

В общем случае, кроме деформации в направлении растяжения
будет происходить и сжатие в поперечном направлении
b b0
b0
Для изотропного материала величина ε’ одинакова для всех направлений в
поперечном сечении (нет предпочтительного направления). Если
деформация – упругая и подчиняется закону Гука, то оказывается, что
отношение поперечной деформации к продольной – величина постоянная
E
Закон Пуассона
коэффициент Пуассона
В трехмерном случае закон Гука для изотропного тела можно представить
следующим образом
2
(39)
ij 2 ij ij K kk
3
модуль сдвига
2
11 2 11 K kk
3
12 2 12
2
22 2 22 K kk
3
……………………..

21.

Просуммируем (39) по i j :
11 22 33 kk 3 p e 3K 11 22 33 3K kk 3K
1
1 V
K
V p e
K модуль всестороннего сжатия или объемный модуль
V V0
V0
Для одноосного растяжения из общей формулы имеем
2
11 2 11 K kk ; 22 33 11
3
kk 11 22 33 11 1 2 и
2
11 2 11 K 1 2 11 E 11 - в соответствии с законом Гука
3
2
2
0 2 22 K kk 2 11 K 1 2 11
3
3
E
2
2
G модуль сдвига (40)
K
;
Отсюда находим
2
1
3 1 2
,
коэффициенты Ламе
E
1 1 2

22.

Учитывая связь (верхняя строка
предыдущего слайда)
kk 3K kk ,
из (39) найдем
2
K
ij
kk ij
kk
3
ij
ij
ij
2
2 3K 2
2 3 2
Обобщенный закон Гука для анизотропного тела:
ij Cij
(41)
(42)
Тензоры напряжений и деформаций обладают рядом интересных свойств.
Рассмотрим некоторые из них
1.Как и всякий симметричный тензор, тензор деформаций можно привести к
0
главным осям. Это означает, что существует такая система координат xi , в
которой тензор деформаций имеет вид
0
11
0
0
0
0
0
22
0
0
0 33
ii0 главные значения тензора деформаций
xi0
главные оси

23.

2.Рассмотрим в элементе объема сферу единичного радиуса, центр которой
находится в начале координат. Ее уравнение в главных осях:
0 2
x1
0 2
x2
0 2
x3
1
После деформации точки сферы будут иметь координаты:
0 0
x10' x10 11
x1 ,
x20' x20 022 x20 ,
0 0
x30' x30 33
x3
и окажутся на поверхности, описываемой следующим уравнением
0 2
x1
0 2
1 11
0 2
x2
2
1 022
0 2
x3
0 2
1 33
1,
т.е., уравнение сферы переходит в уравнение эллипсоида, если все главные
значения тензора деформаций – различны. Если главные значения –
одинаковы, то сфера переходит в сферу.
В теории показывается (обычными средствами математического анализа),
что точки, лежащие на одной прямой до деформации, после деформации
также расположатся на некоторой прямой; параллельные прямые останутся
параллельными и тд.

24.

Температурная деформация
Деформация тел может происходить не только вследствие приложенных к
нему сил, но и в результате изменения его температуры. В пределах
выделенного элемента будем считать температуру однородной.
Изменение температуры:
T T T0
В силу однородности Т внутри объема напряжения не возникают, а происходит
только тепловое расширение или сжатие элемента.
T
1, деформацию элемента можно считать пропорциональной
Если
T0
изменению температуры
duiT Tij dx j ,
Tij
ijT ij T
Температурная
деформация
элемента объема
происходит без
его поворота
тензор теплового расширения
ij коэффициенты линейного теплового расширения
В главных осях:
При температурной деформации сфера Изотропное тело:
переходит в эллипсоид
0
11
0
0
ijT ij T
2
2
2
x10
x20
x30
0
0
1,
0 22
V
2
2
2
T
0
0
0
0
0
ii 3 T
1 11 T
1 22 T
1 33 T
0 33
V
p 3

25.

Термодинамическая теория
Уравнение Гиббса для простой деформируемой среды:
du Tds 1 ij e d ij
(1)
Локальным аналогом изменения удельного объема d будет величина,
связанная с изменением диагональных компонент тензора деформаций
kk 11 22 33
Как перейти от (1) к термодинамической системе в целом?
1
P kk
Введем гидродинамической давление по формуле
3
Известно (для малых
деформаций):
V V0
11 22 33 kk ,
V0
ij e p e ij Sij e ,
Если
ij 1
ij kk ij eij
3
1 ij d ij 1 p e ij Sij e d kk ij eij
(2)
3
ij , ij - шаровые тензоры, то
d
1 ij d ij 1 p e kk ij 1 p e d kk p e d , d 1d kk
3
(3)

26.

du Tds p e d kk
(4)
Домножив (4) на плотность и проинтегрировав по объему, получим
dU TdS p e dV
Уравнения Гиббса можно записать и для единицы объема (обозначения
оставляем прежними)
du Tds ij d ij
df sdT ij d ij
(5)
Как мы уже знаем, если имеется уравнение Гиббса, то имеет место система УРС:
f f T , ij :
s
s
d ij
ds dT
T
ij T
(6)
ij
ij
d
dT
d ij
T
T
(7)
2 f
s
C
T T
T 2
T

27.

2
ij
f
изотермические модули
Cij T
ij
T
ij
ij
d
вместо (7)
d ij
ds
u u s , ij :
s
s
2
ij
u
Cij s адиабатические модули
ij
T
Подчеркнутые слагаемы описывают один из самых известных перекрестных
эффектов
2 f
2 f
s
ij
ij
ij
ij T
T ij
T
T
тензор коэффициентов
термоупругости
ij
C
ds
dT
d ij ,
T
d ij ij dT Cij d
(8)
Последние уравнения – есть уравнения состояния для термоупругого тела
Если тело – изотропное, а деформации – малы, из последнего
соотношения имеем:
ij 2 ij ij kk Kw , w 3 T T T0
Это – соотношения Дюамеля Неймана
(9)