Similar presentations:
Теория упругости сплошных сред. Упругие поля (поля напряжений) вокруг дислокаций. Энергия дислокаций
1. Физика реального кристалла
7. Теория упругости сплошных сред.Упругие поля (поля напряжений)
вокруг дислокаций. Энергия
дислокаций.
Профессор Б.И.Островский
ostr@cea.ru
2.
Типы дислокаций:Краевые дислокации - Edge Dislocation:
A portion of an extra plane of atoms
Винтовые дислокации - Screw Dislocation:
Helical atomic displacement around a
line extending through the crystal
Смешанные дислокации - Mixed Dislocation:
Some edge, some screw nature
3.
Краевая дислокацияСлабые, упругие
искажения идеальной
решетки - «хороший
материал» -
линейная теория
упругости
Ядро дислокации (??)
-сильные искажения решетки,
нелинейные деформации
4.
Свойства вектора БюргерсаFinish-start/ right hand
5.
Свойства дислокацийДислокационная линия не может закончиться внутри кристалла,
а только
- на его поверхности
- на внутренней границе раздела ( на границах зерен)
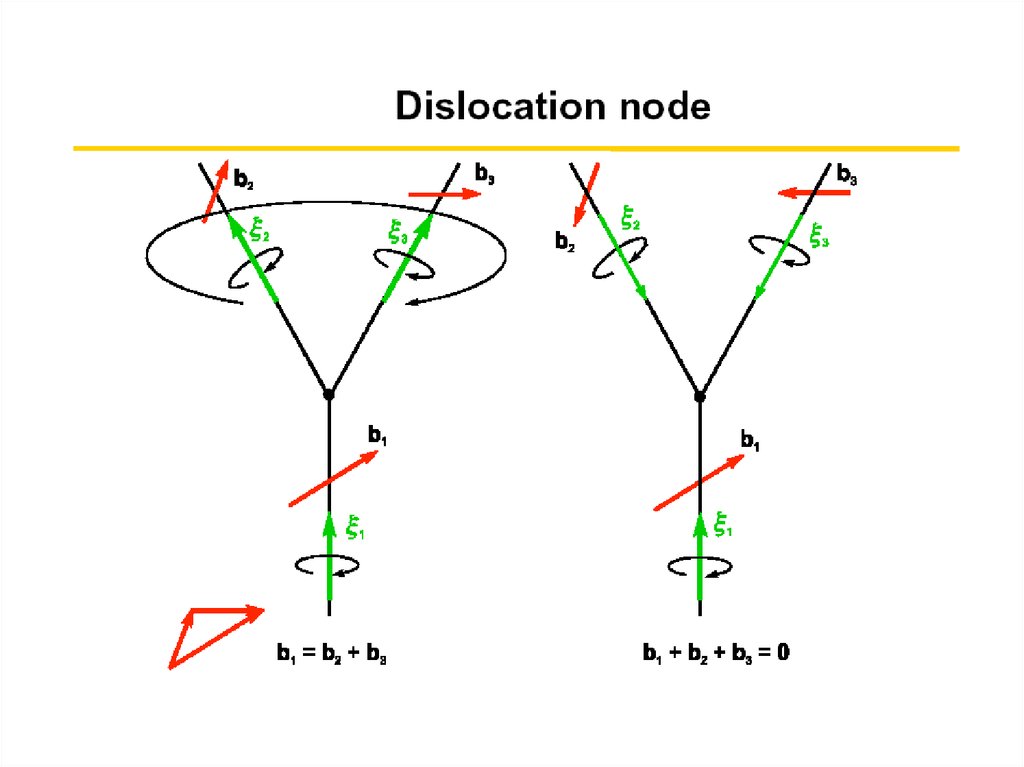
- в дислокационном узле
- с образованием дислокационной петли
6.
7.
Примеры дислокационных петель иузлов в кристаллах
Дислокационная петля
в fcc кристале
Сетка Франка
8.
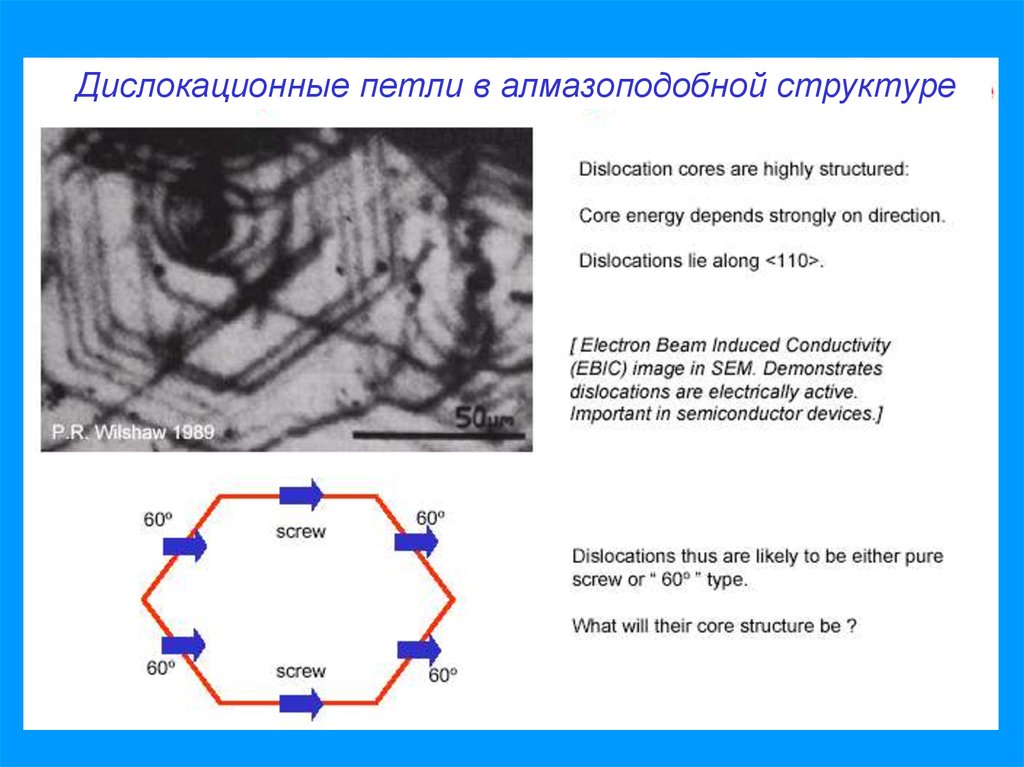
Дислокационные петли в алмазоподобной структуре9.
Плотность дислокацийОпределение плотности дислокаций
см-2
= L/ V
= L/ V = Nl/ V = Nl/ lS = N/ S
Выражается в единицах,
Типичные значения в отожженных металлах
В полупроводниках
После пластической деформации
и выше
-1 = S/ N
-1/2
-1/2 = < r >- среднее расстояние
между дислокациями
10. Элементы теории упругости сплошных сред
11.
Закон Гука,модуль Юнга
Y E
Брусок из однородного
изотропного материала
12.
Коэффициент ПуассонаВ кристаллах:
ij = Cijkl kl
13.
Брусок под действиемгидростатического
давления
14.
15.
Объемный модуль упругости16.
Однородный сдвиг (1)клей
17.
Однородный сдвиг (2)Fi = 0
Mi = 0
18.
Однородный сдвиг (3)сдвиге
19.
Однородный сдвиг (4)-1 < < 1/2
20. Элементы теории упругости кристаллов
21.
22.
ij = dFi /dAj23.
24.
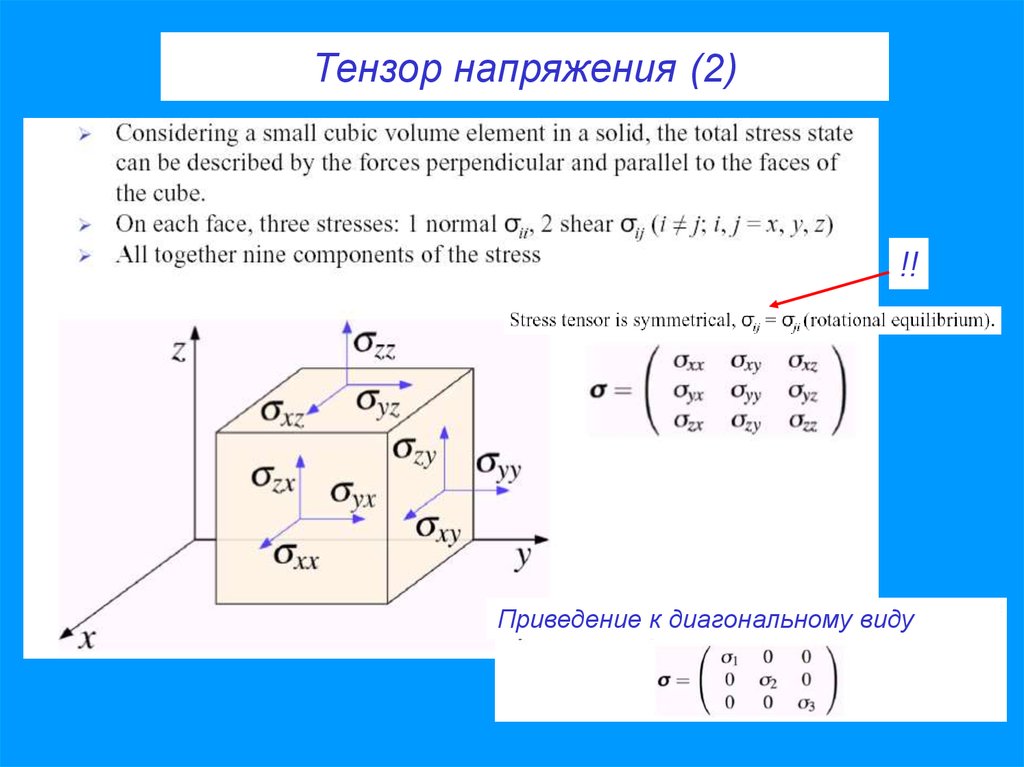
Тензор напряжения (1)25. Тензор напряжения (2)
!!Приведение к диагональному виду
26.
Симметрия тензора напряженияij
ij
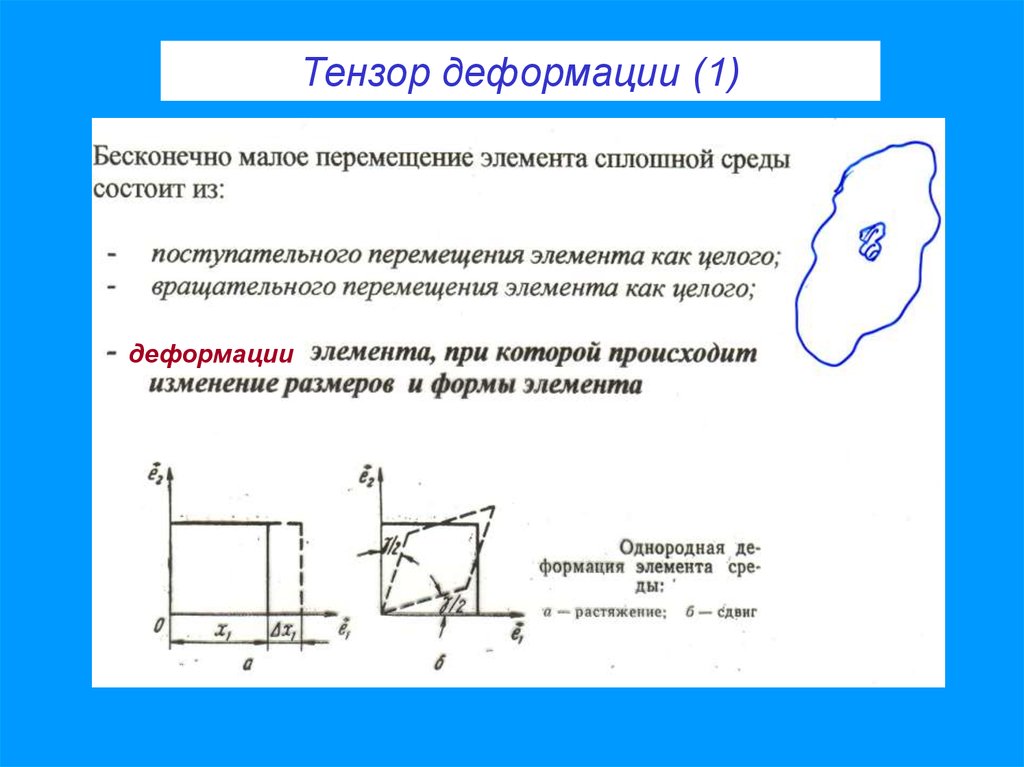
27. Тензор деформации (1)
деформации28.
Тензор деформации (2)u - смещение
частицы
x’ = x + u2 - u1
x’ = x + u
e = lim ( x’ - x)/ x =
x 0
= lim u/ x = du/dx - деформация
x 0
29.
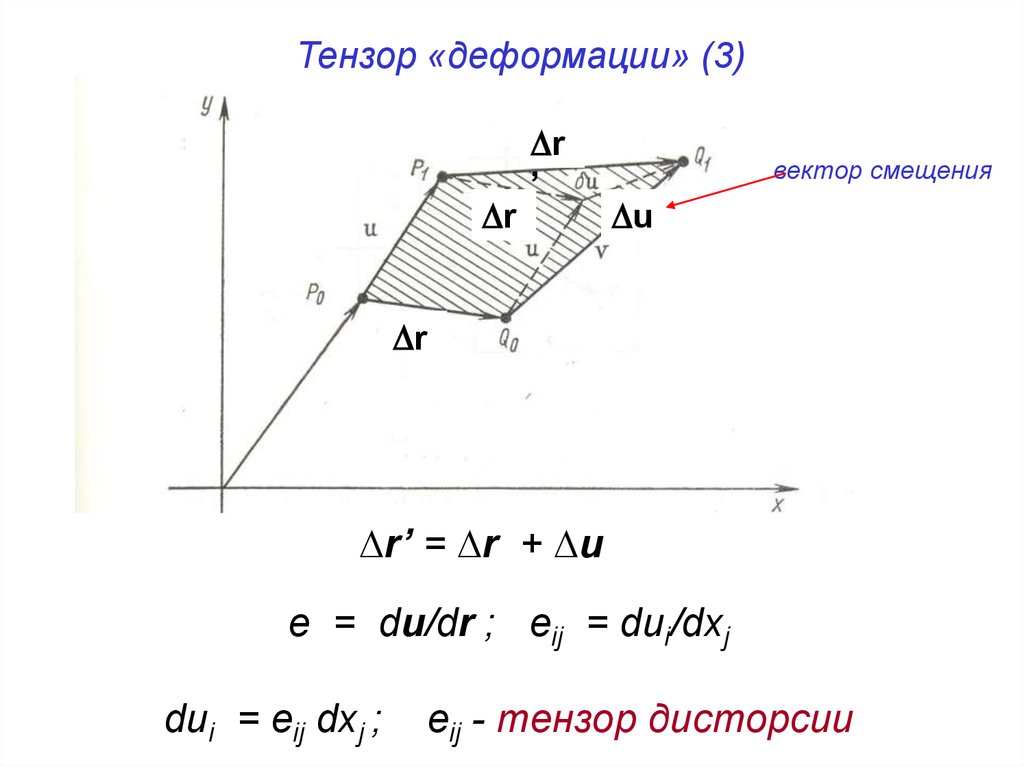
Тензор «деформации» (3)r
r
’
вектор смещения
u
r
r’ = r + u
e = du/dr ; eij = dui/dxj
dui = eij dxj ;
eij - тензор дисторсии
30.
Тензор дисторсии (1)31.
вектор смещенияr’ = r + u
В общем случае:
e = du/dr ; eij = dui/dxj
dui = eij dxj ;
eij - тензор деформации (??)
Легко понять смысл компонент тензора eij
x = ( x1; 0; 0)
ui = eij xj
:
32.
Тензор дисторсии (2)2
33.
Определение тензора деформации- Тензор деформации
- Чистые повороты
34.
Тензор деформации (6)35.
Акивис,Гольдберг,
1969
r’ = r + u
( r’)2 = ( r)2 + 2 r u + u2
( r’)2 - ( r)2 = 2 r u
2 r u =2eij xi xj
Таким образом,
в чистую
деформацию
вносит вклад
только тензор
Вклад равен 0
2 r u =2 ij xi xj
36.
Акивис,Гольдберг,
1969
u = x r
r’
r
37.
Акивис,Гольдберг,
1969
38.
39.
Тензор деформации (5)40.
Тензор деформации (6)41.
Тензор упругостиij
ij
ij
ij = Cijkl kl
42.
Роль симметрииКубические кристаллы
Ромбическая
Тригональная
В кубических кристаллах достаточно трех упругих констант
43. Изотропное твердое тело
GСвязь с константами упругости
кубического кристалла
Связь с модулем Юнга и
коэффициентом Пуассона
E = 2G (1+ )
= /2( +G )
44. Коэффициенты упругости
CCijkl
1.6х10-12
C
C = U/a3
Оценка величины коэффициентов упругости
C11
C12
C44
Кубические кристаллы
Дин/см2 = эрг/см3 = 10 -1 дж/м3
45.
Изотропные телаДин/см2
Дин/см2 = эрг/см3 = 10 -1 дж/м3 = 10 -1 Н/м2
46.
Энергия деформируемого кристалла47.
Когда единичный элемент объема деформируется на малую величину d ij ,напряжения совершают над ним работу:
d Wel = ij d ij = Cijkl kld ij
ij = Cijkl kl
Плотность
энергии!
[эрг/см3]
- Закон Гука
После интегрирования имеем для плотности энергии:
Wel = (1/2)Cijkl ij kl = (1/2) ij ij
Полная упругая энергия деформации получается интегрированием
по всему объему кристалла:
Wel полн = (1/2) Cijkl ij kl d3r
V
В случае однородной деформации: kl = const (r )
Wel полн = (1/2)C 2 V
- одноконстантное приближение
При неоднородной деформации: kl = kl (r ) ;
Wel полн = (1/2) C 2(r)d3r
48.
Энергия деформируемого кристалла49.
В общем случае если деформация производится обратимо и припостоянной температуре, и если вся работа идет на упругую
деформацию, то свободная энергия системы имеет вид:
F = (1/2) Cijkl ij kld3r
V
Плотность энергии деформации в общем случае записывается в
виде:
Wel = Wel ( kl) = (1/2)Cijkl ij kl + (1/6)Cijklтn ij kl mn+
2W
el /
ij kl
+ (1/24)Cijklmnpq ij kl mn pq
Гармоническое приближение
Ангармонические поправки
50. Упругие поля и напряжения вокруг дислокаций
51.
Дислокации в непрерывной упругой средеПостроение
Вольтерра
52.
Образование краевой дислокации в кристалле53.
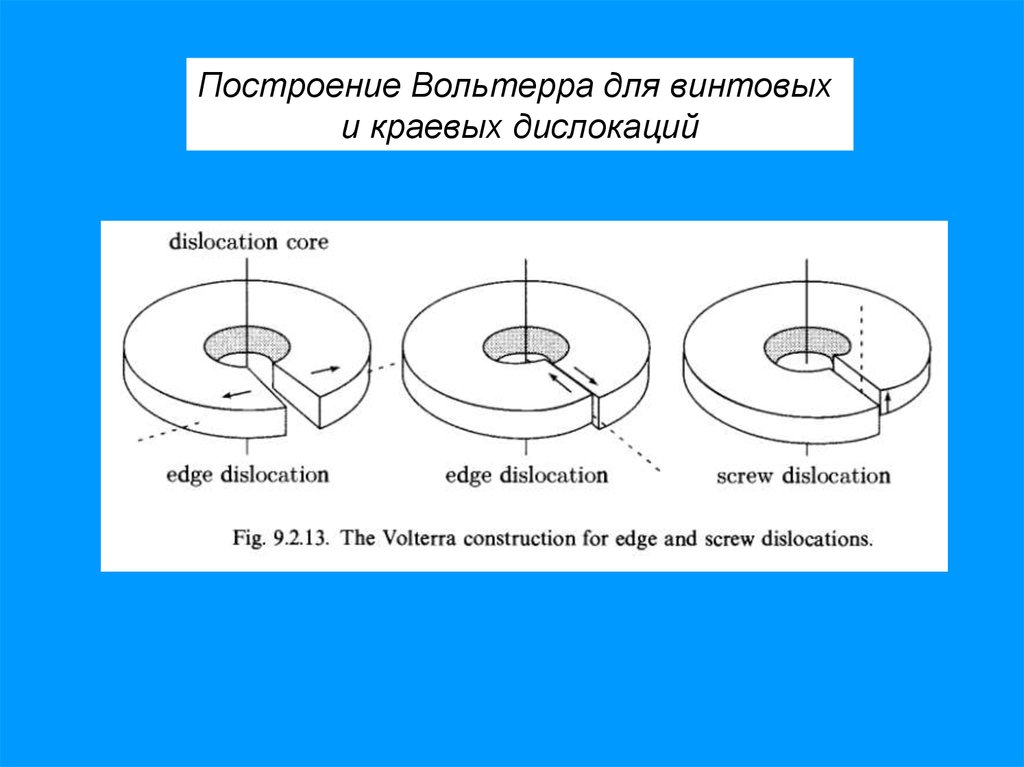
Построение Вольтерра для винтовыхи краевых дислокаций
54.
Поле смещений вокруг винтовой дислокацииarctg (y/x)
Цилиндрические
координаты:
r, , z
x 2 + y 2 = r2;
tg = y/x
uz =
uz(x,y)
55.
Вычисление компонент тензорадеформации (1)
uz = uz(x,y)
ux = 0
uy = 0
56.
Вычисление компонент тензорадеформации (2)
Смещения:
arctg (y/x)
(1/2)duz/dy =(b/4 )d[ arctg(y/x)]/dy =
dy/(y2 +a2)
= (1/a) arctg(y/a)
57.
Вычисление компонент тензорадеформации (3)
xx = yy = zz = xy = yx = 0
xz = zx
Цилиндрические
координаты:
r, , z;
x2 + y2 = r2; tg = y/x
58.
Вычисление компонент тензора напряженийG
59.
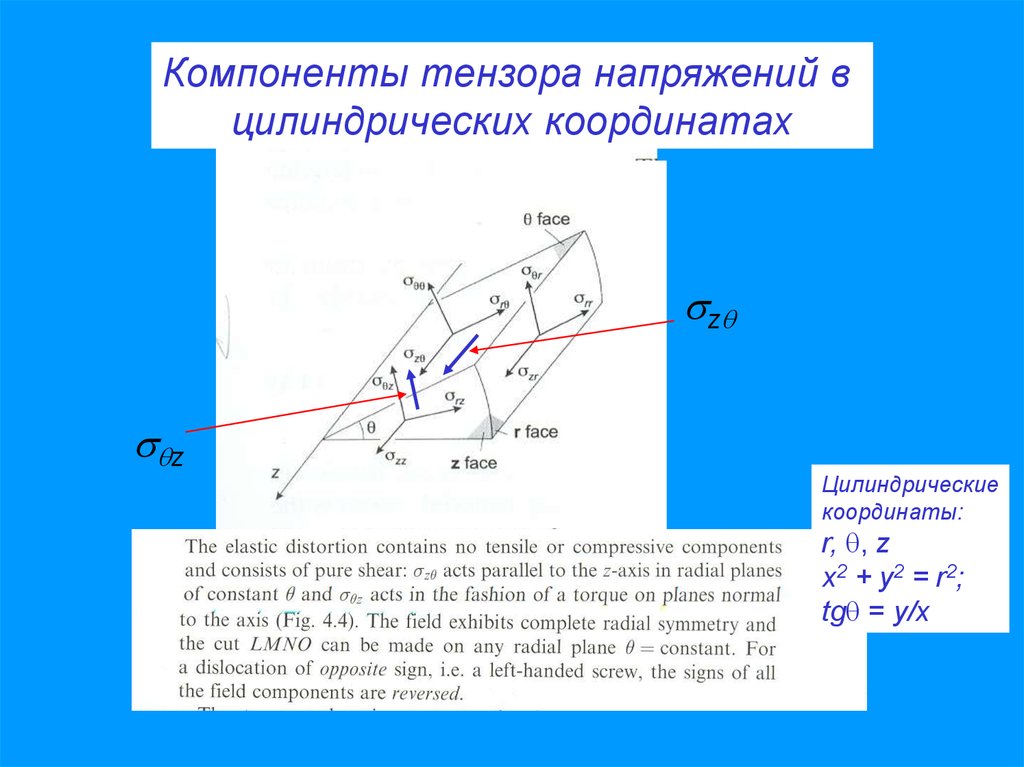
Компоненты тензора напряжений вцилиндрических координатах
z
z
Цилиндрические
координаты:
r, , z
x 2 + y 2 = r 2;
tg = y/x
60.
Компоненты тензоров напряжений и деформаций вцилиндрических координатах
используя соотношения:
и, аналогичным образом, для сдвиговых деформаций,
получаем:
61.
Упругие поля искажений вокруг дислокацийявляются дальнодействующими!
Отличные от нуля компоненты ij и kl убывают с
расстоянием от дислокации как r -1,
r -1
62.
Сравнение законов спадания напряжений с расстоянием r,для точечных дефектов, дислокаций и
дислокационных стенок
63.
в нем имеются внутренние напряжения, источникомкоторых являются дислокации.
64.
Упругая энергия дислокацииПолная энергия дислокации состоит из двух частей:
Wel = (1/2) Cijkl ij kl
= (1/2) ij ij
Плотность упругой энергии, запасенной в дислокации:
8
2
полн
2
=
Полная энергия, запасенная в полом цилиндре радиуса R и длины L :
L
2
R
2/8 2) dz d rdr/r2 = L
=
(Gb
полн
0
0
L
r0
Или на единицу длины дислокации:
полн /L
=
dV
65.
Оценки упругой энергии дислокацииПри обычных значениях плотности дислокаций
=107 см-2, среднее
расстояние между ними составляет R -1/2 3.10-4 см, что дает
для
и
10
полн /L
=
При G 1012 дин.см-2 и b = 2.10 -8 см имеем:
Ebond Gb3
-4 эрг/см
4.10
/L
=
полн
Что в пересчете на одну связь дает:
Ebond
= 4.10 -4 эрг/см x 2.10 -8 см
= 8.10-12 эрг
5 эв
66.
67.
Наименьшей энергией обладают дислокации с наи-!!
68.
Диссоциация дислокаций69.
Ядро дислокацииядро – неупругие искажения
упругие деформации
70.
Оценки, выполненные на основе различных микроскопических подходови результатов компьютерного моделирования взаимодействий в ядре
дислокаций, показывают, что энергия ядра дислокации не превышает
10-15% полной энергии, т.е. большая часть энергии дислокации
связана с упругими деформациями, распространяющимися далеко
в объеме кристалла.






























































 physics
physics








