Similar presentations:
Упругость изотропных сред
1. Лекция 10 Упругость изотропных сред
Содержание1. Тензор деформации
2. Тензор напряжений
3. Условие равновесия. Уравнение
движения.
4. Закон Гука
2.
1. Тензор деформацииИсходные посылки:
Жидкость – свойство текучести, неспособность сохранять форму.
11
Время оседлого образа жизни молекул 10
сек (T 300 K)
частицы жидкости способны легко менять своих соседей
Картина изменения окружения
выделенной частицы жидкости
Из-за легкой смены соседей
любые 2 близкие частицы
могут разойтись со временем
на произвольно большое
расстояние. Обычное в механике
определение положения с помощью
радиус-вектора становится неудобным.
Поэтому вектор перемещения частицы r в качестве меры изменения
ее местоположения не пригоден. Единственной удобной для
использования кинематической характеристикой в гидродинамике
оказывается скорость частицы v (Лагранж) или скорость частиц v в данной
точке пространства (Эйлер).
3.
Твердое тело – текучесть отсутствует, присутствует дальнийпорядок, тела сохраняют форму, окружение частиц не меняется.
Поведение тела удобно отслеживать по изменениям радиус-вектора
частиц – по вектору смещения.
Основные опытные факты
1) Непреложным является факт изменения телами объема и
формы под влиянием поверхностных нагрузок (поверхностнораспределенных сил), массовых сил (действуют на
единичный объем тела), нагрева и охлаждения. Это свойство
тел, выведенное a posteriori (из опыта), называется
деформированием (дословно "изменением формы, вида").
2) Если деформация тела не превышает некоторый предел, то
при медленном снятии внешних воздействий тело
возвращается в исходное недеформированное состояние, а
при мгновенном – совершает колебания относительно
равновесного положения, которые со временем затухают по
причине внешнего или внутреннего трения. Эта способность
деформируемых твердых тел восстанавливать свою форму,
было названа упругостью.
4.
К истолкованию упругостиТеория упругости – изучает изменения
состояния тел при деформировании,
оценивает деформации по геометрическим
показателям, определяет внутренние силы
(напряжения), как реакции на внешние
воздействия.
Концепция сплошности. Вещество непрерывно распределено по
объему тела и такой характер его распределения сохраняется при
деформировании. Реальная атомно-молекулярная структура
вещества игнорируется.
Тело трактуется как трехмерное евклидово пространство, точки которого
совпадают с частицами тела. Распределение массы тела по
точкам-частицам характеризуют плотностью в данной точке, под
которой понимается предел отношения массы M в элементарном
объеме V, к этому объему при его стягивании в точку
M dM
V 0 V
dV
( x, y, z ) lim
M (r)dV
V
Обычные требования – среда однородна ( const) и изотропна.
5.
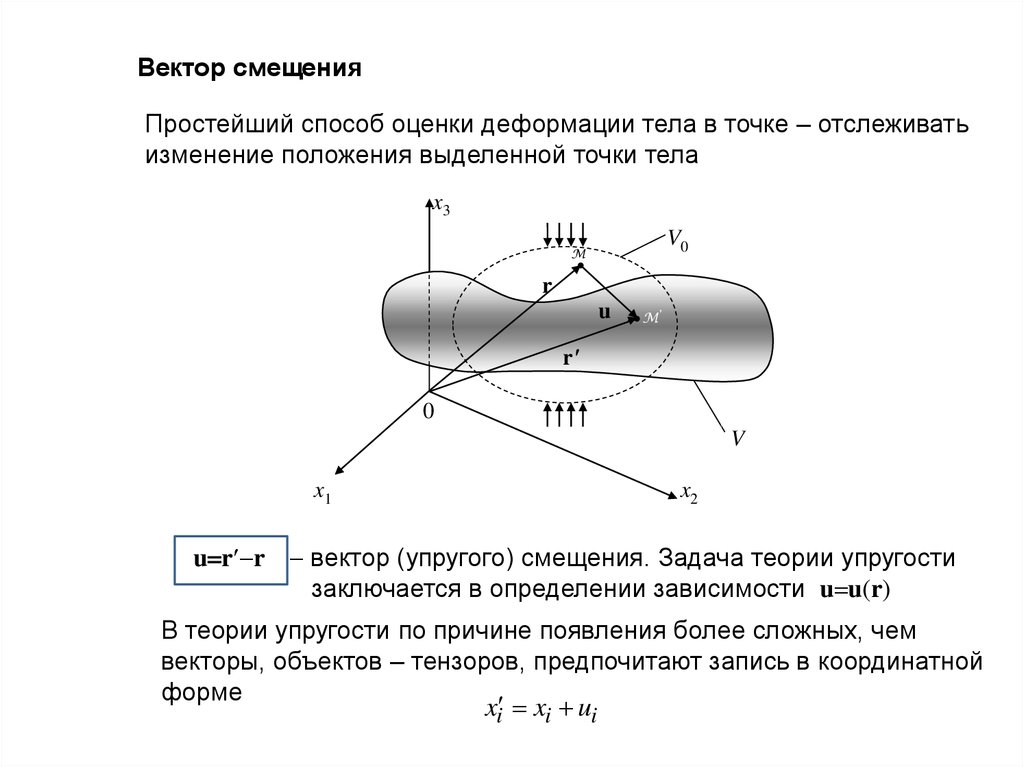
Вектор смещенияПростейший способ оценки деформации тела в точке – отслеживать
изменение положения выделенной точки тела
x3
V0
M
r
u
M'
r'
0
V
x1
x2
u r r вектор (упругого) смещения. Задача теории упругости
заключается в определении зависимости u u(r)
В теории упругости по причине появления более сложных, чем
векторы, объектов – тензоров, предпочитают запись в координатной
форме
xi xi ui
6.
Тензор деформацииДля оценки характера деформирования тела особый интерес
представляют изменения расстояния между двумя сколь угодно
близкими точками тела. Выделим в теле до деформации две
близь лежащие точки, определяемые векторами r и r dr.
dr'
dr
r dr
r
'r' dr
r'
0
dr 2 dxi2 dr '2 (dxi dui ) 2
Т.к. u u(r)
dui
ui
dxk
xk
ui
ui
2
2
dr ' dxi 2dxi
dxk
dxk
xk
xk
ui
ui
2
2
dr ' dxi 2dxi
dxk
dxk
xk
xk
2
2
7.
uiui
2
2
dr ' dr 2dxi
dxk
dxk
xk
xk
2
2
ui
ui
ui
dxk
dxk
dxm
xk
xk
xm
dr '2 dr 2 2dxi
u
u
ui
dxk i dxk i dxm
xk
xk
xm
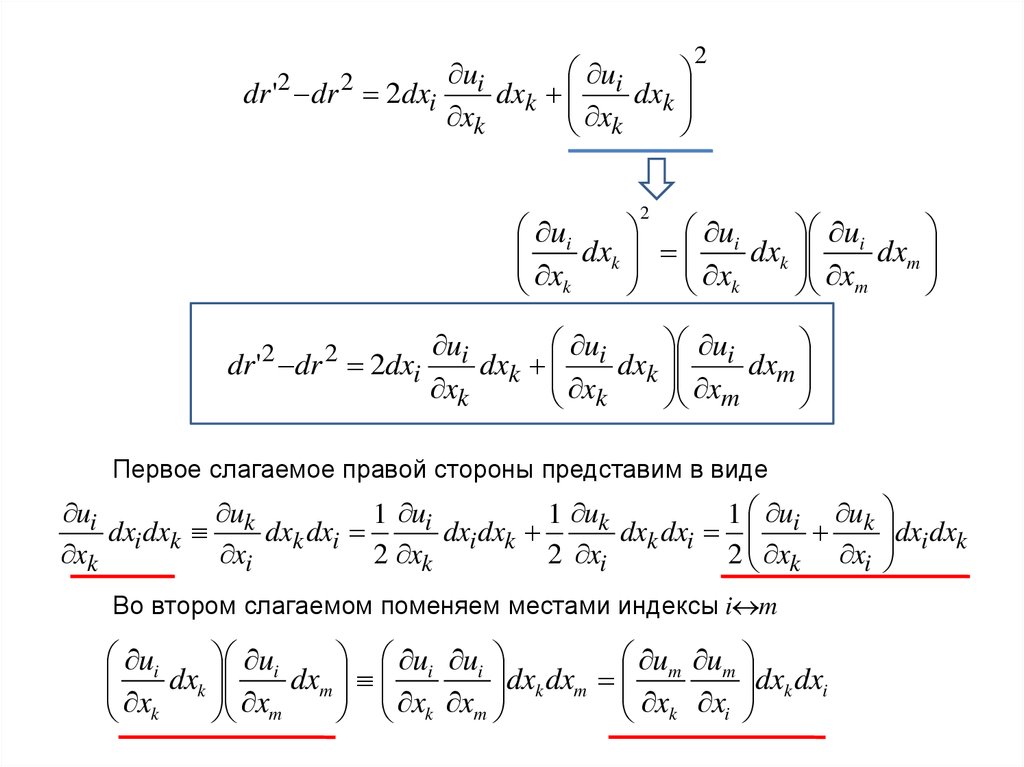
Первое слагаемое правой стороны представим в виде
ui
uk
1 ui
1 uk
1 ui uk
dxi dxk
dxk dxi
dxi dxk
dxk dxi
xk
xi
2 xk
2 xi
2 xk xi
Во втором слагаемом поменяем местами индексы i m
ui
u
u u
u u
dxk i dxm i i dxk dxm m m dxk dxi
xk
xm
xk xm
xk xi
dxi dxk
8.
1 ui uk um um2dxi dxk uik
dr ' dr 2dxi dxk
xi xk
2 xk xi
2
2
1 ui uk um um
uik
2 xk xi xi xk
тензор деформации
Основные свойства тензора деформации
1) Симметричный тензор 2-го ранга uik uki и, поэтому
характеризуется 3 вещественными собственными значениями –
главными деформациями: u xx , u yy , u zz . Тензорная поверхность
представляет эллипсоид с полуосями вдоль собственных направлений
a u xx
b u yy
c u zz
9.
2) Геометрический смысл диагональных компонент тензораdr '2 dr 2 2dxi dxk uik
В случае малых деформаций
(dr ' dr )(dr ' dr ) 2dxi dxk uik
dr ' dr 2dr
относительное удлинение
1 dxi dxk
r (dr ' dr )
uik
элементарного отрезка из-за
dr dr dr
деформации uik
dxi
dxk
Так как
– направляющие косинусы
ni
, nk
dr
dr
элементарного отрезка
r uik ni nk
u xx r , n || x u yy r, n || y
uzz r, n || z
Диагональные компоненты тензора деформации показывают
относительные удлинения элементарного отрезка вдоль
соответствующей оси
10.
3) Линеаризуем тензор деформации1 ui uk
uik
2 xk xi
um um 1 ui uk
xi xk 2 xk xi
Тогда имеем
u y
u z
d
z
dy
1
dy 1
z
y
Перемножая элементы dx , dy , dz получаем
u
dx 1 x dx
x
u x u y u x
dV 1
dV
x
y
x
div u uii
V
dz
dV dV
div u
dV
Сумма диагональных компонент тензора деформации определяет
относительное изменение элементарного объема среды
11.
4) Недиагональные компоненты тензора деформации позволяютоценить изменение угла между векторами вследствие деформации.
В пренебрежении нелинейным членом тензора деформации
cos ' cos 2nk(1) n(j2)ukj
/2
Пусть dr(1)||x1, dr(2)||x2, так что /2 и
cos 0. При этом nk(1) k1, nj(2) j2
cos ' 2 k1 j 2ukj 2u12
B силу малости деформаций ( /2) ' /2 можно
принять cos sin[( /2) '] ( /2) '. В итоге
2u12
u12
2
2
2
Недиагональную компоненту тензора деформации u12 можно
рассматривать как половину углового поворота ' линейных
элементов dr(1) и dr(2) вследствие деформации тела
12.
Недиагональные компоненты тензора деформациихарактеризуют повороты линейного элемента среды при
деформации без изменения его длины. Такого рода
преобразования в чистом виде можно вызвать послойным сдвигом
или кручением материала. По этой причине недиагональные
компоненты тензора деформации называют сдвиговыми
деформациями.
Отсутствие удлинений линейных элементов при сдвиговых
деформациях указывает на то, что они не связаны с изменением
объема тела и характеризуют исключительно изменение его
формы.
2. Тензор напряжений
Деформация – выражает отклонения частиц (молекул) от равновесия
к силе реакции, восстанавливающей равновесие. Имеет молекулярное
происхождение. Силы реакции, распределенные по деформируемому
объему, – внутренние напряжения или просто напряжения.
13.
Силы напряжения имеют близкодействующий характер; радиус ихдействия ограничен межмолекулярным расстоянием (в
континуальном приближении ).
Передача силовой реакции напряжениями с одной части тела на
другую происходит по разграничивающей эти части поверхности.
Напряжения – силы распределенные по поверхности. Их соотносят
к единице площади поверхности
T
x3
F ( n) dF (n)
lim
dS
S 0 S
II
S
(n)
n
dF(n)
I
dS
r
x1
( n)
0
x2
Задание T
требует указания 3-х
компонент вектора силы и ориентации
вектора нормали к элементу dS .
Математически напряжение – объект
более сложный, чем вектор. В общем
случае напряжение в данной точке
среды можно представить набором
из 9 элементов в виде матрицы
размером 3 3
14.
T11 T12Т ik T21 T22
T
31 T32
T13
T23
T33
Тензор напряжений – симметричный
тензор 2-го ранга. Геометрическим
образом является поверхность
тензора в виде эллипсоида с
полуосями, равными главным
значениям (диагональные компоненты
тензора)
Т ik – результат действия
внешней силы F
Т ik и F должны быть связаны между
собой
F – сила, действующая на единицу объема тела
F dV – сила, действующая на элемент объема тела
F FdV – результирующая сила
V
15.
FV
На элемент dS действует поверхностная сила
напряжения
S
dfi Tik nk dS
n
T
По 3 закону Ньютона внешняя сила, приложенная
к объему V, уравновесится результирующей силой
поверхностных напряжений
V
S
Fi dV
Tik
dV
xk
Fi Fi dV Tik nk dS
V
V
S
V
Tik nk dS Tik dS k
S
Fi
Tik
xk
Tik
dV
xk
16.
3. Условие равновесия. Уравнение движения.В статическом состоянии 1) uik , Tik не зависят от времени;
2) внешние силы отсутствуют
T
Tik
Fi ik
0
Fi 0
xk
xk
При наличии массовых сил f , добавляющихся к силам упругости,
необходимо сделать замену F F f . Например, для силы тяготения
в пересчете на единицу объема f g, что дает
T
Fi g i ik
xk
или в равновесии
Tik
gi 0
xk
В динамике единичный объем деформируемого тела может
ускоряться. Тогда
Уравнение
2ui Tik
2
Tik
ui
движения
дает
2
Fi
Fi
xk
t
2
xk
t
17.
Граничные условия.Граница раздела двух упругих сред:
Tik (1) nk(1) S Tik (2) nk(2) S
u(1) S u(2) S
На свободной границе
Tik (1) nk(1) S 0
Для границы жидкость( среда «2») - твердое тело (среда «1»)
напряжения выражаются через давление
Tik ( 2) p ik
Требование непрерывности смещений заменяется условием
непрерывности скоростей смещений.
18.
4. Закон Гука.Важность знания термодинамических условий процесса
деформирования условия измерений деформаций и
напряжений
Исходным является I-ое начало термодинамики dQ dU+dA
dQ TdS
dA определяется по аналогии с механикой:
Tik
dA=Fdx
uik
Знак «минус» берется потому, что
напряжения – это силы реакции
dQ TdS dU Tik duik
Внутренняя энергия U системы только частью связана с
деформированием. Чтобы вычленить из нее энергию теплового
(хаотического) движения молекул нужно перейти к свободной
энергии F U TS (T температура)
19.
dF dUTdS
SdT
dF Tik uik SdT
Tik uik
Из первого начала
U F
Tik
uik S uik T
TdS dU Tik duik
dU Tik duik TdS
Состояние деформируемого изотропного твердого тела
выразится зависимостью F F (uik )
1) Равновесному состоянию отвечает условие T const
При этом Tik 0 , если uik 0
2) В разложении F по степеням uik отсутствует линейный член
(в противном случае F – скалярная по определению величина, зависела бы от знака деформации <растяжение – сжатие были
бы энергетически не эквивалентны>)
20.
3) Так как тензор деформации симметричный из его компонентможно сконструировать только 2 независимые скалярные
константы, квадратичные по uik
2
F F0 C1ull2 C2uik
C1
, C2
2
и – коэффициенты Ламе. С учетом равенства
ull2 (u xx u yy u zz ) 2 (div u) 2
получаем
div u
uik ik
F
ull
2
2
Tik
ull uik ull
2 uik
uik
uik T uik 2
Tik ull ik 2 uik
закон Гука
21.
2K – модуль всестороннего сжатия (всегда K 0)
3
Положительность K , вытекает из условия положительности
свободной энергии и наличия минимума зависимости F F (uik )
4. Основные виды деформаций
uik const
1) Всестороннее сжатие
нет изменения формы
P
P
P
– однородные деформации
Tik P ik (граничное условие)
V
u xx u yy u zz ull
V
1
T
Ku
2
u
u
Закон Гука ik
ik
ll ik
ik ll
3
деформация
3P
Tll Txx T yy Tzz 3Kull 2 ull
P
P
V
Tll 3Kull P K
V
2
( xx yy zz )ull
3
0
22.
2) Простое растяжение (сжатие) стержняF
Отличные от нуля компоненты деформации uik 0 :
l/2
l
d
u xx
, u zz
l
d
uzz uxx
F
Отличная от нуля компонента напряжения :
Txx
S
(граничное условие; на боковой поверхности
напряжения равны нулю)
Условию пропорциональности uzz uxx придают вид
коэффициент Пуассона)
u zz νu xx
l
Закон Гука:
d
z
F
E
Txx Euxx
9 K
1 3K 2
,ν
3K
2 3K
F
l
E
S
l
E модуль
Юнга
Всегда K>0 и обычно
0< <1/2
x
Пены (90-ые годы) имеют 0. У резины 1/2
23.
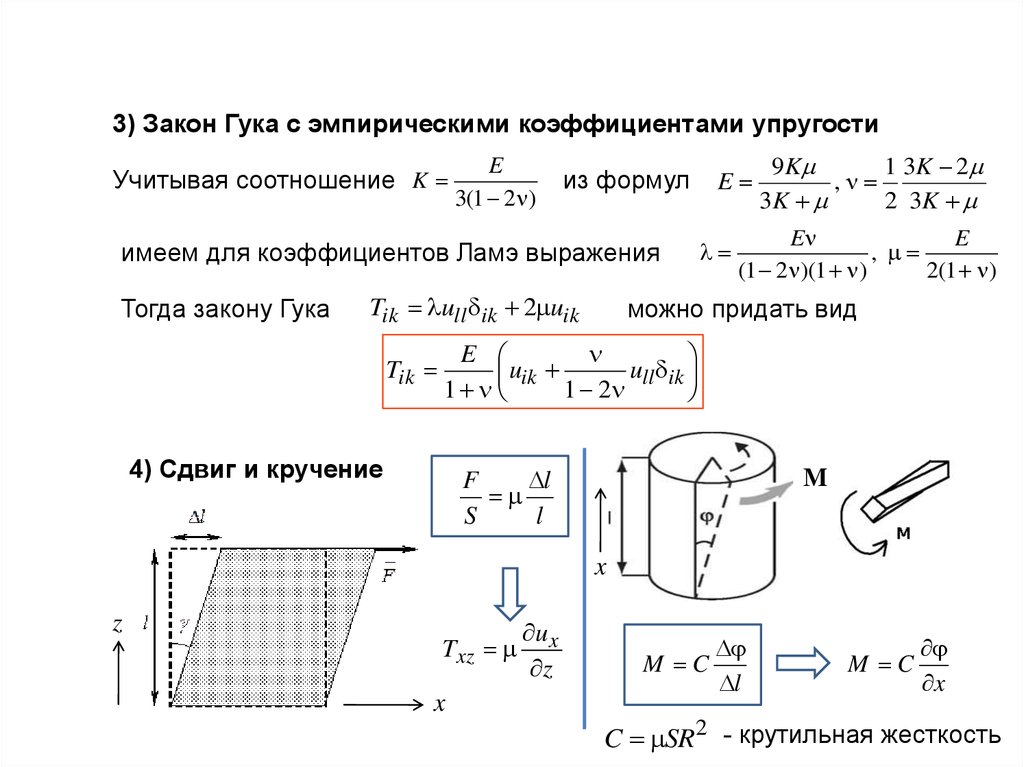
3) Закон Гука с эмпирическими коэффициентами упругостиУчитывая соотношение K
E
3(1 2 )
имеем для коэффициентов Ламэ выражения
Тогда закону Гука
Tik ull ik 2 uik
Tik
E
из формул
9 K
1 3K 2
,ν
3K
2 3K
E
E
,
(1 2 )(1 )
2(1 )
можно придать вид
E
ull ik
uik
1
1 2
4) Сдвиг и кручение
F
l
S
l
M
x
z
Txz
x
u x
z
M C
l
M C
x
C SR2 - крутильная жесткость
24.
5) Изгиб (тип деформации, наблюдающийся в тонких стержнях и пластинах)F
x
M
u(x)
неоднородная
деформация
На каждый элемент стержня (пластины) действуют
поперечные (перерезывающие) силы F и
вращательный момент M, меняющий ориентацию
нейтральной плоскости
dx
u
2u
x
M EI
M EI 2
x
x
F
M
M
F
x
x
x
I – момент инерции поперечного сечения элемента относительно оси,
проходящей через центр масс сечения
25.
5. Уравнение динамики изотропной средыИсходные посылки: однородная среда, малые и быстро
протекающие (адиабатические) деформации
2ui Tik
Используем уравнение движения
2
xk
t
и закон Гука
1
Tik Kull ik 2 uik ik ull
3
имеет такую же форму, как и для статических (изотермических)
деформаций, но с адиабатическими коэффициентами упругости
- одинаковые, K – разные:
1
1 T 2
K S KT C p
Т – абсолютная температура
коэффициент теплового
расширения.
C p изобарическая теплоемкость единицы объема
Условие быстроты процесса: отсутствие заметного теплообмена
за время
26.
Tikull ik 2 uik ull ik 2 uik ik ull 2
xk xk
xk
xk
xk
xk
1 ui uk
2
x
k xi
/ xi
Tik
xk
2
ui
t 2
2
2
u
u
ui
i
k
( )
ull
u
ll
xi
xk
xi
xk2 xi
xk2
u
ll
2ui
2
2 ( )
ull 2 ui
xi
t
xk
div u
Tik
xk
2
2u
2
(
)
grad(div
u
)
u
2
t
27.
6. Волновые уравнения. Продольные и сдвиговые волныu x
2u
2
u u( x, t ) div u
, u 2
x
x
1) Одномерный случай:
2u
2
(
)
grad(div
u
)
u
2
t
2
2
ux
u x
ux
(
)
x x
t 2
x 2
2u x
t
2
( 2 )
1 2u x
cl2 t 2
2u x
x 2
2u x
x 2
Волновое уравнение
для продольных волн
0
2
u y, z
2u y , z
u x
( )
2
y , z x
t
x 2
2
cl
2u y , z
t
2
2u y , z
x 2
1 2 u 2 u
2
2
ct t
x 2
Волновое уравнение
для поперечных волн
ct
28.
2) Обобщение на 3-х мерный случай1 2 ul
2
ul , div ul 0, rot ul 0
2
2
cl t
1 2 ut
2
ut , div ut 0, rot ut 0
2
2
ct t
cl k
ct k
k
u x ul , u ut ,
2
2
x 2
В изотропном упругой среде
способны распространяться без
дисперсии 2 типа волн:
1. продольные – сопровождаются
сжатиями (разрежениями) среды и
имеют большую скорость
2. поперечные (сдвиговые) – не
сопровождаются сжатиями среды,
имеют меньшую скорость
29.
7. Плоские гармонические волны. Особенности рефракции2
1 u l ,t
2
ul ,t ul ,t Ul ,t f (nl ,t r cl ,t )
2
2
cl ,t t
U векторные амплитуды, иначе векторы поляризации, характеризуют
направление и величину смещений в упругих волнах;
n вектор волновой нормали
В случае гармонических волн f тригонометрические функции sin, cos.
Требуется обезразмерить аргументkl ,t
u l ,t U l ,t
u l ,t U l ,t
sin
cos
sin
cos
[kl ,t (nl ,t r cl ,t t )] Ul ,t
sin
(kl ,t nl ,t r kl ,t cl ,t t )]
cos
k l ,t
( k l ,t r t )
ul ,t Ul ,t exp[ i (k l ,t r t )]
kl ,t волновые числа
k l ,t kl ,t n волновые векторы, частота
экспоненциальная форма представления
30.
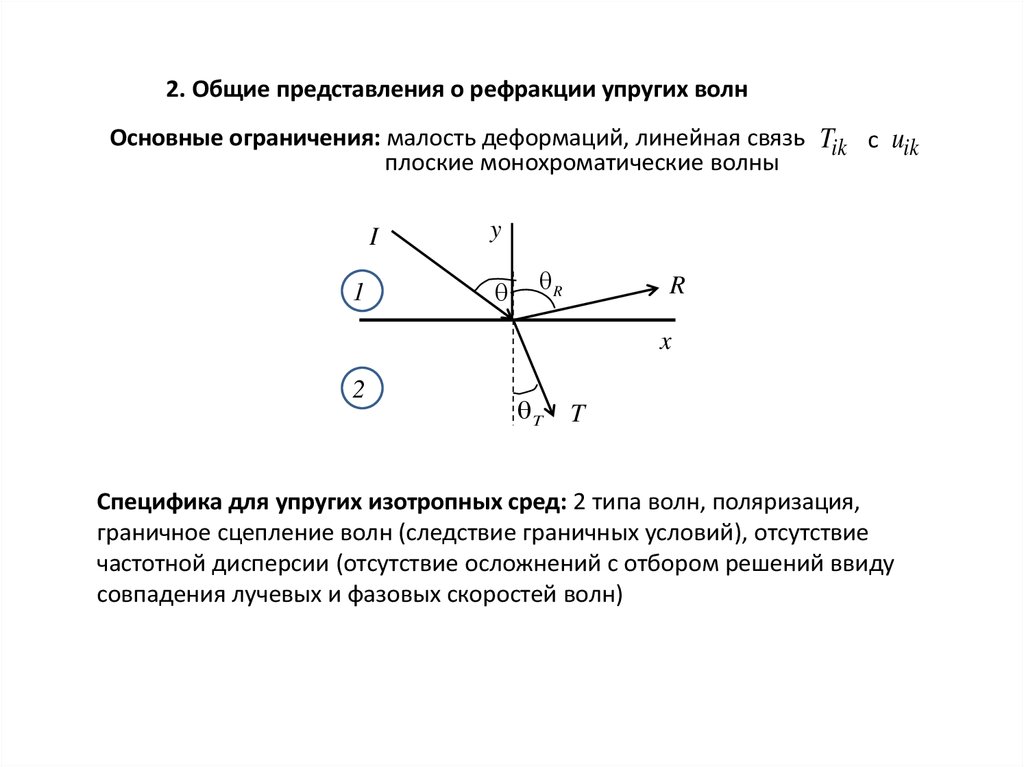
2. Общие представления о рефракции упругих волнОсновные ограничения: малость деформаций, линейная связь Tik c uik
плоские монохроматические волны
I
11
y
θR
R
x
2
θT
T
Специфика для упругих изотропных сред: 2 типа волн, поляризация,
граничное сцепление волн (следствие граничных условий), отсутствие
частотной дисперсии (отсутствие осложнений с отбором решений ввиду
совпадения лучевых и фазовых скоростей волн)
31.
Описание волн:ul ,t Ul ,t exp[ i (k l ,t r t )]
В падающей волне k , и U заданы (излучение создается
источником с известными параметрами). Задачей является
определение аналогичных характеристик для волн, возникающих
при отражении/преломлении.
Направления волновых векторов k (задают направление
распространения волн и направление переноса энергии волной)
в падающей волне к границе
в отраженных/преломленных волнах от границы
Граничные условия:
формулируются для точек границы, разделяющей среды 1, 2,
в терминах результирующих упругих смещений
u
(1)
uI u
j
( R)
j
u ( 2) u (mT )
m
32.
Общая формулировка граничных условий:u(1) y 0 u( 2) y 0 , Tik(1)nk(1) y 0 Tik( 2)nk( 2) y 0
Для выполнения граничных условий (в любой точке границы x ,
в любой момент времени t) экспоненциальные множители в волнах
exp[ i (klx(1) x ωt )] , exp[ i (ktx(1) x ωt )] , exp[ i (klx( 2) x ωt )] , exp[ i (ktx( 2) x ωt )]
должны совпадать
обобщенный закон рефракции
klx(1) ktx(1) klx( 2) ktx( 2) const
В отраженной волне (того же типа поляризации, что и падающая волна)
kl(,It ) sin θ kl(,Rt) sin θ R
θ θ R обычный закон отражения
33.
(1, 2 )(1, 2 )
sin θ (1,2)
Закон преломления: Так как k x k
sin θ (1) sin θ (2)
(2)
(1)
v
v
θ (rT )
θ (rL )
v
(1,2)
sin
θ
(1,2)
обычный закон преломления
Геометрическая интерпретация закона рефракции:
1
ω
L
k x const
T
L
θ t( L )
Трансформация волн при
отражении
2
θ t(T )
34.
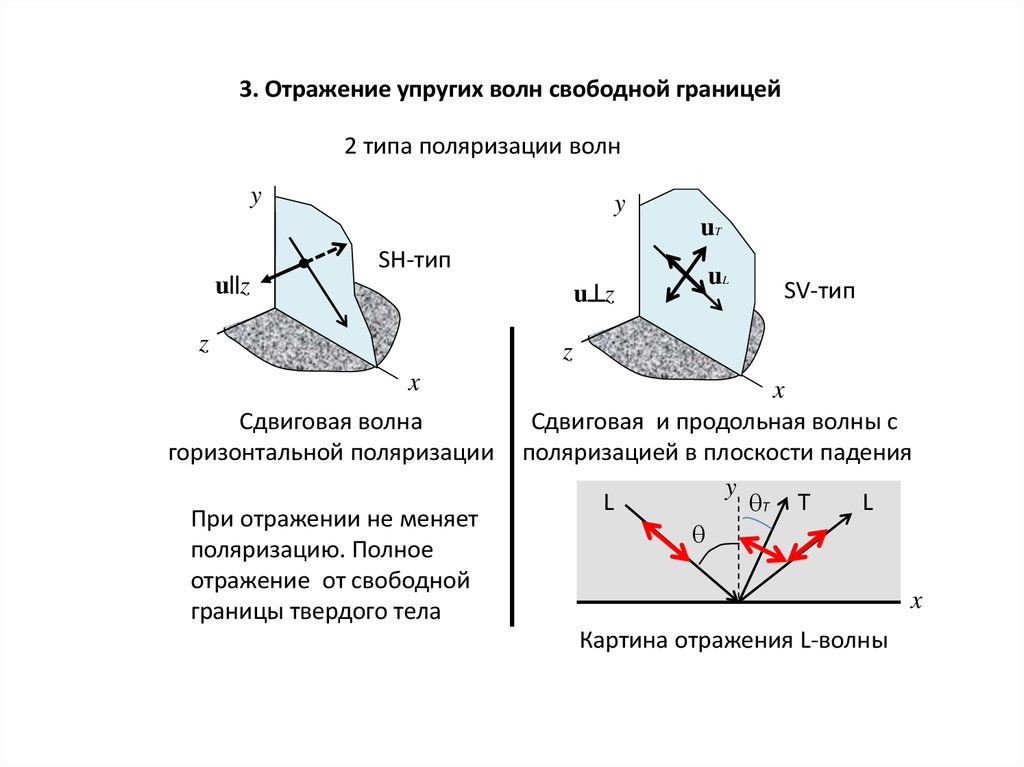
3. Отражение упругих волн свободной границей2 типа поляризации волн
y
y
uT
SH-тип
u||z
u z
z
uL
SV-тип
z
x
Сдвиговая волна
горизонтальной поляризации
При отражении не меняет
поляризацию. Полное
отражение от свободной
границы твердого тела
x
Сдвиговая и продольная волны с
поляризацией в плоскости падения
y
L
L
T T
x
Картина отражения L-волны
35.
Поле упругих смещенийu U 0n 0 exp( ik l n 0r ) U 0 Rl n l exp( ik l n l r )
U 0 Rt [N n t ] exp( ik t n t r )
n 0 (sin θ, - cosθ )
nl (sin θ, cosθ )
nT (sin θt , cosθt )
nT N || z
волновая нормаль падающей L-волны
волновая нормаль отраженной L- волны
волновая нормаль отраженной T- волны
правая тройка векторов
Закон Гука
Tik 2 ct2uik cl2 2ct2 ull ik
36.
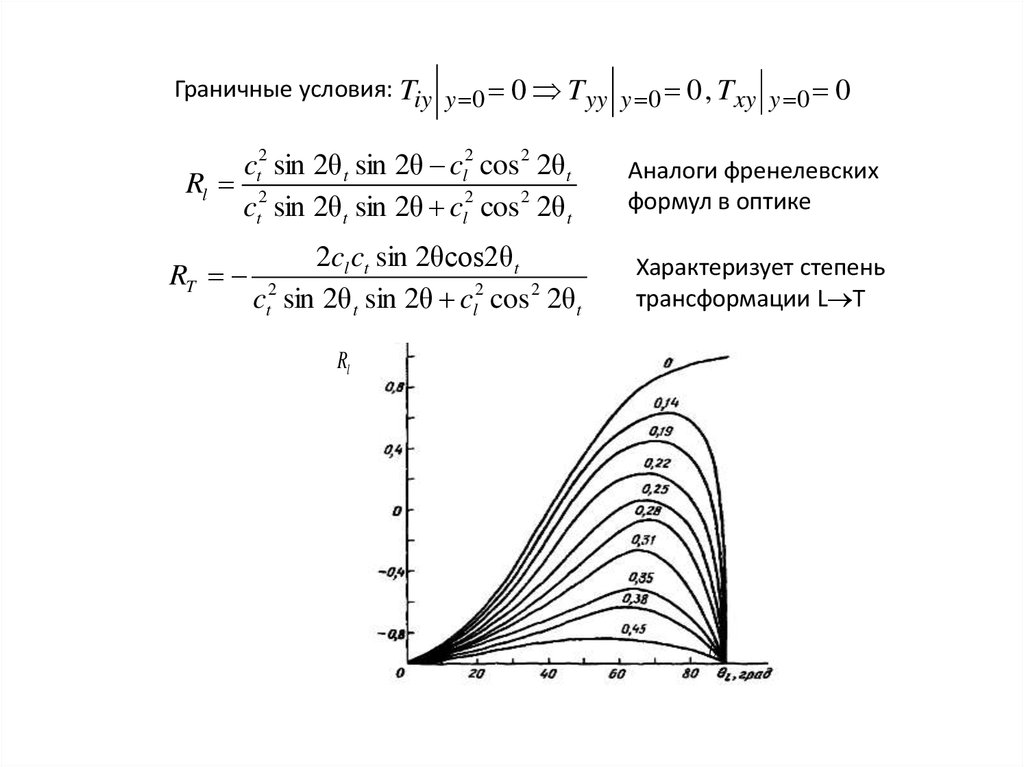
Граничные условия: Tiy y 0 0 T yy y 0 0 , Txy y 0 0ct2 sin 2θ t sin 2θ cl2 cos 2 2θ t
Rl 2
ct sin 2θ t sin 2θ cl2 cos 2 2θ t
Аналоги френелевских
формул в оптике
2cl ct sin 2θcos2θ t
RT 2
ct sin 2θ t sin 2θ cl2 cos 2 2θ t
Характеризует степень
трансформации L T
Rl






























 physics
physics








