Similar presentations:
Упругие волны. Лекция 6
1. Волны
“Путешественнику на кораблекажется, что океан состоит из
волн, а не из воды”
А. Эддингтон, 1929
Лекция 6. Упругие волны
II. Лекция 7. Электромагнитные волны
I.
2. Лекция 6. Упругие волны
3.
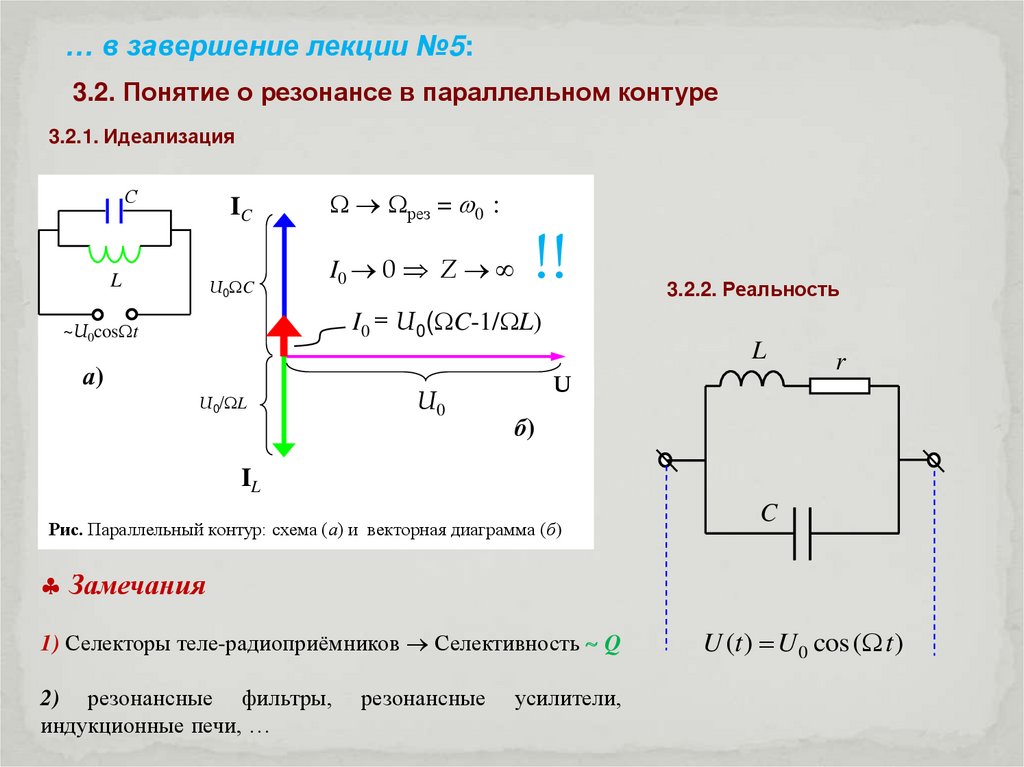
… в завершение лекции №5:3.2. Понятие о резонансе в параллельном контуре
3.2.1. Идеализация
С
IC
L
U0 C
рез = 0 :
I0 0 Z
!!
3.2.2. Реальность
I0 = U0( C-1/ L)
~U0cos t
L
а)
U0/ L
U0
U
r
б)
IL
Рис. Параллельный контур: схема (а) и векторная диаграмма (б)
C
Замечания
1) Селекторы теле-радиоприёмников Селективность Q
2) резонансные фильтры,
индукционные печи, …
резонансные
усилители,
U (t ) U 0 cos ( t )
4.
3.2. Понятие о резонансе в параллельном контуре3.2.2. Реальность
L
UL
UL,R UC U
r
Iобщ
C
IC
IR,L
рез 0 :
I0 0 Z
U (t ) U 0 cos ( t )
!!
5.
Глава III. Волны“Путешественнику на корабле
кажется, что океан состоит из
волн, а не из воды”
А. Эддингтон, 1929
“Опр.” Волна – процесс распространения
колебаний в пространстве
…?
6.
7.
8.
9.
10.
11.
12.
13.
1.1. Дифференциальное волновое уравнение1
2
l
1
n
n–1
n+1
N–1
N
l
2
n
n–1
x–l
x
n+1
N–1
x+l
X
1) система состоит из длинной цепочки большого количества одинаковых
связанных атомов массы m (“химическая аналогия”);
2) амплитуды колебаний малы, силы квазиупруги и моделируются пружинами
жёсткости k;
3) система консервативна;
4) расстояние l между соседними осцилляторами очень мало;
5) соседние шарики-атомы движутся почти одинаково (исключаем из
рассмотрения наиболее высокочастотные моды колебаний).
14.
К выводу дифференциального волнового уравнения1
2
l
n
n–1
n+1
N–1
N
l
1
2
n
n–1
x–l
x
n+1
N–1
x+l
X
m n к( n n 1 ) к( n 1 n )
n ( x, t )
l
n 1 ( x l , t ) ( x, t )
l 2
x
x 2
2
2
2 l 2
n 1 ( x l , t ) ( x, t )
l 2
x
x 2
15.
2m 2 кl
t
x 2
2
2
Обозначим
кl 2 v 2
m
2
t
2
v2
2
x
2
Это одномерное
“Классическое Дифференциальное
Волновое Уравнение”
2
2
v
2
t
“Трёхмерный” случай
2
2
2
" оператор Лапласа " :
2
2
2
x
y
z
16.
Замечания1)
“Опр.” Волна называется продольной, если колебания происходят
вдоль направления распространения возмущений
2
кl
2) Для поперечной вместо v
:
m
2
к
T
l
v2
Tl
m
1.2. Уравнение волны
“Опр.” Уравнением упругой волны называется соотношение,
описывающее зависимость смещения колеблющихся частиц (х,t) от
координат и времени в явной форме:
( x, t )
или
( x, y, z, t )
Уравнение волны – вид решения волнового уравнения
2
v
2
2
t
x
2
2
17. Уравнение волны (2)
12
l
1
n
n–1
2
x–l
n–1
n
x
(0, t ) A cos t
( x, t ) A cos (t ) ;
2
T
N–1
n+1
x+l
n+1
N
l
N–1
x
X
x /v
запаздывание на
( x, t ) A cos t x / v ;
“Длина волны” :
;
N
2 x 2
x
v
T v
v T
“Волновое число” :
k
2
2
2
( x, t ) A cos( t kx) ; или ( x,t) Acos t x
T
18. Уравнение волны (3)
“Опр.” Уравнением гармонической бегущей волны называется функциякоординат и времени вида:
( x, t ) A cos( t kx)
Замечания
1) “недиспергирующая” среда; … любая (t – x/v);
2) гармоническая; “бегущая”; “плоская” (?); в среде без поглощения.
Продольные волны
Поперечные волны
19. Уравнение волны (4)
“Опр.” Волновой поверхностью называют такуюповерхность, колебания во всех точках которой,
происходят в одной и той же фазе
Волновая поверхность, служащая «передней» границей
«возмущенной» области пространства, называется
волновым фронтом
“Опр.” Длиной волны называется расстояние, на которое фронт волны
(или любая волновая поверхность) смещается за один период колебаний
Замечания
( x, t )
… 2) Эта волна …
а. гармоническая;
б. “бегущая” («+»);
в. в среде без поглощения;
г. “плоская”.
A cos( t kx)
20. Уравнение волны (5)
… “плоская” …?
Если фронт волны и волновые поверхности – плоскости,
то волну называют плоской
x D
( D размер источника)
21.
Плоская волнаволновая поверхность
r
O
v
k X
x
k x k r cos k r
(r , t ) Acos( t k r )
22.
1.3. “Другие” волныСферическая волна
Если волновые поверхности имеют сферическую
форму, волну называют сферической
D x, r
A0
( r, t ) cos( t kr)
r
Замечания
1) нет поглощения средой, но энергия “разбегается”;
2) А если есть?
A( х) A0e x
а. Плоская волна:
б.Сферическая волна:
A0 r
A( r )
e
r
23.
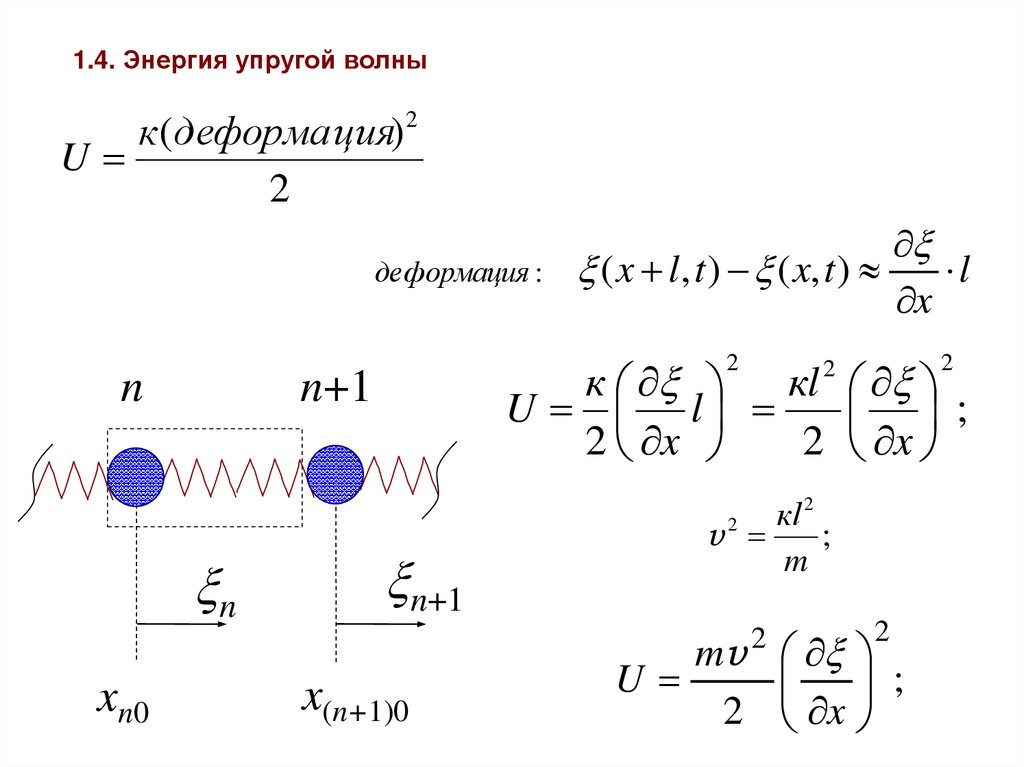
1.4. Энергия упругой волнык ( деформация) 2
U
2
деформация :
n
к кl
U l
;
2 x
2 x
2
n+1
n
( x l , t ) ( x, t )
l
x
n+1
2
кl
v2
;
m
x(n+1)0
2
mv
U
;
2 x
2
xn0
2
2
24.
2m
T
;
2 t
2
mv
U
;
2 x
2
W T U ;
2
2
m
2
W
v
2 t
x
dW
w
dV
( плотность энергии)
2
2
2
w
v
2 t
x
25.
wкинwпот
2
2 2
2
A
sin
( t kx)
2 t
2
v
2
2
v 2
A2 k 2 sin 2 ( t kx)
2 x
2
(с учётом v / k )
w wкин wпот ;
wпот
2
A2 2 sin 2 ( t kx)
w A2 2 sin 2 ( t kx)
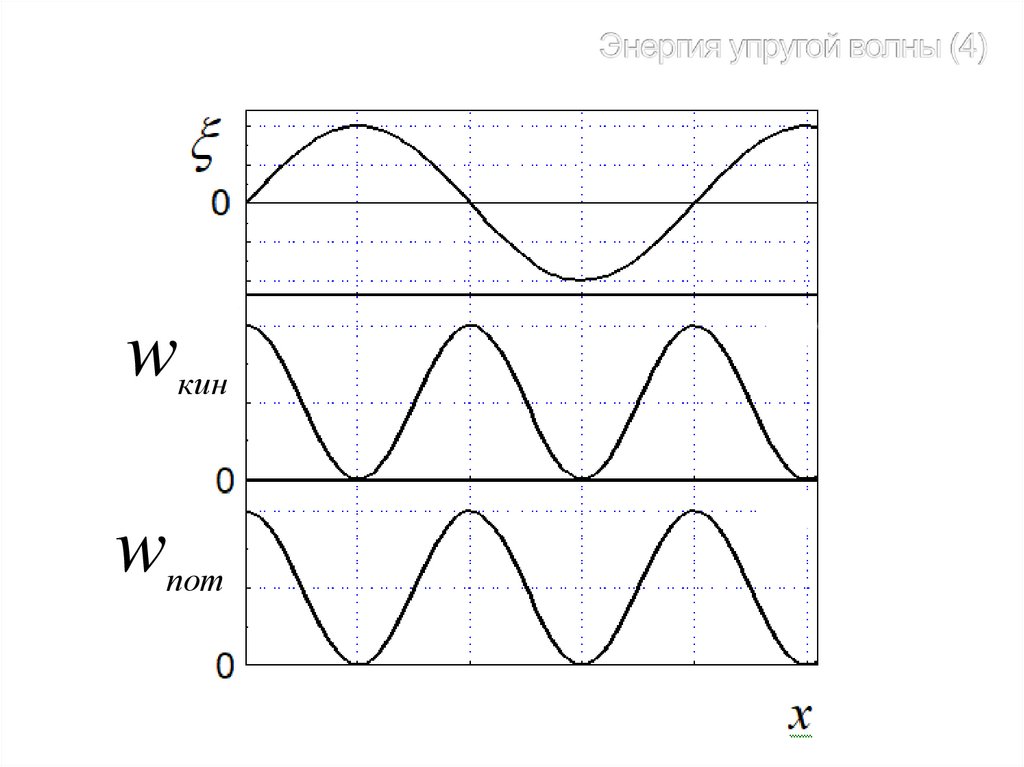
26.
wкинwпот
27.
Характеристики переноса энергии упругой волныw w( x, t )
S (t ) w(t ) v
Плотность потока энергии – энергия, переносимая волной в
единицу времени через «единичную площадку»,
перпендикулярную направлению распространения волны
Интенсивностью волны называется среднее по времени значение
плотности потока её энергии
1
w t A sin ( t kx) A2 2
t
2
2 2
2
1
2 2
I S t w t v A v
2
28.
S w(t ) vВектор Умова:
«векторная интенсивность»:
1
2 2
S w v A v
2
Поток энергии:
S ds S n ds






















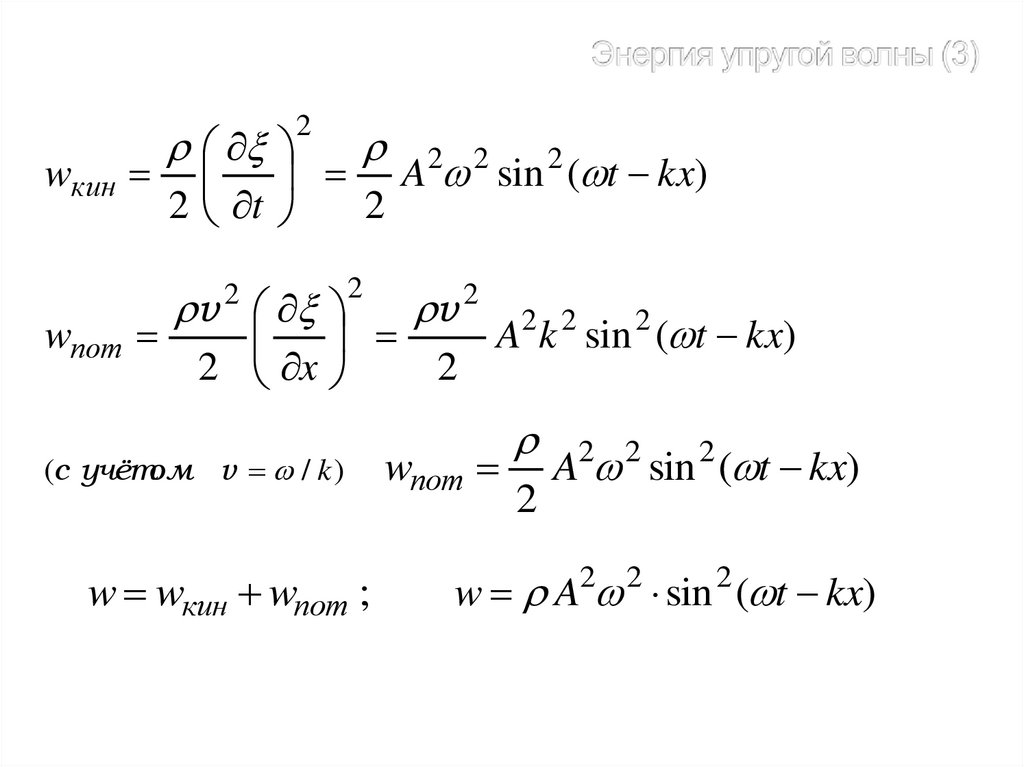


 physics
physics








