Similar presentations:
Энергия упругих волн. Акустика Электромагнитные волны
1.
Общая физика, 4-ый семестрВолны и оптика
Лекция 04
Энергия упругих волн.
Акустика
Электромагнитные волны
9 марта 2022 года
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович
2.
Плотность энергии волныКаждый элемент среды, в которой распространяется упругая волна,
обладает кинетической и потенциальной энергиями, плотности
которых [Дж/м3] пропорциональны квадратам производных от
смещения:
2
2
2
w wk w p
В бегущей волне:
v
2 t
2 x
v
t
x
wk w p
В бегущей гармонической волне плотности кинетической и
потенциальной энергий равны и меняются софазно:
wk wwk p
2
2
a 2 2
2
sin 2 t kx
3.
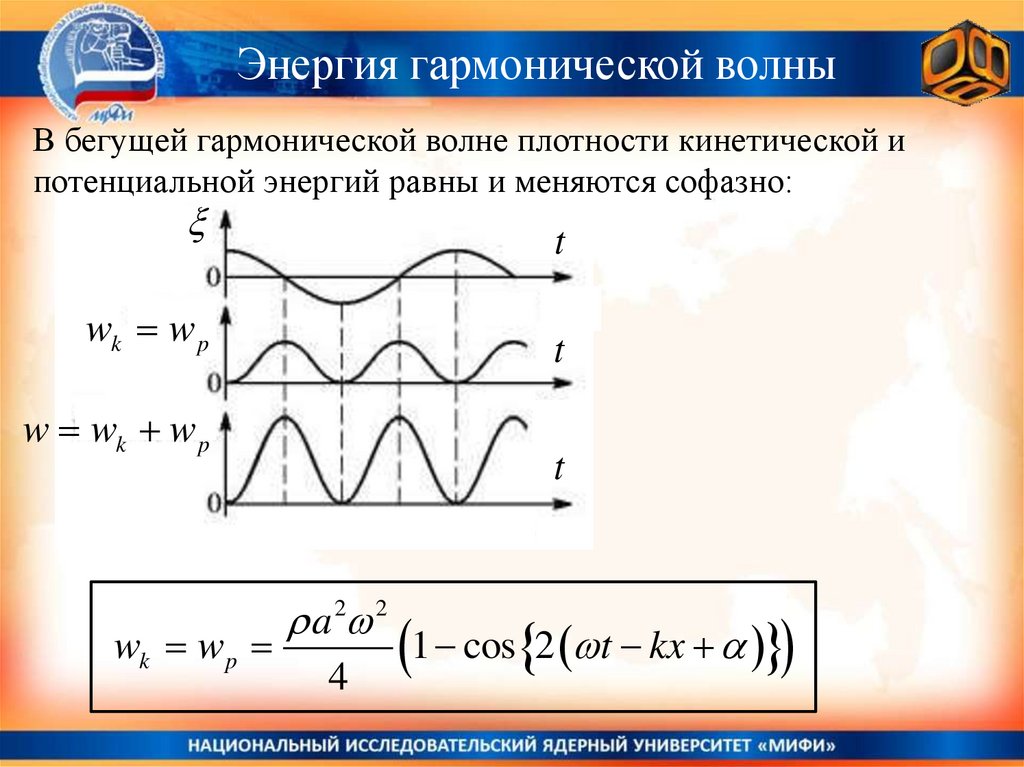
Энергия гармонической волныВ бегущей гармонической волне плотности кинетической и
потенциальной энергий равны и меняются софазно:
t
wk w p
t
w wk w p
wk w p
t
a 2 2
4
1 cos 2 t kx
4.
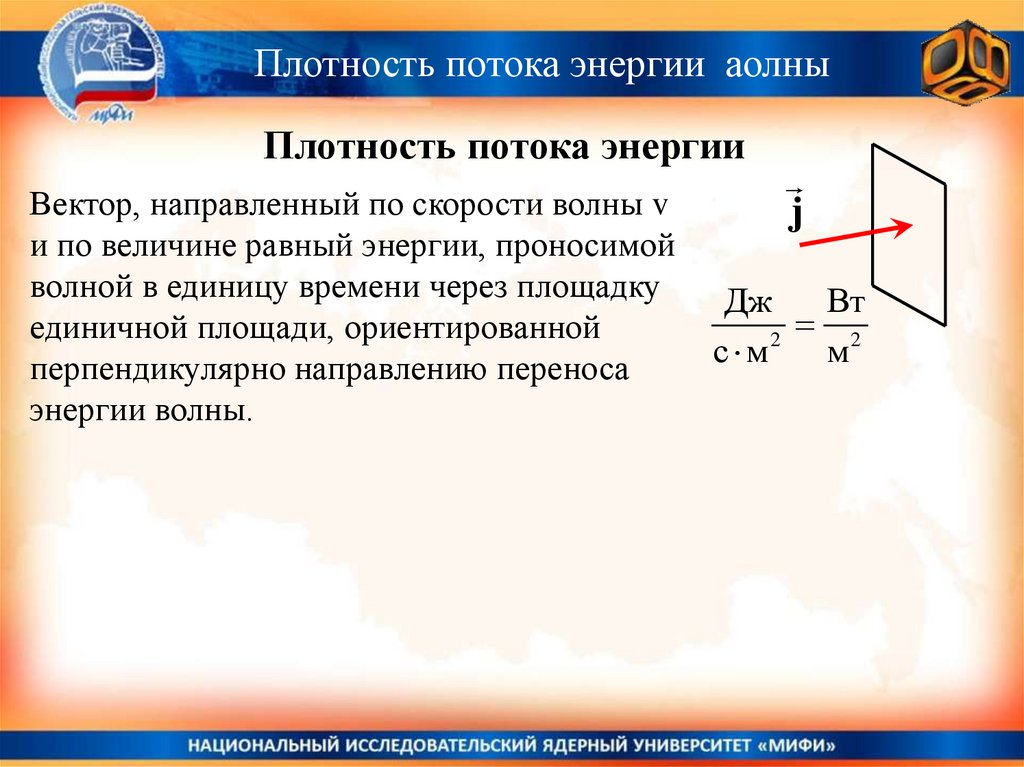
Плотность потока энергии аолныПлотность потока энергии
Вектор, направленный по скорости волны v
и по величине равный энергии, проносимой
волной в единицу времени через площадку
единичной площади, ориентированной
перпендикулярно направлению переноса
энергии волны.
j
Дж
Вт
2
2
с м
м
5.
Непрерывность потока энергииjx
dW jx x, t jx x x, t Sdt
xSdt
x
V , dt
j x x, t
j x, t
V xS
x
x
x
x x
jx
dW
Vdt
x
jx
w
t
x
2
2
2
w v
2
2 t tt 2v x xt
t t 2 t
2 x 2
6.
Плотность потока энергии волныjx
w
t
x
=>
2
2
2
w v
2
2
2v
x xt
t tt
t t 2 t
2 x 2
tt v xx
2
w
2
2
v t xx x xt v
t x
t
x
jx
w
t
x
jx v
t x
2
7.
Плотность потока энергии в средахjx
w
t
x
jx v
t x
2
В газе можно выразить производные от смещений через
отклонения давления и плотности от равновесных :
P
2
2
P
v 0 v
x
S
2
jx v
P
t x
t
В твердом теле роль добавочного давления
∆Р играет механическое напряжение σ:
jx
t
8.
Плотность потока энергии и интенсивностьПлотность потока энергии в бегущей волне
jx v
t x
2
v
t
x
jx v 2vw p vw j wv
x
Интенсивность волны
2
2
I j
Вт
м2
вектор Умова
Это модуль средней по времени
плотности потока энергии.
9.
Интенсивность упругих волн в средахjx P
Pv
P v
t
x
0
Идеальный газ:
P v P P
2
0 v
0 v
2
I jx
I
P 2
0 v
В твердом теле величину ∆Р надо заменить на σ
В гармонической волне
P 2
2
Pmax
2
2
Pmax
I
2 0 v
10.
Интенсивность гармонической волныПлоская гармоническая волна
jx v w 2v wk a 2 2 v 2 sin 2 t kx
sin t kx
2
1
2
1 2 2
I a v
2
a 2 2
j w
2
Сферическая гармоническая волна
r0
I I0
r
2
I 0 I r0
11.
ПОТОК ЭНЕРГИИпоток энергии:
Ф jdS jndS jn dS
среднее значение:
Ф j dS I cos dS
S
S
S
для сферической волны:
Ф
S
S
j dS j S j 4 r 2 P const
S
r0
I I0
r
2
P – мощность источника
12.
Затухание волнПлоская квазигармоническая волна
x, t a exp x cos t kx
- коэффициент затухания. В вязкой среде
I
2 - коэффициент
I0
поглощения
I I 0 exp x
x
13.
Затухание волнСферически-симметричная волна
r02
I I 0 2 exp r
r
I 0 I r0
14.
Звуковые волныАкустика
15.
Скорость звука в средахСкорость звука в газе v P
PV const
S
v
1,4, T 290 K, M 29 г/моль v
Скорость звука в жидкости
RT
M
RT
M
v 1,5 км/с
Скорость звука в твердом теле:
2
vl 2
2
t
x
2
P
v
S
2
vl
E
0
340 м/
16.
Звук в твердом телеПродольная волна (P-волна).
cp ~= (E/ρ)1/2
Материал
E,
ГПа
ср,
км/с
сs,
км/с
Поперечная волна (S-волна).
cs ~= (G/ρ)1/2
Модуль Юнга Е[Па] характеризует
упругие и прочностные свойства
вещества по отношению к объемному
растяжению и сжатию.
Модуль сдвига G[Па] характеризует
упругие и прочностные свойства
вещества по отношению сдвиговой
деформации
с, км/с
в
стержне
Al
70
6,26
3,08
5,08
W
350400
5,46
2,62
4,31
Лёд
3
3,98
1,99
3,28
Cu
110130
4,70
2,26
3,71
Pb
14-18
2,16
0,70
1,20
Fe
200
5,85
3,23
5,17
Чугун
210
4,50
2,40
3,85
17.
Звуковые волны в воздухеШкала звуковых волн
0 16 Гц
16 2 104 Гц
2 10 10 Гц
4
9
>10 Гц
9
18.
Звуковые волны в газеp
t
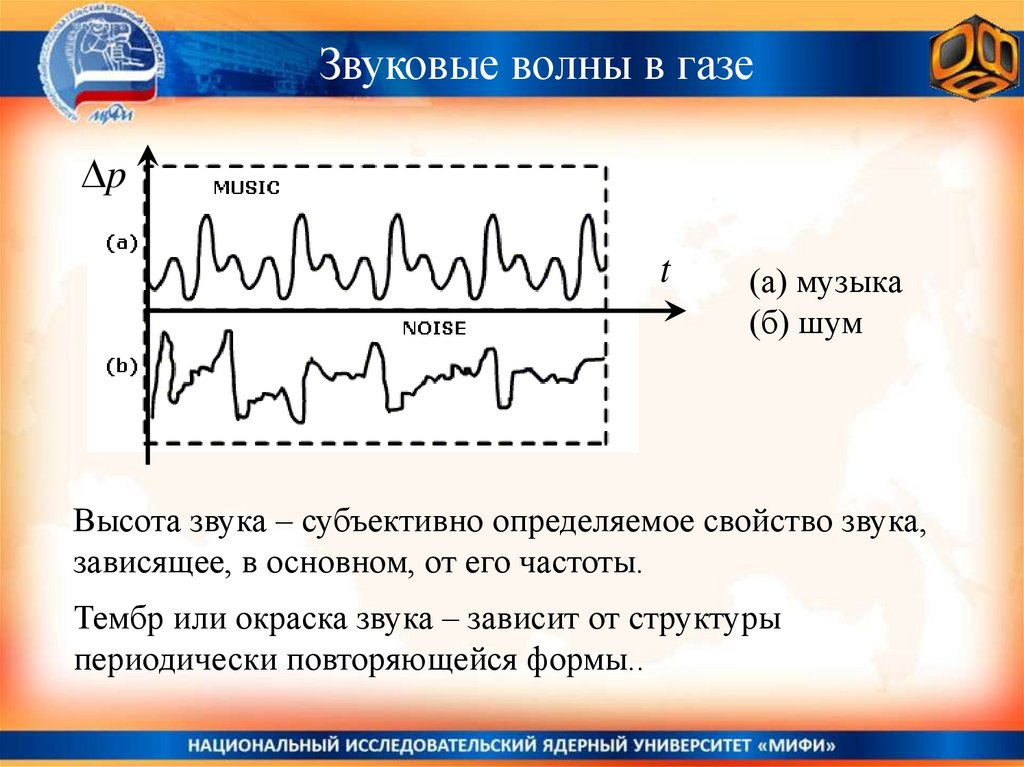
(а) музыка
(б) шум
Высота звука – субъективно определяемое свойство звука,
зависящее, в основном, от его частоты.
Тембр или окраска звука – зависит от структуры
периодически повторяющейся формы..
19.
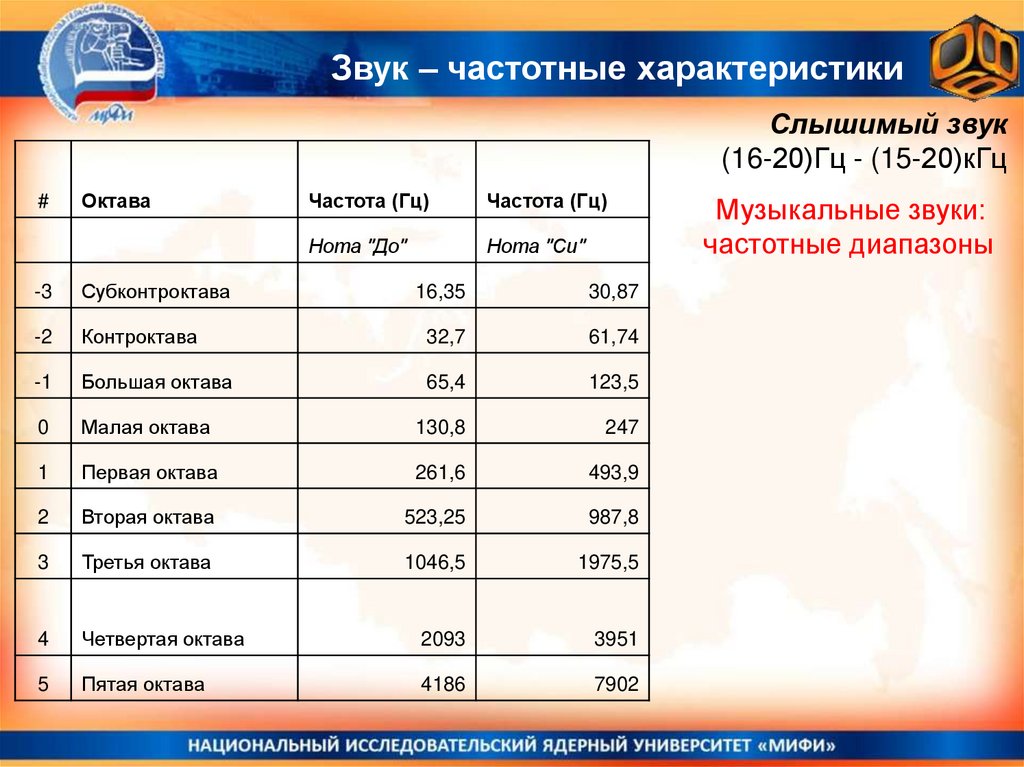
Звук – частотные характеристикиСлышимый звук
(16-20)Гц - (15-20)кГц
#
Октава
-3
Субконтроктава
-2
Частота (Гц)
Частота (Гц)
Нота "До"
Нота "Си"
16,35
30,87
Контроктава
32,7
61,74
-1
Большая октава
65,4
123,5
0
Малая октава
130,8
247
1
Первая октава
261,6
493,9
2
Вторая октава
523,25
987,8
3
Третья октава
1046,5
1975,5
4
Четвертая октава
2093
3951
5
Пятая октава
4186
7902
Музыкальные звуки:
частотные диапазоны
20.
Сила звукаЗвук
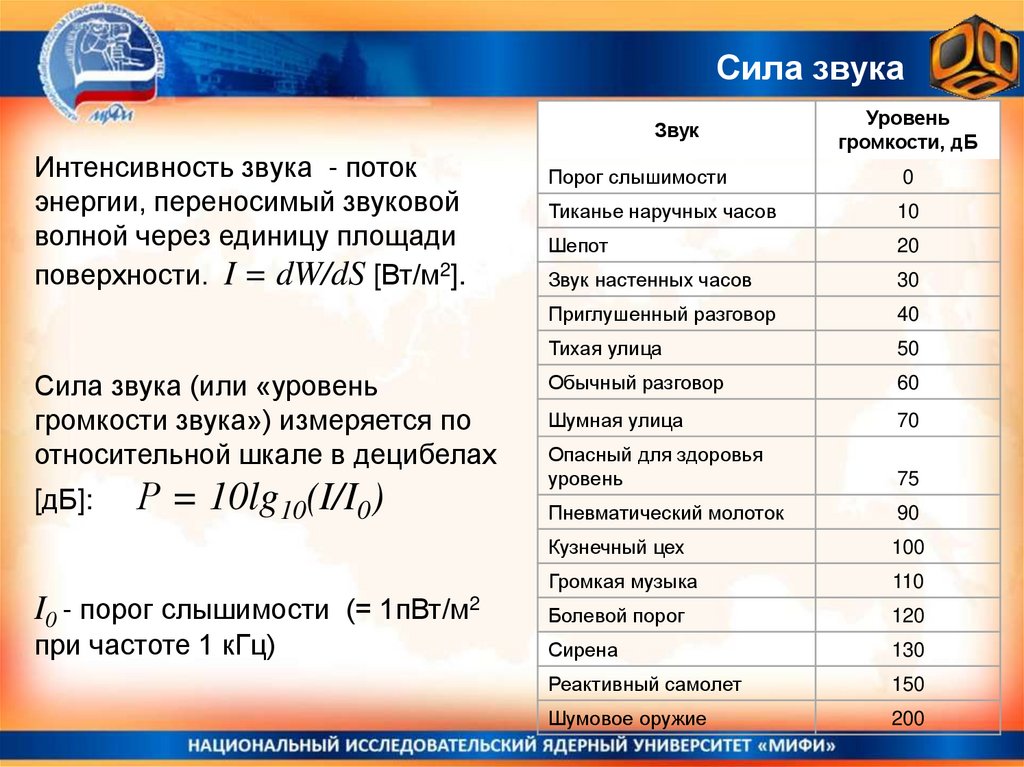
Интенсивность звука - поток
энергии, переносимый звуковой
волной через единицу площади
поверхности. I = dW/dS [Вт/м2].
Сила звука (или «уровень
громкости звука») измеряется по
относительной шкале в децибелах
[дБ]:
Р = 10lg10(I/I0)
I0 - порог слышимости (= 1пВт/м2
при частоте 1 кГц)
Уровень
громкости, дБ
Порог слышимости
0
Тиканье наручных часов
10
Шепот
20
Звук настенных часов
30
Приглушенный разговор
40
Тихая улица
50
Обычный разговор
60
Шумная улица
70
Опасный для здоровья
уровень
75
Пневматический молоток
90
Кузнечный цех
100
Громкая музыка
110
Болевой порог
120
Сирена
130
Реактивный самолет
150
Шумовое оружие
200
21.
ШКАЛА УРОВНЕЙ ГРОМКОСТИ ЗВУКАПорог болевого ощущения –
значение
интенсивности,
при
котором
волна
перестает
восприниматься как звук, вызывая в
ухе лишь ощущение боли и
давления.
I
L 10lg
I0
L – уровень громкости [Дб]
I0 – исходная интенсивность: 10-12 Вт/м2
22.
Распространение звуковых волнПри распространении звуковых волн в среде возникают те-же
характерные эффекты, что и при распространении световых
(электромагнитных) волн:
- Дисперсия (зависимость скорости волны от частоты) – для звуковых волн
в однородных средах выражена слабо
- Затухание (потеря энергии звуковой волной за счет вязкости среды)
- Дифракция (изменение направления распространения волны при
огибании препятствия)
- Интерференция (эффект наложения двух волн одной длины, при котором
амплитуда колебаний в разных точках пространства становится разной)
- Стоячие волны (эффект сложения двух волн одной длины,
распространяющихся навстречу друг-другу)
- Эффект Доплера (зависимость слышимой частоты звука от скорости
источника или приемника звука)
- …..
23.
Эффект ДоплераЭффект Доплера (зависимость слышимой частоты
звука от скорости источника или приемника звука)
Эффект был впервые описан Кристианом
Доплером в 1842 году.
24.
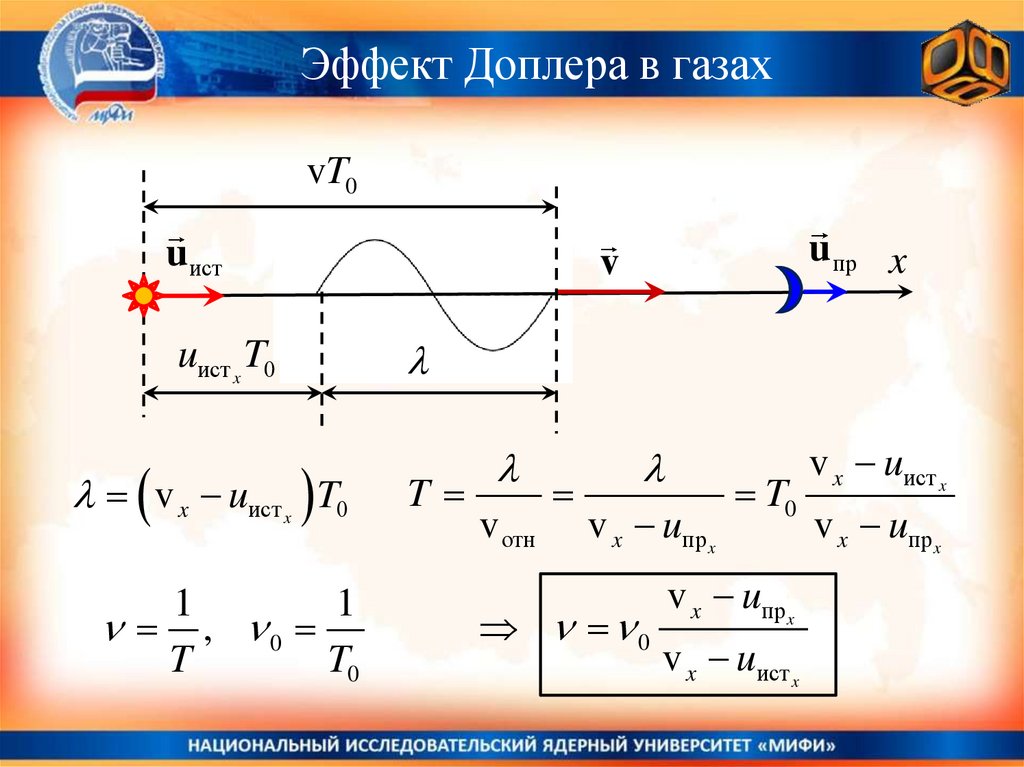
Эффект Доплера в газахvT0
u ист
u пр x
v
uист x T0
v x uист T0
x
1
1
, 0
T
T0
T
v отн
v x uпр x
0
T0
v x uпр x
v x uист x
v x uист x
v x uпр x
25.
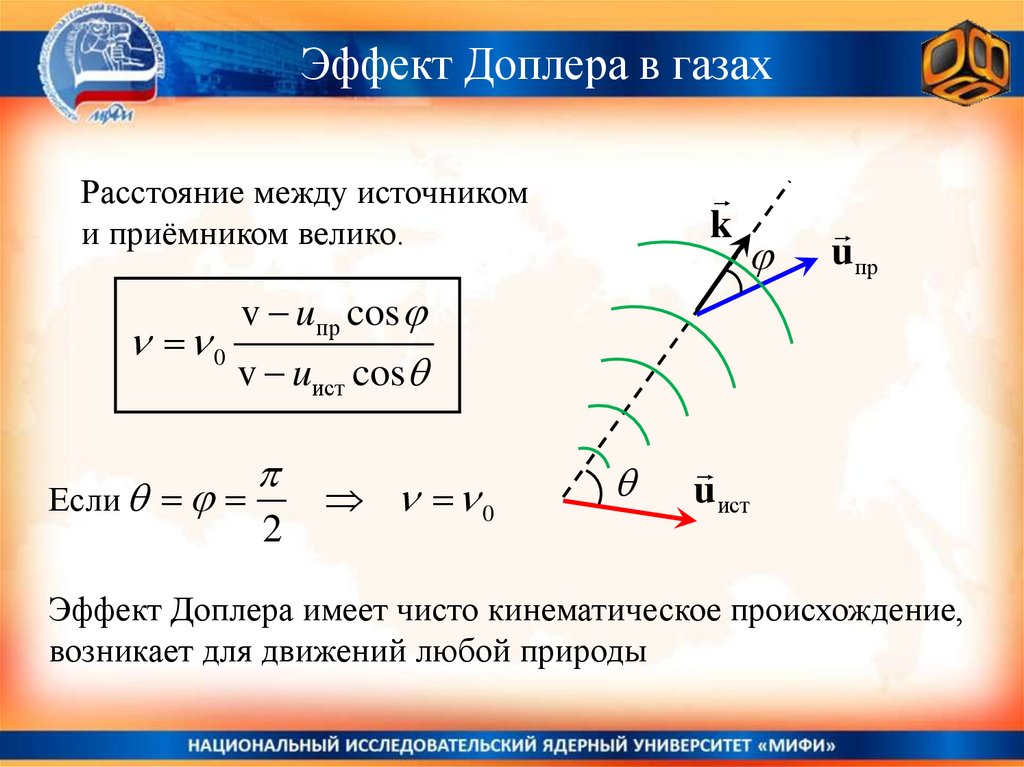
Эффект Доплера в газахРасстояние между источником
и приёмником велико.
0
k
u пр
v uпр cos
v uист cos
Если
2
0
u ист
Эффект Доплера имеет чисто кинематическое происхождение,
возникает для движений любой природы
26.
Ударная волна в газахЕсли uист v , то возникает ударная волна.
Ударная волна и конус Маха, возникшие в результате
сверхзвукового полёта пули с числом Маха 2,45.
27.
Электромагнитные волныH
E 0
t
H E
0
t
2E
2
v
E
2
t
1 c
v
2H
2
v
H
2
t
1
0 0
1
0 0
E 0
H 0
3 10 м/с
8
v
c
28.
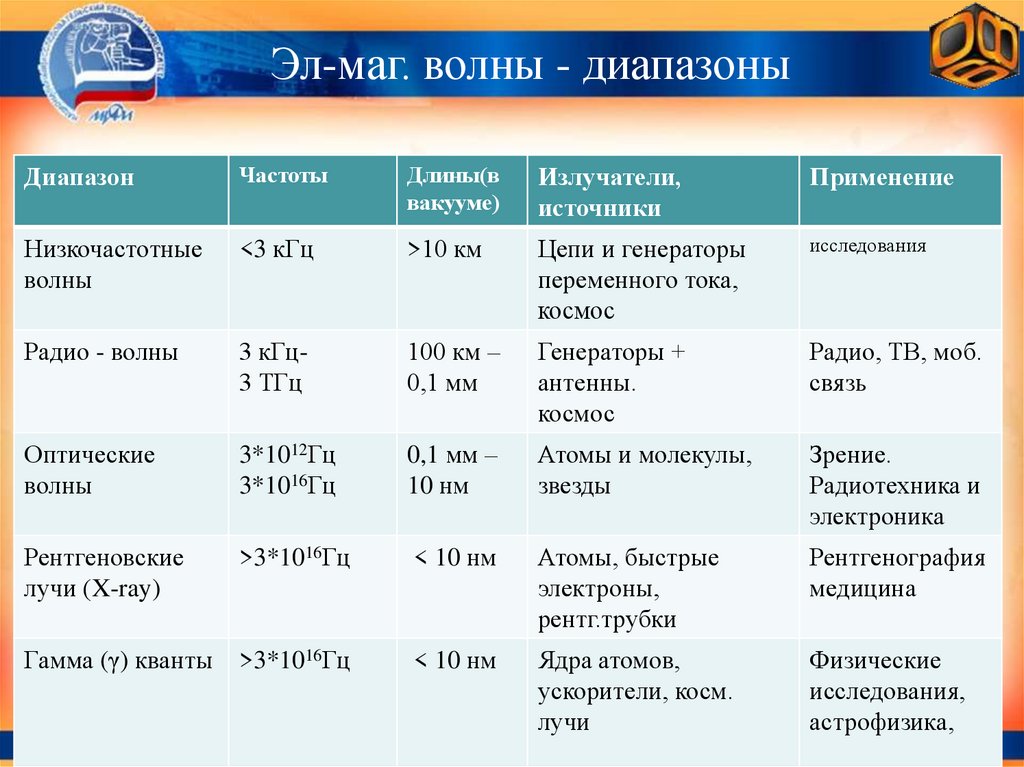
Эл-маг. волны - диапазоныДиапазон
Частоты
Длины(в
вакууме)
Излучатели,
источники
Применение
Низкочастотные
волны
<3 кГц
>10 км
Цепи и генераторы
переменного тока,
космос
исследования
Радио - волны
3 кГц3 ТГц
100 км –
0,1 мм
Генераторы +
антенны.
космос
Радио, ТВ, моб.
связь
Оптические
волны
3*1012Гц
3*1016Гц
0,1 мм –
10 нм
Атомы и молекулы,
звезды
Зрение.
Радиотехника и
электроника
Рентгеновские
лучи (X-ray)
>3*1016Гц
< 10 нм
Атомы, быстрые
электроны,
рентг.трубки
Рентгенография
медицина
Гамма (γ) кванты
>3*1016Гц
< 10 нм
Ядра атомов,
ускорители, косм.
лучи
Физические
исследования,
астрофизика,
29.
Оптический и квантовый диапазоныДиапазон
Длины, частоты,
энергии квантов
Получение и использование
Инфракрасные волны
0,75-100 мкм
3 – 400 ТГц
0,01-1,6 эВ
Тепловое излучение.
Инфракрасные приборы
Видимый свет
380-760 нм
400-800 ТГц
1,6-3,2 эВ
Свет звезд. Атомы.
Зрение
Ультрафиолетовые
волны
380-100 нм
8*1014-3*1015 Гц
3 -10 эВ
Атомы. Звезды. Космос.
Медицина. исследования
Рентгеновское
излучение
0,01 -100 нм
3*1015-3*1019 Гц
10 эВ – 100 кэВ
Атомы, тормозное излучение.
Исследования, медицина
Гамма излучение
< 0,01 нм
>3*1019 Гц
>100 кэВ
Ядра атомов, ускорители,
космические лучи
Физические исследования
30.
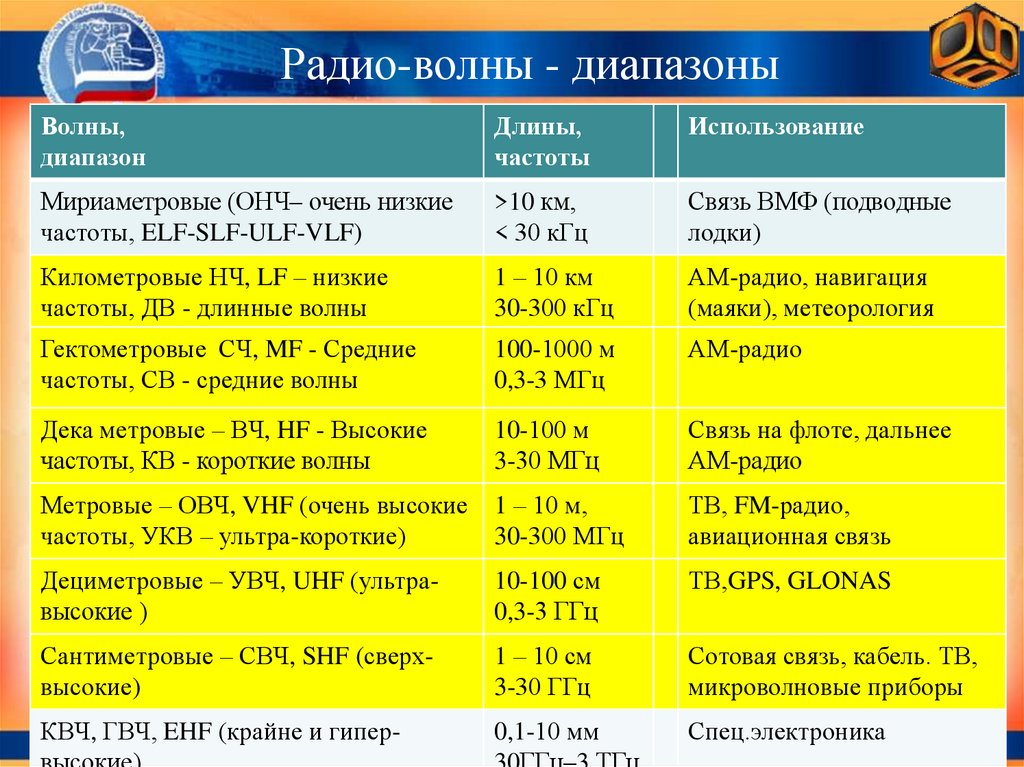
Радио-волны - диапазоныВолны,
диапазон
Длины,
частоты
Использование
Мириаметровые (ОНЧ– очень низкие
частоты, ELF-SLF-ULF-VLF)
>10 км,
< 30 кГц
Связь ВМФ (подводные
лодки)
Километровые НЧ, LF – низкие
частоты, ДВ - длинные волны
1 – 10 км
30-300 кГц
АМ-радио, навигация
(маяки), метеорология
Гектометровые СЧ, MF - Средние
частоты, СВ - средние волны
100-1000 м
0,3-3 МГц
АМ-радио
Дека метровые – ВЧ, HF - Высокие
частоты, КВ - короткие волны
10-100 м
3-30 МГц
Связь на флоте, дальнее
АМ-радио
Метровые – ОВЧ, VHF (очень высокие
частоты, УКВ – ультра-короткие)
1 – 10 м,
30-300 МГц
ТВ, FM-радио,
авиационная связь
Дециметровые – УВЧ, UHF (ультравысокие )
10-100 см
0,3-3 ГГц
ТВ,GPS, GLONAS
Сантиметровые – СВЧ, SHF (сверхвысокие)
1 – 10 см
3-30 ГГц
Сотовая связь, кабель. ТВ,
микроволновые приборы
КВЧ, ГВЧ, EHF (крайне и гипер-
0,1-10 мм
Спец.электроника
31.
Излучение электромагнитных волн32.
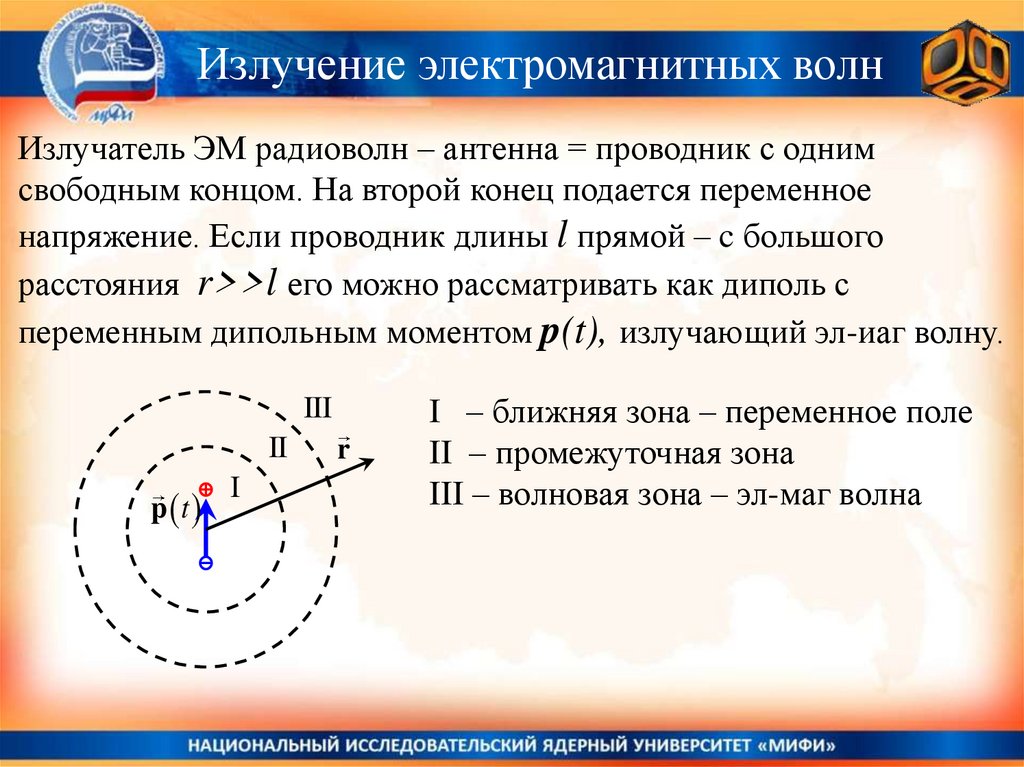
Излучение электромагнитных волнИзлучатель ЭМ радиоволн – антенна = проводник с одним
свободным концом. На второй конец подается переменное
напряжение. Если проводник длины l прямой – c большого
расстояния r>>l его можно рассматривать как диполь с
переменным дипольным моментом p(t), излучающий эл-иаг волну.
III
II
p t
I
r
I – ближняя зона – переменное поле
II – промежуточная зона
III – волновая зона – эл-маг волна
33.
Излучение электромагнитных волнIII
II
p t
I
r
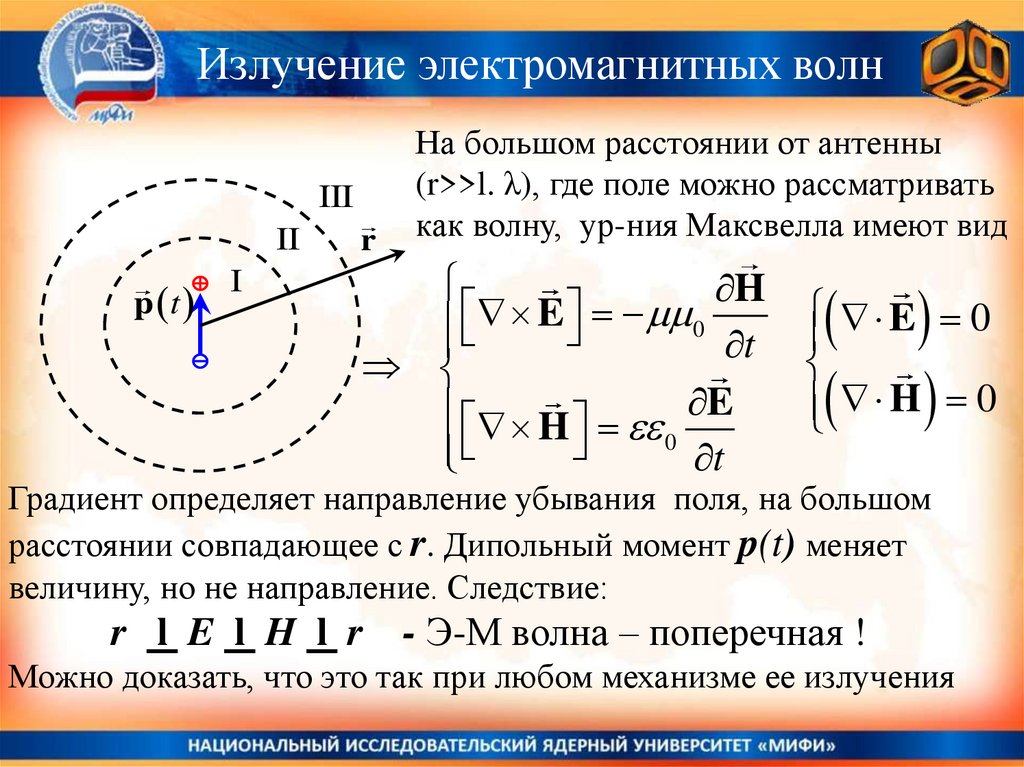
На большом расстоянии от антенны
(r>>l. λ), где поле можно рассматривать
как волну, ур-ния Максвелла имеют вид
H
E 0
t
H E
0
t
E 0
H 0
Градиент определяет направление убывания поля, на большом
расстоянии совпадающее с r. Дипольный момент p(t) меняет
величину, но не направление. Следствие:
r l E l H l r
- Э-М волна – поперечная !
Можно доказать, что это так при любом механизме ее излучения
34.
Излучение электромагнитных волнВектора E l H l r образуют правую
тройку, причем векторное произведение
III
II
r S = [E, H ] || r и имеет размерность
[Вт/м2]. Это вектор Пойнтинга I
p t
плотность потока энергии ЭМ-волны –
аналог вектора Умова для волн упругих.
В следующей лекции мы строже
покажем, что это действительно так.
I = |<S>| = абсолютная величина усредненного по времени
вектора Пойнтинга = интенсивность волны.
Закон сохранения энергии требует, чтобы средний по времени
полный поток вектора Пойнтинга через любую поверхность,
окружающую источник излучения, был одним и тем же и равным
средней мощности источника <Р> [Вт]
35.
Излучение электромагнитных волнНа больших расстояниях от диполя – источника волны
p
= K sin2θ / r2
2
0
0
0
2
2
r
d
I
r
,
sin
d
2
r
<Р>
I r, sin d
=> <Р> = (8π /3)K => I = 3<Р>sin2θ /8πr2
I
36.
Излучение электромагнитных волнЕсли излучатель – диполь с
моментом р(t), можно показать, что
P
p
I = 3<Р>sin2θ /8πr2
2
I
6 c 0
3
p
2
sin
2
16 2 c 3 0 r 2
Мощность излучения пропорциональна квадрату второй
производной по времени от меняющегося дипольного момента.
Если p(t) ~ cos(ωt), то средняя мощность излучения
<P> ~ ω4
(!)
37.
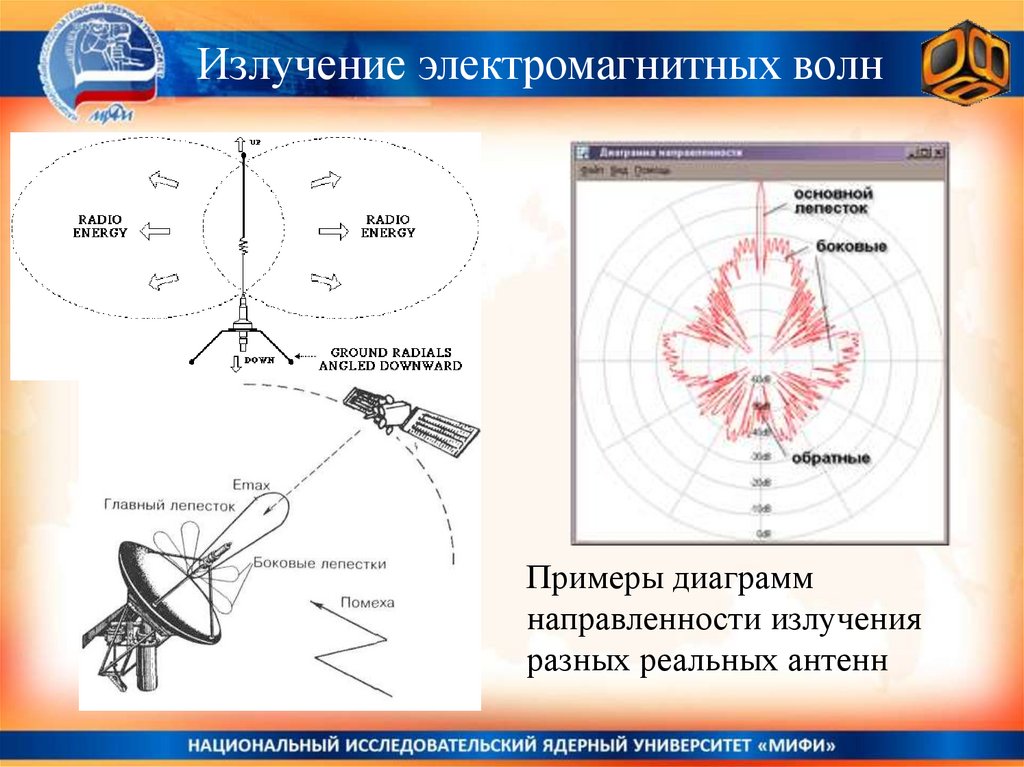
Излучение электромагнитных волнПримеры диаграмм
направленности излучения
разных реальных антенн
38.
Излучение электромагнитных волнИзлучение зарядов, движущихся с ускорением
p qr
p qr qa
39.
Излучение электромагнитных волн40.
Эффект Доплера для электромагнитных волнЭффект Доплера = изменение частоты и/или длины волны,
воспринимаемой приёмником при относительном движении
источника и приёмника волн.
В отличие от звуковых волн, скорость ЭМ-волн в вакууме
одинакова для любого наблюдателя и равна с. Но время для
разных наблюдателей может течь по разному!
c - скорость света в вакууме
u - относительная скорость источника и приёмника
t0 - собственный период колебаний источника
t1 - период колебаний, воспринимаемых приемником
t1 t0
t0
1 u 2 c2
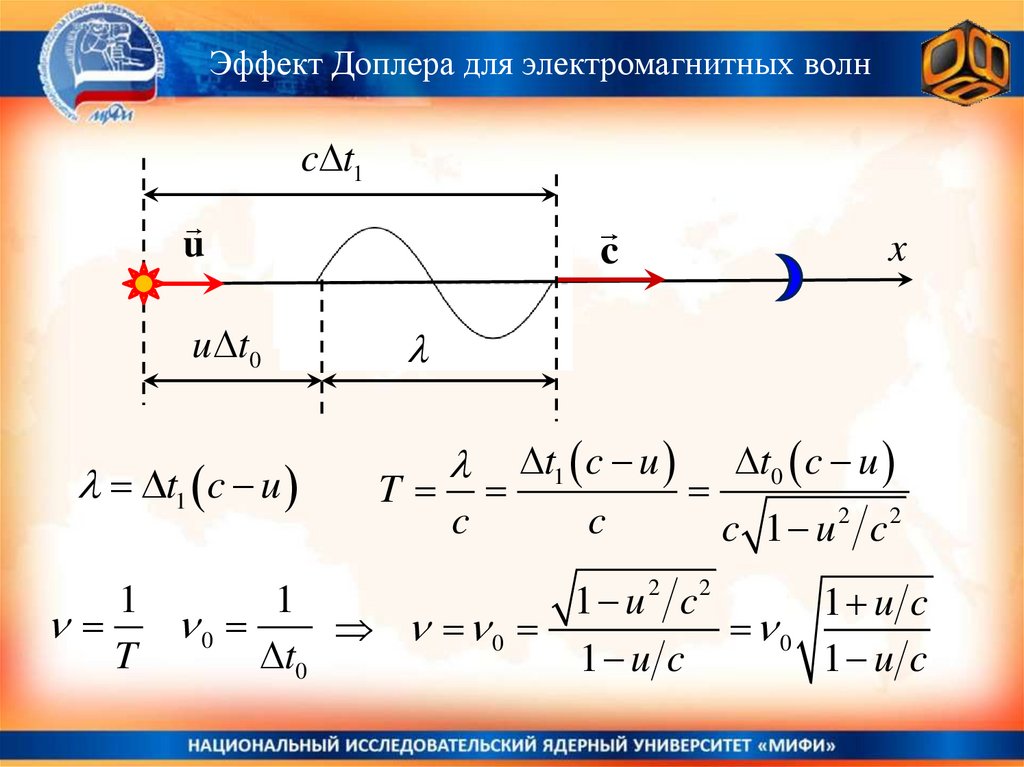
41.
Эффект Доплера для электромагнитных волнc t1
u
u t 0
t1 c u
c
x
t1 c u t0 c u
T
2
2
c
c
c 1 u c
1
1
1 u 2 c2
1 u c
0
0
0
T
t0
1 u c
1 u c
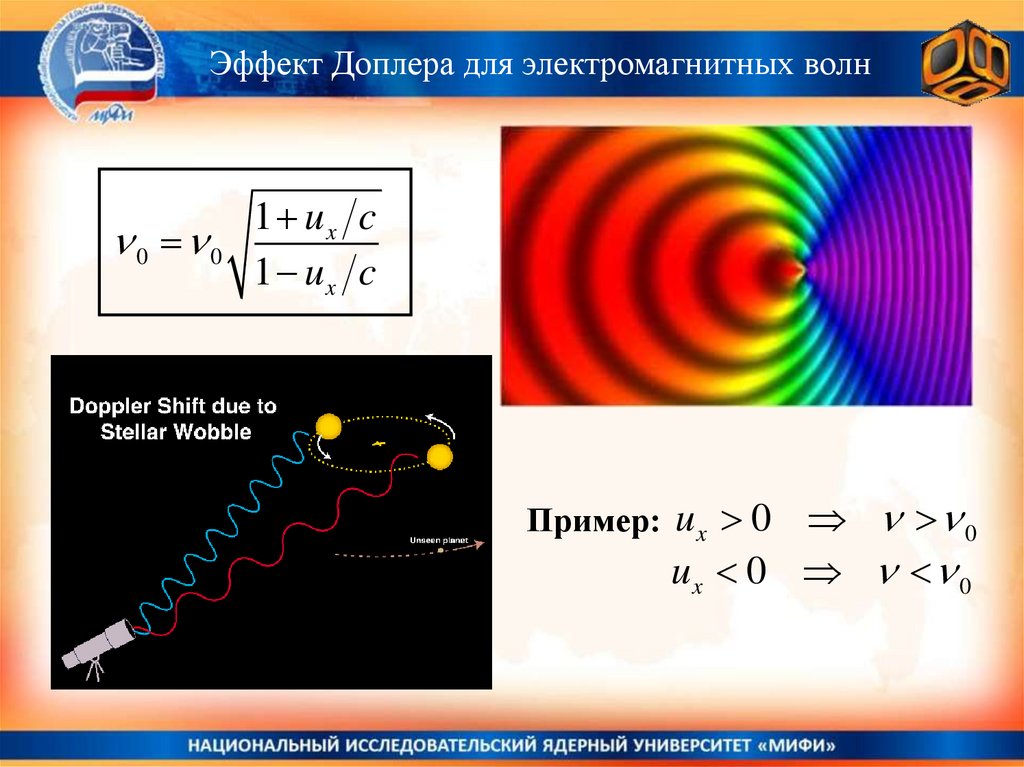
42.
Эффект Доплера для электромагнитных волн0 0
1 ux c
1 ux c
0
ux 0 0
Пример: u x 0
43.
Примеры решения задачПример 1. Звуковая волна распространяется вдоль трубы
длиной l 50 м, заполненной воздухом. Коэффициент
затухания звука в трубе 0,010 м-1. Каков уровень
громкости звука у конца трубы, если у её начала он равен
L1 60 дБ?
k
0
x
l
I
L 10lg
I0
a a1 exp x
44.
Примеры решения задачk
x
0
l
I I1 exp 2 x
I1
L 10lg 20 l lg e
I0
L L1 20 l lg e 56 дБ
45.
Примеры решения задачПример 2. В упругой струне массы m возбудили стоячую
волну основного тона с частотой 1 . Амплитуда колебаний
струны в пучности смещений составила a1. Найти
максимальное значение кинетической энергии струны.?
x, t Asin kx sin t
0, t l , t 0
sin kl 0
kl n, n 1,2,3...
46.
Примеры решения задачkn n l , n 1,2,3...
A a1
1
x, t a1 sin
wк
2 t
2
wк
a12 12
2
sin
2
x
x
l
l
k l
sin 1t
cos2 1t
47.
Примеры решения задачdV Sdx
l
dWк wк dV
sin
0
Wк
2 x
Wк
Sa12 12
2
l
cos 1t sin
2
0
2 x
l
dx 1 cos
dx
l
l
2
0
l
lSa
2
1
4
2
1
cos 1t
2
Wmax
ma
Wк
cos2 1t
4
ma12 12
4
2
1
2
1
2
x
l
dx
48.
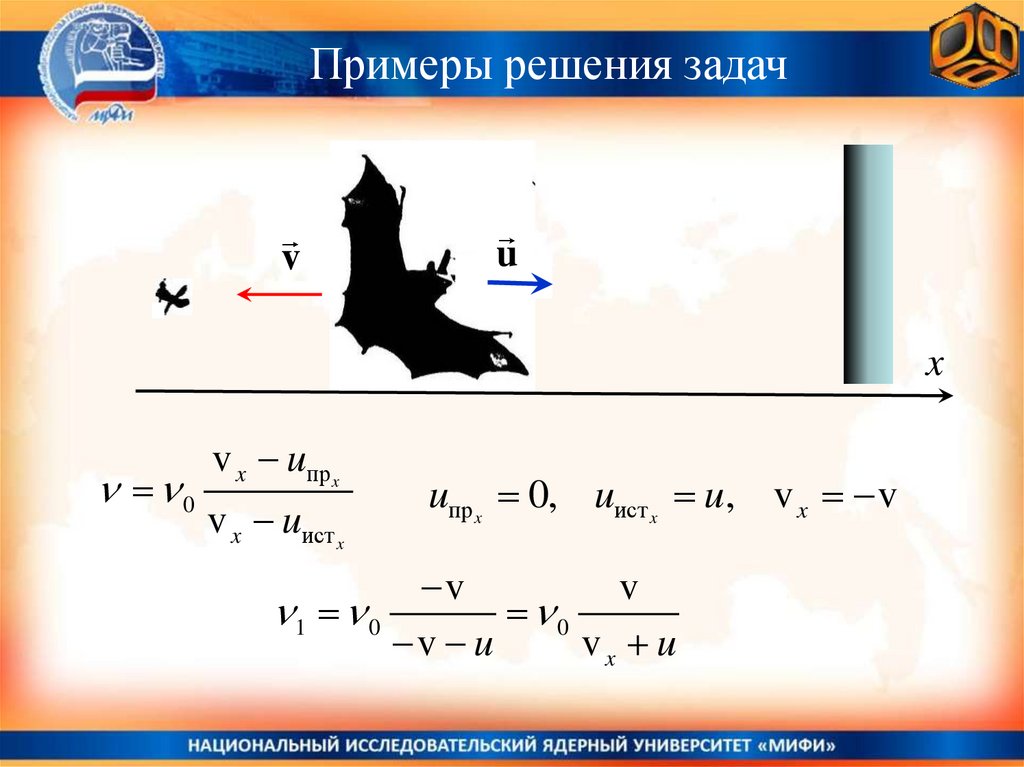
Примеры решения задачПример 3. Летучая мышь летит перпендикулярно к стенке со
скоростью u 6,0 м/с , излучая при этом ультразвуковую волну
с частотой 0 46 кГц . Насекомое, расположенное за спиной
летучей мышью на линии её движения, слышит акустические
биения. Какова частота этих биений? Скорость звука 340 м/с.
u
x
49.
Примеры решения задачv
u
x
0
v x uпр x
v x uист x
uпр x 0, uист x u, v x v
v
v
1 0
0
v u
vx u
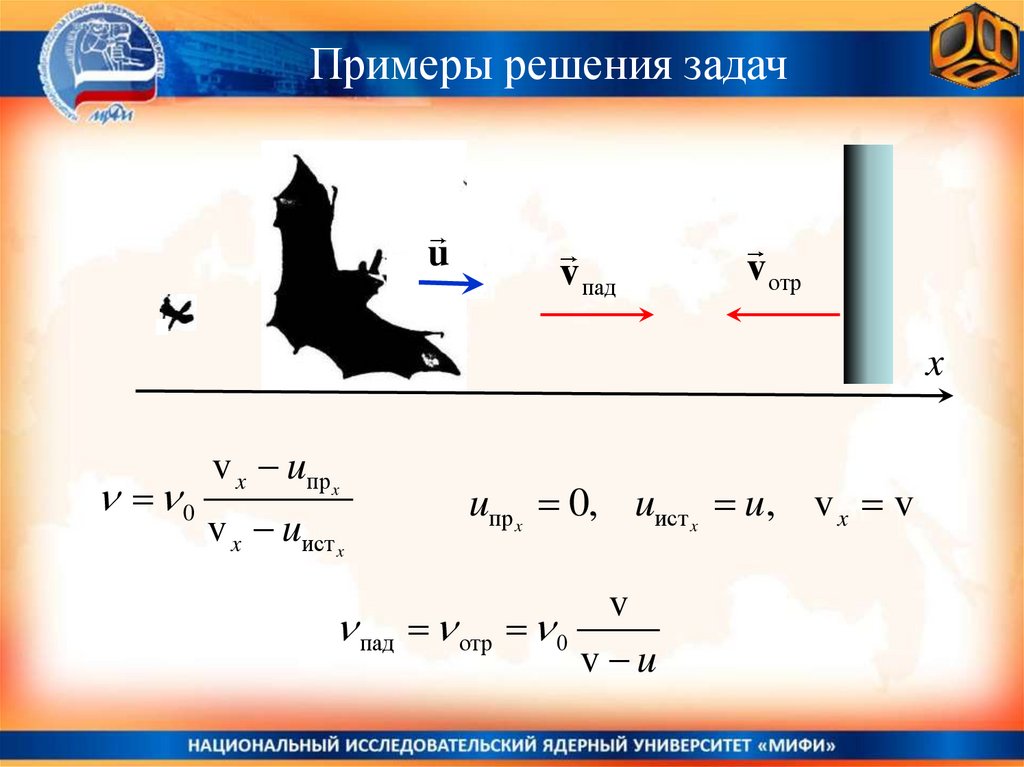
50.
Примеры решения задачu
v пад
v отр
x
0
v x uпр x
v x uист x
uпр x 0, uист x u, v x v
пад отр
v
0
v u
51.
Примеры решения задачu
v пад
v отр
x
v
v
б отр 1 0
0
v u
v u
2vu
2u
3 2 6
3
б 0 2 2 0
46 10
1,6 10 Гц
v u
v
340
52.
Общая физика, 4-ый семестрСпасибо за внимание!
Следующая лекция
16 марта




































 physics
physics








