Similar presentations:
Упругие волны. Электромагнитные волны
1.
Кафедра физикиЛЕКЦИЯ 10
ПЛАН ЛЕКЦИИ
1. Упругие волны:
- уравнения плоской и сферической волн;
- волновое уравнение;
- звуковые волны. Эффект Доплера (самостоятельно).
2. Электромагнитные волны:
- волновое уравнение;
- энергия электромагнитной волны;
- интенсивность;
- импульс электромагнитной волны.
Общая физика. «Волны»
1
2.
Упругие волныКафедра физики
Основные виды волн:
- упругие (например, звуковые и сейсмические волны);
- волны на поверхности жидкости;
- электромагнитные волны (в том числе световые и радиоволны).
Характерная особенность волн - при их распространении происходит
перенос энергии без переноса вещества.
Упругая волна - процесс распространения возмущения в упругой
среде.
Гармоническая волна - изменение состояния среды происходит по
закону синуса или косинуса.
Параметры упругих гармонических волн
Фронт волны (волновой фронт) - геометрическое место точек, до
которых доходят колебания к некоторому моменту времени t.
Общая физика. «Волны»
2
3.
Упругие волныКафедра физики
Волновая поверхность - геометрическое место точек, колеблющихся
в одинаковой фазе.
Простейшие волновые поверхности - плоскость или сфера. Волна
соответственно плоская или сферическая.
Пусть плоская гармоническая
волна распространяется со
скоростью v. вдоль оси x .
0
x
Общая физика. «Волны»
Графически волна изображается в
виде функции x,t (дзета) для
фиксированного
момента
времени.
3
4.
Упругие волныB
Функция
x,t - зависимость
смещения
точек с различными
значениями x от
положения
равновесия.
v
0
x
x
Кафедра физики
х - это расстояние от источника
колебаний
О,
на
котором
находится, например, частица В.
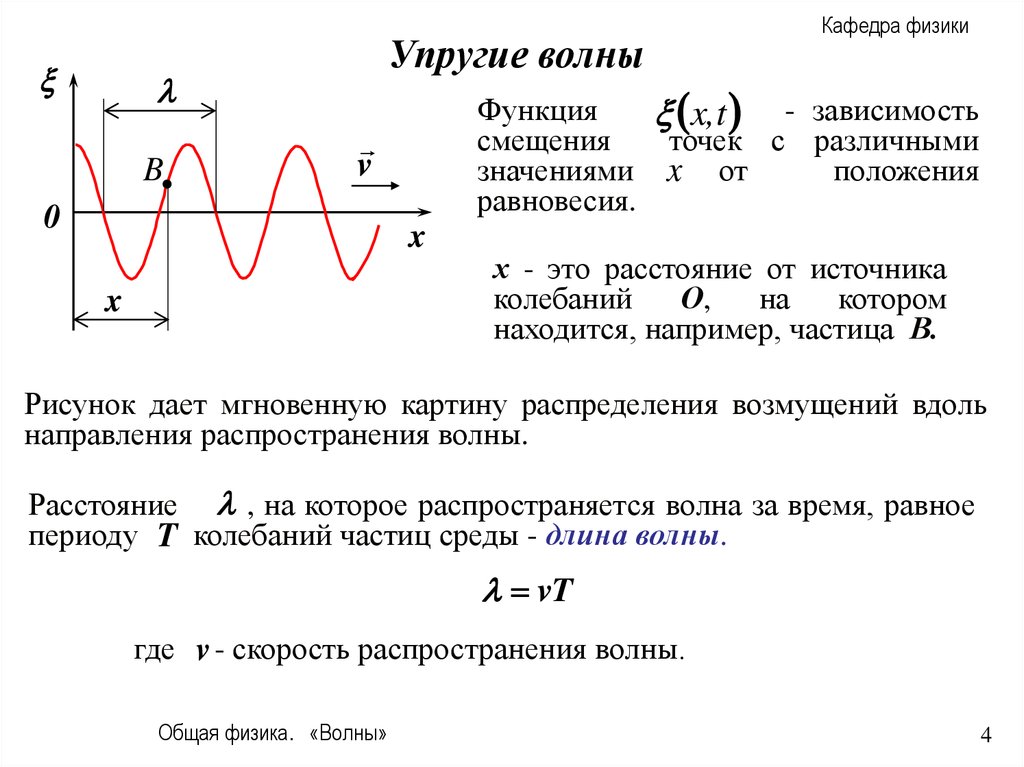
Рисунок дает мгновенную картину распределения возмущений вдоль
направления распространения волны.
Расстояние , на которое распространяется волна за время, равное
периоду T колебаний частиц среды - длина волны.
vT
где v - скорость распространения волны.
Общая физика. «Волны»
4
5.
Кафедра физикиУпругие волны
Уравнения плоской и сферической волн.
Уравнение волны – это уравнение,
выражающее зависимость смещения
колеблющейся частицы, участвующей
в волновом процессе, от координаты ее
равновесного положения и времени:
x , y , z; t
B
0
v
x
x
Рассмотрим плоскую гармоническую волну, распространяющуюся
вдоль положительного направления оси х в среде, не поглощающей
энергию.
Волновые поверхности будут перпендикулярны оси х, а все величины,
характеризующие колебательное движение частиц среды, зависят
только от времени t и координаты х.
Общая физика. «Волны»
5
6.
Упругие волныКафедра физики
Уравнения плоской и сферической волн.
Смещение будет зависеть только от
иx : t
x,t
B
.
0
v
x
x
Пусть колебание точки с координатой x 0 (источник колебаний)
задается функцией вида
0 , t A cos t 0
Задача: найти вид колебания точек в плоскости, соответствующей
произвольному значению х.
Для того, чтобы пройти путь от плоскости x 0 до искомой плоскости,
волне требуется время x v .
Следовательно, колебания частиц, лежащих в плоскости x , будут
отставать по фазе на время от колебаний частиц в плоскости x 0 .
Тогда уравнение колебаний частиц в плоскости x будет иметь вид:
x
x , t Acos t 0 Acos t 0
v
Общая физика. «Волны»
6
7.
Упругие волныКафедра физики
Уравнения плоской и сферической волн.
B
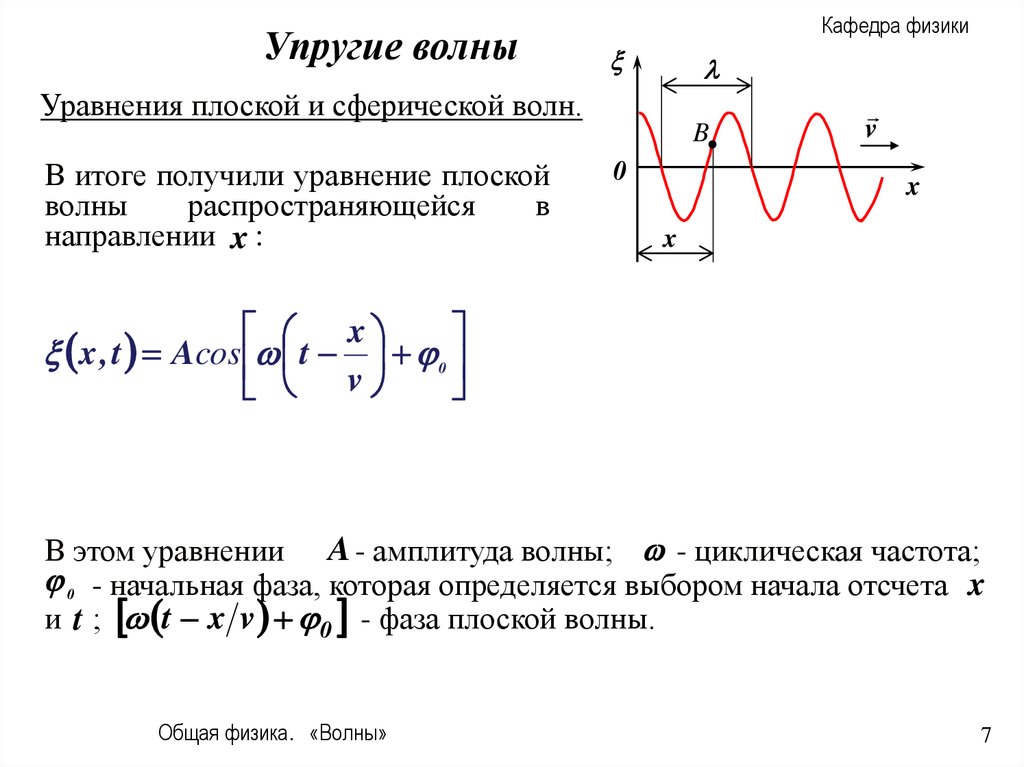
В итоге получили уравнение плоской
волны
распространяющейся
в
направлении x :
0
v
x
x
x
x , t Acos t 0
v
В этом уравнении A - амплитуда волны; - циклическая частота;
. 0 - начальная фаза, которая определяется выбором начала отсчета x
и t ; t x v 0 - фаза плоской волны.
Общая физика. «Волны»
7
8.
Упругие волныКафедра физики
Уравнения плоской и сферической волн.
B
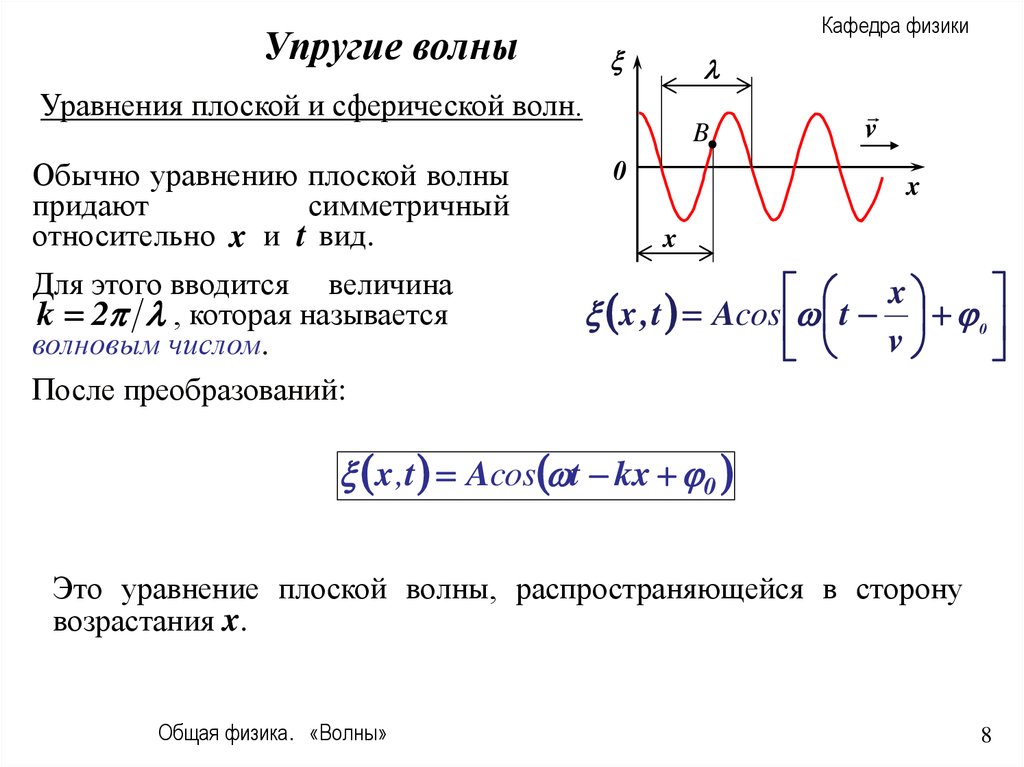
Обычно уравнению плоской волны
придают
симметричный
относительно x и t вид.
Для этого вводится величина
.k 2 , которая называется
волновым числом.
После преобразований:
0
v
x
x
x
x , t Acos t 0
v
x ,t Acos t kx 0
Это уравнение плоской волны, распространяющейся в сторону
возрастания x.
Общая физика. «Волны»
8
9.
Кафедра физикиУпругие волны
Уравнения плоской и сферической волн.
Уравнение сферической волны.
Будем считать источник колебаний точечным.
Волна от такого источника в изотропной и однородной среде будет
сферической.
Точки лежащие на волновой поверхности
радиуса r , будут колебаться с фазой
r
t 0
v
1
Амплитуда колебаний убывает с расстоянием от источника как .
r
Следовательно, уравнение сферической волны имеет вид:
A
x ,t cos t kr 0
r
Общая физика. «Волны»
9
10.
Кафедра физикиУпругие волны
Уравнения плоской и сферической волн.
Уравнение плоской волны
Уравнение сферической волны
x ,t Acos t kx 0
A
r , t cos t kr 0
r
Общая физика. «Волны»
10
11.
Упругие волныКафедра физики
Волновое уравнение.
Все возможные волны описываются волновыми уравнениями.
Уравнение конкретной волны - это решение волнового уравнения.
Вид волнового уравнения:
В этом уравнении
2
1
2
2 2
v t
v - фазовая скорость,
2
2
2
2
2 2 2
x
y
z
- оператор набла (оператор Лапласа)
Волновому уравнению удовлетворяют уравнения плоской и
сферической волн.
Для плоской волны, распространяющейся в направлении x , волновое
уравнение имеет вид:
d 2ξ
1 2ξ
2 2
2
dx
v t
Это одномерное волновое уравнение второго
порядка в частных производных.
Общая физика. «Волны»
11
12.
Упругие волныКафедра физики
Звуковые волны.
Звуковые волны (звук) – это распространяющийся в упругой среде
волновой процесс, воспринимаемый человеческим ухом.
Диапазон звуковых частот – 20 Гц – 20 кГц.
Инфразвук - волны с частотами меньше 20 Гц.
Ультразвук - волны с частотами больше 20 кГц
Акустика - учение о звуке.
Эффект Доплера.
Общая физика. «Волны»
12
13.
Кафедра физикиЭлектромагнитные волны.
Волновое уравнение
Все возможные волны, описываются
волновыми уравнениями вида:
2
1
2 2 2
v t
Из уравнений Максвелла следует пара уравнений вида:
H
2
H 0 0 2
t
Это волновые уравнения для полей E и H .
E
2
E 0 0 2
t
2
2
В волновом уравнении
2
1
2
2 2
v t
множитель
перед второй производной в правой части – это величина, обратная
квадрату фазовой скорости волны.
Общая физика. «Волны»
13
14.
Кафедра физикиЭлектромагнитные волны.
Волновое уравнение
E
2
E 0 0 2
t
2
H
2
H 0 0 2
t
2
1
Следовательно, 0 0
.
2
v
В вакууме эта скорость для электромагнитной
волны равна скорости света.
Тогда волновые уравнения для полей E и H можно записать как
1 H
2 H 2
с t 2
2
1 E
2
E 2 2
с t
2
Эти уравнения указывают на то, что электромагнитные поля могут
существовать в виде электромагнитных волн, фазовая скорость
которых в вакууме равна скорости света.
Общая физика. «Волны»
14
15.
Электромагнитные волны.Кафедра физики
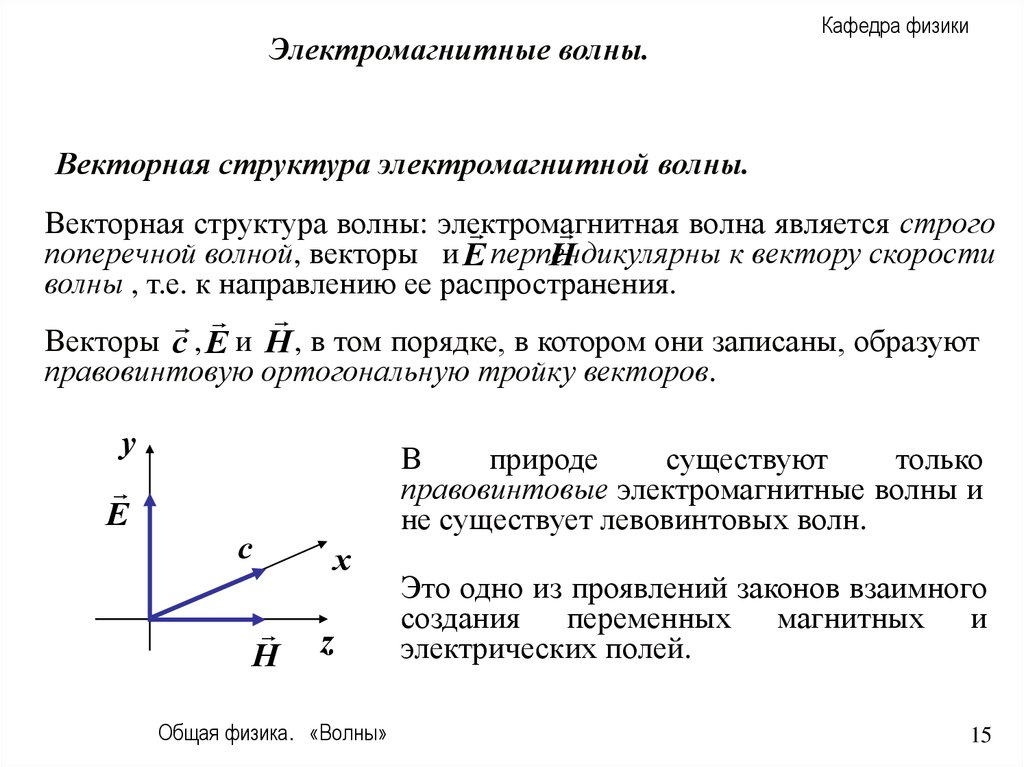
Векторная структура электромагнитной волны.
Векторная структура волны: электромагнитная
волна является строго
поперечной волной, векторы и E перпендикулярны
к вектору скорости
H
волны , т.е. к направлению ее распространения.
Векторы c , E и H , в том порядке, в котором они записаны, образуют
правовинтовую ортогональную тройку векторов.
y
E
В
природе
существуют
только
правовинтовые электромагнитные волны и
не существует левовинтовых волн.
c
H
x
z
Общая физика. «Волны»
Это одно из проявлений законов взаимного
создания переменных магнитных и
электрических полей.
15
16.
Электромагнитные волны.Кафедра физики
Из уравнений Максвелла
следует также, что в электромагнитной
волне векторы E и H всегда колеблются в одинаковых фазах, а
мгновенные значения E и H в любой точке пространства связаны
соотношением
E 0 H 0
Рассмотрим для простоты вид и свойства одномерного волнового
уравнения электромагнитной волны.
Пусть электромагнитная
волна будет строго монохроматической
(волны E и H имеют одну и ту же частоту) и распространяется в
направлении x.
Векторы E и H перпендикулярны направлению распространения
волны, следовательно, их проекции на ось x равны нулю.
Общая физика. «Волны»
16
17.
yE
Электромагнитные волны.
c
H
x
z
Кафедра физики
Волновые уравнения такой волны будут
иметь вид:
Ey 1 Ey
2 Hz 1 2 Hz
2
,
2
2
2
2
x
с t
x
с t 2
2
2
E y E0 cos t kx 0
H z H 0 cos t kx 0
Индексы y и z означают, что векторы E и H направлены вдоль
взаимно перпендикулярных осей y и z . E0 и H 0 соответственно
Этим уравнениям удовлетворяют
плоские линейно поляризованные
монохроматические волны
амплитуды напряженностей электрического и магнитного полей
волны; - частота волны; k v - волновое число; 0 - начальные
фазы колебаний в точках с координатой x 0.
Колебания электрического и магнитного векторов в электромагнитной
волне происходят в одной фазе, так что в уравнениях 0 одинаково.
Общая физика. «Волны»
17
18.
Кафедра физикиЭлектромагнитные волны.
Мгновенная картина электромагнитной волны в некоторый момент
времени:
x
y
E0
λ
E
0
H
Общая физика. «Волны»
H0
z
y
E
c
H
x
z
18
19.
Кафедра физикиЭлектромагнитные волны.
Энергия электромагнитной волны.
Электромагнитные волны переносят в пространстве энергию.
Объемная плотность энергии электромагнитной волны складывается
из объемных плотностей энергии электрического и магнитного полей:
w w эл w магн
0 E 2
2
0 H 2
2
Мгновенные значения E и H связаны соотношением E 0 H 0
Следовательно,
выражение для объемной плотности энергии
электромагнитной волны в произвольный момент времени в
рассматриваемой точке пространства можно представить в виде:
E 0 E 0 H 0 H 0
w
2
2
Общая физика. «Волны»
19
20.
Электромагнитные волны.Кафедра физики
Энергия электромагнитной волны.
E 0 E 0 H 0 H 0
w
w 0 0 EH
2
2
1
1
w EH
0 0 2
c
v
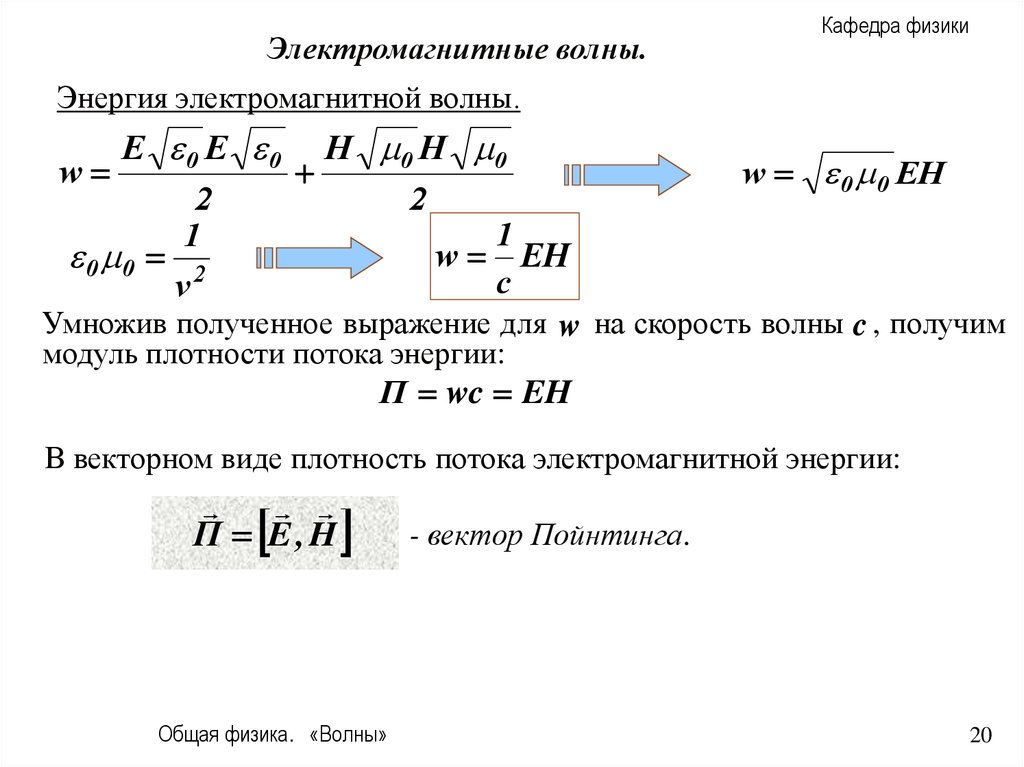
Умножив полученное выражение для w на скорость волны c , получим
модуль плотности потока энергии:
П wc EH
В векторном виде плотность потока электромагнитной энергии:
П E,H
Общая физика. «Волны»
- вектор Пойнтинга.
20
21.
Кафедра физикиЭлектромагнитные волны.
Интенсивность электромагнитной волны.
Для периодической электромагнитной волны значение вектора
Пойнтинга, усредненное по периоду волны – это интенсивность I:
1
1 0 2
I П П dt
Em
T0
2 0
T
Импульс электромагнитной волны.
Перенос энергии электромагнитной волной сопровождается
переносом импульса. Импульс электромагнитного поля
где W - энергия электромагнитного поля.
P W c,
и
Запишем это выражение для плотностей импульса и энергии т.е., для
величин, отнесенных к единице объема: p w c
Если умножить и разделить числитель и знаменатель этого
выражения на с , получим в числителе плотность потока энергии wc ,
которая равна модулю вектора Пойнтинга.
1
p 2 E,H
c
Общая физика. «Волны»
21
















 physics
physics