Similar presentations:
Волны и оптика. Лекция 03
1.
Общая физика, 4-ый семестрВолны и оптика
Лекция 03
Упругие волны в средах
Энергия волн.
Акустика
2 марта 2022 года
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович
2.
Упругие волны в средах0
x
0 2
x
x
x
2
P P
x S x
1 P
1 P
2 P 2
0 2 2
0 x
0 S
x
S x
Одномерное волновое
уравнение
2
2
2
v
2
t
x 2
Скорость упругих волн
P
v
S
м/с
3.
Упругие волны в газеP
v
S
Скорость звука в газе
PV const
P P0
0
P
P0
1
P0
S
0
0
P
v
S
1,4, T 290 K, M 29 г/моль v
P0
v
RT
M
0 RT
M
RT
M
340 м/с
4.
Упругие волны в жидкостиP
Скорость звука в жидкости v
S
P A 1
0
v
A
0
P
v
S
1
A
0
0
A 3,75 108 Па, 6,0, 0 =103 кг/м3 ,
v 1,5 км/с
5.
Упругие волны в твёрдом телеПродольная упругая волна в стержне со
свободной боковой поверхностью
l
P
v
S
dF
dx
dP= dF/S = Eε = Edx/l = Edρ/ρ0
dP/dρ = E/ρ0
2
vl 2
2
t
x
2
2
vl
E
0
Железо
Vl = 5,1 км/c
6.
Упругие волны в твёрдом телеE
x
Продольная волна
vl vt
G
x
Поперечная волна
Поперечная упругая волна в стержне
2
2
2
vt 2
2
t
x
vt
G
железо
0
v t 3,15 км/с
7.
Звук в твердом телеПродольная волна (P-волна).
cp ~= (E/ρ)1/2
Материал
E,
ГПа
ср,
км/с
сs,
км/с
Поперечная волна (S-волна).
cs ~= (G/ρ)1/2
Модуль Юнга Е[Па] характеризует
упругие и прочностные свойства
вещества по отношению к объемному
растяжению и сжатию.
Модуль сдвига G[Па] характеризует
упругие и прочностные свойства
вещества по отношению сдвиговой
деформации
с, км/с
в
стержне
Al
70
6,26
3,08
5,08
W
350400
5,46
2,62
4,31
Лёд
3
3,98
1,99
3,28
Cu
110130
4,70
2,26
3,71
Pb
14-18
2,16
0,70
1,20
Fe
200
5,85
3,23
5,17
Чугун
210
4,50
2,40
3,85
8.
Плотность энергии волныПлотность кинетической энергии
2
m
Рассмотрим малый элемент среды: Ek
2
E k m 2
wk
V V 2
wk
2 t
2
9.
Плотность энергии волныПлотность потенциальной энергии
d x
d x x
F S
F S
x x
x
x
x
1) Малые смещения d 2) справа и слева одинаково
dE p d Aвнешн Sd x x Sd x
10.
Плотность энергии волныd x
d x x
F S
F S
x x
x
x
dE p Sd x x x Sd x
x
V S x
E
S x d
x
x
x
11.
Плотность энергии волныdE p Sd x x x Sd x
x
V S x
E
S x d
x
x
E
v
dE p VE
d V d V
d
x x
2 x
2 x
2
2
E p
v
wp
E p V
V
2 x
2
wp
v
2
2 x
2
w wk w p
2
2
v
2
2 t
2 x
2
2
12.
Плотность энергии волныwp
v
2
2
2 x
В бегущей волне:
w wk w p
v
t
x
2
v
2
2 t
2 x
wk w p
2
13.
Плотность потока энергии и интенсивностьПлотность потока энергии
Модуль вектора плотности потока энергии равен энергии,
проносимой волной в единицу времени через площадку
единичной площади, ориентированной перпендикулярно
направлению переноса энергии волны.
j
Дж
Вт
2
2
с м
м
14.
Плотность потока энергии и интенсивностьjx
dW jx x, t jx x x, t Sdt
xSdt
x
V , dt
j x x, t
j x, t
V xS
x
x
x
x x
jx
dW
Vdt
x
jx
w
t
x
2
2
2
w v
2
2
2v
t
tt
x
xt
t t 2 t
2 x 2
15.
Плотность потока энергии и интенсивность2
2
2
w v
2
2
2v
x xt
t tt
t t 2 t
2 x 2
tt v xx
2
w
2
2
v t xx x xt v
t x
t
x
jx
w
t
x
jx v
t x
2
16.
Плотность потока энергии и интенсивностьjx
w
t
x
jx v
t x
2
P
2
2
Идеальный газ: P
v 0 v
x
S
jx v
P
t x
t
2
Твёрдое тело:
jx
t
17.
Плотность потока энергии и интенсивностьПлотность потока энергии в бегущей волне
jx v
t x
2
v
t
x
jx v 2vw p vw j wv
x
Интенсивность волны
2
2
I j
Вт
м2
вектор Умова
Это модуль средней по времени
плотности потока энергии.
18.
Плотность потока энергии и интенсивностьjx P
Pv
P v
t
x
0
Идеальный газ:
P v P P
2
0 v
0 v
2
В гармонической
волне
I jx
P 2
2
Pmax
2
I
P 2
0 v
2
Pmax
I
2 0 v
19.
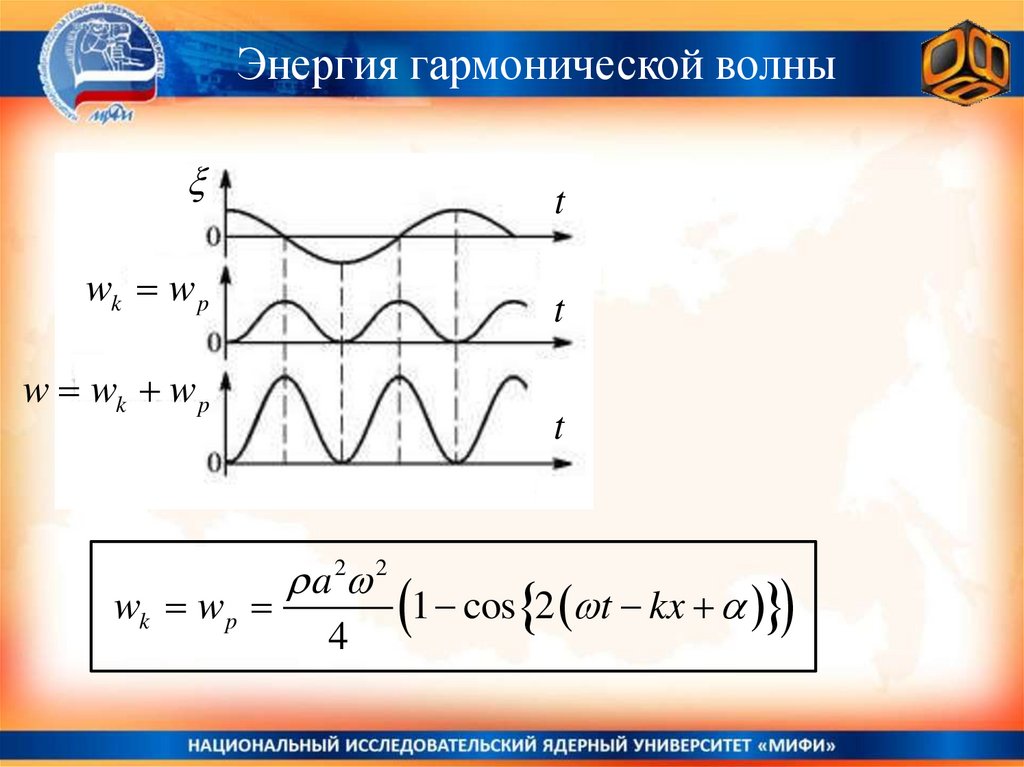
Энергия гармонической волныПлотность энергии в гармонической волне
a cos t kx
wk
2
2
a 2 2
wk w p
2
sin 2 t kx
a 2 2
4
a sin t kx
wk w p
1 cos 2 t kx
20.
Энергия гармонической волныt
wk w p
t
w wk w p
wk w p
t
a 2 2
4
1 cos 2 t kx
21.
Энергия гармонической волныИнтенсивность гармонической волны
Плоская гармоническая волна
jx v w 2v wk a 2 2 v 2 sin 2 t kx
sin t kx
2
1
2
1 2 2
I a v
2
a 2 2
j w
2
22.
Энергия гармонической волныИнтенсивность гармонической волны
Плоская гармоническая волна
jx v w 2v wk a 2 2 v 2 sin 2 t kx
sin t kx
2
1
2
1 2 2
I a v
2
Сферическая гармоническая волна
r0
I I0
r
2
I 0 I r0
23.
ПОТОК ЭНЕРГИИпоток энергии:
Ф jdS jndS jn dS
среднее значение:
Ф j dS I cos dS
S
S
S
для сферической волны:
Ф
S
S
j dS j S j 4 r 2 P const
S
r0
I I0
r
2
P – мощность источника
24.
Затухание волнПлоская квазигармоническая волна
x, t a exp x cos t kx
- коэффициент затухания. В вязкой среде
I
2 - коэффициент
I0
поглощения
I I 0 exp x
x
25.
Затухание волнСферически-симметричная волна
r02
I I 0 2 exp r
r
I 0 I r0
26.
Звуковые волны в газеАкустика
27.
Звуковые волны в газеШкала звуковых волн
0 16 Гц
16 2 104 Гц
2 10 10 Гц
4
9
>10 Гц
9
28.
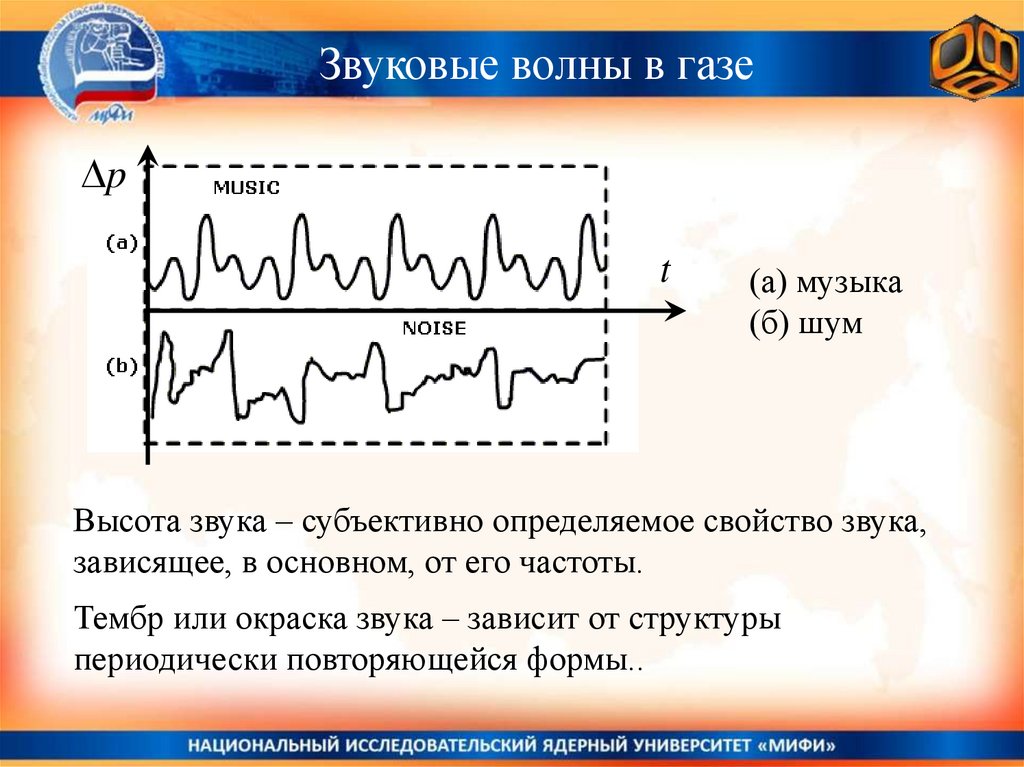
Звуковые волны в газеp
t
(а) музыка
(б) шум
Высота звука – субъективно определяемое свойство звука,
зависящее, в основном, от его частоты.
Тембр или окраска звука – зависит от структуры
периодически повторяющейся формы..
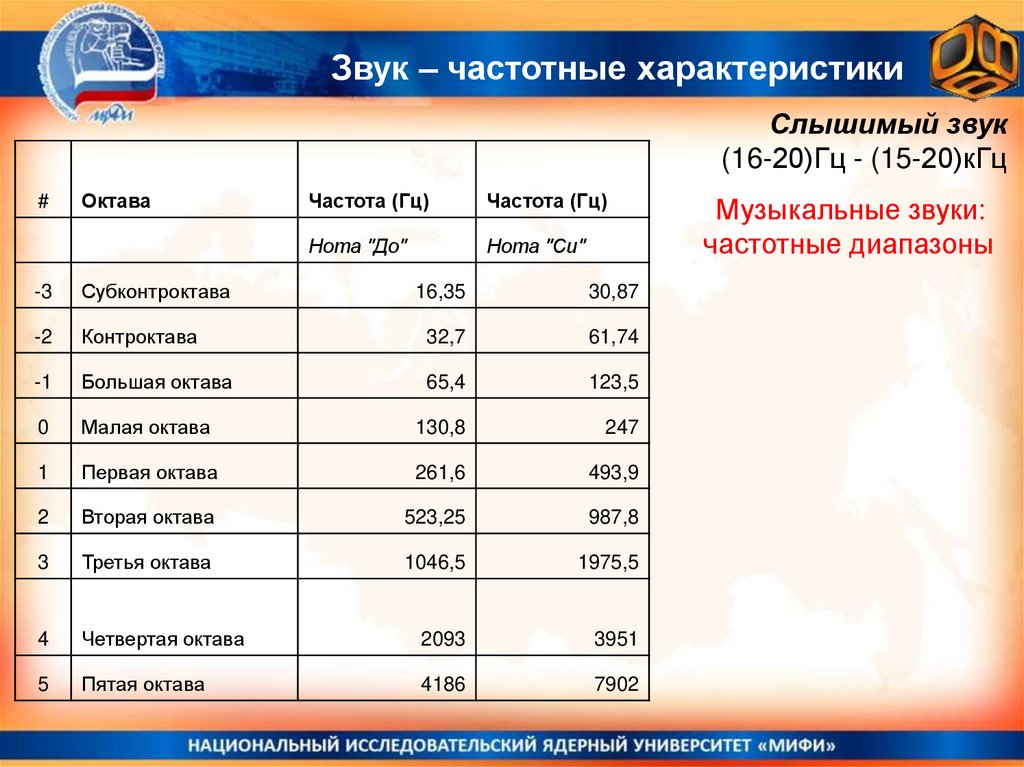
29.
Звук – частотные характеристикиСлышимый звук
(16-20)Гц - (15-20)кГц
#
Октава
-3
Субконтроктава
-2
Частота (Гц)
Частота (Гц)
Нота "До"
Нота "Си"
16,35
30,87
Контроктава
32,7
61,74
-1
Большая октава
65,4
123,5
0
Малая октава
130,8
247
1
Первая октава
261,6
493,9
2
Вторая октава
523,25
987,8
3
Третья октава
1046,5
1975,5
4
Четвертая октава
2093
3951
5
Пятая октава
4186
7902
Музыкальные звуки:
частотные диапазоны
30.
Звук – частотные характеристикиСлышимый звук
16-20)Гц - (15-20)кГц
#
Октава
-3
Субконтроктава
-2
Частота (Гц)
Частота (Гц)
Нота "До"
Нота "Си"
16,35
30,87
Контроктава
32,7
61,74
-1
Большая октава
65,4
123,5
0
Малая октава
130,8
247
1
Первая октава
261,6
493,9
2
Вторая октава
523,25
987,8
3
Третья октава
1046,5
1975,5
4
Четвертая октава
2093
3951
5
Пятая октава
4186
7902
Музыкальные звуки:
частотные диапазоны
31.
Сила звукаЗвук
Интенсивность звука - поток
энергии, переносимый звуковой
волной через единицу площади
поверхности. I = dW/dS [Вт/м2].
Сила звука (или «уровень
громкости звука») измеряется по
относительной шкале в децибелах
[дБ]:
Р = 10lg10(I/I0)
I0 - порог слышимости (= 1пВт/м2
при частоте 1 кГц)
Уровень
громкости, дБ
Порог слышимости
0
Тиканье наручных часов
10
Шепот
20
Звук настенных часов
30
Приглушенный разговор
40
Тихая улица
50
Обычный разговор
60
Шумная улица
70
Опасный для здоровья
уровень
75
Пневматический молоток
90
Кузнечный цех
100
Громкая музыка
110
Болевой порог
120
Сирена
130
Реактивный самолет
150
Шумовое оружие
200
32.
ШКАЛА УРОВНЕЙ ГРОМКОСТИ ЗВУКАПорог болевого ощущения –
значение
интенсивности,
при
котором
волна
перестает
восприниматься как звук, вызывая в
ухе лишь ощущение боли и
давления.
I
L 10lg
I0
L – уровень громкости [Дб]
I0 – исходная интенсивность: 10-12 Вт/м2
33.
Распространение звуковых волнПри распространении звуковых волн в среде возникают те-же
характерные эффекты, что и при распространении световых
(электромагнитных) волн:
- Дисперсия (зависимость скорости волны от частоты) – для звуковых волн
в однородных средах выражена слабо
- Затухание (потеря энергии звуковой волной за счет вязкости среды)
34.
Затухание волнПлоская квазигармоническая волна
x, t a exp x cos t kx
- коэффициент затухания. В вязкой среде
I
2 - коэффициент
I0
поглощения
I I 0 exp x
x
35.
Затухание волнСферически-симметричная волна
r02
I I 0 2 exp r
r
I 0 I r0
- коэффициент затухания. В вязкой среде
36.
Распространение звуковых волнПри распространении звуковых волн в среде возникают те-же
характерные эффекты, что и при распространении световых
(электромагнитных) волн:
- Дисперсия (зависимость скорости волны от частоты) – для звуковых волн
в однородных средах выражена слабо
- Затухание (потеря энергии звуковой волной за счет вязкости среды)
- Дифракция (изменение направления распространения волны при
огибании препятствия)
- Интерференция (эффект наложения двух волн одной длины, при котором
амплитуда колебаний в разных точках пространства становится разной)
37.
Интерференция звуковых волнИнтерференция (эффект наложения двух (или
более) когерентных волн (одной длины), при
котором амплитуда колебаний в разных точках
пространства становится разной)
38.
Распространение звуковых волнПри распространении звуковых волн в среде возникают те-же
характерные эффекты, что и при распространении световых
(электромагнитных) волн:
- Дисперсия (зависимость скорости волны от частоты) – для звуковых волн
в однородных средах выражена слабо
- Затухание (потеря энергии звуковой волной за счет вязкости среды)
- Дифракция (изменение направления распространения волны при
огибании препятствия)
- Интерференция (эффект наложения двух волн одной длины, при котором
амплитуда колебаний в разных точках пространства становится разной)
- Стоячие волны (эффект сложения двух волн одной длины,
распространяющихся навстречу друг-другу)
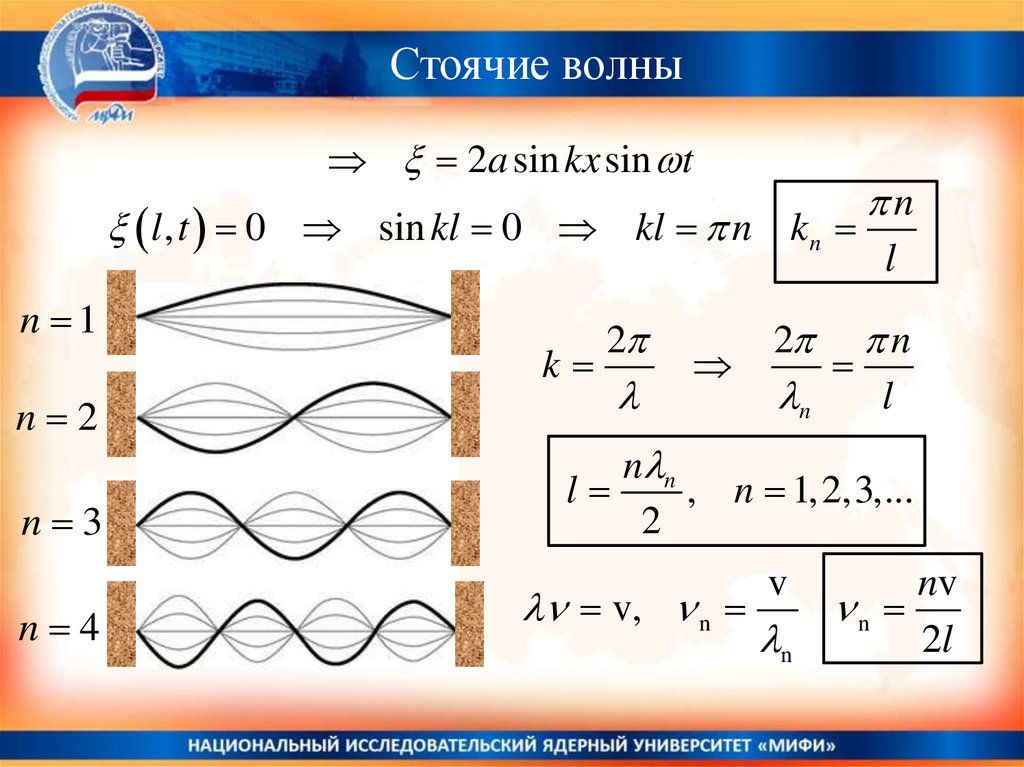
39.
Стоячие волны2a sin kx sin t
l , t 0 sin kl 0 kl n kn
n 1
n 2
n 3
n 4
k
2
2
n
n
l
n
l
n n
l
, n 1,2,3,...
2
v, n
v
n
nv
n
2l
40.
Стоячие волныСтоячие волны (эффект сложения двух плоских волн одной длины и
амплитуды, распространяющихся навстречу друг-другу)
A cos(ωt–kx) + A cos(ωt+kx) =
= 2A cos(kx) cos(ωt)
kl/2 = π/2 + πn – условие
существования стоячей волны
На правом конце узел - А(0) = 0
На левом конце пучность - А(l) = 2А
k = 2π/λ
41.
Распространение звуковых волнПри распространении звуковых волн в среде возникают те-же
характерные эффекты, что и при распространении световых
(электромагнитных) волн:
- Дисперсия (зависимость скорости волны от частоты) – для звуковых волн
в однородных средах выражена слабо
- Затухание (потеря энергии звуковой волной за счет вязкости среды)
- Дифракция (изменение направления распространения волны при
огибании препятствия)
- Интерференция (эффект наложения двух волн одной длины, при котором
амплитуда колебаний в разных точках пространства становится разной)
- Стоячие волны (эффект сложения двух волн одной длины,
распространяющихся навстречу друг-другу)
- Эффект Доплера (зависимость слышимой частоты звука от скорости
источника или приемника звука)
- …..
42.
Эффект ДоплераЭффект Доплера (зависимость слышимой частоты
звука от скорости источника или приемника звука)
Эффект был впервые описан Кристианом
Доплером в 1842 году.
43.
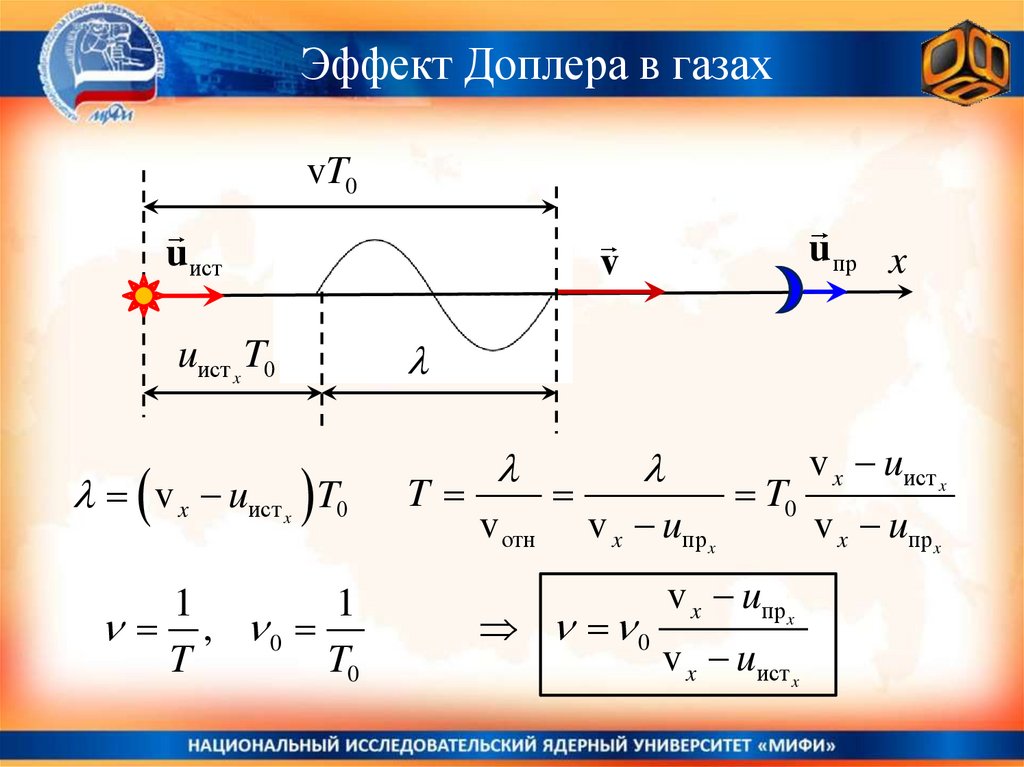
Эффект Доплера в газахvT0
u ист
u пр x
v
uист x T0
v x uист T0
x
1
1
, 0
T
T0
T
v отн
v x uпр x
0
T0
v x uпр x
v x uист x
v x uист x
v x uпр x
44.
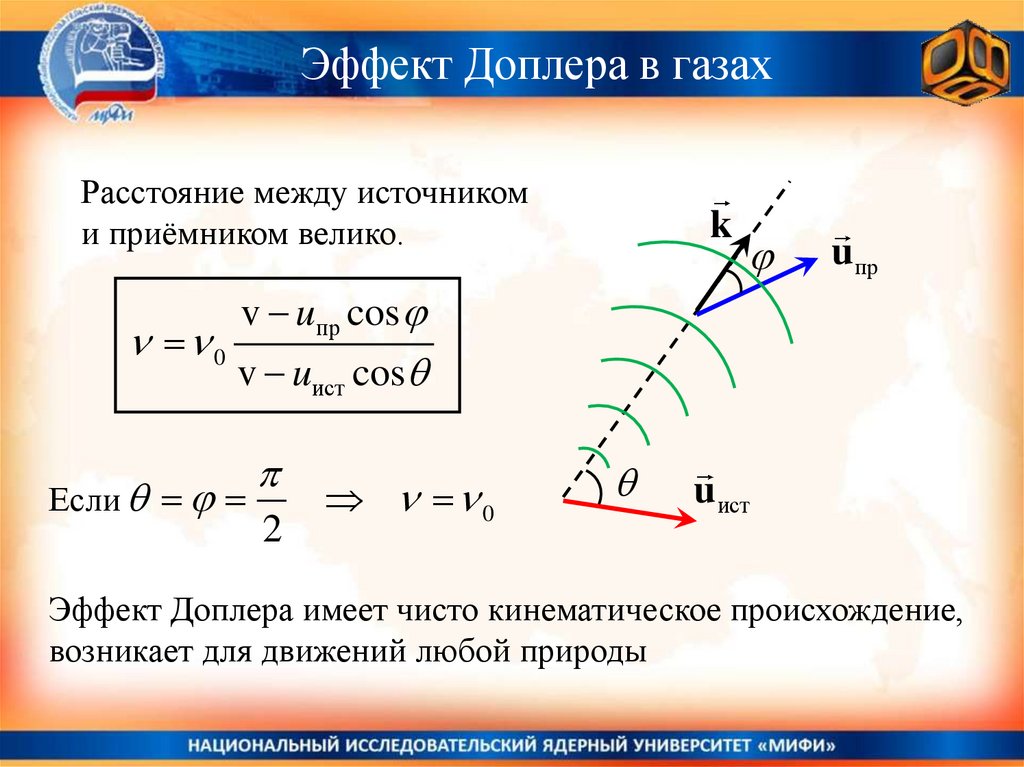
Эффект Доплера в газахРасстояние между источником
и приёмником велико.
0
k
u пр
v uпр cos
v uист cos
Если
2
0
u ист
Эффект Доплера имеет чисто кинематическое происхождение,
возникает для движений любой природы
45.
Ударная волна в газахЕсли uист v , то возникает ударная волна.
Ударная волна и конус Маха, возникшие в результате
сверхзвукового полёта пули с числом Маха 2,45.
46.
Общая физика, 4-ый семестрСпасибо за внимание!
47.
Примеры решения задачПример 1. Звуковая волна распространяется вдоль трубы
длиной l 50 м, заполненной воздухом. Коэффициент
затухания звука в трубе 0,010 м-1. Каков уровень
громкости звука у конца трубы, если у её начала он равен
L1 60 дБ?
k
0
x
l
I
L 10lg
I0
a a1 exp x
48.
Примеры решения задачk
x
0
l
I I1 exp 2 x
I1
L 10lg 20 l lg e
I0
L L1 20 l lg e 56 дБ
49.
Примеры решения задачПример 2. В упругой струне массы m возбудили стоячую
волну основного тона с частотой 1 . Амплитуда колебаний
струны в пучности смещений составила a1. Найти
максимальное значение кинетической энергии струны.?
x, t Asin kx sin t
0, t l , t 0
sin kl 0
kl n, n 1,2,3...
50.
Примеры решения задачkn n l , n 1,2,3...
A a1
1
x, t a1 sin
wк
2 t
2
wк
a12 12
2
sin
2
x
x
l
l
k l
sin 1t
cos2 1t
51.
Примеры решения задачdV Sdx
l
dWк wк dV
sin
0
Wк
2 x
Wк
Sa12 12
2
l
cos 1t sin
2
0
2 x
l
dx 1 cos
dx
l
l
2
0
l
lSa
2
1
4
2
1
cos 1t
2
Wmax
ma
Wк
cos2 1t
4
ma12 12
4
2
1
2
1
2
x
l
dx
52.
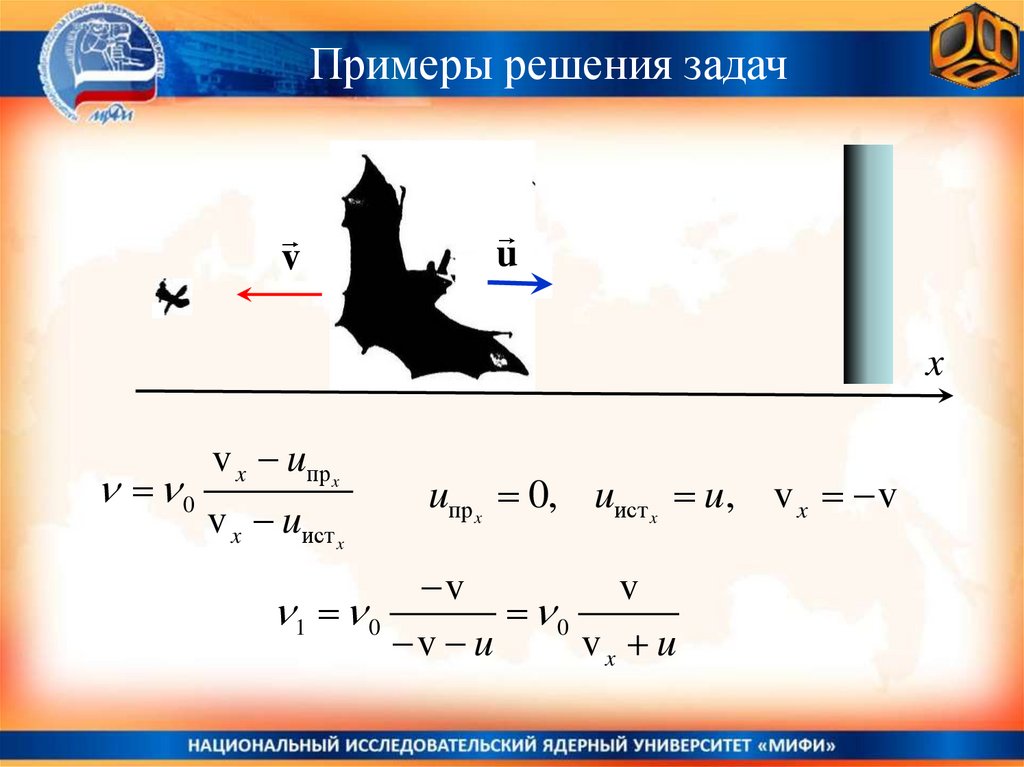
Примеры решения задачПример 3. Летучая мышь летит перпендикулярно к стенке со
скоростью u 6,0 м/с , излучая при этом ультразвуковую волну
с частотой 0 46 кГц . Насекомое, расположенное за спиной
летучей мышью на линии её движения, слышит акустические
биения. Какова частота этих биений? Скорость звука 340 м/с.
u
x
53.
Примеры решения задачv
u
x
0
v x uпр x
v x uист x
uпр x 0, uист x u, v x v
v
v
1 0
0
v u
vx u
54.
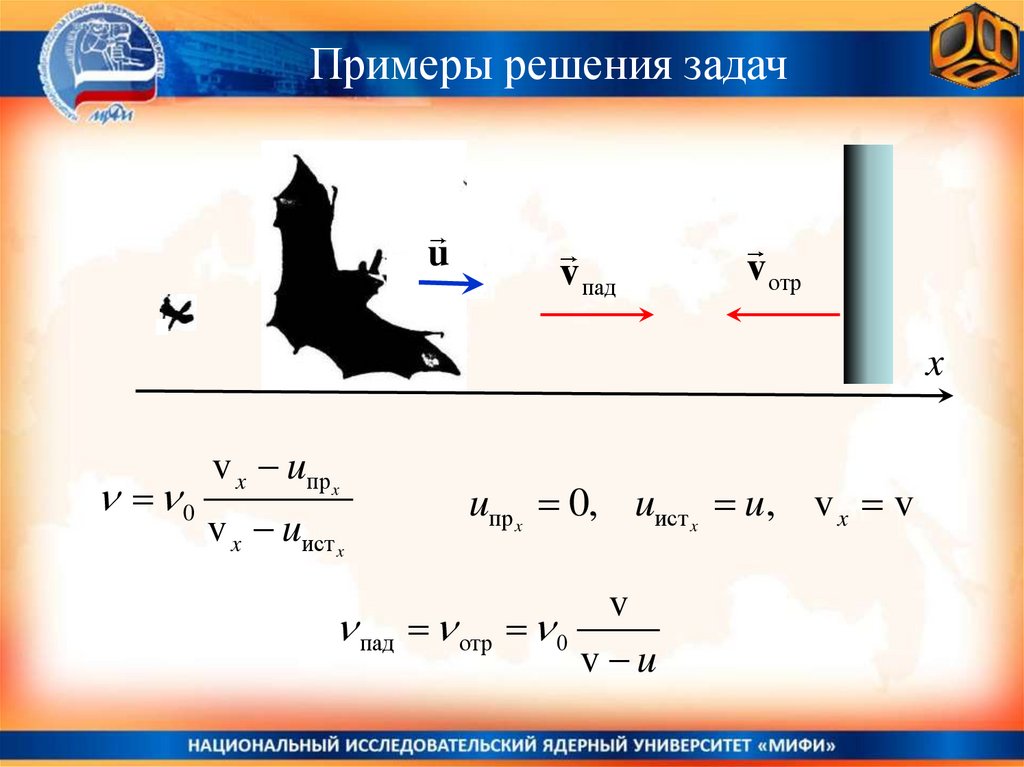
Примеры решения задачu
v пад
v отр
x
0
v x uпр x
v x uист x
uпр x 0, uист x u, v x v
пад отр
v
0
v u
55.
Примеры решения задачu
v пад
v отр
x
v
v
б отр 1 0
0
v u
v u
2vu
2u
3 2 6
3
б 0 2 2 0
46 10
1,6 10 Гц
v u
v
340
56.
Общая физика, 4-ый семестрСпасибо за внимание!
Следующая лекция
9 марта
57.
Общая физика, 4-ый семестрВолны и оптика
Лекция 04
Электромагнитные волны
9 марта 2022 года
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович

















































 physics
physics








