Колебания и волны. Волновая оптика

1. ФИЗИКА

Лекция № 2

2. КОЛЕБАНИЯ

2

3.

Колебаниями называются процессы, в той или
иной степени повторяющиеся с течением времени.
Наименьшее время повторения состояния
называется периодом Т колебаний. Период – это время
одного полного колебания.
Число полных колебаний, совершаемых за 1 секунду,
называется частотой колебаний:
1 T
Число полных колебаний за 2 секунд называется
циклической частотой:
2 2 T
Единицы измерения:
[ T ] c ; [ ] c
1
Гц ; [ ] рад с
3

4.

,
Если изменение колеблющейся величины с
течением времени происходит по закону синуса
(или косинуса), то колебания называются
гармоническими:
x x m cos( t 0 )
Систему, совершающую гармонические
колебания, называют гармоническим
осциллятором.
4

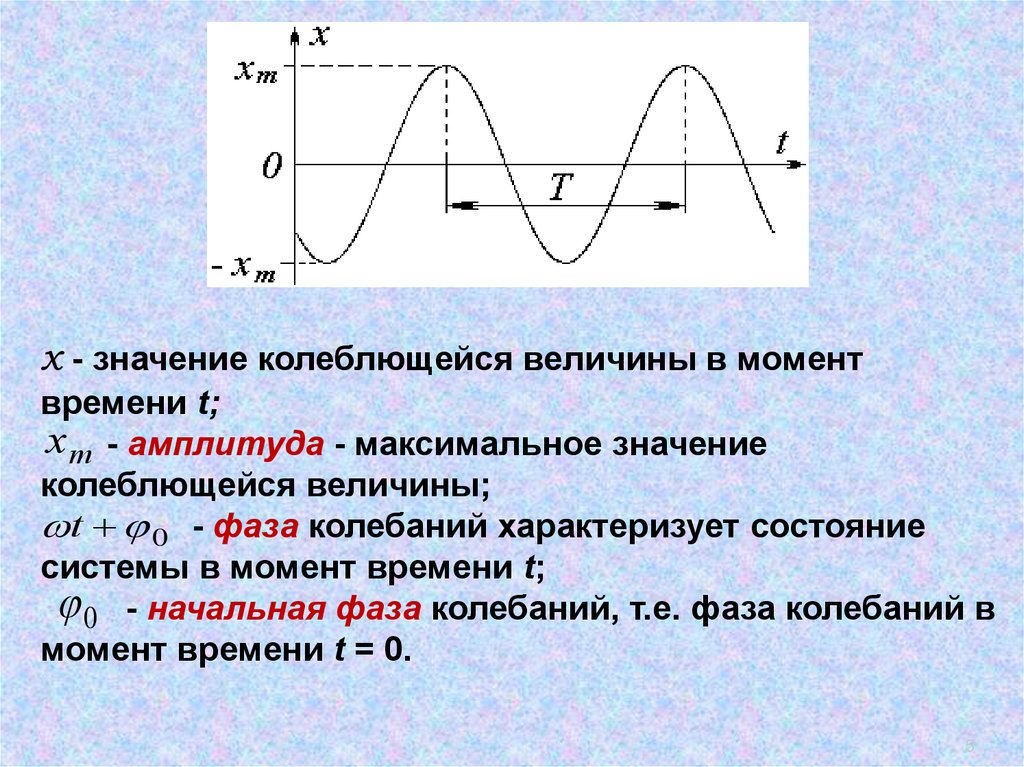
5.

х - значение колеблющейся величины в момент
времени t;
x m - амплитуда - максимальное значение
колеблющейся величины;
t 0 - фаза колебаний характеризует состояние
системы в момент времени t;
0 - начальная фаза колебаний, т.е. фаза колебаний в
момент времени t = 0.
5

6.

.
Условия существования
колебаний:
После выведения системы из состояния
равновесия в ней должна действовать
упругая или квазиупругая сила, которая в
любой момент времени направлена к
положению равновесия, а её величина
пропорциональна смещению от состояния
равновесия.
Система должна обладать инертностью.
6

7.

происходят в системе, выведенной из
состояния равновесия и
предоставленной самой себе.
Собственные незатухающие колебания
совершаются без участия внешних сил.
7

8.

Пружинный маятник
Уравнение движения
F ma m
d 2r
dt
2
F Fупр kr
d 2r
dt
2
k
k
2
r 0 0
m
m
Решением является гармоническая
функция
r rm cos( 0 t 0 )
m
T0 2
k

9.

)
.
Физический маятник – это
твердое тело, способное вращаться
вокруг оси, не проходящей через его
центр инерции.
2
Уравнение движения
M J J
Момент силы тяжести
l
d
dt 2
M mgl sin
Для малых углов ( < 10 ) sin
d 2
dt
2
mgl
mgl
2
0 0
J
J
Решением является гармоническая
функция
m cos( 0 t 0 )
J
T0 2
mgl
l – расстояние между центром инерции и осью вращения тела

10.

Математический маятник –
это материальная точка на
тонкой, невесомой,
нерастяжимой нити.
Для материальной точки момент инерции
J ml
2
. Период колебаний математического маятника
l
T0 2
g
Это уравнение используется для измерения
ускорения свободного падения.
10

11.

.
.
Электрический
колебательный контур – это
последовательно соединенные
емкость C и индуктивность L.
По закону Ома для замкнутой цепи сумма
напряжений равна действующей в цепи ЭДС
U C Eis
q
UC
C
dI
Eis L
dt
dq
I
dt
dq
q
L
0
dt
LC
2
2
Решением является гармоническая функция
q qm cos( 0 t 0 )
Сила тока
в контуре
2
0
1
LC
T0 2 LC
dq
I qm 0 sin( o t o ) I m sin( o t o )
dt

12. Энергия гармонического осциллятора

Характерным признаком любых колебаний
является взаимные превращения одного вида энергии в
другой:
o в механических колебаниях - это взаимные
превращения кинетической и потенциальной энергии
системы;
o в электрическом колебательном контуре - это
взаимные превращения энергии электрического поля
конденсатора и энергии магнитного поля катушки
индуктивности.
o Если в системе действуют только консервативные
силы и система замкнута, то полная энергия системы
постоянна.

13.

Механические
колебания
(без трения)
Электромагнитные
колебания
(активное сопротивление
R = 0)
kx 2 k 2
Wp
xm cos 2 ( 0t 0 )
2
2
q2
1 2
WЭ
qm cos 2 ( 0 t 0 )
2C 2C
mv 2 m 2 2 2
Wk
xm 0 sin ( 0t 0 )
2
2
LI 2 L 2 2 2
WM
qm 0 sin ( 0t 0 )
2 2
W W p Wk
2
kx m
2
W WЭ WM
2
qm
2C
Энергия гармонического осциллятора
пропорциональна квадрату амплитуды колебаний.
13

14. Затухающие колебания

Затухание колебаний в механических
колебательных системах вызвано трением,
а в электрическом колебательном контуре активным сопротивлением R.
14

15.

Закон Ома в этом случае имеет вид:
E U U
C
is
dI
dq
E L
L
;
dt
dt
2
is
2
R
q
U ;
C
C
dq
I
dt
U IR ;
R
2
d q R dq 1
q
0
2
dt L dt LC
Решение этого дифференциального уравнения
q q e cos( t )
t
m0
0

16.

16

17.

qm 0
- начальная амплитуда колебаний;
t - амплитуда колебаний в момент
qm 0 e
времени t;
1
LC
0
2
- собственная частота колебаний;
2
- частота затухающих колебаний;
o
R 2 L
1
- коэффициент затухания;
- время релаксации – это время, за
которое амплитуда колебаний
уменьшается в е раз;
xm (t )
ln
- логарифмический декремент
xm (t T ) затухания - характеризует изменение
T
амплитуды за один период колебаний.
17

18. Вынужденные колебания

Совершаются благодаря
периодическому внешнему
воздействию.
В случае механических колебаний – это
периодическая сила,
в случае электрических колебаний – это
переменная ЭДС.
18

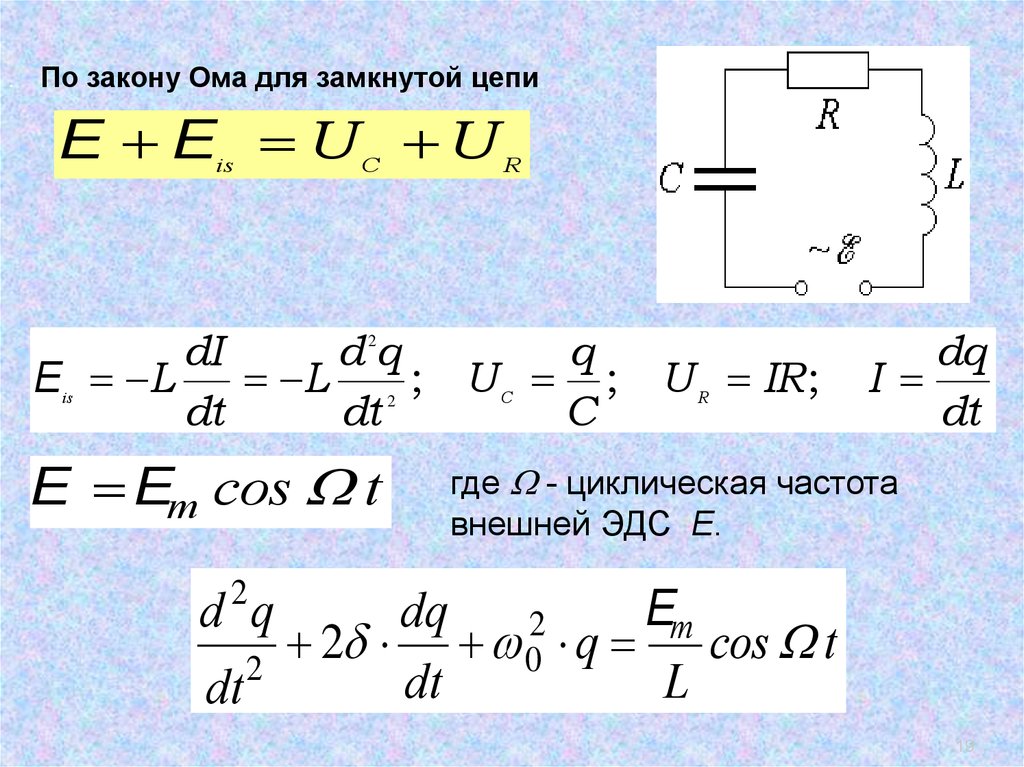
19.

.
По закону Ома для замкнутой цепи
E E U U
is
C
R
dI
dq
q
E L
L
; U ; U IR ;
dt
dt
C
2
is
2
E Em cos t
C
R
dq
I
dt
где - циклическая частота
внешней ЭДС Е.
2
d q
Em
dq
2
2
q
cos
t
0
2
dt
L
dt
19

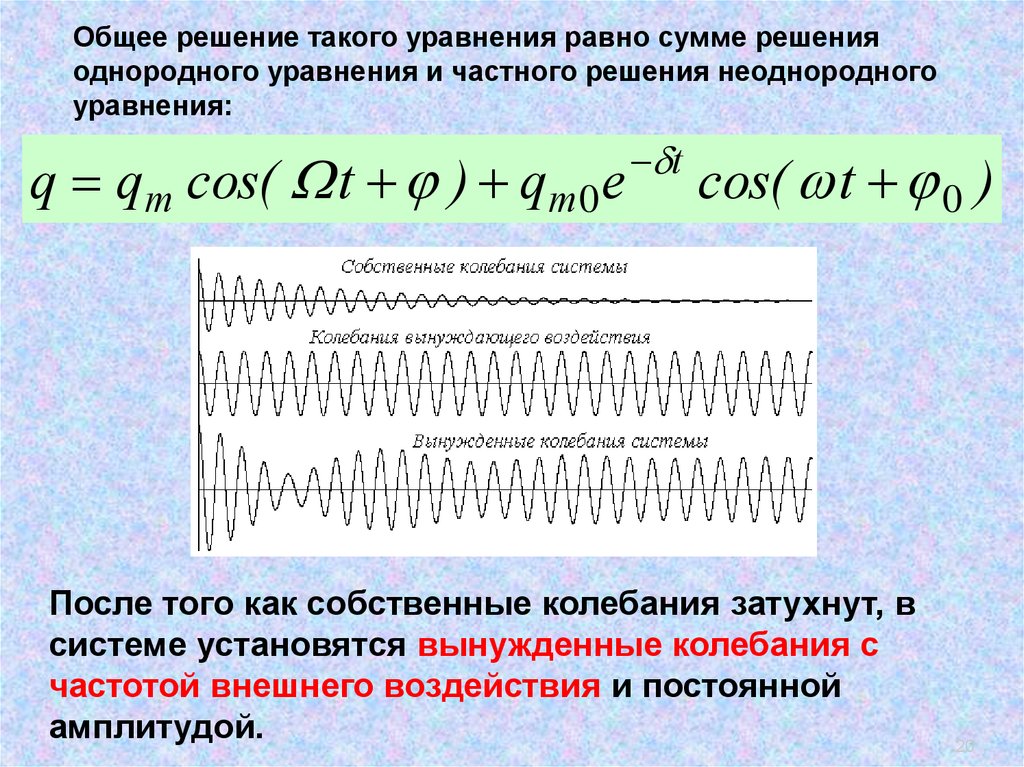
20.

.
Общее решение такого уравнения равно сумме решения
однородного уравнения и частного решения неоднородного
уравнения:
q qm cos( t ) qm 0 e
t
cos( t 0 )
После того как собственные колебания затухнут, в
системе установятся вынужденные колебания с
частотой внешнего воздействия и постоянной
амплитудой.
20

21.

Амплитуда вынужденных
колебаний зависит не только
от амплитуды внешней ЭДС и
параметров контура, но и от
частоты колебаний.
qm
Амплитуда вынужденных
колебаний достигает
максимального значения при
частоте внешнего
воздействия, близкой к
частоте собственных
колебаний системы. Это
явление называется
резонансом.
рез
2
0
2
2
Em
L
2
( 0
) 4
2 2
2
2
Резонансная кривая –
зависимость амплитуды
вынужденных колебаний от
частоты вынуждающего
воздействия
21

22. ВОЛНЫ

22

23.

Волна – это процесс
распространения колебаний (или
возмущения) в пространстве.
Тела, вызывающие эти колебания,
называются источником волны.
23

24. Волны в упругой среде

В упругой среде при распространении
волны частицы среды лишь колеблются
около своих равновесных положений.
Поэтому волна не переносит вещество;
вместе с волной переносится энергия
колебательного движения.
Основное свойство всех волн –
перенос энергии без переноса вещества
24

25.

,
В поперечной волне частицы среды
колеблются перпендикулярно направлению
распространения волны.
(Волны вдоль натянутой струны, поверхностные
волны).
В продольной волне частицы среды
колеблются вдоль направления
распространения волны.
(Волны в газах, жидкостях и твердых телах).
25

26.

Геометрическое место точек, в
которых фаза колебаний имеет одинаковое
значение, называется волновой
поверхностью (или волновым фронтом).
Различают плоские и сферические волны.
Если колебание частиц среды
является гармоническим, то волна
называется монохроматической (или
синусоидальной).
26

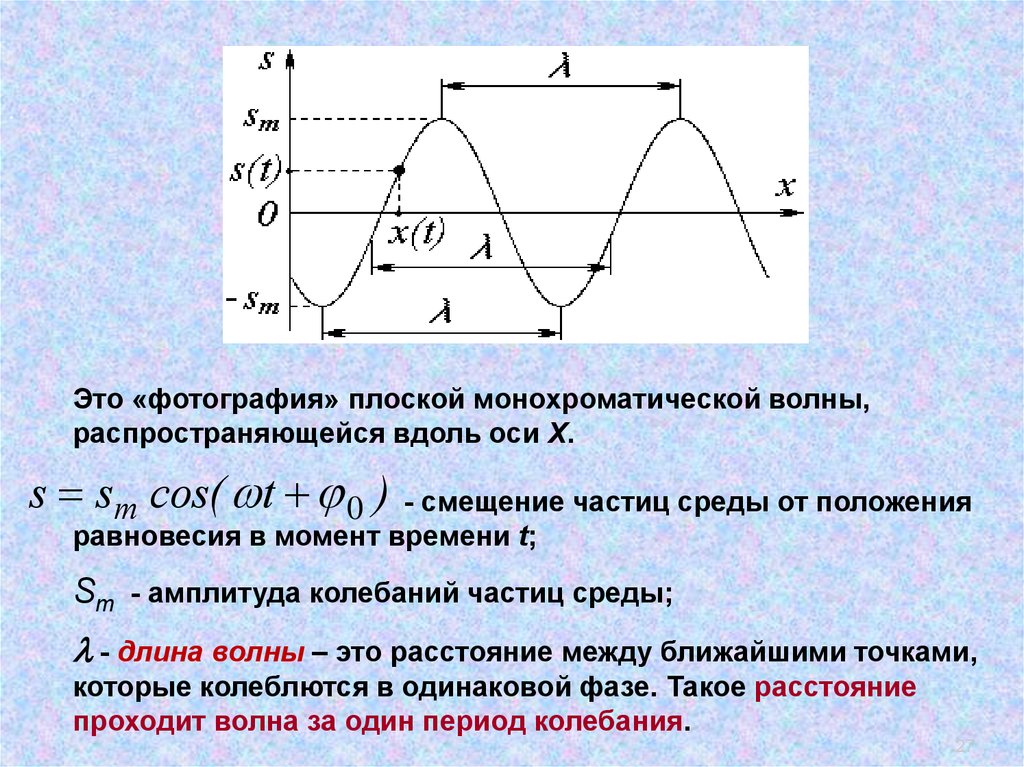
27.

.
Это «фотография» плоской монохроматической волны,
распространяющейся вдоль оси Х.
s sm cos( t 0 ) - смещение частиц среды от положения
равновесия в момент времени t;
Sm - амплитуда колебаний частиц среды;
- длина волны – это расстояние между ближайшими точками,
которые колеблются в одинаковой фазе. Такое расстояние
проходит волна за один период колебания.
27

28.

В любой точке среды с координатой х колебания частиц
происходят
по гармоническому закону, но с некоторым
,
где
запозданием
по сравнению с источником волны на время
= x/v, необходимое для прохождения волной расстояния х;
v
- скорость распространения волны.
Уравнение колебаний для точки с координатой х
имеет вид:
s sm cos( t kx 0 )
2
k
- волновое число.
v
v
vT
v
28

29.

Каждая колеблющаяся частица упругой среды в любой момент
времени имеет полную энергию
ks
W
2
k
2
m0
Так как
2
m
1
W m0 2 sm2
2
, то
k - коэффициент упругости среды; mo - масса частицы среды;
sm - амплитуда колебаний частиц среды.
Средняя плотность энергии волны:
1
1
w m n s s
2
2
2
0
2
m
2
2
m
n – концентрация частиц среды;
- плотность среды.
29

30.

Средняя энергия, переносимая волной за
единицу времени через единицу поверхности,
называется интенсивностью волны или плотностью
потока энергии
1
2 2
J w v v sm
2
где v - это фазовая скорость волны.
Вектор Пойнтинга характеризует величину и
направление переноса энергии при волновом процессе:
u w v
u J
30

31. Электромагнитные волны

Существование электромагнитных
волн теоретически предсказал
Дж. Максвелл в 1864 году.
Джеймс Клерк Максвелл
1831-1867
Г. Герц экспериментально
подтвердил существование
электромагнитных волн в 1888 году.
Генрих Герц
1857-1894
31

32.

Электрический заряд, движущийся с ускорением,
создаёт переменное магнитное поле, которое создает
переменное вихревое электрическое поле. Т.е.
происходит образование переменного
электромагнитного поля, которое, «оторвавшись» от
источника поля, распространяется в пространстве.
Процесс распространения в
пространстве переменного
электромагнитного поля называется
электромагнитной волной.
32

33.

Скорость распространения электромагнитных волн
v
1
0
v
0
м
c 299792458
с
1
0
0
c
Для вакуума = 1 и = 1
В вакууме электромагнитные волны
распространяются со скоростью света.

34.

Электромагнитные волны поперечны
Векторы напряженностей электрической E и H
магнитной составляющих волны синфазно
колеблются во взаимно перпендикулярных плоскостях
и перпендикулярны направлению распространения
волны.
34

35.

.
Электромагнитные волны переносят энергию
Объемная плотность энергии ЭМВ равна сумме объемных
плотностей энергии электрического и магнитного полей:
w w w
e
m
1
1
w E H
2
2
2
0
2
0
Модули векторов E и H связаны соотношением
H E
0
0
EH
w E H
v
2
0
2
0
Вектор плотности потока энергии ЭМВ называется
вектором Пойнтинга:
S w v [E H ]
35

36.

.
Электромагнитные волны излучаются только
движущимися с ускорением электрическими зарядами
Простейшей системой, излучающей ЭМВ,
является электрический диполь:
pe ql
Для излучения необходимо, чтобы дипольный
момент изменялся с течением времени,
например, по гармоническому закону:
e
p p0 cos t
Интенсивность излучения диполя максимальна в плоскости,
перпендикулярной оси диполя.
Вдоль своей оси диполь не излучает.
36

37.

Виды электромагнитных волн
Низкочастотные
Радиоволны
Инфракрасное излучение
Свет
Ультрафиолетовое излучение
Рентгеновское излучение
Гамма-излучение
37

38. ВОЛНОВЫЕ СВОЙСТВА СВЕТА

38

39.

Свет – это электромагнитная волна
с ~ 0,7 ... 0,4 мкм.
Свет излучается атомом при переходе из
возбужденного состояния в стационарное состояние.
В стационарном состоянии атом не излучает.
Процесс излучения длится приблизительно ~ 10 – 8 с.
За это время излучается порция электромагнитной
волны, которая называется цугом. Длина цуга: ~ 3 м.
Свет – это поток небольших порций («кусочков") ЭМВ.
Такая порция ЭМВ называется
квантом
света
или фотоном
.
Свет проявляет и волновые и квантовые свойства!

40.

.
Волновые свойства света
Оптические свойства среды характеризует
абсолютный показатель преломления, который
равен отношению скорости света в вакууме к
фазовой скорости света в данной среде:
c
n
v
Показатель преломления любой среды n 1.
Чем более оптически плотной является среда,
тем больше значение n , и тем медленнее в ней
распространяется свет.
40

41. Интерференция

– это процесс наложения двух
или более волн, в результате которого происходит
усиление или ослабление колебаний.
В тех точках пространства, в которых волны
встречаются в одинаковой фазе, колебания усиливают
друг друга, происходят с наибольшей амплитудой, здесь
наблюдается максимум (светлое пятно). Там, где волны
встречаются в противофазе, колебания гасят друг друга,
наблюдается минимум (темное пятно).
При интерференции не нарушается закон
сохранения энергии: энергия в минимуме не исчезает, а
перераспределяется в пространстве.
41

42.

42

43.

Необходимым условием
интерференции является
согласованность колебаний –
когерентность волн.
Волны являются когерентными, если:
частоты их колебаний одинаковы;
колебание векторов E и H происходит в
одном или близком направлениях (одинаковая
или близкая поляризация);
разность фаз накладывающихся волн
постоянна во времени.
43

44.

Свет, излучаемый обычными источниками света (не
лазерами), представляет собой набор плоско
поляризованных порций волн со всевозможными
направлениями колебаний векторов
и ,
E H
и хаотично изменяющейся начальной фазой. Поэтому
интерференция света от обычных источником света
не возможна.
Однако, если разделить одну волны на две
когерентные волны, то интерференция окажется
возможной. Это можно сделать, пропустив свет от
одного источника через два малых отверстия, или
отразив от плоскопараллельной пластинки, или от
двух зеркал с углом, близким к ..
44

45.

Пусть точечные источники S1 и S2
излучают две плоские
монохроматические волны.
Встречаясь на экране, эти волны
возбуждают
в точке А колебания с амплитудой
E E E 2E E cos
2
2
2
m
1m
2m
1m
k x
x x x
0
2
1
2m
- разность фаз колебаний;
- разность хода лучей;
- разность начальных фаз колебаний.
0
45

46.

Если 0 хаотично изменяется с течением времени (волны не
когерентны), то средний косинус cos 0 и тогда это обычное
сложение интенсивностей от двух источников (без интерференции).
Если o const , то в формуле для интенсивности
появляется интерференционный член
J J J 2 J J cos
1
2
1
2
который зависит от x, и на экране наблюдаются области с
различной освещенностью:
максимум, если в эту точку обе волны приходят в одинаковой
фазе, а это будет, если разность хода равна целому числу длин волн
(или четному числу длин полуволн):
x m
минимум, если волны встречаются в противофазах, а это будет,
если разность хода равна нечетному числу длин полуволн:
x (2m 1)
2
46

47.

Условие максимума интерференции
.
L m
Условие минимума интерференции
L (2m 1)
где
2
L = n x
- оптическая разность хода;
n - показатель преломления среды;
( m = 0, 1, 2, ...),
Применение интерференции:
просветление оптики;
измерение показателя преломления газов;
измерение длины;
контроль качества обработки поверхности…
47

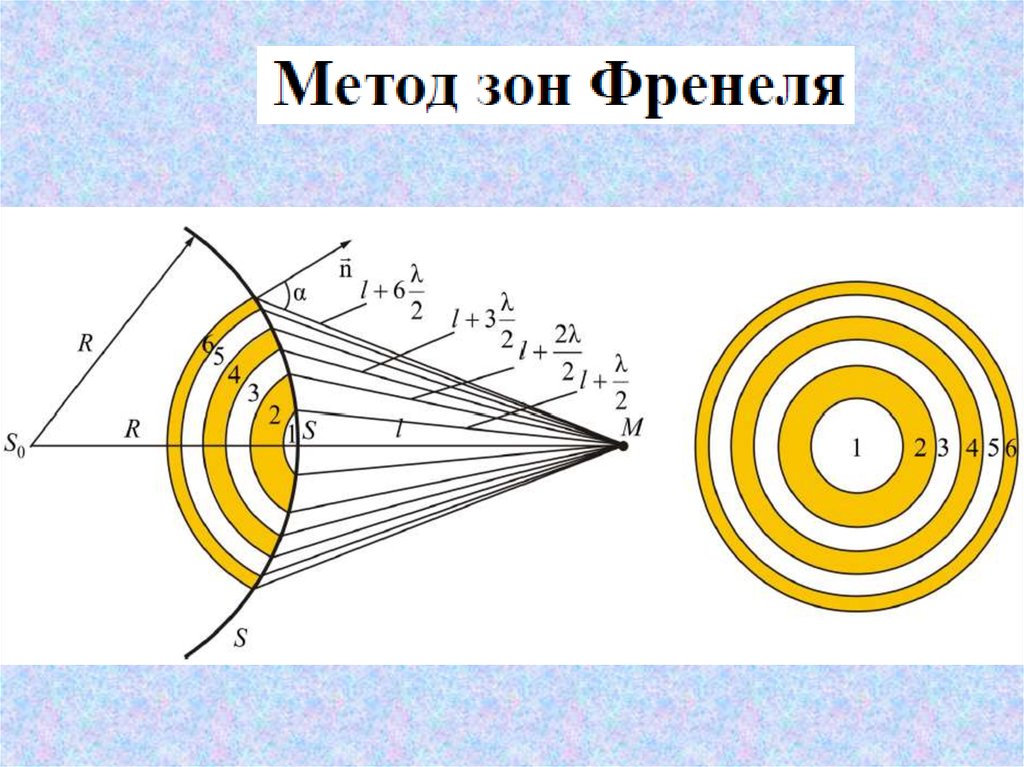
48. Дифракция света

Дифракцией
называется
совокупность явлений, которые проявляются
при распространении света в среде с резкими
неоднородностями, в результате наблюдаются
отклонения от законов геометрической оптики.
Условие неоднородности:
2b
max
b
дифракция плоских волн (дифракция Фраунгофера);
1
l
b
дифракция сферических волн (дифракция Френеля);
~1
b
l
1 геометрическая оптика.
l
2
2
2
Дифракция света определяет четкость изображения на экране
и предел разрешения оптических приборов.
48

49.

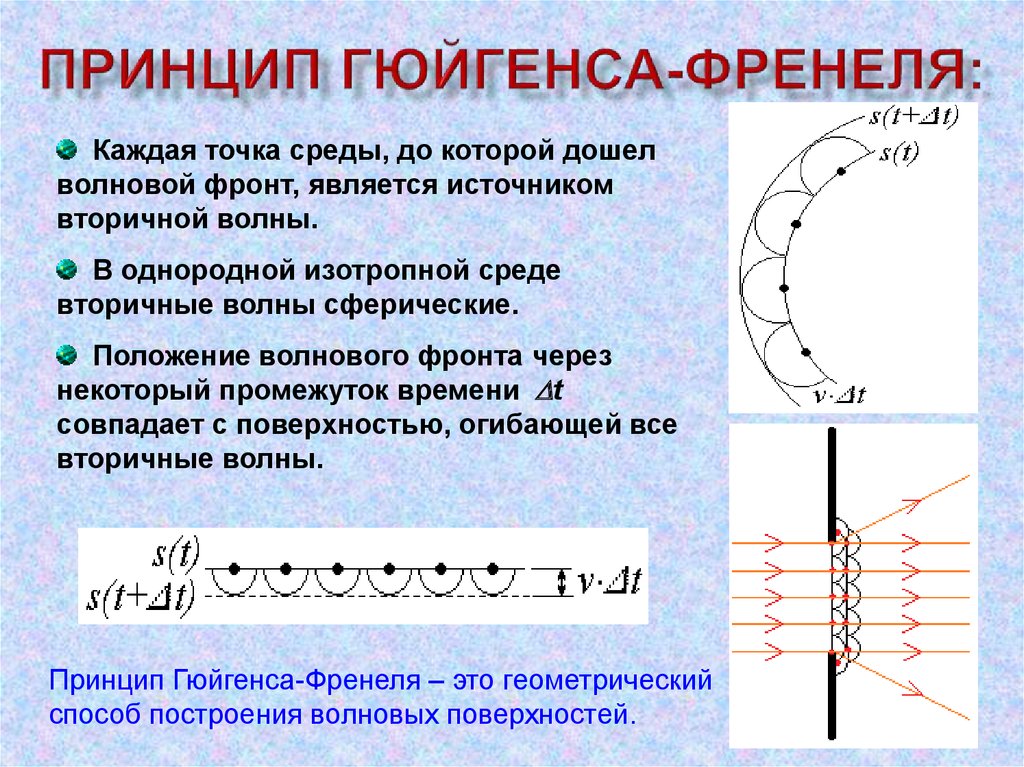
49

50. Принцип гюйгенса-френеля:

Каждая точка среды, до которой дошел
волновой фронт, является источником
вторичной волны.
В однородной изотропной среде
вторичные волны сферические.
Положение волнового фронта через
некоторый промежуток времени t
совпадает с поверхностью, огибающей все
вторичные волны.
Принцип Гюйгенса-Френеля – это геометрический
способ построения волновых поверхностей.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61.

62.

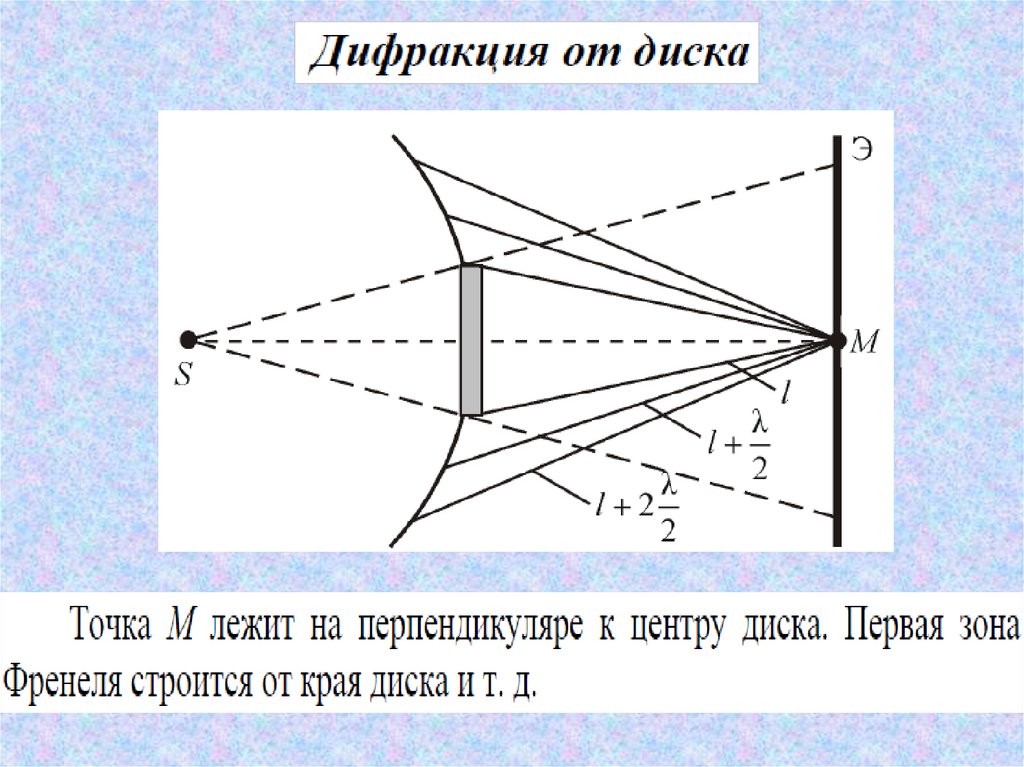
На щель шириной b падает плоская монохроматическая волна.
Условие минимума при
дифракции на щели:
b sin m

63.

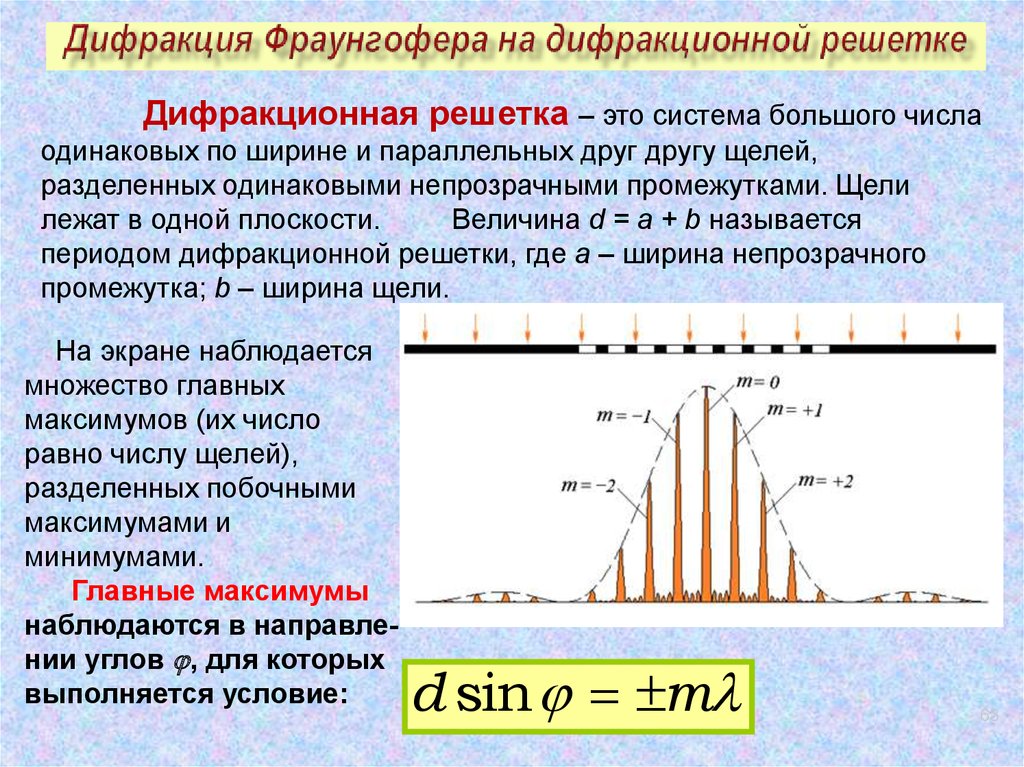
Дифракционная решетка – это система большого числа
одинаковых по ширине и параллельных друг другу щелей,
разделенных одинаковыми непрозрачными промежутками. Щели
лежат в одной плоскости.
Величина d = a + b называется
периодом дифракционной решетки, где а – ширина непрозрачного
промежутка; b – ширина щели.
На экране наблюдается
множество главных
максимумов (их число
равно числу щелей),
разделенных побочными
максимумами и
минимумами.
Главные максимумы
наблюдаются в направлении углов , для которых
выполняется условие:
d sin m
63

64.

Дифракция наблюдается и на двумерной решетке (сетке),
в которой штрихи расположены в одной плоскости, но по взаимно
перпендикулярным направлениям.
Но наиболее интересна дифракция на трехмерных
пространственных решетках, каковыми являются,
например, кристаллические вещества. Но для этого
подходит лишь рентгеновское излучение с
~ 10 12 10 8 м.
Максимумы
интенсивности наблюдаются в
тех направлениях,
в которых отраженные
атомными плоскостями волны
находятся в одинаковой фазе.
Это будет, если разность хода
лучей удовлетворяет условию:
L 2d sin m
64

65.

L 2d sin m
Это формула Вульфа-Бреггов,
которая используется для решения двух важных задач:
Наблюдая дифракцию монохроматического рентгеновского
излучения с известной длиной волны, по измеренным значениям
углов θ, можно рассчитать значение межплоскостного расстояния d,
т.е. исследовать структуру кристалла.
Это принцип рентгеноструктурного анализа.
Если исследуемое вещество бомбардировать быстрыми
электронами, то вещество излучает характеристическое
рентгеновское излучение с линейчатым спектром. Излучение с
неизвестной длиной волны направляют на кристалл с известными
значениями d. По измерениям углов θ можно определить длину
волны наблюдаемого излучения, а по ее значению судить о
химическом составе исследуемого вещества.
В этом суть рентгеноспектрального анализа.
65

66. Поляризация света

Свет, излучаемый обычными источниками (не
лазерами), это электромагнитная волна, в которой вектор
E (и вектор H ) колеблется перпендикулярно вектору
скорости v по всевозможным направлениям.
Вследствие хаотичности излучения средняя
амплитуда колебаний вектора E одинакова по всем
направлениям.
Свет с хаотичным направлением колебания вектора E
и одинаковой амплитудой колебаний по всем
направлениям называется естественным светом.

67.

При отражении или преломлении света на границе раздела двух
сред может происходить частичное или полное упорядочивание
направлений колебаний вектора E . Этот процесс называется
поляризацией света.
В частично поляризованном свете есть направление, в
котором амплитуда колебаний вектора E максимальна.
Если есть только одно направление колебаний вектора E , то
такой свет называется плоско поляризованным.
67

68.

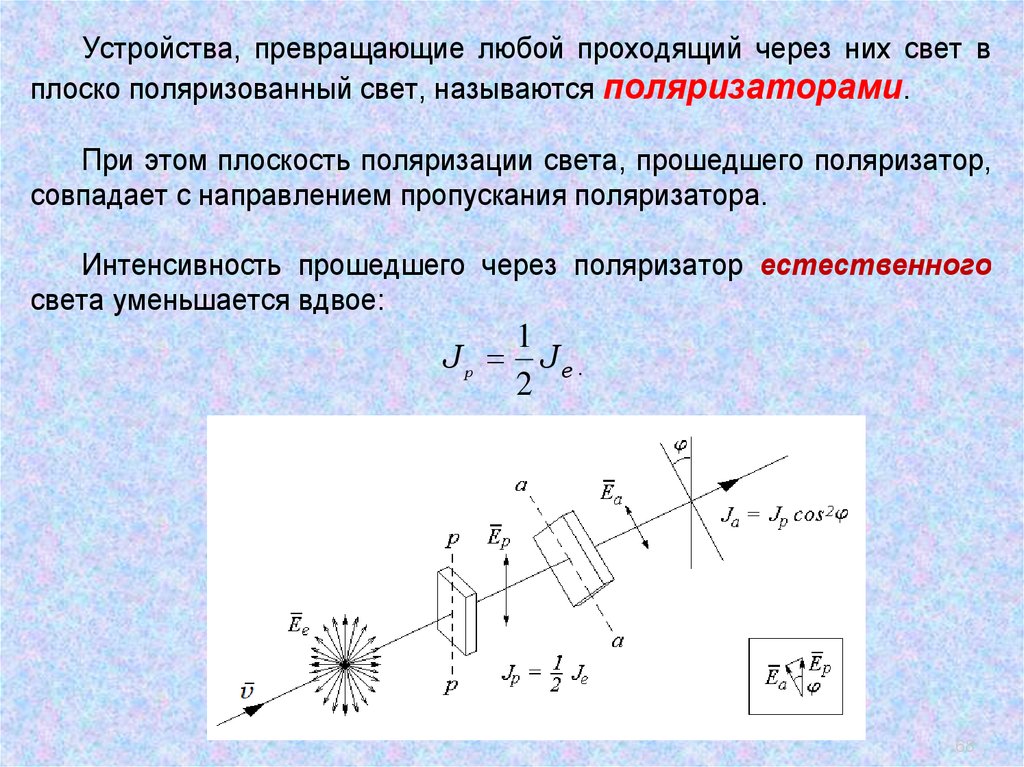
Устройства, превращающие любой проходящий через них свет в
плоско поляризованный свет, называются поляризаторами.
При этом плоскость поляризации света, прошедшего поляризатор,
совпадает с направлением пропускания поляризатора.
Интенсивность прошедшего через поляризатор естественного
света уменьшается вдвое:
1
J Je .
2
p
68

69. Закон Малюса

Если на пути плоско поляризованного света расположить второй
поляризатор (анализатор), то интенсивность прошедшего через
анализатор света будет зависеть от угла между направлениями
пропускания поляризатора и анализатора.
Так как J ~ E , а E E cos , то
2
a
p
J J cos
2
a
p
Закон Малюса: интенсивность плоско поляризованного
света, прошедшего анализатор, пропорциональна квадрату
косинуса угла между направлением поляризации падающего
света и направлением пропускания анализатора.
69

70. Поляризация при отражении

Поляризация естественного света происходит на границе раздела двух
сред. При этом преломленный луч поляризован в плоскости падения, а в отраженном свете максимальная амплитуда колебаний вектора E наблюдается в
направлении, перпендикулярном плоскости падения.
Степень поляризации обоих лучей зависит от угла падения.
При углу падения Б отраженный свет плоско поляризован.
Угол Б называется углом Брюстера, который определяется из условия:
n1
n
tg n
n
Б
n2
2
21
1
70

71. Дисперсия света

Дисперсией
называется зависимость фазовой скорости
волны от частоты колебаний:
v ( )
c
Так как скорость света в среде определяется выражением v , то
n
дисперсия приводит к зависимости показателя преломления от частоты:
n ( )
Эта зависимость проявляется, например, при прохождении белого
света через призму.
71

72.

На каждой границе раздела свет испытывает преломление, так что
sin
n
v
n
sin
n v
2
1
1
2
21
Зависимость скорости волны от частоты приводит к различным
углам преломления света различной частоты (или различного цвета):
( )
При переходе волны из одной среды в другую частота света не
изменяется, но изменяется длина волны.
72

73.

73

74.

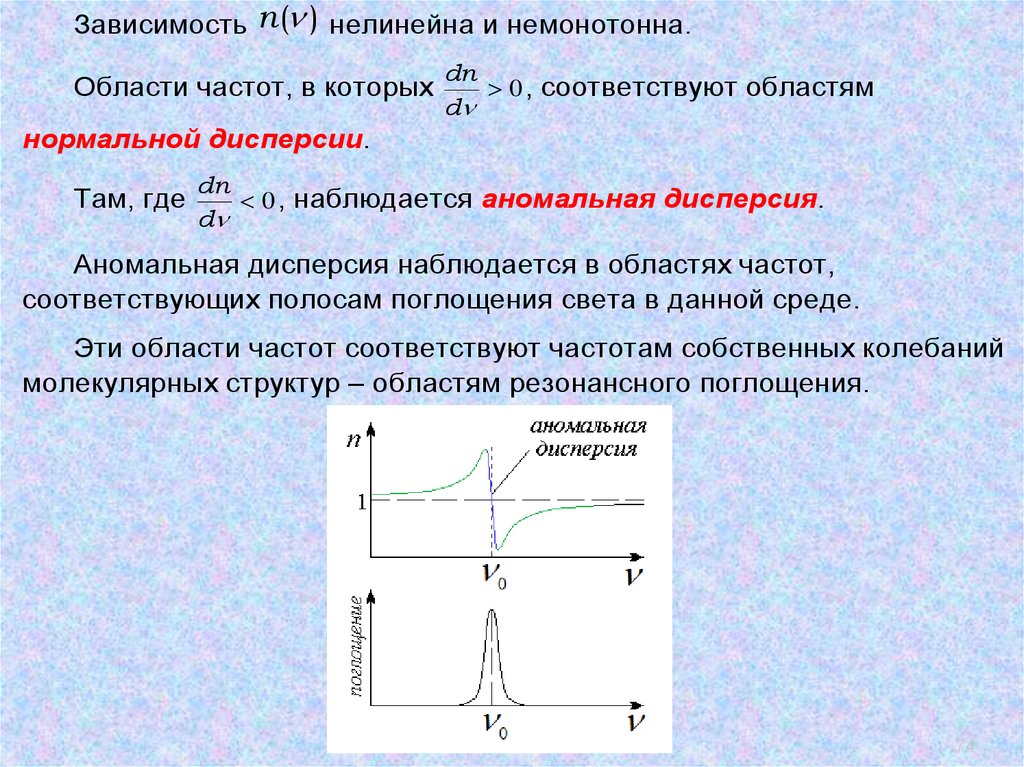
Зависимость n ( ) нелинейна и немонотонна.
Области частот, в которых
dn
0 , соответствуют областям
d
нормальной дисперсии.
Там, где
dn
0 , наблюдается аномальная дисперсия.
d
Аномальная дисперсия наблюдается в областях частот,
соответствующих полосам поглощения света в данной среде.
Эти области частот соответствуют частотам собственных колебаний
молекулярных структур – областям резонансного поглощения.
74

75.

Объяснение дисперсии в классической электронной теории
Переменное электрическое поле световой волны, распространяющейся в диэлектрической среде, вызывает вынужденные колебания внешних
(оптических) электронов. Эти осцилляторы имеют собственные частоты
колебаний.
При вынужденных колебаниях периодически изменяется дипольный
момент молекулы, и они излучают вторичные когерентные волны. Эти
волны интерферируют, и в среде распространяется волна в направлении,
совпадающем с направлением первичной волны.
Фазовая скорость волны зависит от частоты колебаний. Согласно теории Максвелла фазовая скорость v
c
.
Оптически прозрачные среды немагнитны, для них 1, поэтому
n .
2
Дисперсию света можно рассматривать как следствие зависимости диэлектрической проницаемости от частоты колебаний .
75

76. Спасибо за внимание!

76