Similar presentations:
Колебания и волны
1.
ФизикаКолебания и волны
1
2.
Колебаниями называются движения или процессы, которыехарактеризуются определенной повторяемостью во времени.
Процесс распространения колебаний в пространстве
называется волной. Основным свойством всех волн,
независимо от их природы, является перенос энергии без
переноса вещества.
Между различными видами колебаний, такими как
механические, электромагнитные, химические и т.д.,
происходящих в замкнутых и открытых системах,
существуют много общего. Поэтому, в этом разделе
наряду с рассмотрением отдельных видов колебаний
изучается и то, что их объединяет, а именно: общие для них
понятия (период Т, амплитуда А, фазаколебаний φ и т.д.),
дифференциальные уравнения и их решения.
2
3.
По характеру воздействия на колебательную системувыделяют:
• Свободные (или собственные) колебания – колебания,
совершаемые за счет первоначально сообщенной энергии
при отсутствии внешних воздействий на колебательную
систему
• Затухающие колебания - колебания, совершаемые за счет
первоначально сообщенной энергии в системе при
наличии сил трения либо сопротивления
• Вынужденные колебания – колебания, в процессе которых
колебательная система подвергается воздействию внешней
периодически действующей силы
3
4.
Механические колебания и волныГармонические колебания и их характеристики
Колебаниями называются движения или процессы, которые
характеризуются определенной повторяемостью во времени.
Гармоническими колебаниями называются колебания,
при которых колеблющаяся величина изменяется со временем по
закону синуса или косинуса.
s(t ) A cos( 0t ).
А — амплитудой колебания, максимальное значение величины,
0 — круговая (угловая) частота,
— начальная фаза колебания, в момент времени t=0,
( 0t+ ) — фаза колебания в момент времени t.
4
5.
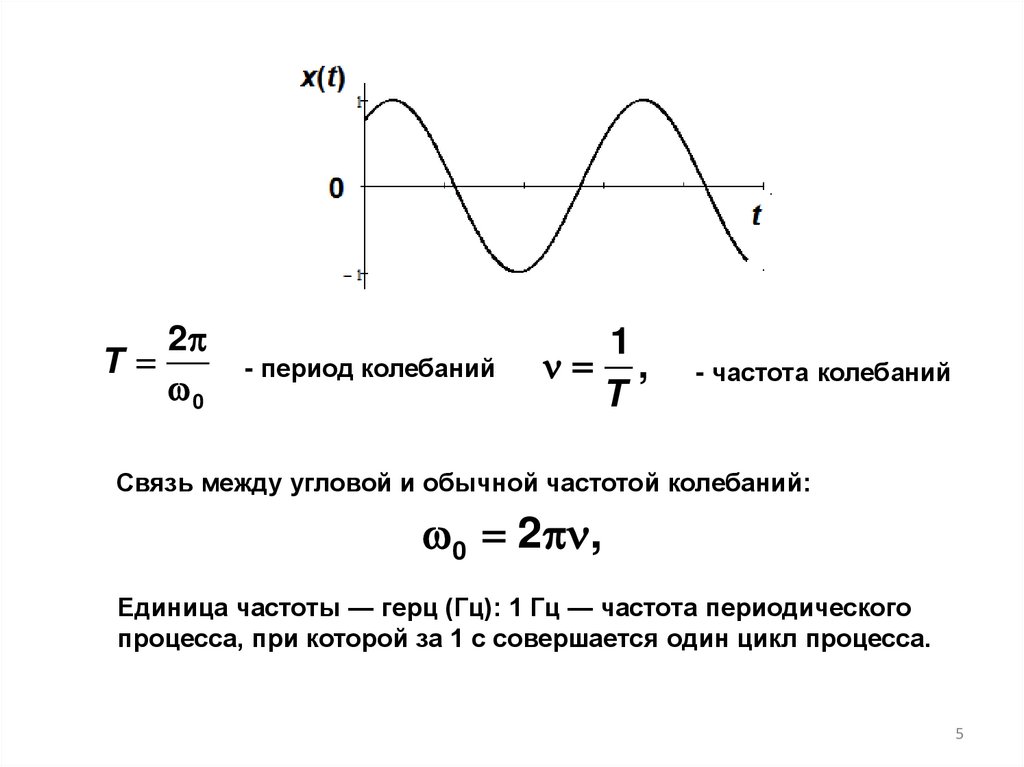
2T
0
- период колебаний
1
,
T
- частота колебаний
Связь между угловой и обычной частотой колебаний:
0 2 ,
Единица частоты — герц (Гц): 1 Гц — частота периодического
процесса, при которой за 1 с совершается один цикл процесса.
5
6.
Дифференциальное уравнение гармонических колебаний:d 2s
2
0 s 0,
2
dt
Решение дифференциального уравнения:
s(t ) A cos( 0t ).
6
7.
Гармонический осциллятор. Пружинный, физический иматематический маятники
Гармоническим осциллятором называется система,
совершающая колебания, описываемые уравнением вида;
2
d s
2
0 s 0,
2
dt
Физические примеры гармонических осцилляторов.
1. Пружинный маятник — это груз массой т,
подвешенный на абсолютно упругой пружине и совершающий
гармонические колебания под действием упругой силы
F=–
kx.
7
8.
Уравнение движения маятника:ma kx ;
d2 x k
x 0;
2
dt
m
Пружинный маятник совершает гармонические колебания по
закону:
x (t ) A cos( 0t )
и периодом
с циклической частотой
T 2
m
.
k
0
k
.
m
8
9.
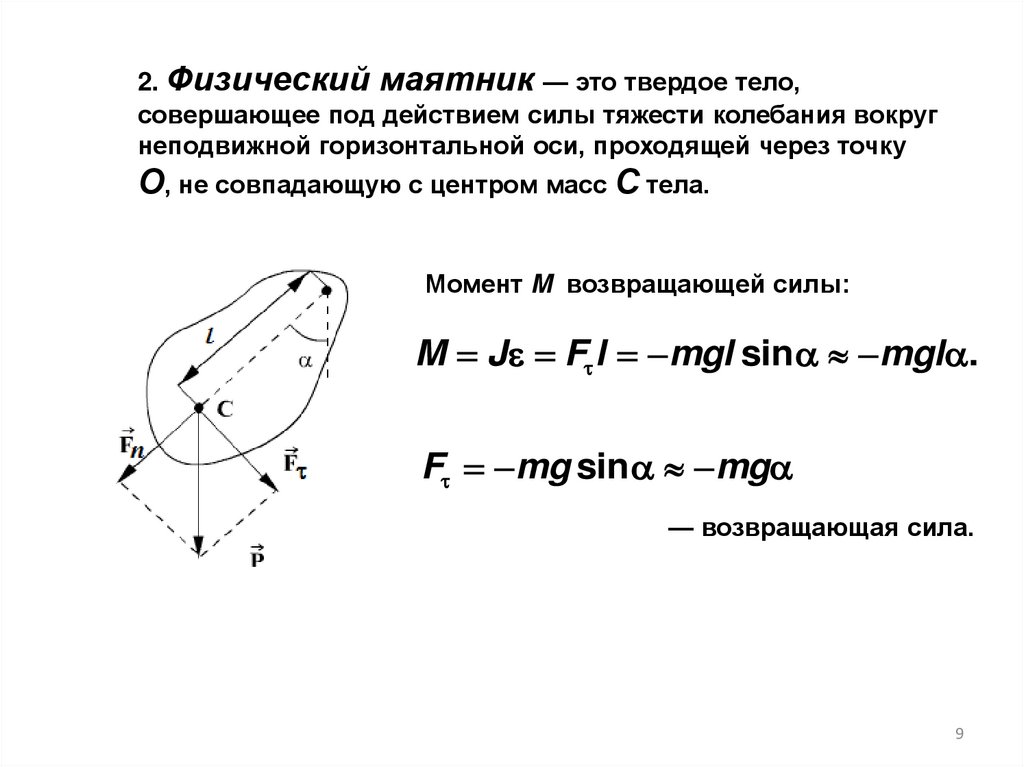
2. Физический маятник — это твердое тело,совершающее под действием силы тяжести колебания вокруг
неподвижной горизонтальной оси, проходящей через точку
О, не совпадающую с центром масс С тела.
Момент M возвращающей силы:
M J F l mgl sin mgl .
F mg sin mg
— возвращающая сила.
9
10.
Уравнение динамики физического маятника:d2
J 2 mgl 0;
dt
или:
d2
2
0 0;
2
dt
d2 mgl
0;
2
dt
J
где:
0
mgl
.
J
Решение динамического уравнения:
(t ) 0 cos( 0t ).
10
11.
3. Математический маятник — это идеализированнаясистема, состоящая из материальной точки массой т, подвешенной
на нерастяжимой невесомой нити, и колеблющаяся под действием
силы тяжести.
x
ma F mg sin ;
l
g
ma m x ;
l
g
; 0
l
2
0
Период малых колебаний
математического маятника:
g
;
l
2
l
T
2
.
0
g
11
12. Характеристики колебаний:
1213.
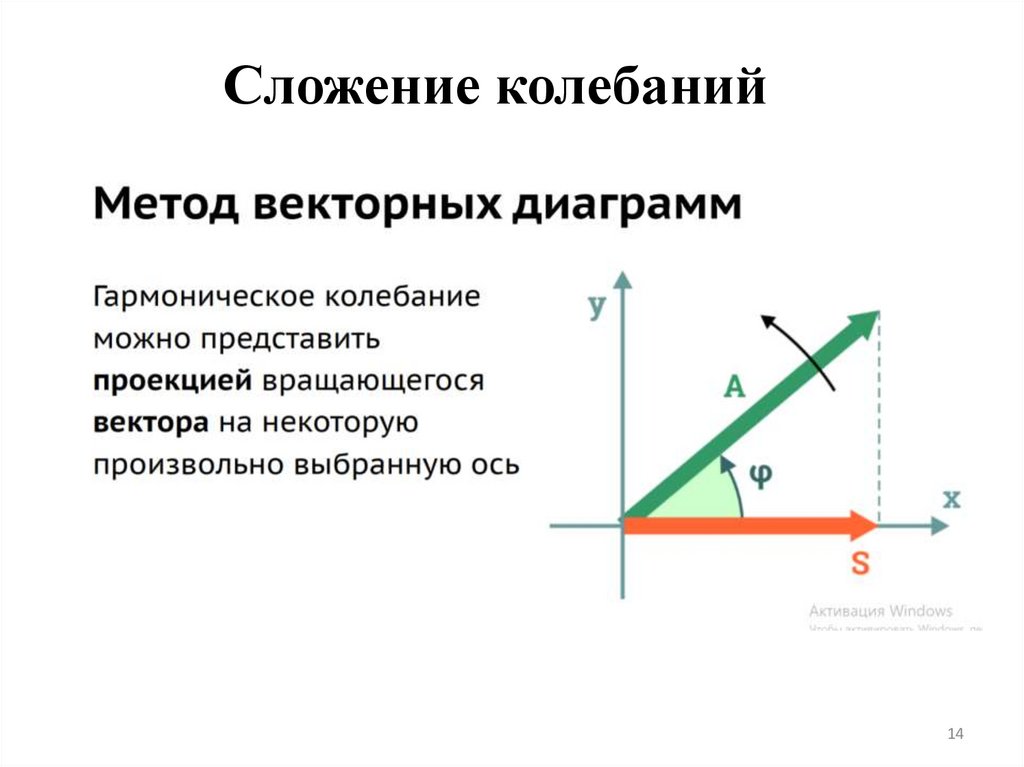
1314.
Сложение колебаний14
15.
Для дальнейшего рассмотрения теории колебаний вспомнимнекоторые моменты теории комплексных переменных
15
16.
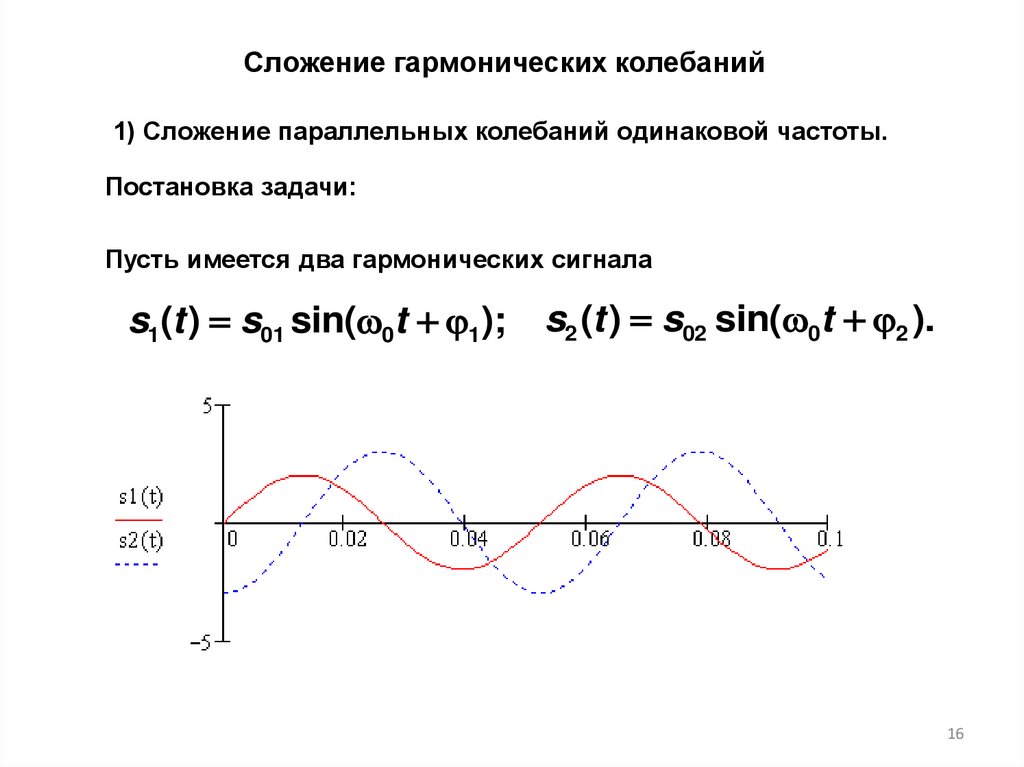
Сложение гармонических колебаний1) Сложение параллельных колебаний одинаковой частоты.
Постановка задачи:
Пусть имеется два гармонических сигнала
s1(t ) s01 sin( 0t 1);
s2 (t ) s02 sin( 0t 2 ).
16
17.
Необходимо сложить два колебания с одинаковыми частотами:s(t ) s1(t ) s2 (t ) s01 sin( 0t 1 ) s02 sin( 0t 2 )
s 1 s01e
j 1
;
s 2 s02e
j 2
.
17
18.
1819.
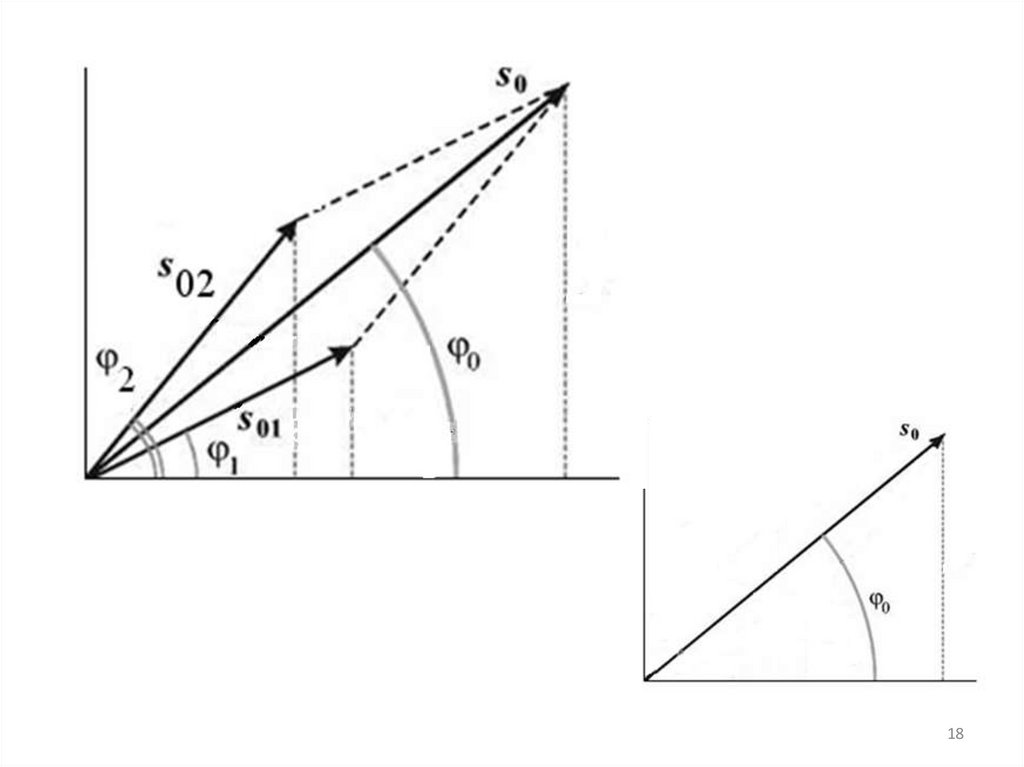
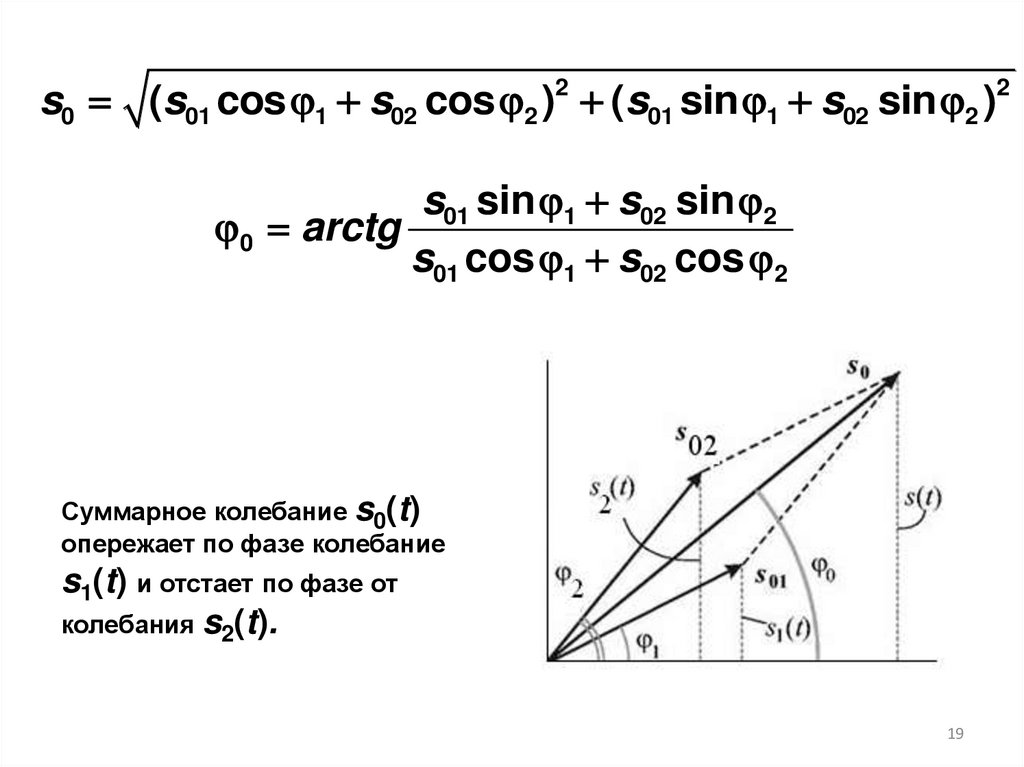
s0 (s01 cos 1 s02 cos 2 )2 (s01 sin 1 s02 sin 2 )2s01 sin 1 s02 sin 2
0 arctg
s01 cos 1 s02 cos 2
Суммарное колебание s0(t)
опережает по фазе колебание
s1(t) и отстает по фазе от
колебания s2(t).
19
20.
2) Сложение параллельных гармонических колебанийс близкими частотами.
Найдем сумму двух гармонических колебаний, частоты которых
различны, но близки по величине:
s1 A cos 1t ;
s2 A cos 2t ;
cos cos 2Cos (
) cos(
);
2
2
( 2 1 )
( 2 1 )
s s1 s2 2 A cos
t cos
t
2
2
2 A cos( t )cos( t ).
20
21.
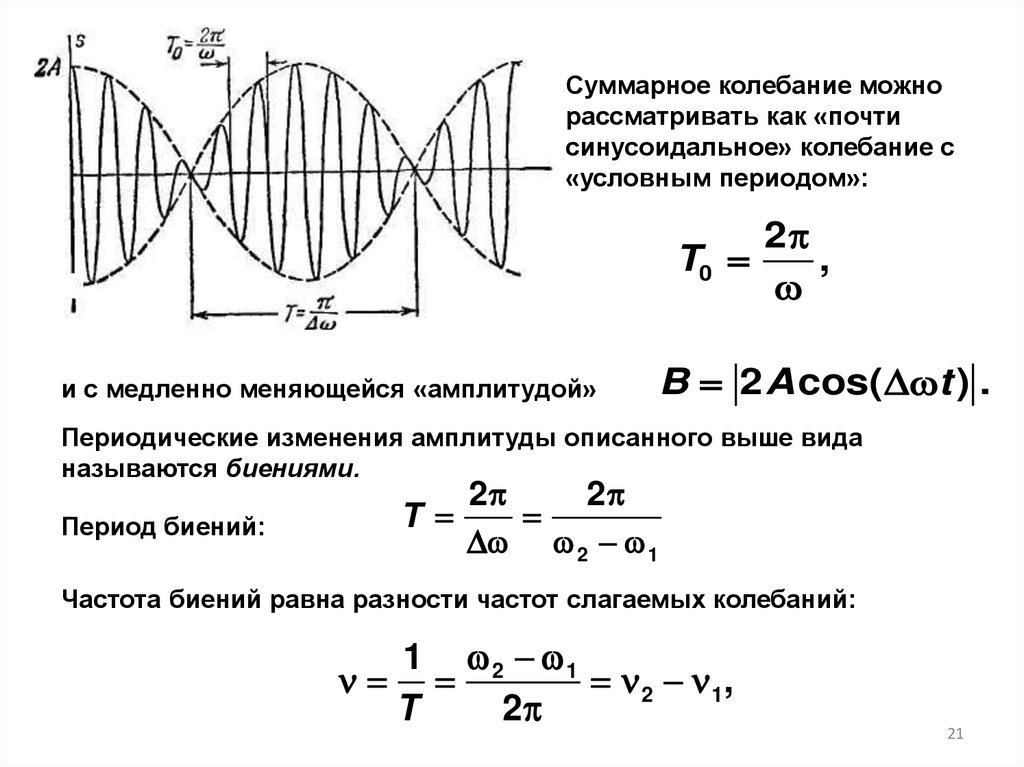
Суммарное колебание можнорассматривать как «почти
синусоидальное» колебание с
«условным периодом»:
2
T0
,
и с медленно меняющейся «амплитудой»
B 2 A cos( t ) .
Периодические изменения амплитуды описанного выше вида
называются биениями.
Период биений:
2
2
T
2 1
Частота биений равна разности частот слагаемых колебаний:
1 2 1
2 1,
T
2
21
22.
3) Сложение взаимно перпендикулярных колебаний содинаковыми частотами.
s1 s01 sin( 0t 1 );
s2 s02 sin( 0t 2 ).
Чтобы получить траекторию движения, исключим из выражений
текущее время и преобразуем синус по формулам тригонометрии:
sin( ) sin cos cos sin ;
s1
sin 0t cos 1 cos 0t sin 1;
s01
s2
sin 0t cos 2 cos 0t sin 2 .
s02
22
23.
Умножим первое уравнение на cos φ2, а второе — на cos φ1 ивычтем второе уравнение из первого
s1
s2
cos 2 cos 1 cos 0t sin( 1 2 ).
s01
s02
Теперь умножим первое уравнение на sin φ2, а второе — на sin φ1 ,
повторим вычитание, получим:
s1
s2
sin 2 sin 1 sin 0t sin( 2 1 ).
s01
s02
Возведем в квадрат каждое из равенств и сложим их.
В результате время будет исключено, а уравнение траектории
движения будет уравнением эллипса:
2
2
s1 s2
s1 s2
2
2
cos(
)
sin
( 2 1 ).
2
1
s01 s02
s01 s02
23
24.
В результате будут совершатьcя периодические движения поэллиптической траектории. Направление движения вдоль траектории и
ориентация эллипса относительно осей s1 и s2 зависят от разности
фаз
Δφ = φ2 – φ1 .
При разности фаз 0 < Δφ < π вектор движется по часовой стрелке,
а при π < Δφ < 2 π -против часовой стрелки.
24
25.
2526.
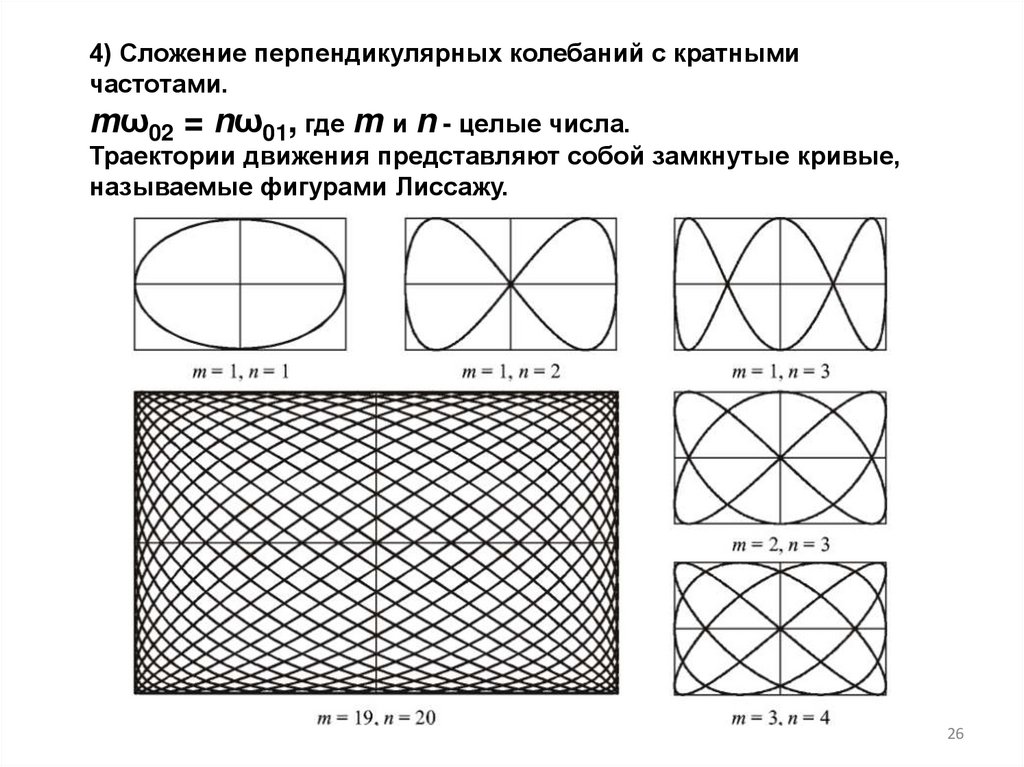
4) Сложение перпендикулярных колебаний с кратнымичастотами.
mω02 = nω01, где m и n - целые числа.
Траектории движения представляют собой замкнутые кривые,
называемые фигурами Лиссажу.
26
27.
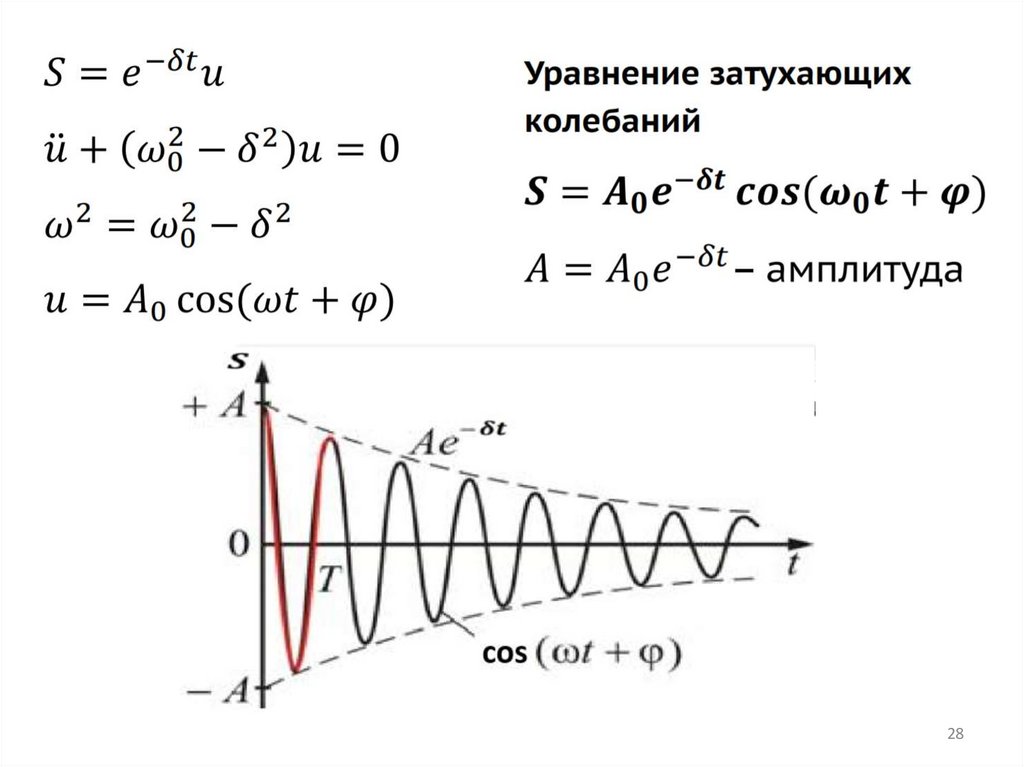
Затухающие механические колебанияЗатухающие колебания происходят в замкнутой механической
системе (Fвнеш=0), в которой имеются потери энергии на
преодоление сил сопротивления, в следствие чего амплитуда
затухающих колебаний с течением времени уменьшается .
27
28.
2829.
Характеристики затухающих колебаний29
30.
3031.
3132.
3233.
Вынужденные колебанияДля получения незатухающих колебаний необходимо
воздействие дополнительной переменной внешней силы,
которая подталкивала бы тело то в одну, то в другую сторону и
работа которой непрерывно восполняла бы убыль энергии,
затрачиваемой на преодоление трения. Подобная переменная
сила называется вынуждающей силой, а возникающие под ее
действием незатухающие колебания - вынужденными.
В простейшем случае вынуждающая сила изменяется по
закону синуса или косинуса, т.е
- амплитуда вынуждающей силы,
вынуждающей силы.
- частота колебаний
33
34.
3435.
3536.
3637. Электромагнитные колебания. Свободные электромагнитные колебания. Электрический колебательный контур. Формула Томсона.
Электромагнитные колебания могут возникать в цепи, содержащейиндуктивность L и емкость C. Такая цепь называется колебательным
контуром. Возбудить колебания в таком контуре можно, например,
предварительно зарядив конденсатор от внешнего источника напряжения,
соединить его затем с катушкой индуктивности.
С
L
Поскольку внешнее напряжение к контуру не приложено, сумма падений
напряжений на емкости и индуктивности должна быть равна нулю в любой
момент времени:
q
dI
C
L
dt
0,
откуда, учитывая, что сила тока I q , получаем дифференциальное уравнение
свободных незатухающих колебаний электрического заряда в колебательном
контуре
1
.
q q 0
LC
38.
Если ввести обозначение0
1
LC
то полученное уравнение принимает вид:
,
q 02 q 0
.
Решением этого уравнения, как известно, является функция
q qm cos( 0 t ) .
Таким образом, заряд на обкладках конденсатора изменяется по гармоническому
закону с частотой ω0, называемой собственной частотой колебательного контура.
Период колебаний определяется по формуле Томсона (Thomson W., 1824-1907):
Напряжение на конденсаторе:
2
T 2 LC
0
q q
U C m cos( 0t ) U m cos( 0t )
C C
- амплитуда напряжения.
,
q
Um m
C
Сила тока в контуре: I q 0 qm sin( 0t ) I m cos( 0t )
. 2
где
39.
Сопоставляя полученные выражения, видим, что когда напряжение наконденсаторе, а значит энергия электрического поля, обращается в нуль,
сила тока, а, следовательно, энергия магнитного поля, достигает
максимального значения. Таким образом, электрические колебания в
контуре сопровождаются
взаимными превращениями энергий
электрического и магнитного полей.
Амплитуды тока Im и напряжения Um связаны между собой очевидным
соотношением:
I m 0 qm 0 CU m
C
Um
L
.
40.
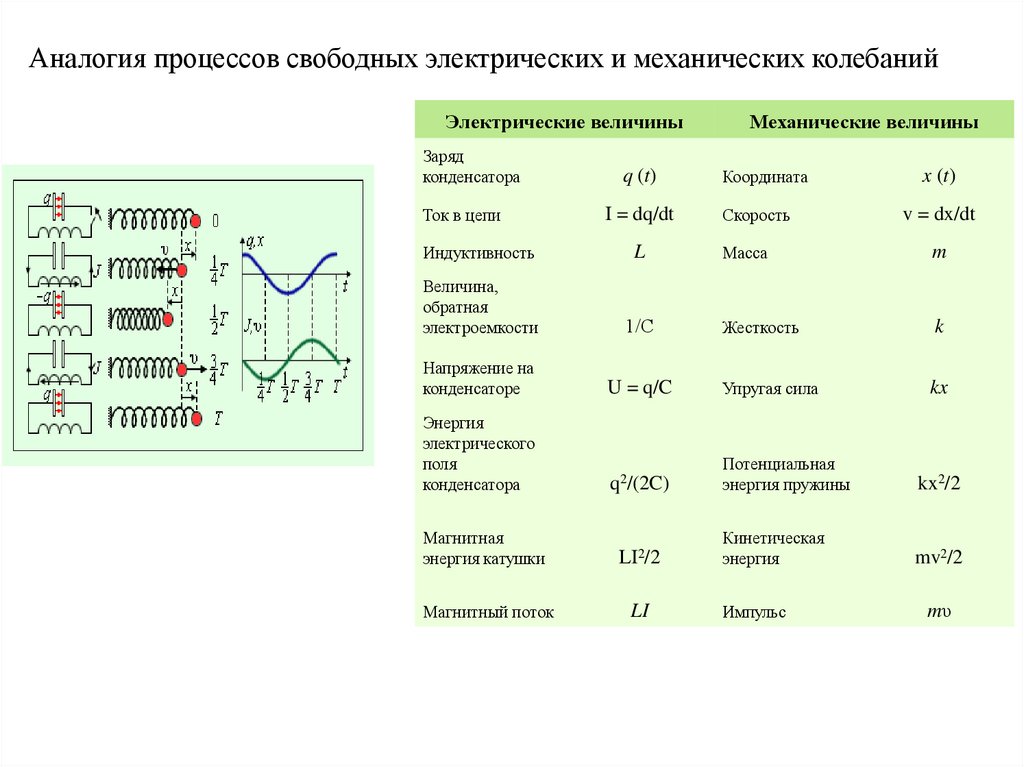
Аналогия процессов свободных электрических и механических колебанийЭлектрические величины
Механические величины
Заряд
конденсатора
q (t)
Координата
x (t)
Ток в цепи
I = dq/dt
Скорость
v = dx/dt
Индуктивность
L
Масса
m
Величина,
обратная
электроемкости
1/С
Жесткость
k
Напряжение на
конденсаторе
U = q/C
Упругая сила
kx
Энергия
электрического
поля
конденсатора
q2/(2C)
Потенциальная
энергия пружины
kx2/2
Магнитная
энергия катушки
LI2/2
Кинетическая
энергия
mv2/2
Магнитный поток
LI
Импульс
mυ
41. Свободные затухающие колебания. Добротность колебательного контура.
Всякий реальный колебательный контур обладает сопротивлением. Энергияэлектрических колебаний в таком контуре постепенно расходуется на нагревание
сопротивления, переходя в джоулево тепло, вследствие чего колебания затухают.
С
L
R
Уравнение свободных затухающих колебаний можно получить, исходя из того, что в
отсутствии внешнего источника напряжения, сумма падений напряжений на
индуктивности, емкости и сопротивлении равна нулю для любого момента времени:
L
или, поскольку
I q ,
Введя обозначение 2 1 LC
0
R
2L
dI
q
IR 0
dt
C
R
1
q q q 0
L LC
этому уравнению можно придать вид:
.
q 2 q 02 q 0
.
,
42.
Решение полученного уравнения имеет вид:q q0 (t ) cos( t )
, где q0 (t ) qm exp( t )
2
02 2
T
Мы видим, что частота свободных затухающих колебаний ω′ меньше собственной
частоты ω0. Подставив значения ω0 и β, получим:
1 R2
2
LC 4 L
Амплитуда затухающих колебаний заряда конденсатора q0(t) уменьшается со
временем по экспоненциальному закону. Коэффициент β называется
коэффициентом затухания.
43.
Затухание колебаний принято характеризовать декрементом колебаний λ,определяемым как:
q(t )
ln
T
.
q(t T )
Легко видеть, что декремент колебаний обратен по величине числу
колебаний Ne, совершаемых за время, в течение которого амплитуда
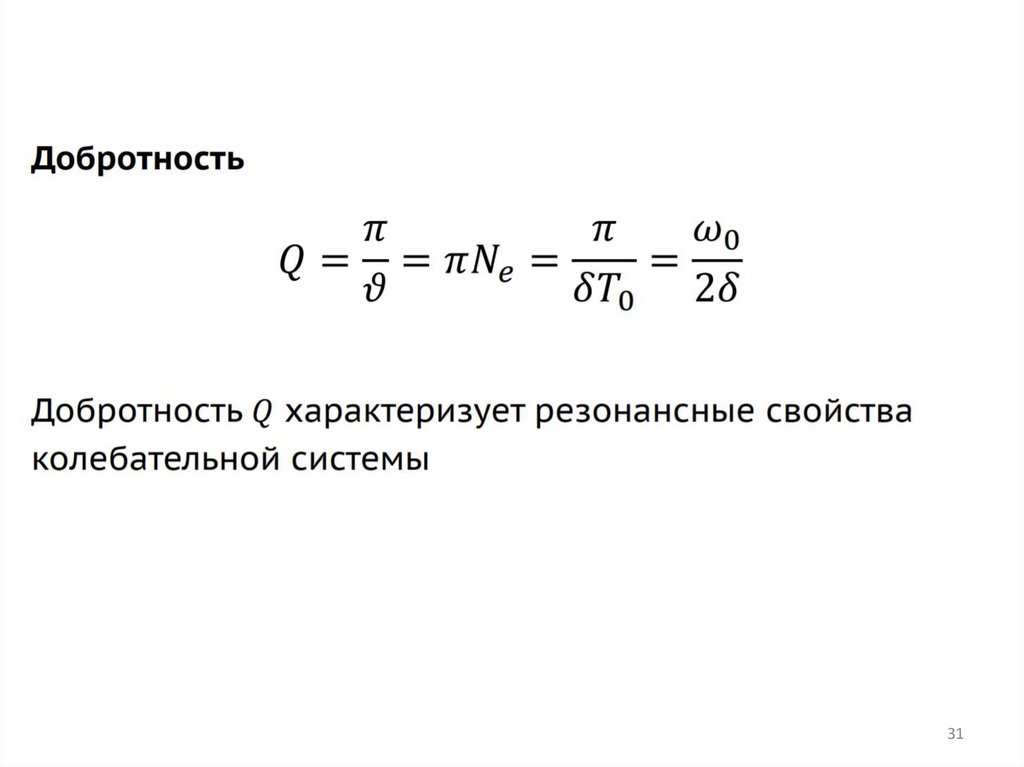
колебаний уменьшается в е раз: λ=1/Ne. Добротностью колебательного
контура называется величина:
Q N e
T
Из этой формулы видно, что добротность тем выше, чем
меньше
коэффициент затухания β. При малых затуханиях (λ<<1) можно приближенно
считать, что
Q
0
1 L 1 L
2 2
LC R R C
.
Амплитуда тока в контуре, как и заряд на конденсаторе, убывает со временем
по закону e-βt. Энергия W, запасенная в контуре, пропорциональна квадрату
амплитуды тока (или квадрату напряжения на конденсаторе). Следовательно,
W убывает со временем по закону e-2βt. Относительное уменьшение энергии
за период колебания Т (при малом затухании) есть:
W W (t ) W (t T )
2
1 e 2 t 2 T
W
W (t )
Q
.
Таким образом, потери энергии в колебательном контуре тем меньше, чем
выше его добротность.
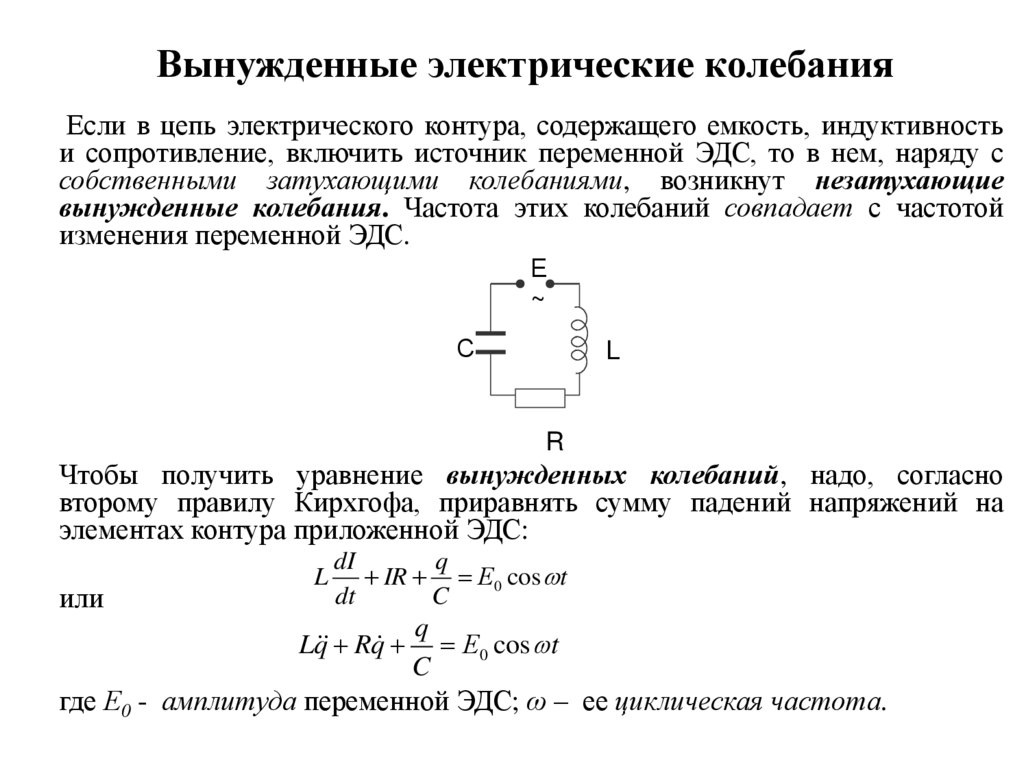
44. Вынужденные электрические колебания
Если в цепь электрического контура, содержащего емкость, индуктивностьи сопротивление, включить источник переменной ЭДС, то в нем, наряду с
собственными затухающими колебаниями, возникнут незатухающие
вынужденные колебания. Частота этих колебаний совпадает с частотой
изменения переменной ЭДС.
Е
~
С
L
R
Чтобы получить уравнение вынужденных колебаний, надо, согласно
второму правилу Кирхгофа, приравнять сумму падений напряжений на
элементах контура приложенной ЭДС:
или
L
dI
q
IR Е0 cos t
dt
C
q
Е0 cos t
C
где Е0 - амплитуда переменной ЭДС; ω – ее циклическая частота.
Lq Rq
45.
Интересующее нас частное решение этого дифференциального уравнения имеет вид:q t q0 cos t
где
E0
q0 ( )
R 2 ( L
tg ( )
1 2
)
C
,
R
1
L
C
Решение соответствующего однородного уравнения, представляет собой свободные затухающие
колебания, которые с течением времени становятся исчезающе малыми, и их можно в дальнейшем не
учитывать.
Выпишем формулы для силы тока в цепи и падений напряжений на каждом из элементов контура.
,
I (t ) q (t ) I 0 ( ) cos( t )
2
E0
I 0 ( ) q0
.
1 2
2
R ( L )
C
По аналогии с законом Ома для полной цепи по постоянному току величину
Сила тока:
Z ( ) R 2 ( L
1 2
)
C
называют полным сопротивлением цепи по переменному току. Эта величина называется
также импедансом цепи. Сопротивление R называют активным сопротивлением (на нем
выделяется тепло). Чисто мнимые сопротивления ωL и 1
C
называют соответственно индуктивным и емкостным реактивными сопротивлениями
(на них тепло не выделяется).
46.
Напряжение на сопротивлении R:U R (t ) RI (t ) U R 0 ( ) cos( t ,)
2
E0
U R 0 ( ) RI 0 ( )
R 2 ( L
Напряжение на конденсаторе С:
q(t )
U C (t )
U C 0 ( ) cos( t ,)
C
q ( )
U C 0 ( ) 0
C
E0
1
C R 2 ( L )2
C
Напряжение на катушке индуктивности L:
U L (t ) I (t ) L q (t ) L U L0 ( ) cos( t ) ,
.
1 2
)
C
R
U L0 ( ) q0 ( ) 2 L
.
.
LE0
R 2 ( L
1 2
)
C
Сравнивая написанные формулы, видим, что изменение напряжения на
сопротивлении следует за изменением силы тока в цепи без отставания
или опережения по фазе,
изменение напряжение на конденсаторе
отстает по фазе на 2 , а на индуктивности опережает по фазе на 2
изменение тока.
47.
4748.
4849.
4950.
5051.
5152.
5253.
5354.
5455.
5556.
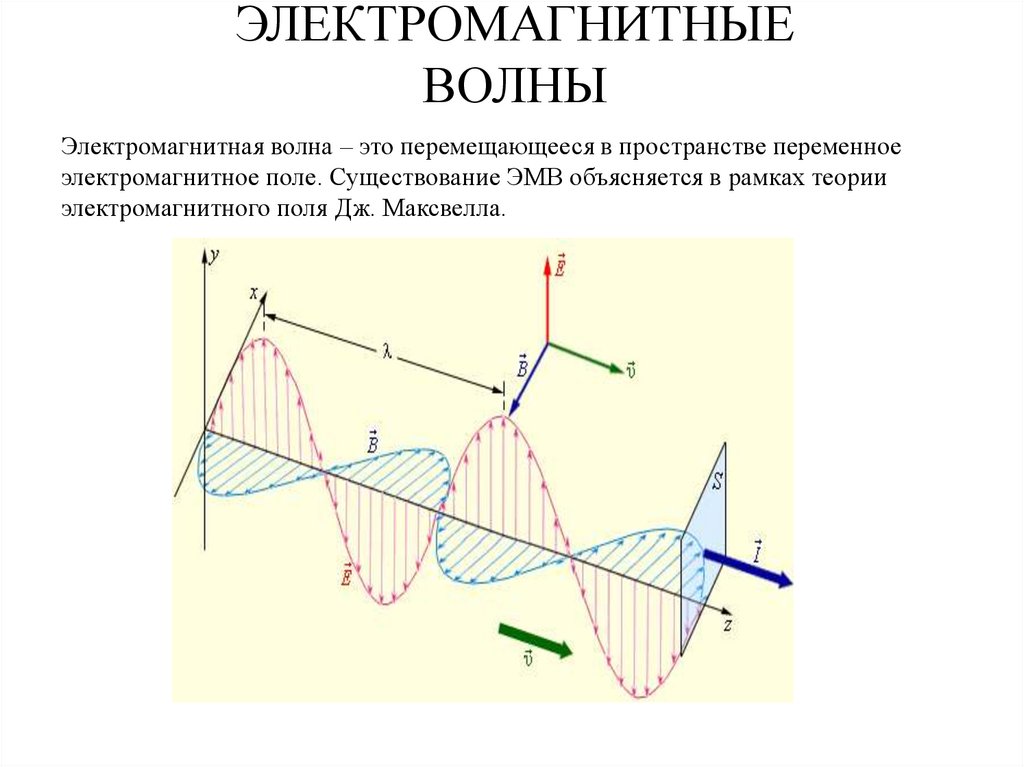
5657. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Электромагнитная волна – это перемещающееся в пространстве переменноеэлектромагнитное поле. Существование ЭМВ объясняется в рамках теории
электромагнитного поля Дж. Максвелла.
58. Свойства электромагнитных волн
1. Э/м волны поперечны2. Э/м волны распространяются со скоростью
1
0 0
3. Объемные плотности электрического и магнитного полей равны друг другу
0 E 2 B 2
2
2 0
4. Э/м волны переносят энергию. Например, через площадку S за малое время
Δt будет перенесена энергия:
W E M S t























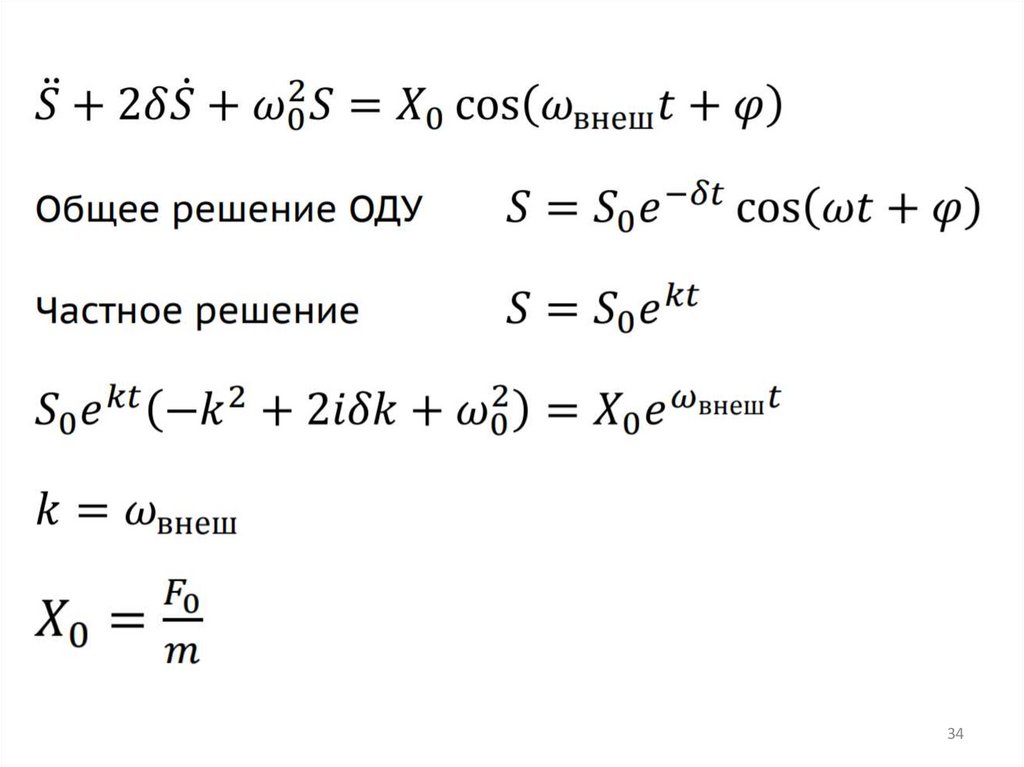





















 physics
physics








