Similar presentations:
Лекции 01-15. Волны и оптика
1.
Общая физика, 4-ый семестрВолны и оптика
Лекции 01_15
Февраль – Май 2014 года
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович
2.
Поперечные и продольные волныy
x
Поперечная волна: направление колебаний материальных точек и
направление распространения волны взаимно перпендикулярны.
Продольная волна: направление колебаний материальных точек и
направление распространения волны совпадают.
Волна - процесс распространения колебаний в пространстве.
3.
Упругие волныВолна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
x, t f x vt
x, t g x vt
v
x
t1
t2 t1
Волны неизменного профиля, распространяющиеся с
постоянной скоростью, называют бегущими волнами
4.
КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕОдиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
Цугом волн называется ограниченный
ряд повторяющихся возмущений.
Если длительность цуга значительно
превышает период колебаний τ/T >> 1,
то такой цуг волн называется
квазимонохроматической волной.
Когда τ/T → ∞ волна становится
монохроматической. (если колебания
происходят по гармоническому закону)
t2 t1
5.
КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕОдиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
Цугом волн называется ограниченный
ряд повторяющихся возмущений.
x, t f x vt
Если длительность цуга значительно
превышает период колебаний τ/T >> 1,
то такой цуг волн называется
квазимонохроматической волной.
x, t g x vt
Когда τ/T → ∞ волна становится
монохроматической. (если колебания
происходят по гармоническому закону)
t2 t1
6.
Волновое уравнениеx, t f x vt
1
<=> 2 2
x, t g x vt
t
2
2
2
2
2
2
2 2 2 =Δξ
x
y
z
Проверка решения: ξ(x, t) = f(α), α = x - vt
f
vf
t
t
f
f
x
x
2
2
v f
2
t
f
2
x
2
2
v
2
t
x 2
2
2
7.
Гармоническая волнаx, t f x vt
1
<=> 2 2
x, t g x vt
t
x
x 0 : 0, t a cos t
2
2
x, t a cos t x v
v
x, t a cos t x v
v
Фазовая
скорость
волны
- циклическая частота волны
T 2 - период волны 1 T 2 - частота волны
t x v - фаза - начальная фаза
a 0 - амплитуда волны
8.
Гармоническая волнаДлина волны – это наикратчайшее расстояние между
двумя точками среды, фазы которых отличаются на 2 .
v
vT
v
k
2
- волновое число
k
v
2
2
k
vT
9.
Плоские гармонические волныl
( r, t ) a cos t a cos( t kl )
nr rcos l
Волновая поверхность (плоскость) –
геометрическое место точек, колеблющихся в
одной фазе
a cos( t knr )
k kn – волновой вектор
2
k
Re ae
i ( t kr )
r , t a cos t k r
k k x ex k y e y k z ez
a cos t k x x k y y k z z
10.
Трехмерное волновое уравнение( r, t ) a cos( t kr )
2
2
2
2
2
v 2 2 2
2
t
y
z
x
2
2
v
2
t
Волновой вектор в любой точке перпендикулярен волновой
поверхности.
Форма волновой поверхности зависит от симметрии задачи.
Для плоских волн это плоскости
Для сферически симметричных волн – концентрические сферы
Для цилиндрически симметричных - соосные цилиндры или (в
двумерном случае) концентрические окружности
11.
Сферические волныЕсли r >> λ и d, то источник можно считать точечным, а
волну на этих расстояниях – сферической.
2
2
2
2 1
2
v 2 v 2 r
2
t
t
r r r
f r vt g r vt
r, t
r
a cos t kr
r, t
r
vф
k
a0
a(r)
r
12.
Цилиндрические волны2 1
v
2
t
2
v
v
,t
v
v
f vt g vt
ξ(ρ,t) = (a0/√ρ)cos(ωt + kρ +α)
vф
k
a(ρ) = (a0/√ρ)
13.
Стоячие волныНаложение двух распространяющихся во встречных направлениях
бегущих плоских волн может образовать стоячую волну:
пад отр a cos t kx a cos t kx
2a cos
t kx t kx
2
cos
t kx t kx
2
2a cos kx cos t 2a sin kx sin t
2
2
Граничные условия:
0, t l , t 0
0, t 0 cos
2
0
2
2
14.
Стоячие волны2a sin kx sin t
l , t 0 sin kl 0 kl n kn
n 1
n 2
n 3
n 4
k
2
2
n
n
l
n
l
n n
l
, n 1,2,3,...
2
v, n
v
n
nv
n
2l
15.
Стоячие волныСтоячие волны (эффект сложения двух плоских волн одной длины и
амплитуды, распространяющихся навстречу друг-другу)
A cos(ωt–kx) + A cos(ωt+kx) =
= 2A cos(kx) cos(ωt)
kl/2 = π/2 + πn – условие
существования стоячей волны
На правом конце узел - А(0) = 0
На левом конце пучность - А(l) = 2А
k = 2π/λ
16.
Упругие волны в газе и жидкостиРассмотрим плоский слой объёмом V0 S x с массой m const
x0 , t
F x0
m
0
V0
x0 x, t
x0 x
x0
x
m
V
F x0 x
m
m
V
2 V 2 V 0
V
V0
V0
x0
x0
V S x0 x x0 S
x V0
x
x
17.
Упругие волны в газе и жидкостиx0 , t
F x0
V
V0
x
x
x0 x, t
x0 x
x0
x
V
0
V0
F x0 x
0
x
18.
Упругие волны в газе и жидкостиx0 , t
F x0
x0 x, t
x0 x
x0
x
F x0 P x0 S
F x0 x
F x0 x P x0 x S
P x0
mx Fx S P x0 P x0 x S
x
x
x x0 x0 , t , x x0 , t , x x0 , t
19.
Упругие волны в газе и жидкостиx0 , t
F x0
x0 x, t
x0 x
x0
x
F x0 x
P
1 P
m V0
x
0 x
Уравнение состояния
Уравнение процесса
P P
S const
20.
Упругие волны в газе и жидкости0
x
0 2
x
x
x
2
P P
x S x
1 P
1 P
2 P 2
0 2 2
0 x
0 S
x
S x
Одномерное волновое
уравнение
2
2
2
v
2
t
x 2
Скорость упругих волн
P
v
S
м/с
21.
Упругие волны в газе и жидкостиP
v
S
Скорость звука в газе
PV const
P P0
0
P
P0
1
P0
S
0
0
P
v
S
1,4, T 290 K, M 29 г/моль v
P0
v
RT
M
0 RT
M
RT
M
340 м/с
22.
Упругие волны в газе и жидкостиP
v
S
Скорость звука жидкости
P A 1
0
v
A
0
P
v
S
1
A
0
0
A 3,75 108 Па, 6,0, 0 =103 кг/м3 ,
v 1,5 км/с
23.
Упругие волны в твёрдом телеF x
F x x
m
V0
x
F
S
E
x x
x
E
x
m S x x x S
x V0
x
x
2
m V0 E 2
x
V0 2 E 2
E 2
m x
0 x 2
24.
Упругие волны в твёрдом телеV0 2 E 2
E 2
m x
0 x 2
2
vl 2
2
t
x
2
2
vl
E
0
железо
0 =7,9 103 кг/м3 , E 2 1011 Па v l 5,1 км/с
25.
Упругие волны в твёрдом телеE
x
Продольная волна
vl vt
G
x
Поперечная волна
Поперечная упругая волна в стержне
2
2
2
vt 2
2
t
x
vt
G
железо
0
v t 3,15 км/с
26.
Плотность энергии волныПлотность кинетической энергии
2
m
Рассмотрим малый элемент среды: Ek
2
E k m 2
wk
V V 2
wk
2 t
2
27.
Плотность энергии волныПлотность потенциальной энергии
d x
d x x
F S
F S
x x
x
x
x
1) Малые смещения d 2) справа и слева одинаково
dE p d Aвнешн Sd x x Sd x
28.
Плотность энергии волныd x
d x x
F S
F S
x x
x
x
dE p Sd x x x Sd x
x
V S x
E
S x d
x
x
x
29.
Плотность энергии волныdE p Sd x x x Sd x
x
V S x
E
S x d
x
x
E
v
dE p VE
d V d V
d
x x
2 x
2 x
2
2
E p
v
wp
E p V
V
2 x
2
wp
v
2
2 x
2
w wk w p
2
2
v
2
2 t
2 x
2
2
30.
Плотность энергии волныwp
v
2
2
2 x
В бегущей волне:
w wk w p
v
t
x
2
v
2
2 t
2 x
wk w p
2
31.
Плотность потока энергии и интенсивностьПлотность потока энергии
Модуль вектора плотности потока энергии равен энергии,
проносимой волной в единицу времени через площадку
единичной площади, ориентированной перпендикулярно
направлению переноса энергии волны.
j
Дж
Вт
2
2
с м
м
32.
Плотность потока энергии и интенсивностьjx
dW jx x, t jx x x, t Sdt
xSdt
x
V , dt
j x x, t
j x, t
V xS
x
x
x
x x
jx
dW
Vdt
x
jx
w
t
x
2
2
2
w v
2
2
2v
t
tt
x
xt
t t 2 t
2 x 2
33.
Плотность потока энергии и интенсивность2
2
2
w v
2
2
2v
x xt
t tt
t t 2 t
2 x 2
tt v xx
2
w
2
2
v t xx x xt v
t x
t
x
jx
w
t
x
jx v
t x
2
34.
Плотность потока энергии и интенсивностьjx
w
t
x
jx v
t x
2
P
2
2
Идеальный газ: P
v 0 v
x
S
jx v
P
t x
t
2
Твёрдое тело:
jx
t
35.
Плотность потока энергии и интенсивностьПлотность потока энергии в бегущей волне
jx v
t x
2
v
t
x
jx v 2vw p vw j wv
x
Интенсивность волны
2
2
I j
Вт
м2
вектор Умова
Это модуль средней по времени
плотности потока энергии.
36.
Плотность потока энергии и интенсивностьjx P
Pv
Pv
t
x
0
Идеальный газ:
P v P P
2
0 v
0 v
2
В гармонической
волне
I jx
P 2
2
Pmax
2
I
P 2
0 v
2
Pmax
I
2 0 v
37.
Энергия гармонической волныПлотность энергии в гармонической волне
a cos t kx
wk
2
2
a 2 2
wk w p
2
sin 2 t kx
a 2 2
4
a sin t kx
wk w p
1 cos 2 t kx
38.
Энергия гармонической волныt
wk w p
t
w wk w p
wk w p
t
a 2 2
4
1 cos 2 t kx
39.
Энергия гармонической волныИнтенсивность гармонической волны
Плоская гармоническая волна
jx v w 2v wk a 2 2 v 2 sin 2 t kx
sin t kx
2
1
2
1 2 2
I a v
2
a 2 2
j w
2
40.
Энергия гармонической волныИнтенсивность гармонической волны
Плоская гармоническая волна
jx v w 2v wk a 2 2 v 2 sin 2 t kx
sin t kx
2
1
2
1 2 2
I a v
2
Сферическая гармоническая волна
r0
I I0
r
2
I 0 I r0
41.
ПОТОК ЭНЕРГИИпоток энергии:
Ф jdS jndS jn dS
среднее значение:
Ф j dS I cos dS
S
S
S
для сферической волны:
Ф
S
S
j dS j S j 4 r 2 P const
S
r0
I I0
r
2
P – мощность источника
42.
Затухание волнПлоская квазигармоническая волна
x, t a exp x cos t kx
- коэффициент затухания. В вязкой среде
I
2 - коэффициент
I0
поглощения
I I 0 exp x
x
43.
Затухание волнСферически-симметричная волна
r02
I I 0 2 exp r
r
I 0 I r0
44.
Звуковые волны в газеШкала звуковых волн
0 16 Гц
16 2 104 Гц
2 104 109 Гц
>109 Гц
45.
Сила звукаЗвук
Интенсивность звука - поток
энергии, переносимый звуковой
волной через единицу площади
поверхности. I = dW/dS [Вт/м2].
Сила звука (или «уровень
громкости звука») измеряется по
относительной шкале в децибелах
[дБ]:
Р = 10lg10(I/I0)
I0 - порог слышимости (= 1пВт/м2
при частоте 1 кГц)
Уровень
громкости, дБ
Порог слышимости
0
Тиканье наручных часов
10
Шепот
20
Звук настенных часов
30
Приглушенный разговор
40
Тихая улица
50
Обычный разговор
60
Шумная улица
70
Опасный для здоровья
уровень
75
Пневматический молоток
90
Кузнечный цех
100
Громкая музыка
110
Болевой порог
120
Сирена
130
Реактивный самолет
150
Шумовое оружие
200
46.
ШКАЛА УРОВНЕЙ ГРОМКОСТИ ЗВУКАПорог болевого ощущения –
значение
интенсивности,
при
котором
волна
перестает
восприниматься как звук, вызывая в
ухе лишь ощущение боли и
давления.
I
L 10lg
I0
L – уровень громкости [Дб]
I0 – исходная интенсивность: 10-12 Вт/м2
47.
Распространение звуковых волнПри распространении звуковых волн в среде возникают те-же
характерные эффекты, что и при распространении световых
(электромагнитных) волн:
- Дисперсия (зависимость скорости волны от частоты) – для звуковых волн
в однородных средах выражена слабо
- Затухание (потеря энергии звуковой волной за счет вязкости среды)
- Дифракция (изменение направления распространения волны при
огибании препятствия)
- Интерференция (эффект наложения двух волн одной длины, при котором
амплитуда колебаний в разных точках пространства становится разной)
- Стоячие волны (эффект сложения двух волн одной длины,
распространяющихся навстречу друг-другу)
- Эффект Доплера (зависимость слышимой частоты звука от скорости
источника или приемника звука)
- …..
48.
Эффект ДоплераЭффект Доплера (зависимость слышимой частоты
звука от скорости источника или приемника звука)
Эффект был впервые описан Кристианом
Доплером в 1842 году.
49.
Эффект Доплера в газахvT0
u ист
u пр x
v
uист x T0
v x uист T0
x
1
1
, 0
T
T0
T
v отн
v x uпр x
0
T0
v x uпр x
v x uист x
v x uист x
v x uпр x
50.
Эффект Доплера в газахРасстояние между источником
и приёмником велико.
0
k
u пр
v uпр cos
v uист cos
Если
2
0
u ист
Эффект Доплера имеет чисто кинематическое происхождение,
возникает для движений любой природы
51.
Общая физика, 4-ый семестрВолны и оптика
Лекции 4_7
Электромагнитные волны
3, 10, 17, 24 марта 2013 года
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович
52.
Уравнения Максвелла в локальной формеОсновные уравнения электромагнитного поля в неподвижных
средах.
B
E
t
D
D
H jпров
t
B 0
стор
Джеймс Клерк
Ма́ксвелл,
1831- 1879
53.
Уравнения МаксвеллаСвойства уравнений Максвелла
1. Уравнения выполняются во всех инерциальных системах отсчёта.
Они являются релятивистски инвариантными.
2. Уравнения линейные – отражение принципа суперпозиции для
магнитных и электрических полей.
3.Уравнения содержат известные законы электродинамики: закон
Кулона, закон Био-Савара-Лапласа, уравнение непрерывности и т.п.
4. Уравнения не симметричны относительно векторов E и B.
5. Из уравнений Максвелла вытекает возможность
распространения электромагнитных волн в средах и в вакууме.
54.
Волновое уравнение для электромагнитных волнРассмотрим однородную, изотропную диэлектрическую среду
или вакуум , const, 0, 0 j E 0
B
E
t
H D
t
H
E 0
t
H E
0
t
D 0
B 0
D 0E
B 0 H
E 0 Уравнения стали
симметричны
относительно
H 0 векторов E и Н.
55.
Волновое уравнение для электромагнитных волнH
E 0
t
H E
0
t
E 0
H 0
H
E 0
t
a
b c
b a c c a b
E E E
E 0,
E E
E E
56.
Волновое уравнение для электромагнитных волнH
E 0
t
H E
0
t
E 0,
E E
E 0
H 0
E E
H
E 0
E 0 H
t
t
E
2E
H 0
E 0 0 2
t
t
57.
Волновое уравнение для электромагнитных волнE
2E
H 0
E 0 0 2
t
t
2E
2
v
E
2
t
1 c
v
2H
2
v
H
2
t
1
0 0
1
0 0
3 10 м/с
8
v
c
58.
Плоская электромагнитная волнаСвязь E и H в бегущей волне
Рассмотрим волну, распространяющуюся вдоль оси x.
Формально:
0
y z
E 0
Ex
0
x
Ex const Ex 0
H 0
H x
0 H x const H x 0
x
Вывод: электромагнитная волна – поперечная.
59.
Плоская электромагнитная волнаЭлектромагнитная волна –
ex
поперечная.
Направим ось Y вдоль
E
x
направления вектора Е
ey
ez
0
0
E || y E E y e y
Ey
0
0
E y
x
ez
E y
H
H
|| e z
e z 0
t
x
t
E
Вывод: электромагнитная волна – поперечная;
H
E 0
t
, причём эти векторы
образуют правую тройку векторов.
v
H
60.
Плоская электромагнитная волнаПусть E y f x vt
E y
H z
0
x
t
1 f
H z
Oz :
0
=>
v t
t
f
f
Hz
dt
const
v 0 t
v 0
1
f
1 f
x
v t
0
Hz
f x vt
0
0 E y x vt 0 H z x vt
61.
Плоская электромагнитная волна0 E y x vt 0 H z x vt
wE
0 E 2
2
wH
0 H 2
2
wE wH
62.
Плоская электромагнитная волнаСвойства бегущей электромагнитной волны
E
1) электромагнитная волна – поперечная;
, причём эти векторы
образуют правую тройку векторов.
2) Векторы E и H одинаковым образом
зависят от координат и времени.
3) В электромагнитной бегущей волне
плотности электрической и магнитной
энергий одинаковы, т.е. wE wH
v
H
H
E
v
63.
Плоская электромагнитная волнаПлоская гармоническая (монохроматическая) волна
E y Em cos t kx
H z H m cos t kx
0 Em 0 H m
k
v
Фазы колебаний E и H
совпадают, причём
Плоскость, в которой лежат векторы E и k , называется
плоскостью поляризации.
64.
Поляризация плоских гармонических волнПусть k || z . Складываются волны одинаковой частоты
y
E
Ey
Пусть E1 || x, E2 || y
x
E E1 E2
z k Ex
E = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey
2 1
.
65.
Поляризация плоских гармонических волнE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
Ey
A1
Плоская (линейная)
0,
=>
поляризация
Ex
A2
y
y
E
E
x
x
k
k
Плоскость поляризации сохраняет своё положение.
66.
Поляризация плоских гармонических волнE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
A1 = A2 = A; δ = +π/2
Ex = Acos(ωt – kz); Ey = +Asin(ωt – kz)
=>
Круговая
(циркулярная)
поляризация
При круговой поляризации конец вектора E равномерно
вращается по окружности в плоскости колебаний x, y .
y
y
E
E
x
x
k
Правая круговая поляризация.
k
Левая круговая поляризация.
67.
Поляризация плоских гармонических волнE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
A1 A2 , 0, 2,
Эллиптическая
=> поляризация
либо A1 A2 , 2
При эллиптической поляризации вектор E вращается с
постоянной угловой скоростью, а его конец движется по эллипсу
в плоскости колебаний x, y .
y
y
E
E
x
x
k
Правая эллиптическая
поляризация.
k
Левая эллиптическая
поляризация.
68.
Вектор ПойнтингаE
В однородной, изотропной
H 0 t
диэлектрической среде или в
вакууме
E H
0
t
2
2
0 H
0 E
E H H E
t 2
2
w
E H
t
S E H
Вт
м2
w
S
t
E
H
w
t
69.
Вектор ПойнтингаS E H
Вт
м2
w
S
t
Рассмотрим бегущую волну:
0 2
0 E 2
S EH
E
2vwэл vw
0
0 0
Интенсивность бегущей волны
I S
S wv
70.
Энергия электромагнитных волнИнтенсивность плоской гармонической волны
0 2
S EH
Em cos2 t kx
0
cos t kx
2
1
2
I S
0 Em2
I
0 2
В слабо проводящей среде: E Em exp x cos t kx
I I 0 exp x
2 - коэффициент поглощения
71.
Импульс электромагнитных волнСТО: p
c2
v
Электромагнитная волна в вакууме
как поток фотонов (m = 0, v = c): p c 2 c
w
S
K 2 c - объёмная плотность импульса K 2
c
c
S K E H
В среде: K 2
0
0
v
K D B
0 E 0 H D B
72.
Давление электромагнитных волнdV Scdt
dp dp отр dp
S
dp
dpотр
cdt
dp
x
dp dp dp отр
Ox : dp dp dpотр
K Kотр cdt S
F
1 dp K K отр cdt S
P
c K Kотр w wотр
S S dt
Sdt
73.
Импульс и давление электромагнитных волнF
1 dp K K отр cdt S
P
c K Kотр w wотр
S S dt
Sdt
P w wотр
S
dp
dpотр
dp
cdt
P 1 w
x
wотр w , 0 1
0
1
P w
P 2 w
74.
Излучение электромагнитных волнПоле излучения диполя
III
II
p t
I
r
I – ближняя зона
II – промежуточная зона
III – волновая зона
p ql
r l
75.
Излучение электромагнитных волнI – ближняя зона, r
III
II
p t
I
r
3 r p r
E
p
3
2
4 0 r
r
1
p r
H
4 r 3
76.
Излучение электромагнитных волнb
S
a
p
H
r
E
c
d
Ш – волновая зона, r
r
T
c
c
t t r c
E E t r c
D
E
0
По контуру abcd идёт ток смещения
t
t
генерация переменного поля H
77.
Излучение электромагнитных волнS
p
H
r
E
p t r c er
H
4 cr
0
H e r
E
0
H
E
er
H
p sin
4 cr
0
E
H
0
78.
Излучение электромагнитных волнДиаграмма направленности излучения
p
I
0 2
S EH
H
0
2
0 1 0 c 2 S
p sin 2
16 2 c 3 0 r 2
79.
Излучение электромагнитных волнI S
I
p
2
sin 2
16 2 c 3 0 r 2
80.
Излучение электромагнитных волнПримеры диаграмм
направленности излучения
разных антенн
81.
Излучение электромагнитных волнМощность излучения
d IdS Ir 2 sin d d
P
2
0
0
0
r 2 d I r , sin d 2 r 2 I r , sin d
4
0 sin d 3
3
p
2
4
2 r
3 16 2 c 3 0 r 2
2
P
p
2
6 c 3 0
82.
Излучение электромагнитных волнИзлучение зарядов, движущихся с ускорением
p qr
p qr qa
83.
Эффект Доплера для электромагнитных волнЭто изменение частоты или длины волны, воспринимаемой
приёмником при относительном движении источника и
приёмника волн.
c - скорость света в вакууме
u - относительная скорость источника и приёмника
t0 - собственный период колебаний источника
t1 - период колебаний, воспринимаемых источником
t0
t1 t0
1 u 2 c2
84.
Эффект Доплера для электромагнитных волнc t1
u
u t 0
t1 c u
c
x
t1 c u t0 c u
T
2
2
c
c
c 1 u c
1
1
1 u 2 c2
1 u c
0
0
0
T
t0
1 u c
1 u c
85.
Эффект Доплера для электромагнитных волн0 0
1 ux c
1 ux c
0
ux 0 0
Пример: u x 0
86.
Шкала электромагнитных волнВ широком смысле под светом понимают не только видимый свет, но и
примыкающие к нему области инфракрасного и ультрафиолетового излучений.
87.
Интенсивность светаc
n
v
v
Если
Em2
I
2
0
0
c
n
1 n
n n
nA2
1 I
2
0
0
88.
Отражение и преломление плоской ЭМ волныez
O
k1 1 1 k1
r
2
E1 E2
τ 1 n1
2 n2
k2
1
1
1
H1 H 2
Из симметрии задачи следует,
что k 1 и k 2 лежат в
плоскости векторов k 1 и e z .
E
E A exp i t k r
E1 A1 exp i 1t k1 r
1
стор 0
На границе
2
A 2 exp i 2t k 2 r 2
1
A1 exp i 1t k1r sin 1 A1 exp i 1 t k1 r sin 1 1
A2 exp i 2t k2 r sin 2 2 = E1 E1 E2
89.
Отражение и преломление плоской ЭМ волныA1 exp i 1t k1r sin 1 A1 exp i 1 t k1 r sin 1 1
A2 exp i 2t k2 r sin 2 2
Равенство верно для любого t.
ez
O
k1 1 1 k1
r
2
k2
1 1 2
τ 1 n1
2 n2
Равенство верно для любого r.
k1 sin 1 k1 sin 1 k2 sin 2
где k1 k1
v1
, k2
1 1
v2
90.
Отражение и преломление плоской ЭМ волныez
O
k1 1 1 k1
r
2
k2
sin 1 k2 v1 n2
sin 2 k1 v 2 n1
τ 1 n1
2 n2
n1 sin 1 n2 sin 2
Векторы k1 , k1 , k 2 и e z лежат в одной плоскости, причём
(1) Угол падения равен углу отражения, т.е. 1 1 ,
(2) Угол падения связан с углом преломления соотношением:
n1 sin 1 n2 sin 2
91.
Отражение и преломление плоской ЭМ волныЯвление полного внутреннего отражения
Если n1 n2 , то первая среда называется оптически более
плотной, а вторая – менее плотной.
Пусть n1 n2 . sin 1
крит
k1
z
n2
sin 2
n1
2 1
2 .2
n2
1 arcsin крит
n1
Если
k1
2 k 2
n1 x
n2
Полным внутренним отражением
называется явление исчезновения
преломлённой волны при 1 крит
92.
Отражение и преломление плоской ЭМ волныk2 z k22 k22x k22 k12x k22 k12 sin 2 1
крит
k1
Если k2 k1 sin 1
z
k1
2 k 2
n1 x
n2
k2 z i
z 0
Поле E2 экспоненциально затухает
вглубь среды 2.
93.
Отражение и преломление плоской ЭМ волныРефракция – отклонение света от прямолинейного распространения в
среде с переменным показателем преломления.
94.
Отражение и преломление плоской ЭМ волныАмплитуда и фаза отражённой
волны при нормальном падении
H1
E1
n1
S1
n2 H
E2
2
S1
E1
H1
τ
τ0
S2
A1 A1 A2
τ 0 : H1 H1 H 2
τ:
Пусть
и
E1 E2 H1 H 2
Пусть A1 , A1 , A2 и H1 , H1 , H 2
- комплексные амплитуды.
0
0
H A
nA
0
0
95.
Отражение и преломление плоской ЭМ волныH1
E1
n1
S1
n2 H
E2
2
S2
S1
E1
H1
τ
τ0
A1 A1 A2
n1 A1 A1 n2 A2
n1 A1 A1 n2 A1 A1
n1 n2
A1
A1
n1 n2
2n1
A2 A1 A1 A2
A1
0, n1 n2
n1 n2
1
Если n1 n2 , то знакиA1 и A1 совпадают.
, n1 n2
Если n1 n2 , то знаки A1 и A1 противоположны. 2 0
96.
Отражение и преломление плоской ЭМ волныКоэффициенты отражения и пропускания
I1
- коэффициент отражения
I1
I2
- коэффициент пропускания
I1
2
2
n1 n2
A1
2
A1
n
n
1 2
n2 A22
n1 A12
4n1n2
n1 n2
2
1
97.
Геометрическая оптикаУсловия применимости законов
геометрической оптики
l – характерный размер
препятствий, отверстий и т.п.
Луч – это линия, касательная к которой в каждой точке
совпадает с направлением вектора S .
1. В оптически однородной среде свет распространяется
прямолинейно, т.е. лучи – прямые линии.
2. Лучи не влияют друг на друга.
3. Справедливы законы отражения и преломления света.
98.
Геометрическая оптикаПринцип Ферма
Световая энергия распространяется из одной точки в другую
по пути, на прохождение которого требуется минимальное
время (точнее экстремальное время).
2
2
1
2
1
L
ndl
c1
c
dl
c
, n
v
v
1
2
L ndl min
1
99.
Геометрическая оптикаПримеры использования принцип Ферма
B
A
1. Однородная среда
2. Отражение света от зеркала
Докажем, что
1 1
1 1
дл. SRA = дл. S’RA <
< дл. S’R’A = дл. SR’A
1 1
100.
Геометрическая оптика3. Преломление света
Задано L, h1 , h2 , найти x .
A
S n1 x h n2
2
1
h1 1
n1
B
x
L
2
2
n2
h2
C
dS
dx
2
1
n1 x
x 2 h12
L x
2
h22
n2 L x
2
L
x
h
2
2
dS
0 n1 sin 1 n2 sin 2
dx
101.
Рефракцияn - dn
β
dβ
β
n
n0 β0
β<<1 – угол наклона луча к горизонтали
n sin(π/2-β) = (n-dn)sin(π/2 -β+dβ)
n cos(β) = (n-dn)cos(β-dβ) cos(x<<1) ~= 1 – x2/2
n(1 – β2/2) = (n-dn)(1 – β2/2 + βdβ) =>
dn(1–β2/2)=nβdβ =>dn/n=βdβ=> β2/2 = C +ln(n)
=> β2 = β02 +2ln(n/n0) = β02 - 2ln(n0/n)
102.
ФотометрияЭто раздел физической оптики, в котором изучаются
энергетические характеристики светового излучения.
Световой поток
d э - спектральная плотность потока
d электромагнитной энергии
э d
0
На видимую область спектра приходится
40% энергии излучения Солнца.
Зрительное ощущение таково, что воспринимаемая
интенсивность света максимальна при = 0,555 мкм.
103.
ФотометрияЧувствительность глаза к интенсивности ЭМ излучения
характеризуется кривой относительной спектральной
чувствительности (функция видности).
0,4 мкм 0,76 мкм
104.
ФотометрияЧувствительность среднего глаза к интенсивности ЭМ
излучения характеризуется кривой относительной спектральной
чувствительности (функция видности).
Элементарный световой
поток:
d KV d
э 1 Вт 1 лм
K 683 лм Вт
0,4 мкм 0,76 мкм
KV d
0
105.
ФотометрияСила света
Точечный источник света
z
x
d исп
I
d
d
I I ,
I 1 кд
y
исп
Изотропный
I
источник света:
4
106.
ФотометрияОсвещённость
d пад
E
dS
E 1 лк
лм
1 лк 2
м
Освещённость, создаваемая
точечным источником света
n
dS
d пад d исп
I
Id 2
r
d пад I
I cos
E
2
dS
r dS
r2
I cos
E
2
r
107.
Фотометрияd исп - световой поток, испускаемый
площадкой источника dS в
определенном направлении
Яркость
L ,
I ,
d
I I ,
n
S
I ,
S cos
d исп
I
d
d исп
L
d S cos
кд
L 2
м
Источник света, яркость которого не зависит от направления,
называется ламбертовским.
L const
108.
ФотометрияСветимость
d исп
M
dS
лм
M 2
м
d исп - световой поток, испускаемый
площадкой источника dS по всем
направлениям.
Светимость ламбертовского источника
L const
исп Ld S cos
2
исп
M
L cos d L d
S
0
d sin d d
2
cos sin d
0
M L
109.
Курс общей физики НИЯУ МИФИ – 4-ый семестрВолны и оптика
Лекция 7
Интерференция света
31 марта 2014 года
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович
110.
Интерференция волнM
S1
E E1 E2
I S , S E H
S2
I I1 I 2 I12
Интерференцией называется такое сложение волн, при
котором в некоторых областях пространства I12 0
.
111.
Интерференция монохроматических волнE1 || E2 || y
E1 y A1 cos t 1 , E2 y A2 cos t 2
E E1 y E2 y Re A1 exp i t 1 A2 exp i t 2
Re exp i t A1 exp i 1 A2 exp i 2 Re A exp i t
A1
1
A A1 exp i 1 A2 exp i 2
A
Im A
2
1 2
2
A2
Re A
A A12 A22 2 A1 A2 cos
A12 A22 2 A1 A2 cos 1 2
112.
Интерференция монохроматических волн1 2
A
Im A
2
A A12 A22 2 A1 A2 cos
A1
1
2
A2
Re A
A12 A22 2 A1 A2 cos 1 2
I I1 I 2 2 I1 I 2 cos
I12 2 I1 I 2 cos
1 2
113.
Интерференция монохроматических волнx
r1
S1
P
x
d
r2
O
S2
A
E2
cos t kr2
r2
l
r2 r1
k r2 r1
A
E1
cos t kr1
r1
1 2 kr1 kr2
v
r2 r1
n
c
r2 r1
2
0
n r2 r1
114.
Интерференция монохроматических волн2
0
n r2 r1
n2 dl2 n1dl1
L2
L1
I I1 I 2 2 I1 I 2 cos
Условия интерференционного максимума:
cos 1 2 m m 0, 1, 2,... m 0
m - порядок интерференционного максимума.
I max I1 I 2 2 I1 I 2
I1 I 2
2
I1 I 2 I max 4 I1
115.
Интерференция монохроматических волнУсловия интерференционного минимума:
cos 1 2 m 1 2 m 1 2 0
m 0, 1, 2,... - порядок интерференционного минимума.
I min I1 I 2 2 I1 I 2
I1 I 2
2
I1 I 2 I min 0
Волны усиливают друг друга.
Амплитуда увеличивается.
Волны ослабляют друг друга.
Амплитуда уменьшается.
116.
Интерференция монохроматических волнШирина и видность интерференционных полос
x
r1
S1
P
x
d
r2 r1 d sin d
r2
O
S2
l
r2 r1
max: m 0
x
tg
l
x
n r2 r1 n d nd
l
x
nd m 0
l
xmax m
0l
nd
m
l
d
117.
Интерференция монохроматических волнШирина интерференционной полосы – это расстояние между
серединами двух соседних интерференционных полос.
m 1 x
l
d
r1 r2
I1 I 2
2
2
I 2 I1 2 I1 cos 2 I1 1 cos
4 I1 cos
0
0
x
n r2 r1 n d nd
l
xd
I 4 I1 cos
l
2
118.
Интерференция монохроматических волнI
S2
Видность интерференционных
полос.
I max I min
V
I max I min
S1
x
119.
Интерференция монохроматических волнI
S2
Видность интерференционных
полос.
I max I min
V
I max I min
S1
x
Реальная картина
интерференционных
полос.
120.
Классические интерференционные опытыОпыт Юнга
l
L
a
b
d
СФ
Э1
Э2
Размер щели a ?
Э3
121.
Бипризма Френеляn 1
d 2a
l a b
a b
x
d
2a
l
a b
x
2a n 1
122.
Бипризма ФренеляP
PQ 2b
2b n 1
PQ
N
x
Q
a b
x
2a n 1
N
n 1
a b
4ab
2
2
123.
Бипризма ФренеляP
N
2
m* min
Q
ког d 2a
ког 2a n 1
124.
Зеркало ЛлойдаИсточник света S и его мнимое изображение S’, полученное
с помощью зеркала Ллойда AB, позволяют наблюдать
интерференционную картину на экране, расположенном
перпендикулярно зеркалу.
125.
Временная когерентностьВолновой цуг.
Схема, поясняющая как из волновых цугов, испускаемых
отдельными атомами (а и б) возникает колебание
электрического поля в произвольной точке пространства (в).
ц – длительность отдельного цуга.
126.
Временная когерентностьКогерентностью называется согласованное протекание во
времени и пространстве двух или нескольких колебательных
или волновых процессов.
t kr t
t – случайная функция
tког
Характерное время, за которое случайные изменения фазы
α(t) достигнут величины ~π , называется временем
когерентности.
127.
Временная когерентностьНаблюдение интерференции с помощью метода
деления волнового фронта.
S1 и S2 – вторичные когерентные, но
не монохроматические источники
1 t 2 t t
r1
r2
Для точки наблюдения P.
t k r2 r1 t t
r2 r1
– время задержки.
v
P
128.
Временная когерентностьt t
Если
, то
t
I12 2 I1 I 2 cos 0
ctког
cos cosk r2 r1
r2 r1 n r2 r1
v
c
c
lког ctког
lког
129.
Временная когерентностьI12 2 I1 I 2 cos 0
|<cos δ>| < 1
Степень когерентности
I I1 I 2 2 I1 I 2 cos
для цилиндрических волн k r2 r1
для плоских волн k 2 k1 r
0 1
130.
Временная когерентностьI
Оценка длины когерентности
2
x
m* 1 2 m* 2
m* 0 lког
– максимальный порядок
интерференции
131.
Временная когерентностьОценка длины и времени когерентности
lког
2 1
1
c
c c
Спектральная линия:
Излучение лазера:
k
2
132.
Временная когерентностьНестационарная интерференция.
Световые биения
Рассмотрим независимые источники S1 и S 2 с одинаковой
1 t и 2 t - случайные статистически независимые функции
t 1 2 k r2 r1 1 t 2 t
I12 2 I1I 2 cos t
cos t 0 I12 0
Если
Если
I12 0 - световые биения
133.
Пространственная когерентностьA
B
a
d
L
Объём когерентности:
x
I
Точки A и B излучают
независимо. Колебания
в щелях согласованы,
если
.
Радиус
когерентности:
134.
ИнтерференцияИнтерференция на тонких пленках.
Интерференция при отражении
135.
Интерференция света при отраженииПлоскопараллельная пластина толщины b
I
D 1
1
x
n1
B
A
n2
n1
2
2
Если n1 < n2 , то при отражении
в точке B появляется
дополнительная фаза .
n2 AC CB n1DB
0
2
b
AC CB
cos 2
b
DB AB sin 1 2btg 2 sin 1
C
0
0
2b
n2 AC CB n1DB n2
n1 2btg 2 sin 1
2
cos 2
2
136.
Интерференция света при отражении0
0
2b
n2 AC CB n1DB n2
n1 2btg 2 sin 1
2
cos 2
2
I
1
D 1
A
B
n1 sin 1 n2sin 2
n1
n2
n1
2
2
C
0
2b
n2 n1sin 2 sin 1
2
x cos 2
b
0
2b
2
n2 n2sin 2
cos 2
2
2bn2 cos2 2 0
cos 2
2
137.
Интерференция света при отражении2bn2 cos 2
0
n2 cos 2 n22 n22 sin 2 2
2
n22 n12 sin 2 1
I
1
D 1
A
B
2b n n sin 1
2
2
n1
2
2
C
2
x
n1
n2
2
1
0
2
Экран равномерно освещён
b
m 0
m 1 2 0
I I max
I I min
138.
Интерференция света при отражении2b n n sin 1
2
2
2
1
2
Условия наблюдения
интерференции:
0
2
I
1
D 1
A
B
x
n1
n2
n1
2
2
C
b
b <<
2
2n2
т.е., пластинка
тонкая
139.
Интерференция света при отраженииПолосы равного наклона
Схема наблюдения полос равного наклона.
140.
Интерференция света при отраженииm 0
m 1
m 2
Интерференционные полосы равного наклона в форме колец
возникают при сложении лучей, падающих под одинаковыми к
поверхности пластины.
141.
Интерференция света при отраженииУсловия интерференционного
максимума:
n1 1
2b n sin 1
2
2
2
0
2
m 0
Максимальный порядок
интерференции при 1 0 .
m 0 2bn2
m
2bn2
0
1
2
0
2
142.
Интерференция света при отраженииПлоский клин. Полосы равной толщины
b x
x
143.
Интерференция света при отраженииЭтот вид интерференции называется «полосы равной толщины»,
т.к. каждая полоса возникает в результате отражения волн от
участка клина с фиксированной толщиной.
144.
Интерференция света при отраженииКольца Ньютона
R
b
r
145.
Немного геометрииAO2 = AC2 – R2 =
D
= (AD – R)2 – R2 =
=
AD2
– 2AD·R =
R
C
= AD(AD – 2R) =
= AD·AB
- ч.т.д.
B
O
A
AB AD AO 2
146.
Интерференция света при отраженииAB AD AO
D
2
AB b,
AD 2 R
2
r
AO r r 2 2 Rb b
2R
2b n n sin 1
2
2
2
1
2
0
C
B
O
A
2
n2 1, 1 0
r 2 0
2b
2
R 2
R
R
0
При отражении света в точке А
появляется дополнительная фаза .
b
r
147.
Интерференция света при отражении0
r 2 0
2b
2
R 2
r 2 0
m 0 ,
R 2
m 0,1,2,...
R
rсветл
b
r
1
R 0 m
2
1
m 0 ,
2
rтемн R 0m
148.
ИнтерферометрыИнтерферометр Фабри -Перо
Строго параллельные поверхности тщательно отшлифованы,
отклонения менее 0,01 . Поверхности покрыты многослойным
диэлектрическим покрытием с = 0,85 – 0,98.
Стеклянные или кварцевые пластины
149.
Интерферометрыb
A0 , I 0
1
2
A1 , I1
f
A2 , I 2
A3 , I 3
A4 , I 4
2 0 2b m 0 m 2b 0
150.
Интерферометры2
1
1
2 m I I min
I0
2
1
I I0
I ) 0,046
II ) 0,27
III ) 0,64
IV ) 0,87
151.
Интерферометры152.
ИнтерферометрыПодвижное зеркало с
микрометрическим
винтом
Полупрозрачное
зеркало отражает
половину
падающего пучка
Монохроматический
источник света
Интерференция двух
пучков с разными
оптическими длинами
Неподвижное
зеркало
Компенсационная
пластина из такого же
материала и такой
толщины как и
полупрозрачное зеркало
153.
ИнтерферометрыИнтерферометр Маха-Цендера
Схема интерферометра Маха-Цендера
154.
Просветление оптикиПросветле́ние о́птики —
это уменьшение
коэффициента отражения
путём нанесения на
поверхность линз,
граничащих с воздухом,
тонких плёнок, что приводит
к деструктивной
интерференции отражённого
света.
155.
Просветление оптикиПотери энергии в многолинзовых приборах более 50%.
Для эффективной интерференции
необходимо, чтобы I1 I 2 .
n1 I 0
n
n2
I1
I0
I2
I1 1 I 0
I 2 12 2 I 0
1 1 I 2 2 I0
2
2
I1 1 n1 n n2 n
1
I 2 2 n1 n n2 n
n1 n n2 n n2 n n1 n
156.
Просветление оптикиn1 I 0
n
I1
I0
Пусть n1 n n2
I2
b
n2
n1 n n n1
n2 n n2 n
n n1 n2 n n2 n n1 n
nn2 n 2 n1n2 nn1 n2 n1 nn2 nn1 n 2
n n1n2
Дважды отражение от оптически более плотной среды 2bn
1
2bn m 0
2
2m 1 0
b
4n
2m 1
b
4
157.
Дифракцияl – расстояние до точки наблюдения
b – размер отверстия (препятствия)
l <~ b
геометрическая
оптика
l ~> b
l >> b
дифракция
Фраунгофера
l >>b и много отверстий (щелей) –
дифракция + интерференция
дифракция Френеля
ВАЖНО: есть дополнительные условия,
зависящие от длины волны
158.
Принцип Гюйгенса – ФренеляКаждая точка
волновой поверхности
является источником
вторичных волн.
Результирующая
волна является
суперпозицией волн,
излучаемых
вторичными
источниками.
159.
Принцип Гюйгенса – ФренеляКаждая точка волновой поверхности является источником вторичных волн.
Результирующая волна является суперпозицией волн, излучаемых
вторичными источниками.
160.
Принцип Гюйгенса – ФренеляАмплитуда первичной волны в
точке, где расположен вторичный
dS
источник
C0
A
exp ikr0
r0
Амплитуда вторичной волны в точке
наблюдения P (Френель, 1816)
A
dAP exp ikr K dS
r
AP dAP
K K
(Кирхгоф, 1883)
161.
Зоны ФренеляЗоны Френеля – «полуволновые» зоны на фронте волны.
Каждая следующая граница между зонами Френеля отстоит от точки
наблюдения на пол длины волны дальше, чем предыдущая
rm+1 – rm = λ/2; m = 0, 1, 2, 3, .. ; r0 = l
S m
rm
S
l 3 2
l 2 2
l 2
P
a
a
l
162.
Зоны Френеля для плоской волныЗоны Френеля – «полуволновые» зоны на фронте волны.
Каждая следующая граница между зонами Френеля отстоит от точки
наблюдения на пол длины волны дальше, чем предыдущая
rm+1 – rm = λ/2; m = 0, 1, 2, 3, .. ; r0 = l
rm2 = (l + mλ/2)2 – l2 = lmλ
λ<<l
Sm = πrm2 – πrm-12 = πlλ
mmax = b2 / lλ ; b – радиус отверстия
163.
Зоны Френеля для сферической волныλ<<l
rm2 = (l + mλ/2)2 – (l +d)2 =
= lmλ – 2ld – d2
a
b
d
a – расстояние от
источника до края отверстия
d – расстояние от передней
точки фронта волны до
центра отверстия
b – радиус отверстия
rm2 = a2 – (a – d)2 = 2ad – d2
lmλ = 2(a + l)d
d = lmλ/2(a + l) <<a, l
rm2 = 2ad = lmλa/(a + l)
Sm = πrm2 – πrm-12 = πlλa/(a + l)
mmax = (a + l)b2/ alλ
164.
Зоны Френеляrm2 = klmλ; Sm = kπlλ; mmax= b2/ klλ
a
b
d
k = 1 для плоской волны
k = a/(a + l) для сферической волны
b2< klλ - «открыта» только первая зона Френеля или часть ее
Вторичные волны, испускаемые фронтом волны, усиливают друг-друга в
точке наблюдения
b2 = 2klλ - «открыты» две зоны Френеля. Вторичные волны, испускаемые
фронтом волны 2-й зоны приходят в точку наблюдения в противофазе к
волнам от первой зоны. Они гасят друг-друга
Если «открыто» четное число зон Френеля – интенсивность волны близка к
нулю. Если нечетное – она максимальна ( I ~ 4Io)
165.
Дифракцияl – расстояние до точки наблюдения
b – размер отверстия (препятствия)
l << b2/λ
l ~ b2/λ
l >> b2/λ
Геометрическая оптика
дифракция Френеля
дифракция Фраунгофера
l ~ 1 м; λ ~ 10-6м
b >> 10-3 м
l ~ 1 м; λ ~ 10-6м
b ~ 10-3 м
l ~ 1 м; λ ~ 10-6м
b << 10-3 м
166.
Дифракция Френеля на круглом отверстииA
AP dAP ⌠ exp ikr K dS
r
A1 2 A0
I1 4 I 0 ;
Am 2 A0 1
m 1
A1 A2 0 I1 2 0
K медленно убывает, поэтому A1 A2 A3 ...
Спираль
Френеля
I1 4 I 0
I1 2 0
I1 2 3 4 I 0
167.
Дифракция Френеля на круглом отверстииПример. Для точки наблюдения P
открыты 1,5 зоны Френеля.
A1,5 2 A0
A1,5
A0
I1,5 2 I 0
Дифракция Френеля на
круглом отверстии по мере
приближения к экрану с
отверстием.
Число открытых полуволновых зон увеличивается слева направо с 2 до 6.
Размер картины уменьшается, приближаясь к диаметру отверстия.
168.
Дифракция Френеля на круглом отверстииЕсли точка P находится не в
центре, то зоны Френеля
располагаются не
симметрично
Дифракция лазерного луча
с длиной волны 650 нм,
прошедшего через отверстие
диаметром 0,2 мм
Дифракционные картины при нечётном
(а) и четном (б) числе открытых зон
Френеля
169.
Дифракционные линзы и зонные пластиныЕсои открыть только четные или только нечетные зоны Френеля –
волны будут усиливаться и фокусироваться
Зонная пластинка Френеля.
Площади зон одинаковы
Синусоидальная зонная
пластинка Френеля. Этот тип
пластин имеет одну фокальную
точку.
170.
Дифракционные линзы и зонные пластиныЗонная (a), фазовая (b) пластинки и фазовая линза (c) Френеля.
171.
Идея голографииa
b
d
=>
=>
=>
172.
Дифракция Френеля на препятствииb rN 1
AN
P
начало N-ой зоны
173.
Дифракция Френеля на препятствииДифракция Френеля на непрозрачном диске.
В центре пятно Пуассона
174.
Дифракция Френеля на препятствииНа рисунке изображена блок-схема для получения увеличенной картины
дифракции Френеля на различного рода препятствиях. Установка состоит из
лазера (ЛГ-52), микрообъектива (М), точечной диафрагмы (S), объекта (О),
на котором наблюдается дифракция, и плоскости наблюдения
175.
Дифракция Френеля на препятствииДифракция на шарике диаметром 2,4
мм.
Шарик аккуратно приклеивался
пластилином к плоскопараллельной
стеклянной пластинке и устанавливался
в расходящийся пучок света.
Распределение освещенности
при дифракции от шарика
176.
Зоны Шустера для плоской волны- волновая поверхность
d1
dm
rm
l
r1
P
rm l m
m 1,2,3,...
d m rm2 l 2 rm2 1 l 2
- экран
rm2 l 2 rm l rm l 2lm
d m 2lm 2l m 1 2l m m 1
d1 d 2 d 3 ...
177.
Спираль Корню- волновая поверхность
d1
dm
rm
l
r1
P
- экран
Графическое сложение
комплексных амплитуд
Если перейти к пределу 0, то получится плавная кривая,
называемая спиралью Корню.
178.
Дифракция Френеля на крае полуплоскости179.
Дифракция Френеля на щели2
v
b const
l
b
I I0
l
v
x
180.
Дифракция Френеля на щели181.
Дифракция Френеля на щелиДифракция Френеля на
узкой и широкой щели
182.
Дифракция Френеля на крае полуплоскостиv 1
v 2
2
v 2 2
1
v
2
1
v
2
183.
Дифракция Френеля на круглом отверстииSQP : r 2 a 2 a l 2a a l cos
rdr
2rdr 2a a l sin d sin d
a a l
Рассмотрим
2
dS 2 a sin d
2
2 ardr
a l
Рассмотрим поле
кольца: r1 r r2 .
184.
Дифракция Френеля на круглом отверстииA
AP dAP K r exp ikr dS
r
S
S
r2
r2
A
2 ar
2 aA
K r exp ikr
dr
K r exp ikr dr
r
a l
a l r1
r1
r2
r2
2 aA K r
1 dK
exp ikr
exp ikr dr
a l ik
ik r1 dr
r
1
0
r r r
1
2
r2
1 dK
exp ikr dr
ik r1 dr
r2
K exp ikr dr
r1
185.
Дифракция Френеля на круглом отверстии2 aA
Ap
K r2 exp ikr2 K r1 exp ikr1
ik a l
Найдём амплитуду волны, излучаемой всей волновой
поверхностью в отсутствие преграды.
r1 l , r2 l 2a 2
K l K 0 , K r2 K 2 0
2 aA
A0
K l exp ikl
ik a l
186.
Дифракция Френеля на круглом отверстииНайдём амплитуду волны, создаваемой m-ой зоной Френеля в
точке P. Для этого используем формулу:
2 aA
Ap
K r2 exp ikr2 K r1 exp ikr1
ik a l
r1 l m 1 2, r2 l m 2
kr1 kl m 1 k 2 kl m 1 , kr2 kl m
K r1 K r2 K l
2 aAK l
Am
exp ikl i m exp ikl i m 1
ik a l
187.
Дифракция Френеля на круглом отверстии2 aAK l
exp ikl i m 1 exp i
ik a l
exp i 1, exp i m 1
m
4 aAK l
m
Am
exp ikl 1
ik a l
2 aA
Сравниваем с выражением: A0
K l exp ikl
ik a l
Am 2 A0 1
m 1
188.
Дифракция Френеля на круглом отверстииAm 2 A0 1
A1 2 A0
I1 4 I 0 ;
m 1
A1 A2 0 I1 2 0
K медленно убывает, поэтому A1 A2 A3 ...
Графическое сложение амплитуд. Спираль Френеля
I1 4 I 0
I1 2 0
I1 2 3 4 I 0
189.
Дифракция Френеля на крае полуплоскостиx
dx
x
AP K
S
x
l
A
K 0 exp ikr dS
l S
r l x
P
A
exp ikr dS
r
dS Ldx , где L – длина полосы
exp ikr exp ikl exp ik x
x
AP
exp ik x dx
0
2
2
x
x
2
2
x r l l x l l 1 2 l
2l
2l
190.
Дифракция Френеля на крае полуплоскости2
2
2 x
x
k x
2l
l
2
s x
l
s 2 x 2
Новая переменная:
2 l
2
x v x
l
i s 2
F v exp
ds
2
0
v
Ap
Интегралы v cos s ds
0 2
Френеля:
v
2
F v v i v
s2
v sin
ds
2
0
v
191.
Дифракция Френеля на крае полуплоскостиF1
A0
d id dF
i v 2
exp
dv dv
2
v- длина дуги,
отсчитываемая от начала
координат, F1 и F2 - фокусы
F2
sin v 2 2
v2
d
v2
tg
tg
2
d cos v 2
2
2
192.
Дифракция Фраунгофера на щелиДействие первой линзы:
a
f1
b
f
P
x
dx
x
x sin
Действие второй линзы:
l
AP ?
Пусть фаза центральной
зоны равна нулю.
x sin
193.
Дифракция Фраунгофера на щели2
2 x
sin x,
2
sin
Вклад полоски dx :
f1
b
x
dx
x
x sin
dx
dAp exp i
b
b2
dx
Ap exp i
b
b 2
b2
f
P
dx
exp i x
b
b 2
194.
Дифракция Фраунгофера на щелиexp i x
exp i b 2 exp i b 2
i b b 2
i b
2
b
b b sin
sin ,
b
2
2
dx
b
2
x
x
sin
2
I AP
x sin
b2
f1
f
P
I Im
sin 2
2
b sin
195.
Дифракция Фраунгофера на щелиРаспределение интенсивности на экране
0 0 sin 2 2 1 I I m
I Im
0,045
sin 2
2
Минимум I, если m
196.
Дифракция Фраунгофера на щелиb
m,
sin m
I Im
Условие минимума:
b sin m , m 1, 2,...
m
sin
1
b
b
m
197.
Дифракция Фраунгофера на щелиУгловой размер центрального максимума
m 1 b sin
I
2
sin
x
2
2
b
2 f
x f
b
198.
Дифракция Фраунгофера на отверстии2 J 1
I Im
D
I Im
1
0,017
2
D
sin
199.
Дифракция Фраунгофера на отверстииm 1 D sin 1,22
I Im
sin
2
2,44
D
I
1
0,017
1,22
D
sin
2,44
D
200.
Дифракция Фраунгофера на отверстииРазрешающая сила оптического прибора
Пучок параллельных лучей собирается
линзой не в точку, а в пятно.
201.
Дифракция Фраунгофера на отверстии- наименьшее угловое
расстояние, при котором
источники воспринимаются
раздельно
S1
S2
R
1
2
D
R
1,22
Выполнен критерий Рэлея
202.
Принципы работы дифракционной решёткиb
d - период
d
решётки
b - ширина
щели
N - число
щелей
f
d sin
203.
Принципы работы дифракционной решёткиb
I1 I m
d
A1 Am
sin
,
2
,
b
sin
Многолучевая
интерференция N волн
f
A2 A1 exp i ,
A3 A2 exp i ,...
sin 2
N
A Ak
k 1
2
2
d sin
204.
Принципы работы дифракционной решёткиA A1 1 exp i exp 2i ... exp i N 1
1 exp iN
A1
1 exp i
I AA A A
*
*
1 1
1 exp iN 1 exp iN
1 exp i 1 exp i
1 cos N
2 exp iN exp iN
I1
I1
1 cos
2 exp i exp i
205.
Принципы работы дифракционной решёткиsin 2 N 2
sin 2 N
d
I1
I I1
,
sin
2
2
sin 2
sin
2
sin
I1 I m
sin sin N
I Im
sin
2
2
b sin
d sin
,
206.
Принципы работы дифракционной решёткиГлавные максимумы
sin N
sin N
N
2
N
lim
lim
2
2
sin 2
sin
0
0
2
lim
m
m 0, 1,...
2
2
Главные максимумы определяют направления, в которых
излучение от всех щелей приходит в фазе (разность фаз кратна 2 ).
d sin
m d sin m , m 0, 1, 2,...
2
m – называется порядком
2
2 sin
I max I1 N I m N
главного максимума.
m d
207.
Принципы работы дифракционной решёткиДополнительные минимумы, если sin N 0 , а sin 0 .
Nd
k
N k ,
sin k , sin
Nd
k mN 1, mN 2,... k mN
Между двумя главными максимумами располагаются N 1
дополнительных минимумов и N 2 дополнительных
максимумов.
208.
Дифракционная картинаy1
sin
y2
sin
y1 y2
sin
минимум y2, если k,
следовательно b sin k.
sin 2 N
y1 sin
sin 2
y2 sin
sin 2
2
y2 1 (максимум)
b sin 0
b sin k , k 1, 2,...
I min 0,
k b
209.
Угловая ширина главных максимумовk
Дополнительные минимумы, если sin
, k mN 1
Nd
2
sin cos
sin
Nd
2
2
2
cos
,
Nd
Nd cos Nd 1 sin 2
m
2
1
sin
, m
d
Nd 1 m d 2
2
0
Nd
210.
Дифракционная картинаN 4, d 3b
Im N
2
sin
2
2
211.
Дифракция Фраунгофера на отверстииДлиной дифракционной расходимости называется характерная
длина, на которой пучок света расширяется на величину
порядка размера щели или радиуса отверстия.
Ld d
Ld
b
b2
212.
Дифракция Фраунгофера на отверстииУсловия для наблюдения дифракций Френеля
и Фраунгофера
Дифракция
Фраунгофера
Заметное отклонение в
область геометрической
тени
Дифракция
Френеля
Слабое отклонение в
область геометрической
тени
Геометрическая
оптика
Выполняются законы
геометрической оптики
213.
Дифракция Фраунгофера на отверстииДифракция Фраунгофера
Дифракция Френеля
В центре всегда светлое пятно
(максимум).
Светлые и тёмные пятна в
центре картины «чередуются».
Интенсивность центрального
максимума на 1-2 порядка
больше, чем у соседних.
Интенсивность центрального и
соседних максимумов
сопоставимы.
В точках минимума
интенсивность близка к нулю.
В точках минимума
интенсивность не нуль.
При наблюдении без линзы
размер центрального
максимума намного больше
размера отверстия.
Размер центрального
максимума порядка диаметра
отверстия.
214.
Дифракционная решеткакак спектральный прибор
Белый свет
m 1
ф
m : 3
2
порядок спектра
1
0
кр
d sin ф ф
ф 0,4 мкм
1
d sin кр кр
кр 0,76 мкм
2
3
215.
Дифракционная решётка как спектральный приборДисперсионной областью спектрального прибора называется
максимальная ширина спектрального интервала , при
спектры разных порядков ещё не пересекаются.
d sin m
d sin m 1
m
m m 1
m 1
m
216.
Угловая дисперсияd
D
d
d sin m
m
D
d sin
где d - угловое расстояние между близкими
спектральными линиями, длины волн которых
различаются на d .
d cos d md
D
m
d 2 m2 2
tg
d
m
D
d d cos
cos 1 m2 2 d 2
d
m
tg
m
D
d d cos
d 2 m2 2
217.
Разрешающая сила (способность)R
где - наименьшая разность длин волн двух близких
спектральных линий и + , при которой эти линии
видны раздельно.
Критерий Рэлея
d sin k N
Точка А
d sin m
k mN 1
I
sin
А
mN 1
N m
mN
R mN
218.
Качества дифракционной решётки1. Большая дисперсионная область m .
2. Большая угловая дисперсия.
Nd l
3. Большая разрешающая сила: R mmax N
0,1
5
l Nd 10 см, 0,5 мкм R
2
10
0,5 10 6
Интерферометр
Майкельсона
Дифракционная
решётка
m
N
, мкм
R
106
2
5 10 7
2 106
3
105
0,17
3 105
219.
Дифракция рентгеновского излученияДлина волны рентгеновского излучения
Период кристаллической решётки d
Лауэ, 1912 г.
0,1 нм
0,3 нм
220.
Дифракция на пространственных структурах- угол скольжения
AB BC 2d sin
2d sin m
m 1,2,...
Формула Брэгга- Вульфа
221.
Дифракция на пространственных структурахЛауэграмма берилла
Лауэграмма ориентированного
кристалла каменной соли. Ось
падающего пучка параллельна оси
симметрии четвертого порядка.
222.
Дифракция на пространственных структурахПрименение дифракции рентгеновского излучения
1. Рентгеновская спектроскопия используется для анализа
спектра рентгеновского излучения и измерения длин волн.
Используются монокристаллы известной структуры.
2. Рентгеноструктурный анализ – метод исследования
структуры вещества, основанный на дифракции
рентгеновского излучения на исследуемом объекте.
Используются поликристаллы и монохроматическое
излучение (Метод Дебая – Шеррера).
223.
Дифракция на пространственных структурахМетод Дебая - Шеррера
рентгеновское
излучение
рентгеновская трубка
детектор
коллиматоры
фильтры
поликристалл
дифракция на одном из
монокристаллов
224.
Дифракция на пространственных структурахДебаеграмма меди.
225.
Курс общей физики НИЯУ МИФИ – 4-ый семестрВолны и оптика
Лекции 13.14.15
Лектор: доцент НИЯУ МИФИ,
ОЛЬЧАК Андрей Станиславович
226.
Плоская электромагнитная волнаПлоская гармоническая (монохроматическая) волна
E y Em cos t kx
H z H m cos t kx
Фазы колебаний E и H
совпадают, причём
0 Em 0 H m
k
v
Плоскость, в которой лежат векторы E и k , называется
плоскостью поляризации.
227.
Поляризация плоских гармонических волнПусть k || z . Складываются волны одинаковой частоты
y
E
Ey
Пусть E1 || x, E2 || y
x
E E1 E2
z k Ex
E = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey
2 1
.
228.
Поляризация плоских гармонических волнE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
Ey
A1
Плоская (линейная)
0,
=>
поляризация
Ex
A2
y
y
E
E
x
x
k
k
Плоскость поляризации сохраняет своё положение.
229.
Поляризация плоских гармонических волнE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
A1 = A2 = A; δ = +π/2
Ex = Acos(ωt – kz); Ey = +Asin(ωt – kz)
=>
Круговая
(циркулярная)
поляризация
При круговой поляризации конец вектора E равномерно
вращается по окружности в плоскости колебаний x, y .
y
y
E
E
x
x
k
Правая круговая поляризация.
k
Левая круговая поляризация.
230.
Поляризация плоских гармонических волнE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
A1 A2 , 0, 2,
Эллиптическая
=> поляризация
либо A1 A2 , 2
При эллиптической поляризации вектор E вращается с
постоянной угловой скоростью, а его конец движется по эллипсу
в плоскости колебаний x, y .
y
y
E
E
x
x
k
Правая эллиптическая
поляризация.
k
Левая эллиптическая
поляризация.
231.
Поляризованный и естественный светE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
y
E
Ey
z
x
k
Ex
Свет называется естественным, если
разность фаз колебаний проекций Ex и
Ey меняется случайным образом,
причём E x2 E y2 .
A1 A2 , t - случайная функция
I I1 I 2
232.
Поляризованный и естественный светE = A1cos(ωt – kz + α1)ex + A2cos(ωt – kz + α2)ey 2 1
Свет называется частично поляризованным, если
A1 A2 , t - случайная функция, либо
A1 A2 , t - случайная функция, меняющаяся в небольших
пределах
Частично поляризованный свет представляет собой смесь
естественного и поляризованного света.
Пример: Смесь естественного и плоскополяризованного света.
I I ест I пол
I пол
P
I
0 P 1
233.
Поляризаторы. Закон МалюсаПоляризатором называется любой прибор, служащий для
получения поляризованного света.
E
E
k
В кристалле поляризатора есть
выделенное направление O O или
оптическая ось анизотропного
кристалла.
Плоскость P, содержащая оптическую
ось O O и волновой вектор k ,
называется плоскостью поляризации
данного кристалла.
234.
Поляризаторы. Закон Малюсаk
Длинные молекулы вытянуты перпендикулярно оптической оси
поляризационного фильтра. Составляющая
электрического
поля волны, параллельная оптической оси и перпендикулярная
этим молекулам, проходит через фильтр, в то время как
составляющая
, параллельная этим молекулам, поглощается.
235.
Поляризаторы. Закон МалюсаСхематическое изображение
продольных колебаний
электронов в длинных
молекулах. Эти колебания
поглощают энергию и
уменьшают интенсивность
соответствующей компоненты
поля.
Поперечные колебания
электронов в длинной молекуле
более слабые.
236.
Поляризаторы. Закон Малюса1). Плоскополяризованный свет падает по нормали на
поверхность поляризатора.
E
O
E
y
O
k
E
k
x
I
I0
E2
I I 0 cos2 - закон Малюса
237.
Поляризаторы. Закон Малюса2). Падает естественный свет
E
E
k
I
I ест
I ест
I
2
E2
238.
Поляризаторы. Закон Малюса3). Естественный свет падает на
два скрещенных поляризатора
P1
P2
k
P2
E
E
I ест
k
P1
I ест
I ест
cos2
2
2
I ест
I
cos2
2
239.
Поляризаторы. Закон Малюса4). Измерение степени поляризации при падении смеси
естественного и плоскополяризованного света
I max
E
E
k
I ест
I пол
2
I min
I ест
2
I max I min I пол I ест
I max I min I пол
I пол
P
I пол I ест
I max I min
P
I max I min
240.
Поляризация света при отражении и преломлениина границе двух диэлектриков. Закон Брюстера
1 1
n1
n2
2
Диаграмма направленности
2
излучения диполя: I I 0 sin
Падающая волна:
В диэлектрике 2 возбуждаются
колебания E2 в плоскости падения ( ) и перпендикулярно ей ( )
241.
Поляризация света при отражении и преломлениина границе двух диэлектриков. Закон Брюстера
Пусть:
1 2 2 в направлении отражённого луча I 0
n1 sin 1 n2 sin 2
1 1
n1
n2
2
n1 sin 1 n2 sin 1
2
n2
tg Бр
n2 cos 1
n1
При падении света под углом
Брюстера отражённый свет
полностью поляризован.
242.
Вращение плоскости поляризацииЕстественное вращение (оптическая активность)
l
l
При прохождении света через оптически активные вещества
плоскость поляризации поворачивается на некоторый угол
243.
Вращение плоскости поляризацииПример оптически активных веществ: кварц (вдоль оптической
оси), скипидар, водный раствор сахара.
В растворах:
l
- удельное вращение
- плотность оптически активного вещества
E
E
k
k
Левовращающее
вещество
Правовращающее
вещество
244.
Вращение плоскости поляризацииХиральность (др.
греч. χειρ — рука) —
свойство молекулы
не совмещаться в
пространстве со
своим зеркальным
отражением.
245.
Вращение плоскости поляризацииПлоскополяризованную
волну представим как
сумму левой и правой E
л
круговых поляризаций.
E
E Eпр Eл
2
Eл
Eпр
k
nл nпр l
2
E
n
nпр l
0
0
2 l
л
Eпр
k
nл nпр
0
246.
Вращение плоскости поляризацииМагнитное вращение (эффект Фарадея)
При распространении плоскополяризованного
света вдоль внешнего магнитного поля в
некоторых веществах возникает вращение
плоскости поляризации
VlH
V V , T - постоянная
Верде
H - напряжённость
магнитного поля
E
H
l
E
k
247.
Вращение плоскости поляризацииЕсли поворот плоскости поляризации связан с направлением H
правилом правого винта, то вещество называется
положительным V 0 , если правилом левого винта,
то – отрицательным V 0 .
В ферромагнетиках:
klJ
J - намагниченность
E
H
ферромагнетика
Замечание. Направление вращения
определяется
E
вектором H , а не
k
направлением луча.
l
248.
Двойное лучепреломлениеРаспространение света в одноосном кристалле
3
Di 0 ik Ek
i, k x, y , z
E
k 1
ik - тензор диэлектрической
D
проницаемости
k перпендикулярен плоскости D, H
H
S
k
S E H перпендикулярен плоскости E, H
Следовательно, в анизотропной среде S не параллельно k .
249.
Двойное лучепреломлениеОбыкновенные и необыкновенные волны
Кристаллы, в которых есть только одно выделенное
направление z называются оптически одноосными.
zz
xx yy
ik 0, i k
1) Направление луча параллельно плоскости x,y.
Главным сечением называется плоскость,
z
параллельная лучу и оптической оси z.
o
В обыкновенной (ordinary) волне E
y перпендикулярно главному сечению.
x
e
o
S
250.
Двойное лучепреломлениеВ необыкновенной (extraordinary) волне вектор E колеблется
в плоскости главного сечения.
Обе волны (o и e)
линейно поляризованные
2) Луч параллелен оптической оси z.
При любой поляризации волны
z
o
o
x
S
y
Поляризация волны может быть любой:
линейной, круговой, эллиптической.
251.
Двойное лучепреломление3) Луч направлен под углом к оптической оси.
не зависит от .
z
e o
x
v e cos v z
S
y
252.
Двойное лучепреломлениеne
c
v e
1) Скорость и показатель преломления обыкновенной волны
не зависят от направления луча. Вектор E колеблется
перпендикулярно главному сечению.
2) Скорость и показатель преломления необыкновенной волны
зависят от направления луча. Вектор E колеблется в плоскости
главного сечения.
253.
Двойное лучепреломлениеЭто пространственное разделение обыкновенной и
необыкновенной волн в одноосном кристалле.
Если v o v e ne no , то одноосный
кристалл называется положительным.
Пример: кварц (SiO2), ne 1,553; no 1,544 при
Если v e v o no ne , то одноосный
кристалл называется отрицательным.
ve
vo
589,3 нм
vo
Пример: исландский шпат (CaCO3), no 1,658; ne 1,486
ve
254.
Двойное лучепреломлениеz
ke
e o
ke
z
Se
So
ko
Положительный кристалл
o
Se
ko
e
Отрицательный кристалл
So
255.
Двойное лучепреломлениеO
O
o
So
e
Se
Необыкновенный луч в кристалле отклоняется от нормали.
Для необыкновенной волны закон преломления с показателем
ne справедлив только для вектора k e и не справедлив для S e .
256.
Двойное лучепреломлениеO
O
O
O
O
O
So
Se
So
Se
Наклонное падение света на одноосный кристалл
257.
Двойное лучепреломлениеДвухосные кристаллы
У таких кристаллов есть две оптические оси. В главных осях
тензора диэлектрической проницаемости
.
В двухосных кристаллах оба луча необыкновенные.
В некоторых кристаллах один луч поглощается сильнее
другого. Это явление называется дихроизм.
Пример: турмалин – природный одноосный кристалл. Для
жёлтого цвета 1 2 40 мм 1, 3 8 мм 1.
Поляроиды – синтетические дихроичные материалы.
258.
Поляризация света при прохождении через кристаллОптическая разность хода обыкновенного и
необыкновенного лучей
O
k
y
x
z
d
O
Монохроматический свет
падает по нормали на
пластинку, вырезанную
параллельно оптической оси
отрицательного кристалла.
Главное сечение
259.
Поляризация света при прохождении через кристаллd no ne
E Ex e x E y e y E x - обыкновенная волна
E y - необыкновенная волна
v e v o no ne
2
2 d
n
n
o
e
O
0
e
k
o
d
O
0
а) падает естественный свет
E x и E y не когерентны, следовательно
на выходе естественный свет
б) поляризованный свет
На выходе поляризованный свет, но
тип поляризации зависит от .
260.
Поляризация света при прохождении через кристаллПластинка в четверть длины волны
y
Ee
x
z k Eo
Если 0,
0
E
m 0
4
2
m 0, 1, 2,...
а) Линейно поляризованный свет
2 , то на выходе линейная поляризация.
Если 4 , то на выходе круговая поляризация.
Левая круговая поляризация, если 0 4, 1 2
Правая круговая поляризация, если 3 0 4, 1 3 2
Если 0, 4, 2 , то на выходе эллиптическая поляризация
261.
Поляризация света при прохождении через кристаллб) Падает свет круговой поляризации (например, правой)
Пластинка из исландского шпата, т.е. v e v o
no ne
E x A cos t
E
На входе:
E y A cos t 2
x
Внутри: E x Eo , E y Ee
k
На выходе: d no ne
2
o e
E y A cos t e
0
2
2
A cos t o A cos t o E x
2
2
y
262.
Поляризация света при прохождении через кристаллy
y
E
E
x
k
k
На выходе линейная
поляризация
Если падающий
свет имел левую
x круговую
поляризацию, то
на выходе также
линейная
поляризация
в) Падает естественный свет
На выходе естественный свет.
Вывод: Чтобы отличить естественный свет от света с круговой
поляризацией, надо использовать пластинку в четверть длины
волны.
263.
Поляризация света при прохождении через кристаллг) Падает эллиптически поляризованный свет
Вращая пластинку, можно совместить
y E O
одну ось эллипса поляризации с
оптической осью ОО пластинки.
x За пластиной ставим поляризатор.
k
O
Вращая пластинку, и поляризатор можно
добиться полного затемнения
д) Падает частично поляризованный свет
Никакими поворотами пластинки и поляризатора нельзя
добиться полного затемнения.
Вывод: Чтобы отличить эллиптически поляризованный свет
от частично поляризованного надо использовать пластинку в
четверть длины волны.
264.
Поляризация света при прохождении через кристаллEвых
Пластинка в полдлины волны
Ee O
0
Eпад
m 0 m 0, 1, 2,...
2
Eo k Eo
2m 1
O
Если на пластину падает линейно поляризованный свет, то
происходит поворот плоскости поляризации на угол 2 .
Общий случай. Если линейно поляризованный свет падает на
пластину произвольной толщины, то на выходе будет
эллиптически поляризованный свет.
265.
Поляризация света при прохождении через кристаллКристаллическая пластинка между двумя
поляризаторами
P
O
естеств.
свет
Свет монохроматический
A естественный плоскополяризованный
эллиптически поляризованный
плоскополяризованный
I и E - интенсивность и амплитуда
света после поляризатора PP.
P
O
A
Отражением света и поглощением
в пластине пренебрегаем
266.
Поляризация света при прохождении через кристаллP
E
Ee
Eo
O
P
O
A
В пластине:
Ee E cos
E2
Eo E sin
1) Поляризатор
и анализатор
параллельны.
O
Ee
E1
Eo
O
A
E1 Eo sin E sin 2
I1 I sin 4
E2 Ee cos E cos2
I 2 I cos4
267.
Поляризация света при прохождении через кристаллI1 I 2 2 I1 I 2 cos
A
I sin 4 cos4 2sin 2 cos2 cos E2
cos 1 sin 2 2
I sin cos
2
2
Ee
E1
Eo
2
2
4sin cos sin 2
2
O
2
O
A
268.
Поляризация света при прохождении через кристалл2) Поляризатор и анализатор перпендикулярны.
P
Eo
E1 E0 cos E sin cos
E2 Ee sin E sin cos
O
Ee
I1 I 2 I sin cos
2
A
E1
E2
O
P
A
2
Знаки проекций E1 и E2 различны.
2 I1 2 I1 cos 2 I1 1 cos 4 I1 sin 2
2
I sin 2 2 sin 2 2
269.
Поляризация света при прохождении через кристаллI
I sin 2 2
0
2
4
6
270.
Искусственное двойное лучепреломлениеФотоупругость (пьезооптический эффект)
Фотоупругость это возникновение оптической анизотропии под
действием механических напряжений в веществе.
Искусственная оптическая ось параллельна приложенной силе.
Соотношение Брюстера для упругих деформаций
n k
n no ne
F S
k - коэффициент фотоупругости
271.
Искусственное двойное лучепреломлениеЭффект Керра
Эффект Керра (квадратичный электрооптический эффект) это
возникновение двойного лучепреломления в изотропных
веществах под действием электрического поля.
Оптическая ось направлена вдоль электрического поля
A
4 4
P
P
A
E
272.
Искусственное двойное лучепреломлениеn E 2
Оптическая разность хода
обыкновенного и
необыкновенного лучей на
длине l образца: l n
2
0
2
0
l E 2
2 BlE 2
B 0 - постоянная Керра
Ячейка Керра – устройство,
применяемое в качестве
оптического затвора или
модулятора света
273.
Вращение плоскости поляризацииВремя установления
ориентации молекул
вдоль поля порядка 10 10
с (полярные молекулы)
или 10 12 с (неполярные).
Ячейка Керра – наиболее быстродействующее устройство
для управления интенсивностью светового потока.
274.
Дисперсия и затухание волнПонятие о дисперсионном уравнении
Пример слабопроводящей среды.
H
E 0
t
, , const
E 0 H
t
E E E
E 0 E 0 H
t
275.
Дисперсия и затухание волнE
H E 0
t
2 E E
1
2
2
v E, v
2
t
0 t
0 0
y
E
v
z
H
E
E
H
0 2
t
t
t
2
x
2 Ey
t 2
2
Ey
2
E y
v
2
x
0 t
E y E0 exp i t kx
v k
2
2
2
i
0
276.
Дисперсия и затухание волнi - дисперсионное
i
k 2
k
1
2
уравнение
v
0 v
v
0
2
2
Дисперсионным уравнением называется зависимость k
или k , которая вытекает из волнового уравнения.
i
k 1
k ik
v 2 0
k , k
E y E0 exp i t k x k x
v
2 0 v
k - коэффициент затухания волн
277.
Дисперсия и затухание волнДисперсией волн называется
зависимость фазовой скорости
гармонической волны от частоты
если
0 vф
v ф
k
1
0 0
Дисперсия световых волн:
n
c
v ф
или
n 0
c
v ф 0
278.
Дисперсия и затухание волнГрупповая скорость волн
Волновой пакет – это распространяющееся волновое
возмущение, занимающее в каждый момент времени
ограниченную область пространства.
v
E
x
E A exp i k t kx
x
E x, t
A k exp i k t kx dk
279.
Дисперсия и затухание волнk
A
v
E
x
k
k0
x
E x, t
x lког
A k exp i k t kx dk
2
k 2 2
k k
k
k0
2
x k 2
280.
Дисперсия и затухание волнx k 2 x 0
d
k k0
dk
E x, t
k k0
u
k k0
d
dk
k k0
A k exp i t u k k t kx dk
0
0
exp i 0t k0 x A k exp i k0 k x ut dk
E x, t exp i 0t k0 x a x ut
281.
Дисперсия и затухание волнa x ut - огибающая волнового пакета, движущаяся
со скоростью u.
Скорость, с которой волновой пакет движется как
целое, называется групповой скоростью
u
E
x
d
u
dk
k k0
x
Групповая скорость определяет скорость переноса энергии в
волне.
282.
Дисперсия и затухание волнОбозначим v ф v
v
k
vk
d
dv
dv d
u
v k
v k
dk
dk
d dk
2 2
u v
2
dv
d
k
2
,
dk
2
2
d
dv
u v
d
283.
Дисперсия и затухание волнФормулы, применяемые в разделе «Оптика»
0
c
dn
v
,
dv 2 dn v
n 0
n 0
n
n
v
dn
d 0 0
0
dv
n
d
2 dn u v
v
n n
d
n d 0 dn
0 2
n
n
0dn
nd 0
v
v 1
v
u
0 dn
nd 0 0dn
nd 0 0 dn
1
n d 0
c
284.
Дисперсия и затухание волнu
v
0 dn
1
n d 0
dn
а) Нормальная дисперсия, если
0 u v
d 0
dn
0 u v
б) Аномальная дисперсия, если
d 0
285.
Элементарная теория дисперсии светаВзаимодействие света с веществом
Оценим воздействие электромагнитной волны на электроны.
F e E v B
v 0
E
Fм
Fэ
evB
eE
v 0 H
E
0
v
E v 0 0
0
c
Электрон рассматриваем как одномерный осциллятор
me x rx kx eE E E0 exp i t
286.
Элементарная теория дисперсии светаeE0
x 2 x x
exp i t
me
Дипольный момент электрона: p ex
Поляризованность вещества: P Np Nex
2
0
2
e NE0
P 2 P P
exp i t P P0 exp i t
me
2
2
e
NE0 me
e NE0
2
2
P0 2
2i 0 P0
2
0 2i
me
2
0
287.
Элементарная теория дисперсии светаP 0 1 E P0 0 1 E0
2
e
N me 0
P0
1
1 2
0 E0
0 2 2i
1 2
0 2 2i
плазменная частота
2
p
1
2i
2
p
2
0
2
0
2
e
NE0
2
p
me 0
2
2 2
4
2
2
i
288.
Элементарная теория дисперсии светаКомплексный показатель преломления
1
2
0
2
p
2
0
2 2
i
2
4
2
2
2
2
0
2 2
2
p
4
2
Пусть мало, т.е.
i
i
n 1
1
n in
2
n , n
k n in
v c
2
2
289.
Комплексный показатель преломления1
p2 02 2 2i
2
0
2 2
4 2 2
Пусть мало, т.е.
i
2
e NE0
me 0
2
p
плазменная частота
i
i
n 1
1
n in
2
2
2
2
2
2
p 0
p
1
2
2
2
2
2 2
2
2
2 2
0 4
0 4
n , n
2
290.
Взаимодействие света с веществомn , n
2
k n in
v c
E E0 exp i t kx E0 exp i t n in x
c
E E0 exp i t n x exp n x
c
c
I I 0 exp x
I
E2
2 n 0
c
Закон Бугера (Бугера – Ламберта -Бера)
291.
Дисперсия и затухание волнn n
Область, в которой dn
называется областью
нормальной дисперсии.
Область, в которой dn
называется областью
аномальной дисперсии.
d 0
u c
d 0
u c
Для бесцветных газов (воздух, H2) и стекла 0 относится к УФ.
292.
Элементарная теория дисперсии светаСпектры испускания и
поглощения
n
1)
2)
0
1
0
2
0
3
3)
4)
5)
0
1
0
2
0
3
6)
7)
8)
1) Солнечный спектр; 2) Спектр звезды Сириуса;
3) Спектр звезды Геркулеса; 4) Спектр водорода;
9)
5) Спектр азота; 6) Спектр рубидия; 7) Спектр цезия;
8) Спектр поглощения крови (оксигемоглобина); 9) Спектр поглощения хлорофилла
293.
Рассеяние светаПри случайном расположении неоднородностей:
I рас NI1
eE0
x
exp i t
2
me 0
p ex
2
Закон Рэлея
I1
p2
I рас 4
4
294.
Рассеяние светаРассеяние солнечного света
происходит на молекулах
воздуха.
Почему небо голубое?
Закон Рэлея
I рас
4
1
4
кр
Iф
2
16
ф
I кр
295.
Рассеяние светаЗакон Рэлея
I рас
4
1
4
296.
Рассеяние света297.
Курс общей физики НИЯУ МИФИ – 4-ый семестрОБЗОР
Курс общей физики НИЯУ МИФИ – 4-ый
семестр
298.
Курс общей физики НИЯУ МИФИ – 4-ый семестрМеханические волны
1. Стоячие волны в струне с двумя закрепленными концами.
2. Интерференция плоских волн.
3. Поток энергии в упругой волне. Вектор Умова.
4. Плоские и сферические волны (без затухания и с затуханием).
Курс общей
физики
НИЯУ МИФИ – 4-ый звуковой
5. Связь избыточного
давления
с интенсивностью
семестр
волны в газе.
6. Эффект Доплера для звуковых волн.
7. Волновое уравнение для продольных упругих волн в тонком
стержне.
8. Колебания струны с двумя закрепленными концами.
9. Скорость продольных и поперечных упругих волн в тонком
стержне.
10. Волновое уравнение для звука в газе. Скорость звука в газе.
299.
Курс общей физики НИЯУ МИФИ – 4-ый семестрЭлектромагнитные волны
1.Плоская монохроматическая электромагнитная волна.
2. Свойства плоской монохроматической электромагнитной
волны. Виды
поляризации.
Курс общей
физики
НИЯУ МИФИ – 4-ый
3.Волновое уравнение
для
электромагнитных
волн в
семестр
однородном изотропном диэлектрике. Скорость
электромагнитных волн.
4. Энергия электромагнитных волн. Вектор Пойнтинга.
5. Импульс электромагнитной волны и давление на стенку.
6. Эффект Доплера для электромагнитных волн.
7. Коэффициент отражения и пропускания плоской
электромагнитной волны.
300.
Курс общей физики НИЯУ МИФИ – 4-ый семестр3. Геометрическая оптика и фотометрия.
1.Понятие о световом луче. Оптическая длина пути. Принцип
Ферма.
2.Принцип Ферма. Законы отражения и преломления.
3.Кардинальные точки и плоскости центрированной
Курс общей физики НИЯУ МИФИ – 4-ый
оптической системы. Формула
Ньютона.
семестр
4. Формула тонкой линзы. Оптическая сила линзы.
5. Сила света и освещенность.
6 Светимость и яркость. Ламбертовский источник.
7. Кривая относительной спектральной чувствительности
глаза.
8. Поток энергии и световой поток.
301.
Курс общей физики НИЯУ МИФИ – 4-ый семестр4. Интерференция света.
1. Явление интерференции. Сложение двух электромагнитных волн.
Интенсивность суммарной волны.
2. Способы наблюдения интерференции света. Бизеркала или
бипризма Френеля
3. Интерференционные полосы равной толщины.
4. Интерференционные полосы равного наклона.
Курс общей физики НИЯУ МИФИ – 4-ый
5. Кольца Ньютона.
семестр
6. Многолучевая интерференция.
7. Интерференция света на тонких пленках. Просветление оптики
8. Временная когерентность, длина когерентности (на примере опыта
Юнга с узкой щелью).
9. Пространственная когерентность, радиус когерентности. (На
примере опыта Юнга с монохроматическим протяженным
источником).
10. Интерферометры Майкельсона и Фабри-Перро.
302.
Курс общей физики НИЯУ МИФИ – 4-ый семестр5. Дифракция Френеля.
1. Принцип Гюйгенса-Френеля и его аналитическое
выражение в виде интеграла или ряда.
общей физики
НИЯУ МИФИ
4-ый
2. ГрафическоеКурс
сложение
амплитуд.
Зоны –Френеля.
семестр
3. Дифракция Френеля на щели. Спираль Корню.
4. Дифракция Френеля на круглом отверстии и на диске.
5 Дифракция Френеля на крае полуплоскости.
303.
Курс общей физики НИЯУ МИФИ – 4-ый семестр6. Дифракция Фраунгофера. Дифракционная решетка.
1. Дифракция Фраунгофера на щели.
2. Дифракционная решетка.
3. Положение и угловая ширина главных дифракционных
Курс общей физики НИЯУ МИФИ – 4-ый
максимумов дифракционной
решетки.
семестр
4. Дисперсия и разрешающая способность дифракционной
решетки.
5. Дифракция рентгеновских лучей. Формула БрэггаВульфа.
6. Дифракция на моно- и поликристаллах. Лауэграммы и
дабаеграммы (качественно).
304.
Курс общей физики НИЯУ МИФИ – 4-ый семестр7. Поляризация и двойное лучепреломление.
1. Эллиптическая и круговая поляризация света.
2. Частично поляризованный свет. Степень поляризации.
3. Двойное лучепреломление в одноосных кристаллах.
4. Ход лучей в одноосном кристалле.
Курс общей физики НИЯУ МИФИ – 4-ый
5. Поляризация при
отражении
и преломлении (качественно).
семестр
Угол Брюстера.
6. Кристаллическая пластинка между двумя поляризаторами.
7. Прохождение плоско поляризованного света через
кристаллическую пластинку. Пластинка в четверть длины
волны.
305.
Курс общей физики НИЯУ МИФИ – 4-ый семестр8. Дисперсия света и затухание электромагнитных
волн.
1. Элементарная теория дисперсии.
2. Фазовая и групповая скорости волн.
3. Комплексный показатель преломления вещества.
Курс общей физики НИЯУ МИФИ – 4-ый
семестр
9. Излучение электромагнитных волн.
1. Излучение ускоренно движущегося заряда. Мощность
дипольного излучения.
2. Излучение дипольного осциллятора. Диаграмма
направленности.
.


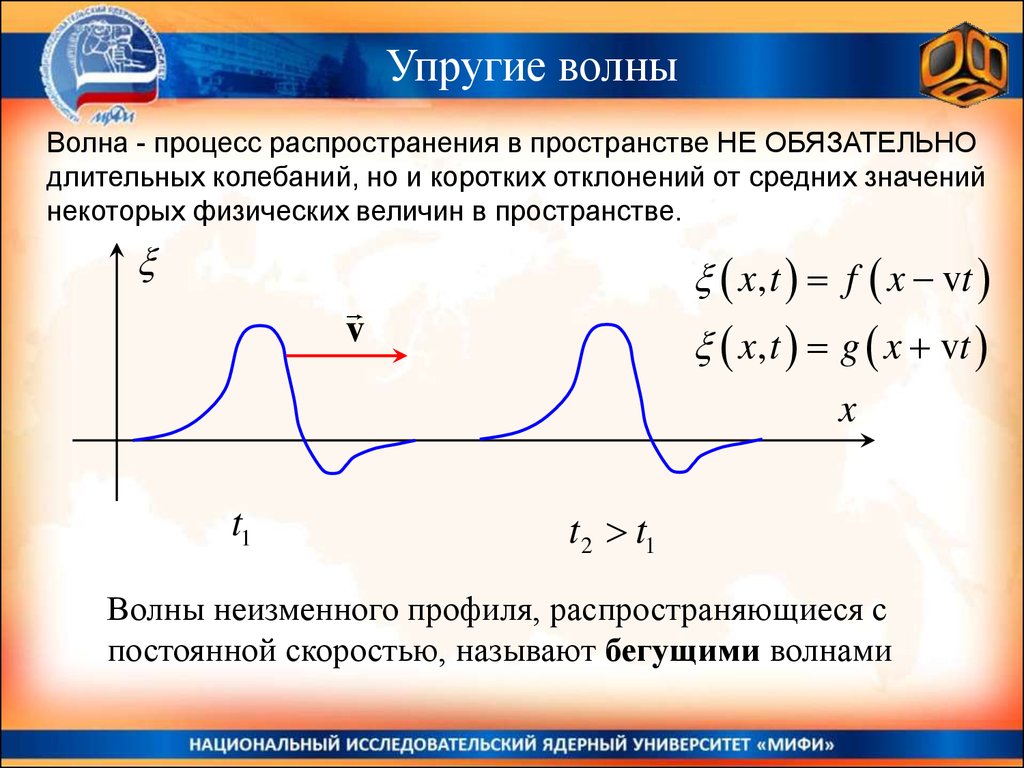

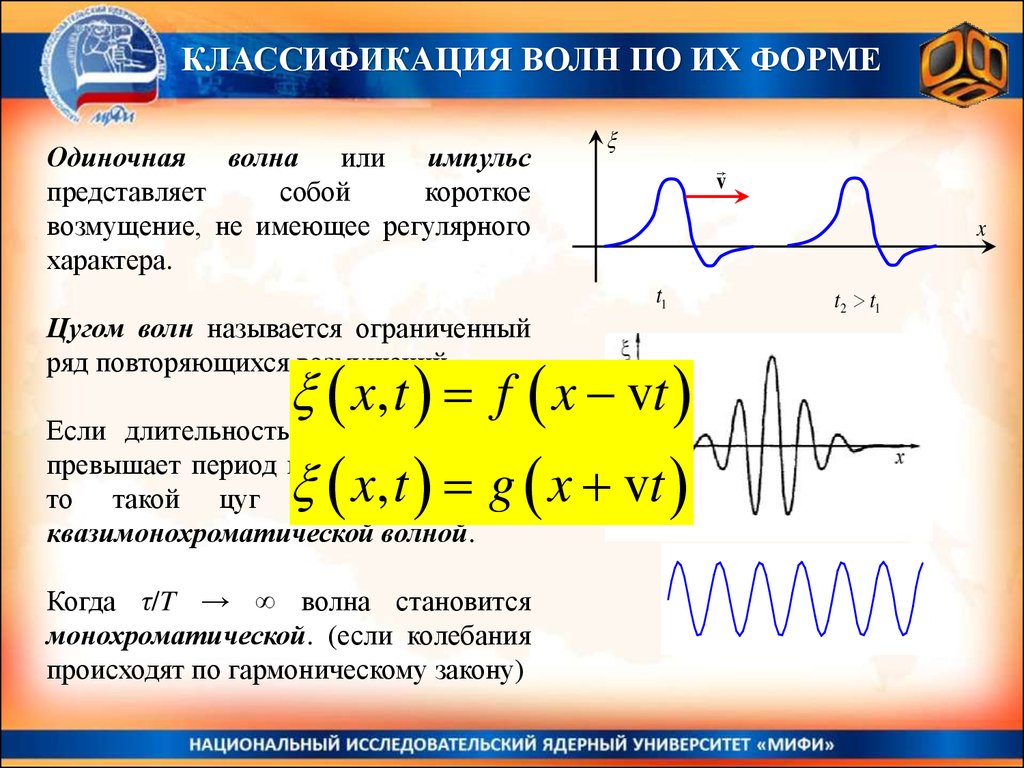






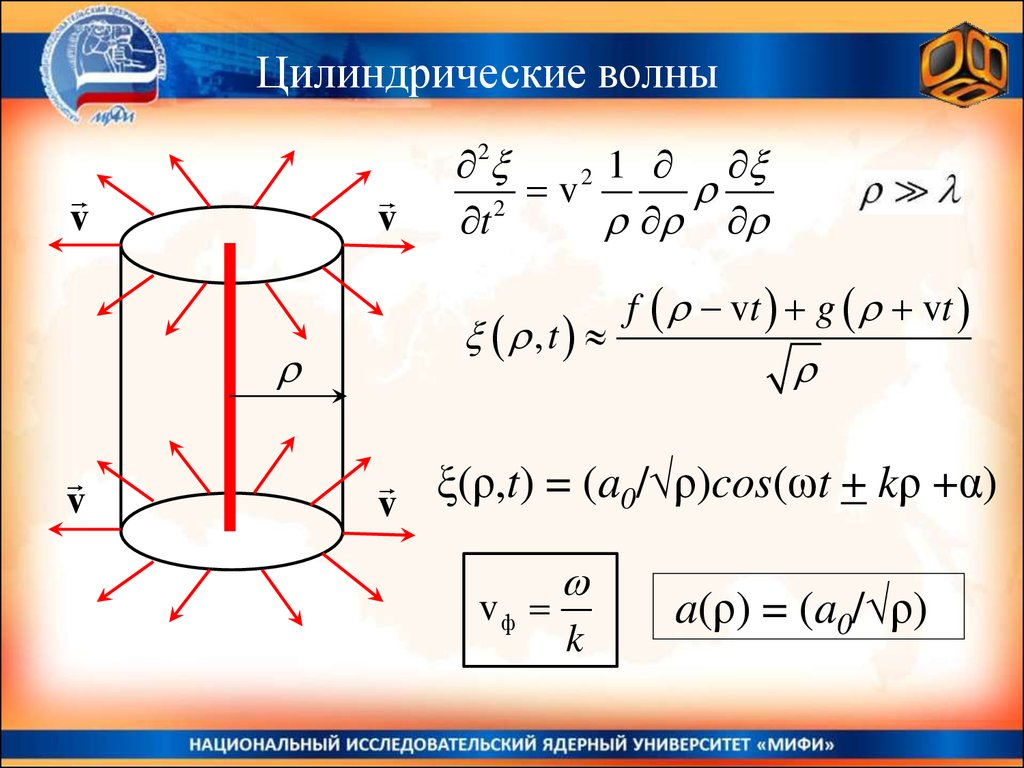

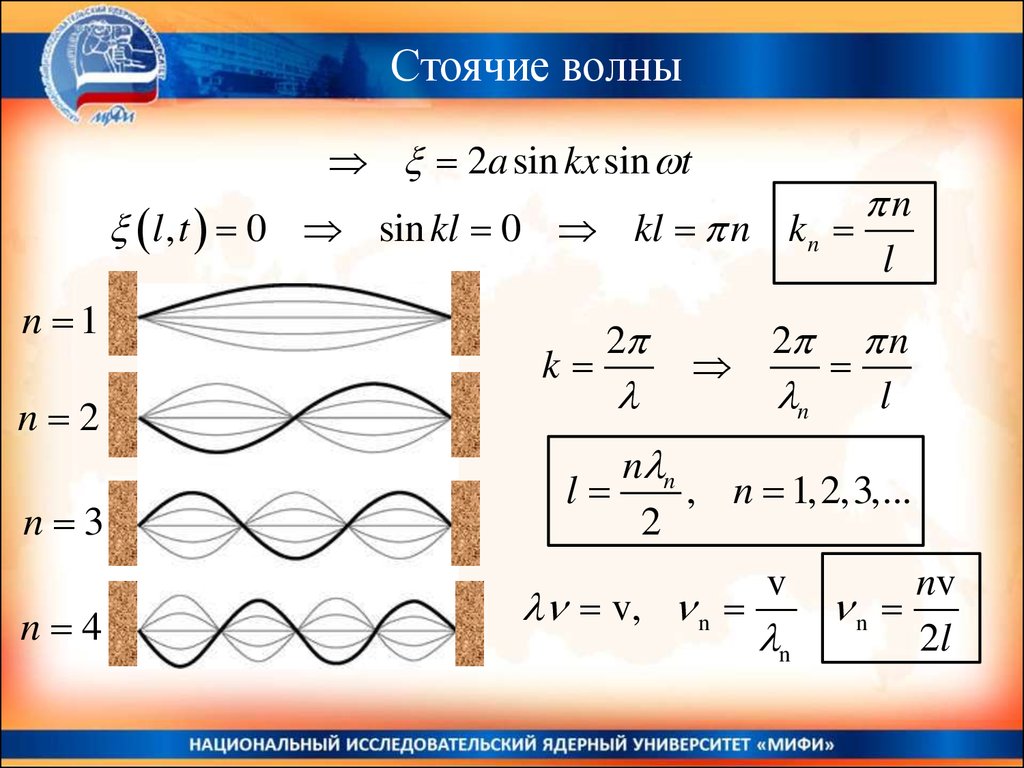























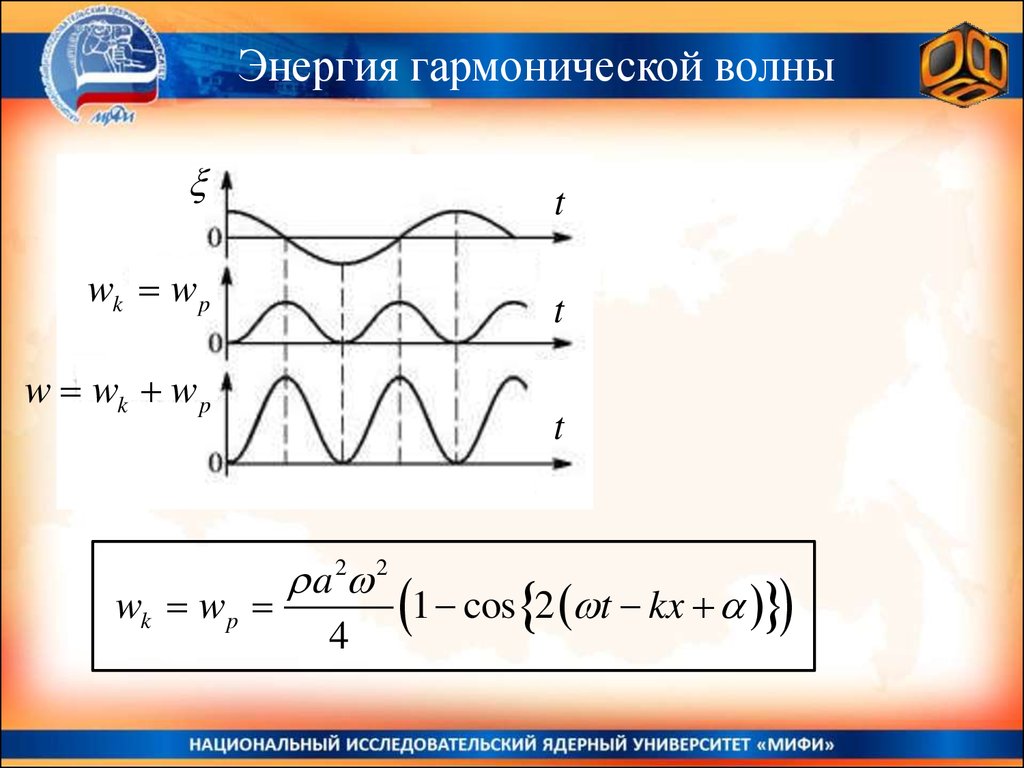






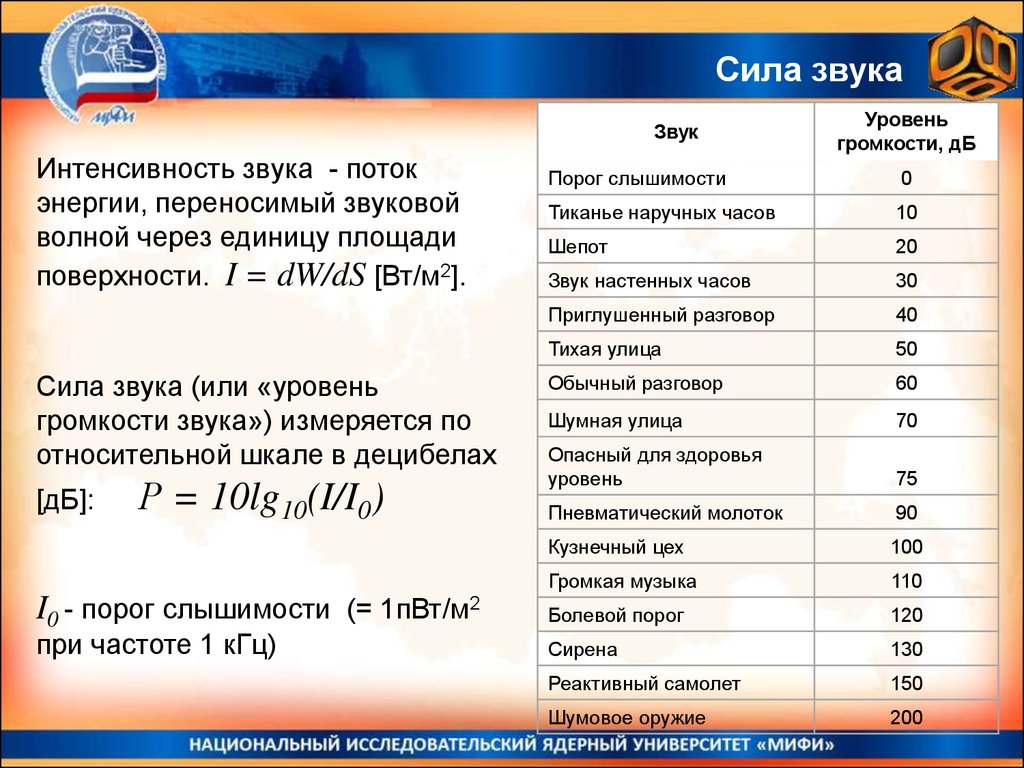
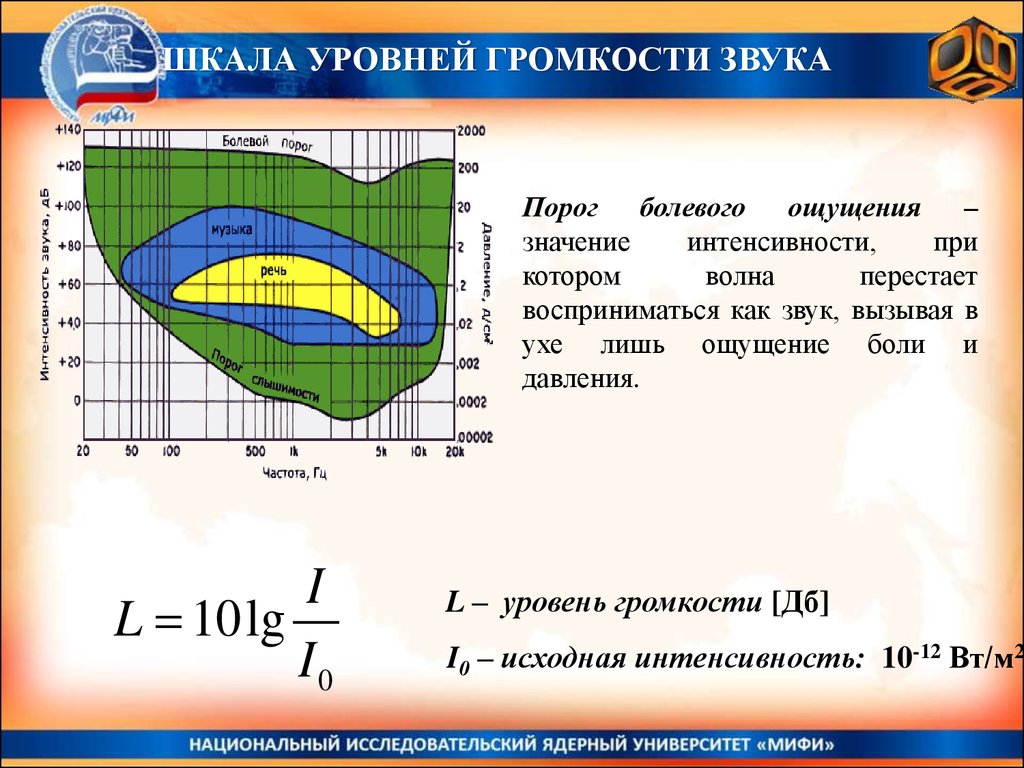



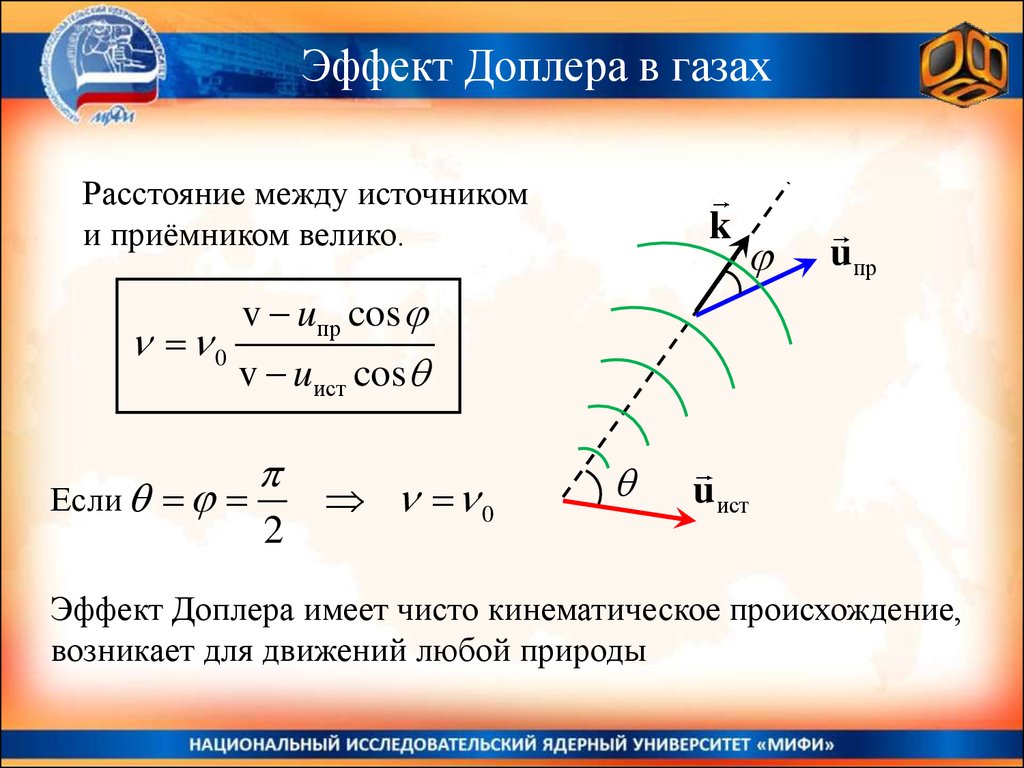






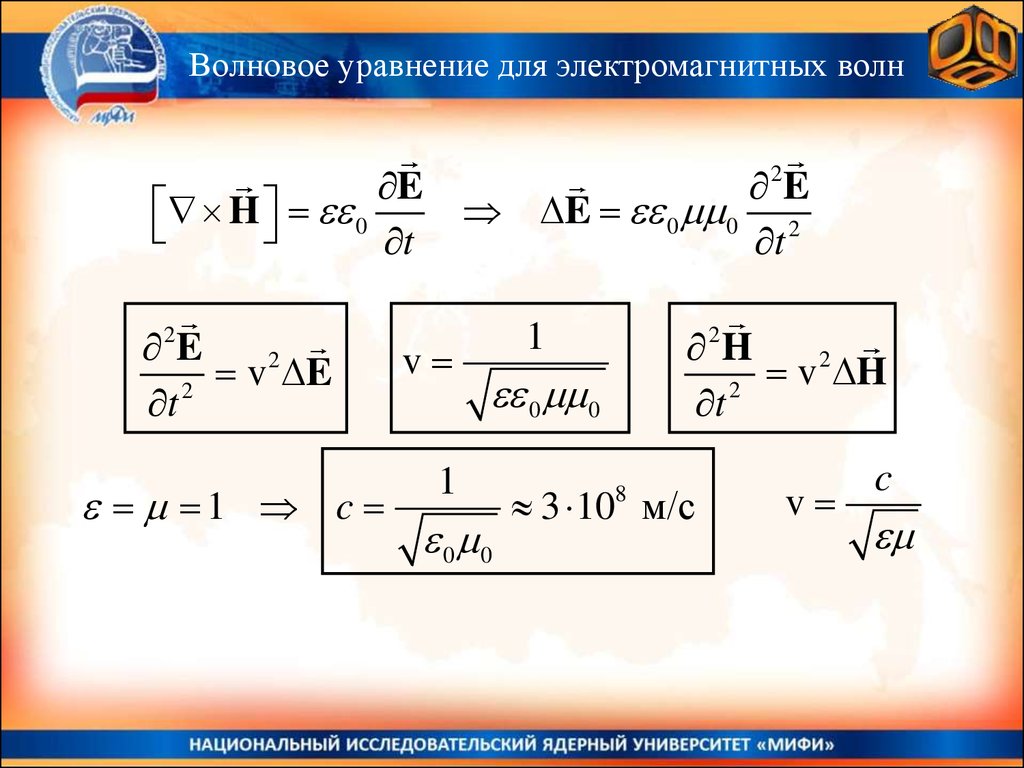
















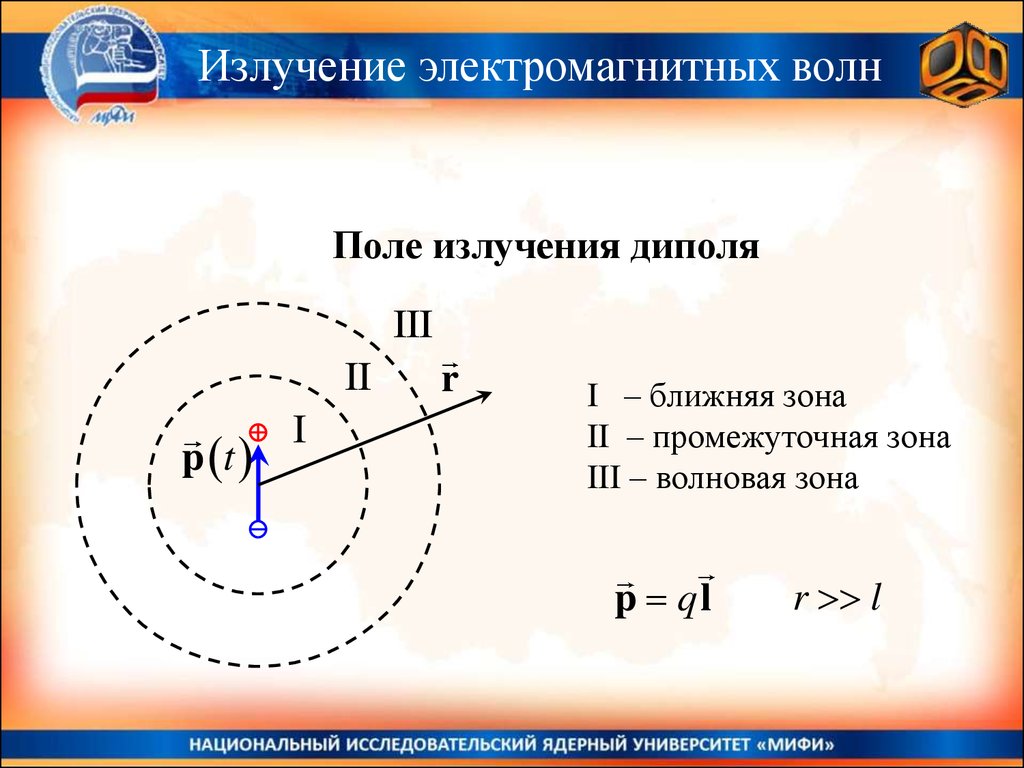
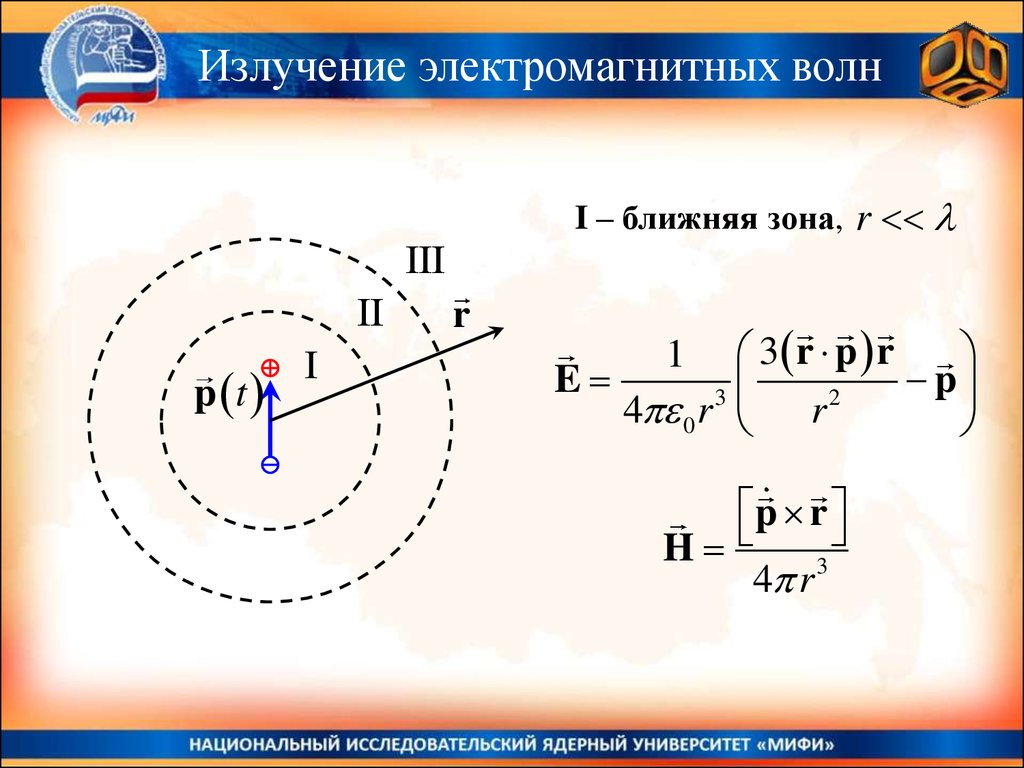

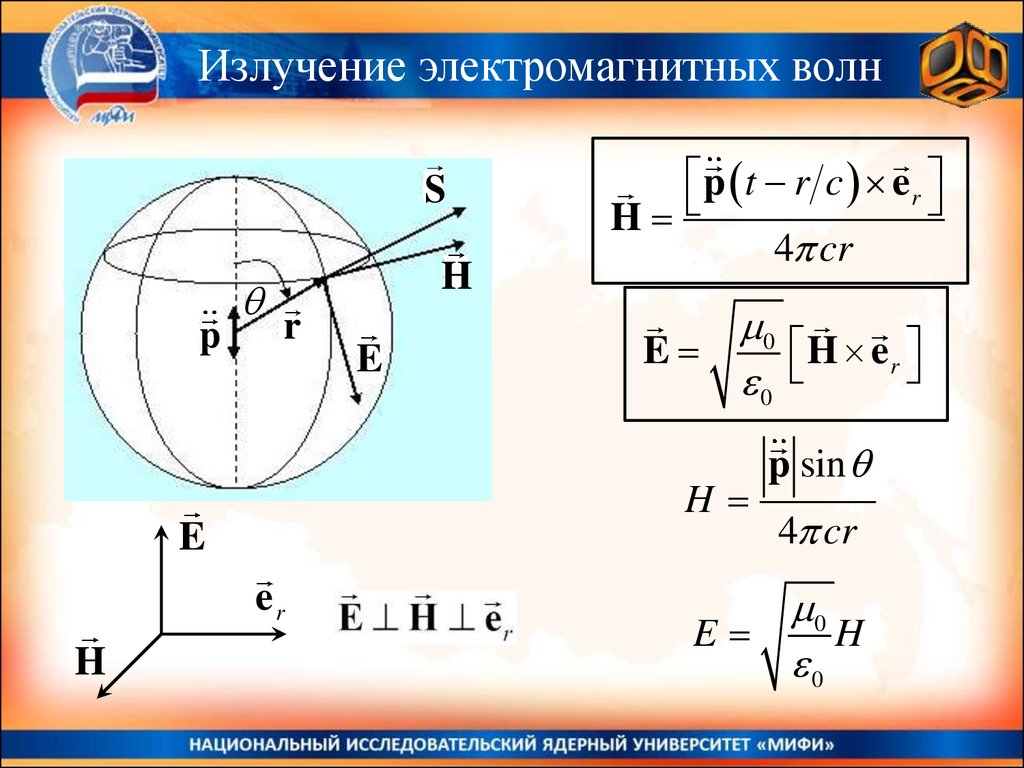






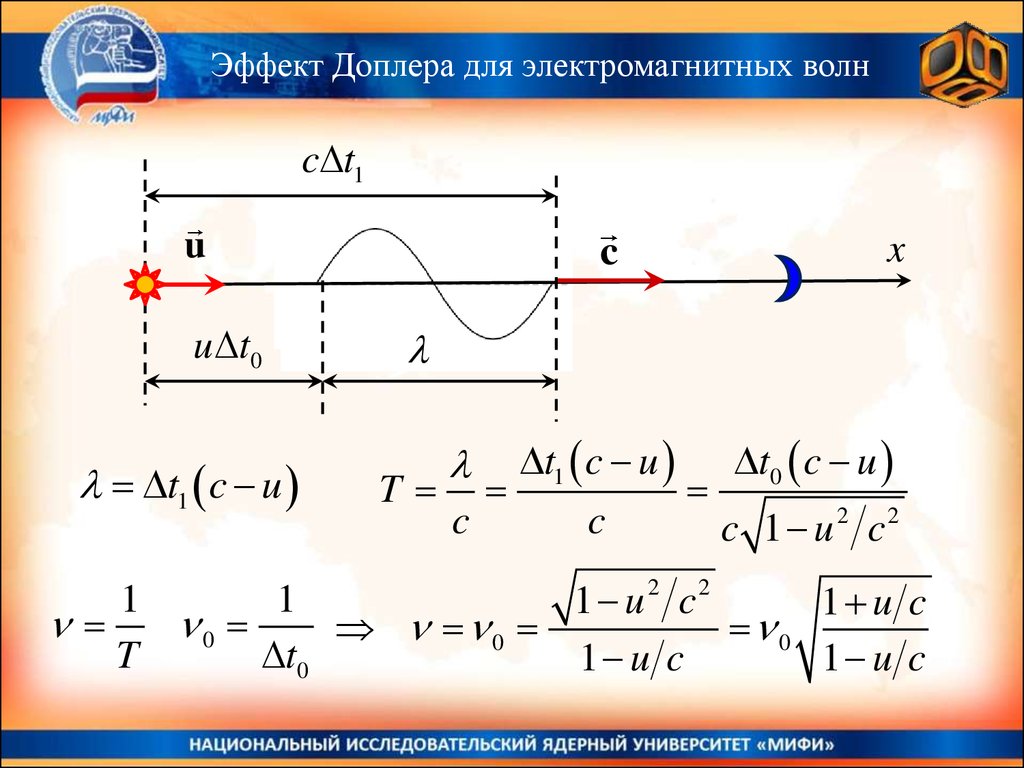

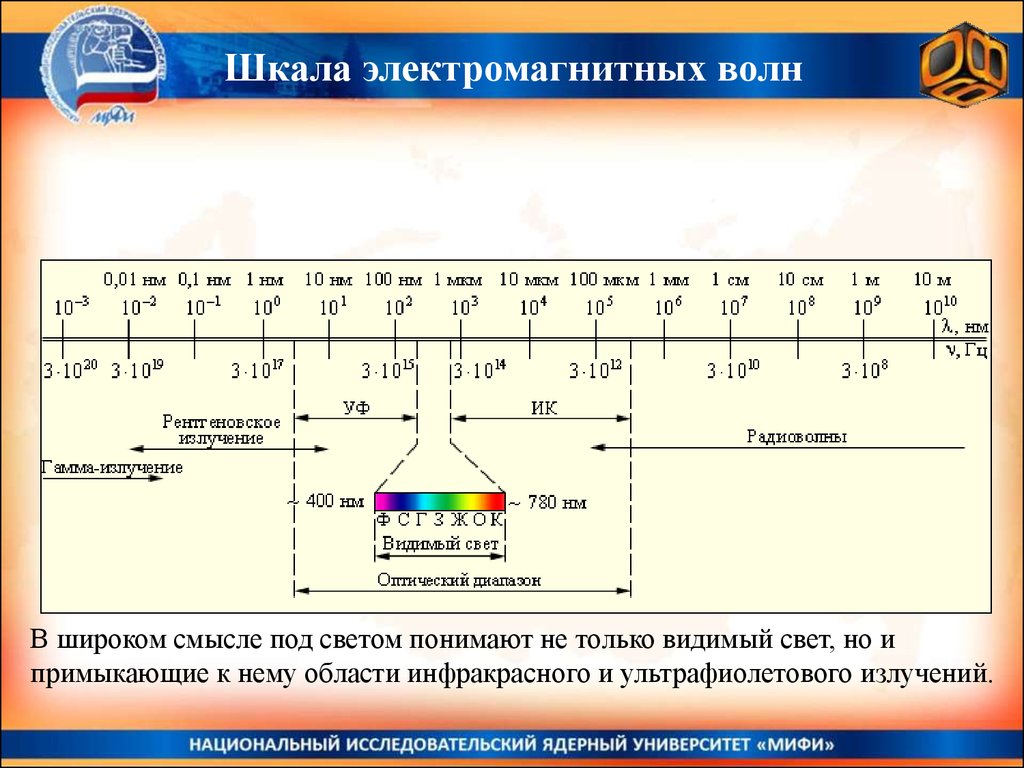






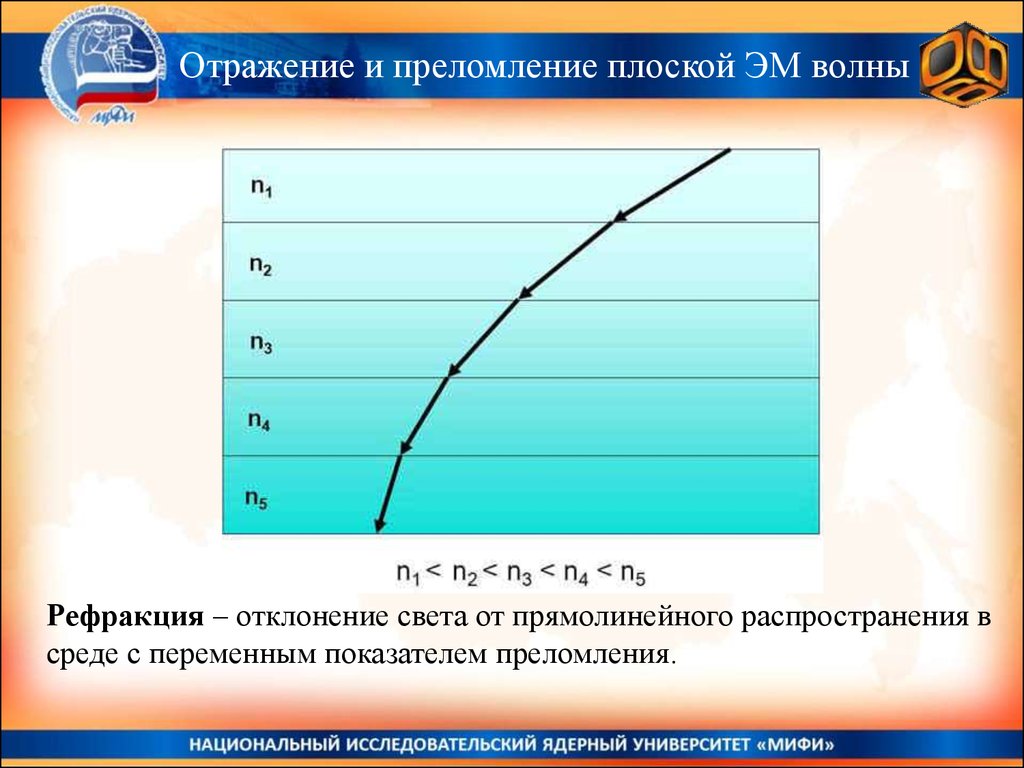

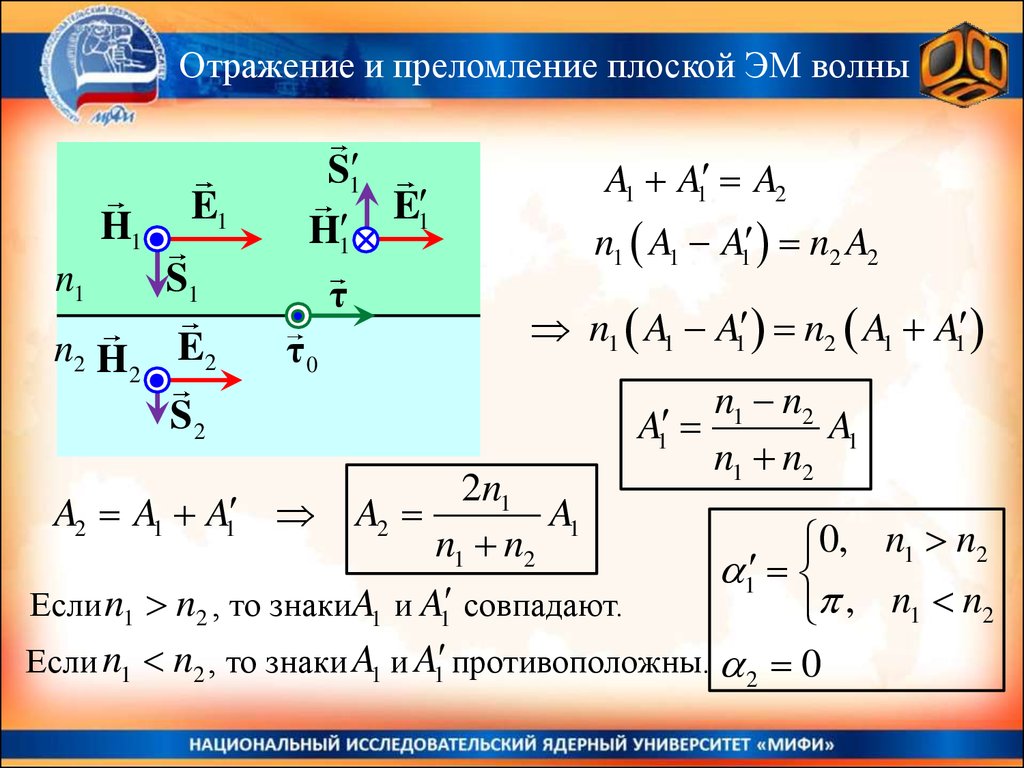



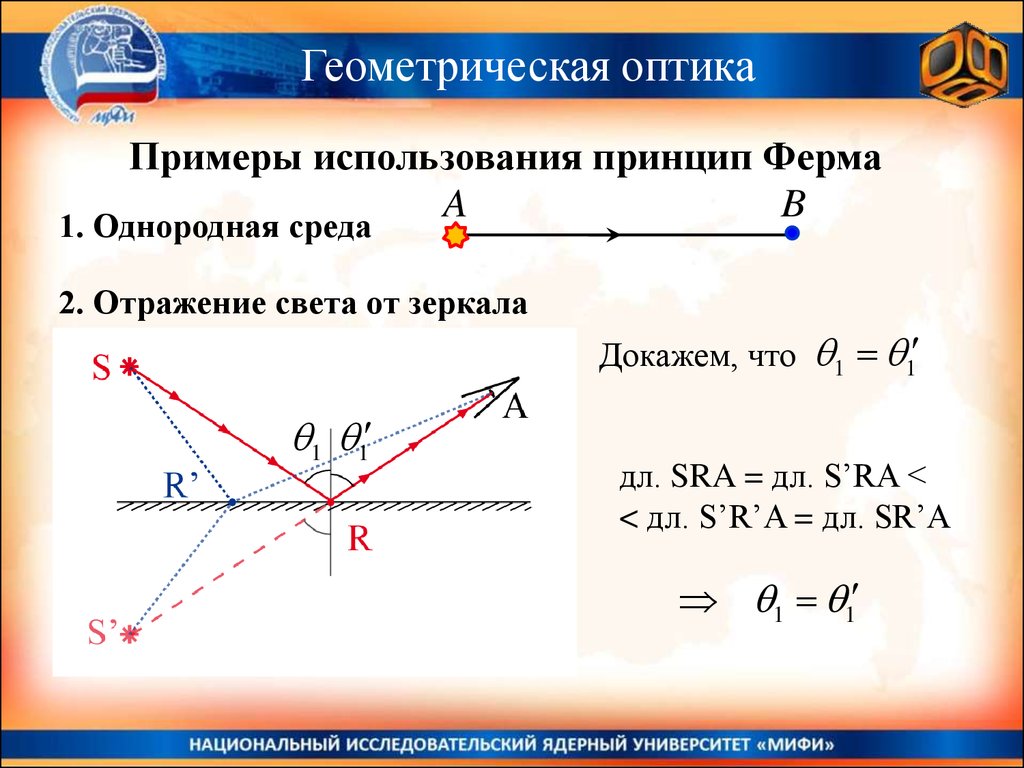



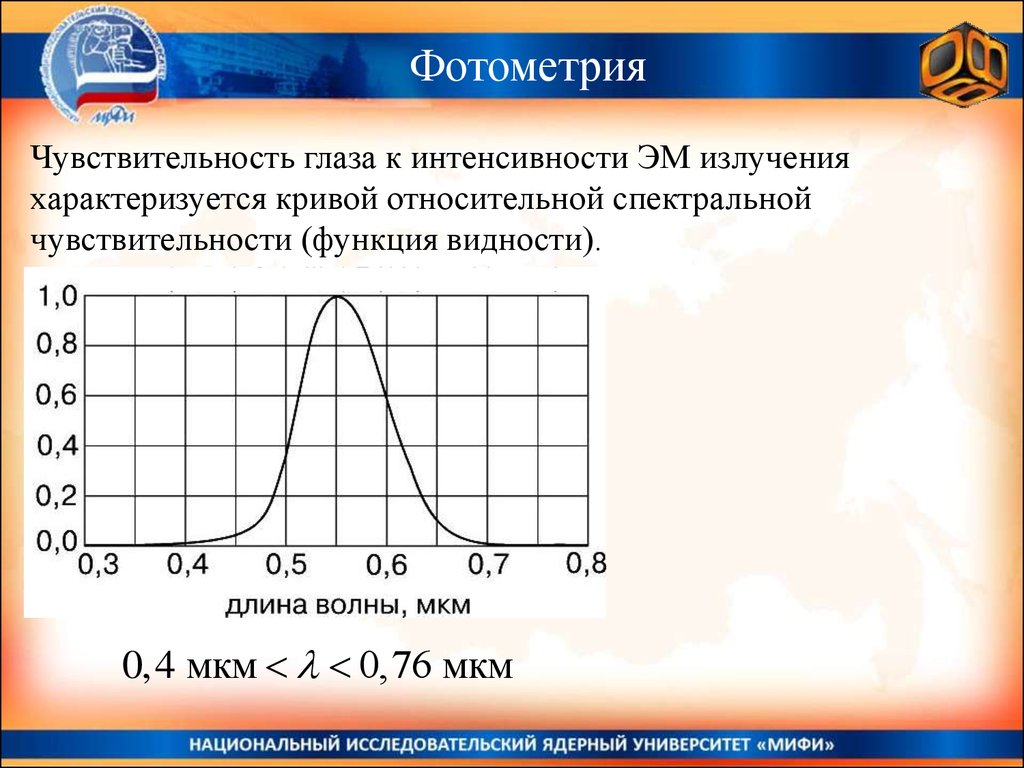
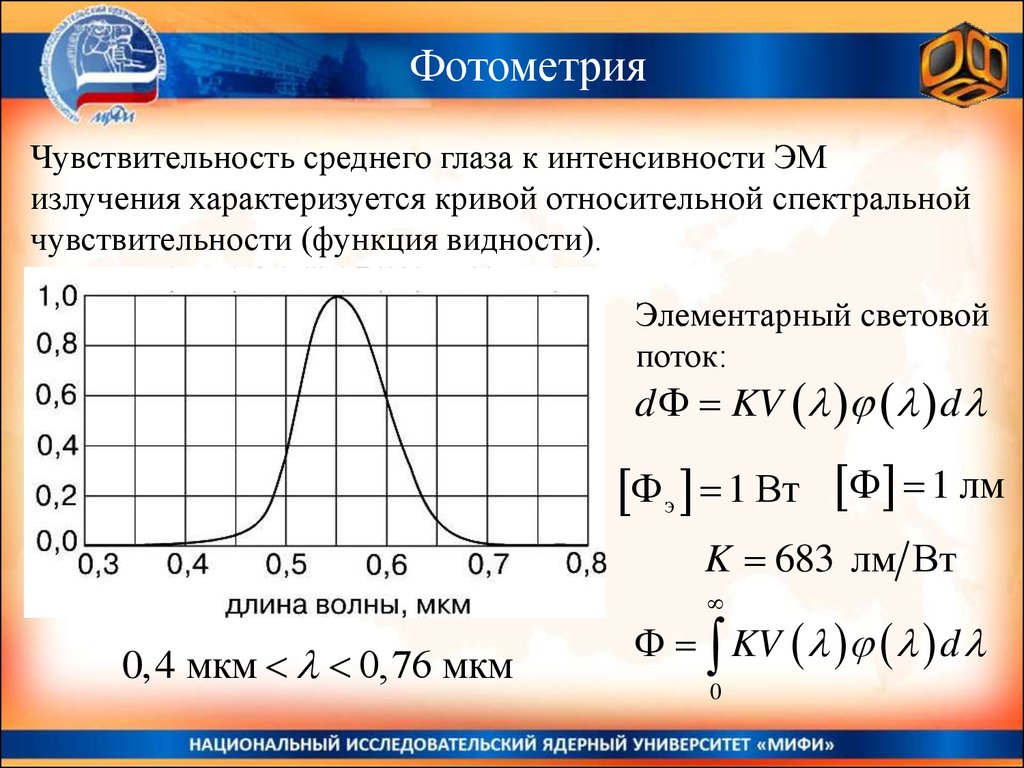








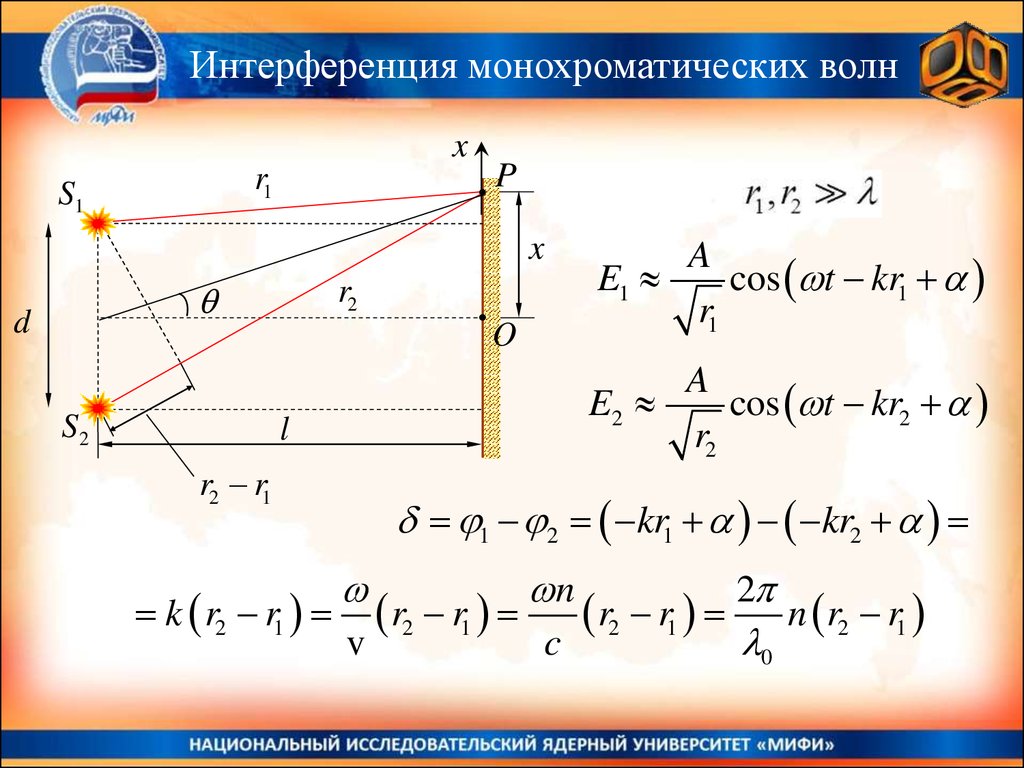





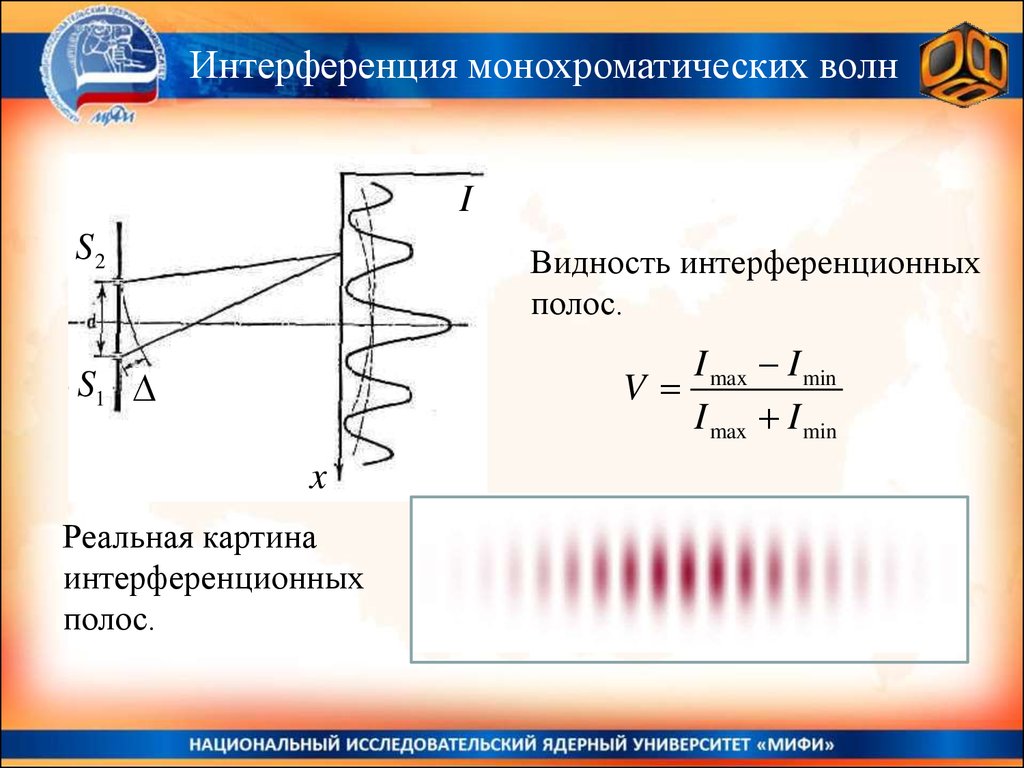













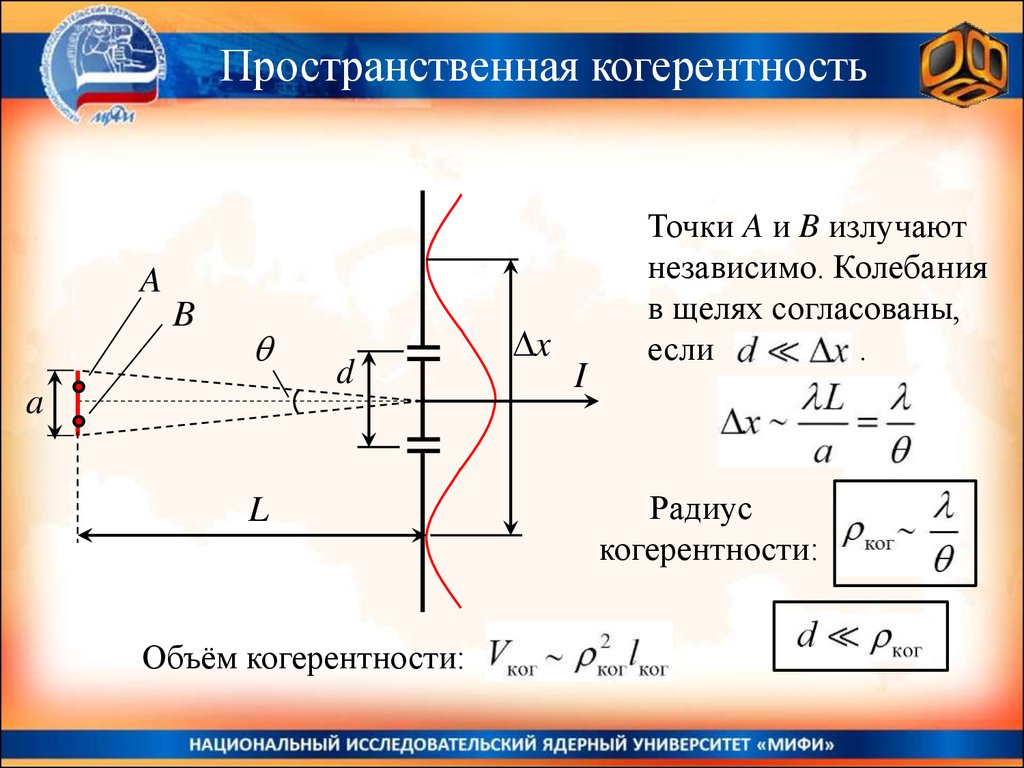




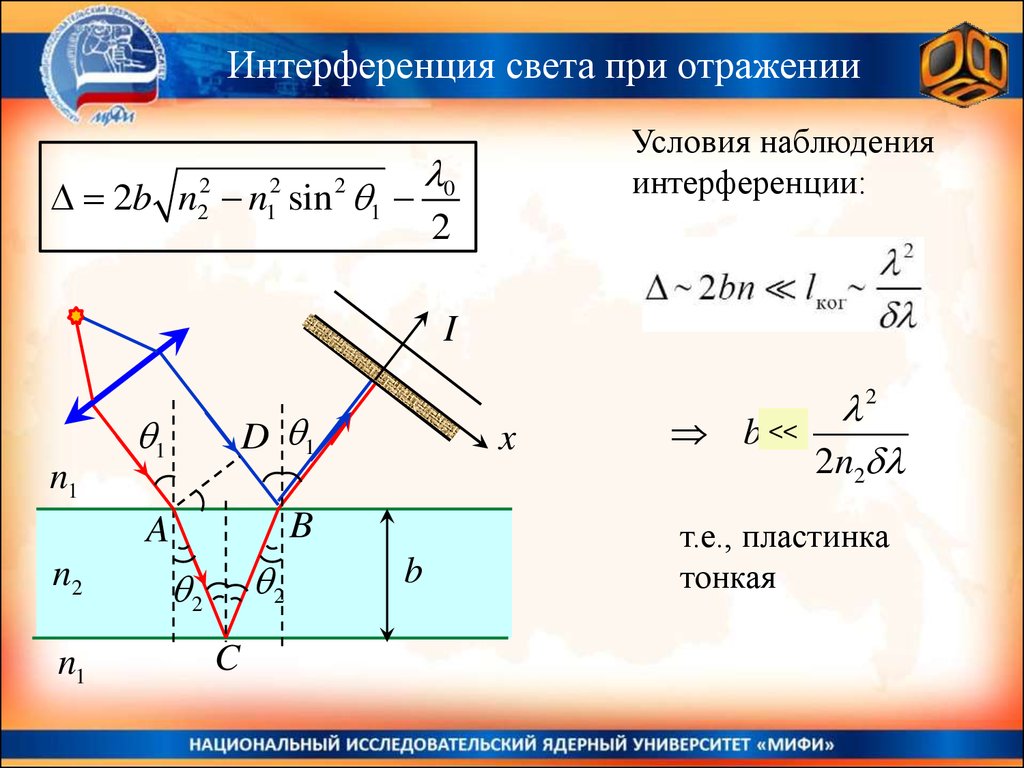
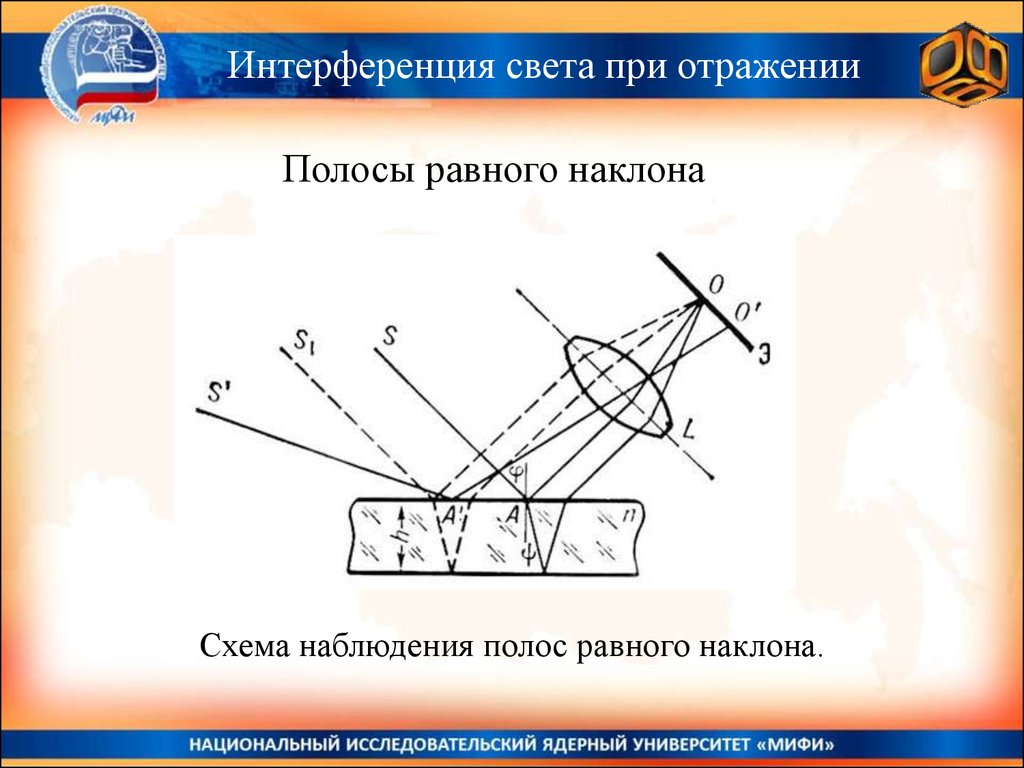



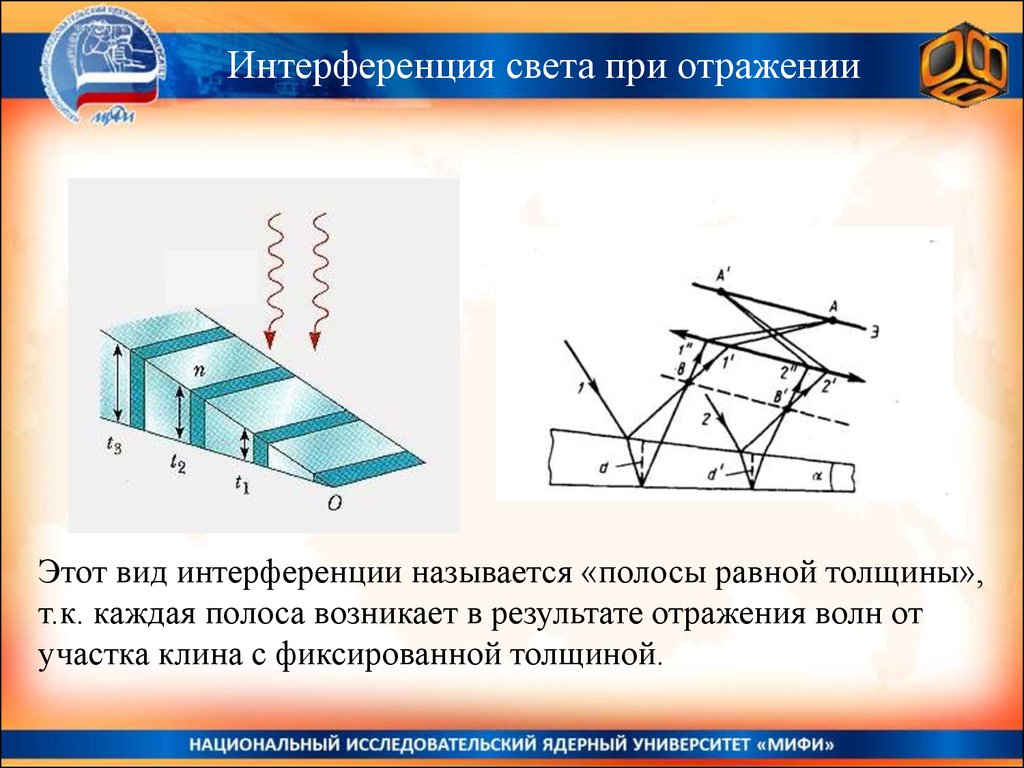





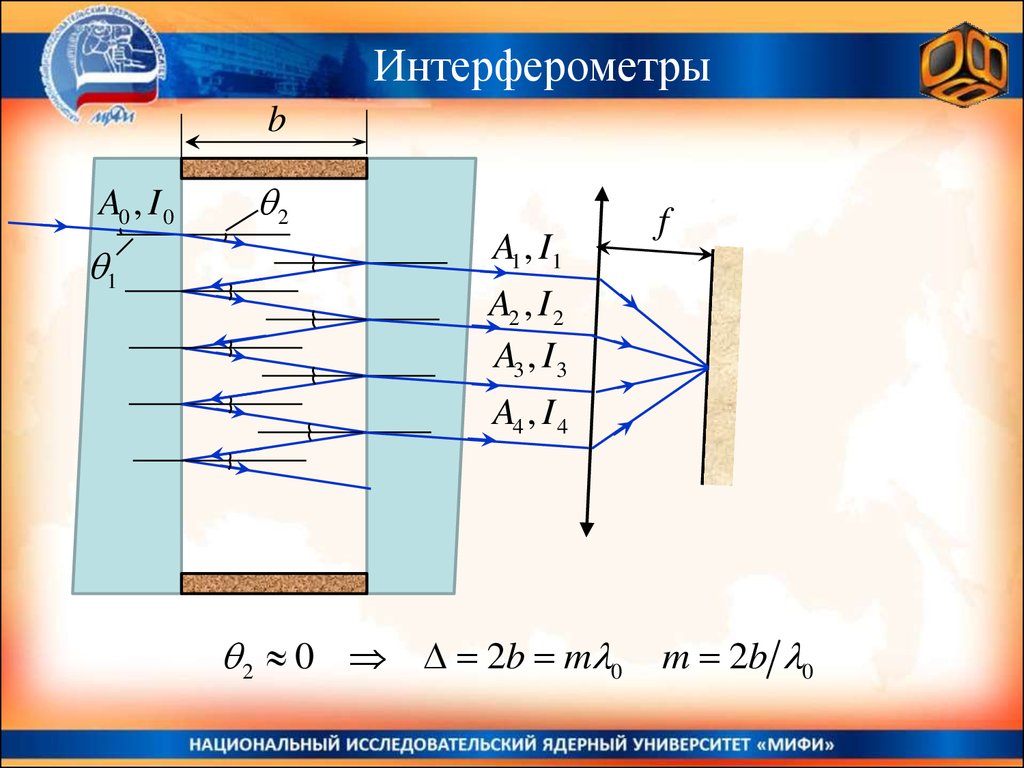


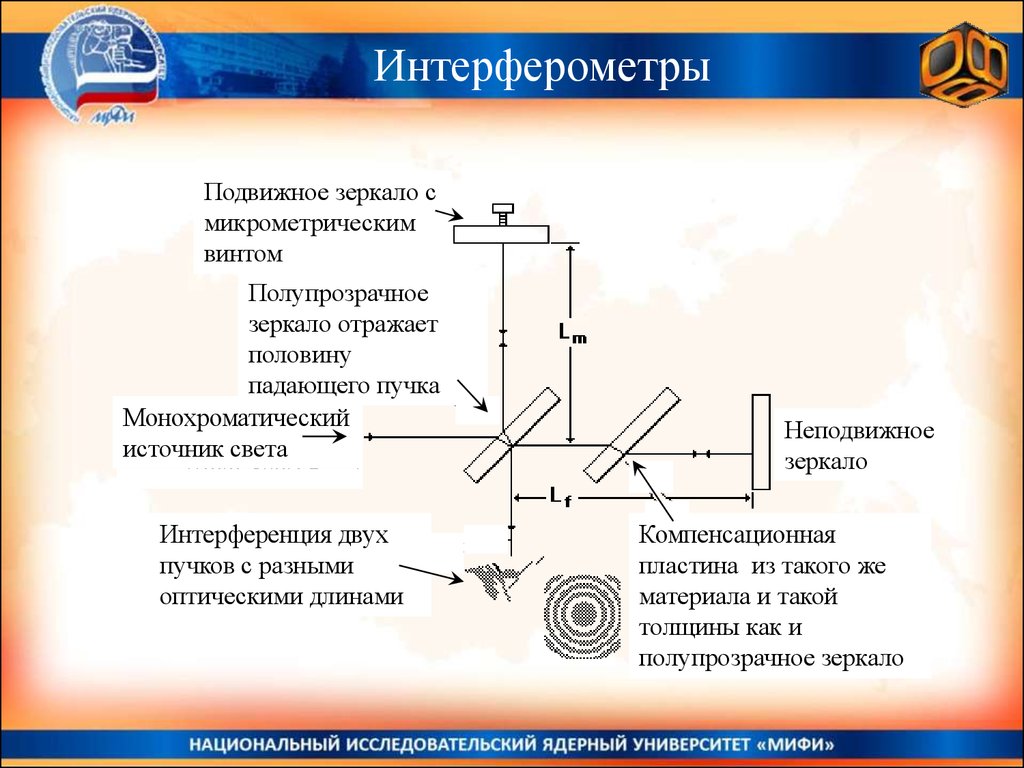
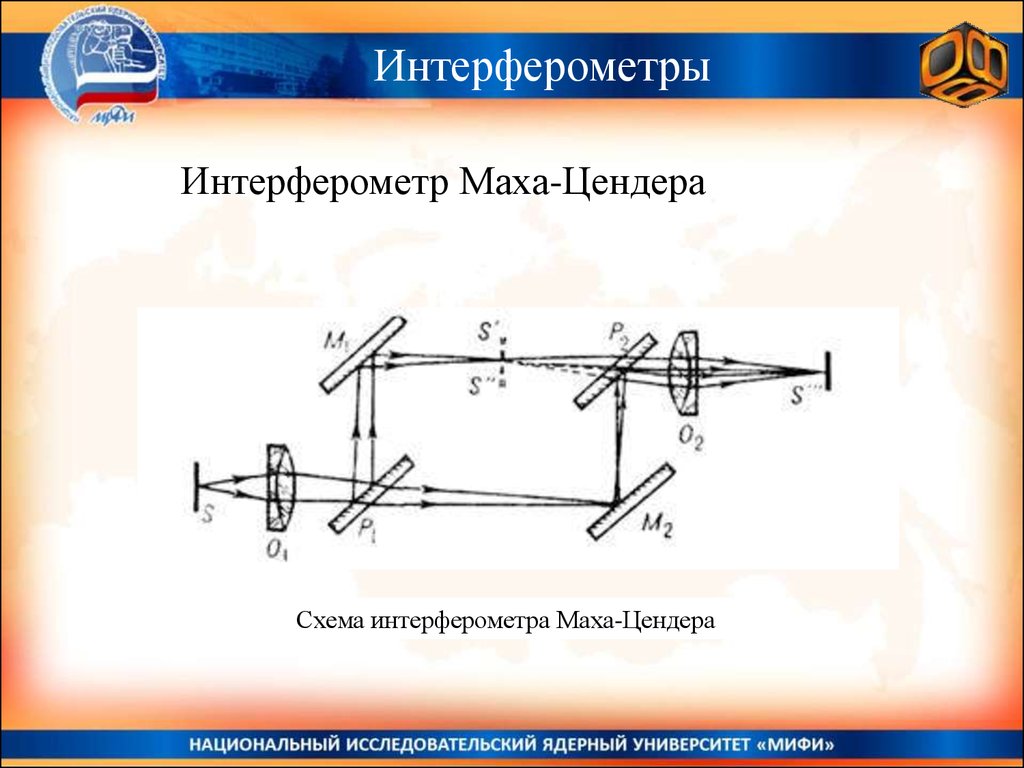




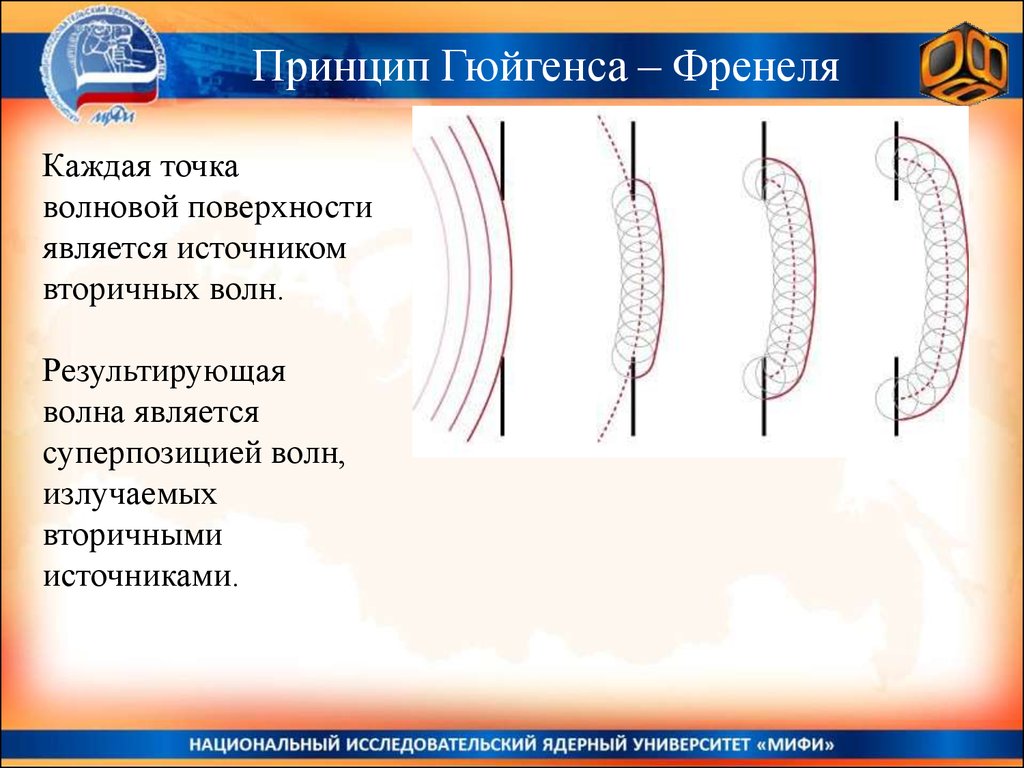
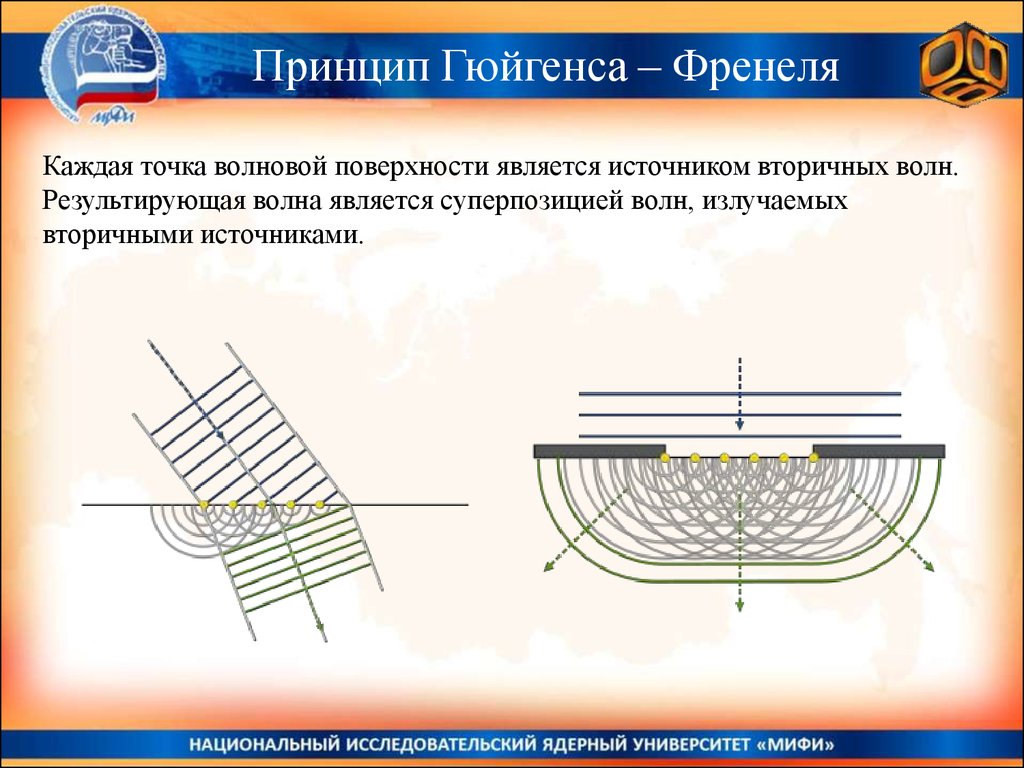

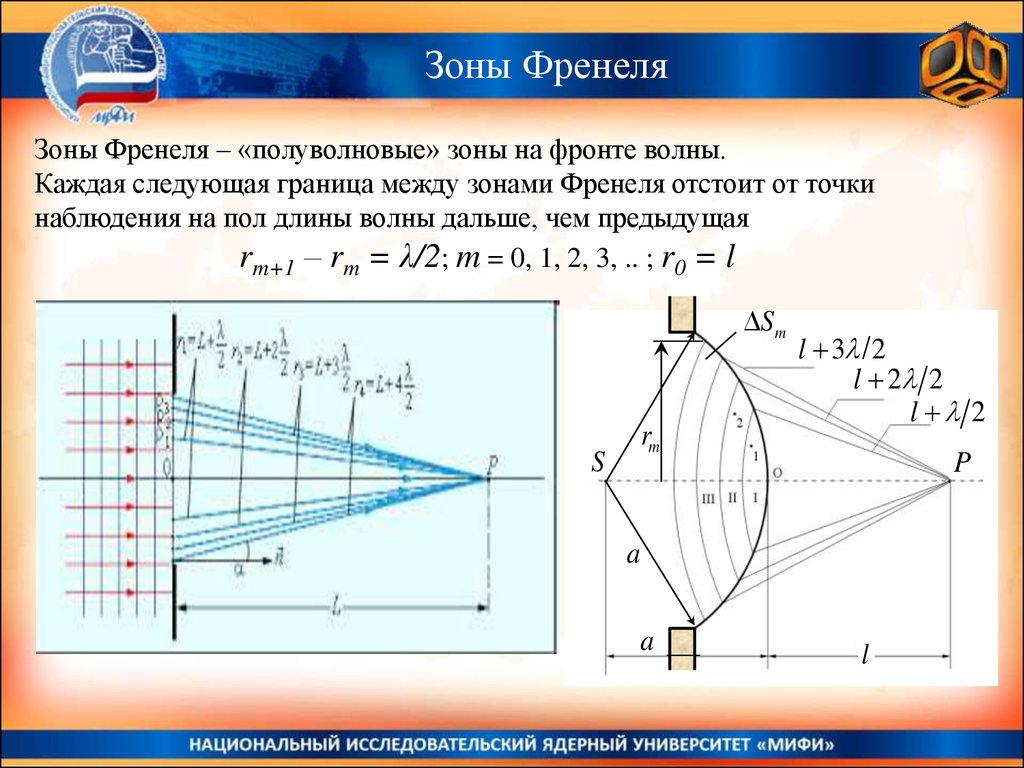








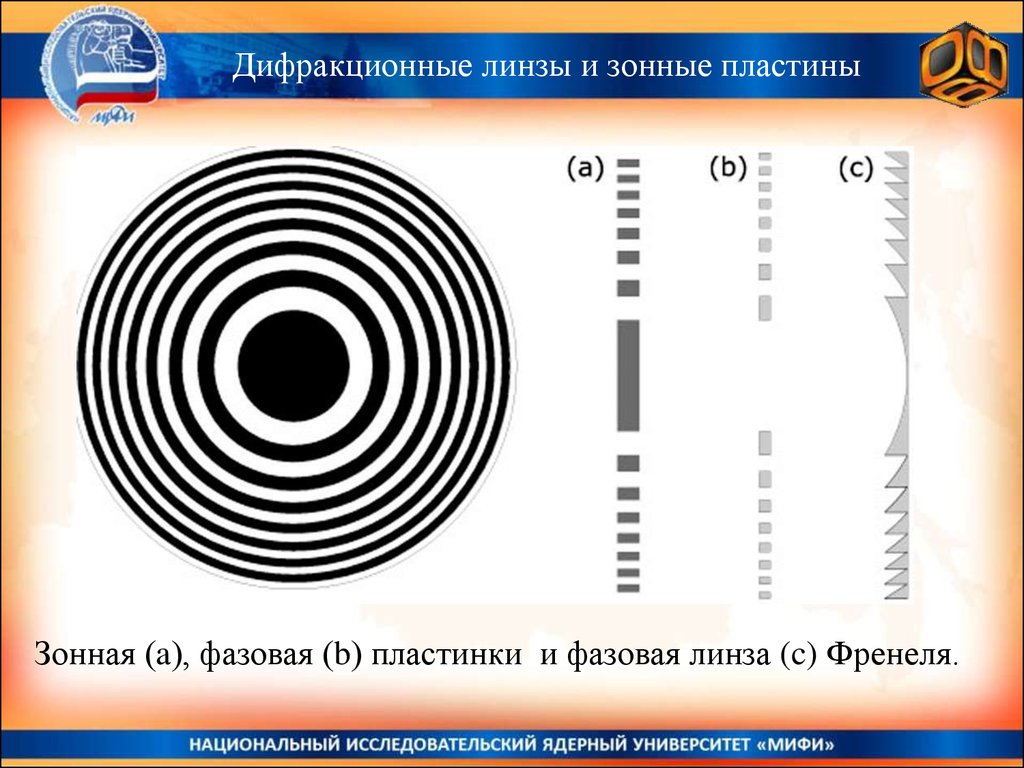

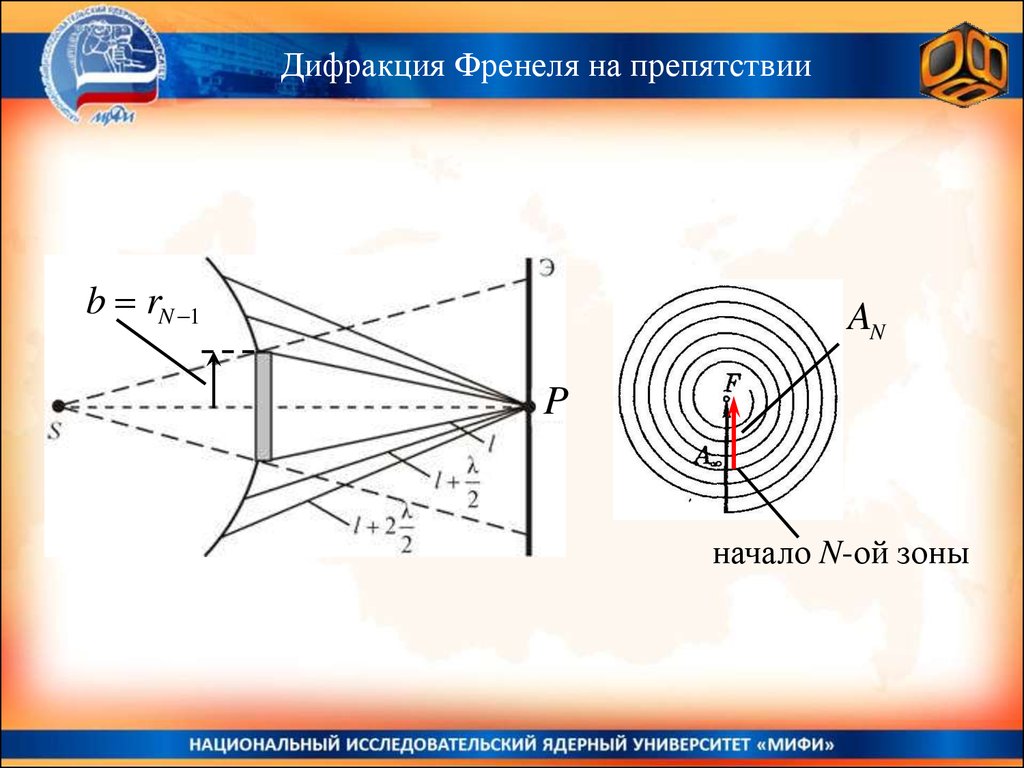






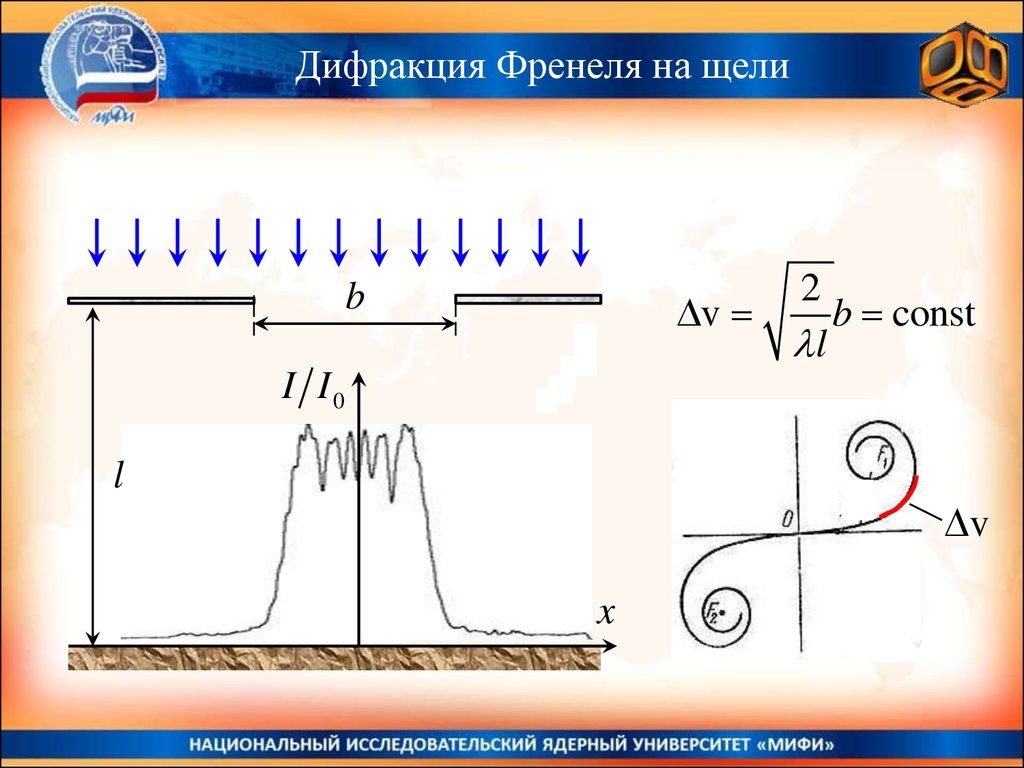
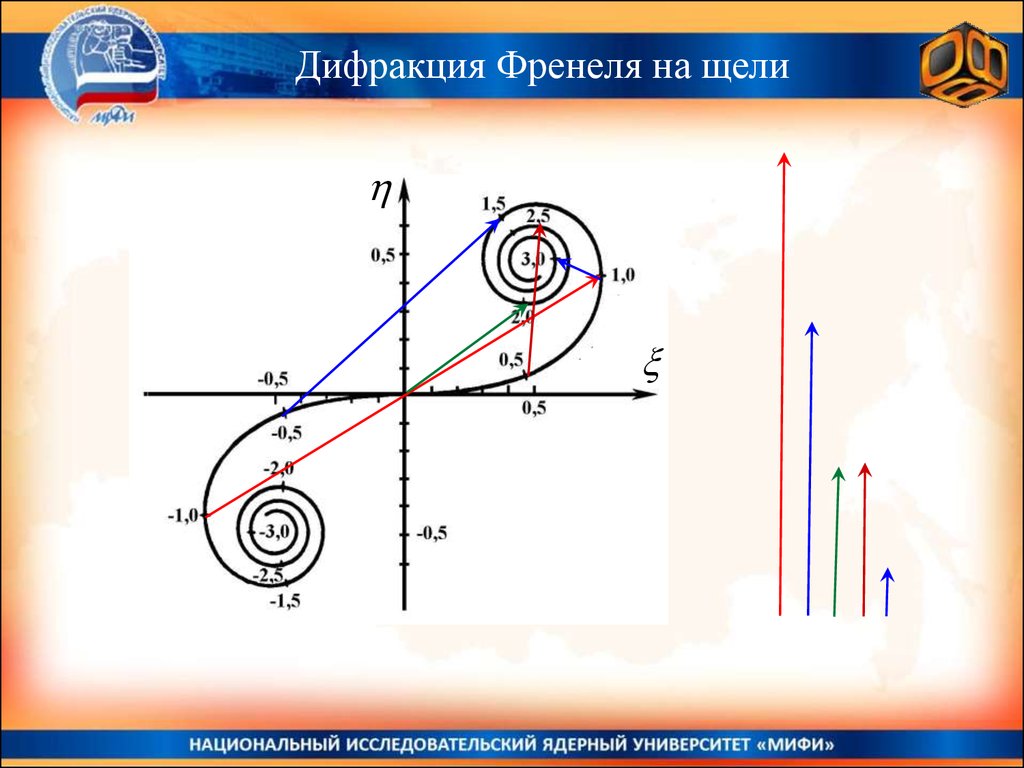
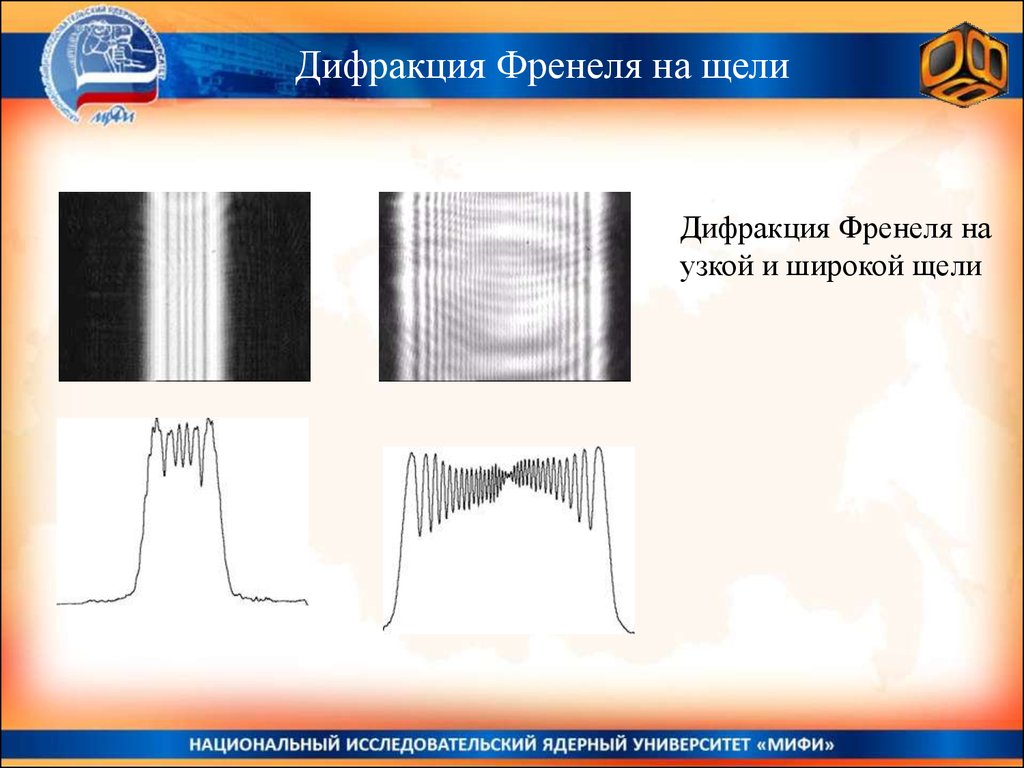
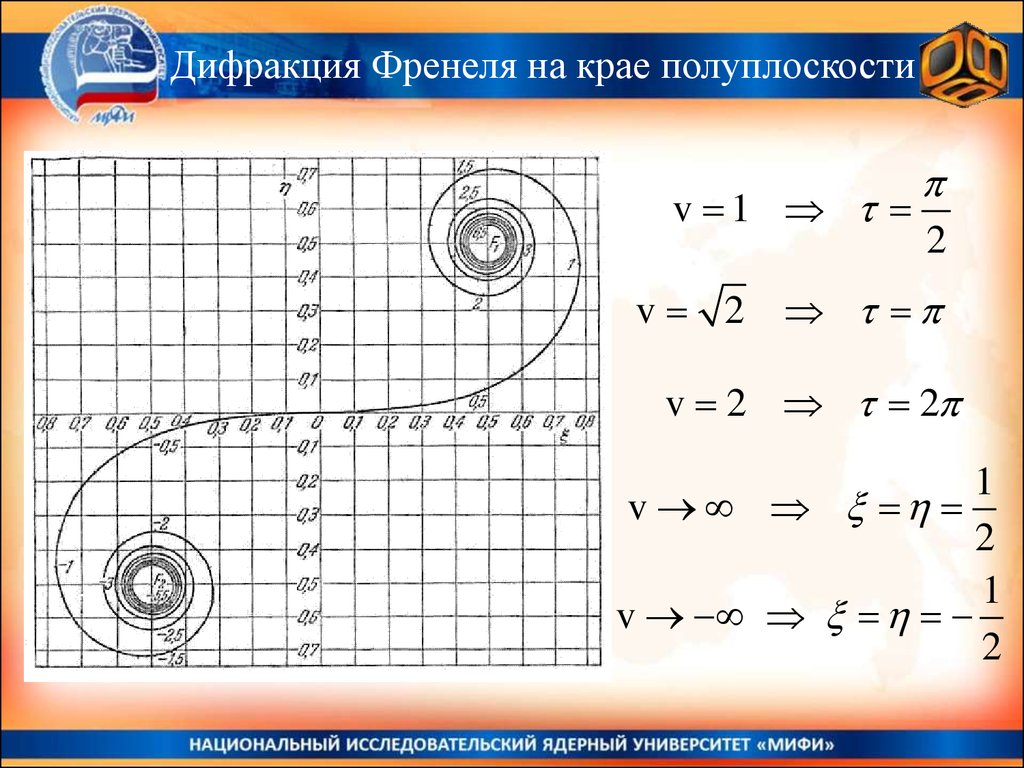










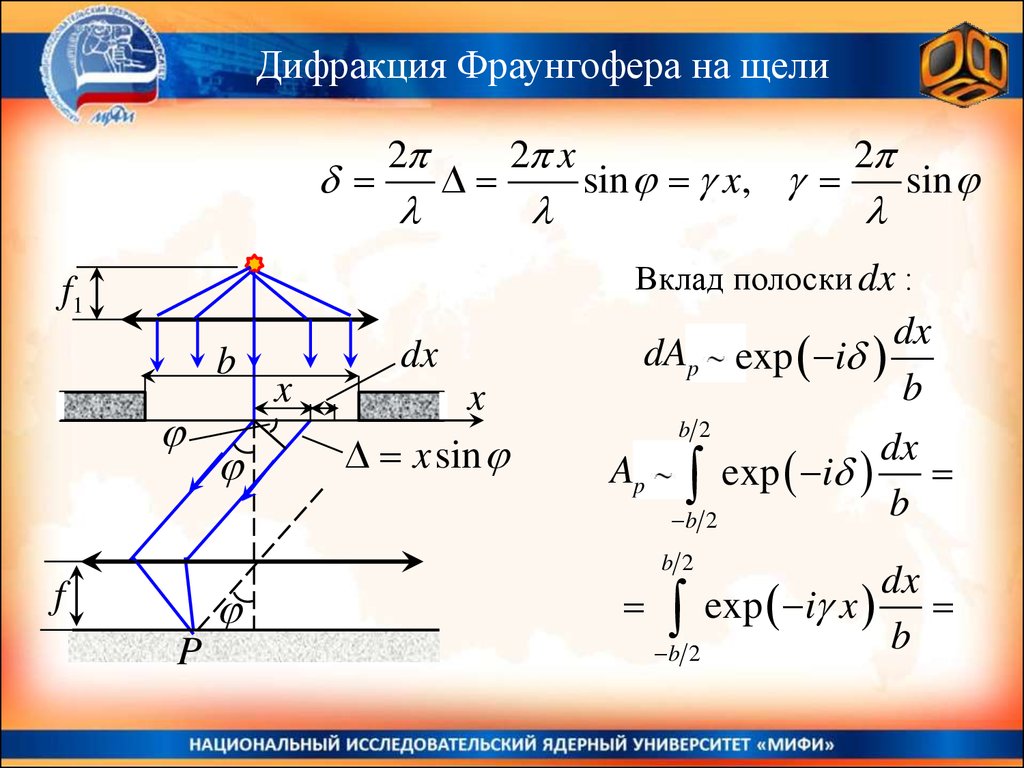

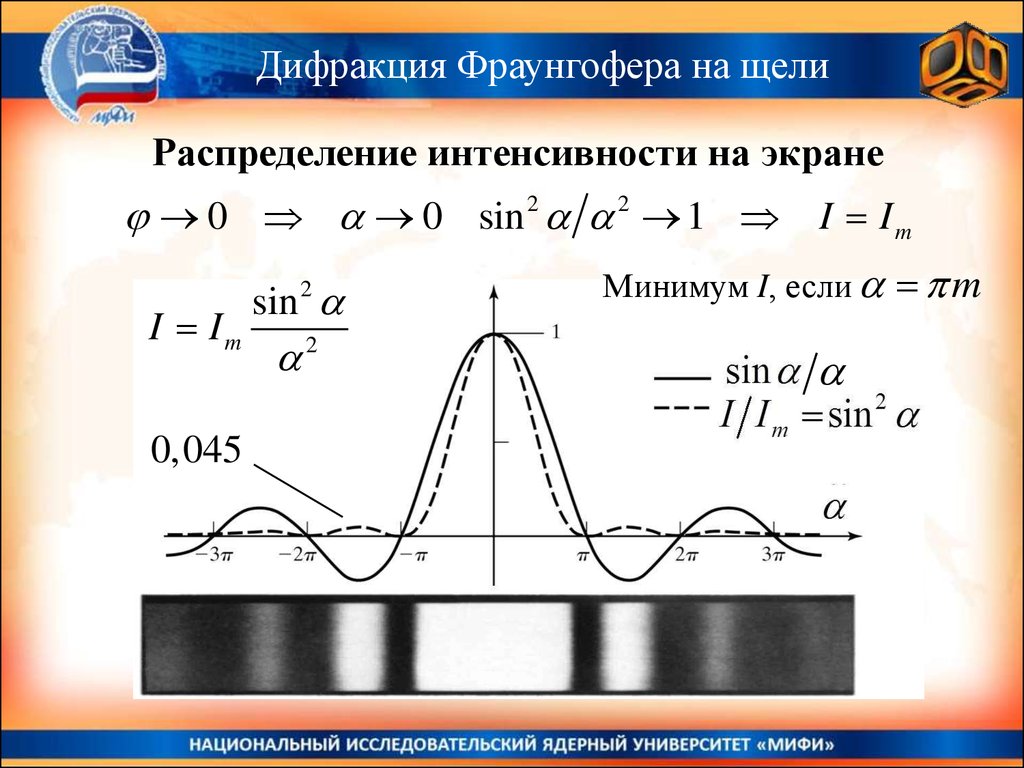

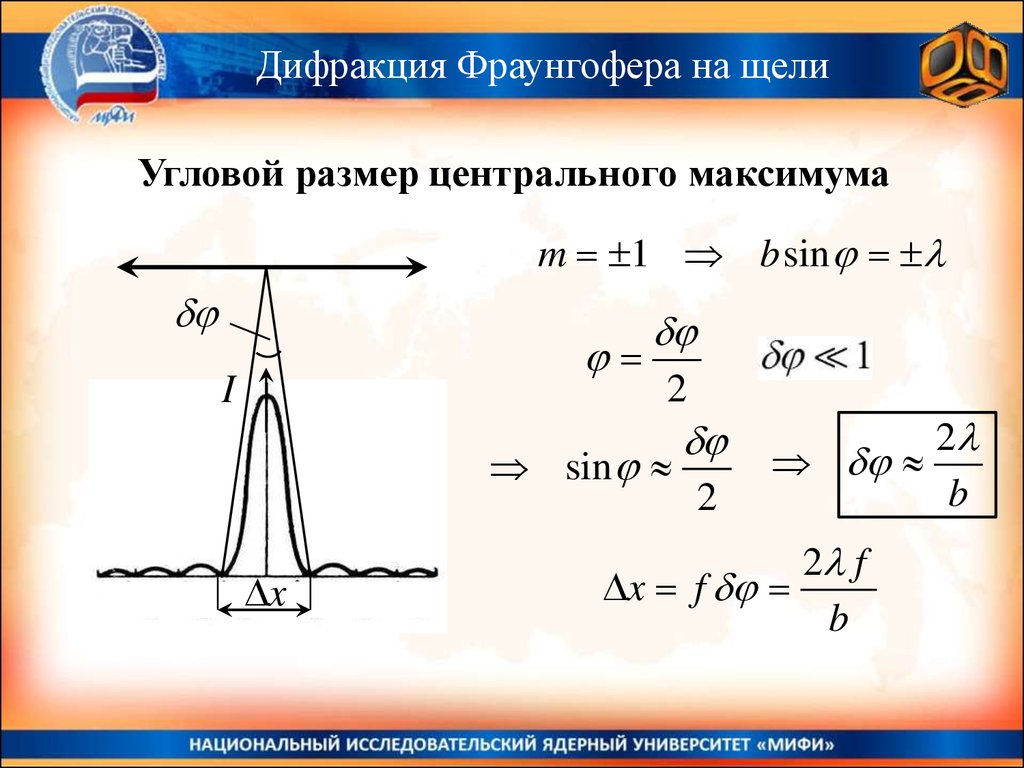
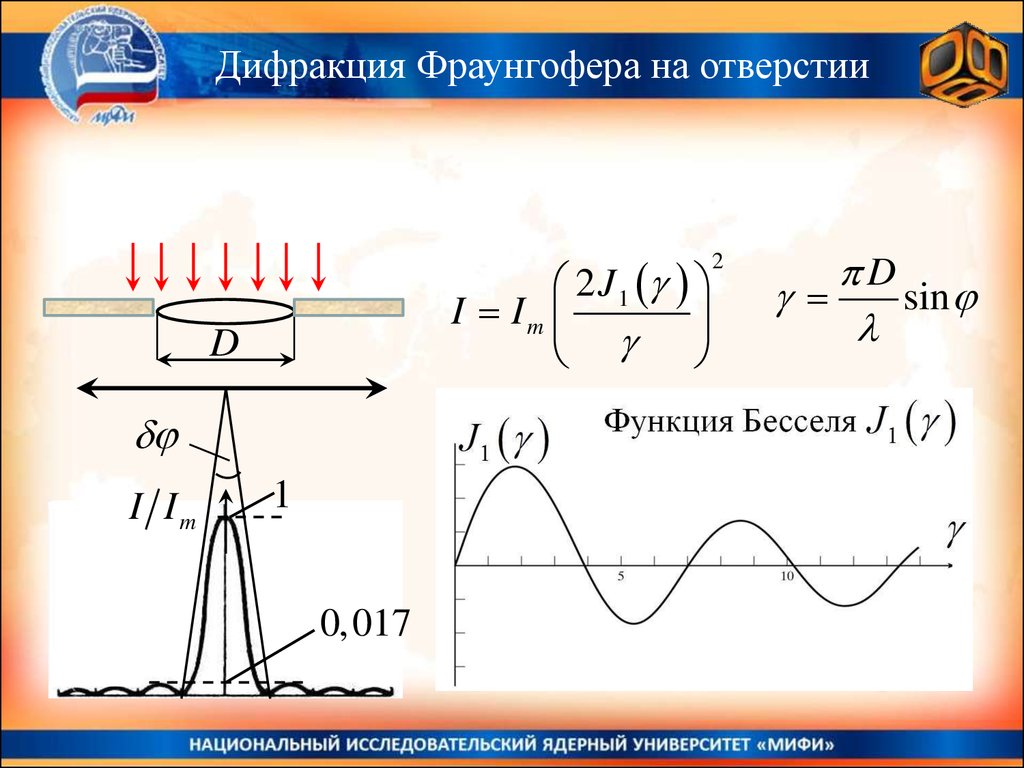



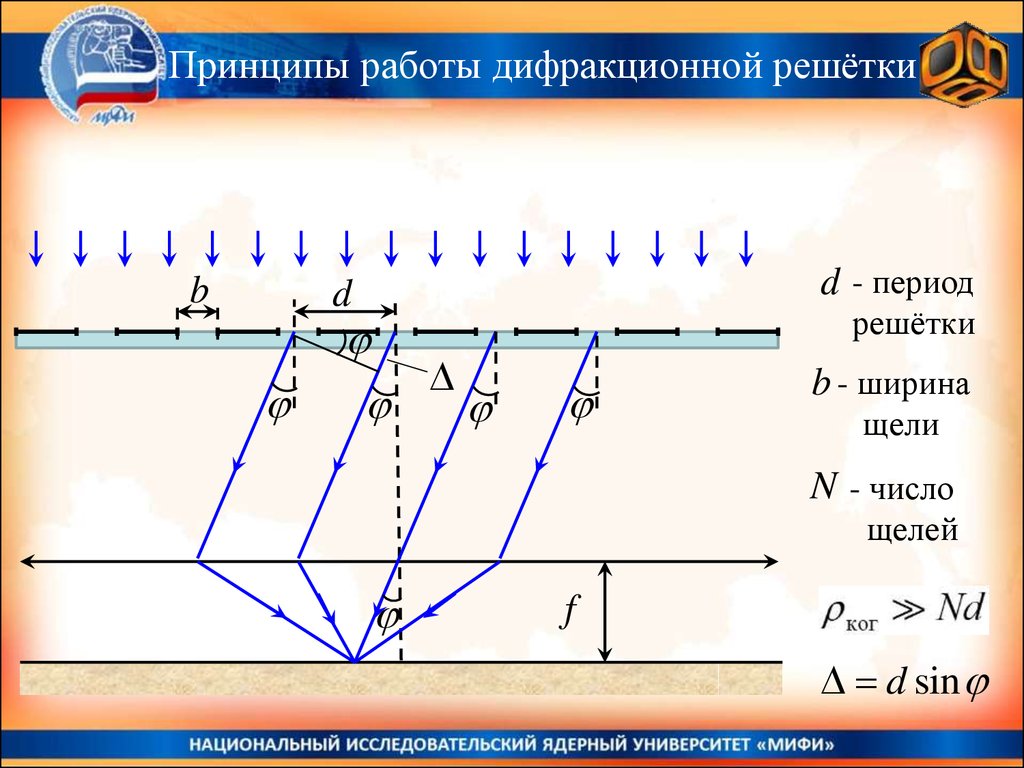





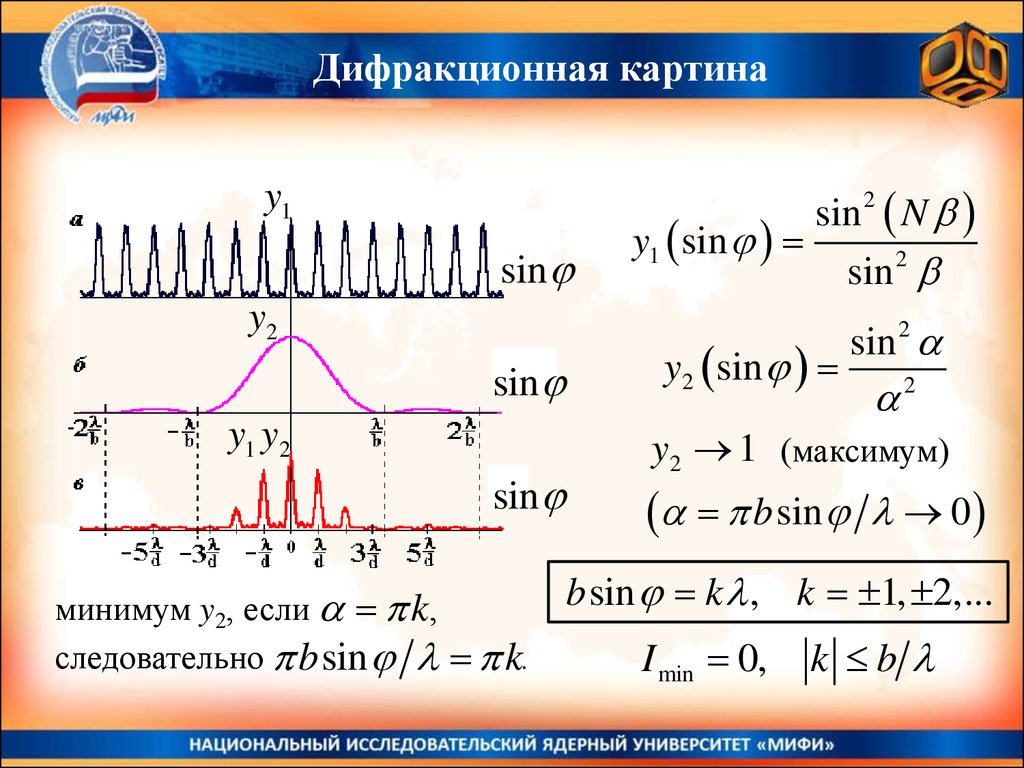

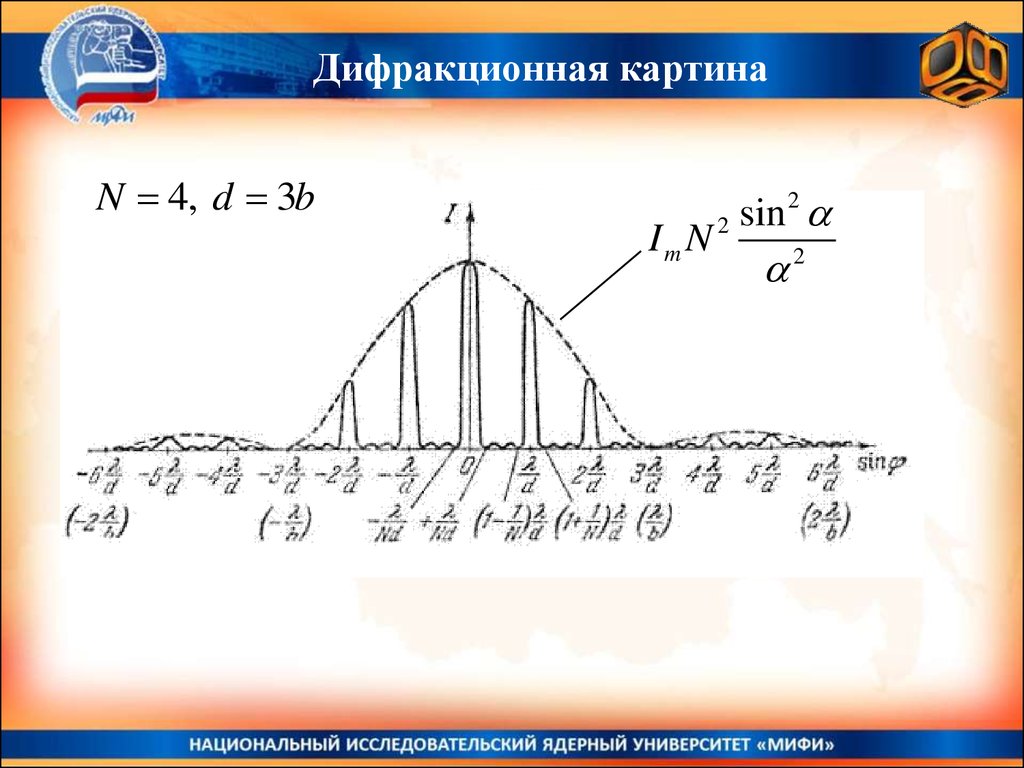






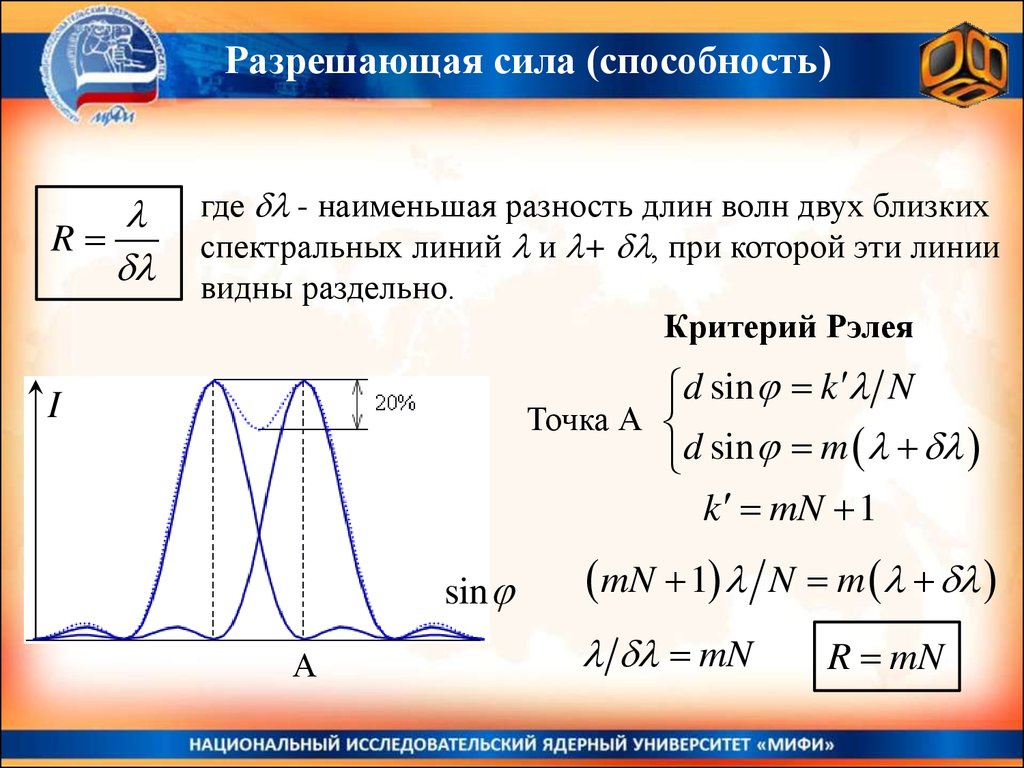

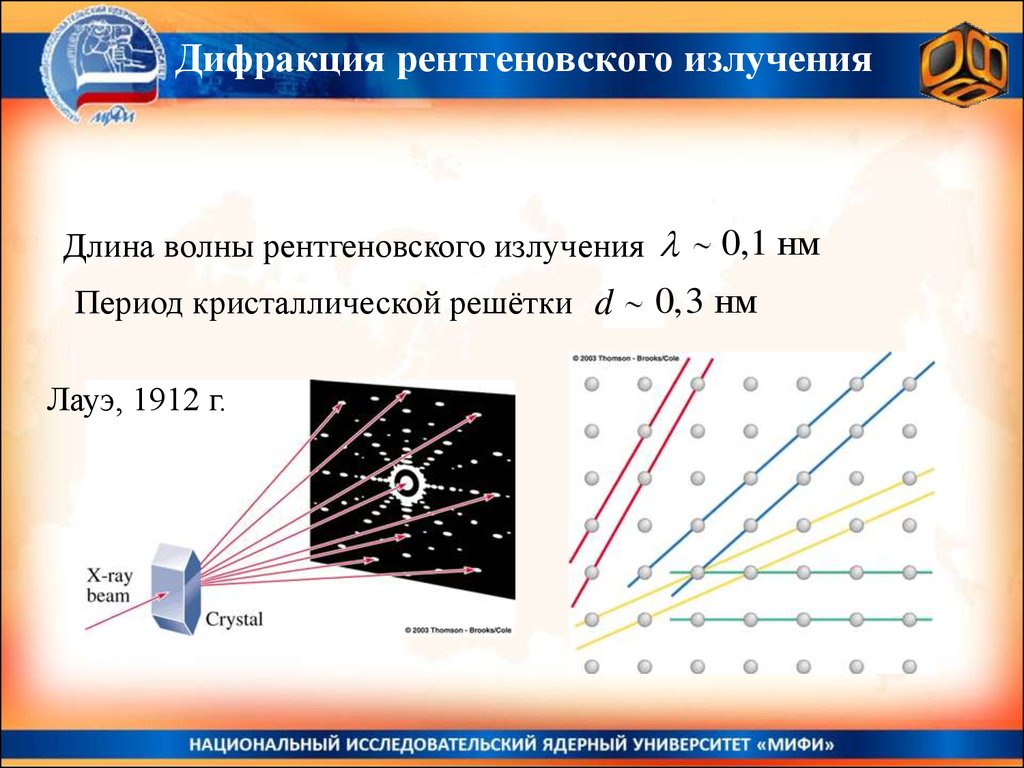
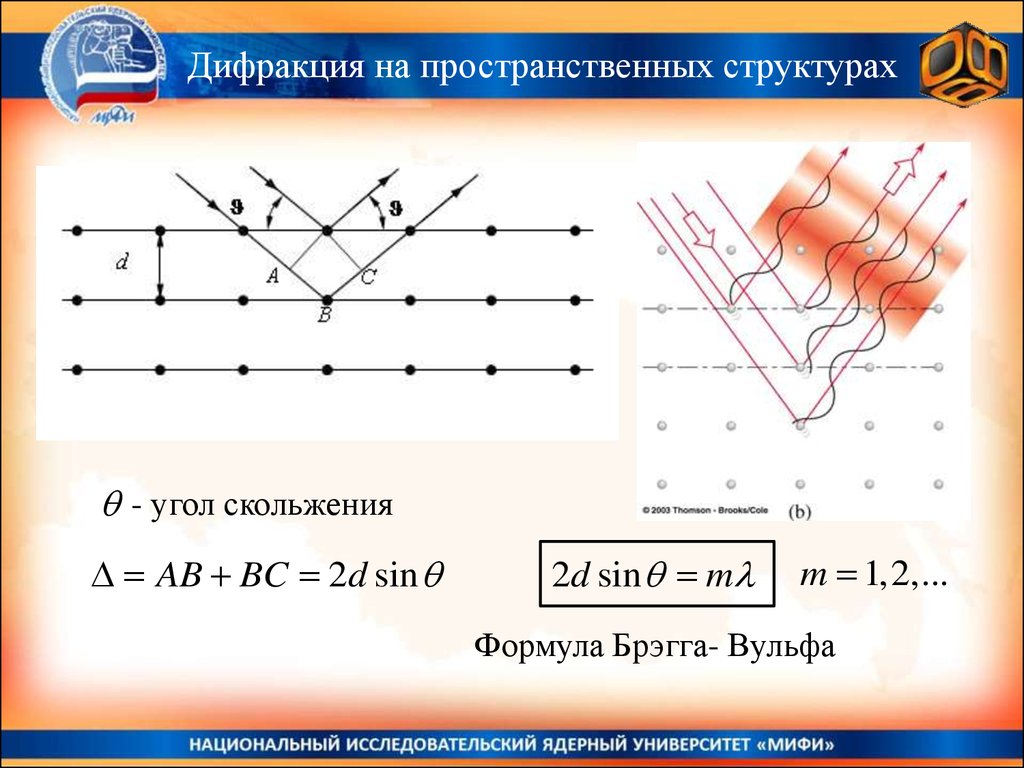


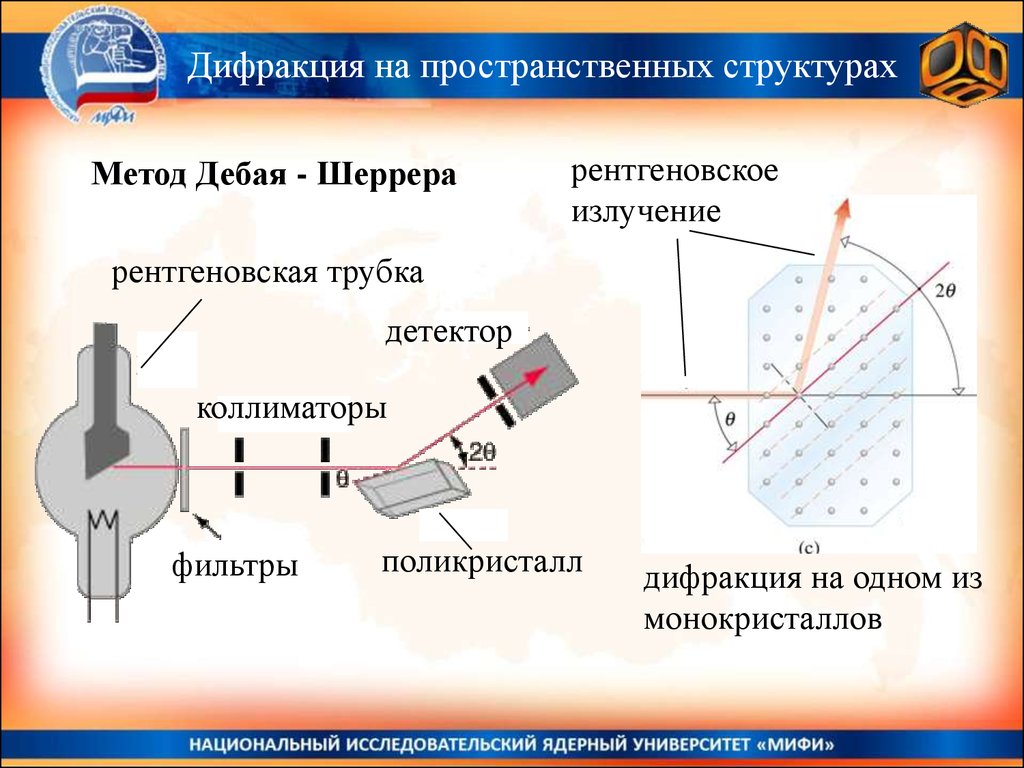









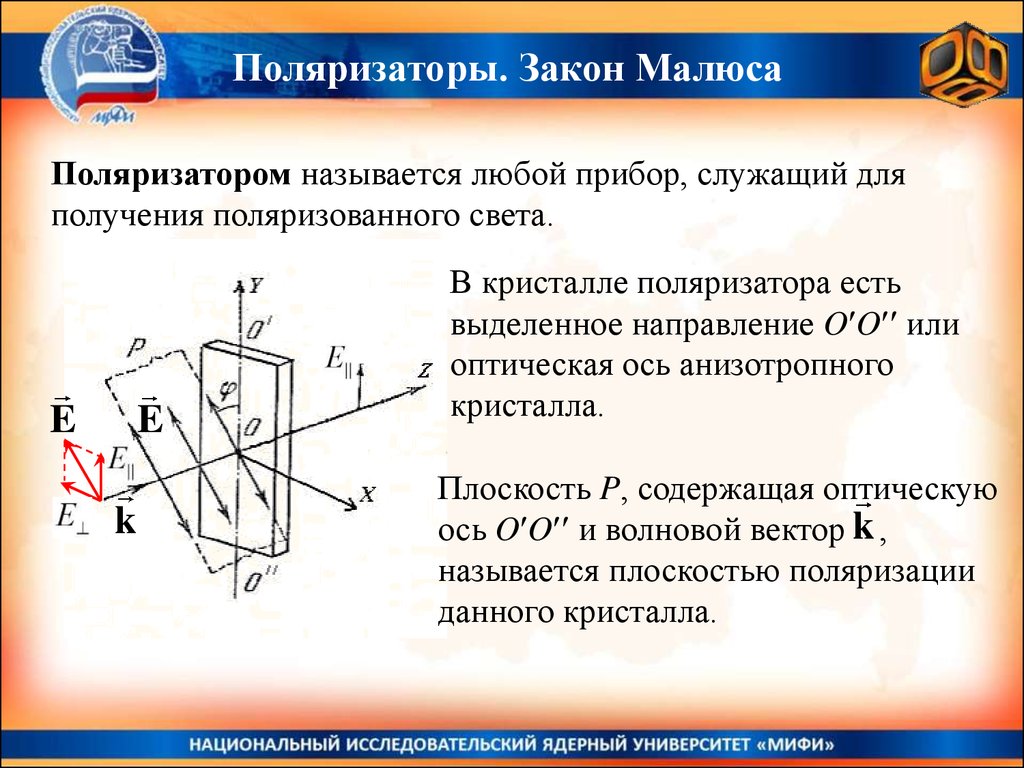
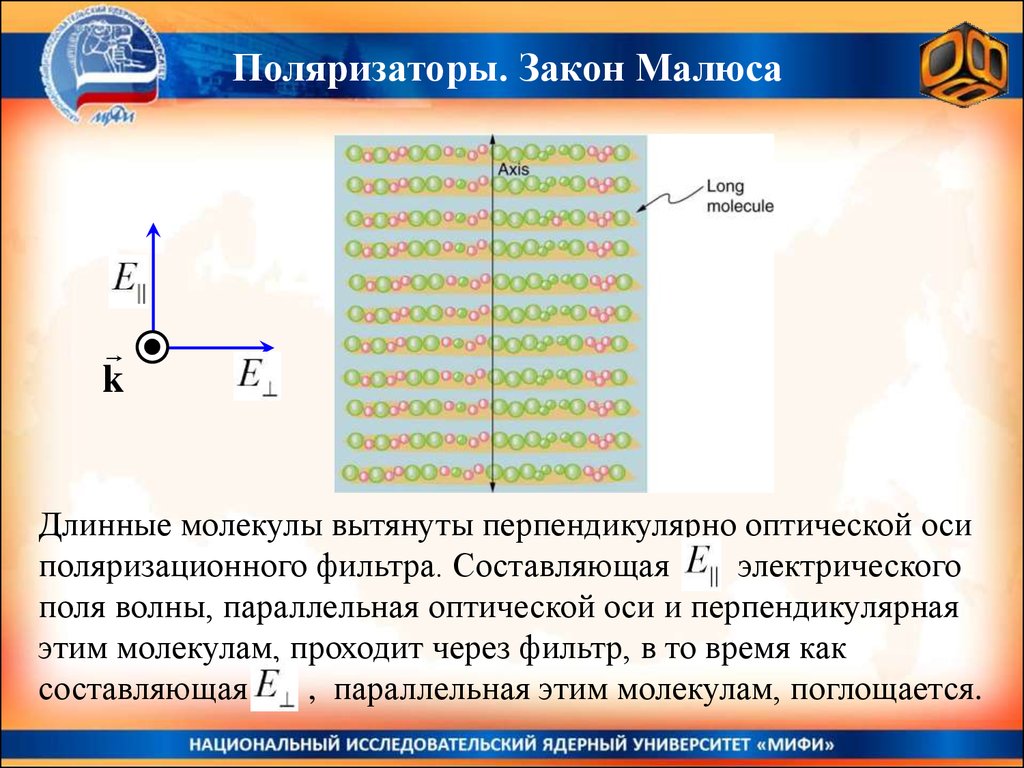


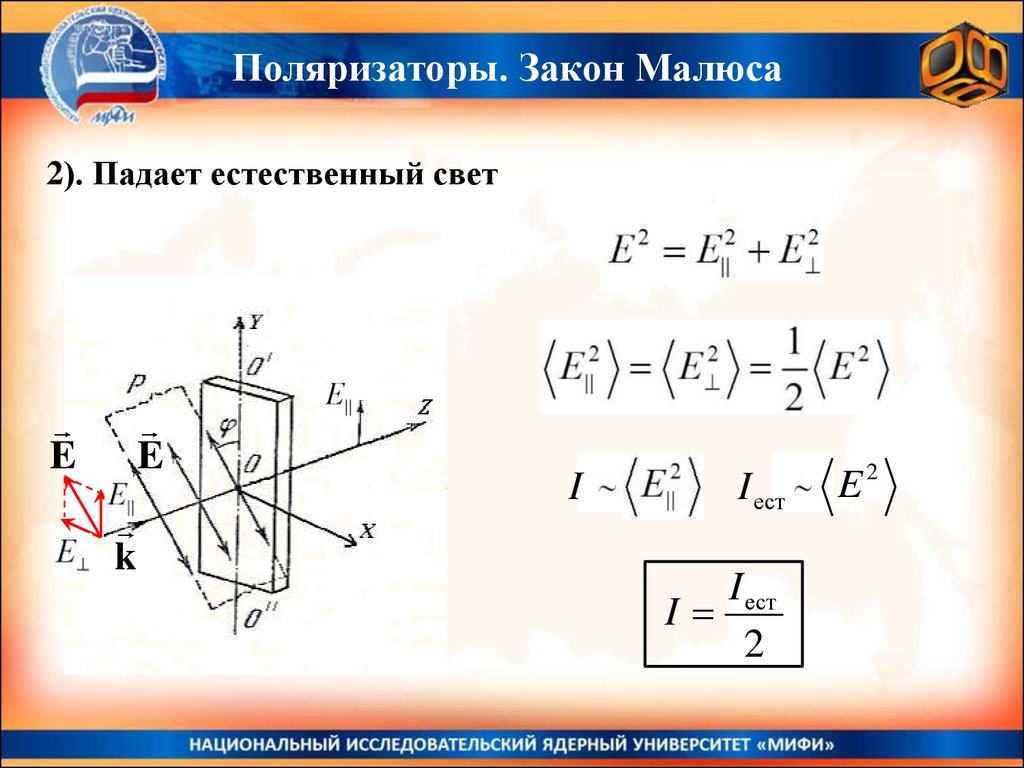
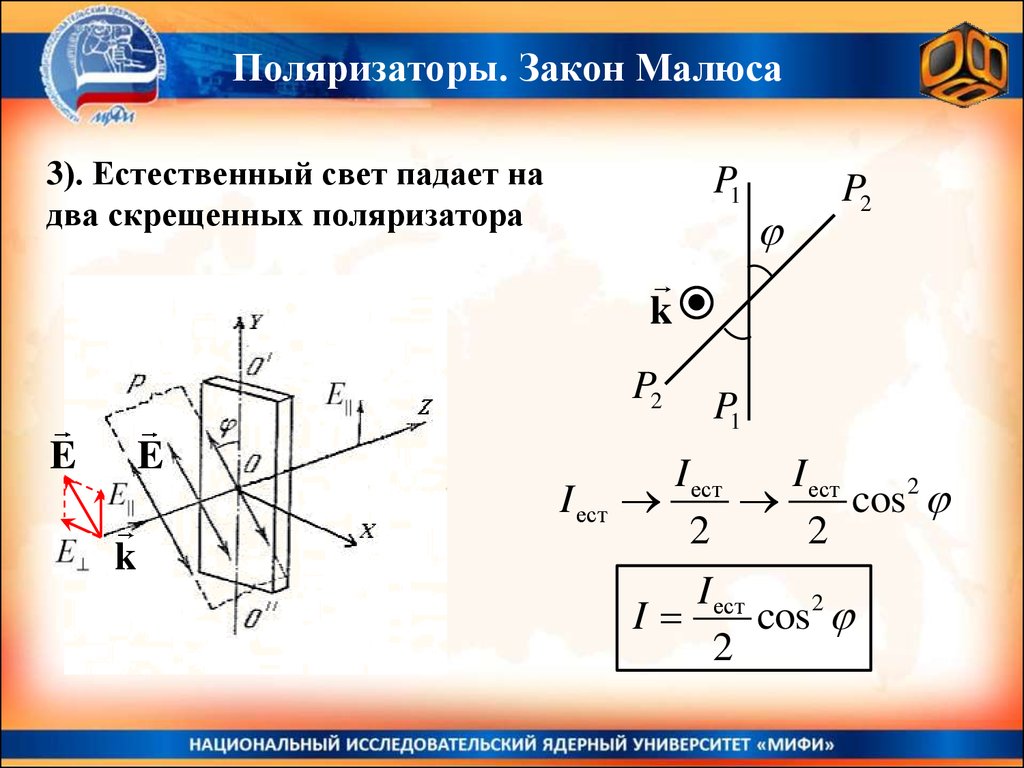
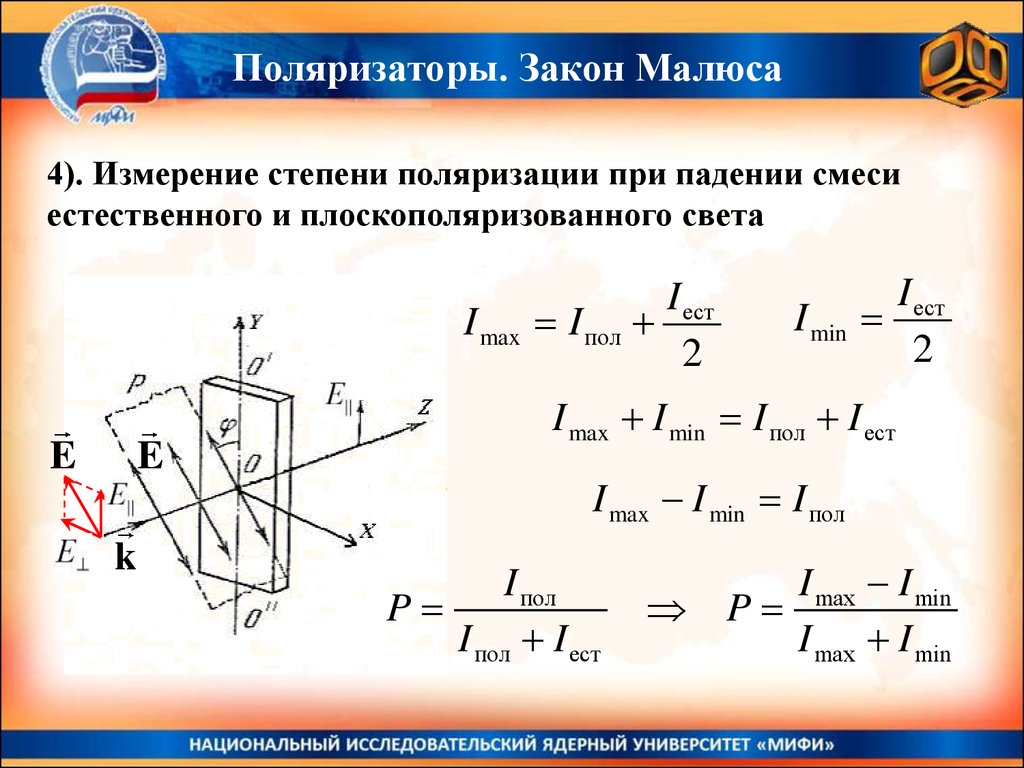
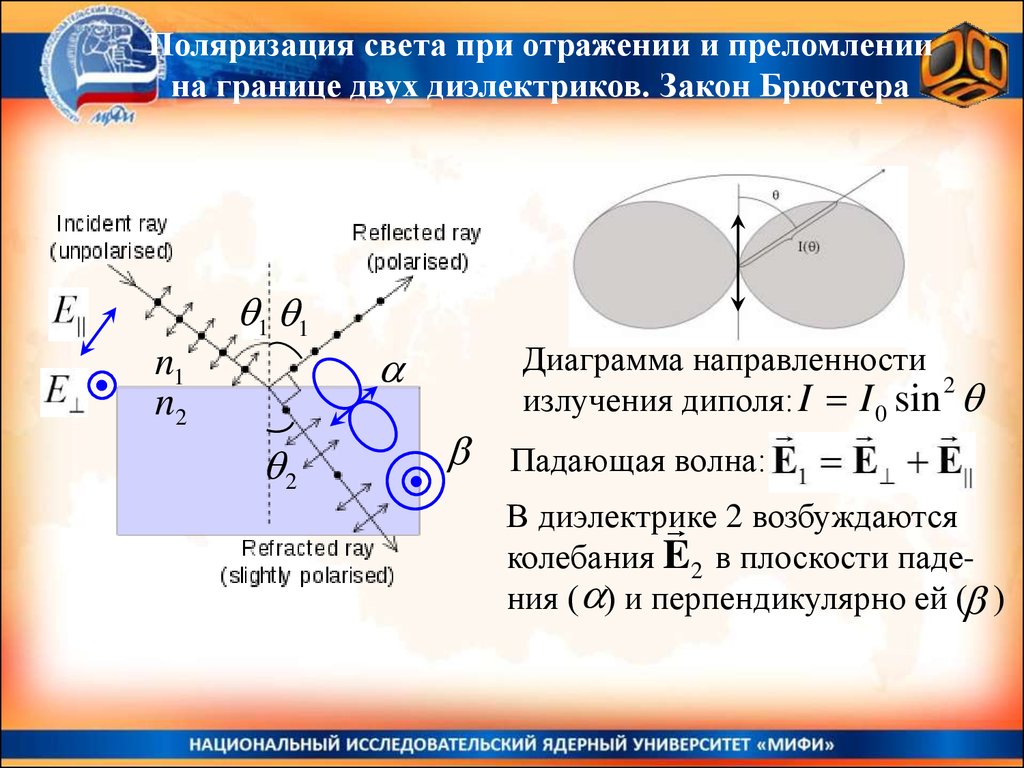


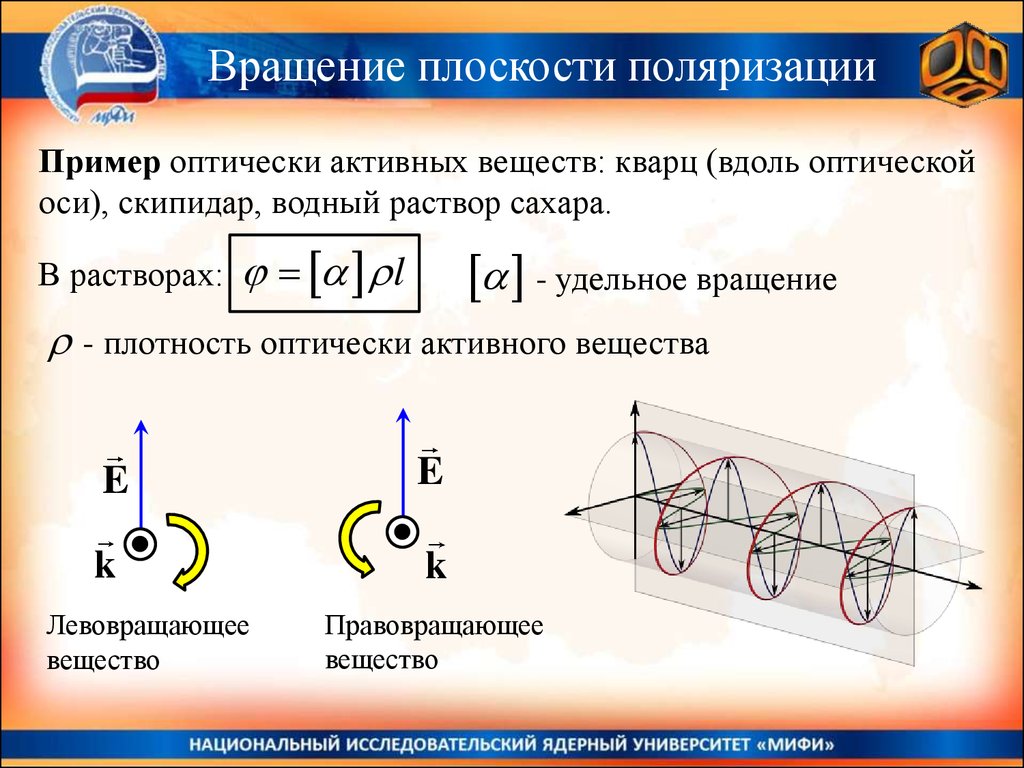

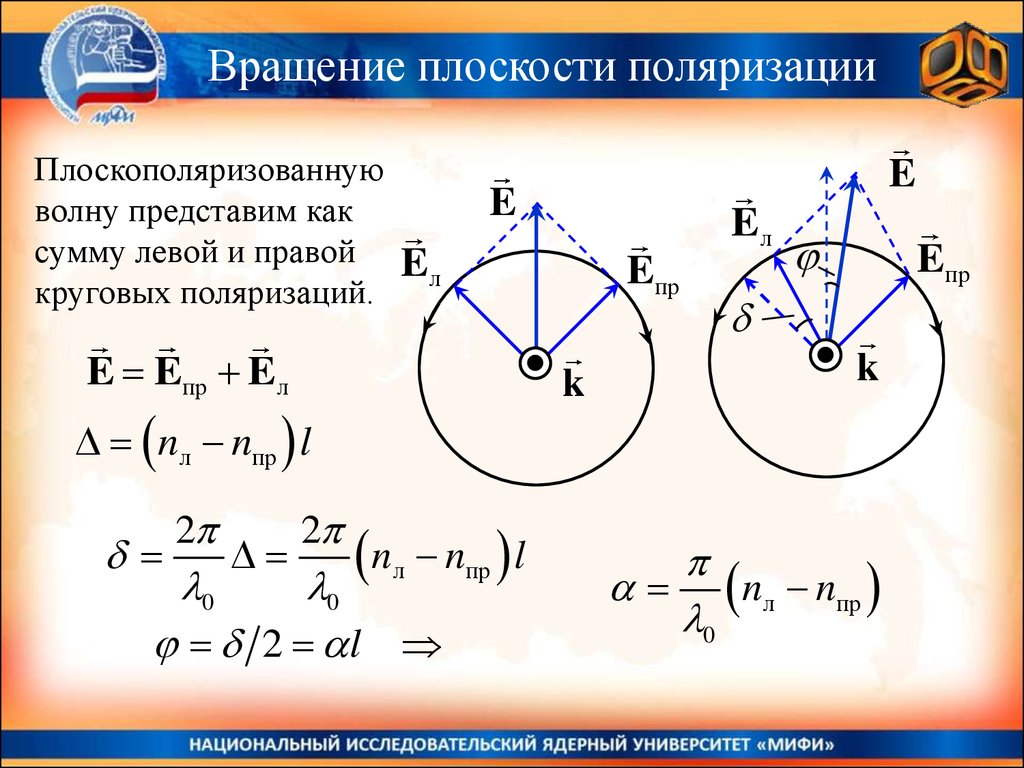
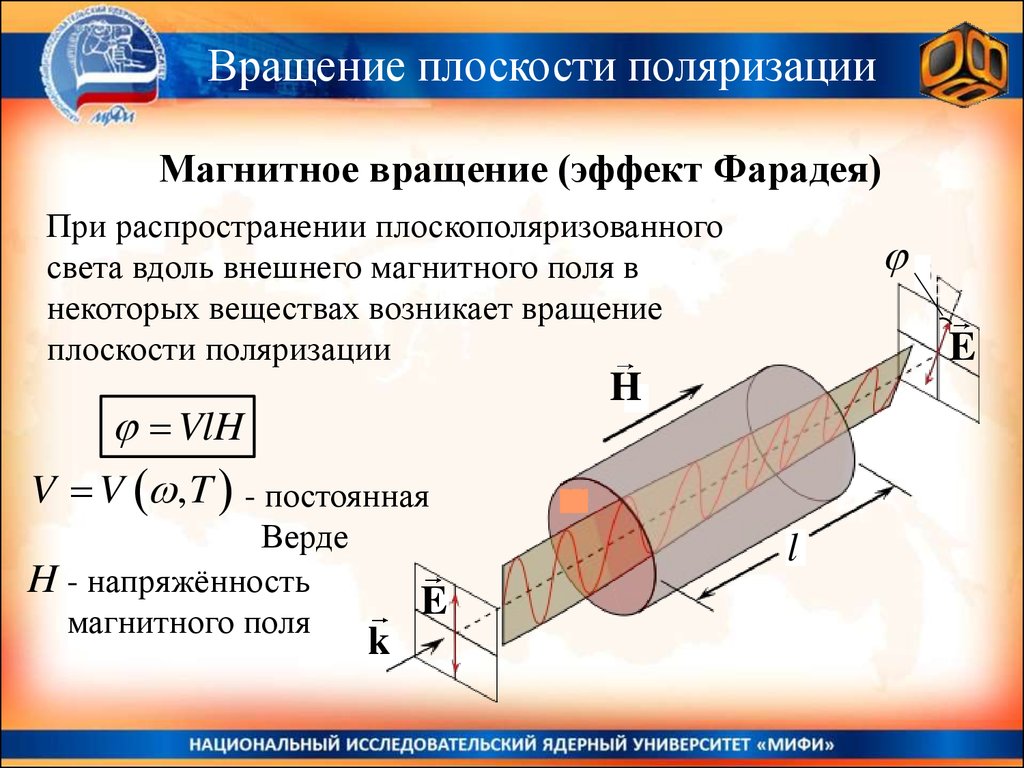

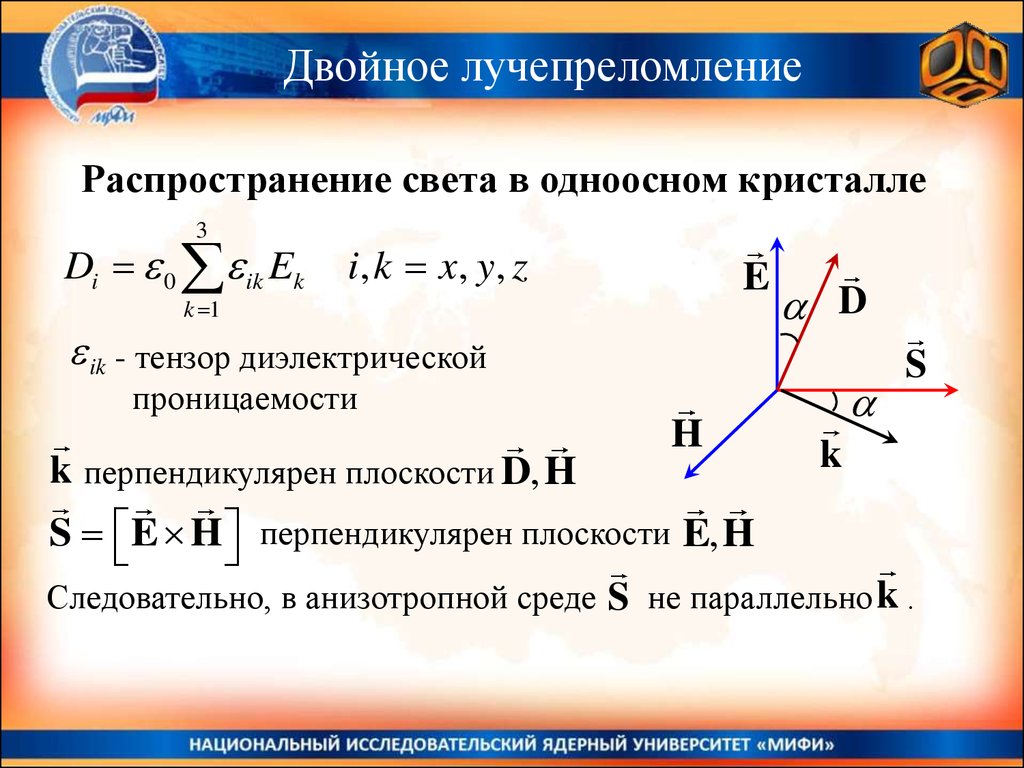





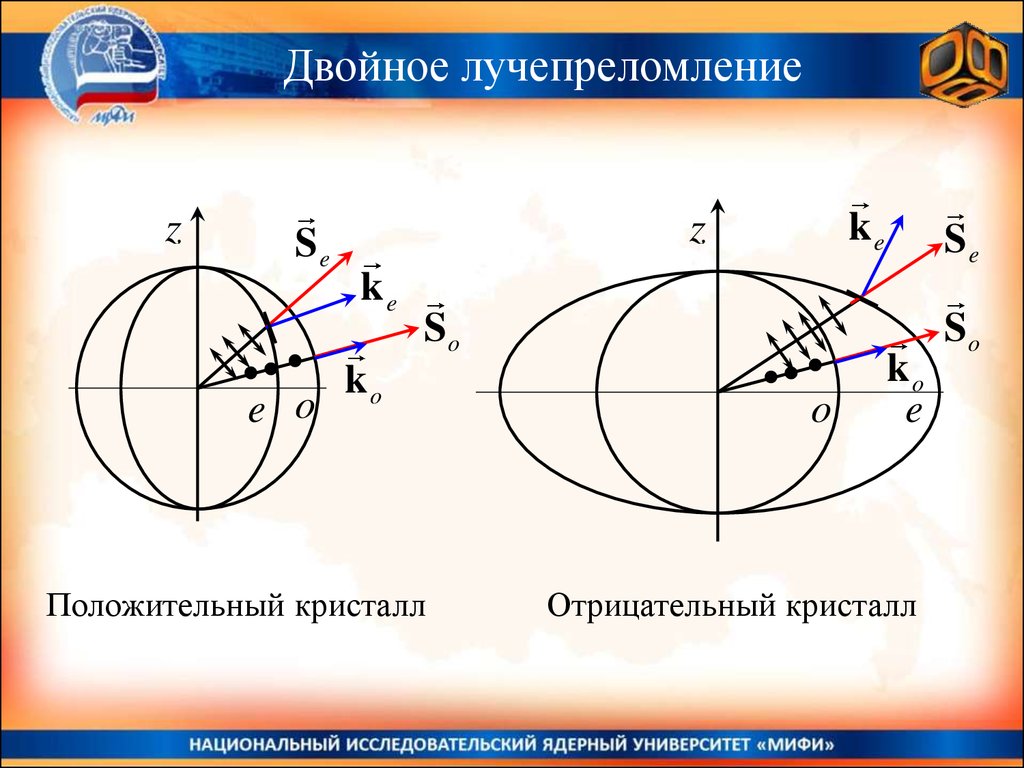

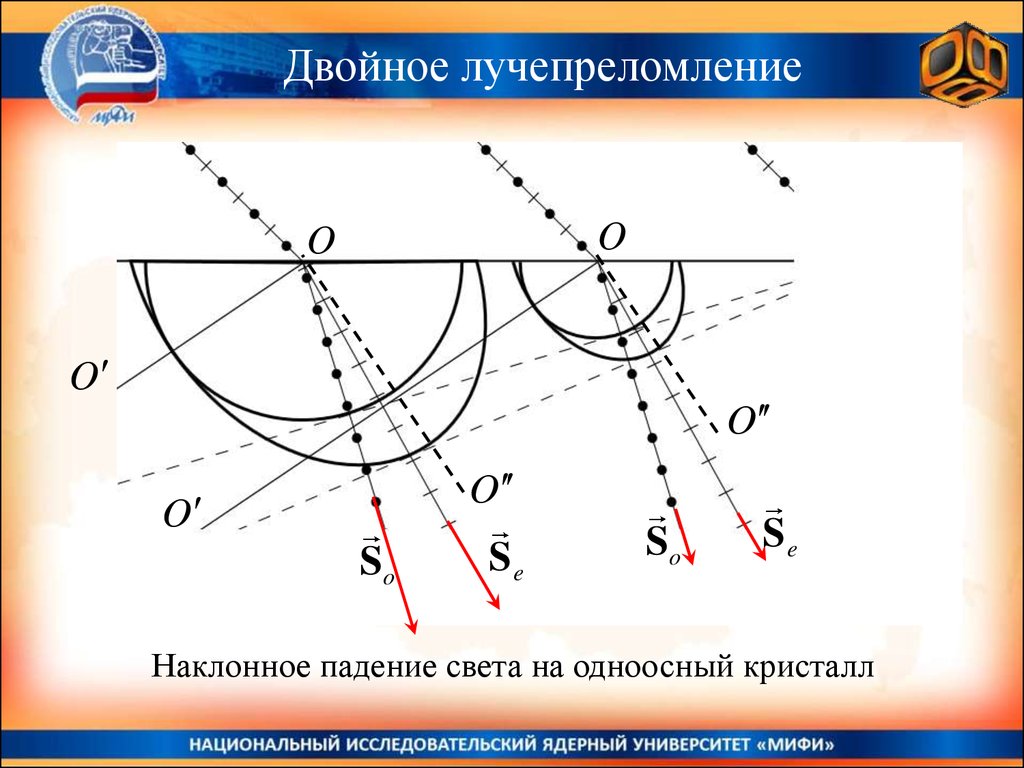









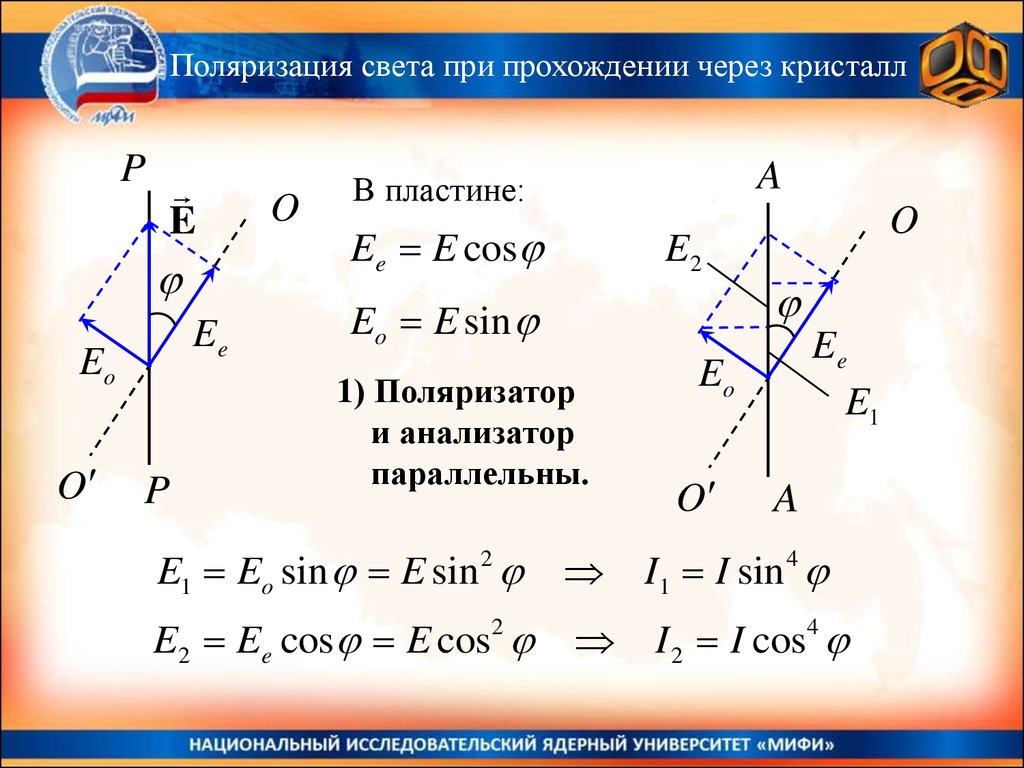


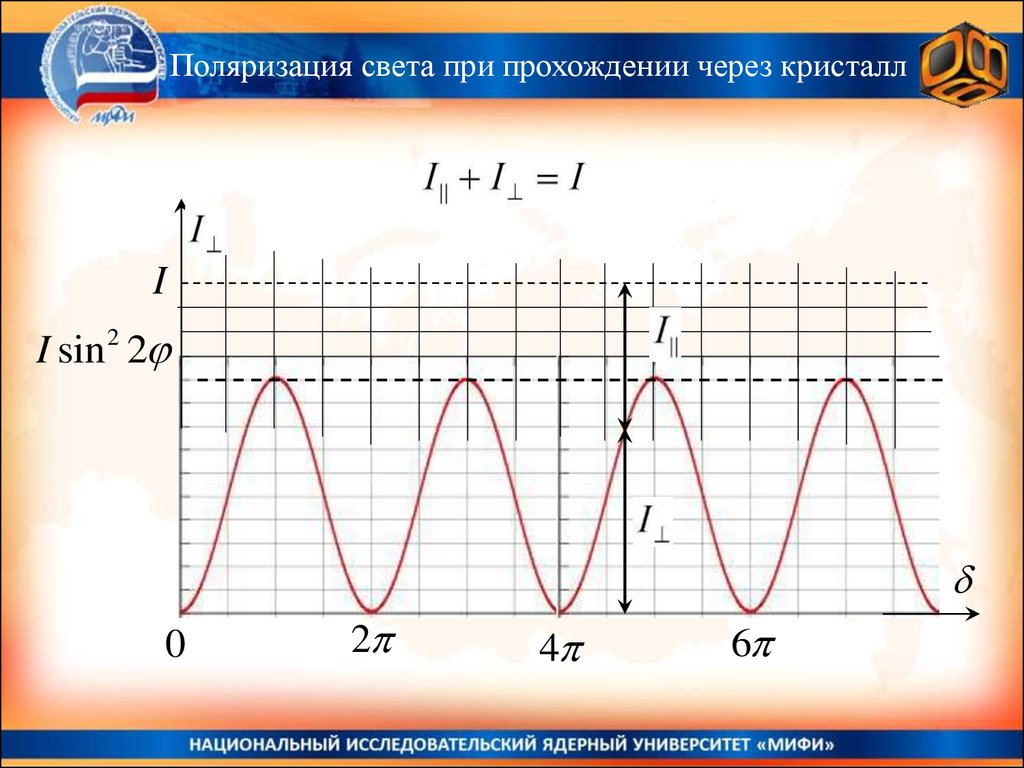


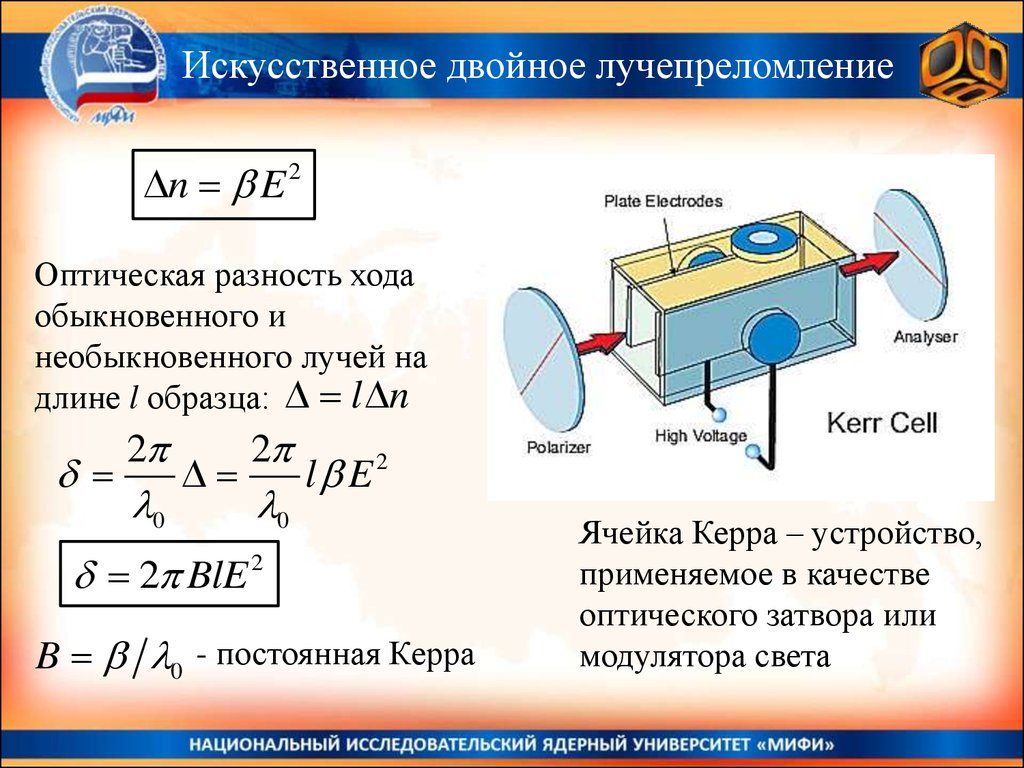





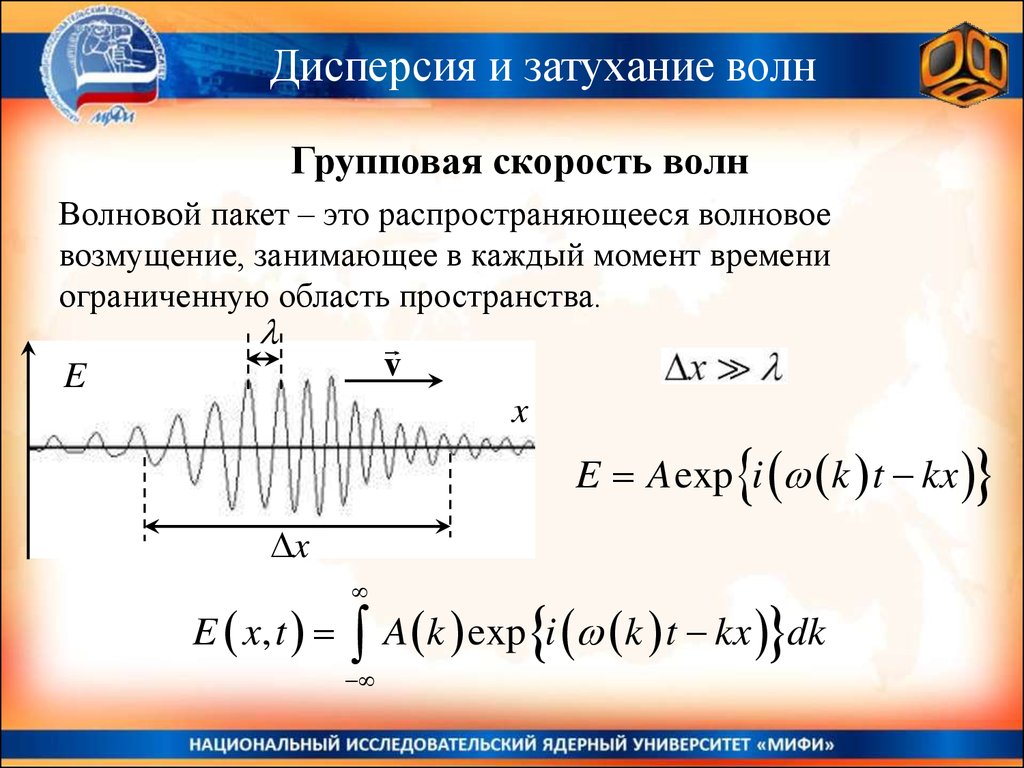












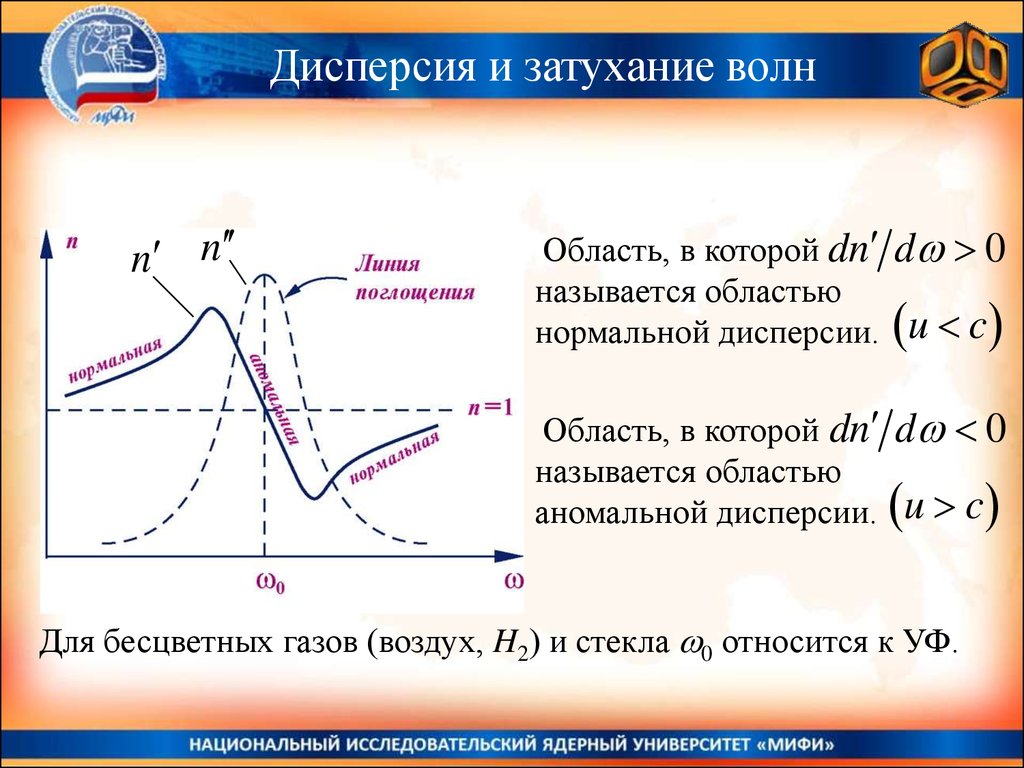
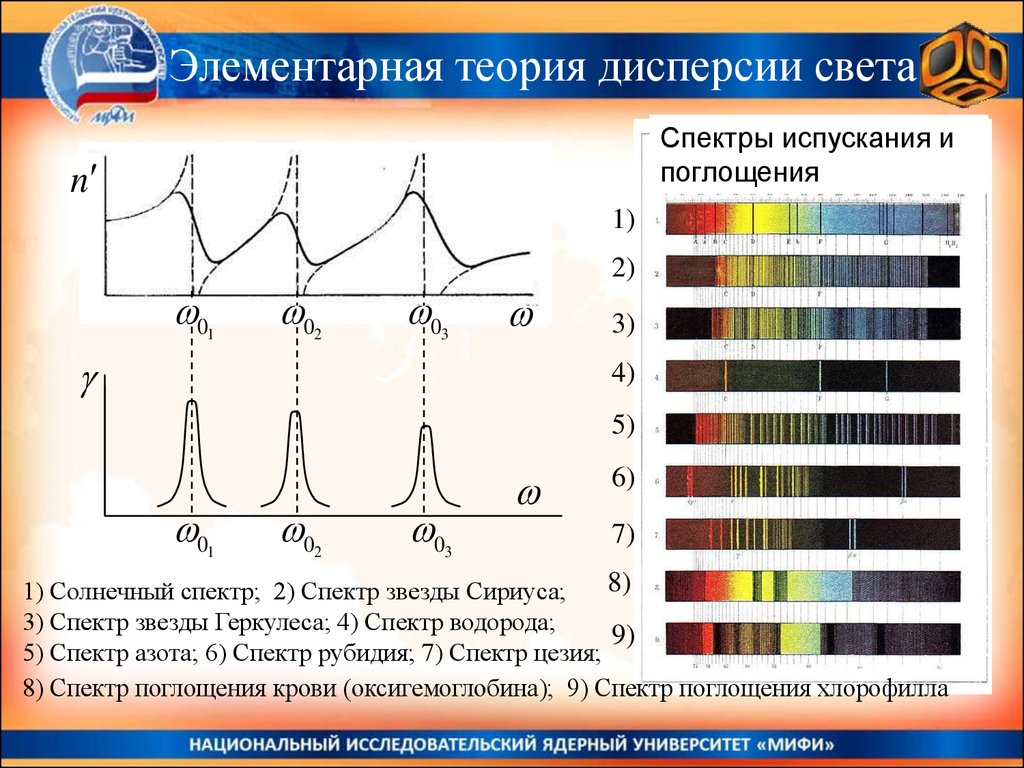












 physics
physics








