Лекция 2: Волновая оптика. Основные понятия. Интерференция. Когерентность

1. Лекция 2: Волновая оптика Основные понятия Интерференция Когерентность

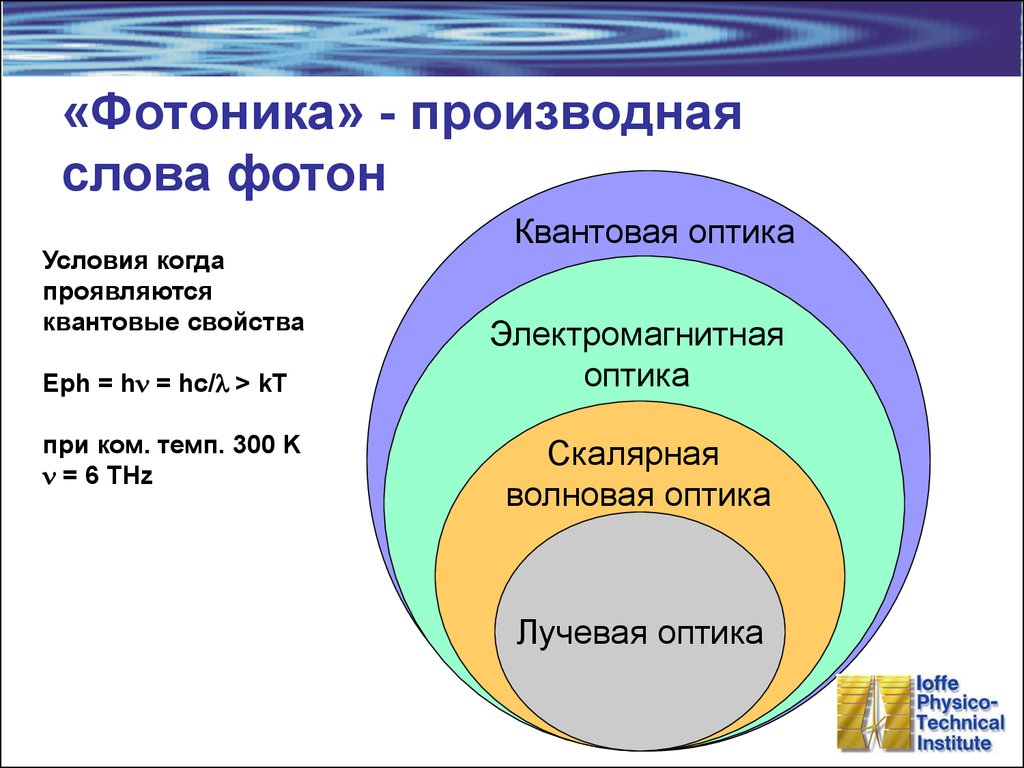
2. «Фотоника» - производная слова фотон

Условия когда
проявляются
квантовые свойства
Eph = hn = hc/l > kT
при ком. темп. 300 K
n = 6 THz
Квантовая оптика
Электромагнитная
оптика
Скалярная
волновая оптика
Лучевая оптика

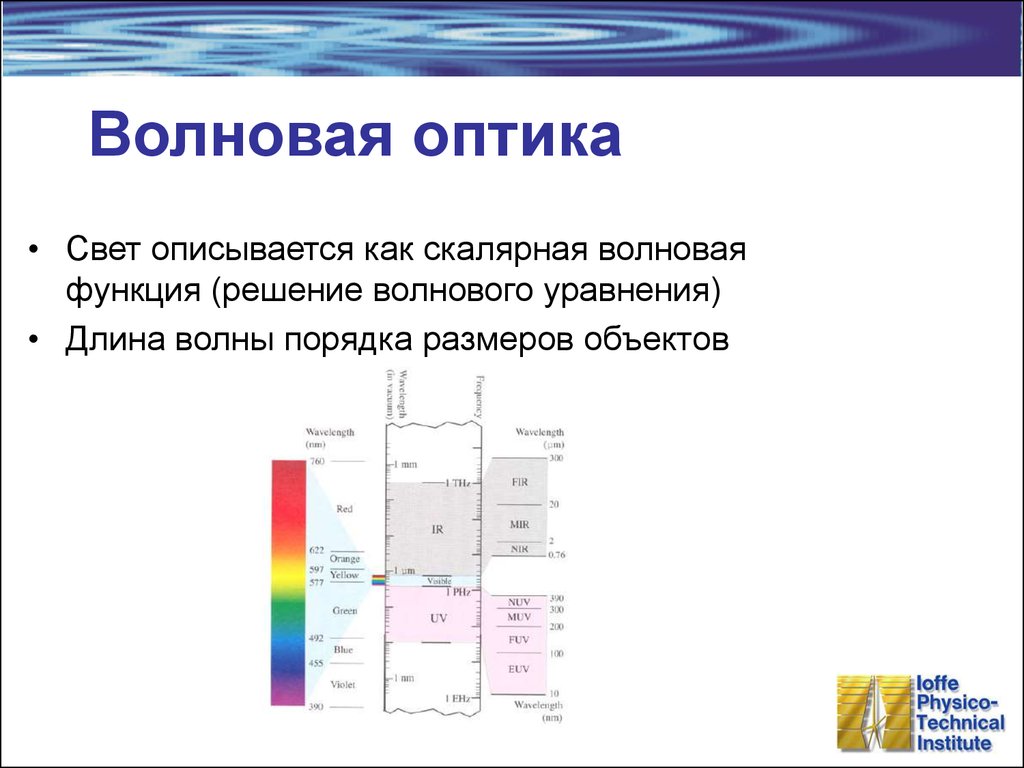
3. Волновая оптика

• Свет описывается как скалярная волновая
функция (решение волнового уравнения)
• Длина волны порядка размеров объектов

4. Постулаты волновой оптики

Свет распространяется в виде волны со скоростью с= c0/n
Амплитуда волны в любой точке пространства r(x,y,z) описывается
волновой функцией u(r,t)
1 2u
2
u 2 2 0
c t
Интенсивность – усредненный по времени квадрат амплитуды
I (r , t ) ~ u 2 r , t ; W m 2
Оптическая мощность – интеграл от интенсивности по площади
P t ~ I (r , t )dA
A
Из линейности волнового уравнения вытекает принцип суперпозиции
u r , t u1 r , t u2 r , t ui r , t
Для определения волновой функции нужно знать граничные условия
Волновая оптика применима для неоднородных сред, с характерными размерами изменения
больше длины волны (локально однородные)
n r c r

5. Монохроматическая волна

u r, t a r cos 2 nt r ; 2 n
Комплексное представление U (r , t ) a r exp j r exp j t U r exp j t
u (r , t ) Re U (r , t )
Уравнение Гемгольца:
2U r k 2U r 0
k
c
; волновой вектор
Волновой фронт – плоскость постоянной фазы
r
I r ~ U r
r const
2 Интенсивность
монохроматической волны
не изменяется во времени

6. Элементарные волны

Плоская волна (в реальности не существует)
Мощный математический аппарат Фурье анализа
Сферическая волна
Параксиальное приближение (Френеля)
Параксиальное приближение
–
(общий вид)
Медленно меняющаяся функция

7. Преломление и отражение

Волновой вектор плоской волны
Аналог импульса
k
2 n 2 n
2
n
n n k0
c
c0
l0
k1 n1 k0 sin 1 ,0, cos 1
k 2 n2 k0 sin 2 ,0, cos 2
k3 n1 k0 sin 3 ,0, cos 3
k
2 n 2 n
2
n
n n k0
c
c0
l0
k1 n1 k0 sin 1 ,0, cos 1
k 2 n2 k0 sin 2 ,0, cos 2
k3 n1 k0 sin 3 ,0, cos 3
На границе раздела фаза должна сохраняться
k1r k2 r k3r
1 3
n1 sin 1 n2 sin 2
Для определения амплитуды скалярной теории недостаточно, нужно определять
граничные условия на амплитуду (электромагнитная теория)

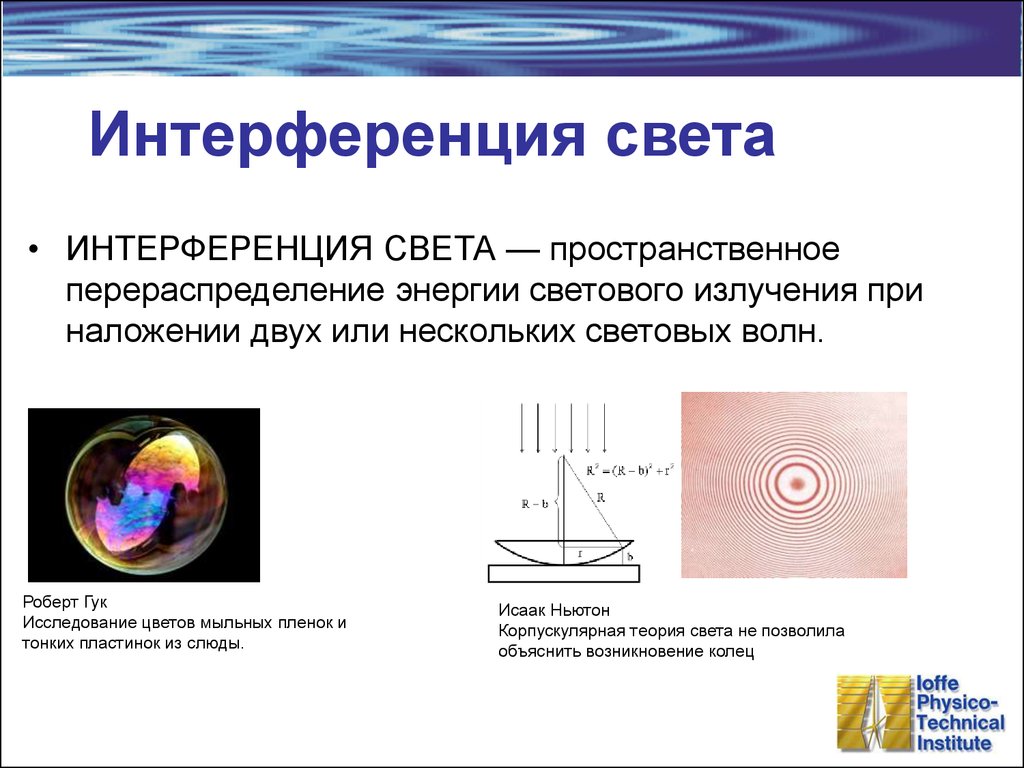
8. Интерференция света

• ИНТЕРФЕРЕНЦИЯ СВЕТА — пространственное
перераспределение энергии светового излучения при
наложении двух или нескольких световых волн.
Роберт Гук
Исследование цветов мыльных пленок и
тонких пластинок из слюды.
Исаак Ньютон
Корпускулярная теория света не позволила
объяснить возникновение колец

9. Интерференция света

ИНТЕРФЕРЕНЦИЯ СВЕТА — проявление волновых свойств (начало XIX века)
Принцип суперпозиции (линейность волнового уравнения)
u r , t u1 r , t u2 r , t ui r , t
Интенсивность не подчиняется принципу суперпозиции.
Нужно учитывать фазу волновой функции
I r , t I1 r , t I 2 r , t I i r , t
(не объясняется лучевой оптикой).
U1 (r ) I1 r exp j 1 r ;
U 2 (r ) I 2 r exp j 2 r
Томас Юнг
Комплексное представление
монохроматических волн
I (r ) U1 (r ) U 2 (r ) I1 r I 2 r 2 I1 r I 2 r cos r ;
2
r 2 r 1 r
2 I1 r I 2 r cos r 0;
конструкти вная интерференция
2 I1 r I 2 r cos r 0;
деструктив ная интерференция
Огюстен Жан Френель
Интерференция объясняет пространственное
перераспределение интенсивности без нарушения закона
сохранения энергии (мощности)

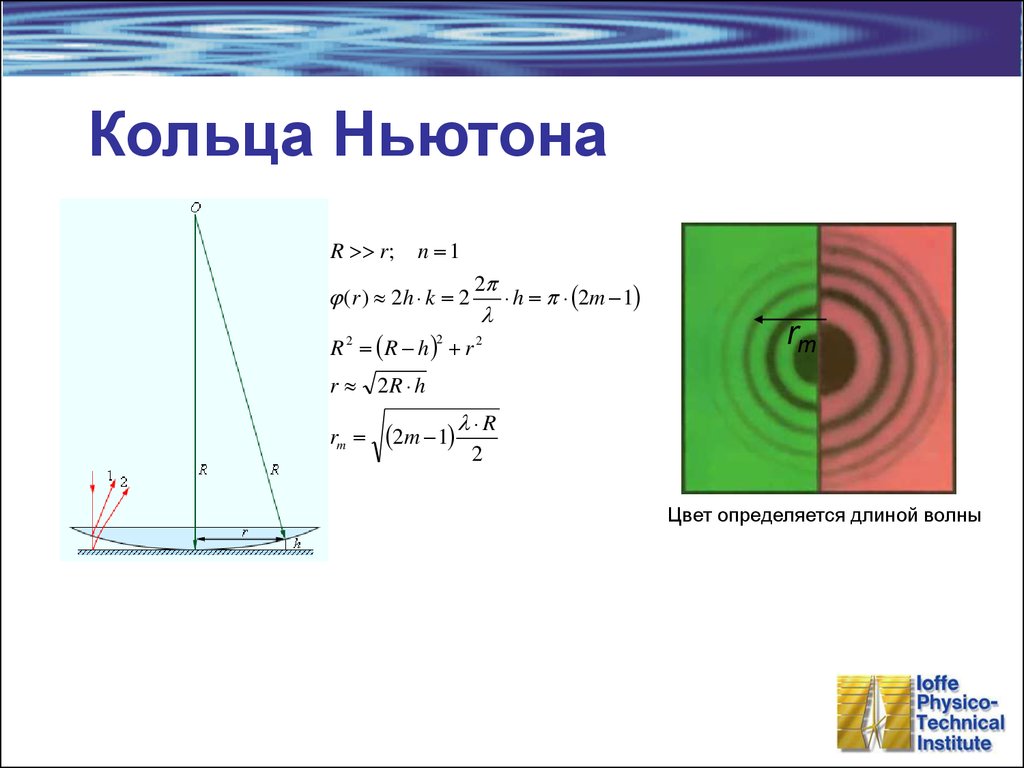
10. Кольца Ньютона

R r ;
n 1
( r ) 2h k 2
2
l
R 2 R h r 2
2
h 2m 1
rm
r 2R h
rm
2m 1 l R
2
Цвет определяется длиной волны

11. Интерференция плоских волн

U1 (r ) I 0 r exp jk z
x,0 k x sin ;
U 2 (r ) I 0 r exp jk x sin z cos
k x
I x,0 4 I 0 cos 2
sin
2
l
sin
период интерферен ционной картины
Опыт Юнга
Узкая щель – источник сферических волн (Принцип Гюйгенса)
L d x, z L k d sin ;
I0
k d
cos 2
sin ;
L
2
x
sin ;
L
I
l L
k d x
I x, d 4 0 cos 2
;
L
d
2L
I x, d 4
Френель использовал бипризму

12. Интерференция нескольких монохроматических плоских волн

U m (r ) I 0 r exp j m 1 r , m 1,2, , M
;
2
2
I (r ) U r U1 r U 2 r U M r
r
sin 2 M
2
I r I 0 r
r
sin 2
2
При большом M очень высока чувствительность к фазе
х
Амплитудная дифракционная решетка
Амплитудная диф. решетка – множество щелей
k d sin 2 m;
ml
sin m
d
d
dsin
L>>d
Дифракционная решетка разбивает
падающую волну на набор плоских волн

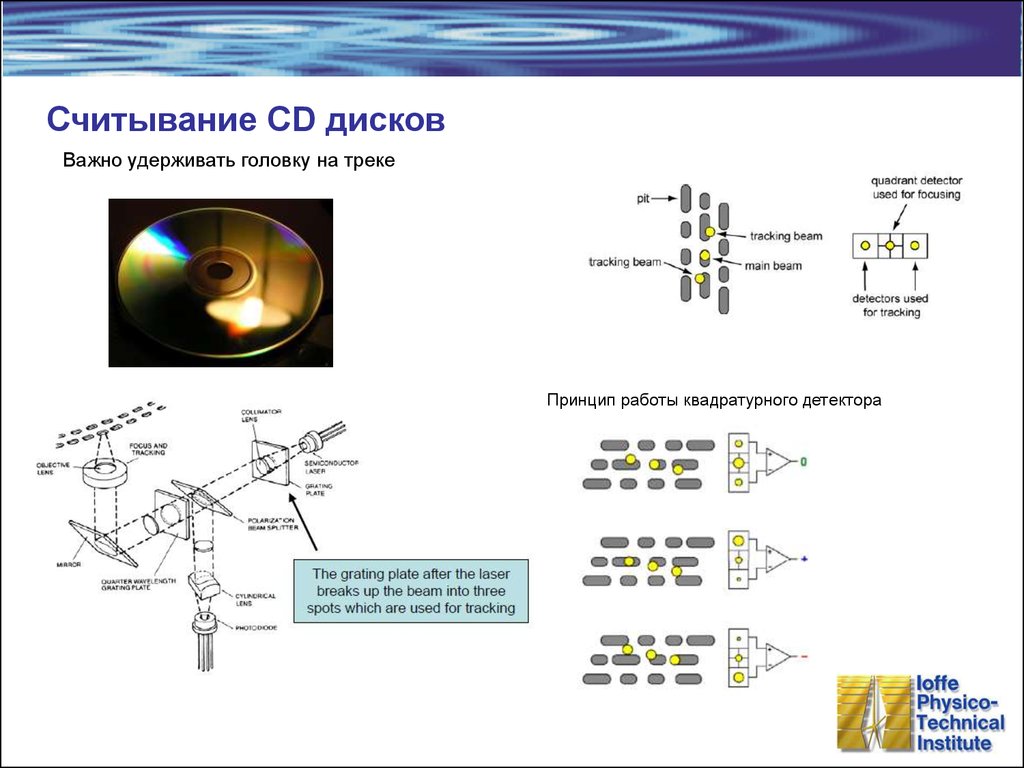
13. Считывание CD дисков

Важно удерживать головку на треке
Принцип работы квадратурного детектора

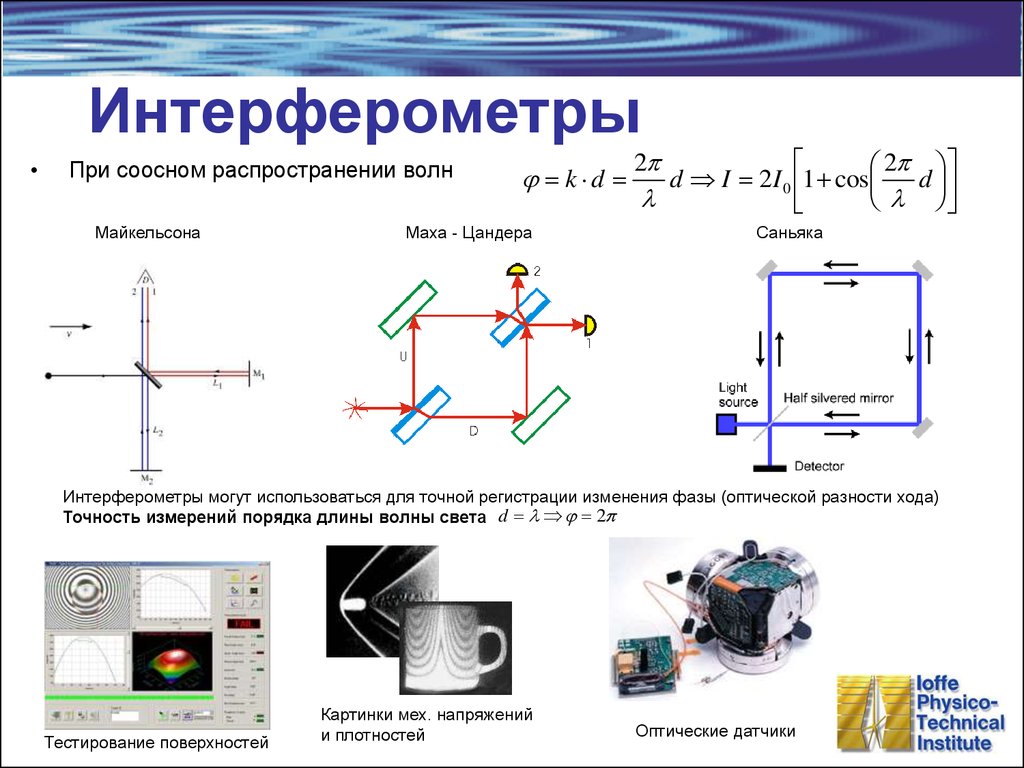
14. Интерферометры

При соосном распространении волн
Майкельсона
k d
Маха - Цандера
2
2
d I 2 I 0 1 cos
d
l
l
Саньяка
Интерферометры могут использоваться для точной регистрации изменения фазы (оптической разности хода)
Точность измерений порядка длины волны света d l 2
Тестирование поверхностей
Картинки мех. напряжений
и плотностей
Оптические датчики

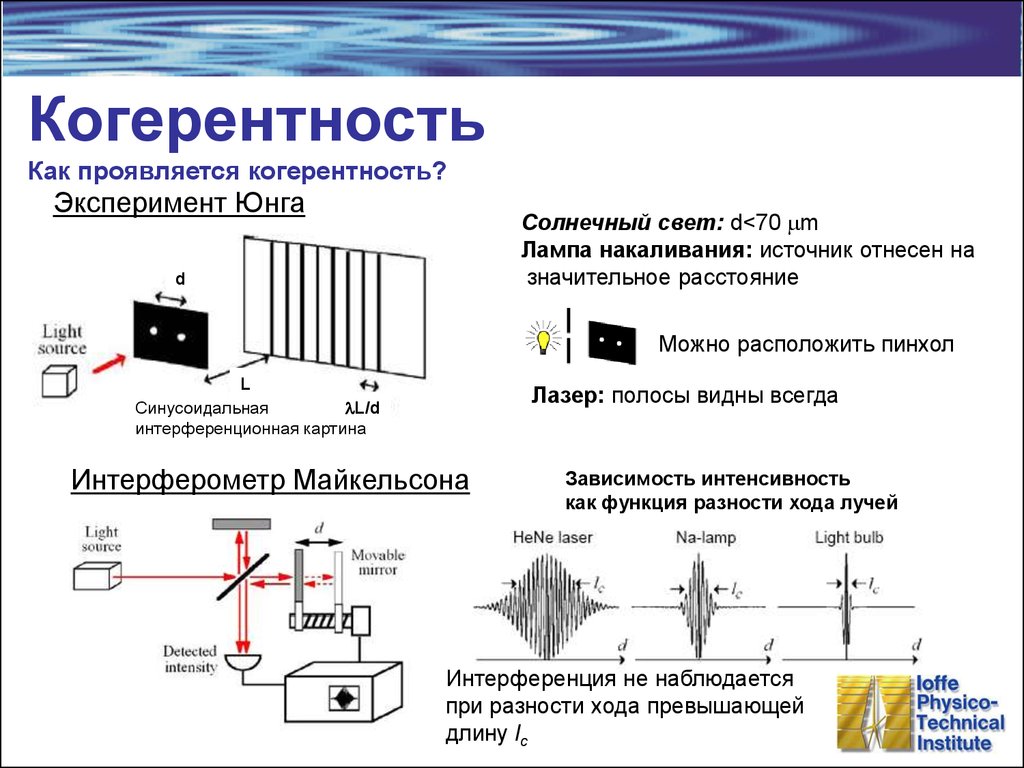
15. Когерентность Как проявляется когерентность?

Эксперимент Юнга
Солнечный свет: d<70 mm
Лампа накаливания: источник отнесен на
значительное расстояние
d
Можно расположить пинхол
L
Синусоидальная
lL/d
интерференционная картина
Лазер: полосы видны всегда
Интерферометр Майкельсона
Зависимость интенсивность
как функция разности хода лучей
Интерференция не наблюдается
при разности хода превышающей
длину lc

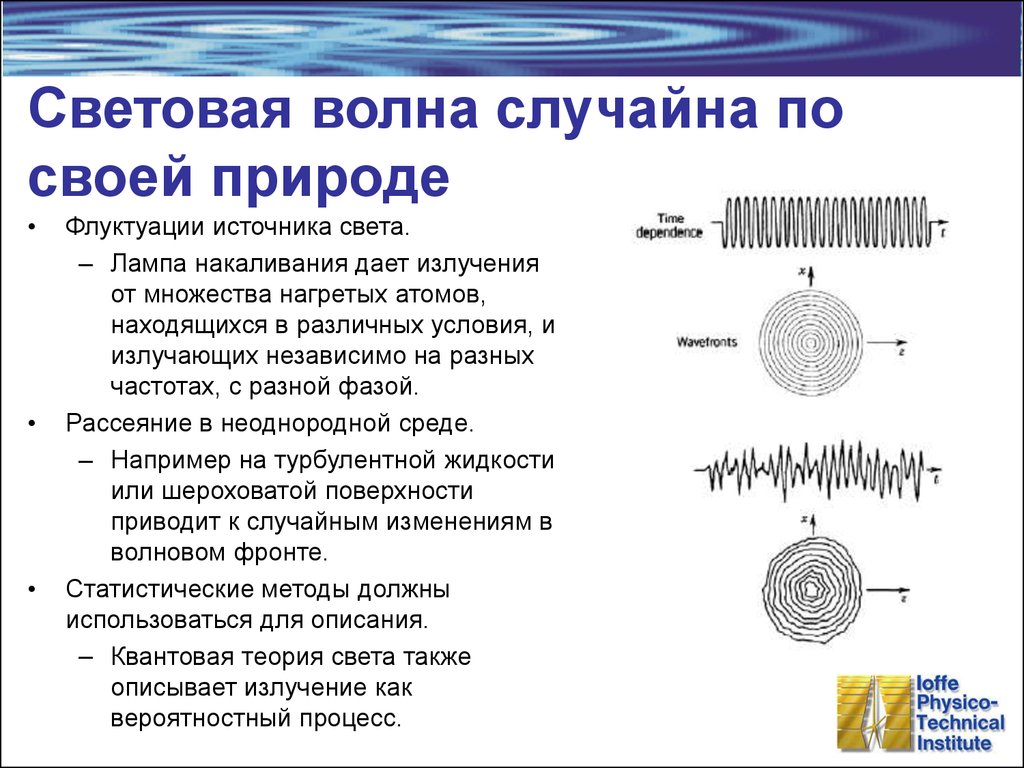
16. Световая волна случайна по своей природе

Флуктуации источника света.
– Лампа накаливания дает излучения
от множества нагретых атомов,
находящихся в различных условия, и
излучающих независимо на разных
частотах, с разной фазой.
Рассеяние в неоднородной среде.
– Например на турбулентной жидкости
или шероховатой поверхности
приводит к случайным изменениям в
волновом фронте.
Статистические методы должны
использоваться для описания.
– Квантовая теория света также
описывает излучение как
вероятностный процесс.

17. Интенсивность

Наблюдаемые в экспериментах (измеряемые) параметры световой волны являются
усреднениями случайной функции по времени измерения.
Случайная волновая функция u(r,t) удовлетворяет волновому уравнению и
граничным условиям. Статистические средние также удовлетворяют этим
законам.
I r , t U r , t
2
Символ <> обозначает усреднение по множеству реализации.
Величина U r ,t 2 называется мгновенная интенсивность.
Для стационарного света
интенсивность не зависит от
времени и выражается через
усреднение по длительному
промежутку времени
1
I r , t lim
T 2T
T
U r , t dt
2
T

18. Когерентность

Корреляционная функция между двумя случайными амплитудами световой
волны, разнесенных в пространстве и времени определяет степень
когерентности света
G r1 , r2 , U r1 , t U r2 , t
*
T
1
*
r1 , t U r2 , t dt
lim
U
T 2T T
Функция взаимной
когерентности
Нормированная корреляционная функция называется комплексной степенью
когерентности
g r1 , r2 , G r1 , r2 , / G r1 , r2 ,0 G r1 , r2 , / I r1 I r1
0 g r1 , r2 , 1
g r1 , r2 , 1;
Пример:
Степень когерентности
лампы накаливания

19. Временная когерентность.

Рассмотрим флуктуации стационарного света (средняя интенсивность постоянна) в
фиксированной точке пространства (r1=r2=r).
G U t U t
*
T
1
*
t U t dt
lim
U
T 2T T
I G 0
g( ) определяет насколько свет близок к монохроматической волне.
g G / G 0 G / I
0 g 1
c
g
2
d
Время когерентности определяет промежуток времени на
котором волна описывается синусоидой
(промежуток времени между сбоями фазы)

20. Временная когерентность.

Расстояние которое проходит световая волна за время когерентности называется
продольной длиной когерентности
lc c c
Если разность ходы лучей в интерферометре превосходит длину когерентности,
интерференционная картина не наблюдается.

21. Оптический спектр.

~ 2
Спектральная интенсивность случайной световой волны U n
усредненное значение преобразования Фурье.
S n lim
T
1
2T
T
U t exp j 2 nt dt
определяется
2
T
S n 0,n 0
I S n dn
0
S - спектральная плотность мощности: средняя мощность через единичную
площадь, переносимая волнами в бесконечно малой полосе частот dn
[Вт/(см2Гц)].
S связана с функцией временной когерентности через преобразование Фурье
S n G exp j 2 n d

22. Оптический спектр.

Ширина спектра излучения напрямую связана с временем когерентности
При определении ширины спектра как FWHM соотношение зависит от формы
спектра
Источник с более узким спектром имеет большую длину когерентности.
Через время
спектральные компоненты приобретаю сдвиг

23. Пространственная когерентность.

Пространственная когерентность описывается корреляционной функцией для
заданной временной задержки , обычно = 0.
Если область когерентности больше апертуры, то свет считают когерентным,
аналогично если область когерентности меньше разрешения, то свет
абсолютно некогерентный.
Для излучения разогретого тела эта площадь порядка l2

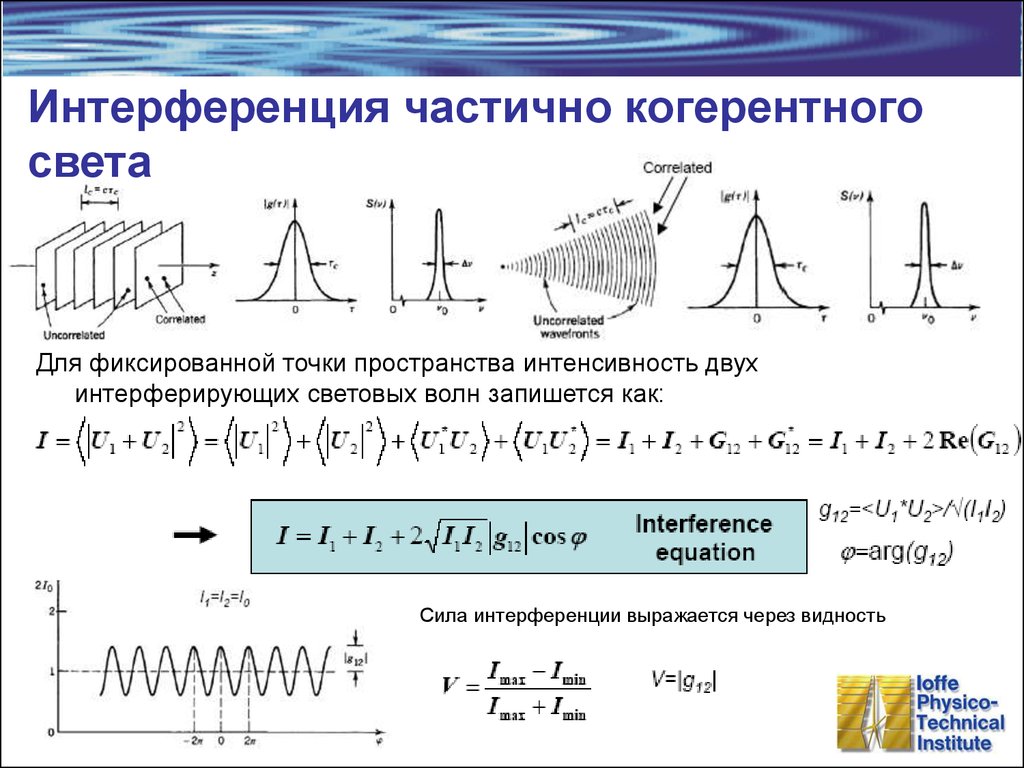
24. Интерференция частично когерентного света

Для фиксированной точки пространства интенсивность двух
интерферирующих световых волн запишется как:
Сила интерференции выражается через видность

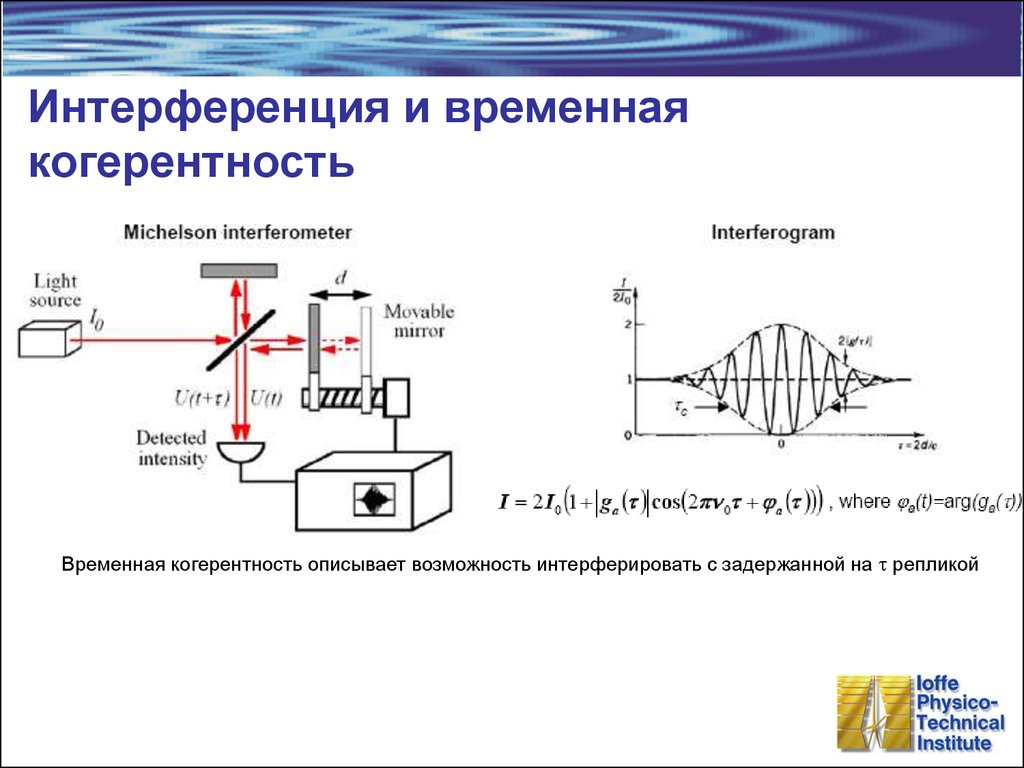
25. Интерференция и временная когерентность

Временная когерентность описывает возможность интерферировать с задержанной на репликой

26. Применения

Фурье спектроскопия (FTIR)
Томография в некогерентном свете
Томограмма кончика пальца

27. Интерференция и пространственная когерентность

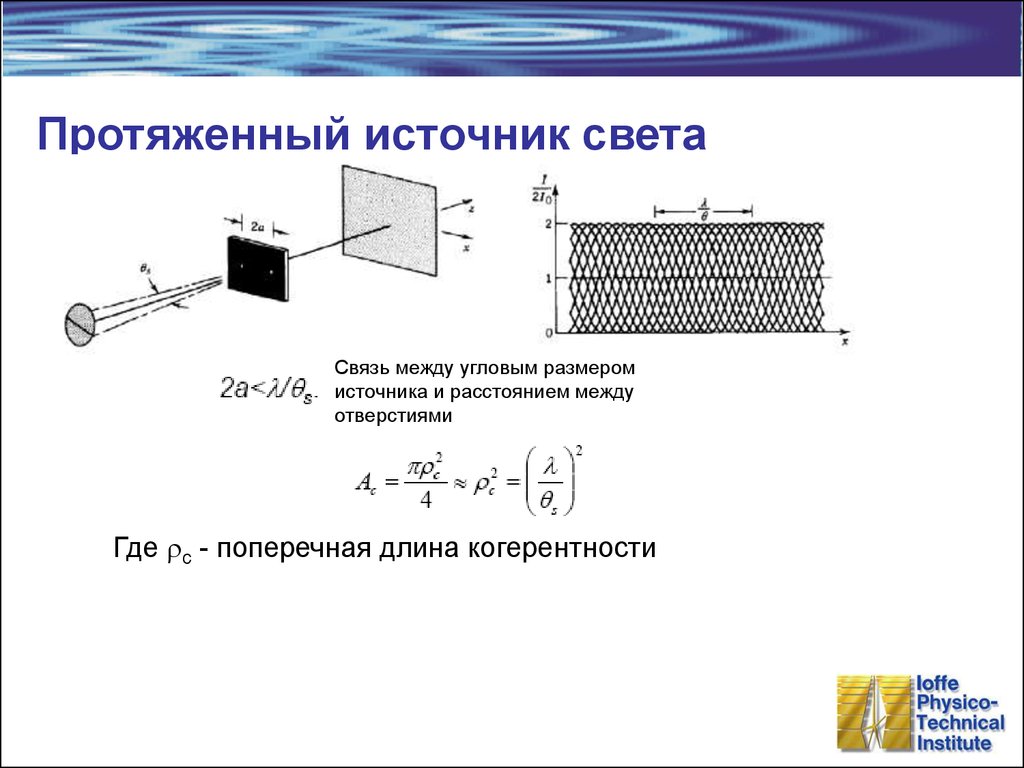
Квазимонохроматический свет

28. Протяженный источник света

Связь между угловым размером
источника и расстоянием между
отверстиями
Где rc - поперечная длина когерентности

29. Влияние ширины спектра

30. Применения

Звездный интерферометр Майкельсона
a -Орион, rc = 3.1 m, l = 0.57mm, s = 22.6 *10-8 rad
(Michelson/Pease, 1920)
Солнце, l = 0.5 mm, s = 0.5 grad, rc = 70 mm

31. Когерентный объем

Используя принцип неопределенности Гейзенберга можно показать, что внутри
данного объема фотоны неразличимы (имеют одинаковую волновую
функцию). Число фотонов в данном объеме зависит от источника, для
лазера ~ 109

32. Спутанные фотоны (entaglemented photons)

Пара фотонов описывается общей волновой функцией
(на примере состояния поляризации)
(1/2)0.5 1,n 2,n
+ 1,m
2,m );
n
m
Измерение поляризации одного фотона строго задает поляризацию второго
Созданы источники на основе понижения частоты в нелинейных кристаллах
Применения: Фотолитография, квантовая криптография

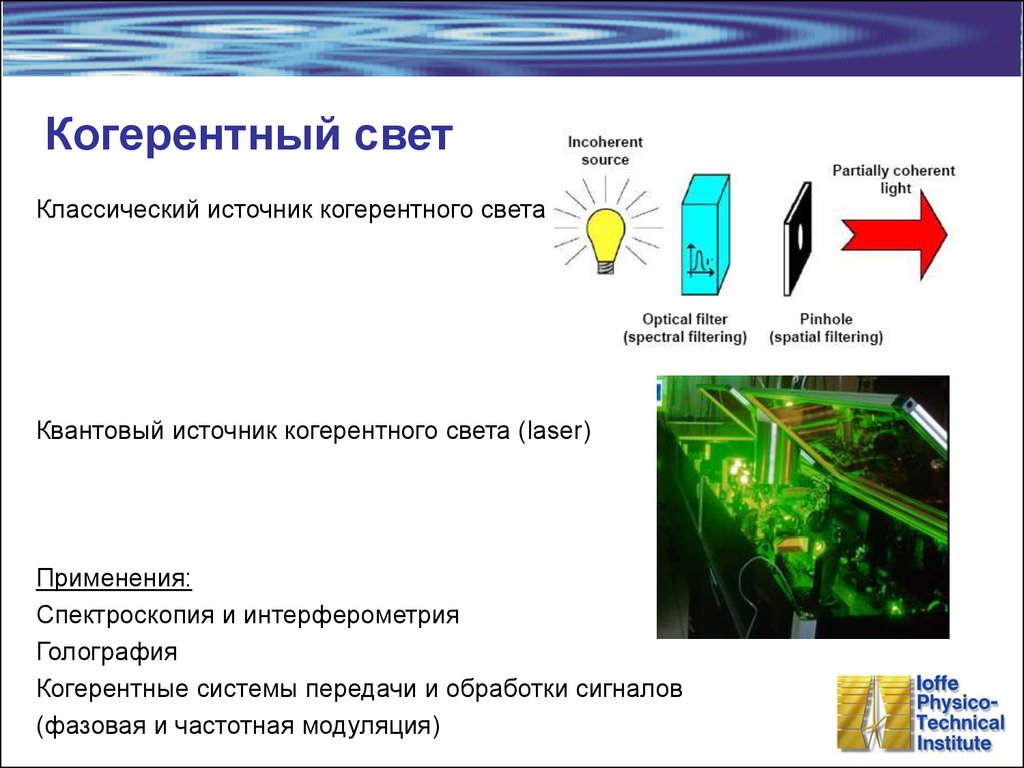
33. Когерентный свет

Классический источник когерентного света
Квантовый источник когерентного света (laser)
Применения:
Спектроскопия и интерферометрия
Голография
Когерентные системы передачи и обработки сигналов
(фазовая и частотная модуляция)