Similar presentations:
Волновая оптика. Cветовые волны. Интерференция света
1.
ВОЛНОВАЯ ОПТИКА2.
Cветовые волны.Интерференция света
3. Лекция 1: Световые волны. Интерференция света
- Световые волны,- Законы геометрической оптики,
- Интерференция света,
- Опыт Юнга,
- Применение интерференции.
Т.И. Трофимова, §170-175, стр:271-284
4.
1. Световые волныСвет – это электромагн. волны.
Световые волны: λ = (10-3 – 10-9) м.
- Инфракрасное излучение, тепло
λ = (10-3 – 10-6) м.
- Видимый свет: λ ≈ (0,4∙10-6 – 0,8∙10-6) м
- Ультрафиолет. изл. λ = (10-7 – 10-9) м.
Световые волны излучают нагретые тела
Солнечный свет глаз воспринимает как белый:
Цвета белого света
0,38 мкм
λ = 0,76 мкм
5.
EZ
Y
H
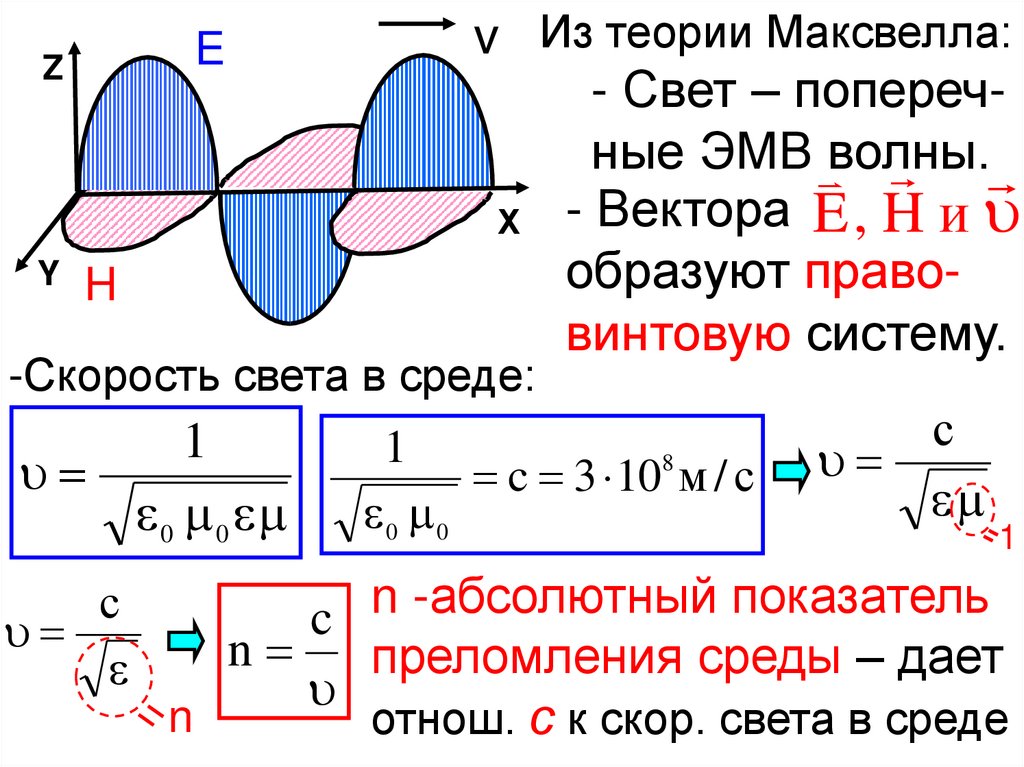
v Из теории Максвелла:
- Свет – поперечные ЭМВ волны.
Х - Вектора E , H и
образуют правовинтовую систему.
-Скорость света в среде:
1
0 0
с
1
8
c 3 10 м / с
0 0
с
1
n
-абсолютный
показатель
c
n
преломления среды – дает
n
отнош. с к скор. света в среде
6.
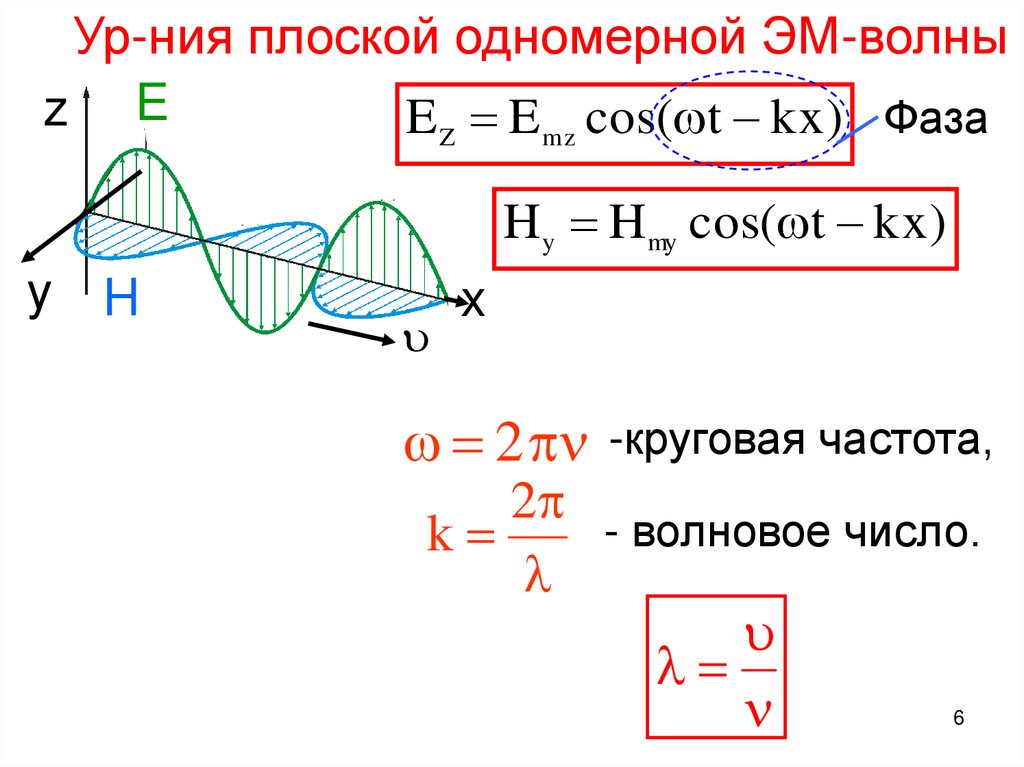
Ур-ния плоской одномерной ЭМ-волныz E
E Z E m z cos( t k x ) Фаза
H y Hmy cos( t k x)
y H
x
2 -круговая частота,
2
- волновое число.
k
6
7.
- Физическое воздействие на глаз,на вещество оказывает вектор Е!
- Интенсивность света J~Em2.
8.
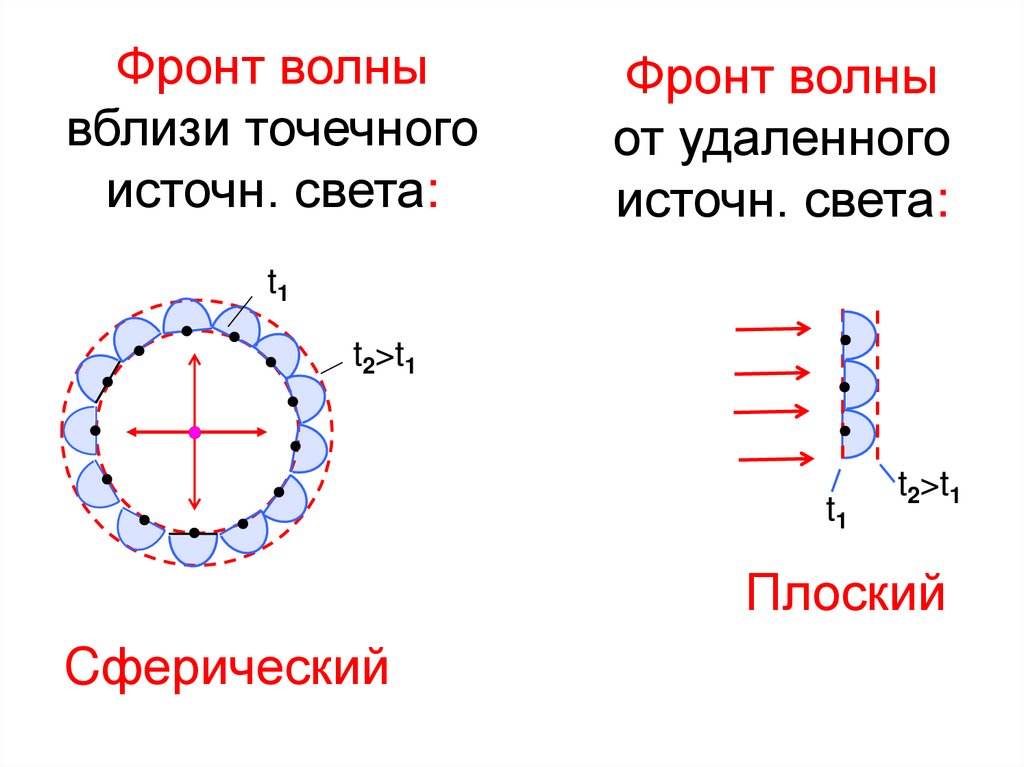
2. Законы геометрической оптикиФронт волны –геометрическое место точек
среды, до которых дошла волна в данное t.
Принцип Гюйгенса:
Каждая точка
дошла волна,
среды,
до
которой
становится точечным
источником вторичных волн, огибающая
которых определяет положение фронта
волны в каждый послед t.
9.
Фронт волнывблизи точечного
источн. света:
Фронт волны
от удаленного
источн. света:
t1
t2>t1
t1
t2>t1
Плоский
Cферический
10.
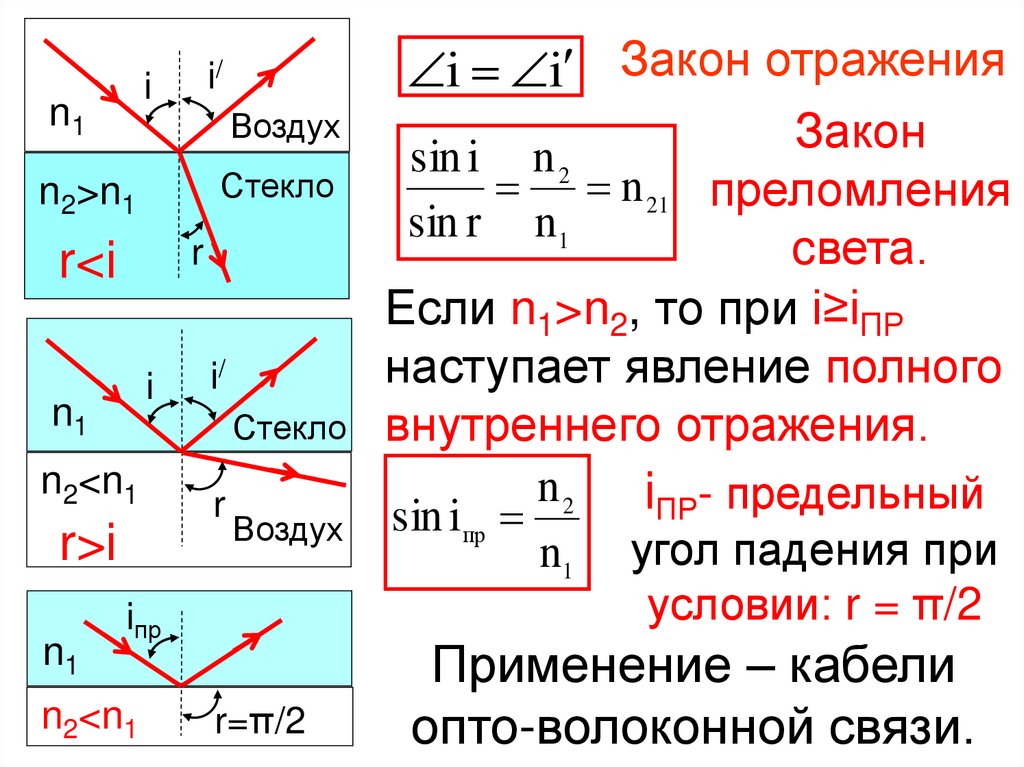
i/i
n1
Воздух
Стекло
n2>n1
r
r<i
i
n1
Стекло
n2<n1
r>i
n1
i/
r
Воздух
iпр
n2<n1
r=π/2
i i Закон отражения
Закон
sin i n 2
n 21 преломления
sin r n1
cвета.
Если n1>n2, то при i≥iПР
наступает явление полного
внутреннего отражения.
n2
i
предельный
ПР
sin i
пр
n1
угол падения при
условии: r = π/2
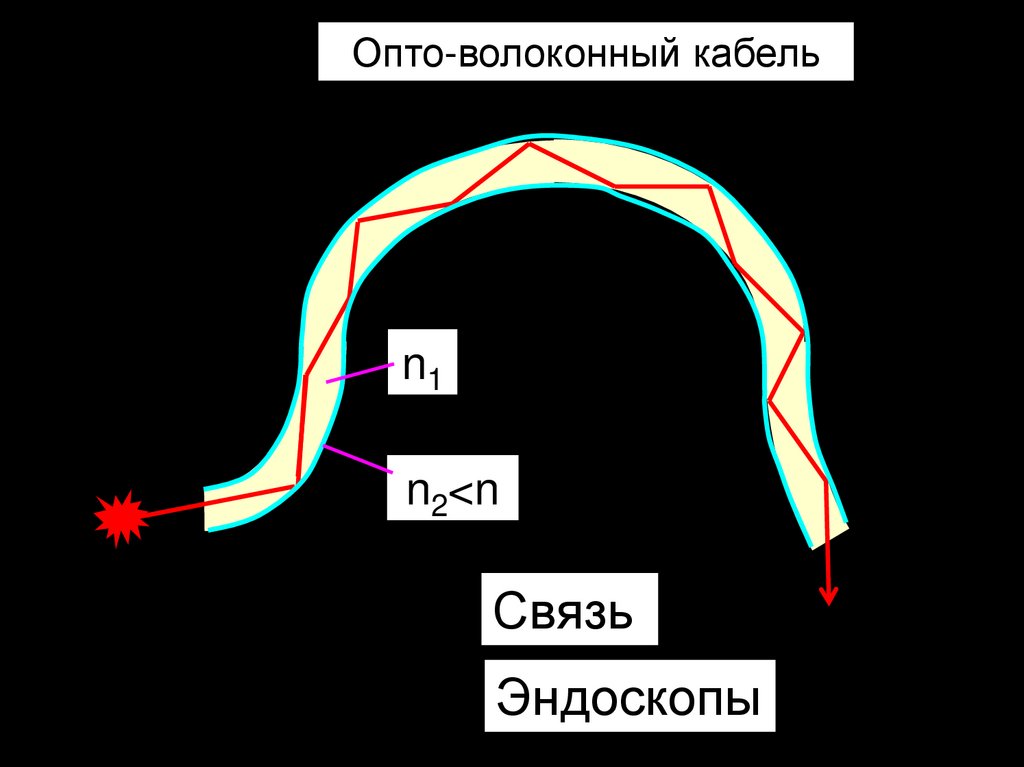
Применение – кабели
опто-волоконной связи.
11.
Опто-волоконный кабельn1
n2<n
1
Связь
Эндоскопы
12.
13.
3. Интерференция светаОпыт
Интерференция - явление наложения
когерентных световых волн, в рез-те чего в
одних местах пр-ва возникают max, а в
других – min освещенности.
У когерентных волн одинаковые λ, и разность фаз не изменяется с t (Δφ(t)=сonst)
Естественный свет – некогерентный,
когерентный – получают искусственно.
14.
Пусть имеются 2 ког. источника света, укоторых Em1=Em2, Е - в одной пл-сти, и лучи
приходят в одну точку. Δφ-разность фаз волн
Δφ=π
EmΣ=2Em
Δφ=0
EmΣ=0
Еm
Еm
Еm
а
JΣ=4J
а
MAX
t
Δφ=0, 2π, 4π
Δφ=2kπ
где k=0,1, 2.
Условие max
интерф-ции света
а
а
Еm
MIN
t
Δφ=π, 3π, 5π
Δφ=(2k+1)π
Условие min
интерф-ции
15.
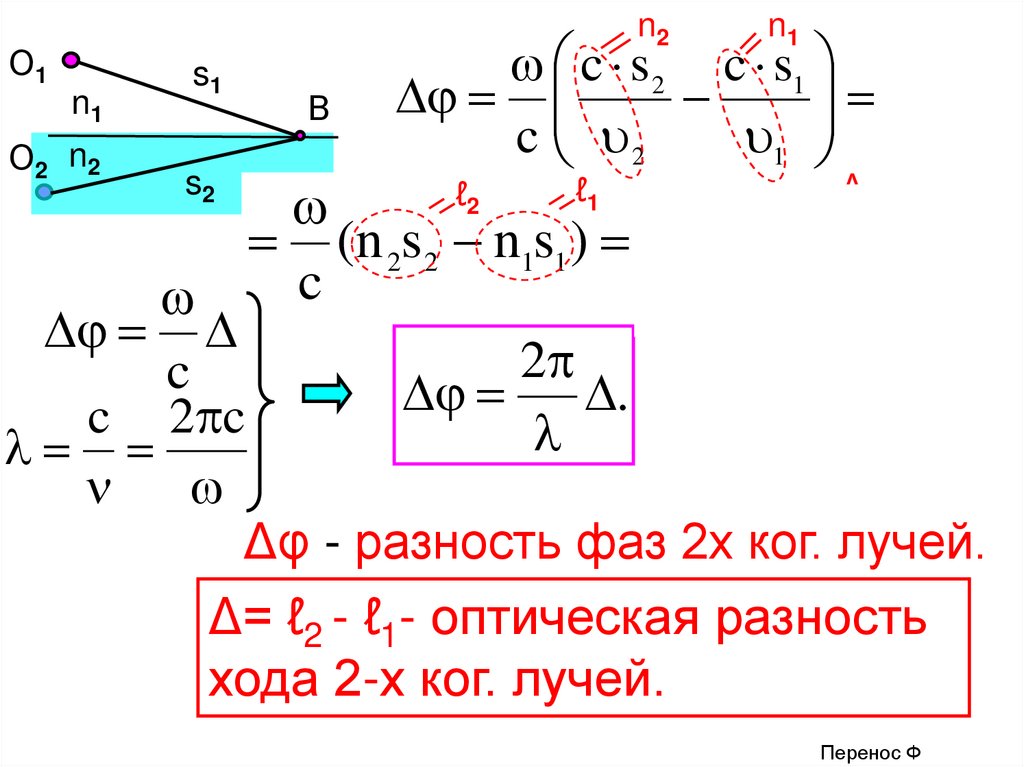
Оптический путь луча и интерф. светаПусть s – геометрический путь луча. Если
луч идет в среде с показ. преломления n,
то ℓ = s∙n – оптический путь луча.
Пусть свет от ког. ист-ков О1 и О2 идет в
т. В через среды с n1 и n2, соотв-но.
2
О1
Ур-ние волн: k
s1
2
n1
В
E E m cos( t k x )
О2 n2
s2
E E m cos ( t s ) Для волн
φ1
s 2 s1 c
E1 E m cos ( t s1 1 )
E 2 E m cos ( t s 2 2 )
1
φ2
2
c
2 1
Перенос Рис. и Ф.
16.
n2О1
n1
О2 n2
s1
В
n1
c s 2 c s1
c 2
1
Δ
(n 2s 2 n1s1 ) ( 2 1 )
c
c
c
2
c
.
c 2 c
s2
ℓ2
ℓ1
Δφ - разность фаз 2х ког. лучей.
Δ= ℓ2 - ℓ1- оптическая разность
хода 2-х ког. лучей.
Перенос Ф
17.
max интерф-ции: Δφ=2kπ2
2k
Δ=kλ=2k λ/2
Условие max интерф-ции:
На опт. разности хода 2-х ког.
2k
2 лучей должно уложиться
k=0,1, 2,.. четное число полуволн.
(2k 1) Условие min интерф-ции:
2
На опт. разности хода 2-х ког. лучей должно уложиться нечетное число полуволн
18.
4.Принципы наблюдения интерф-цииЕстственный свет – некогер-ый. Свет излучают атомы нагретых тел в виде отрезков
волн, цугов, независимо друг от друга.
Длина цуга волн ≈3 м. Цуги волн разных
атомов разл-ся по фазе
свет-некогер-й.
Принцип наблюдения ИН: луч ест. света
разделяют на 2 луча, которые по отношению друг к другу становятся когерентными
Пройдя различные опт. пути эти когер.
лу-чи, сходясь в одной точке, дают картину ИН.
19.
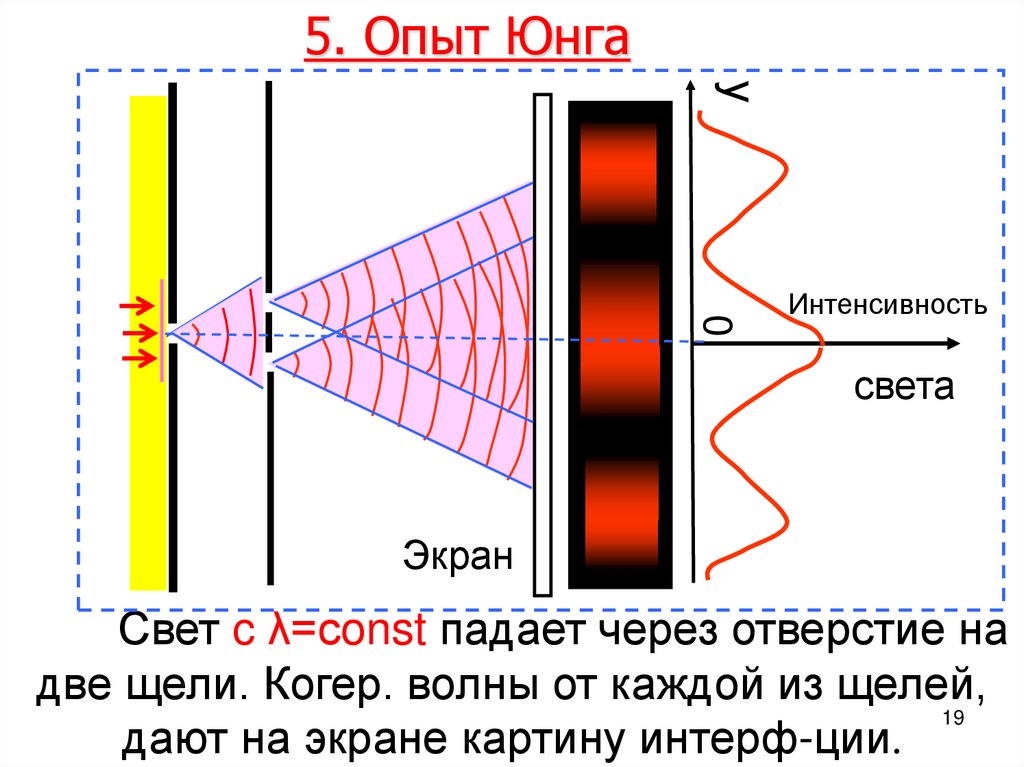
5. Опыт Юнгау
0
Интенсивность
света
Экран
Свет c λ=сonst падает через отверстие на
две щели. Когер. волны от каждой из щелей,
19
дают на экране картину интерф-ции.
20.
d<<ℓo1
A
r1
у
r2
d
d 2
Δ
o2
d 2
ℓ
у
k=1
Найдем Δ=r2- r1.
r22=ℓ2+(y+d/2)2
J
2=ℓ2+(y- d/2)2
r
k=0
1
2-r 2=2dy
Δ
r
k=1
2
1
(r2-r1)(r2+r1) = 2dy
d y
2ℓ
. Опт. разность хода 2-х ког. лучей.
d y
Условие max ИН: 2k 2 y d k
Условие min ИН: y (2k 1)
d
2 k=0,1, 2
У –местоположение max или min интерф.
21.
6. Интерференция на тонких пленкахСвет падает из воздуха (i) на пленку с n и
nв=1
Лучи 1 и 2 ког. и в т.Р интерф.
1
i D
A
d
отражается.
P
2
Δ=ℓ2-ℓ1=(АВ+ВС)n-(AD-λ/2).
C
r
n
B
При отраж. от более плотной
среды ℓ луча уменьш. на λ/2.
Если i=0:
2dn
2d n sin i
2
2
2
2
Δ на пленке в отраж. свете
22.
Условие max ИН:2k ;
2
min ИН: (2k 1)
2
k=0,1, 2
Почему пленки масла на воде цветные?
Пусть белый свет падает на Пл. ┴, max.
2dn 2k
2dn (2k 1)
2
2
2
Пленки имеют разную d.
В белом свете условие max ИН для разных
d выпол-ся при разных λ, (разный цвет).
23.
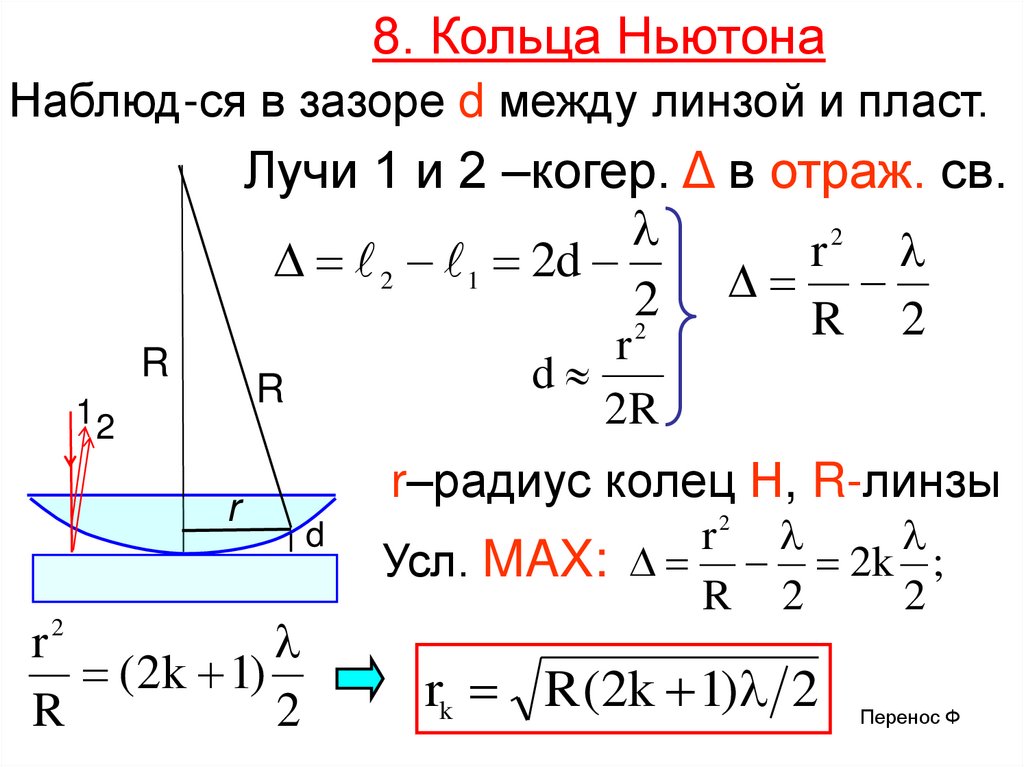
8. Кольца НьютонаНаблюд-ся в зазоре d между линзой и пласт.
Лучи 1 и 2 –когер. Δ в отраж. св.
2
r
2 1 2d
22
R 2
R
r
d
2R
R
12
r
r
(2k 1)
R
2
r–радиус колец Н, R-линзы
d
r2
Усл. MAX: 2k ;
R 2
2
2
rk R (2k 1) 2
Перенос Ф
24.
rk R (2k 1) 2 Радиусы светлых,rk R k
k= 0, 1, 2…
темных колец Н
в отраж. свете.
25. .
Кольца Н в свете с разным λ..
26.
27.
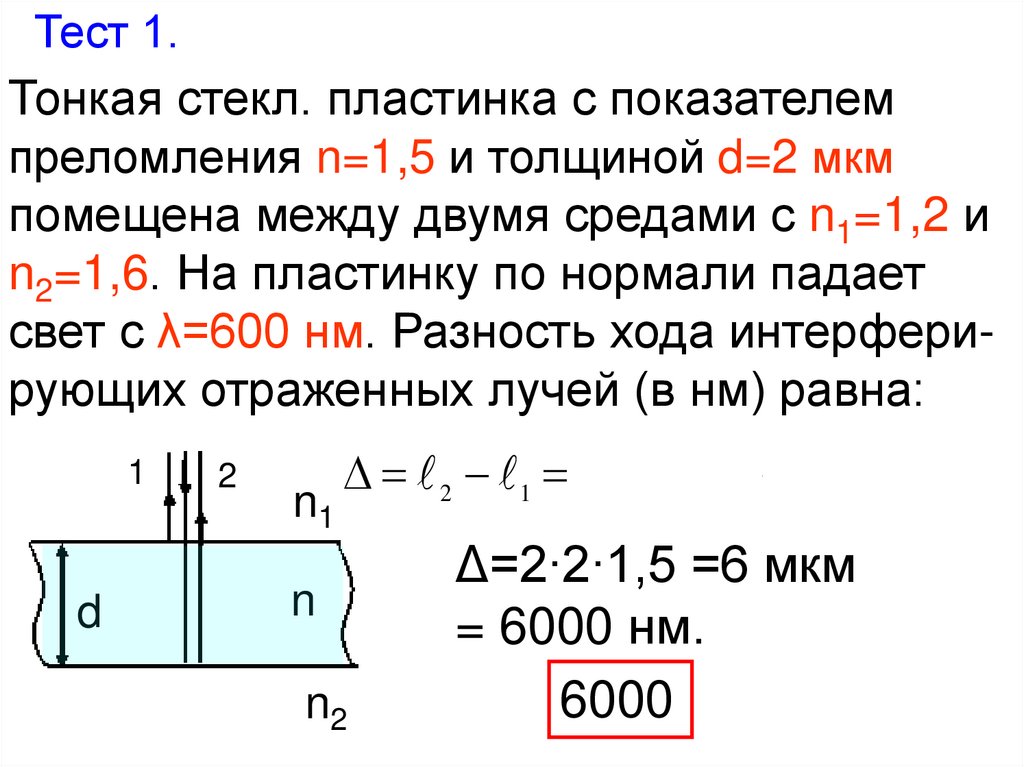
Тест 1.Тонкая стекл. пластинка с показателем
преломления n=1,5 и толщиной d=2 мкм
помещена между двумя средами с n1=1,2 и
n2=1,6. На пластинку по нормали падает
свет с λ=600 нм. Разность хода интерферирующих отраженных лучей (в нм) равна:
1
2
2 1 2 d n (0 ) 2 d n
n1
2
2
d
n
n2
Δ=2∙2∙1,5 =6 мкм
= 6000 нм.
6000
28.
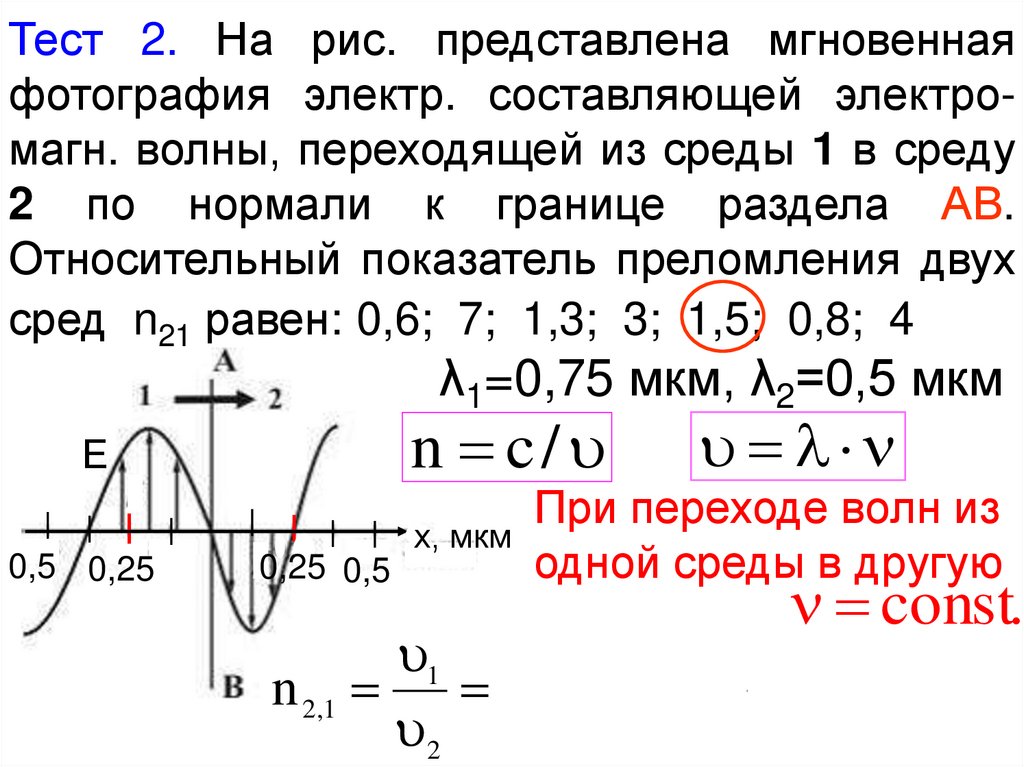
Тест 2. На рис. представлена мгновеннаяфотография электр. составляющей электромагн. волны, переходящей из среды 1 в среду
2 по нормали к границе раздела АВ.
Относительный показатель преломления двух
сред n21 равен: 0,6; 7; 1,3; 3; 1,5; 0,8; 4
λ1=0,75 мкм, λ2=0,5 мкм
Е
0,5 0,25
n c/
При переходе волн из
х, мкм
одной среды в другую
0,25 0,5
const.
1 1 1 0,75
n 2,1
1,5
2 2 2 0,5
29.
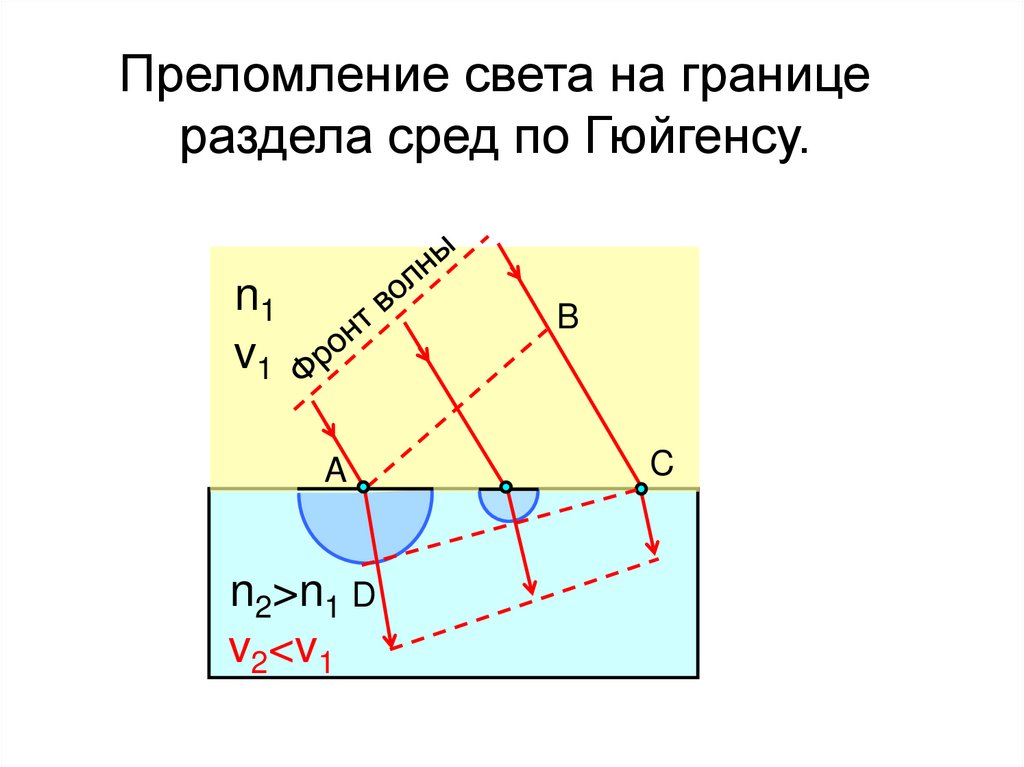
Преломление света на границераздела сред по Гюйгенсу.
n1
v1
B
A
n2>n1 D
v2<v1
C
30.
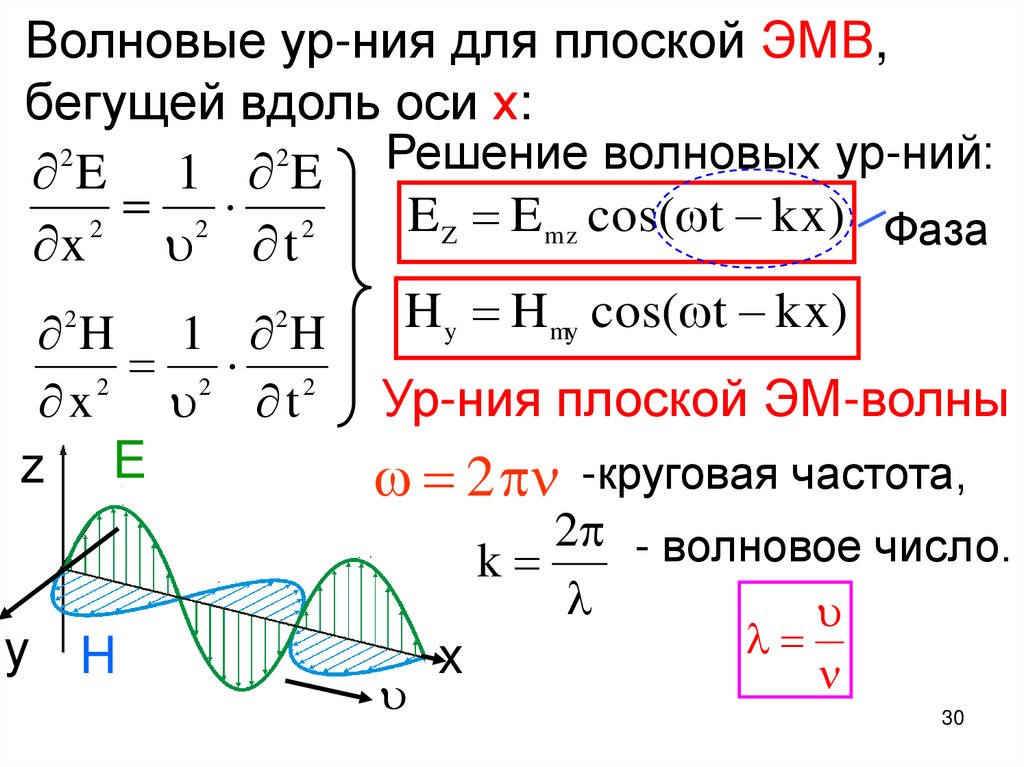
Волновые ур-ния для плоской ЭМВ,бегущей вдоль оси х:
2
2
Решение
волновых
ур-ний:
E 1 E
2 2
E Z E m z cos( t k x ) Фаза
2
x
t
2
2
H
H
cos
(
t
k
x
)
y
my
H 1 H
2 2
2
Ур-ния плоской ЭМ-волны
x
t
z E
2 -круговая частота,
y H
2 - волновое число.
k
x
30
31.
7. Просветление оптикиДля оптики важно, чтобы свет по min отражался и по max проходил через линзы.
Их покрывают пленкой с n<nСТ и d=λ/4n
1
о)
Пусть
свет
падает
нормально
(i=0
nв=1 2
Условие min для отраж. света:
n<nCT
Δ=(2k+1)λ/2
d
nСТ
2 1 2 d n (0 ) 2 d n.
Линза
2
2
2 d n (2 k 1) . d=min, когда k=0
2
Условие просветле2 d min n
d min
2
4n ния (для λ≈0.6 мкм).



















 physics
physics








