Волновая оптика основные сведения

1.

ВОЛНОВАЯ ОПТИКА
ОСНОВНЫЕ СВЕДЕНИЯ
В волновой оптике свет рассматривается как электромагнитная
волна. Вектор напряженности электрического поля называется
световым вектором. Линии, вдоль которых распространяется
световая энергия, называются лучами.
Интенсивность света I - модуль среднего по времени значения
плотности потока энергии световой волны:
I S
S [ E, H ]
I ~ A2
Интенсивность световой волны равна энергии, переносимой
волной за единицу времени через единичную площадку,
перпендикулярную направлению переноса.

2.

Длины волн видимого света заключены в пределах:
0 0,4 0,76мкм
Частоты видимых световых волн заключены в пределах:
0,39 0,75 1015 Гц

3.

Основу волновой теории Гюйгенса составляло следующее
положение (принцип Гюйгенса):
Каждая частица среды, до которой дошла световая
волна, сама становится источником вторичных волн,
внешняя огибающая которых определяет положение
фронта волны в каждый следующий момент времени.

4.

ИНТЕРФЕРЕНЦИЯ СВЕТОВЫХ ВОЛН
Интерференция - это явление наложения когерентных волн,
в результате которого происходит пространственное
перераспределение интенсивности результирующей волны.
Рассмотрим наложение двух когерентных волн в точке Р.
Пусть разделение на две когерентные волны происходит в
точке О.

5.

6.

r1
y1 A1 cos[ ( t )]
1
r2
y 2 A 2 cos[ ( t )]
2
c
c
1
2
n1
n2
Разность фаз колебаний, возбуждаемых волнами в точке Р:
r2 r1
1 2 n 2 r2 n1r1
2 1 c

7.

8.

9.

2 2
Подставим в последнее выражение
c
c
0
2
1 2 n 2 r2 n1r1
0
n r - оптический путь;
( 21 = n2r2 - n1r1) - оптическая разность хода
r2 - r1 - геометрическая разность хода
2
1 2 21
0

10.

Если волны 1 и 2 распространяются в одной среде:
2
1 2 r2 r1
Амплитуда результирующих колебаний:
A 2рез. A12 A 22 2 A1 A 2 cos( 1 2 )
1. const - волны некогерентные.
cos 1 2 0
A 2рез. A12 A 22 ; I I1 I 2

11.

2. const - волны когерентные.
2.1. 1 2 2k ; k 0,1,2.....
A 2рез. A12 A 22 2 A1 A 2
Если А1 = А2 = А (I1 = I2 = I), то:
A 2рез. A 2 A 2 2 A A 4 A 2
I рез. I I 4I

12.

2
1 2 21 2k
2.2. 1 2 (2k 1)
21 k
A 2рез. A12 A 22 2 A1 A 2
Если А1 = А2 = А (I1 = I2 = I), то:
A 2рез. A 2 A 2 2 A A 0
I рез. 0
2
1 2 21 (2k 1)
21 (2k 1)
2

13.

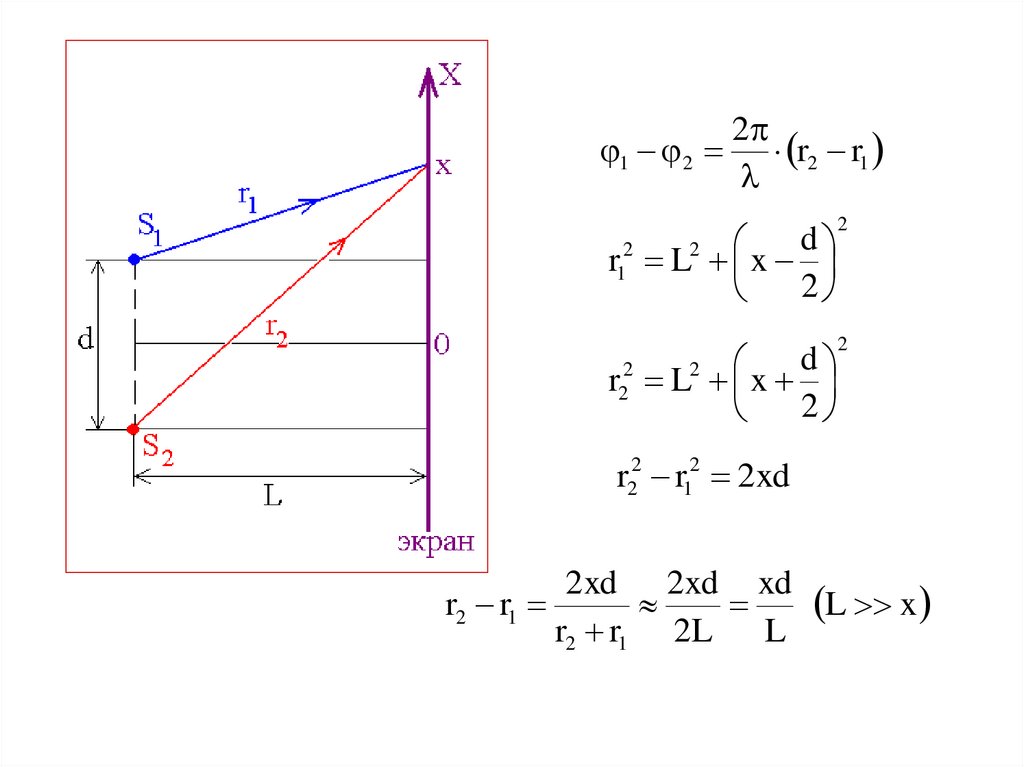
РАСЧЕТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ
ОТ ДВУХ ИСТОЧНИКОВ

14.

2
1 2 r2 r1
d
r12 L2 x
2
2
d
r22 L2 x
2
2
r22 r12 2xd
2xd 2xd xd
r2 r1
L x
r2 r1 2L
L

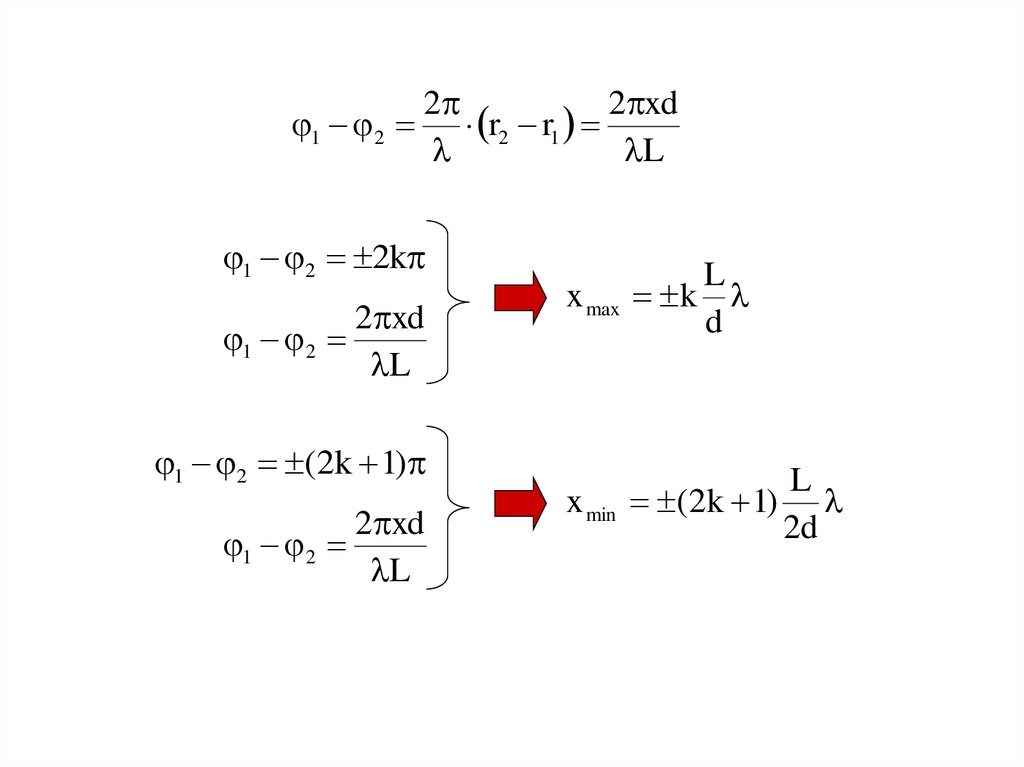
15.

2
2 xd
1 2 r2 r1
L
1 2 2k
2 xd
1 2
L
x max
L
k
d
x min
L
(2k 1)
2d
1 2 (2k 1)
2 xd
1 2
L

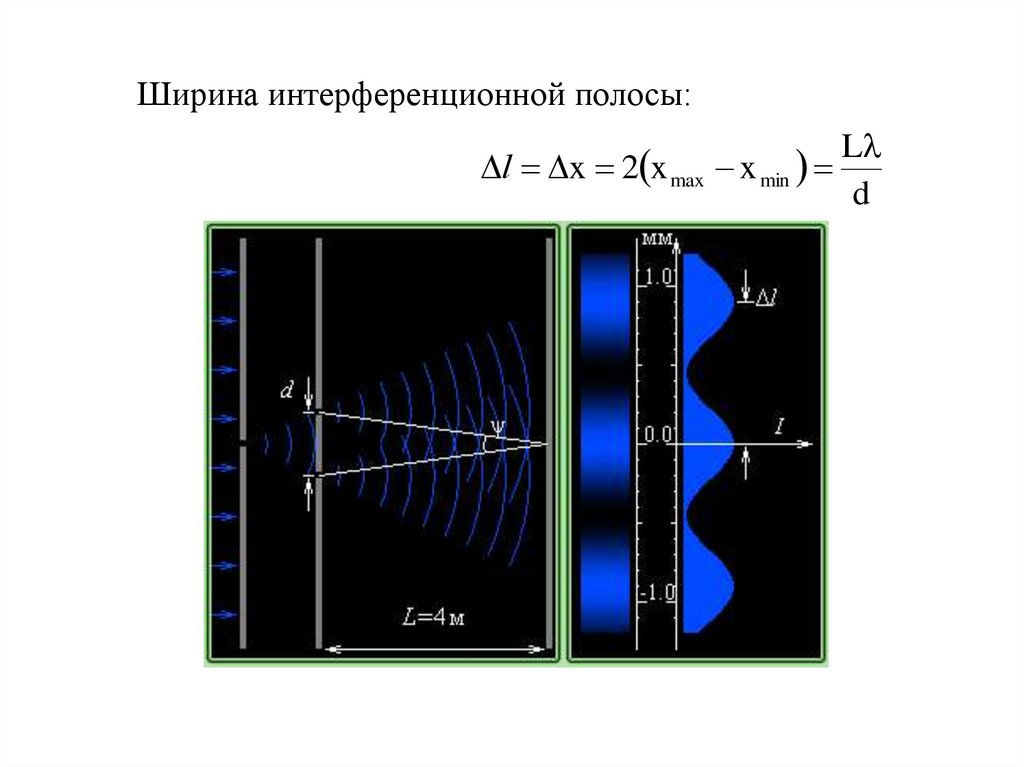
16.

Ширина интерференционной полосы:
l x 2 x max
L
x min
d

17.

Рассмотрим формирование
интерференционной
картины на примере колец
Ньютона
Интерференция возникает при
сложении волн, отразившихся
от двух сторон прослойки
среды (зазора) между линзой и
стеклянной
пластинкой.
«Лучи» 1 и 2 – направления
распространения волн; h –
толщина зазора.

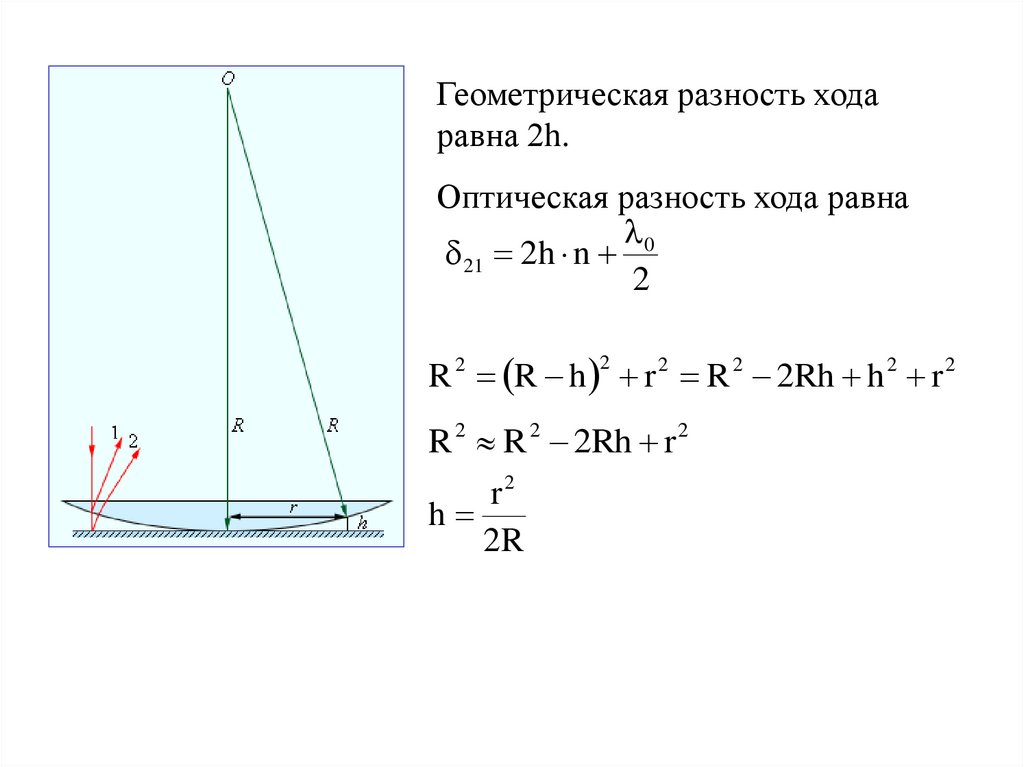
18.

19.

Геометрическая разность хода
равна 2h.
Оптическая разность хода равна
0
21 2h n
2
R R h r 2 R 2 2Rh h 2 r 2
2
2
R 2 R 2 2Rh r 2
r2
h
2R

20.

0
0 r 2
0
r2
21 2h n 2
n n
2
2R
2 R
2
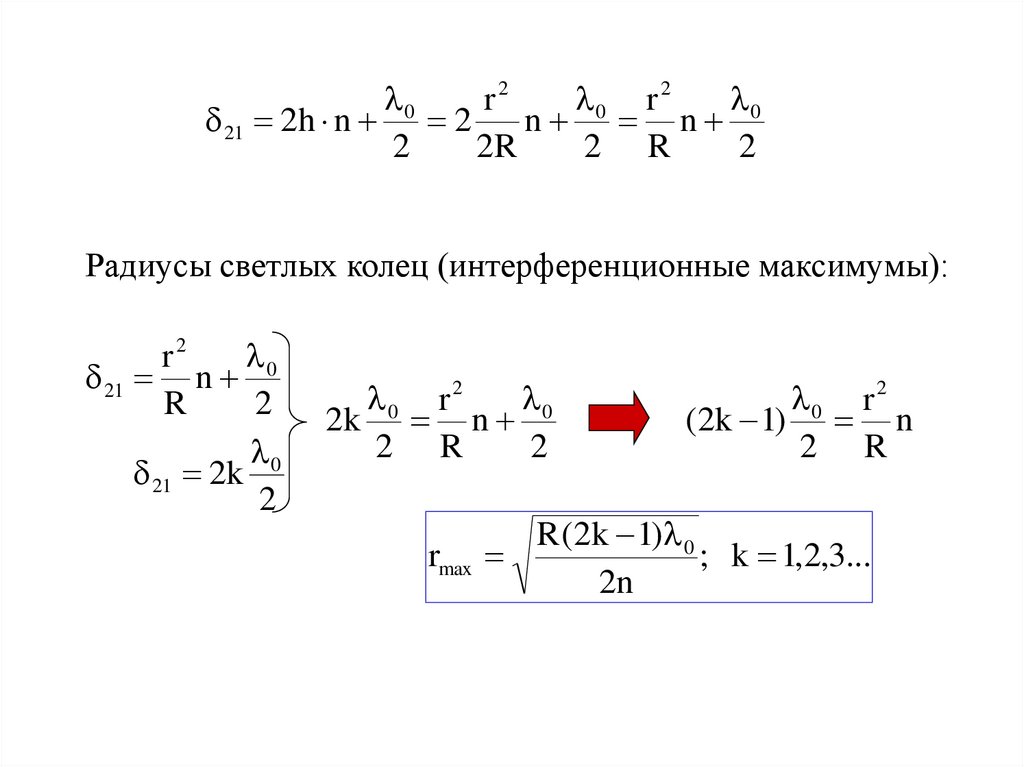
Радиусы светлых колец (интерференционные максимумы):
0
r2
21 n
R
2
0
21 2k
2
0 r 2
2k n 0
2 R
2
rmax
0 r 2
(2k 1) n
2 R
R (2k 1) 0
; k 1,2,3...
2n

21.

Радиусы темных колец (интерференционные минимумы):
0
r2
21 n
R
2
0
21 (2k 1)
2
0 r 2
(2k 1) n 0
2 R
2
rmin
0 r 2
2k n
2 R
Rk 0
; k 0,1,2,3...
n

22.

Кольца Ньютона в зеленом и красном свете

23.

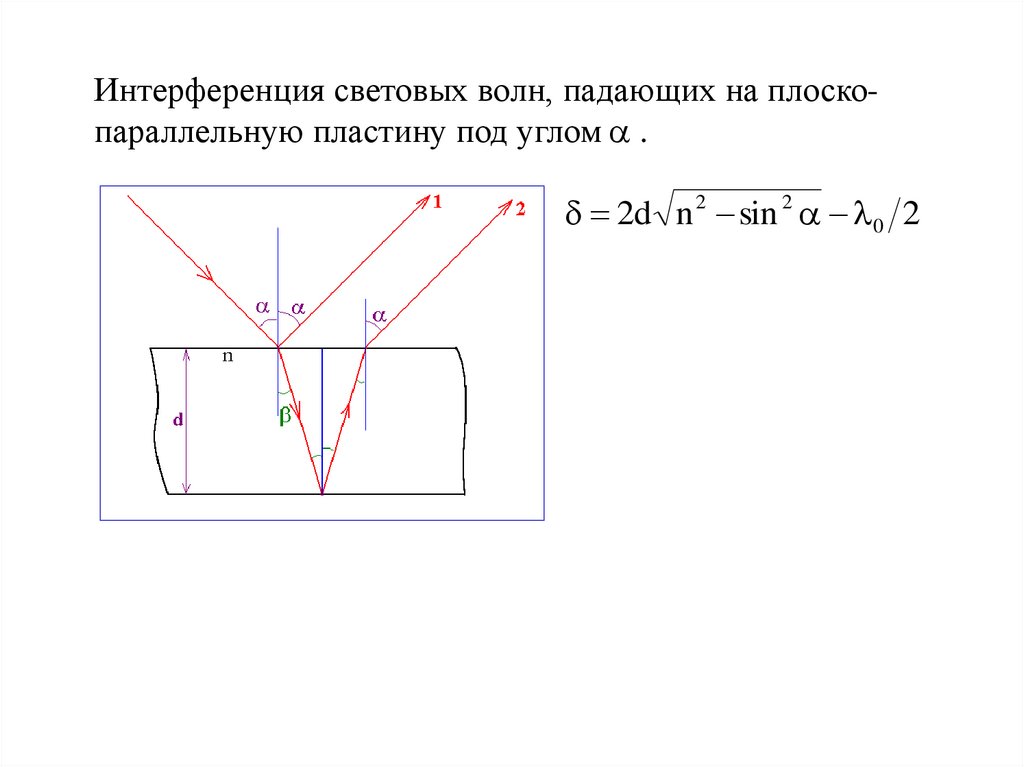
Интерференция световых волн, падающих на плоскопараллельную пластину под углом .
2d n 2 sin 2 0 2

24.

25.

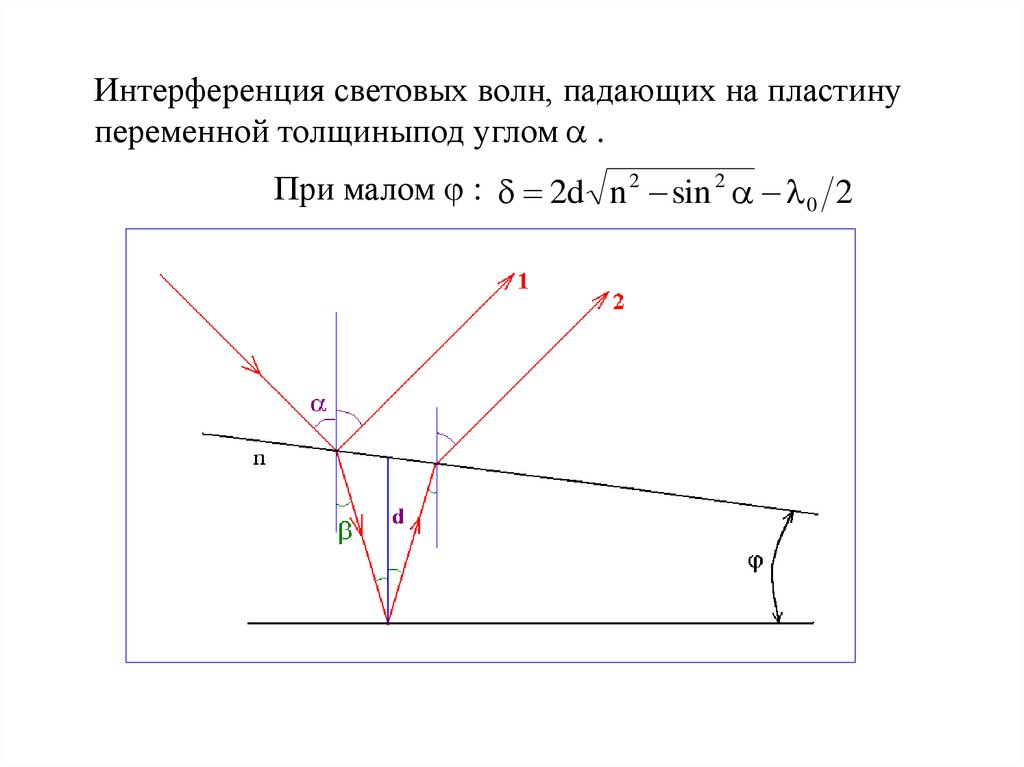
Интерференция световых волн, падающих на пластину
переменной толщиныпод углом .
При малом : 2d n 2 sin 2 0 2

26.

27.

Применение интерференции в технике:
1. Голография.
2. Интерферометры.
3. Просветление оптики.
0
d
4 4n