Лекция 3: Волновая оптика. Дифракция. Фурье оптика

1. Лекция 3: Волновая оптика Дифракция Фурье оптика

2. Волновая оптика

• Свет описывается как скалярная волновая
функция (решение волнового уравнения)
• Длина волны порядка размеров объектов

3. Дифракция света

Дифракция волн (лат. diffractus — буквально разломанный, переломанный)
— явление, которое можно рассматривать как отклонение от законов
геометрической оптики при распространении волн.
Первоначально понятие дифракции относилось к огибанию волнами
препятствий, но в современном, более широком толковании, с дифракцией
связывают весьма широкий круг явлений, возникающих при
распространении волн в неоднородных средах, а также при
распространении ограниченных в пространстве волн.
Дифракция тесно связана с явлением интерференции. Более того, само
явление дифракции зачастую трактуют как частный случай интерференции
(интерференция вторичных волн).

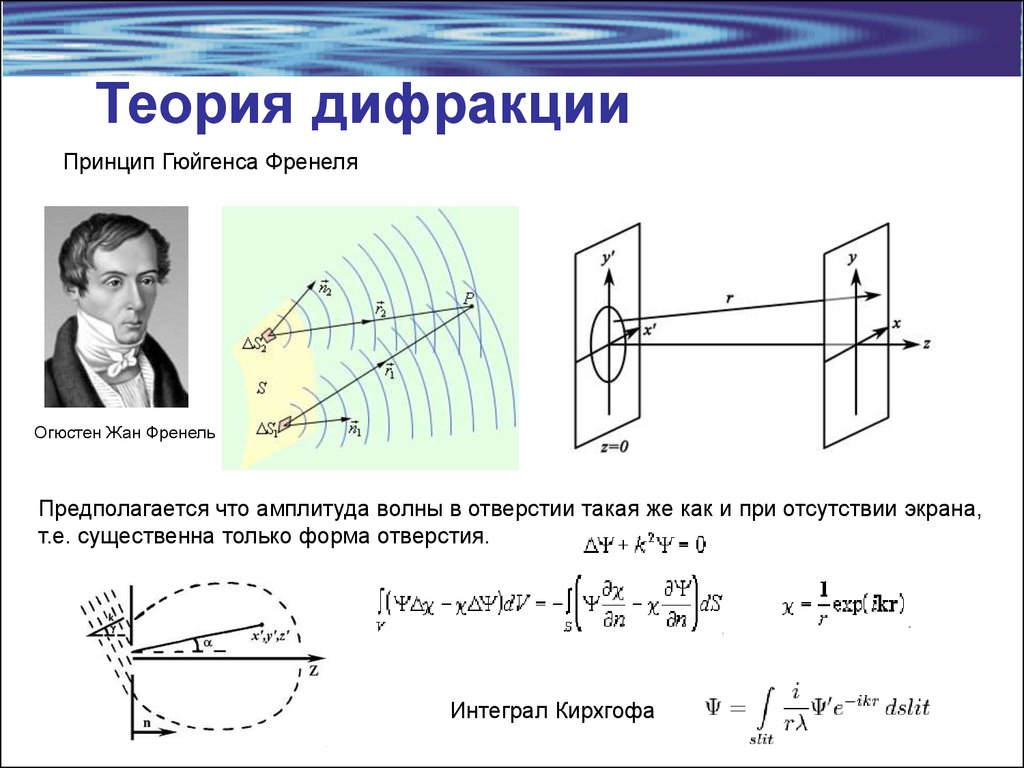
4. Теория дифракции

Принцип Гюйгенса Френеля
Огюстен Жан Френель
Предполагается что амплитуда волны в отверстии такая же как и при отсутствии экрана,
т.е. существенна только форма отверстия.
Интеграл Кирхгофа

5. Дифракция Френеля

Число зон Френеля

6. Дифракция на круглом отверстии

Метод разбиения волнового фронта на зоны Френеля
m r L mlL m
2
m
2
2
l2
4
mlL
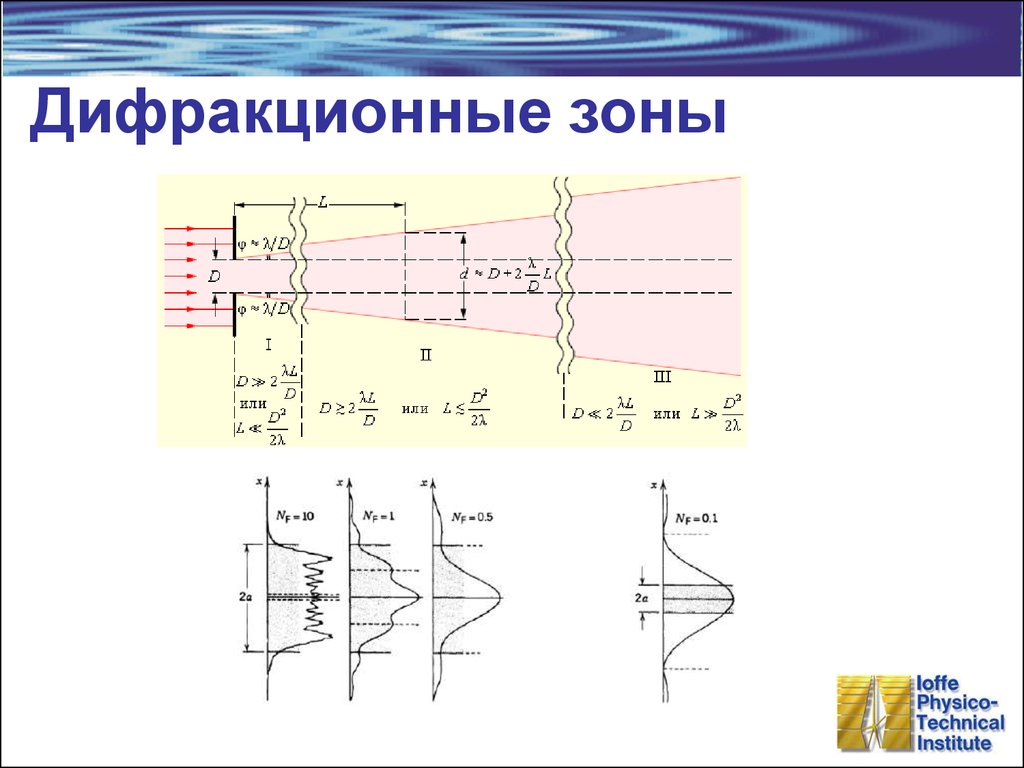
L = 1 м, l = 600 нм
Условие наблюдения
дифракции Френеля
Геометрическая оптика

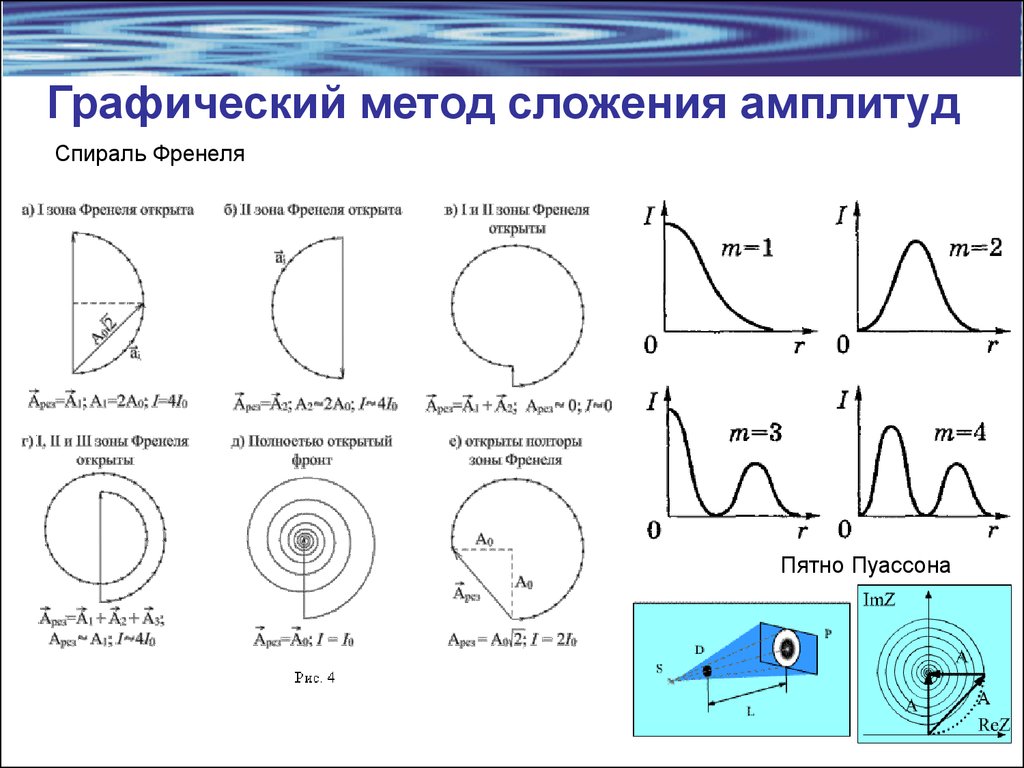
7. Графический метод сложения амплитуд

Спираль Френеля
Пятно Пуассона

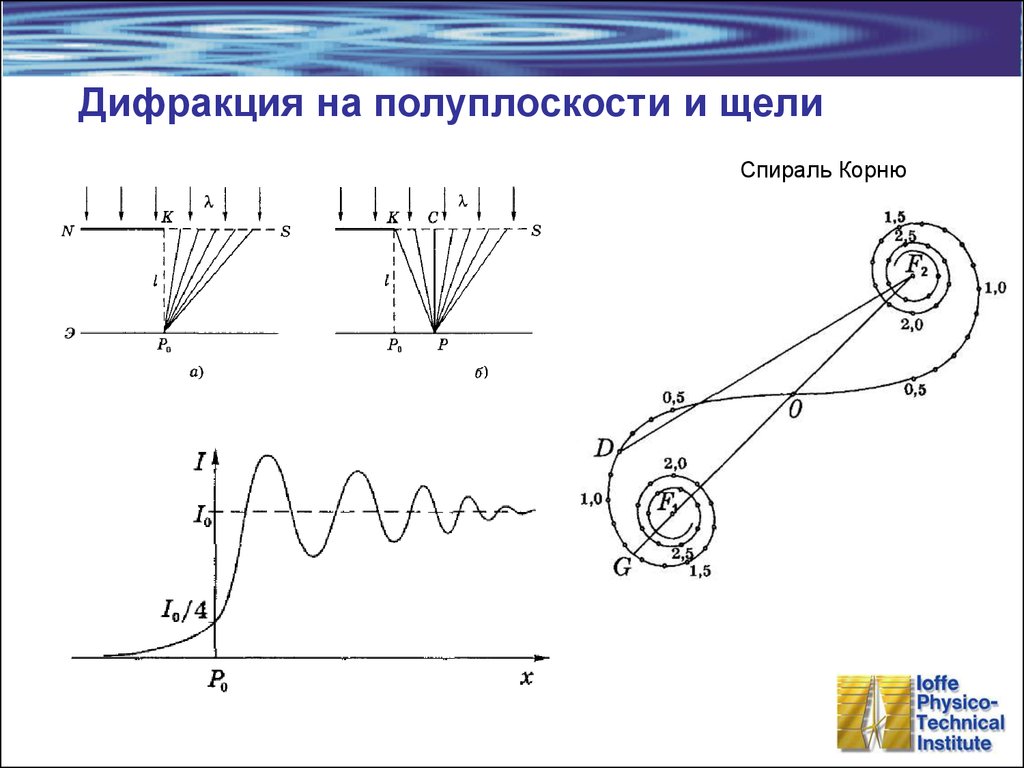
8. Дифракция на полуплоскости и щели

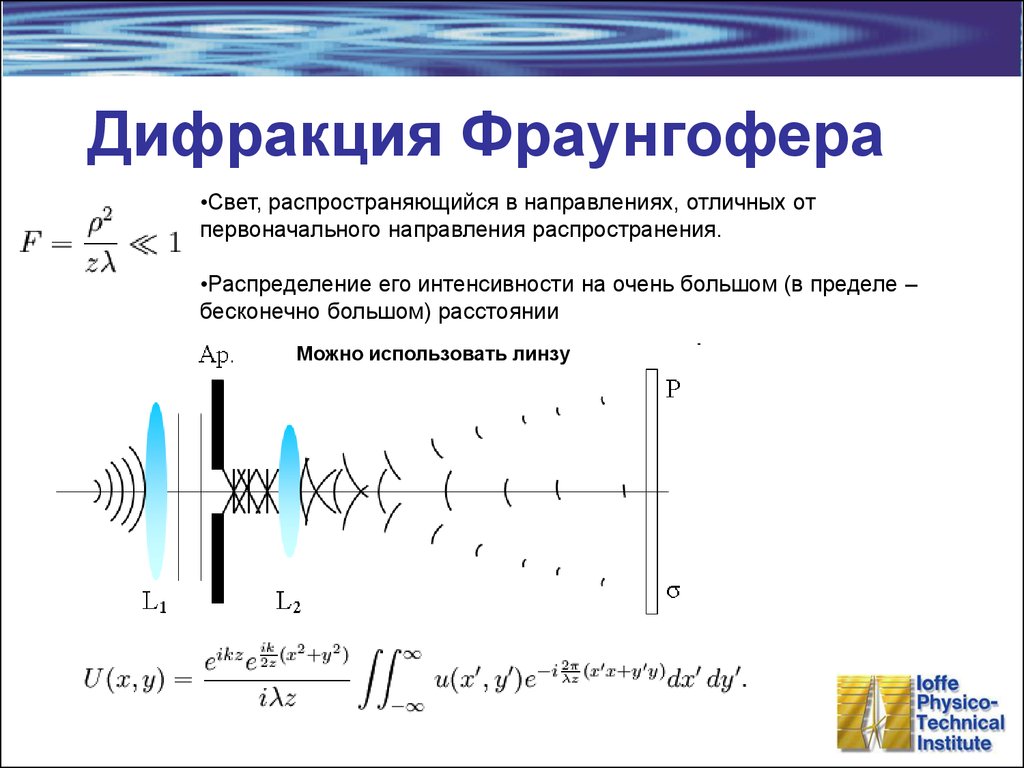
Спираль Корню

9. Дифракция Фраунгофера

•Свет, распространяющийся в направлениях, отличных от
первоначального направления распространения.
•Распределение его интенсивности на очень большом (в пределе –
бесконечно большом) расстоянии
Можно использовать линзу

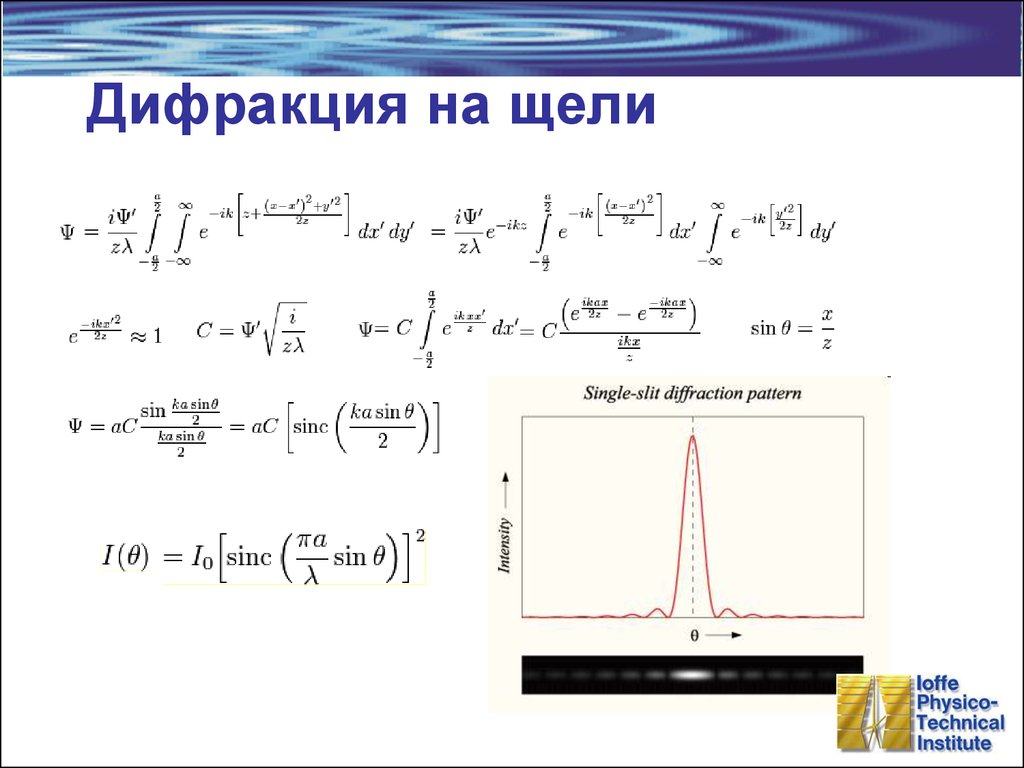
10. Дифракция на щели

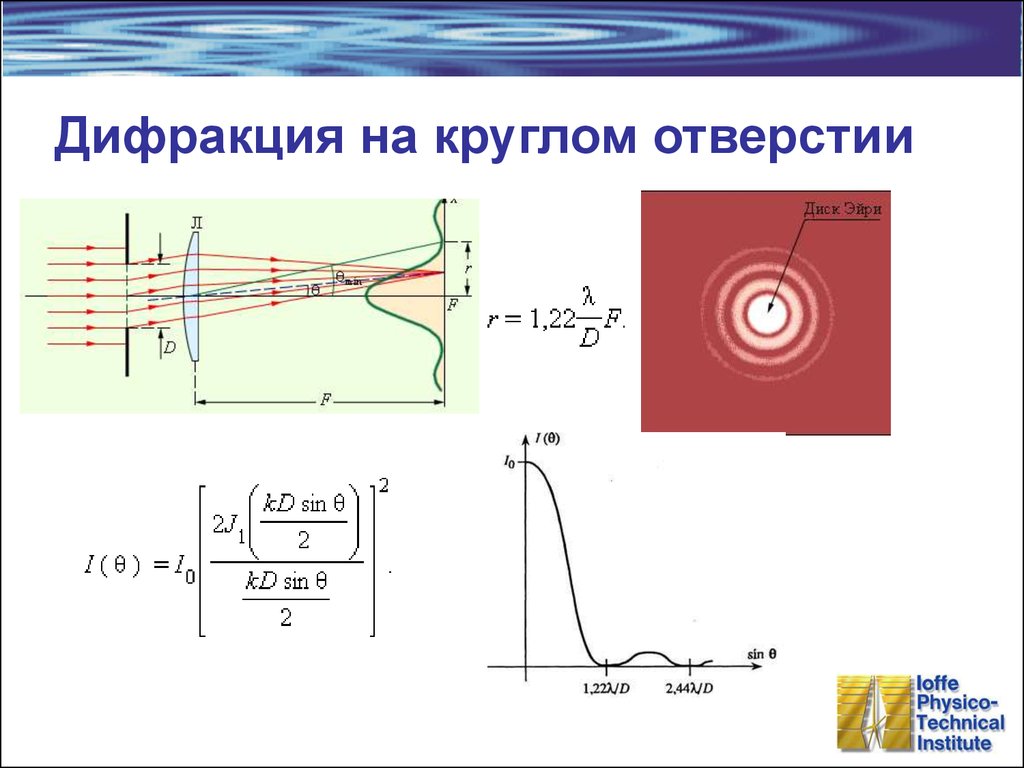
11. Дифракция на круглом отверстии

12. Дифракционная расходимость

Лазерный пучок D0 = 2 мм, L = 100 м
D ≈ D0 + 2λL/D0 = 2 + 50 ≈ 5 см.

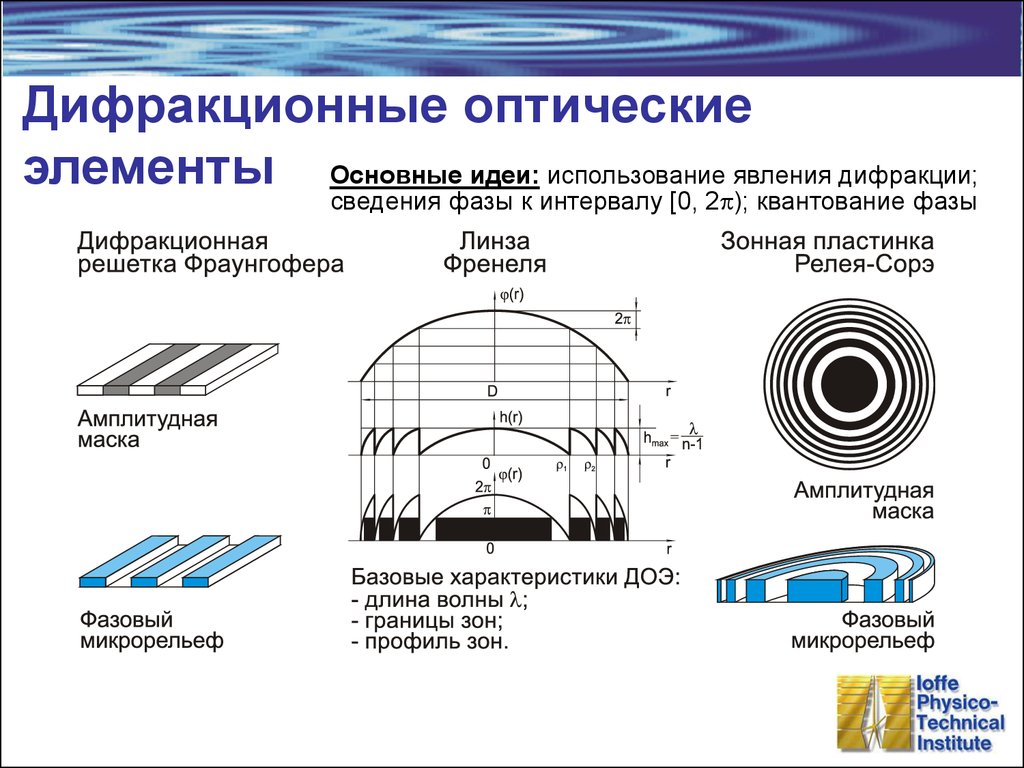
13. Дифракционные оптические элементы

Основные идеи: использование явления дифракции;
сведения фазы к интервалу [0, 2p); квантование фазы

14. Бессель-оптика и сингулярная оптика

Функция
exp
im фазы терпит m разрывов первого рода, m – порядок ДОЭ
Винтовой
фазовый ДОЭ
Винтовая
зонная пластина
Решетка
с «вилкой»
exp im
sgn cos m +kr 2
sgn cos m + x
m=1
1. Березный А.Е., Прохоров А.М.,
Сисакян И.Н., Сойфер В.А.
Бессель-оптика // ДАН, 1984.
2. Khonina S.N., Kotlyar V.V.,
Shinkaryev M.V., Soifer V.A.,
Uspleniev G.V.,
The phase rotor filter
// J. Modern Optics, 1992
1. Heckenberg N.R. et al.
Generation of optical
phase singularities by
computer-generated
holograms
// Opt. Lett., 1992
1. Bazhenov V.Yu., Soskin
M.S., Vasnetsov M.V.
Screw dislocations
in light wavefronts
// J. of Mod. Opt., 1992

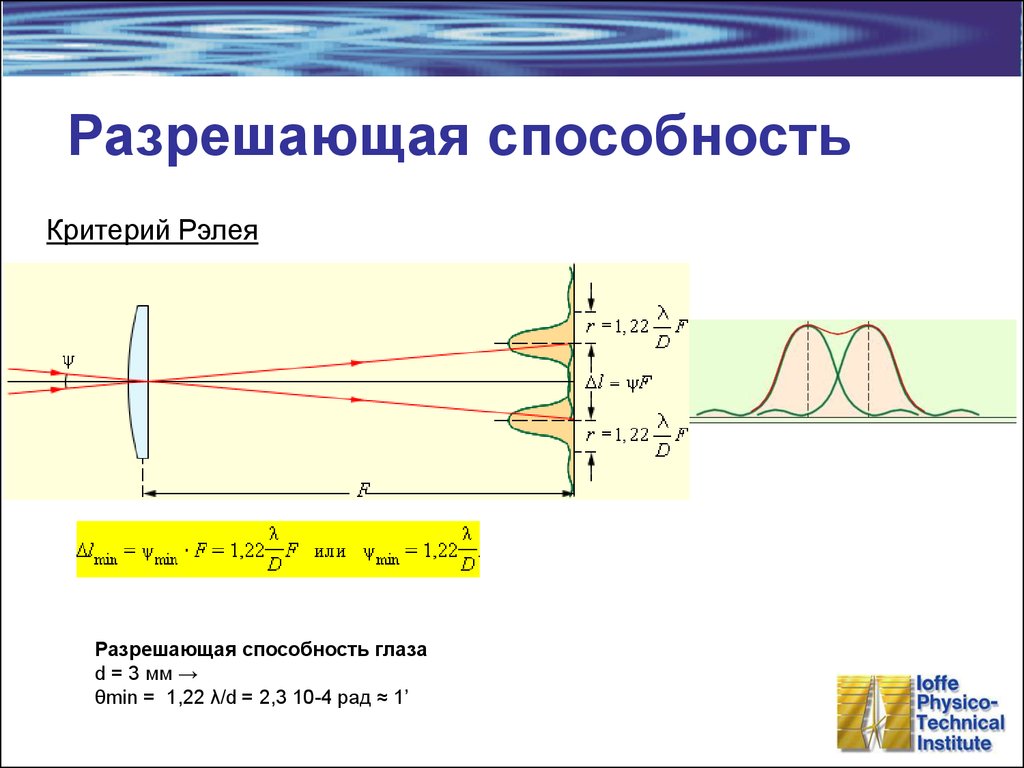
15. Разрешающая способность

Критерий Рэлея
Разрешающая способность глаза
d = 3 мм →
θmin = 1,22 λ/d = 2,3 10-4 рад ≈ 1’

16. Дифракционный предел

Mинимально возможный размер светового пятна,
которое можно получить, фокусируя свет заданной длины волны
в среде с показателем преломления n:
Для микроскопа
Эрнст Аббе 1873

17. Дифракционные зоны

18. Ближнепольная оптика

Дифракция на отверстии меньше длины волны
(волновая оптика не работает)

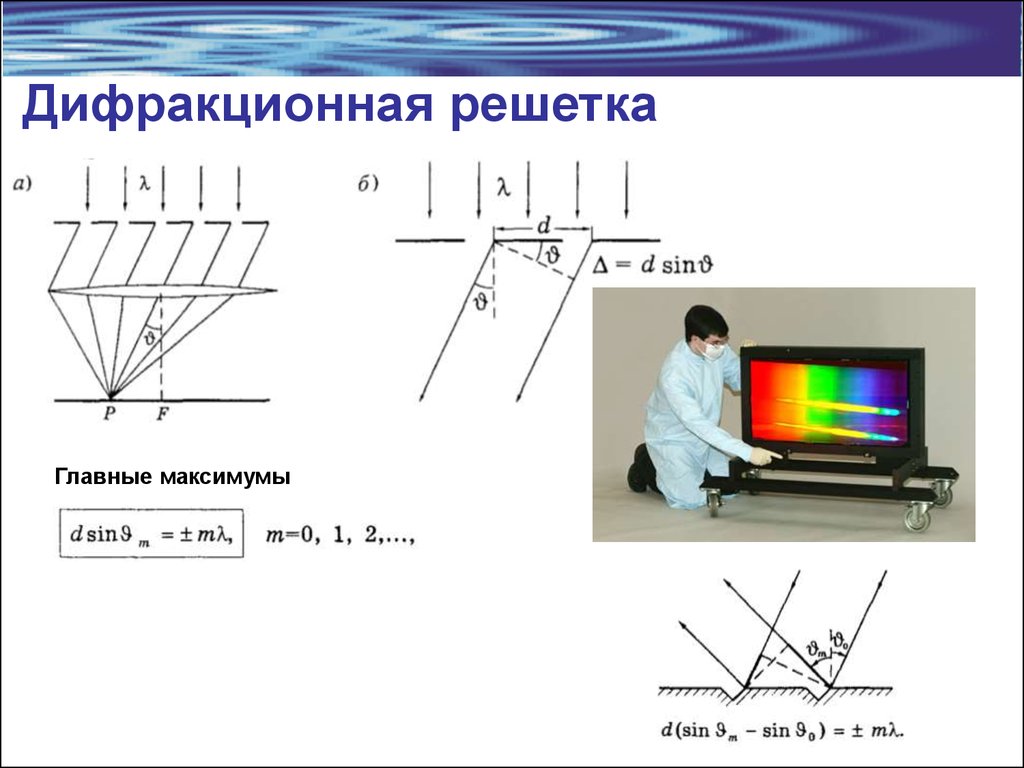
19. Дифракционная решетка

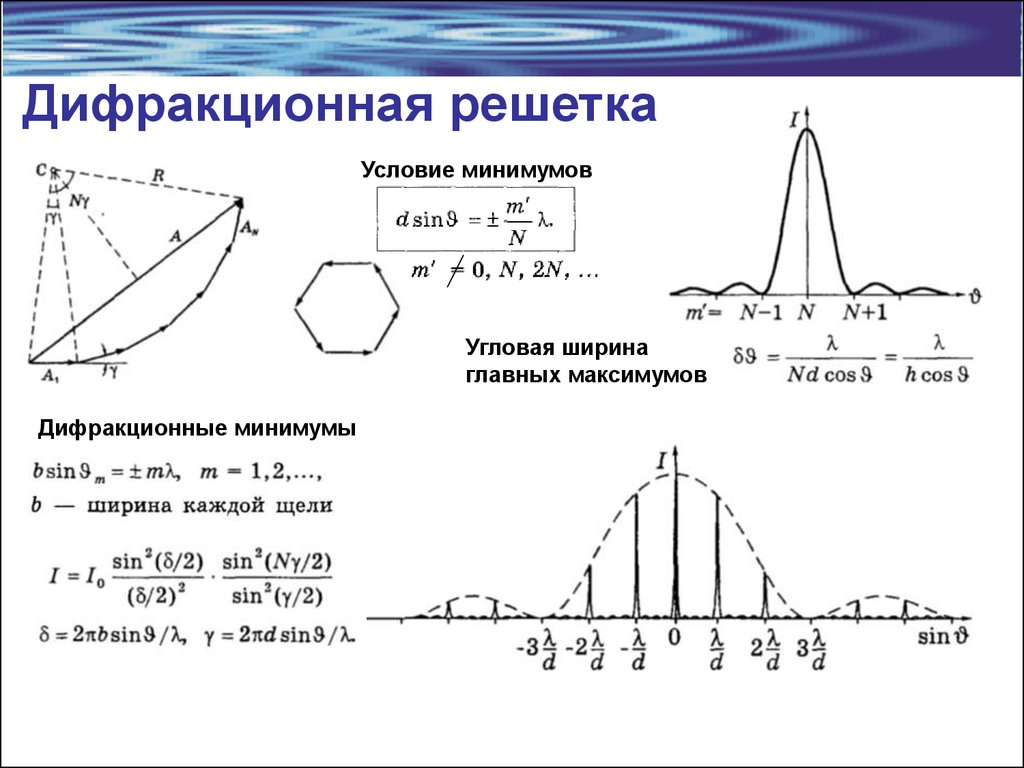
Главные максимумы

20. Дифракционная решетка

Условие минимумов
Угловая ширина
главных максимумов
Дифракционные минимумы

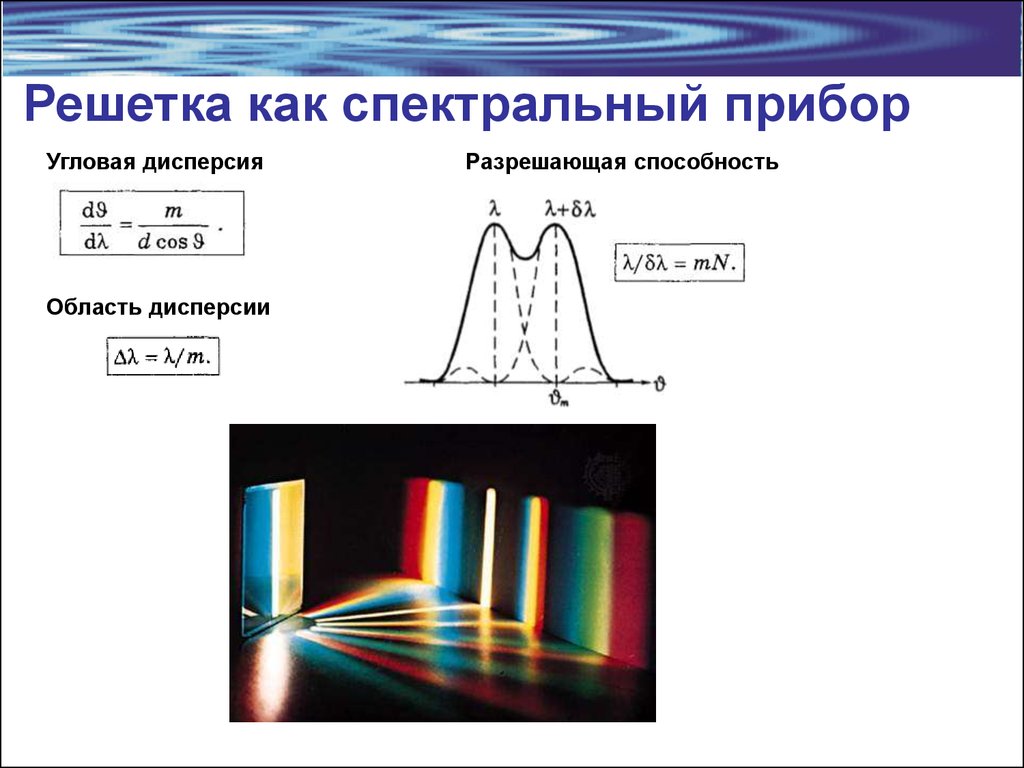
21. Решетка как спектральный прибор

Угловая дисперсия
Область дисперсии
Разрешающая способность

22. Фурье оптика

ФУРЬЕ Жан Батист Жозеф
(1768-1830)
Гармонический анализ (Преобразование Фурье)
– Представление произвольной функции f(t) (волнового фронта) в виде
гармонических функций различных частот (пространственных частот)
f (t ) F exp j 2p t d
Линейная система
– Отклик системы на гармоническую функцию известен
Двумерное преобразование Фурье в пространственных координатах.
Волны считаем монохроматическими.
f ( x, y ) F x , y exp j 2p x y t d x d y

23. Фурье оптика

Плоские волны играют роль гармонических функций
– Произвольная волна раскладывается по плоским волнам
U ( x, y, z ) A exp j k x x k y y k z z ;
z 0;U ( x, y,0) f ( x, y ) A exp j x x y y ;
x
ky
kx
; y
2p
2p
Линейная система характеризуются импульсным откликом и
функцией пропускания (отклик на гармоническую функцию)

24. Свободное пространство

U ( x, y, z ) A exp j k x x k y y k z z ;
k k x , k y , k z ; k k x k y k z
2
x arg sin k x
2
2
2p
l
k
; y arg sin y
k
k
U ( x, y,0) f ( x, y ) A exp j x x y y ;
x
x arg sin l x ;
y arg sin l y
ky
kx
; y
;
2p
2p
Параксиальном приближении
k x k ; k y k x l x ; y l y
По распределению амплитуды можно определить волновые
функции плоских волн (если известна длина волны)
U ( x, y, z ) f ( x, y ) exp j k z z ;
2p
2
2
kz
kx k y
l
2

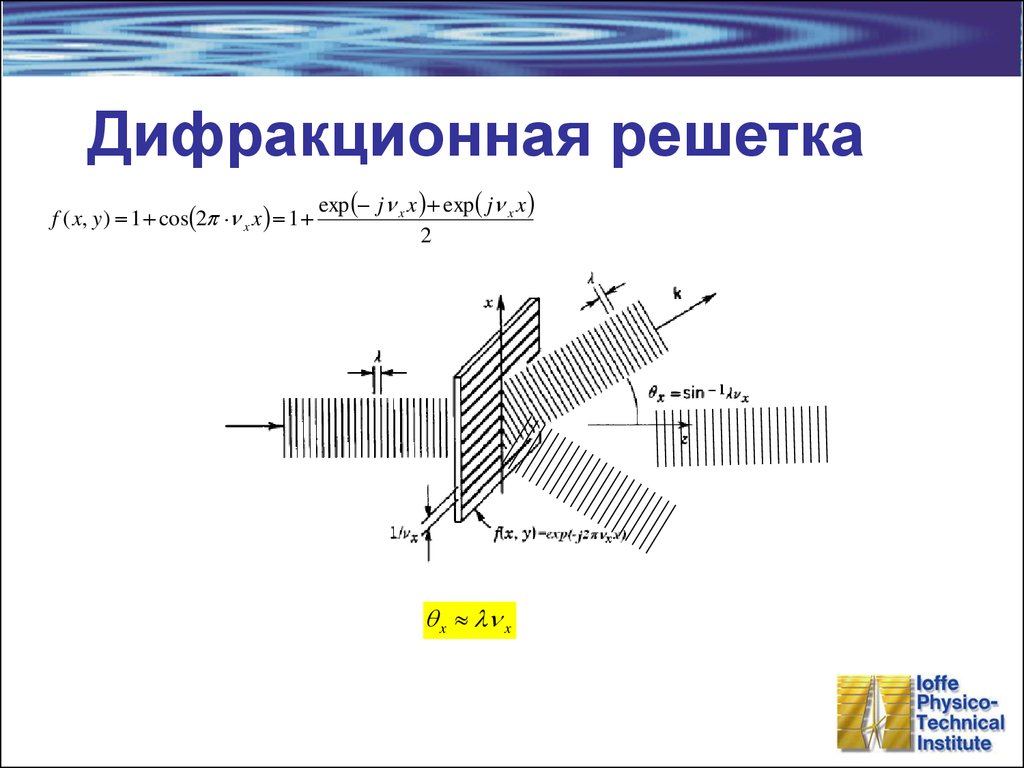
25. Дифракционная решетка

f ( x, y ) 1 cos 2p x x 1
exp j x x exp j x x
2
x l x

26. Сферическая линза

x2 y2
f ( x, y ) exp jp
exp j 2p x, y
l
F
x
x
2
2
x
x
x y
x
l F
F
x, y
y
y
2l F
y
y
x
l F
F

27. Зонная пластика Френеля

x2 y2
0
1; cos p
f ( x, y )
l
F
0; otherwise
x2 y2
, q 0, 1, 2
f ( x, y ) Cq cos qp
l
F
q
x2 y2
x2 y2
exp jqp
exp jqp
2
2
l F
l F
x y
cos qp
l F
2
Зонная пластинка работает как сферическая линза со множеством фокусов
F , F / 2
(высшие порядки дифракции), которые зависят от дины волны F~1/l
В линзе Френеля используется квадратичная модуляция фазы

28. Передаточная функция

Свободное пространство
f ( x, y ) U ( x, y,0); g ( x, y ) U ( x, y, d )
Линейная функция инвариантная к сдвигу системы координат
H ( x , y )
2
2
H ( x , y ) exp j 2pd 1 2 x y
l
g ( x, y ) A exp j k x x k y y k z d
exp jkz d
f ( x, y )
A exp j k x x k y y
H ( x , y ) exp j 2pd
1
2
2
2 x y
l
Плоские волны с пространственными частотами
x 2 y 2 1 2
Испытывают набег фазы при распространении, с более высокими
l
частотами затухают
Детали с размерами менее длины волны не могут быть переданы линейной оптической системой на расстояние более
длины волны (предел разрешения)
Произвольная оптическая система
g ( x, y )
F (
x
, y ) H ( x , y ) exp j 2p x x y y d x d y
F ( x , y )
f ( x, y) exp j 2p
x
x y y dxdy

29. Фурье преобразование

Свободное пространство
x x ld
x y
g
(
x
,
y
)
h
F
,
Приближение Фраунгофера
0
ld ld
y y ld
Одна плоская волна соответствует каждой точке
Нет вклада других волн из-за деструктивной интерференции
Дифракция Фраунгофера
I ( x, y)
Ii
x y
F
,
2
l
d
ld ld

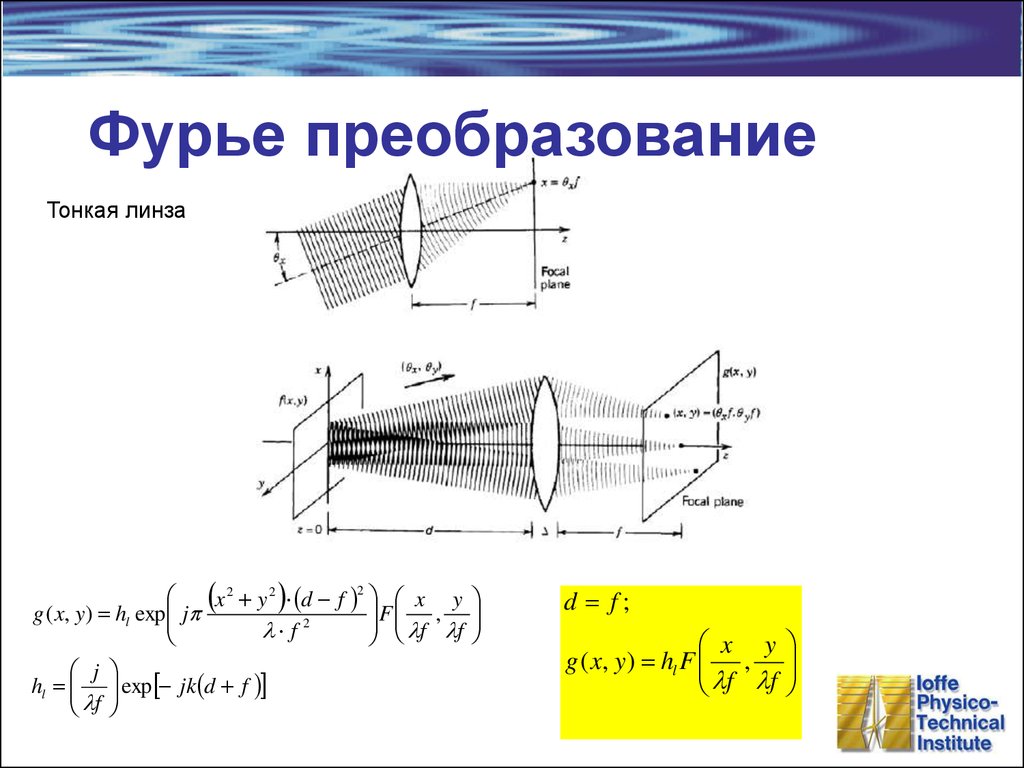
30. Фурье преобразование

Тонкая линза
x 2 y 2 d f 2 x y
F ,
g ( x, y ) hl exp jp
2
lf lf
l f
j
hl exp jk d f
lf
d f;
x y
g ( x, y ) hl F ,
lf lf

31. Формирование изображения

Одна линза (лучевое приближение)
1 1 1
f d1 d 2
p ( x, y ) - апертурная функция
1 1 1
; ps p d 2
f d1 d 2
x
y
h( x, y ) ~ p
,
d
d
2
2
Циркулярная апертура
ps
d 2 D
2
Меньше апертура – больше глубина резкости

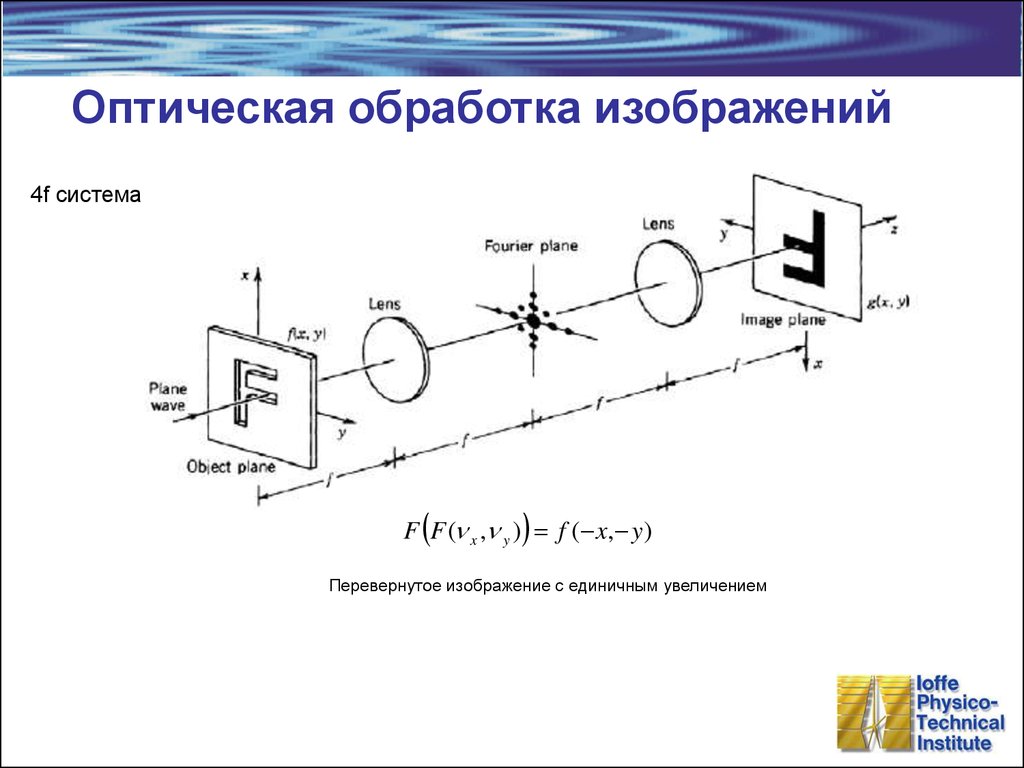
32. Оптическая обработка изображений

4f система
F F ( x , y ) f ( x, y )
Перевернутое изображение с единичным увеличением

33. Пространственная фильтрация

4f система
H ( x , y ) ~ p lf x , lf y - передаточн ая функция 4f системы
h( x, y) ~
1
lf 2
x y
P , - импульсный отклик 4f системы
lf lf

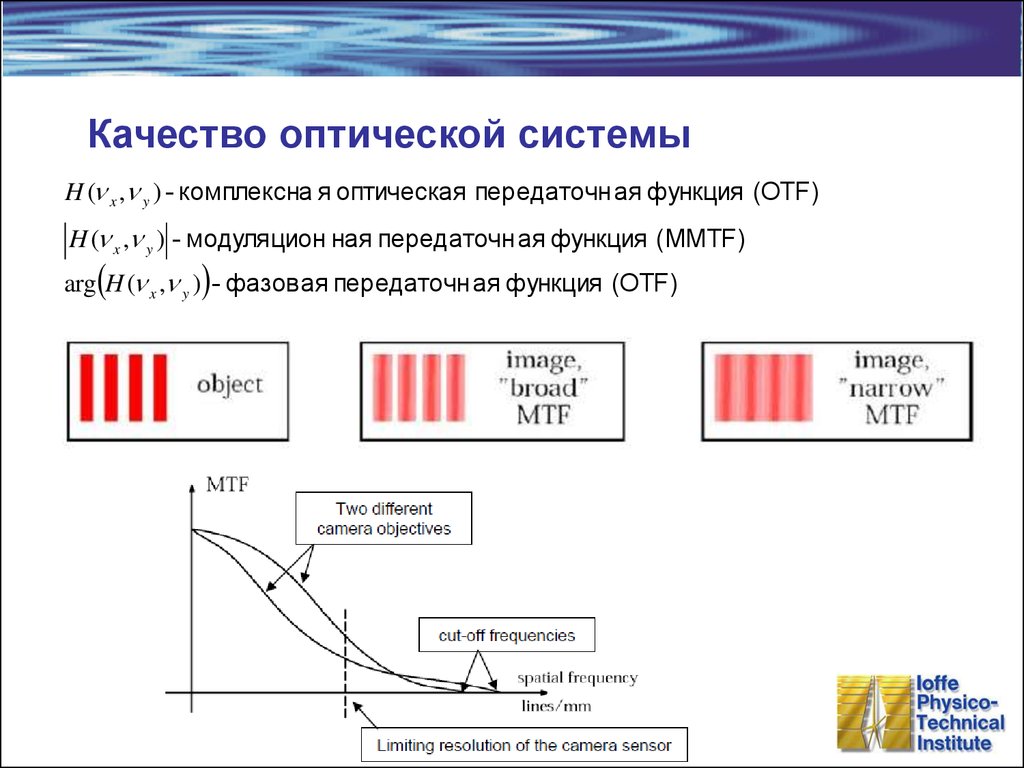
34. Качество оптической системы

H ( x , y ) - комплексна я оптическая передаточн ая функция (OTF)
H ( x , y ) - модуляцион ная передаточн ая функция (ММTF)
arg H ( x , y ) - фазовая передаточн ая функция (OTF)