Similar presentations:
Волны. Упругие волны. Основные понятия
1. Волны
ВоГУЛекция 09
Волны
Кузина Л.А.,
к.ф.-м.н., доцент
2019 г.
1
2. План
1.2.
3.
4.
5.
Упругие волны. Основные понятия.
Дифференциальное уравнение волны.
Стоячие волны.
Скорость упругих волн.
Энергия волны. Групповая скорость. Вектор плотности
потока энергии (вектор Умова). Интенсивность волны.
6. Элементы акустики.
7. Эффект Доплера для звуковых волн.
2
3.
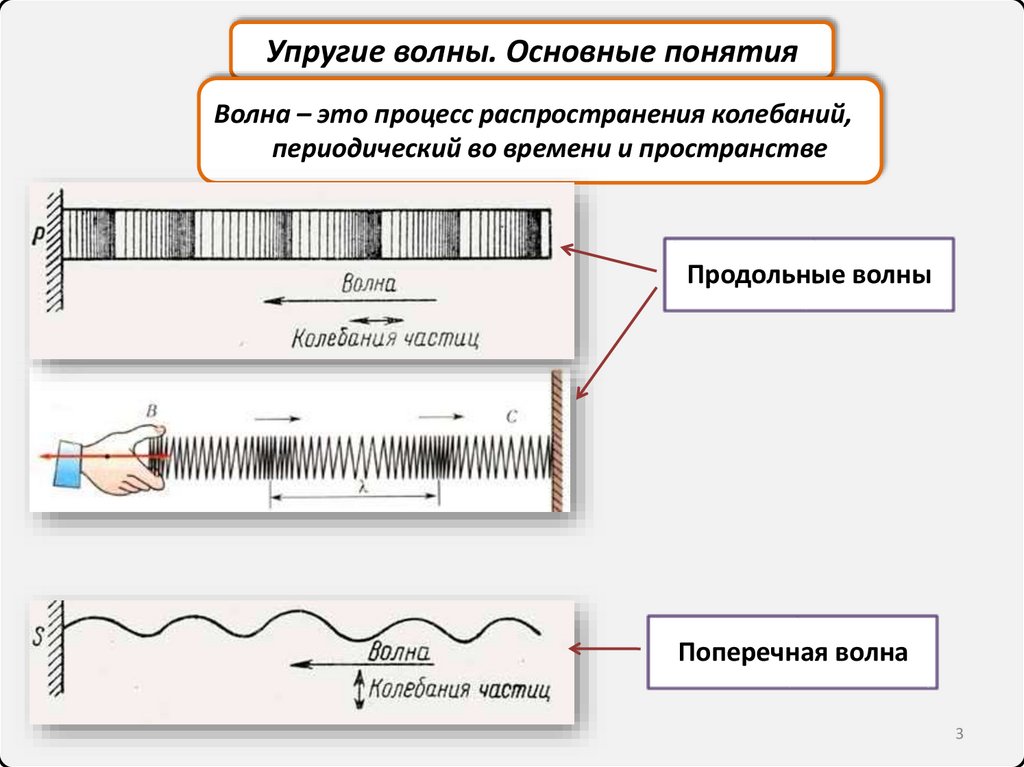
Упругие волны. Основные понятияВолна – это процесс распространения колебаний,
периодический во времени и пространстве
Продольные волны
Поперечная волна
3
4.
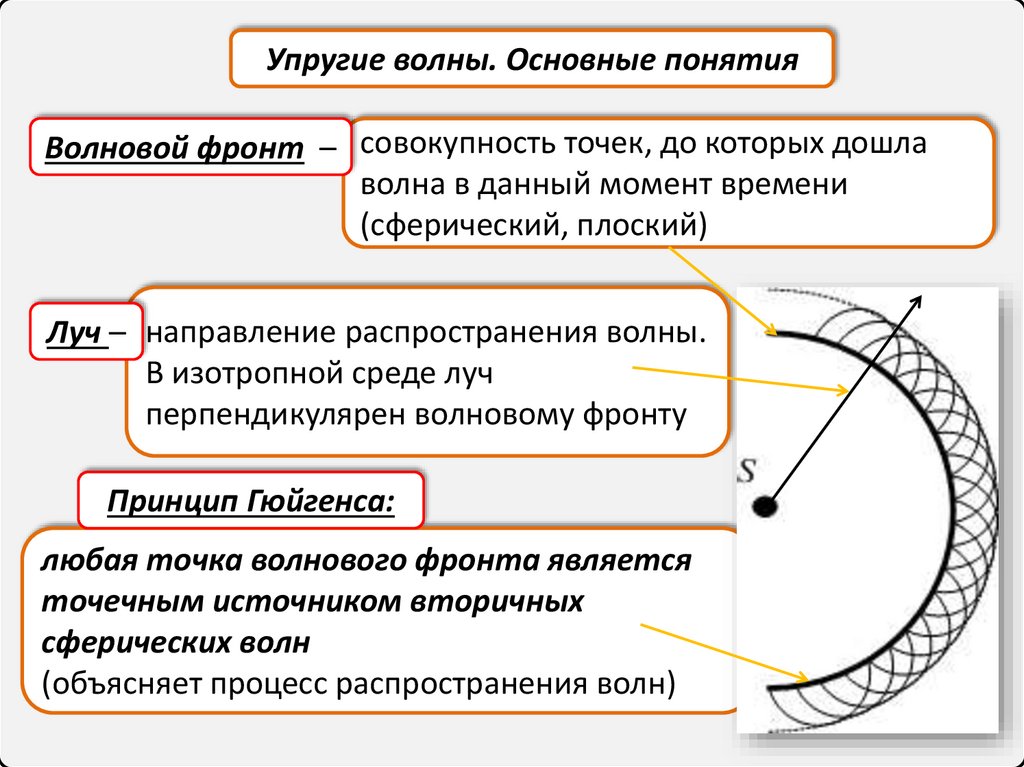
Упругие волны. Основные понятияВолновой фронт – совокупность точек, до которых дошла
волна в данный момент времени
(сферический, плоский)
Луч – направление распространения волны.
В изотропной среде луч
перпендикулярен волновому фронту
Принцип Гюйгенса:
любая точка волнового фронта является
точечным источником вторичных
сферических волн
(объясняет процесс распространения волн)
5.
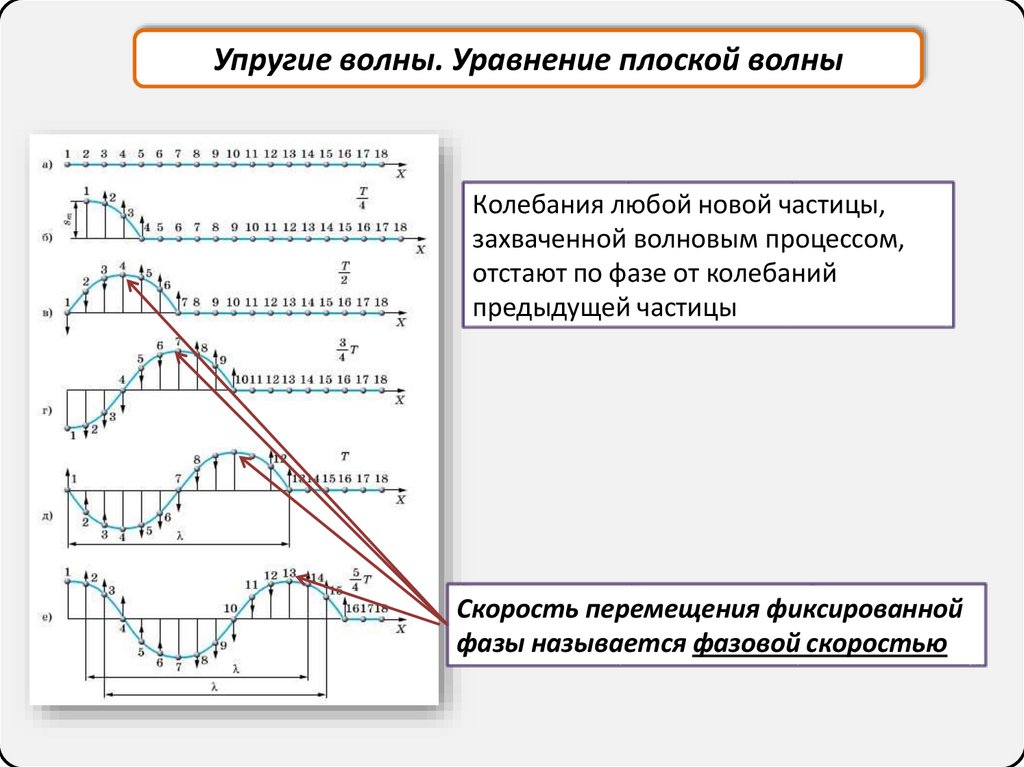
Упругие волны. Уравнение плоской волныКолебания любой новой частицы,
захваченной волновым процессом,
отстают по фазе от колебаний
предыдущей частицы
Скорость перемещения фиксированной
фазы называется фазовой скоростью
6.
67.
78.
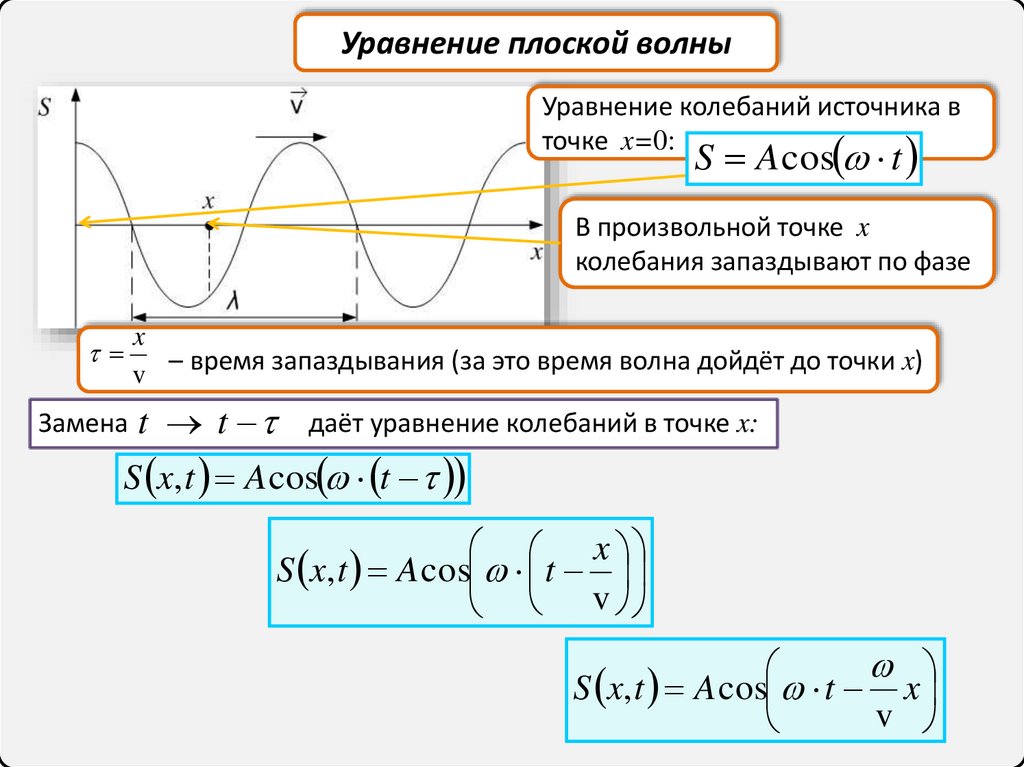
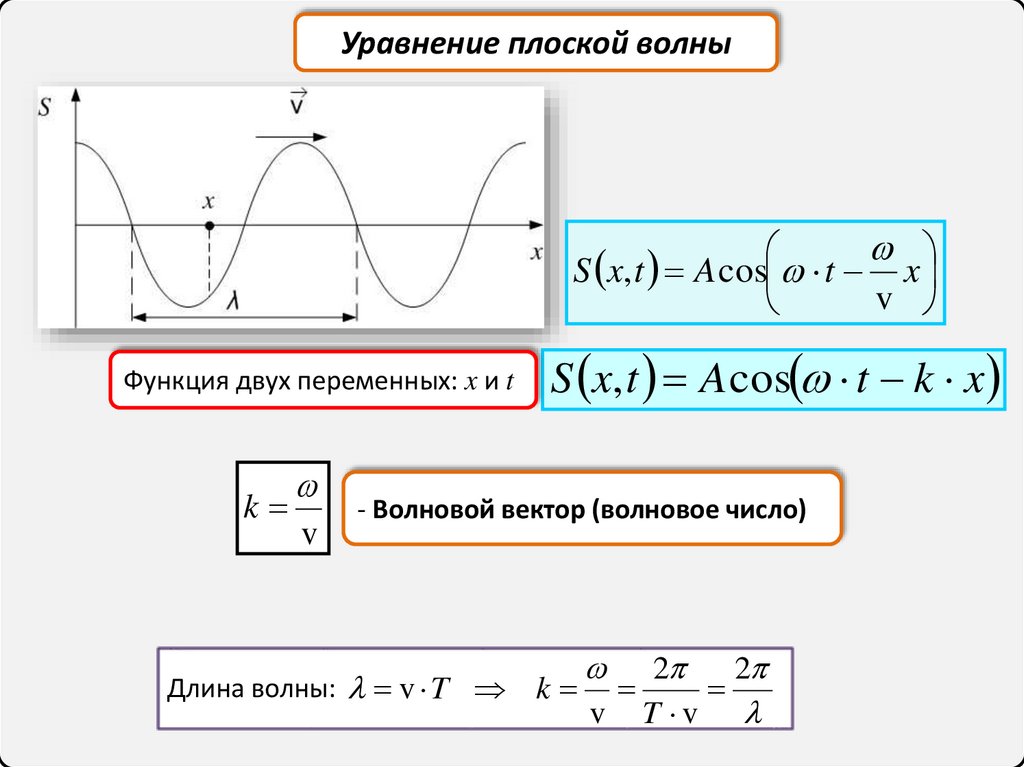
Уравнение плоской волныУравнение колебаний источника в
точке x=0:
S A cos t
В произвольной точке x
колебания запаздывают по фазе
x
– время запаздывания (за это время волна дойдёт до точки x)
v
Замена t t
даёт уравнение колебаний в точке x:
S x, t A cos t
x
S x, t A cos t
v
S x, t A cos t x
v
9.
Уравнение плоской волныS x, t A cos t x
v
Функция двух переменных: x и t
k
v
S x, t A cos t k x
- Волновой вектор (волновое число)
Длина волны: v T
k
v
2
2
T v
10.
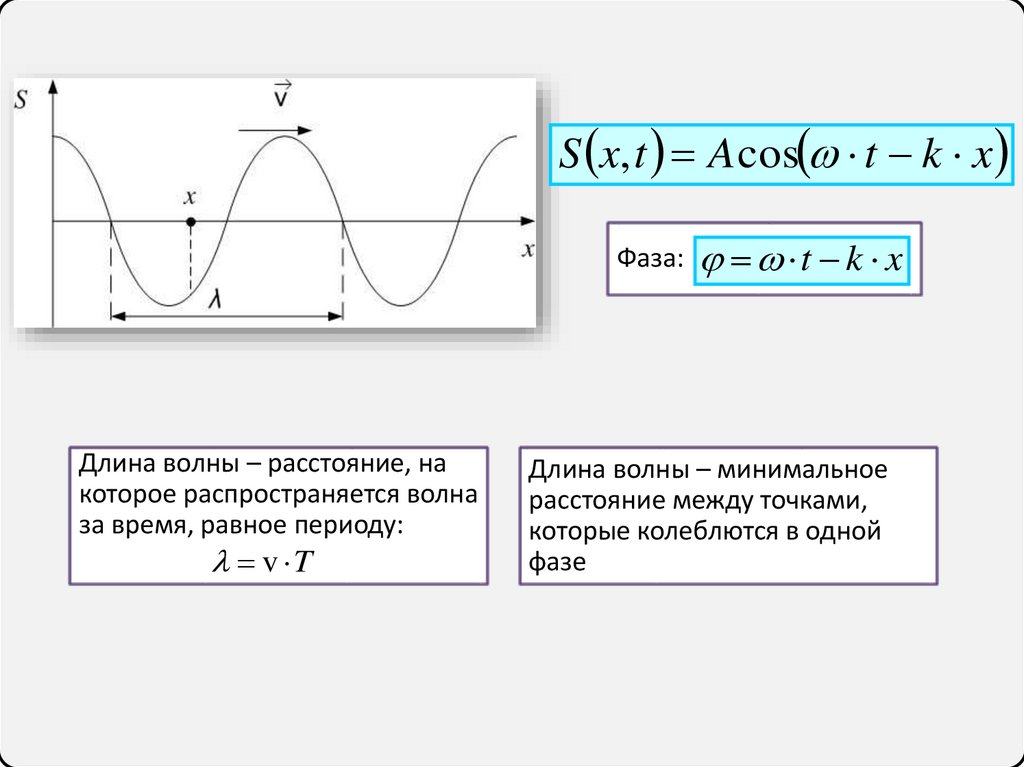
S x, t A cos t k xФаза: t k x
Длина волны – расстояние, на
которое распространяется волна
за время, равное периоду:
v T
Длина волны – минимальное
расстояние между точками,
которые колеблются в одной
фазе
11.
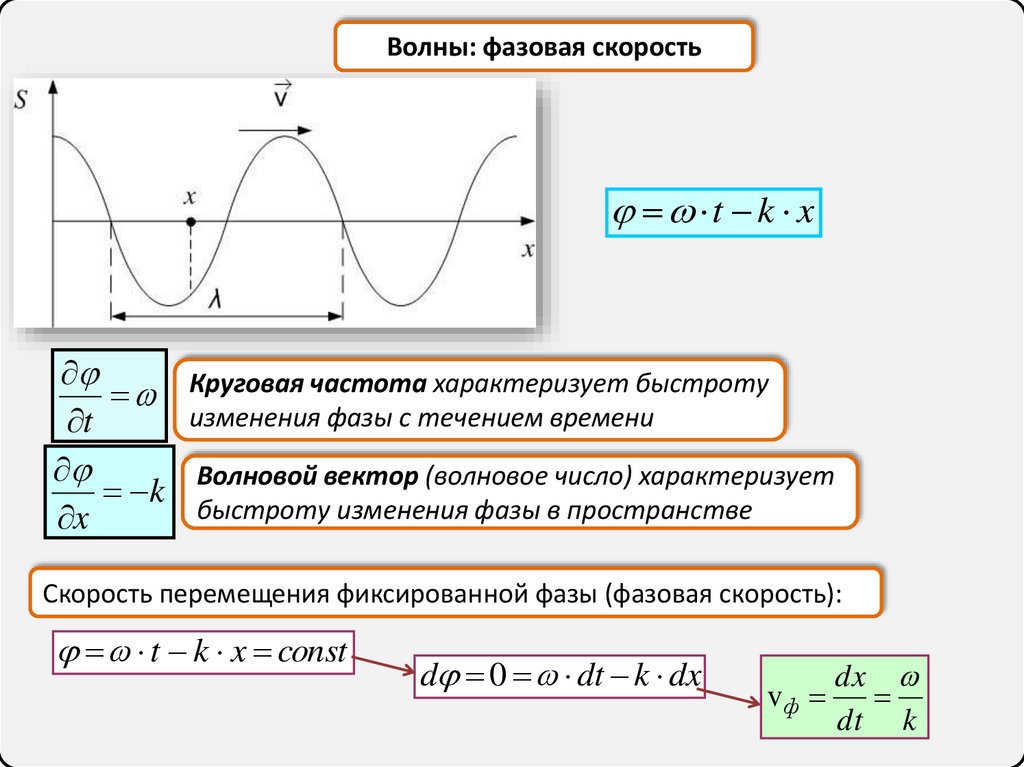
Волны: фазовая скоростьt k x
t
k
x
Круговая частота характеризует быстроту
изменения фазы с течением времени
Волновой вектор (волновое число) характеризует
быстроту изменения фазы в пространстве
Скорость перемещения фиксированной фазы (фазовая скорость):
t k x const
d 0 dt k dx
vф
dx
dt k
12.
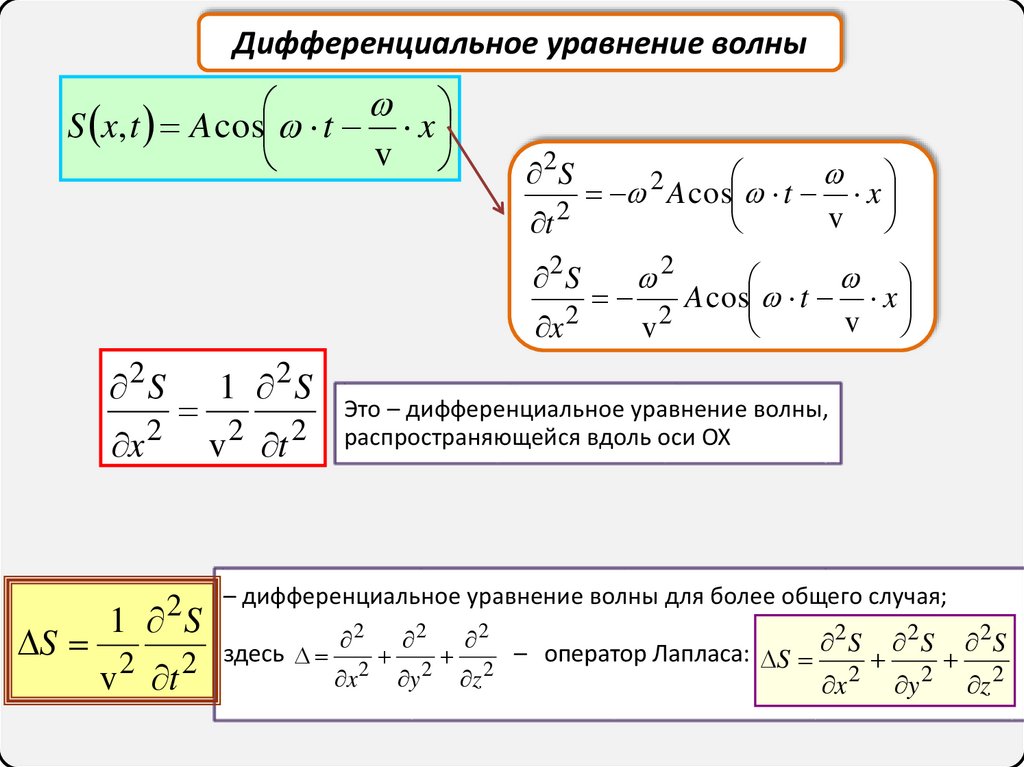
Дифференциальное уравнение волныS x, t A cos t x
v
2 A cos t x
v
t 2
2S
A cos t x
2
2
v
x
v
2S
2S
x 2
S
2
1 S
2
v t
1 2S
v 2 t 2
2
Это – дифференциальное уравнение волны,
распространяющейся вдоль оси OX
– дифференциальное уравнение волны для более общего случая;
2
2
2
2 здесь x 2 y 2 z 2 – оператор Лапласа: S
2S
x
2
2S
y
2
2S
z 2
13.
S1 2S
v 2 t 2
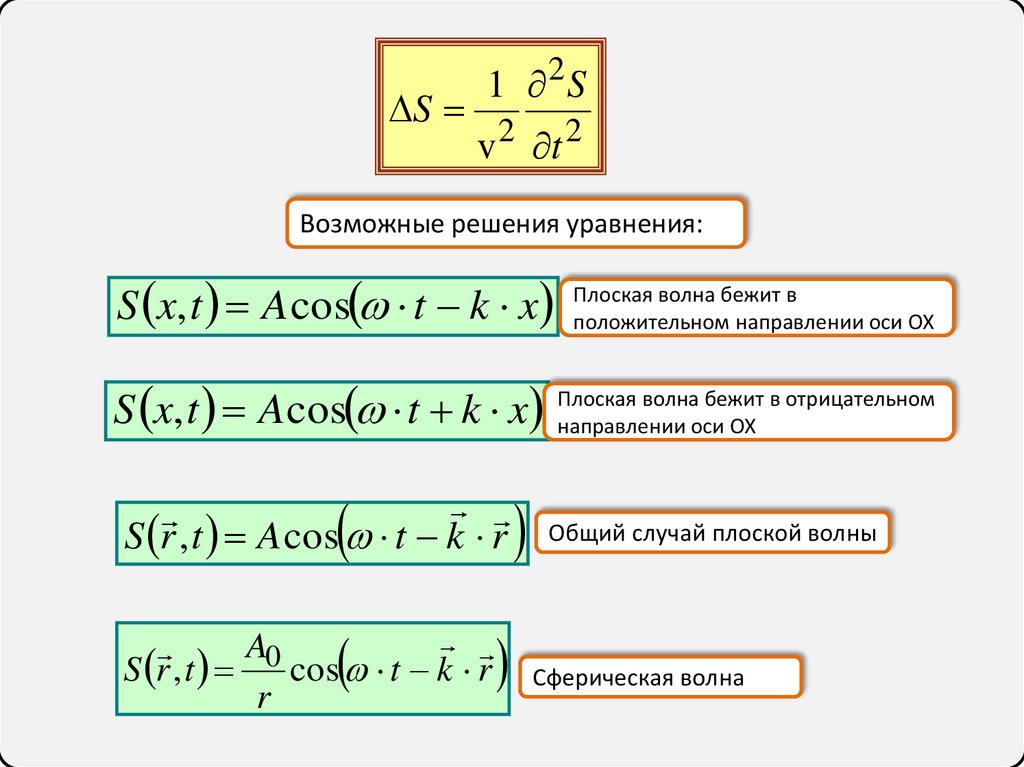
Возможные решения уравнения:
волна бежит в
S x, t A cos t k x Плоская
положительном направлении оси OX
волна бежит в отрицательном
S x, t A cos t k x Плоская
направлении оси OX
Сферическая волна
S r , t A cos t k r
A0
S r , t
cos t k r
r
Общий случай плоской волны
14.
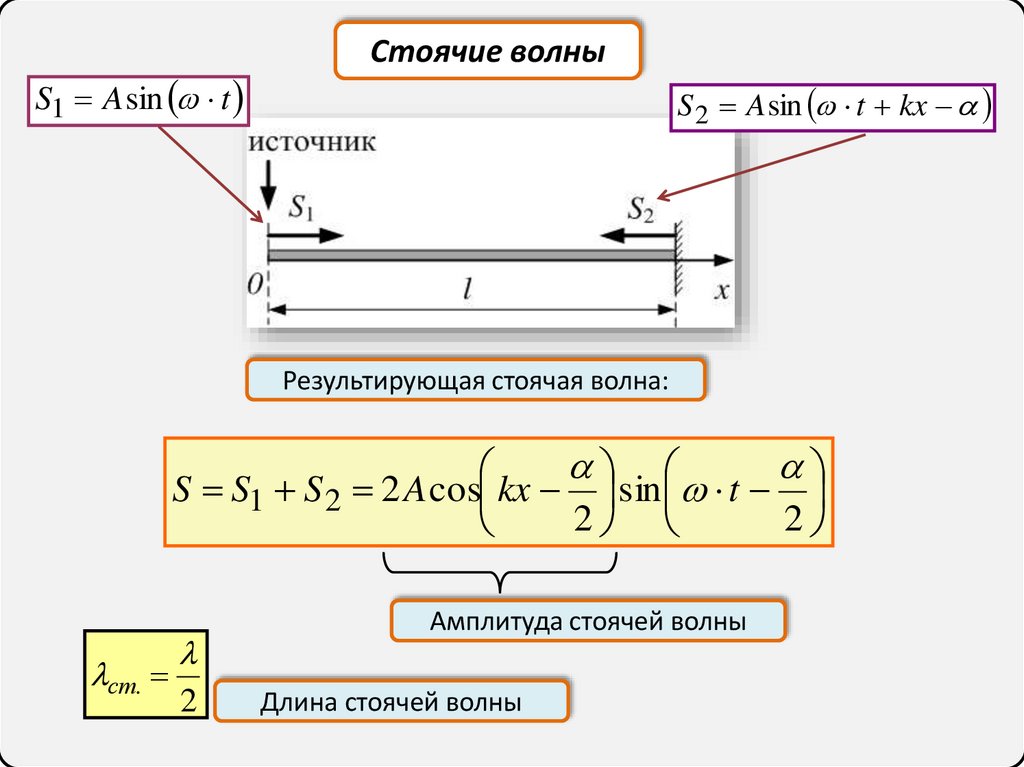
S1 A sin tСтоячие волны
S 2 A sin t kx
Результирующая стоячая волна:
S S1 S 2 2 A cos kx sin t
2
2
ст.
2
Амплитуда стоячей волны
Длина стоячей волны
15.
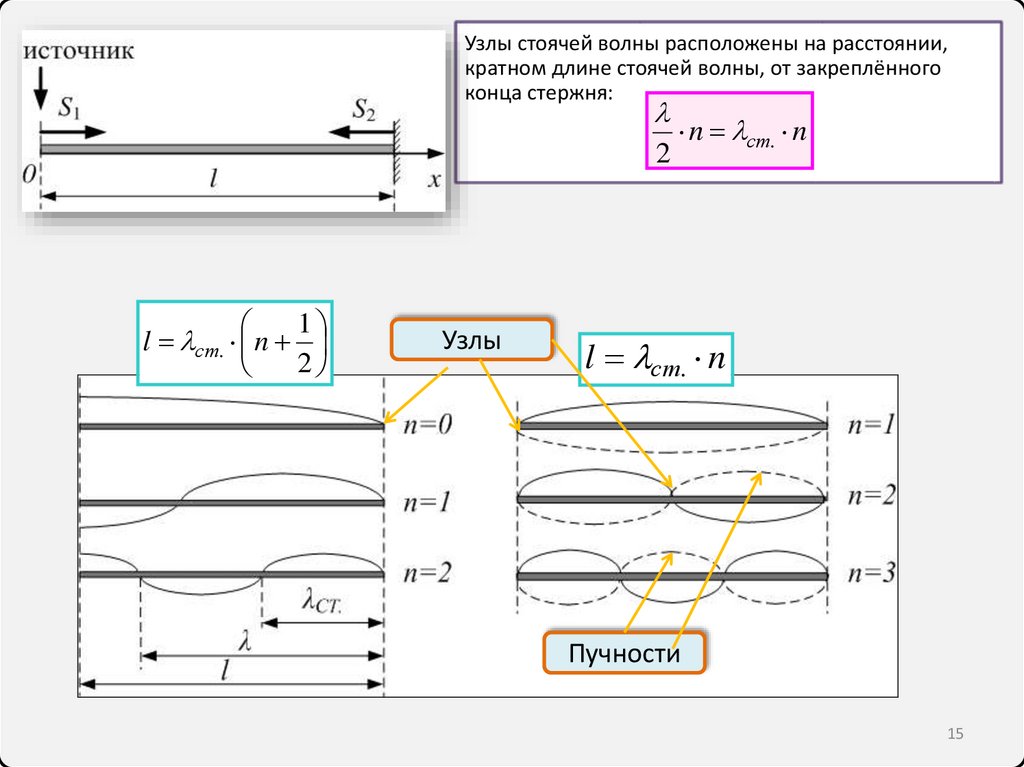
Узлы стоячей волны расположены на расстоянии,кратном длине стоячей волны, от закреплённого
конца стержня:
2
1
l ст. n
2
Узлы
n ст. n
l ст. n
Пучности
15
16.
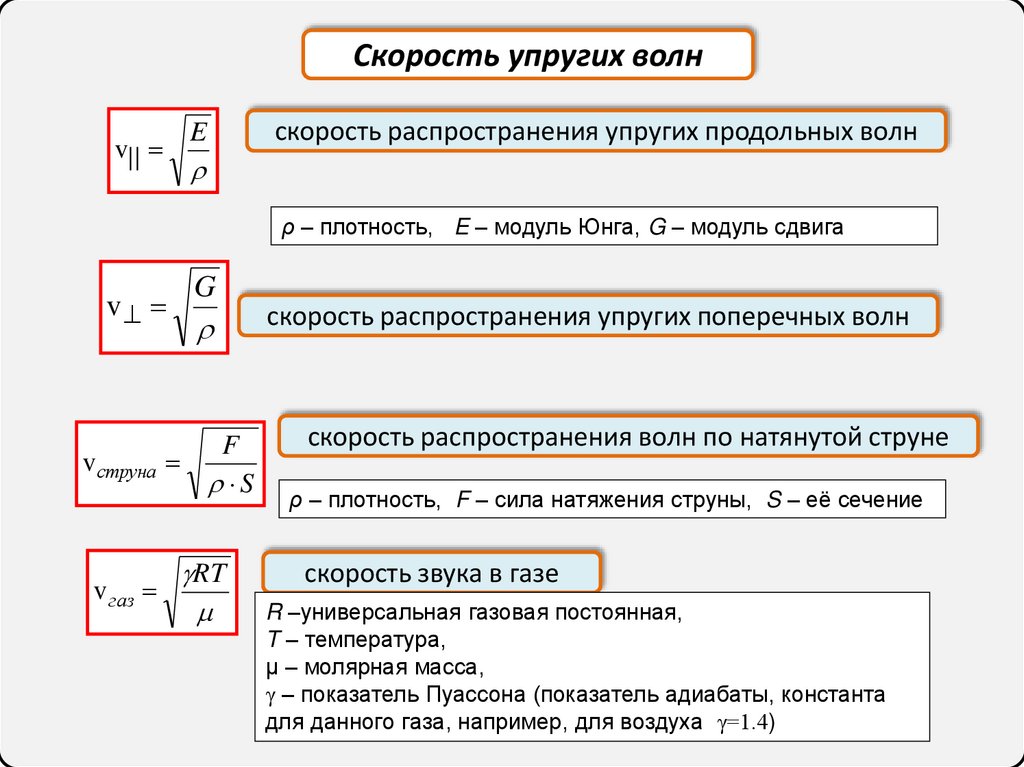
Скорость упругих волнv| |
E
скорость распространения упругих продольных волн
ρ – плотность, E – модуль Юнга, G – модуль сдвига
v
G
F
vструна
S
v газ
RT
скорость распространения упругих поперечных волн
скорость распространения волн по натянутой струне
ρ – плотность, F – сила натяжения струны, S – её сечение
скорость звука в газе
R –универсальная газовая постоянная,
T – температура,
μ – молярная масса,
γ – показатель Пуассона (показатель адиабаты, константа
для данного газа, например, для воздуха γ=1.4)
17.
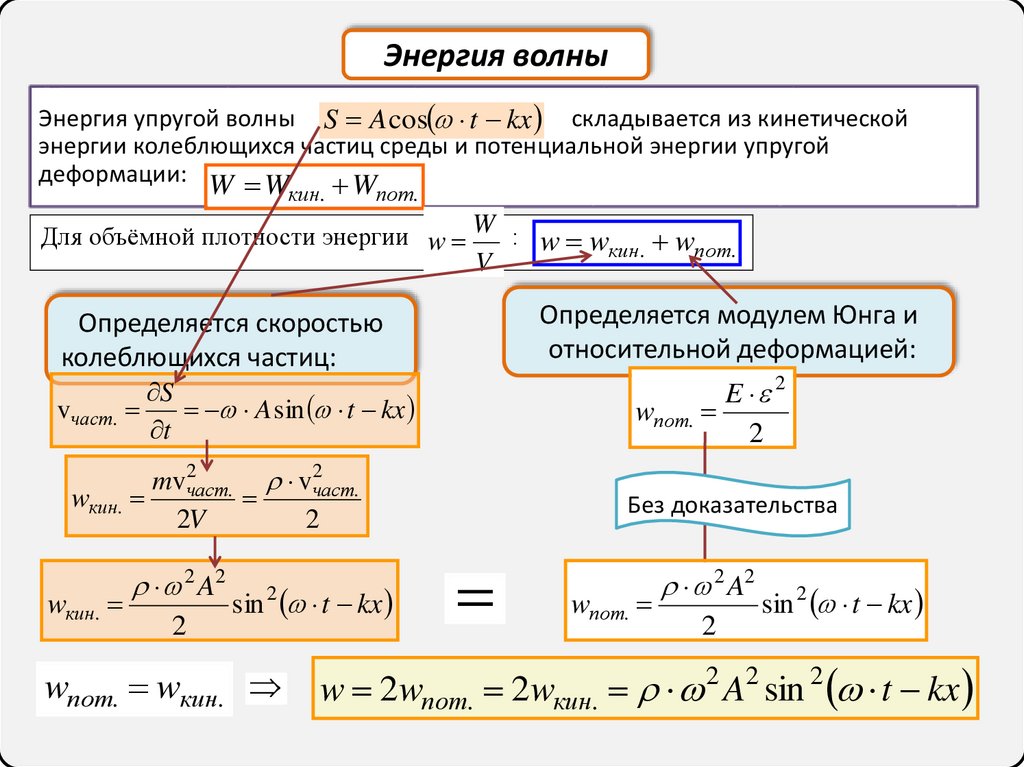
Энергия волныЭнергия упругой волны S A cos t kx складывается из кинетической
энергии колеблющихся частиц среды и потенциальной энергии упругой
деформации: W W
W
кин.
пот.
Для объёмной плотности энергии w W : w wкин. wпот.
V
Определяется модулем Юнга и
относительной деформацией:
Определяется скоростью
колеблющихся частиц:
E 2
wпот.
2
S
vчаст.
A sin t kx
t
2
2
mvчаст
v
.
част.
wкин.
2V
2
wкин.
2 A2
2
sin t kx
2
wпот. wкин.
Без доказательства
wпот.
2 A2
2
sin 2 t kx
w 2wпот. 2wкин. 2 A2 sin 2 t kx
18.
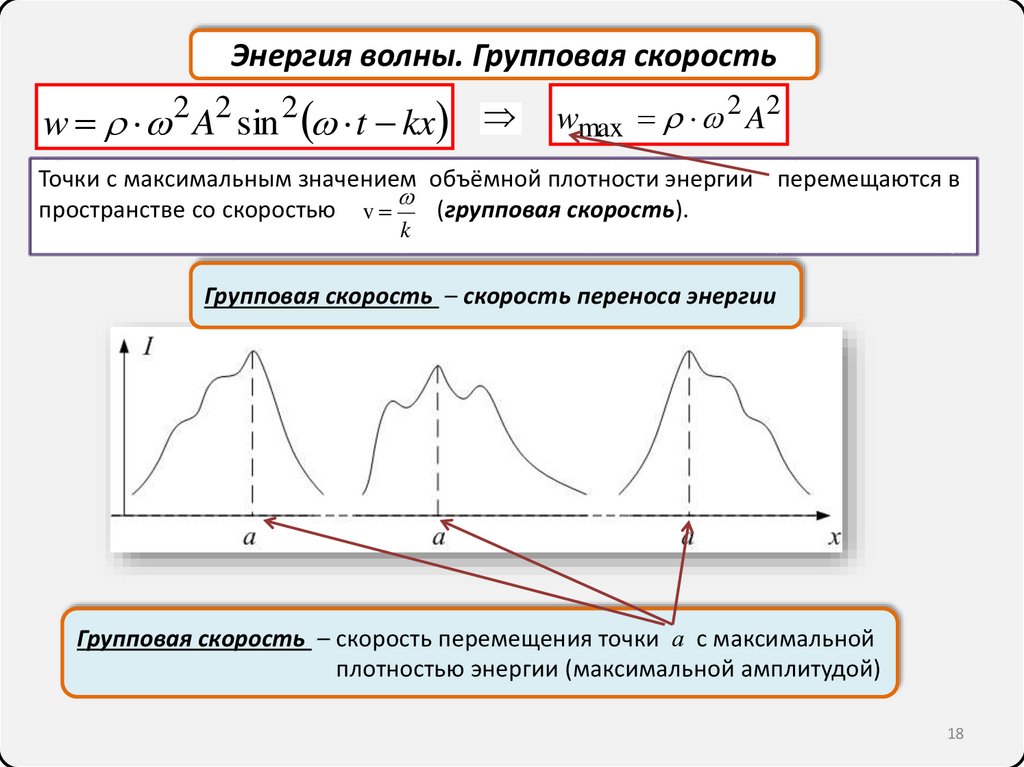
Энергия волны. Групповая скоростьw 2 A2 sin 2 t kx
wmax 2 A2
Точки с максимальным значением объёмной плотности энергии перемещаются в
пространстве со скоростью v (групповая скорость).
k
Групповая скорость – скорость переноса энергии
Групповая скорость – скорость перемещения точки а с максимальной
плотностью энергии (максимальной амплитудой)
18
19.
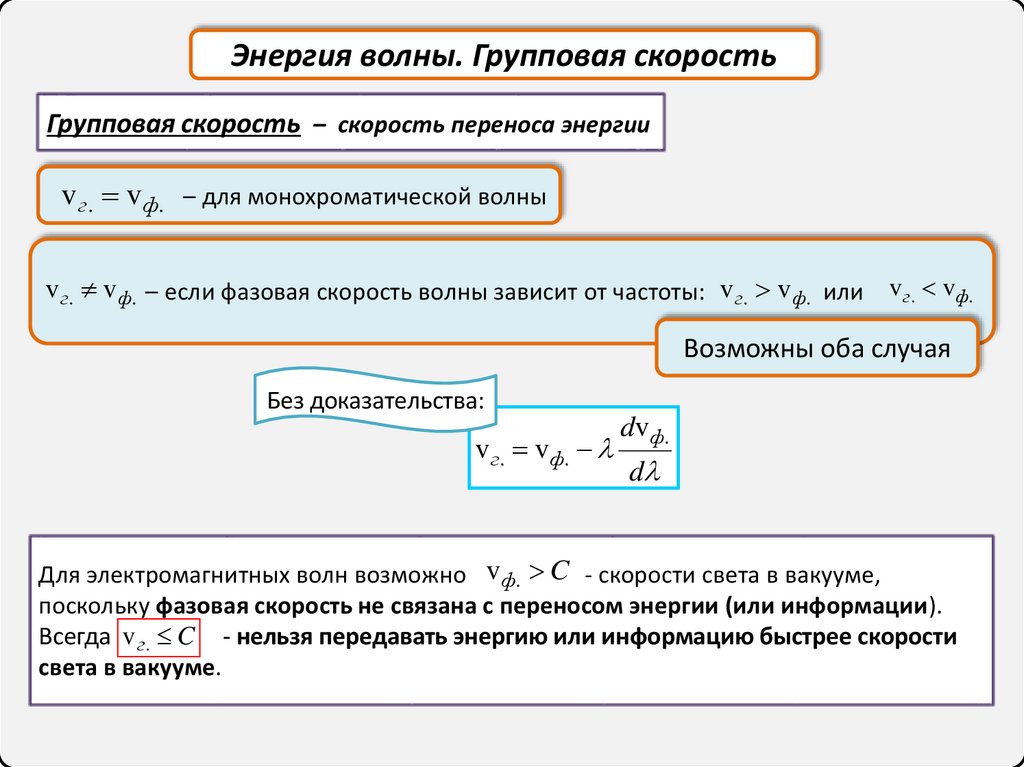
Энергия волны. Групповая скоростьГрупповая скорость – скорость переноса энергии
v г. vф. – для монохроматической волны
v г. vф. – если фазовая скорость волны зависит от частоты: v г. vф. или v г. vф.
Возможны оба случая
Без доказательства:
v г. vф.
dvф.
d
Для электромагнитных волн возможно vф. C - скорости света в вакууме,
поскольку фазовая скорость не связана с переносом энергии (или информации).
Всегда v г. C - нельзя передавать энергию или информацию быстрее скорости
света в вакууме.
20.
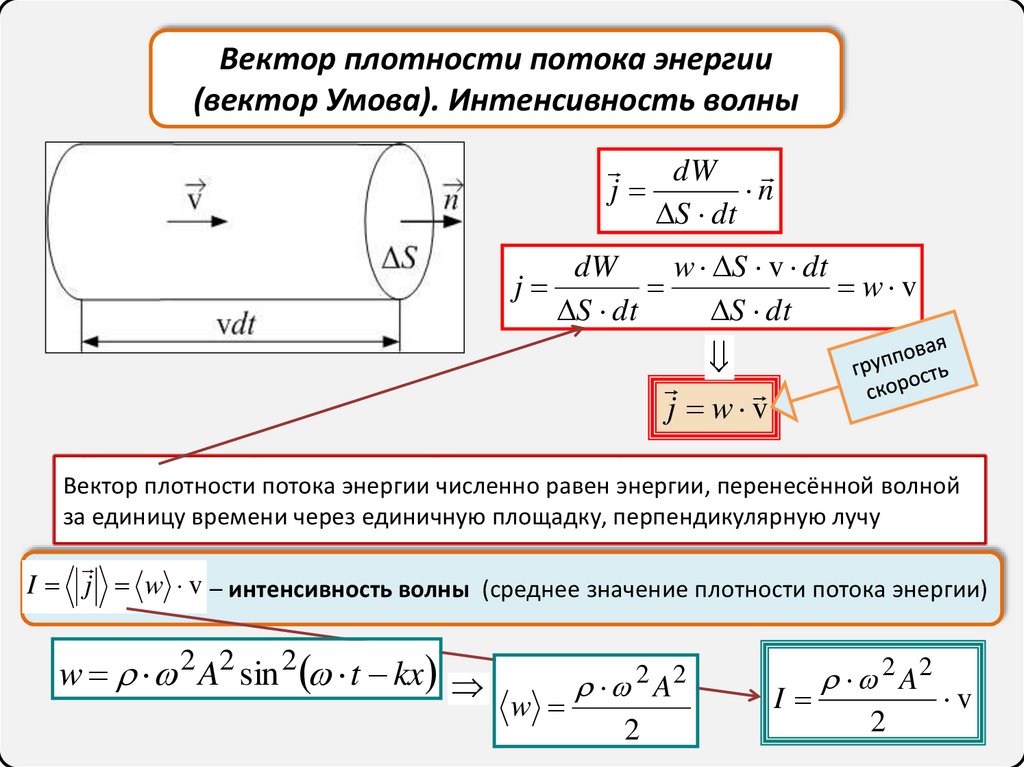
Вектор плотности потока энергии(вектор Умова). Интенсивность волны
dW
j
n
S dt
dW
w S v dt
j
w v
S dt
S dt
j w v
Вектор плотности потока энергии численно равен энергии, перенесённой волной
за единицу времени через единичную площадку, перпендикулярную лучу
I j w v – интенсивность волны (среднее значение плотности потока энергии)
w 2 A2 sin 2 t kx
w
A
2 2
2
I
2 A2
2
v
21.
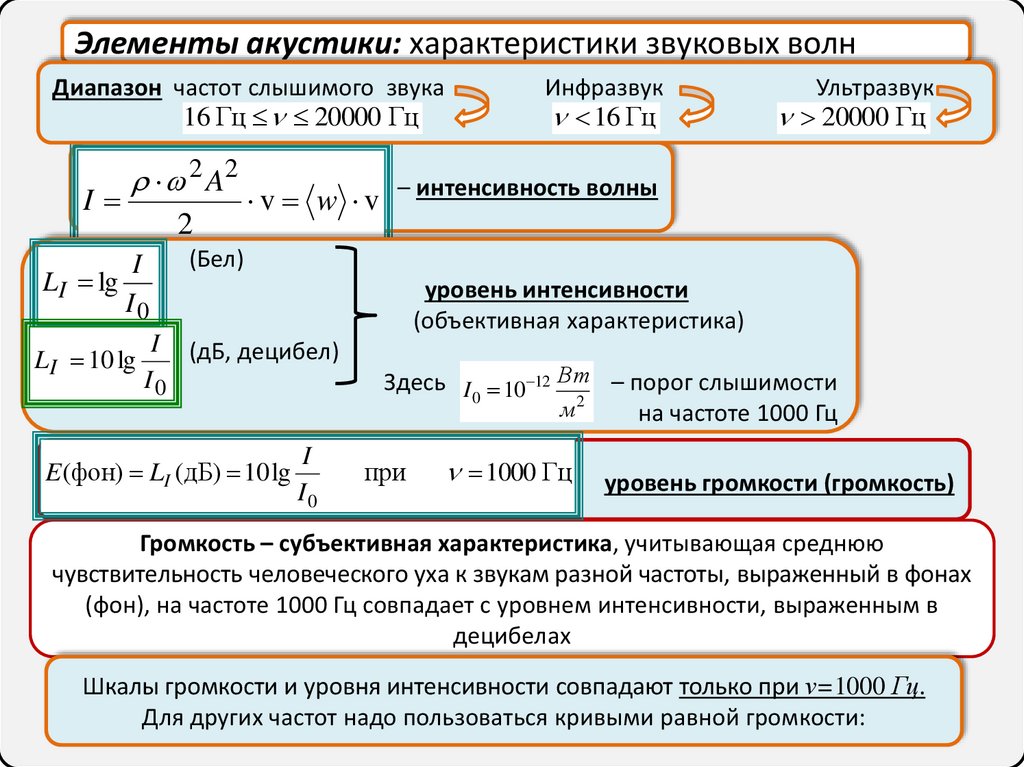
Элементы акустики: характеристики звуковых волнДиапазон частот слышимого звука
16 Гц 20000 Гц
I
2 A2
2
I
LI lg
I0
LI 10 lg
Инфразвук
16 Гц
Ультразвук
20000 Гц
v w v – интенсивность волны
(Бел)
I (дБ, децибел)
I0
E (фон) LI (дБ) 10 lg
I
I0
уровень интенсивности
(объективная характеристика)
Здесь I 0 10 12 Вт – порог слышимости
м2
на частоте 1000 Гц
при
1000 Гц
уровень громкости (громкость)
Громкость – субъективная характеристика, учитывающая среднюю
чувствительность человеческого уха к звукам разной частоты, выраженный в фонах
(фон), на частоте 1000 Гц совпадает с уровнем интенсивности, выраженным в
децибелах
Шкалы громкости и уровня интенсивности совпадают только при ν=1000 Гц.
Для других частот надо пользоваться кривыми равной громкости:
22.
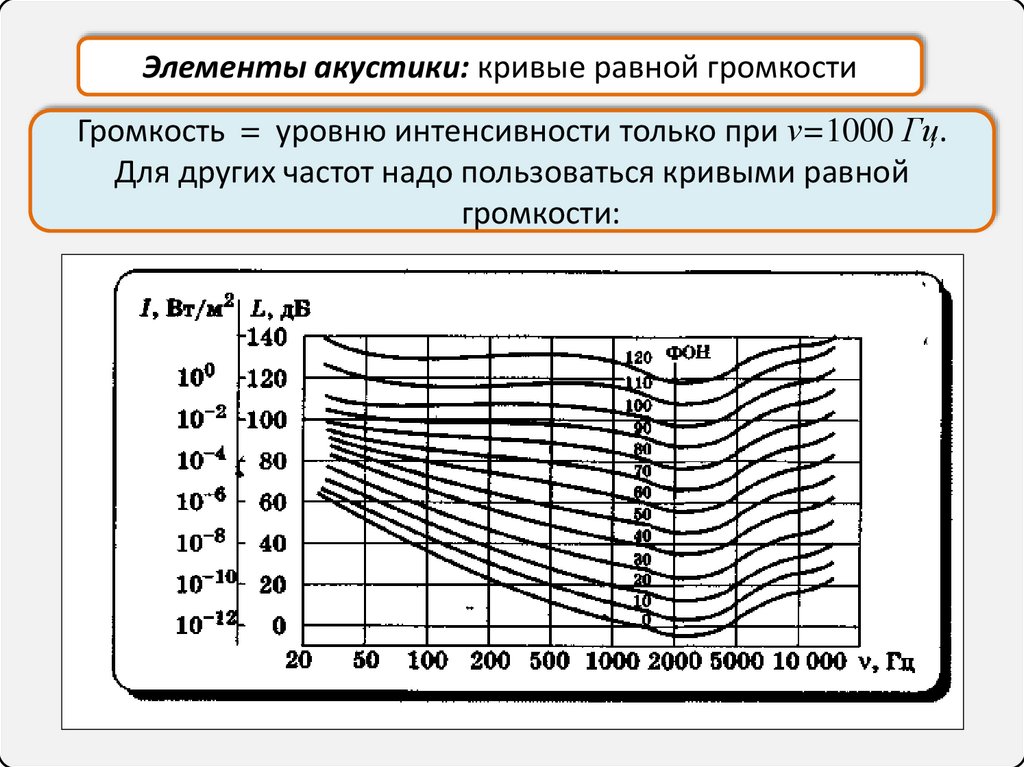
Элементы акустики: кривые равной громкостиГромкость = уровню интенсивности только при ν=1000 Гц.
Для других частот надо пользоваться кривыми равной
громкости:
23.
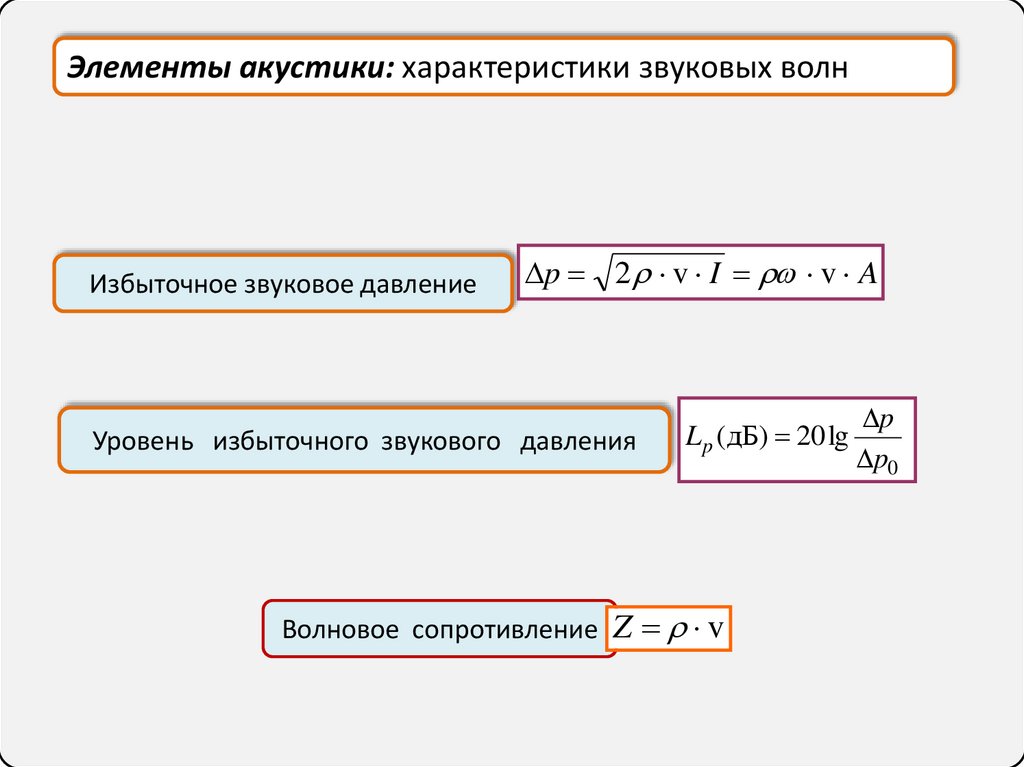
Элементы акустики: характеристики звуковых волнИзбыточное звуковое давление
p 2 v I v A
Уровень избыточного звукового давления
L p (дБ) 20 lg
Волновое сопротивление Z v
p
p0
24.
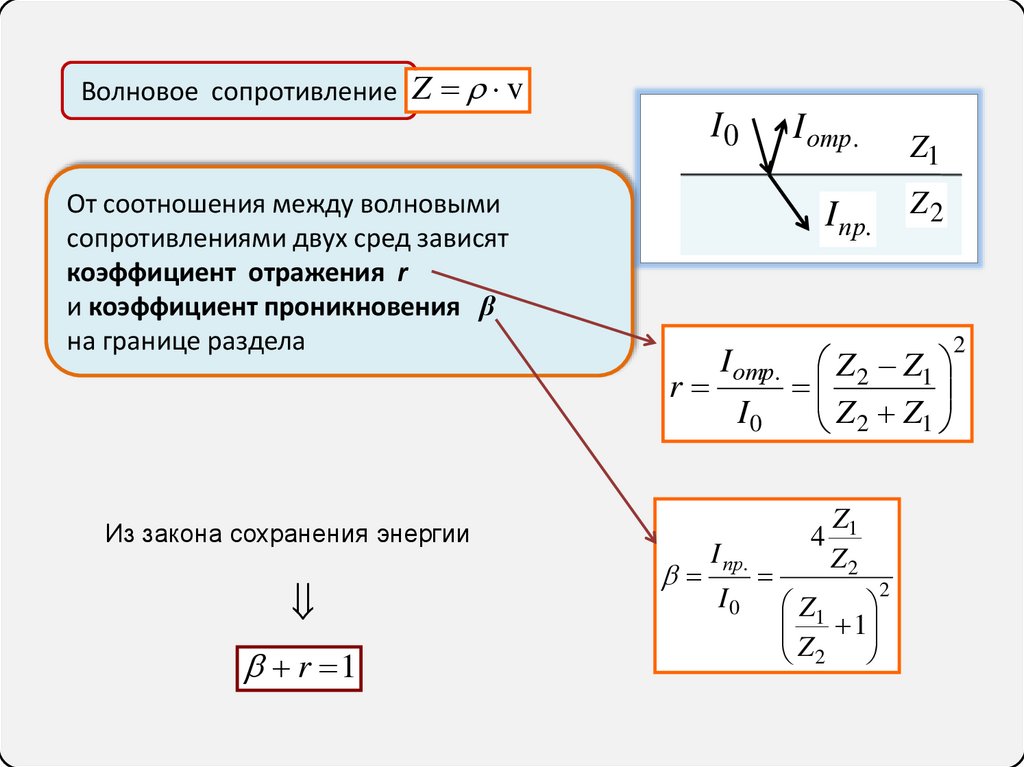
Волновое сопротивление Z vI0
От соотношения между волновыми
сопротивлениями двух сред зависят
коэффициент отражения r
и коэффициент проникновения β
на границе раздела
Из закона сохранения энергии
r 1
Z1
Z2
I пр.
r
I отр .
I отр.
I0
I пр.
I0
Z 2 Z1
Z 2 Z1
4
Z1
Z2
Z1
1
Z2
2
2
25.
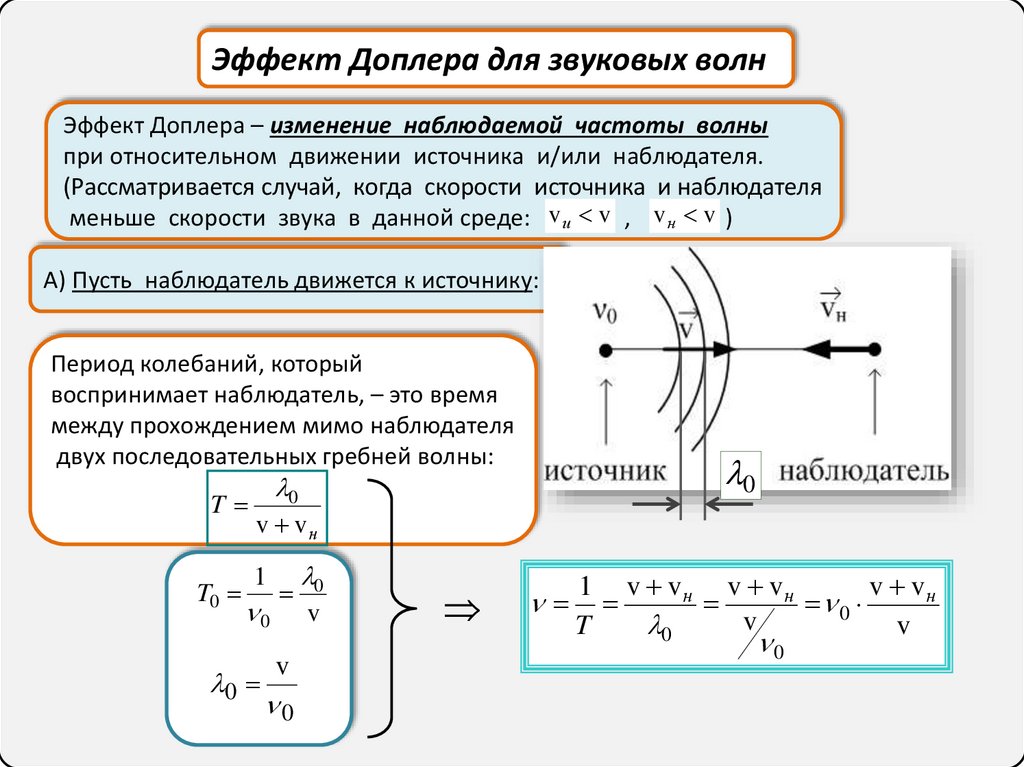
Эффект Доплера для звуковых волнЭффект Доплера – изменение наблюдаемой частоты волны
при относительном движении источника и/или наблюдателя.
(Рассматривается случай, когда скорости источника и наблюдателя
меньше скорости звука в данной среде: vи v , v н v )
А) Пусть наблюдатель движется к источнику:
Период колебаний, который
воспринимает наблюдатель, – это время
между прохождением мимо наблюдателя
двух последовательных гребней волны:
T
T0
0
0
v vн
1
0
0
v
0
0
v
1 v vн v vн
v vн
0
v
T
0
v
0
26.
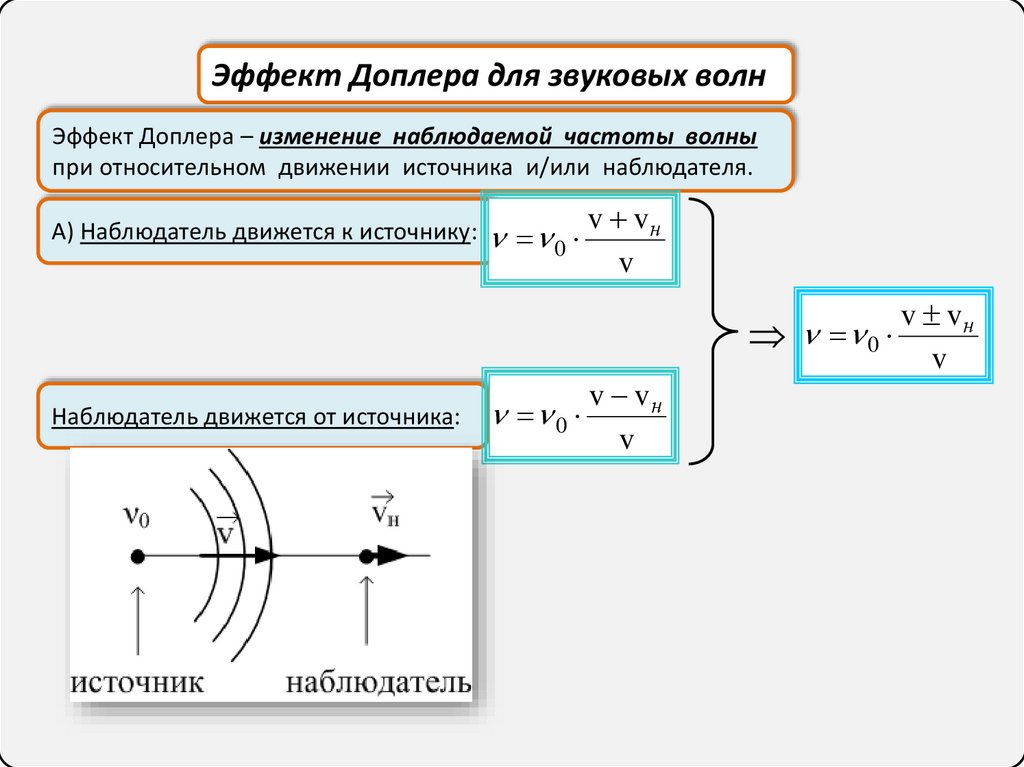
Эффект Доплера для звуковых волнЭффект Доплера – изменение наблюдаемой частоты волны
при относительном движении источника и/или наблюдателя.
А) Наблюдатель движется к источнику:
0
v vн
v
0
Наблюдатель движется от источника:
0
v vн
v
v vн
v
27.
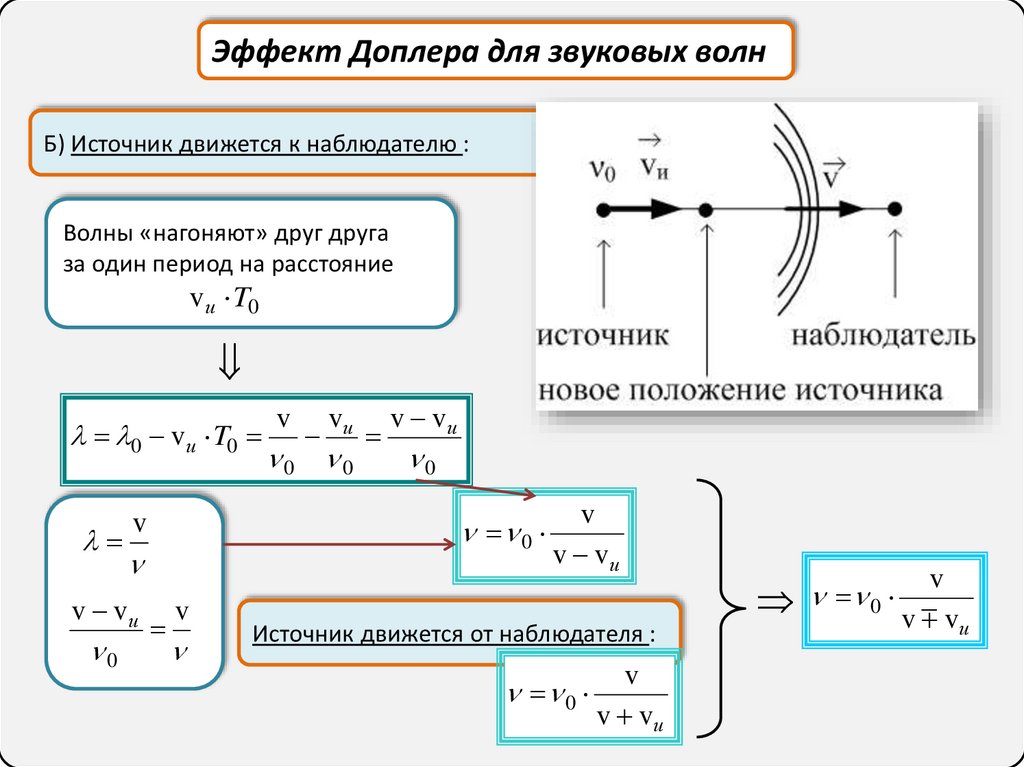
Эффект Доплера для звуковых волнБ) Источник движется к наблюдателю :
Волны «нагоняют» друг друга
за один период на расстояние
vи T0
0 vи T0
0
vи
0 0
v vи
0
v
0
v vи
v
v vи
v
v
Источник движется от наблюдателя :
0
v
v vи
0
v
v vи
28.
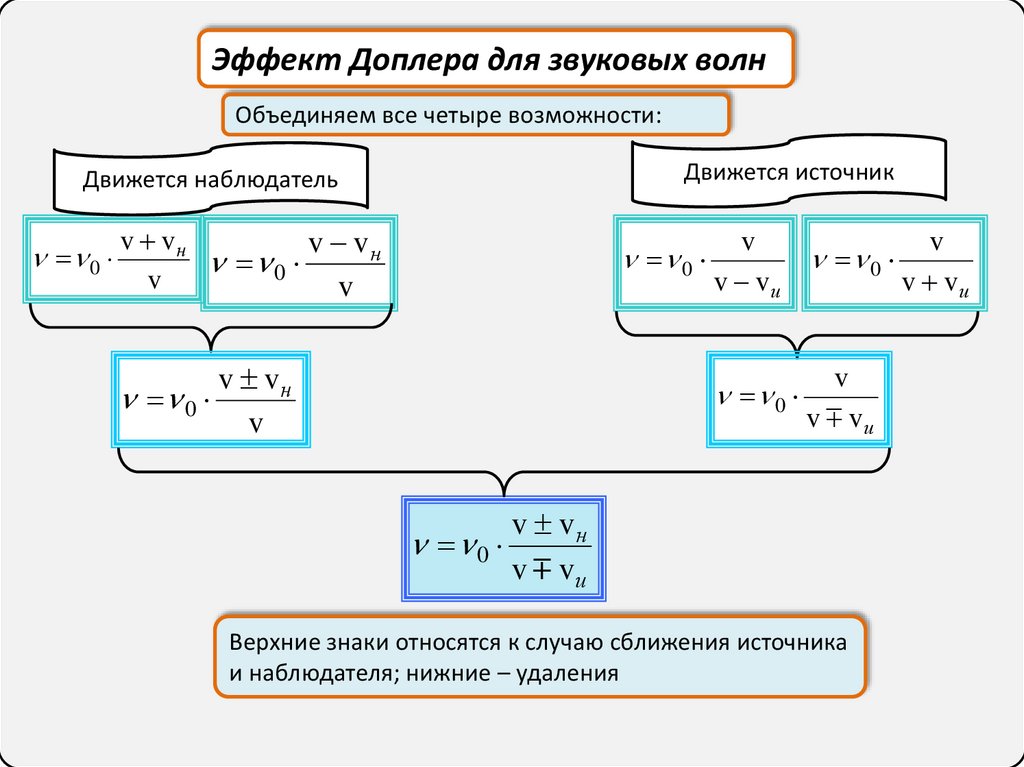
Эффект Доплера для звуковых волнОбъединяем все четыре возможности:
Движется источник
Движется наблюдатель
0
v vн
v vн
0
v
v
0
0
v vн
v
v
v
0
v vи
v vи
0
v
v vи
v vн
0
v vи
Верхние знаки относятся к случаю сближения источника
и наблюдателя; нижние – удаления




 physics
physics








