Механические колебания. Волны

1.

ВоГУ
Лекция 04
Механические колебания
Волны
Кузина Л.А.,
к.ф.-м.н., доцент
2020 г.
1

2.

План
1. Колебательные процессы. Гармонические колебания
2. Дифференциальное уравнение гармонических
колебаний
3. Пружинный и математический маятники
4. Энергия гармонического осциллятора
5. Упругие волны. Основные понятия
6. Уравнение плоской волны
7. Стоячие волны
8. Скорость упругих волн
9. Элементы акустики
10. Эффект Доплера
2

3.

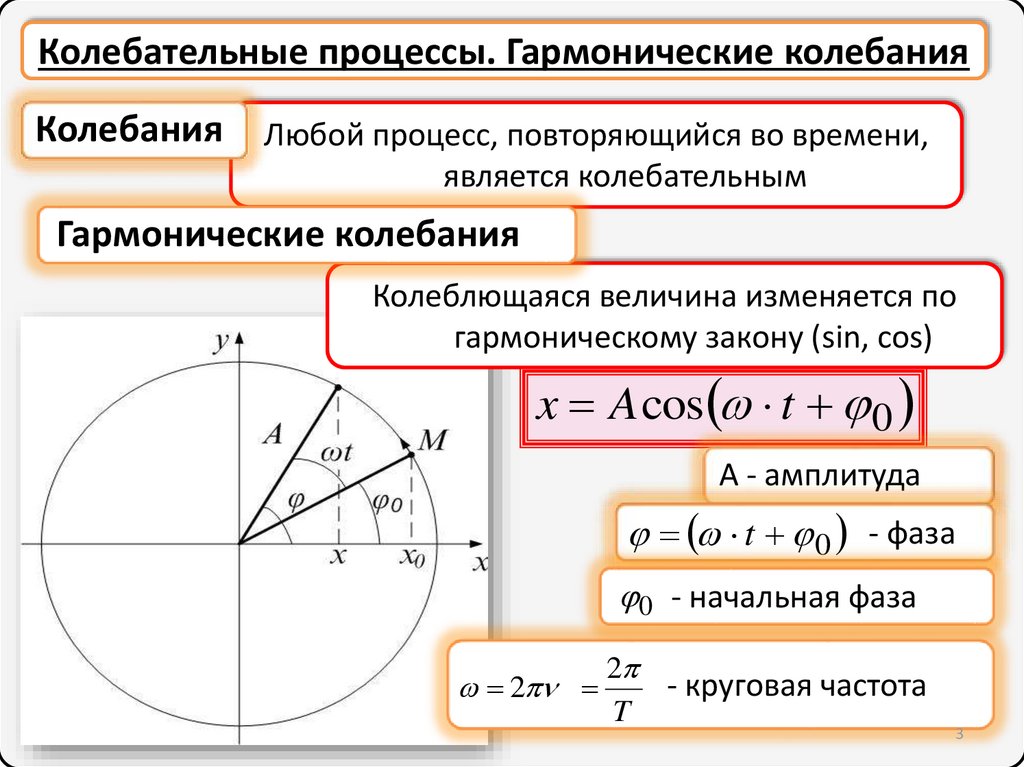
Колебательные процессы. Гармонические колебания
Колебания
Любой процесс, повторяющийся во времени,
является колебательным
Гармонические колебания
Колеблющаяся величина изменяется по
гармоническому закону (sin, cos)
x A cos t 0
А - амплитуда
t 0 - фаза
0 - начальная фаза
2
2
- круговая частота
T
3

4.

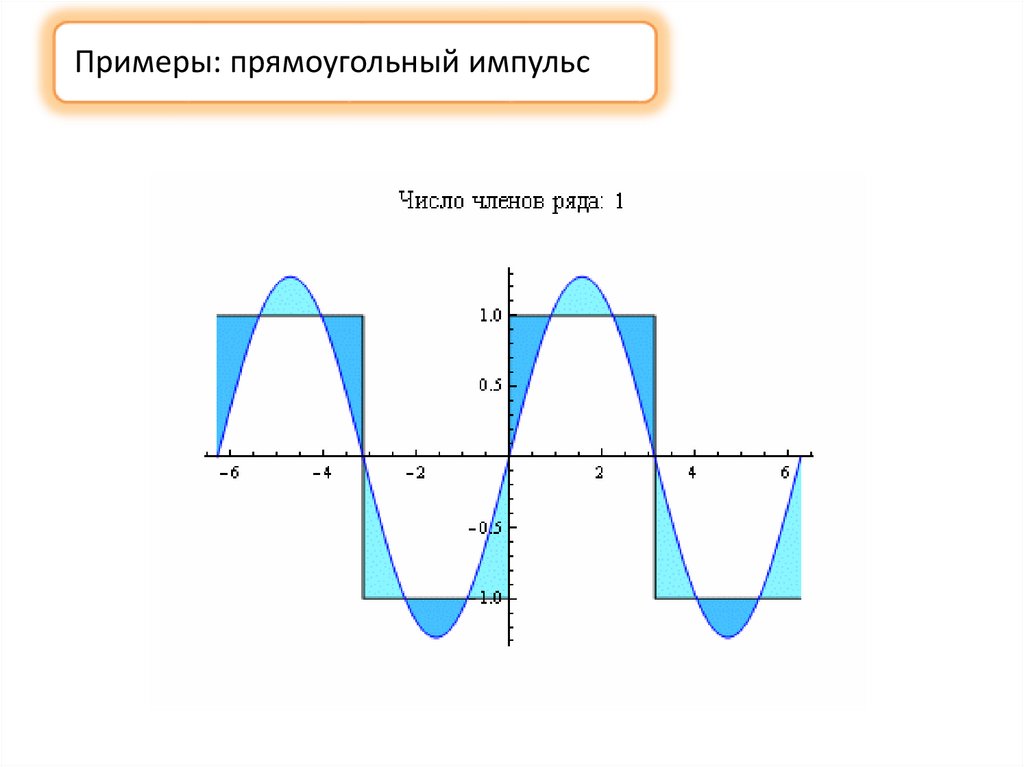
Примеры: «пила» раскладывается на гармонические
составляющие тем точнее, чем больше членов ряда

5.

Примеры: прямоугольный импульс

6.

Дифференциальное уравнение гармонических колебаний
x A cos t 0
x A sin t 0
a x 2 A cos t 0 2 x
2
x x 0
Решение этого дифференциального
уравнения – гармоническая функция:
Сила пропорциональна смещению
F ma m 2 x kx
(квазиупругая, возвращающая)
k m 2

7.

7

8.

Колебательные системы:
1) пружинный маятник
F ma mx
F kx
x x 0
2
k
m
x A cos t 0
2
mx kx
k
x x 0
m
k
m
2
m
T
2
k

9.

9

10.

Колебательные системы: 2) Математический маятник
Математический маятник - материальная точка
(тело, размерами которого можно пренебречь),
подвешенная на нерастяжимой невесомой нити
ma m g F нат.
Fx mg sin mg
Fx ma
a x g
x
g
x
g
x x 0
l
T 2
g

11.

11

12.

Энергия гармонического осциллятора
Полная энергия:
m 2 kx 2
W Wкин. Wпот.
2
2
x A cos t 0
x A sin t 0
k m 2
m 2 A2 sin 2 t 0 k A2 cos2 t 0 m 2 A2
W
2
2
2
Полная энергия сохраняется; переходит из кинетической
в потенциальную и обратно
Максимальные значения:
Wкин. max Wпот. max
m 2 A 2
W
2
m 2 A2 k A2
2
2
Средние значения:
Wкин. Wпот.
W m 2 A2 k A2
2
4
4

13.

13

14.

Сложение взаимно перпендикулярных колебаний кратных
частот (частные случаи). Фигуры Лиссажу
x Ax cos x t
y Ay cos y t
ny
nx
1
2
x x ny
y y nx
Условие замкнутости фигуры:
x nx y n y
nx и n y - число точек пересечения фигуры с осями OX и OY
1
3
2
3
Метод фигур Лиссажу применяется
для точного определения частоты
3
2
14

15.

Фигуры Лиссажу
На осциллографе:
https://youtu.be/hUu653khUlE
Запись песком:
https://youtu.be/rdWWvjH8cPM

16.

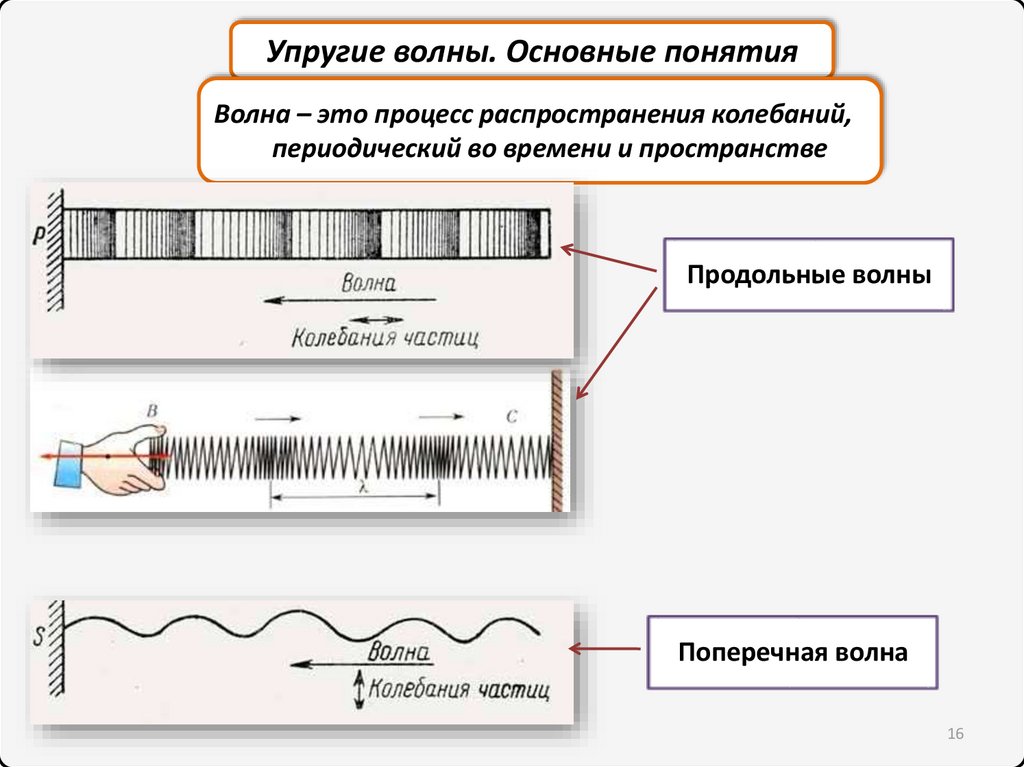
Упругие волны. Основные понятия
Волна – это процесс распространения колебаний,
периодический во времени и пространстве
Продольные волны
Поперечная волна
16

17.

Упругие волны. Основные понятия
Волновой фронт – совокупность точек, до которых дошла
волна в данный момент времени
(сферический, плоский)
Луч – направление распространения волны.
В изотропной среде луч
перпендикулярен волновому фронту
Принцип Гюйгенса:
любая точка волнового фронта является
точечным источником вторичных
сферических волн
(объясняет процесс распространения волн)

18.

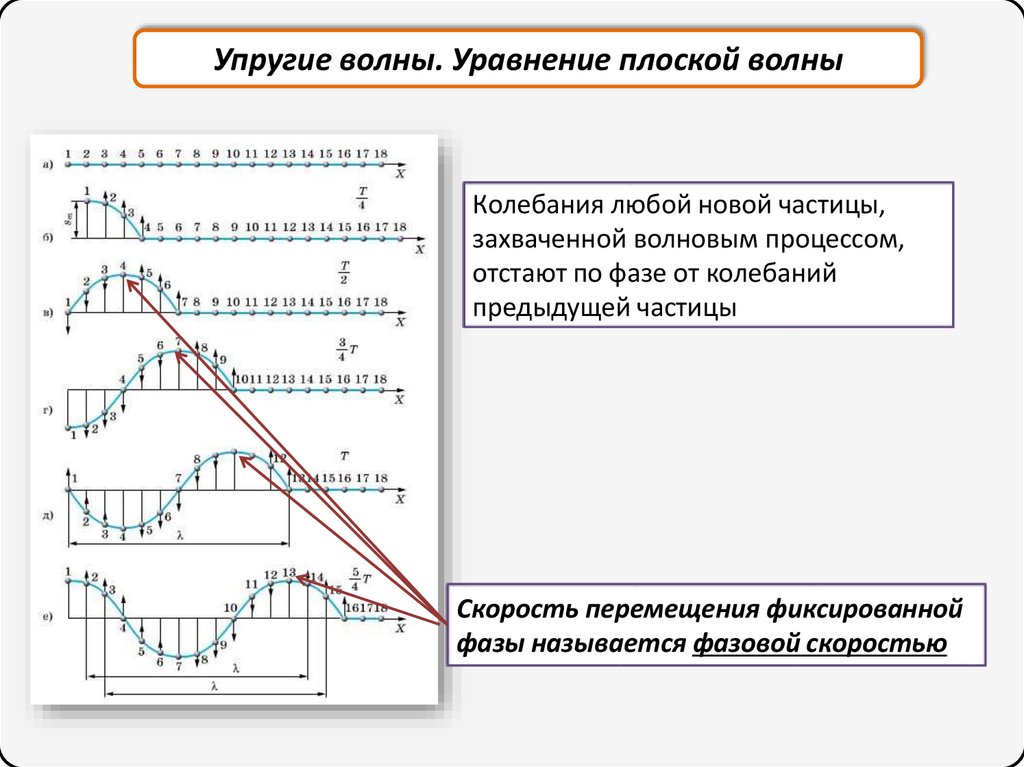
Упругие волны. Уравнение плоской волны
Колебания любой новой частицы,
захваченной волновым процессом,
отстают по фазе от колебаний
предыдущей частицы
Скорость перемещения фиксированной
фазы называется фазовой скоростью

19.

19

20.

20

21.

Уравнение плоской волны
Уравнение колебаний источника в
точке x=0:
S A cos t
В произвольной точке x
колебания запаздывают по фазе
Замена
x
– время запаздывания (за это время волна дойдёт до точки x)
v
t t
даёт уравнение колебаний в точке x:
S x, t A cos t
x
S x, t A cos t
v
S x, t A cos t x
v

22.

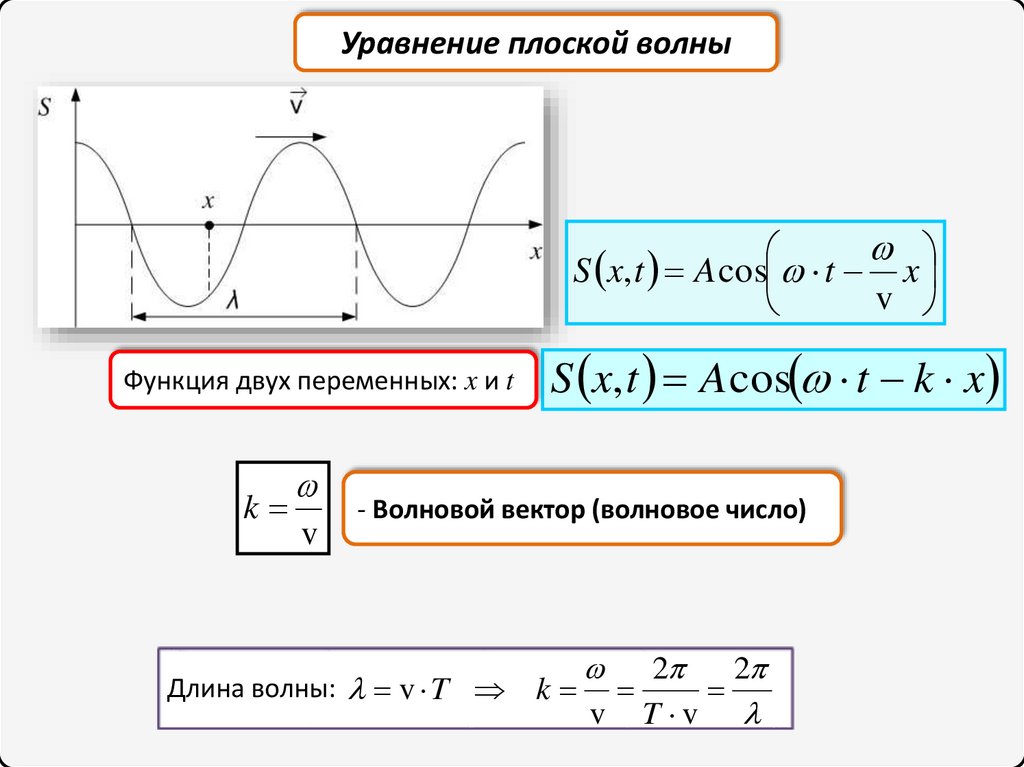
Уравнение плоской волны
S x, t A cos t x
v
Функция двух переменных: x и t
k
v
S x, t A cos t k x
- Волновой вектор (волновое число)
Длина волны: v T
k
v
2
2
T v

23.

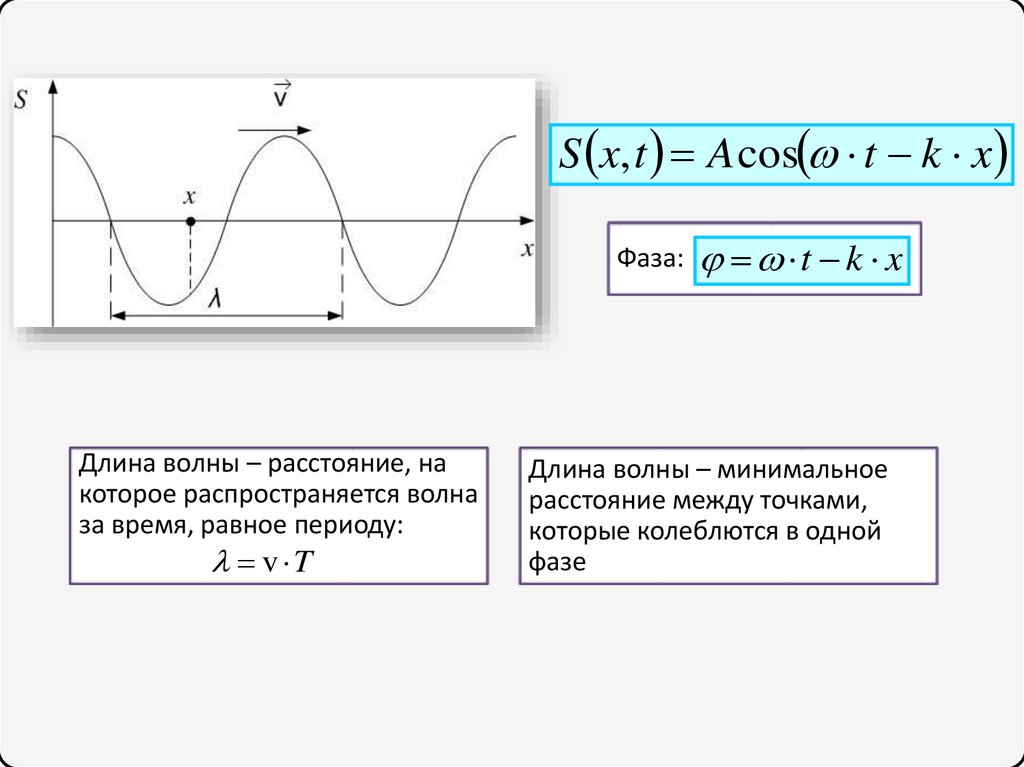
S x, t A cos t k x
Фаза:
Длина волны – расстояние, на
которое распространяется волна
за время, равное периоду:
v T
t k x
Длина волны – минимальное
расстояние между точками,
которые колеблются в одной
фазе

24.

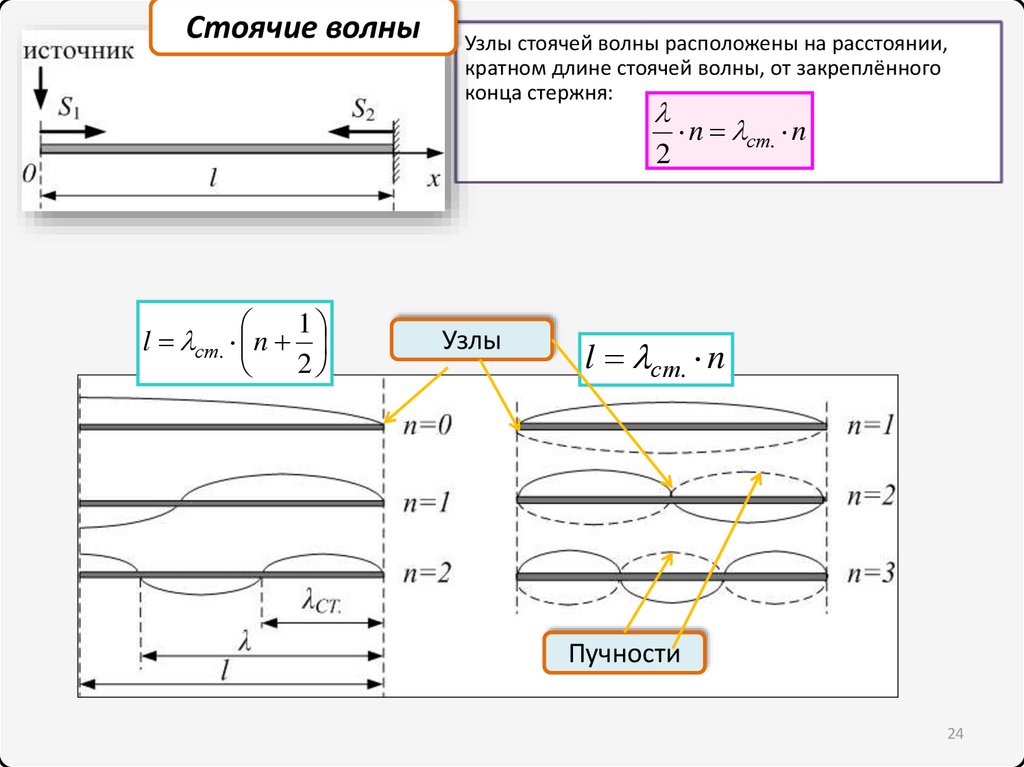
Стоячие волны
Узлы стоячей волны расположены на расстоянии,
кратном длине стоячей волны, от закреплённого
конца стержня:
2
1
l ст. n
2
Узлы
n ст. n
l ст. n
Пучности
24

25.

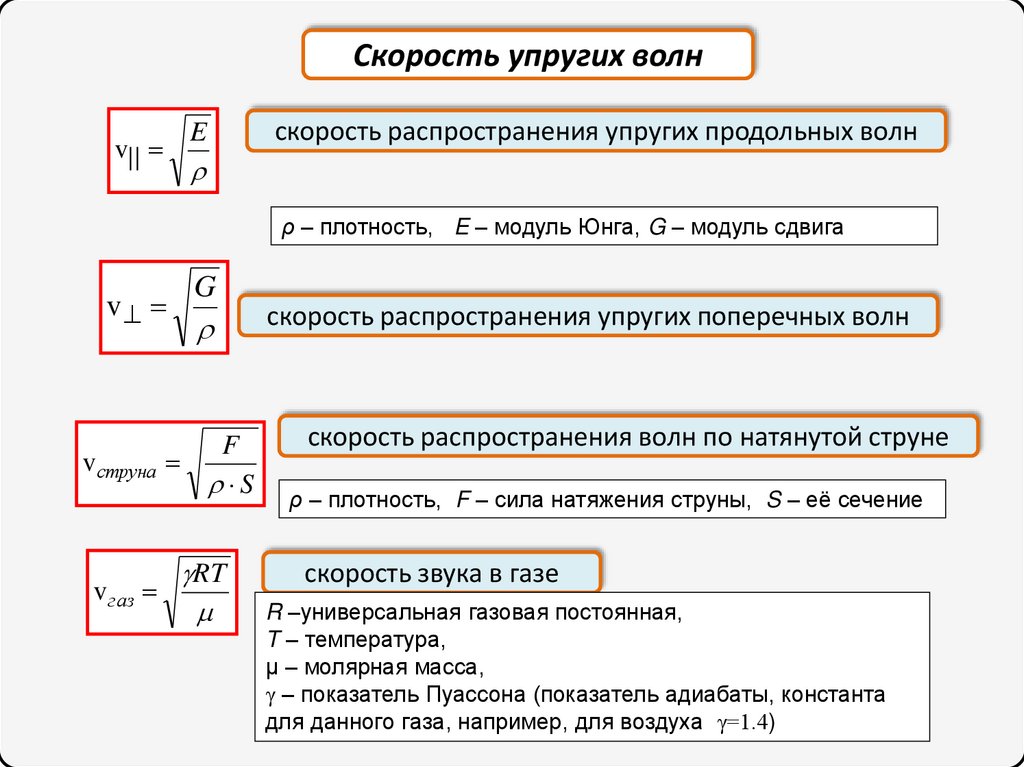
Скорость упругих волн
E
v| |
скорость распространения упругих продольных волн
ρ – плотность, E – модуль Юнга, G – модуль сдвига
v
vструна
v газ
G
F
S
RT
скорость распространения упругих поперечных волн
скорость распространения волн по натянутой струне
ρ – плотность, F – сила натяжения струны, S – её сечение
скорость звука в газе
R –универсальная газовая постоянная,
T – температура,
μ – молярная масса,
γ – показатель Пуассона (показатель адиабаты, константа
для данного газа, например, для воздуха γ=1.4)

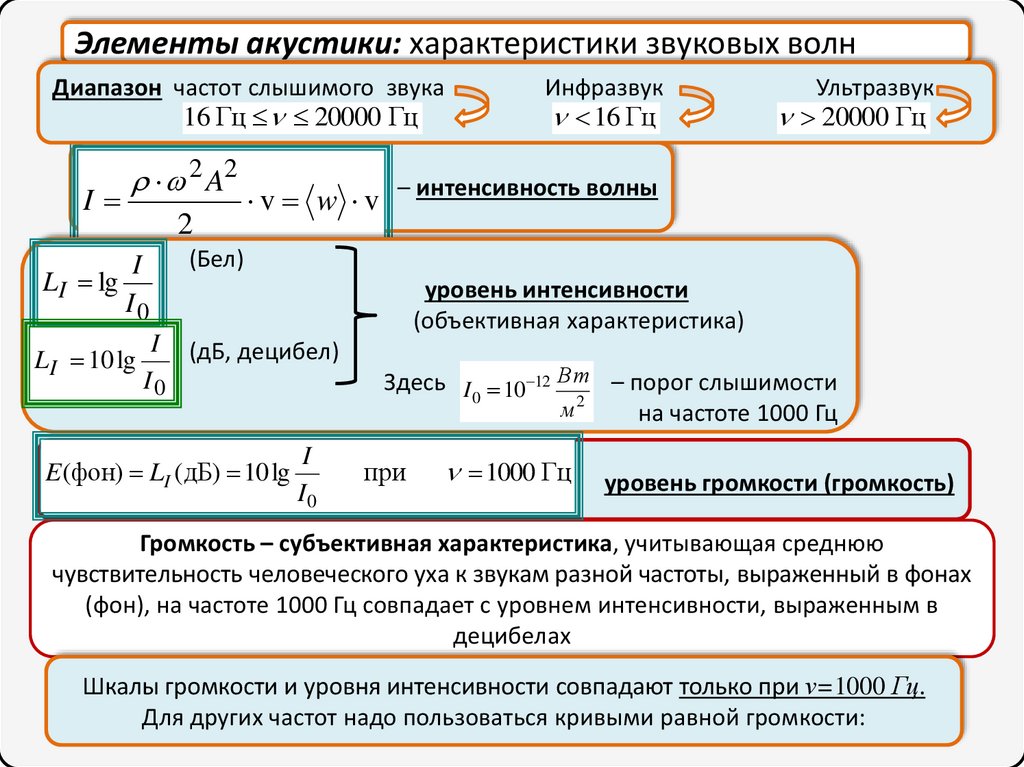
26.

Элементы акустики: характеристики звуковых волн
Диапазон частот слышимого звука
16 Гц 20000 Гц
I
2 A2
2
I
LI lg
I0
LI 10 lg
Инфразвук
16 Гц
Ультразвук
20000 Гц
v w v – интенсивность волны
(Бел)
I (дБ, децибел)
I0
E (фон) LI (дБ) 10 lg
I
I0
уровень интенсивности
(объективная характеристика)
Здесь I 0 10 12 Вт – порог слышимости
м2
на частоте 1000 Гц
при
1000 Гц
уровень громкости (громкость)
Громкость – субъективная характеристика, учитывающая среднюю
чувствительность человеческого уха к звукам разной частоты, выраженный в фонах
(фон), на частоте 1000 Гц совпадает с уровнем интенсивности, выраженным в
децибелах
Шкалы громкости и уровня интенсивности совпадают только при ν=1000 Гц.
Для других частот надо пользоваться кривыми равной громкости:

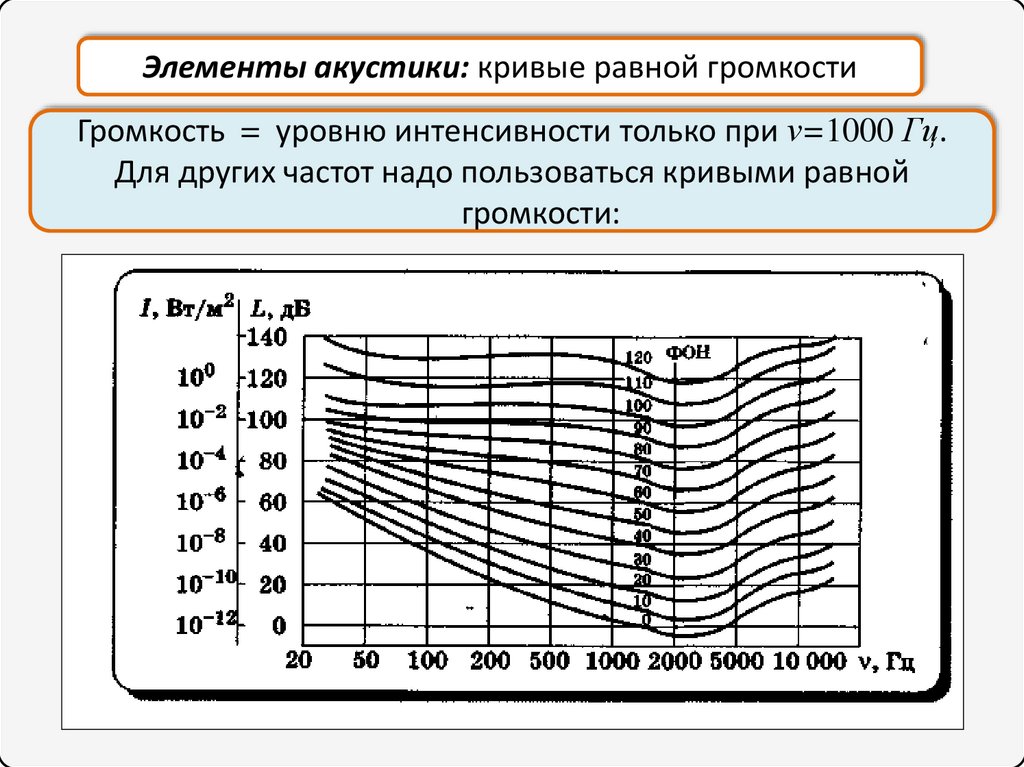
27.

Элементы акустики: кривые равной громкости
Громкость = уровню интенсивности только при ν=1000 Гц.
Для других частот надо пользоваться кривыми равной
громкости:

28.

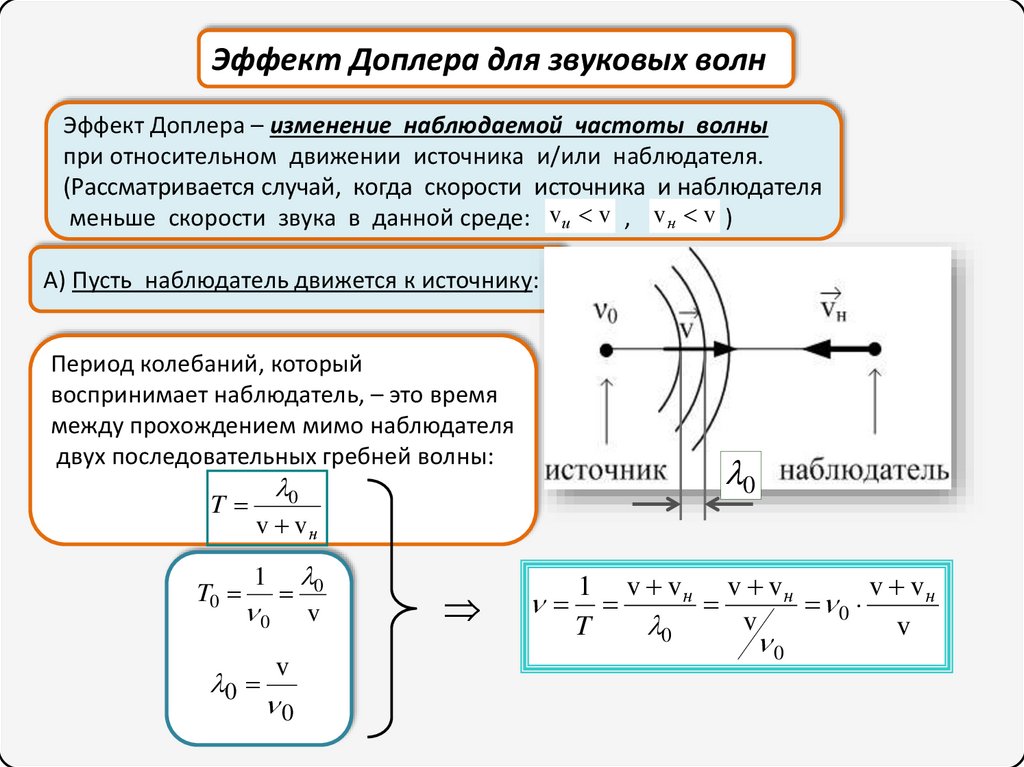
Эффект Доплера для звуковых волн
Эффект Доплера – изменение наблюдаемой частоты волны
при относительном движении источника и/или наблюдателя.
(Рассматривается случай, когда скорости источника и наблюдателя
меньше скорости звука в данной среде: vи v , v н v )
А) Пусть наблюдатель движется к источнику:
Период колебаний, который
воспринимает наблюдатель, – это время
между прохождением мимо наблюдателя
двух последовательных гребней волны:
T
T0
0
0
v vн
1
0
0
v
0
0
v
1 v vн v vн
v vн
0
v
T
0
v
0

29.

Эффект Доплера для звуковых волн
Эффект Доплера – изменение наблюдаемой частоты волны
при относительном движении источника и/или наблюдателя.
А) Наблюдатель движется к источнику:
0
v vн
v
0
Наблюдатель движется от источника:
0
v vн
v
v vн
v

30.

Эффект Доплера для звуковых волн
Б) Источник движется к наблюдателю :
Волны «нагоняют» друг друга
за один период на расстояние
vи T0
0 vи T0
0
vи
0 0
v vи
0
v
0
v vи
v
v vи
v
v
Источник движется от наблюдателя :
0
v
v vи
0
v
v vи

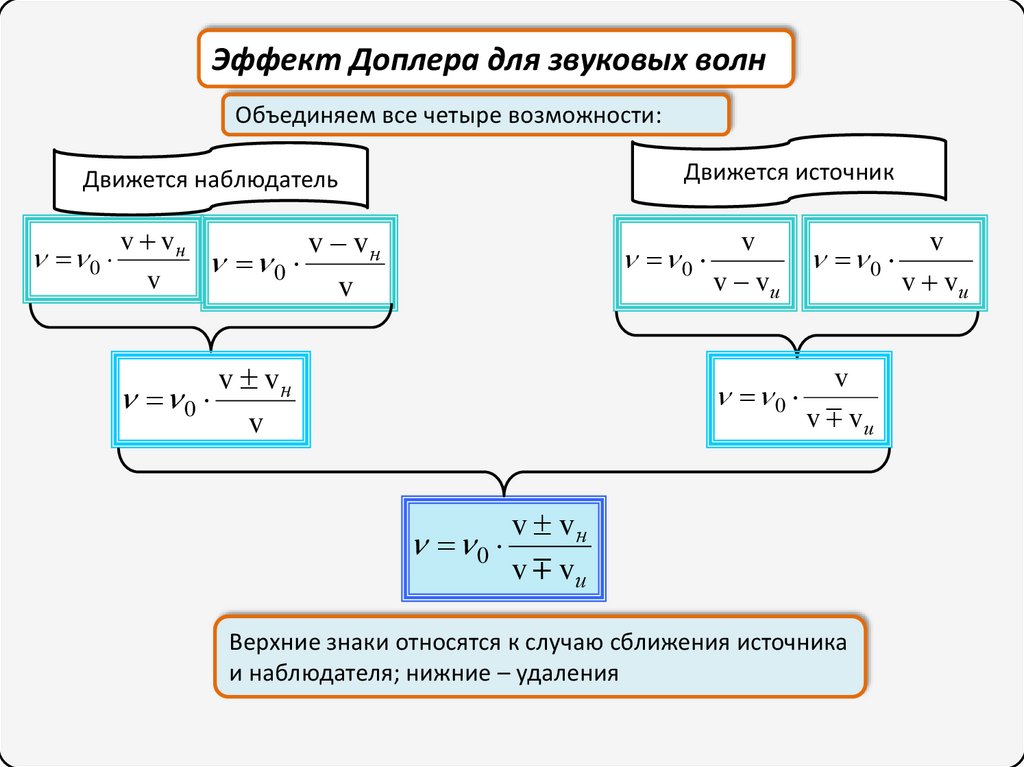
31.

Эффект Доплера для звуковых волн
Объединяем все четыре возможности:
Движется источник
Движется наблюдатель
0
v vн
v vн
0
v
v
0
0
v vн
v
v
v vи
0
0
v
v vи
v vн
0
v vи
Верхние знаки относятся к случаю сближения источника
и наблюдателя; нижние – удаления
v
v vи